A Study on Cubic H-Relations in a Topological Universe Viewpoint

Abstract

We introduce the concrete category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] of cubic H-relational spaces and P-preserving [resp. R-preserving] mappings between them and study it in a topological universe viewpoint. In addition, we prove that it is Cartesian closed over $\mathbf{Set}$. Next, we introduce the subcategory ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] of ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] and investigate it in the sense of a topological universe. In particular, we obtain exponential objects in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] quite different from those in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$].

1. Introduction

In 1984, Nel [1] introduced the concept of a topological universe which implies quasitopos [2]. Its notion has already been put to effective use several areas of mathematics in [3,4,5]. After then, Kim et al. [6] and Lee et al. [7] constructed the category $\mathbf{NSet}(H)$ of neutrosophic H-sets and morphisms between them and the category $\mathbf{NCSet}(H)$ of neutrosophic crisp sets and morphisms between them, and they studied each category in the sense of a topological universe. On the other hand, Cerruti [8] constructed the category of L-fuzzy relations and obtained some of its properties. Hur [9,10] [resp. Hur et al. [11] and Lim et al [12] formed the category $\mathbf{Rel}(H)$ of H-fuzzy relational spaces [resp. $\mathbf{IRel}(H)$ of H-intuitionistic fuzzy relational spaces and $\mathbf{VRel}(H)$ of vague relational spaces] and each category was investigated in topological universe viewpoint.

In 2012, Jun et al. [13] introduced the notion of a cubic set and investigated some of its properties. After that time, Ahn and Ko [14] studied cubic subalgebras and filters of $CI$-algebras. Akram et al. [15] applied the concept of cubic sets to $KU$-algebras. Jun et al. [16] dealt with cubic structures of ideals of $BCI$-algebras. Jun and Khan [17] found some properties of cubic ideals in semigroups. Jun et al. [18] studied cubic subgroups. Zeb et al. [19] defined the notion of a cubic topology and investigated some of its properties. Recently, Mahmood et al. [20] dealt with multicriteria decision making based on cubic sets. Rashed et al. [21] applied the concept of cubic sets to graph theory. Yaqoob et al. [22] introduced the notion of a cubic finite switchboard state machine and studied its various properties. Ma et al. [23] define a cubic relation on $H_v$-LA-semigroup and investigated some of its properties. Kim et al. [24] defined cubic relations and obtained some their properties.

In this paper, we study the category of cubic relations and morphisms between them in the sense of a topological universe proposed by Nel. First, we define the concept of a cubic H-relational space for a Heyting algebra H and introduce the concrete category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] of cubic H-relational spaces and P-preserving [resp. R-preserving] mappings between them, and obtained some categorical structures and give examples. In particular, we prove that the category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is Cartesian closed over $\mathbf{Set}$, where $\mathbf{Set}$ denotes the category consisting of ordinary sets and ordinary mappings between them. Next, we introduce the subcategory ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] of ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] and investigate it in the sense of a topological universe. In particular, we obtain exponential objects in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] quite different from those in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$].

2. Preliminaries

In this section, we list some basic definitions for category theory which are needed in the next sections. Let us recall that a concrete category is a category of sets which are endowed with an unspecified structure. Refer to [25] for the notions of a topological category and a cotopological category.

Definition 1

([25]). Let $\mathbf{A}$ be a concrete category.

(i) 

The $\mathbf{A}$-fiber of a set X is the class of all $\mathbf{A}$-structures on X.

(ii) 

$\mathbf{A}$ is said to be properly fibered over $\mathbf{Set}$, if it satisfies the following:

(a) 

(Fiber-smallness) for each set X, the $\mathbf{A}$-fiber of X is a set,

(b) 

(Terminal separator property) for each singleton set X, the $\mathbf{A}$-fiber of X has precisely one element,

(c) 

if ξ and η are $\mathbf{A}$-structures on a set X such that $id:(X,\xi )\to (X,\eta )$ and $id:(X,\eta )\to (X,\xi )$ are $\mathbf{A}$-morphisms, then $\xi =\eta$.

Definition 2

([26]). A category $\mathbf{A}$ is said to be Cartesian closed, if it satisfies the following conditions:

(i) 

for each $\mathbf{A}$-object A and B, there exists a product $A\times B$ in $\mathbf{A}$,

(ii) 

exponential objects exist in A, i.e., for each $\mathbf{A}$-object A, the functor $A\times -:A\to A$ has a right adjoint, i.e., for any $\mathbf{A}$-object B, there exist an $\mathbf{A}$-object $B^A$ and a $\mathbf{A}$-morphism $e_{A,B}:A\times B^A\to B$ (called the evaluation) such that for any $\mathbf{A}$-object C and any $\mathbf{A}$-morphism $f:A\times C\to B$, there exists a unique $\mathbf{A}$-morphism $\overline{f}:C\to B^A$ such that $e_{A,B}\circ (1_A\times \overline{f})=f$, i.e., the diagram commutes:

   

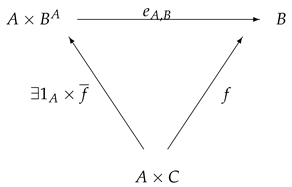
Definition 3

([1]). A category $\mathbf{A}$ is called a topological universe over $\mathbf{Set}$ if it satisfies the following conditions:

(i) 

$\mathbf{A}$ is well-structured, i.e., (a) $\mathbf{A}$ is concrete category; (b) fiber-smallness condition; (c) $\mathbf{A}$ has the terminal separator property,

(ii) 

$\mathbf{A}$ is cotopological over $\mathbf{Set}$,

(iii) 

final episinks in A are preserved by pullbacks, i.e., for any episink ${(g_j:X_j\to Y)}_J$ and any $\mathbf{A}$-morphism $f:W\to Y$, the family ${(e_j:U_j\to W)}_J,$ obtained by taking the pullback f and $g_j$, for each $j\in J$, is again a final episink.

Now refer to [13,27,28,29,30,31,32,33,34] for the concepts of fuzzy sets, fuzzy relations, interval-valued fuzzy sets and interval-valued fuzzy relations, neutrosophic crisp sets, neutrosophic sets and operation between them, respectively.

3. Properties of the Categories ${\mathbf{HRel}}_{\mathit{P}}(\mathit{H})$ and ${\mathbf{HRel}}_{\mathit{R}}(\mathit{H})$

In this section, first, we write the concept of a cubic set introduced by Jun et al. [13] (Also, see [13] for the equality $\mathcal{A}=\mathcal{B}$ and orders $\mathcal{A}⊏\mathcal{B},\mathcal{A}⋐\mathcal{B}$ for any cubic sets $\mathcal{A},\mathcal{B},$ the complement ${\mathcal{A}}^c$ of a cubic set $\mathcal{A}$, and the unions $\mathcal{A}\bigsqcup \mathcal{B},\mathcal{A}⋓\mathcal{B}$ and intersections $\mathcal{A}\sqcap \mathcal{B},\mathcal{A}⋓\mathcal{B}$ of two cubic sets $\mathcal{A},\mathcal{B}$). Next, we introduce the category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] consisting of all cubic H-relational spaces and all P-preserving [resp. R-preserving] mappings between any two cubic H-relational spaces and it has the similar structures as those of ${\mathbf{CSet}}_P(H)$ [resp. ${\mathbf{CSet}}_R(H)$] (See [35]).

Throughout this section and next section, H denotes a complete Heyting algebra (Refer to [36,37] for its definition) and $[H]$ denotes the set of all closed subintervals of H.

Definition 4

([13]). Let X be a nonempty set. Then a complex mapping $\mathcal{A}=<A,\lambda >:X\to [I]\times I$ is called a cubic set in X, where $I=[0,1]$ and $[I]$ be the set of all closed subintervals of I.

A cubic set $\mathcal{A}=<A,\lambda >$ in which $A(x)=\mathbf{0}$ and $\lambda (x)=1$ (resp. $A(x)=\mathbf{1}$ and $\lambda (x)=0$) for each $x\in X$ is denoted by $\ddot{0}$ (resp. $\ddot{1}$).

A cubic set $\mathcal{B}=<B,\mu >$ in which $B(x)=\mathbf{0}$ and $\mu (x)=0$ (resp. $B(x)=\mathbf{1}$ and $\mu (x)=1$) for each $x\in X$ is denoted by $\widehat{0}$ (resp. $\widehat{1}$). In this case, $\widehat{0}$ (resp. $\widehat{1}$) will be called a cubic empty (resp. whole) set in X.

We denote the set of all cubic sets in X by ${([I]\times I)}^X$.

Definition 5.

Let X be a nonempty set. Then a complex mapping $\mathcal{R}=<R,\lambda >:X\times X\to [H]\times H$ is called a cubic H-relation in X. The pair $(X,\mathcal{R})$ is called a cubic H-relational space. In particular, a cubic H-relation from X to X is called a H-relation in or on X. We will denote the set of all cubic H-relations in X as resp. ${([H]\times H)}^{X\times X}$. In fact, each member $\mathcal{R}=<R,\lambda >\in {([H]\times H)}^{X\times Y}$ is a cubic H-set in $X\times X$ (See [35]).

Definition 6.

Let $(X,{\mathcal{R}}_X)=(X,<R_X,{\lambda }_X>)$ and $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$ be two cubic H-relational spaces. Then a mapping $f:(X,{\mathcal{R}}_X)\to (Y,{\mathcal{R}}_Y)$ is called:

(i) 

a P-order preserving mapping, if it satisfies the following condition:

$${\mathcal{R}}_X⊏{\mathcal{R}}_Y\circ f^2=<R_Y\circ f^2,{\lambda }_Y\circ f^2>,\mathrm{i}.\mathrm{e}.,\mathrm{for}\mathrm{each}(x,y)\in X\times X,$$

$$<[R_X^{-}(x,y),R_X^{+}(x,y)],\lambda (x,y)>$$

$${\le }_P<[R_Y^{-}(f(x),f(y)),R_Y^{+}(f(x),f(y))],{\lambda }_Y(f(x),f(y))>,\mathrm{i}.\mathrm{e}.,$$

$$R_X^{-}(x,y)\le (R_Y^{-}\circ f^2)(x,y),R_X^{+}(x,y)\le (R_Y^{+}\circ f^2)(x,y),{\lambda }_X(x,y)\le ({\lambda }_Y\circ f^2)(x,y),$$

(ii) 

a R-order preserving mapping, if it satisfies the following condition:

$${\mathcal{R}}_X⋐{\mathcal{R}}_Y\circ f^2=<R_Y\circ f^2,{\lambda }_Y\circ f^2>,\mathrm{i}.\mathrm{e}.,\mathrm{for}\mathrm{each}(x,y)\in X\times X,$$

$$<[R_X^{-}(x,y),R_X^{+}(x,y)],\lambda (x,y)>$$

$${\le }_R<[R_Y^{-}(f(x),f(y)),R_Y^{+}(f(x),f(y))],{\lambda }_Y(f(x),f(y))>,\mathrm{i}.\mathrm{e}.,$$

$$R_X^{-}(x,y)\le (R_Y^{-}\circ f^2)(x,y),R_X^{+}(x,y)\le (R_Y^{+}\circ f^2)(x,y),{\lambda }_X(x,y)\ge ({\lambda }_Y\circ f^2)(x,y),$$

where $f^2=f\times f$.

Proposition 1.

Let $(X,{\mathcal{R}}_X)=(X,<R_X,{\lambda }_X>)$, $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$ and $(Z,{\mathcal{R}}_Z)=(Z,<R_Z,{\lambda }_Z>)$ be three cubic H- relational spaces.

(1) 

The identity mapping $1_X:(X,{\mathcal{R}}_X)\to (X,{\mathcal{R}}_X)$ is a P-order [resp. R-oder] preserving mapping.

(2) 

If $f:(X,{\mathcal{R}}_X)\to (Y,{\mathcal{R}}_Y)$ and $g:(Y,{\mathcal{R}}_Y)\to (Z,{\mathcal{R}}_Z)$ are P-preserving [resp. R-preserving] mappings, then $g\circ f:(XX,{\mathcal{R}}_X)\to (Z,{\mathcal{R}}_Z)$ is a P-preserving [resp. R-preserving] mapping.

Proof. 

(1) The proof follows from the definitions of P-orders and R-orders, and identity mappings.

(2) Suppose $f:(X,{\mathcal{R}}_X)\to (Y,{\mathcal{R}}_Y)$ and $g:(Y,{\mathcal{R}}_Y)\to (Z,{\mathcal{R}}_Z)$ are P-preserving mappings and let $(x,y)\in X\times X$. Then

$${\mathcal{R}}_X(x,y)=<[R_X^{-}(x,y),R_X^{+}(x,y)],{\lambda }_X(x,y)>$$

$${\le }_P<[(R_Y^{-}\circ f^2)(x,y),R_Y^{+}\circ f^2)(x,y)],{\lambda }_Y\circ f^2)(x,y)>$$

$[\mathrm{Since}$f is a P-preserving mapping]

$=<[R_Y^{-}(f(x),f(y)),R_Y^{+}(f(x),f(y))],{\lambda }_Y(f(x),f(y))>$

${\le }_P[R_Z^{-}(g(f(x)),g(f(y))),R_Z^{+}(g(f(x)),g(f(y)))],{\lambda }_Z(g(f(x)),g(f(y)))>$

$[\mathrm{Since}$g is a P-preserving mapping]

$=[R_Z^{-}\circ {(g\circ f)}^2(x,y),R_Z^{+}\circ {(g\circ f)}^2(x,y)],{\lambda }_Z\circ {(g\circ f)}^2(x,y)>$.

Thus, ${\mathcal{R}}_X⊏{\mathcal{R}}_Z\circ {(g\circ f)}^2$. So $g\circ f$ is a P-preserving mapping. □

We will denote the collection consisting of all cubic H-relational spaces and all P-preserving [resp. R-preserving] mappings between any two cubic H-relational spaces as ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$]. Then from Proposition 1, we can easily see that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] forms a concrete category. In the sequel, a P-preserving [resp. R-preserving] mapping between any two cubic H-spaces will be called a ${\mathbf{CRel}}_P(H)$-mapping [resp. ${\mathbf{CRel}}_R(H)$-mapping].

Lemma 1.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is topological over $\mathbf{Set}$.

Proof. 

Let X be a set and let ${(X_j,{\mathcal{R}}_j)}_{j\in J}=(X_j,<R_j,{\lambda }_j>)$ be any family of cubic H-relational spaces indexed by a class J. Suppose ${(f_j:X\to X_j)}_J$ be a source of mappings. We define a mapping ${\mathcal{R}}_{X,P}=<R_{X,P},{\lambda }_{X,P}>:X\times X\to [H]\times H$ as follows: for each $(x,y)\in X\times X$,

$${\mathcal{R}}_{X,P}(x)=[{\sqcap }_{j\in J}({\mathcal{R}}_j\circ f_j^2)](x,y),\mathrm{i}.\mathrm{e}.,$$

$${\mathcal{R}}_{X,P}(x,y)=<[\underset{j\in J}{\bigwedge }{R}_j^{-}(f_j(x),f_j(y)),\underset{j\in J}{\bigwedge }{R}_j^{+}(f_j(x),f_j(y)),\underset{j\in J}{\bigwedge }{\lambda }_j(f_j(x),f_j(y))>.$$

Then clearly, for each $j\in J$ and $(x,y)\in X\times X$,

$$\begin{gathered} <[R_{X,P}^{-}(x,y),R_{X,P}^{+}(x,y)],{\lambda }_{X,P}(x,y)> \\ {\le }_P<[R_j^{-}(f_j(x),f_j(y)),R_j^{+}(f_j(x),f_j(y)),{\lambda }_j(f_j(x),f_j(y))>. \end{gathered}$$

Thus, ${\mathcal{R}}_{X,P}⊏{\mathcal{R}}_j\circ f_j^2$, for each $j\in J$. So $f_j:(X,{\mathcal{R}}_{X,P})\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_P(H)$-mapping, for each $j\in J$.

For any object $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y)$, let $g:Y\to X$ be any mapping for which $f_j\circ g:(Y,{\mathcal{R}}_Y)\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_P(H)$-mapping, for each $j\in J$ and let $(y,y^{{}^{\prime }})\in Y\times Y$. Then for each $j\in J$,

$${\mathcal{R}}_Y(y,y^{{}^{\prime }}){\le }_P[{\mathcal{R}}_j\circ {(f_j\circ g)}^2](y,y^{{}^{\prime }})=[({\mathcal{R}}_j\circ f_j^2)\circ g^2](y,y^{{}^{\prime }}),\mathrm{i}.\mathrm{e}.,$$

$$<[R_Y^{-}(y,y^{{}^{\prime }}),R_Y^{+}(y,y^{{}^{\prime }})],{\lambda }_Y(y,y^{{}^{\prime }})>$$

$${\le }_P<[(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }})),(R_j^{+}\circ f_j^2)(g(y),g(y^{{}^{\prime }})],({\lambda }_j\circ f_j^2)(g(y),g(y^{{}^{\prime }})>.$$

Thus,

$<[R_Y^{-}(y,y^{{}^{\prime }}),R_Y^{+}(y,y^{{}^{\prime }})],{\lambda }_Y(y,y^{{}^{\prime }})>$

${\le }_P<[{\bigwedge }_{j\in J}(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }}),{\bigwedge }_{j\in J}(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }})],$

${\bigwedge }_{j\in J}({\lambda }_j\circ f_j^2)(g(y),g(y^{{}^{\prime }})>$

$=[{\sqcap }_{j\in J}({\mathcal{R}}_j\circ f_j)](g(y),g(y^{{}^{\prime }})$

$=({\mathcal{R}}_{X,P}\circ g^2)(y,y^{{}^{\prime }}).$ [By the definition of ${\mathcal{R}}_{X,P}$]

So ${\mathcal{R}}_Y⊏{\mathcal{R}}_{X,P}\circ g^2.$ Hence $g:(Y,{\mathcal{R}}_Y)\to (X,{\mathcal{R}}_{X,P})$ is a ${\mathbf{CRel}}_P(H)$-mapping. Therefore ${(f_j:(X,{\mathcal{R}}_{X,P})\to (X_j,{\mathcal{R}}_j))}_J$ is an initial source in ${\mathbf{CRel}}_P(H)$.

Now define a mapping ${\mathcal{R}}_{X,R}=<R_{X,R},{\lambda }_{X,R}>:X\times X\to [H]\times H$ as below: for each $(x,y)\in X\times X$,

$$\begin{array}{c}{\mathcal{R}}_{X,R}(x)=[{⋒}_{j\in J}({\mathcal{R}}_j\circ f_j^2)](x,y),\mathrm{i}.\mathrm{e}.,\\ {\mathcal{R}}_{X,R}(x,y)=<[{\displaystyle \underset{j\in J}{\bigwedge }}{R}_j^{-}(f_j(x),f_j(y)),{\displaystyle \underset{j\in J}{\bigwedge }}{R}_j^{+}(f_j(x),f_j(y)),{\displaystyle \underset{j\in J}{\bigvee }}{\lambda }_j(f_j(x),f_j(y))>.\end{array}$$

Then clearly, for each $j\in J$ and $(x,y)\in X\times X$,

$$\begin{array}{c}<[R_{X,R}^{-}(x,y),R_{X,R}^{+}(x,y)],{\lambda }_{X,R}(x,y)>\\ {\le }_R<[R_j^{-}(f_j(x),f_j(y)),R_j^{+}(f_j(x),f_j(y))],{\lambda }_j(f_j(x),f_j(y))>.\end{array}$$

Thus, ${\mathcal{R}}_{X,R}⋐{\mathcal{R}}_j\circ f_j^2$, for each $j\in J$. So $f_j:(X,{\mathcal{R}}_{X,R})\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_R(H)$-mapping, for each $j\in J$.

For any object $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y)$, let $g:Y\to X$ be any mapping for which $f_j\circ g:(Y,{\mathcal{R}}_Y)\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_R(H)$-mapping, for each $j\in J$ and let $(y,y^{{}^{\prime }})\in Y\times Y$. Then for each $j\in J$,

$${\mathcal{R}}_Y(y,y^{{}^{\prime }}){\le }_R[{\mathcal{R}}_j\circ {(f_j\circ g)}^2](y,y^{{}^{\prime }})=[({\mathcal{R}}_j\circ f_j^2)\circ g^2](y,y^{{}^{\prime }}),\mathrm{i}.\mathrm{e}.,$$

$$\begin{array}{c}<[R_Y^{-}(y,y^{{}^{\prime }}),R_Y^{+}(y,y^{{}^{\prime }})],{\lambda }_Y(y,y^{{}^{\prime }})>\\ {\le }_R<[(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }})),(R_j^{+}\circ f_j^2)(g(y),g(y^{{}^{\prime }})],({\lambda }_j\circ f_j^2)(g(y),g(y^{{}^{\prime }})>.\end{array}$$

Thus,

$<[R_Y^{-}(y,y^{{}^{\prime }}),R_Y^{+}(y,y^{{}^{\prime }})],{\lambda }_Y(y,y^{{}^{\prime }})>$

${\le }_R<[{\bigwedge }_{j\in J}(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }}),{\bigwedge }_{j\in J}(R_j^{-}\circ f_j^2)(g(y),g(y^{{}^{\prime }})],$

${\bigvee }_{j\in J}({\lambda }_j\circ f_j^2)(g(y),g(y^{{}^{\prime }})>$

$=[{⋒}_{j\in J}({\mathcal{R}}_j\circ f_j)](g(y),g(y^{{}^{\prime }})$

$=({\mathcal{R}}_{X,R}\circ g^2)(y,y^{{}^{\prime }}).$ [By the definition of ${\mathcal{R}}_{X,R}$]

So ${\mathcal{R}}_Y⊏{\mathcal{R}}_{X,R}\circ g^2.$ Hence $g:(Y,{\mathcal{R}}_Y)\to (X,{\mathcal{R}}_{X,R})$ is a ${\mathbf{CRel}}_R(H)$-mapping. Therefore ${(f_j:(X,{\mathcal{R}}_{X,R})\to (X_j,{\mathcal{R}}_j))}_J$ is an initial source in ${\mathbf{CRel}}_R(H)$. This completes the proof. □

Example 1.

(1) (Inverse image of a cubicH-relation) Let X be a set, let $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$ be a cubic H-relational space and let $f:X\to Y$ be a mapping. Then there exists a unique initial cubic H-relation of P-order type ${\mathcal{R}}_{X,P}$ [resp. R-order type ${\mathcal{R}}_{X,R}$] in X for which $f:(X,{\mathcal{R}}_{X,P})\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_P(H)$-mapping [resp. $f:(X,{\mathcal{R}}_{X,R})\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_R(H)$-mapping]. In fact,

$${\mathcal{R}}_{X,P}={\mathcal{R}}_Y\circ f^2=<R_Y\circ f^2,{\lambda }_Y\circ f^2>={\mathcal{R}}_{X,R}.$$

In this case, ${\mathcal{R}}_{X,P}$ [resp. ${\mathcal{R}}_{X,R}$] is called the inverse image under f of the cubic H-relation ${\mathcal{R}}_Y$ in Y.

In particular, if $X\subset Y$ and $f:X\to Y$ is the inclusion mapping, then the inverse image ${\mathcal{R}}_{X,P}$ [resp. ${\mathcal{R}}_{X,R}$] of ${\mathcal{R}}_Y$ under f is called a cubic H-subrelation of $(Y,{\mathcal{R}}_Y)$. In fact,

$${\mathcal{R}}_{X,P}(x,y)={\mathcal{R}}_Y(x,y)={\mathcal{R}}_{X,R}(x,y),\mathrm{for}\mathrm{each}(x,y)\in X\times X.$$

(2) (CubicH-product relation) Let ${((X_j,{\mathcal{R}}_j))}_{j\in J}={((X_j,<R_j,{\lambda }_j>))}_{j\in J}$ be any family of cubic H-relational spaces and let $X={\mathsf{\Pi }}_{j\in J}{X}_j$. For each $j\in J$, let $p{r}_j:X\to X_j$ be the ordinary projection. Then there exists a unique cubic H-relation of P-order type, ${\mathcal{R}}_{X,P}$ in X for which $p{r}_j:(X,{\mathcal{R}}_{X,P})\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_P(H)$-mapping, for each $j\in J$. In this case, ${\mathcal{R}}_{X,P}$ is called the cubic H-product relation of ${({\mathcal{R}}_j)}_{j\in J}$ and $(X,{\mathcal{R}}_{X,P})$ is called the cubic H-product relational space of ${((X_j,{\mathcal{R}}_j))}_{j\in J}$, and denoted as the following, respectively:

$${\mathcal{R}}_{X,P}={\mathsf{\Pi }}_{j\in J}{\mathcal{R}}_j$$

and

$$(X,{\mathcal{R}}_{X,P})=({\mathsf{\Pi }}_{j\in J}{X}_j,{\mathsf{\Pi }}_{j\in J}{\mathcal{R}}_j)=({\mathsf{\Pi }}_{j\in J}{X}_j,<{\mathsf{\Pi }}_{j\in J}{R}_j,{\mathsf{\Pi }}_{j\in J}{\lambda }_j>).$$

In fact, ${\mathcal{R}}_{X,P}(x)=[{\sqcap }_{j\in J}({\mathcal{R}}_j\circ p{r}_j)](x,y)$, for each $(x,y)\in X\times X$.

Similarly, there exists a unique cubic H-relation of R-order type, ${\mathcal{R}}_{X,R}$ in X for which $p{r}_j:(X,{\mathcal{R}}_{X,R})\to (X_j,{\mathcal{R}}_j)$ is a ${\mathbf{CRel}}_R(H)$-mapping, for each $j\in J$. In this case, ${\mathcal{R}}_{X,R}$ is called the cubic H-product${}^{*}$ relation of ${({\mathcal{R}}_j)}_{j\in J}$ and $(X,{\mathcal{R}}_{X,R})$ is called the cubic H-product${}^{*}$ relational space of ${((X_j,{\mathcal{R}}_j))}_{j\in J}$, and denoted as the following, respectively:

$${\mathcal{R}}_{X,R}={\mathsf{\Pi }}_{j\in J}^{*}{\mathcal{R}}_j$$

and

$$(X,{\mathcal{R}}_{X,R})=({\mathsf{\Pi }}_{j\in J}{X}_j,{\mathsf{\Pi }}_{j\in J}^{*}{\mathcal{R}}_j)=({\mathsf{\Pi }}_{j\in J}{X}_j,<{\mathsf{\Pi }}_{j\in J}{R}_j,{\mathsf{\Pi }}_{j\in J}^{*}{\lambda }_j>).$$

In fact, ${\mathcal{R}}_{X,R}(x,y)=[{⋒}_{j\in J}({\mathcal{R}}_j\circ p{r}_j)](x,y)$, for each $(x,y)\in X\times X$.

In particular, if $J=\{1,2\}$, then for each $(x_1,y_1),(x_2,y_2)\in X_1\times X_2$,

$({\mathcal{R}}_1\times {\mathcal{R}}_2)((x_1,y_1),(x_2,y_2))$

$=<[R_1^{-}(x_1,x_2)\wedge R_2^{-}(y_1,y_2),R_1^{+}(x_1,x_2)\wedge R_2^{+}(y_1,y_2)],{\lambda }_1(x_1,x_2)\wedge {\lambda }_2(y_1,y_2)>$

and

$({\mathcal{R}}_1{\times }^{*}{\mathcal{R}}_2)((x_1,y_1),(x_2,y_2))$

$=<[R_1^{-}(x_1,x_2)\wedge R_2^{-}(y_1,y_2),R_1^{+}(x_1,x_2)\wedge R_2^{+}(y_1,y_2)],{\lambda }_1(x_1,x_2)\vee {\lambda }_2(y_1,y_2)>$.

The following is obvious from Lemma 3.9 and Theorem 1.6 in [25] or Proposition in Section 1 in [38].

Corollary 1.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is complete and cocomplete over $\mathbf{Set}$.

Furthermore, we can easily see that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is well-powered and cowell-powered. It is well-known that a concrete category is topological if and only if it is cotopological (See Theorem 1.5 in [25]). However, we prove directly that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is cotopological.

Lemma 2.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is cotopological over $\mathbf{Set}$.

Proof. 

Let X be any set and let ${(X_j,{\mathcal{R}}_j)}_{j\in J}=(X_j,<R_j,{\lambda }_j>)$ be any family of cubic H-relational spaces indexed by a class J. Suppose ${(f_j:X_j\to X)}_{j\in J}$ is a sink of mappings. We define a mapping ${\mathcal{R}}_{X,P}=<R_{X,P},{\lambda }_{X,P}>:X\times X\to [H]\times H$ as follows: for each $(x,y)\in X\times X$,

$${\mathcal{R}}_{X,P}(x,y)=({\bigsqcup }_{j\in J}{\bigsqcup }_{(x_j,y_j)\in f^{-2}(x,y)}{\mathcal{R}}_j)(x_j,y_j)=\underset{j\in J}{\bigvee }\underset{(x_j,y_j)\in f^{-2}(x,y)}{\bigvee }{\mathcal{R}}_j(x_j,y_j).$$

Then we can easily see that

$$f_j:(X_j,{\mathcal{R}}_j)\to (X,{\mathcal{R}}_{X,P})\mathrm{is}\mathrm{a}{\mathbf{CRel}}_P(H)-\mathrm{mapping},\mathrm{for}\mathrm{each}j\in J.$$

For any cubic H-relational space $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$, let $g:X\to Y$ be any mapping such that $g\circ f_j:(X_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_P(H)$-mapping, for each $j\in J$ and let $(x,y)\in X\times X$. Then for each $j\in J$ and each $(x_j,y_j)\in f_j^{-2}(x,y)$,

${\mathcal{R}}_j(x_j,y_j)$

$=<[R_j^{-}(x_j,y_j),[R_j^{+}(x_j,y_j)],{\lambda }_j(x_j,y_j)>$

${\le }_P<[(R_Y^{-}\circ {(g\circ f_j)}^2)(x_j,y_j),(R_Y^{+}\circ {(g\circ f_j)}^2)(x_j,y_j)],({\lambda }_Y\circ {(g\circ f_j)}^2)(x_j,y_j)>$

$=<[(R_Y^{-}\circ g^2)(f_j(x_j),f_j(y_j)),(R_Y^{+}\circ g^2)(f_j(x_j),f_j(y_j))],({\lambda }_Y\circ g^2)(f_j(x_j),f_j(y_j))>$

$=<[(R_Y^{-}\circ g^2)(x,y),(R_Y^{+}\circ g^2)(x,y),({\lambda }_Y\circ g^2)(x,y)>$

$=({\mathcal{R}}_Y\circ g^2)(x,y).$

Thus, by the definition of ${\mathcal{R}}_{X,P}$, ${\mathcal{R}}_{X,P}(x,y){\le }_P({\mathcal{R}}_Y\circ g^2)(x,y).$ So ${\mathcal{R}}_{X,P}⊏{\mathcal{R}}_Y\circ g^2$. Hence $g:(X,{\mathcal{R}}_{X,P})\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_P(H)$-mapping. Therefore ${\mathbf{CRel}}_P(H)$ is cotopological over $\mathbf{Set}$.

Now we define a mapping ${\mathcal{R}}_{X,R}=<R_{X,R},{\lambda }_{X,R}>:X\times X\to [H]\times H$ as follows: for each $(x,y)\in X\times X$,

${\mathcal{R}}_{X,R}(x,y)$

$=({⋓}_{j\in J}{⋓}_{(x_j,y_j)\in f^{-2}(x,y)}{\mathcal{R}}_j)(x_j,y_j)$

$=<[{\bigvee }_{j\in J}{\bigvee }_{(x_j,y_j)\in f^{-2}(x)}{R}_j^{-}(x_j,y_j),{\bigvee }_{j\in J}{\bigvee }_{(x_j,y_j)\in f^{-2}(x,y)}{R}_j^{+}(x_j,y_j)],$

${\bigwedge }_{j\in J}{\bigwedge }_{x_j\in f^{-2}(x,y)}{\lambda }_j(x_j,y_j)>.$

Then we can easily see that

$$f_j:(X_j,{\mathcal{R}}_j)\to (X,{\mathcal{R}}_{X,R})\mathrm{is}\mathrm{a}{\mathbf{CRel}}_R(H)-\mathrm{mapping},\mathrm{for}\mathrm{each}j\in J.$$

For any cubic H-relational space $(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$, let $g:X\to Y$ be any mapping such that $g\circ f_j:(X_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_R(H)$-mapping, for each $j\in J$ and let $(x,y)\in X\times X$. Then for each $j\in J$ and each $(x_j,y_j)\in f_j^{-2}(x,y)$,

${\mathcal{R}}_j(x_j,y_j)$

$=<[R_j^{-}(x_j,y_j),[R_j^{+}(x_j,y_j)],{\lambda }_j(x_j,y_j)>$

${\le }_R<[(R_Y^{-}\circ {(g\circ f_j)}^2)(x_j,y_j),(R_Y^{+}\circ {(g\circ f_j)}^2)(x_j,y_j)],({\lambda }_Y\circ {(g\circ f_j)}^2)(x_j,y_j)>$

$=<[(R_Y^{-}\circ g^2)(f_j(x_j),f_j(y_j)),(R_Y^{+}\circ g^2)(f_j(x_j),f_j(y_j))],({\lambda }_Y\circ g^2)(f_j(x_j),f_j(y_j))>$

$=<[(R_Y^{-}\circ g^2)(x,y),(R_Y^{+}\circ g^2)(x,y)],({\lambda }_Y\circ g^2)(x,y)>$

$=({\mathcal{R}}_Y\circ g^2)(x,y).$

Thus, by the definition of ${\mathcal{R}}_{X,R}$, ${\mathcal{R}}_{X,R}(x,y){\le }_R({\mathcal{R}}_Y\circ g^2)(x,y).$ So ${\mathcal{R}}_{X,R}⋐{\mathcal{R}}_Y\circ g^2$. Hence $g:(X,{\mathcal{R}}_{X,R})\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_R(H)$-mapping. Therefore ${\mathbf{CRel}}_R(H)$ is cotopological over $\mathbf{Set}$. This completes the proof. □

Example 2.

(CubicH-quotient relation) Let $(X,\mathcal{R})=(X,<R,\lambda >)$ be a cubic H-relational space, let ∼ be an equivalence relation on X and let $\pi :X\to X/\sim$ be the canonical mapping. We define a mapping ${\mathcal{R}}_{X/\sim ,P}:X/\sim \times X/\sim \to [H]\times H$ as below: for each $([x],[y])\in X/\sim \times X/\sim$,

${\mathcal{R}}_{X/\sim ,P}([x],[y])$

$=[{\bigsqcup }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}\mathcal{R}](x^{{}^{\prime }},y^{{}^{\prime }})$

$=<[{\bigvee }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{21}([x],[y])}{R}^{-}(x^{{}^{\prime }},y^{{}^{\prime }}),{\bigvee }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}{R}^{+}(x^{{}^{\prime }},y^{{}^{\prime }})],$

${\bigvee }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}\lambda (x^{{}^{\prime }},y^{{}^{\prime }})>.$

Then we can easily see that ${\mathcal{R}}_{X/\sim ,P}$ is a cubic H-relation in $X/\sim$. Furthermore, $\pi :(X,\mathcal{R})\to (X/\sim ,{\mathcal{R}}_{X/\sim ,P})$ is a ${\mathbf{CRel}}_P(H)$-mapping. Thus, ${\mathcal{R}}_{X/\sim ,P}$ is the final cubic H-relation in $X/\sim$.

Now we define a mapping ${\mathcal{R}}_{X/\sim ,R}:X/\sim \times X/\sim \to [H]\times H$ as follows: for each $([x],[y])\in X/\sim \times X/\sim$,

${\mathcal{R}}_{X/\sim ,R}([x])=[{⋓}_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}\mathcal{R}](x^{{}^{\prime }},y^{{}^{\prime }})$

$=<[{\bigvee }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}{R}^{-}(x^{{}^{\prime }},y^{{}^{\prime }}),{\bigvee }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}{R}^{+}(x^{{}^{\prime }},y^{{}^{\prime }})],$

${\bigwedge }_{(x^{{}^{\prime }},y^{{}^{\prime }})\in {\pi }^{-2}([x],[y])}\lambda (x^{{}^{\prime }},y^{{}^{\prime }})>.$

Then we can easily see that ${\mathcal{R}}_{X/\sim ,R}$ is a cubic H-relation in $X/\sim$. Furthermore, $\pi :(X,\mathcal{R})\to (X/\sim ,{\mathcal{A}}_{X/\sim ,R})$ is a ${\mathbf{Crel}}_R(H)$-mapping. Thus, ${\mathcal{R}}_{X/\sim ,R}$ is the final cubic H-relation in $X/\sim$.

In this case, ${\mathcal{R}}_{X/\sim ,P}$ [resp. ${\mathcal{A}}_{X/\sim ,R}$] is called the cubic H-quotient [resp. H-quotient${}^{*}$] relation in X induced by ∼.

Definition 7

([38]). Let $\mathbf{A}$ be a concrete category and let $f,g:A\to B$ be two $\mathbf{A}$-morphisms. Then a pair $(E,e)$ is called an equalizer in $\mathbf{A}$ of f and g, if the following conditions hold:

(i) 

$e:E\to A$ is an $\mathbf{A}$-morphism,

(ii) 

$f\circ e=g\circ e$,

(iii) 

for any $\mathbf{A}$-morphism $e^{{}^{\prime }}:E^{{}^{\prime }}\to A$ such that $f\circ e^{{}^{\prime }}=g\circ e^{{}^{\prime }}$, there exists a unique $\mathbf{A}$-morphism $\overline{e}:E^{{}^{\prime }}\to E$ such that $e^{{}^{\prime }}=e\circ \overline{e}$.

In this case, we say that $\mathbf{A}$ has equalizers.

Dual notion: Coequalizer.

Proposition 2.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] has equalizers.

Proof. 

Let $f,g:(X,{\mathcal{R}}_X)\to (Y,{\mathcal{R}}_Y)$ be two ${\mathbf{CRel}}_P(H)$-mappings, where ${\mathcal{R}}_X=<R_X,{\lambda }_X>$ and ${\mathcal{R}}_Y=<R_Y,{\lambda }_Y>$. Let $E=\{a\in X:f(a)=g(a)\}$ and define a mapping ${\mathcal{R}}_{E,P}:E\times E\to [H]\times H$ as follows: for each $(a,b)\in E\times E$,

$${\mathcal{R}}_{E,P}(a,b)={\mathcal{R}}_X(a,b))=<[R_X^{-}(a,b),R_X^{+}(a,b)],{\lambda }_X(a,b)>.$$

Then clearly, ${\mathcal{R}}_{E,P}$ is a cubic H-relation in E and ${\mathcal{R}}_{E,P}⊏{\mathcal{R}}_X$. Consider the inclusion mapping $i:E\to X$. Then clearly, $i:(E,{\mathcal{A}}_{P,E})\to (X,\mathcal{A})$ is a ${\mathbf{CSet}}_P(H)$-mapping and $f\circ i=g\circ i$.

Let $k:(E^{{}^{\prime }},{\mathcal{R}}_{E^{{}^{\prime }}})\to (X,{\mathcal{A}}_X)$ be a ${\mathbf{CRel}}_P(H)$-mapping such that $f\circ k=g\circ k$. We define a mapping $\overline{k}:E^{{}^{\prime }}\to E$ as follows: for each $e^{{}^{\prime }}\in E^{{}^{\prime }}$,

$$\overline{k}(e^{{}^{\prime }})=i^{-1}\circ k(e^{{}^{\prime }}).$$

Then clearly, $k=i\circ \overline{k}$.

Let $(e^{{}^{\prime }},f^{{}^{\prime }})\in E^{{}^{\prime }}\times E^{{}^{\prime }}$. Since $k:(E^{{}^{\prime }},{\mathcal{R}}_{E^{{}^{\prime }}})\to (X,{\mathcal{R}}_{E,P})$ is a ${\mathbf{CRel}}_P(H)$-mapping,

${\mathcal{R}}_{E,P}\circ {(\overline{k})}^2(e^{{}^{\prime }},f^{{}^{\prime }})={\mathcal{R}}_{E,P}\circ {(\overline{k})}^2(e^{{}^{\prime }},f^{{}^{\prime }})$

$={\mathcal{R}}_{E,P}\circ (i^{-2}\circ k^2(e^{{}^{\prime }},f^{{}^{\prime }}))$

$={\mathcal{R}}_{E,P}\circ k^2(e^{{}^{\prime }},f^{{}^{\prime }})$

${\ge }_P{\mathcal{R}}_{E^{{}^{\prime }}}(e^{{}^{\prime }},f^{{}^{\prime }}).$

Thus, ${\mathcal{R}}_{E^{{}^{\prime }}}⊏{\mathcal{R}}_{E,P}\circ {(\overline{k})}^2$. So $\overline{k}:(E^{{}^{\prime }},{\mathcal{R}}_{E^{{}^{\prime }}})\to (E,{\mathcal{R}}_{E,P})$ is a ${\mathbf{CRel}}_P(H)$-mapping.

Now in order to prove the uniqueness of $\overline{k}$, let $\overline{r}:E^{{}^{\prime }}⟶E$ such that $i\circ \overline{r}=k$. Then $\overline{r}=i^{-1}\circ k=\overline{k}.$ Thus, $\overline{k}$ is unique. Hence ${\mathbf{CRel}}_P(H)$ has equalizers.

Similarly, we can prove that ${\mathbf{CRel}}_R(H)$ has the equalizer ${\mathcal{R}}_{E,P}$. □

For two cubic H-relations ${\mathcal{R}}_X=<R_X,{\lambda }_X>$ in X and ${\mathcal{R}}_Y=<R_Y,{\lambda }_Y>$ in Y, the product of P-order type [resp. R-order type], denoted by ${\mathcal{R}}_X{\times }_P{\mathcal{Y}}_Y$ [resp. ${\mathcal{R}}_X{\times }_R{\mathcal{R}}_Y$], is a cubic H-relation in $X\times Y$ defined by: for any $(x,y),(x^{{}^{\prime }},y^{{}^{\prime }})\in X\times Y$,

$$({\mathcal{R}}_X{\times }_P{\mathcal{R}}_Y)((x,y),(x^{{}^{\prime }},y^{{}^{\prime }}))=<R_X(x,x^{{}^{\prime }})\wedge R_Y(y,y^{{}^{\prime }}),{\lambda }_X(x,x^{{}^{\prime }})\wedge {\lambda }_X(y,y^{{}^{\prime }})>$$

[resp. ${({\mathcal{R}}_X{\times }_R\mathcal{R})}_Y((x,y),(x^{{}^{\prime }},y^{{}^{\prime }}))=<R_X(x,x^{{}^{\prime }})\wedge R_Y(y,y^{{}^{\prime }}),{\lambda }_X(x,x^{{}^{\prime }})\vee {\lambda }_X(y,y^{{}^{\prime }})>$].

Lemma 3.

Final episinks in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] are preserved by pullbacks.

Proof. 

Let ${(g_j:(X_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_Y))}_{j\in J}$ be any final episink in ${\mathbf{CRel}}_P(H)$ and let $f:(W,{\mathcal{R}}_W)\to (Y,{\mathcal{R}}_Y)$ be any ${\mathbf{CRel}}_P(H)$-mapping, where ${\mathcal{R}}_j=<R_j,{\lambda }_j>$, ${\mathcal{R}}_Y=<R_Y,{\lambda }_Y>$ and ${\mathcal{R}}_W=<R_W,{\lambda }_W>$. For each $j\in J$, let

$$U_j=\{(w,x_j)\in W\times X_j:f(w)=g_j(x_j)\}$$

and let us define a mapping ${\mathcal{R}}_{U_j,P}=<R_{U_j,P},{\lambda }_{U_j,P}>:U_j\times U_j\to [H]\times H$ as follows: for each $((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in U_j\times U_j$,

${\mathcal{R}}_{U_j,P}((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=({\mathcal{R}}_W{\times }_P{\mathcal{R}}_j){\mid }_{U_j\times U_j}((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=({\mathcal{R}}_W{\times }_P{\mathcal{R}}_j)((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=<R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_j(x_j,x_j^{{}^{\prime }})>$

$=<(R_W\times R_j)((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }})),({\lambda }_W\times {\lambda }_j)((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))>$, i.e.,

$${\mathcal{R}}_{U_j,P}=<R_W\times R_j{\mid }_{U_j\times U_j},{\lambda }_W\times {\lambda }_j{\mid }_{U_j\times U_j}>.$$

For each $j\in J$, let $e_j:U_j\to W$ and $p_j:U_j\to X_j$ be the usual projections. Then clearly, $e_j:(U_j,{\mathcal{R}}_{U_j,P})\to (W,{\mathcal{R}}_W)$ and $p_j:(U_j,{\mathcal{R}}_{U_j,P})\to (X_j,{\mathcal{R}}_j)$ are ${\mathbf{CRel}}_P(H)$-mappings and $g_j\circ p_j=f\circ e_j$, for each $j\in J$. Thus, we have the following pullback square in ${\mathbf{CRel}}_P(H)$:

   

We will prove that ${(e_j:(U_j,{\mathcal{R}}_{U_j,P})\to (W,{\mathcal{R}}_W))}_{j\in J}$ is a final episink in ${\mathbf{CRel}}_P(H)$. Let $w\in W$. Since ${(g_j)}_{j\in J}$ is an episink in ${\mathbf{CSet}}_P(H)$, there is $j\in J$ such that $g_j(x_j)=f(w)$, for some $x_j\in X_j$. Thus, $(w,x_j)\in U_j$ and $e_j(w,x_j)=w$. So ${(e_j)}_{j\in J}$ is an episink in ${\mathbf{CRel}}_P(H)$.

Finally, let us show that ${(e_j)}_J$ is final in ${\mathbf{CRel}}_P(H)$. Let ${\mathcal{R}}_W^{*}$ be the final structure in W regarding ${(e_j)}_{j\in J}$ and let $(w,w^{{}^{\prime }})\in W\times W$. Then

${\mathcal{R}}_W(w,w^{{}^{\prime }})=<R_W(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})>$

$=<R_W(w,w^{{}^{\prime }})\wedge R_W(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_W(w,w^{{}^{\prime }})>$

${\le }_P<R_W(w,w^{{}^{\prime }})\wedge R_Y\circ f^2(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_Y\circ f^2(w,w^{{}^{\prime }})>$

$[\mathrm{Since}$$f:(W,{\mathcal{R}}_W)\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_P(H)$-mapping]

$=<R_W(w,w^{{}^{\prime }})\wedge [{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}{R}_j(x_j,x_j^{{}^{\prime }})],$

${\lambda }_W(w,w^{{}^{\prime }})\wedge [{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}{\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$[\mathrm{Since}$${(g_j:(R_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_Y))}_{j\in J}$ is a final episink in ${\mathbf{CRel}}_P(H)$]

$=<{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}[R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }})]],$

${\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}[{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$=<{\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }})]],$

${\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$=<{\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[R_{U_j,P}((w,x_j,(w^{{}^{\prime }},x_j^{{}^{\prime }})],$

${\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[{\lambda }_{U_j,P}((w,x_j,(w^{{}^{\prime }},x_j^{{}^{\prime }})]>$

$={\mathcal{R}}_W^{*}(w,w^{{}^{\prime }})$.

Thus, ${\mathcal{R}}_W⊏{\mathcal{R}}_W^{*}$. Since ${(e_j:(U_j,{\mathcal{R}}_{U_j})\to (W,{\mathcal{R}}_W))}_{j\in J}$ is final, $1_W:(W,{\mathcal{R}}_W^{*})\to (W,{\mathcal{R}}_W)$ is a ${\mathbf{CRel}}_P(H)$-mapping. So ${\mathcal{R}}_W^{*}⊏{\mathcal{R}}_W$. Hence ${\mathcal{R}}_W^{*}={\mathcal{R}}_W$. Therefore ${(e_j)}_{j\in J}$ is final.

Now we define a mapping ${\mathcal{R}}_{U_j,R}=<R_{U_j,R},{\lambda }_{U_j,R}>:U_j\to [H]\times H$ as follows: for each $((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in U_j\times U_j$,

${\mathcal{R}}_{U_j,R}((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=({\mathcal{R}}_W{\times }_R{\mathcal{R}}_j){\mid }_{U_j\times U_j}((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=({\mathcal{R}}_W{\times }_R{\mathcal{R}}_j)((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))$

$=<R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\vee {\lambda }_j(x_j,x_j^{{}^{\prime }})>.$

For each $j\in J$, let $e_j:U_j\to W$ and $p_j:U_j\to X_j$ be the usual projections. Then we can similarly prove that final episinks in ${\mathbf{Rel}}_R(H)$ are preserved by pullbacks. This completes the proof. □

For any singleton set $\left\{a\right\}$, since the cubic set ${\mathcal{R}}_{\left\{a\right\}}$ in $\left\{a\right\}$ is not unique, the category $\mathbf{CRel}(H)$ is not properly fibered over $\mathbf{Set}$. Then from Definitions 1 and 3, Lemmas 2 and 3, we have the following result.

Theorem 1.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] satisfies all the conditions of a topological universe over $\mathbf{Set}$ except the terminal separator property.

Theorem 2.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is Cartesian closed over $\mathbf{Set}$.

Proof. 

From Lemma 1, it is clear that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] has products. Then it is sufficient to prove that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] has exponential objects.

For any cubic H-relational spaces $\mathbf{X}=(X,{\mathcal{R}}_X)=(X,<R_X,{\lambda }_X>)$ and $\mathbf{Y}=(Y,{\mathcal{R}}_Y)=(Y,<R_Y,{\lambda }_Y>)$, let $Y^X$ be the set of all ordinary mappings from X to Y. We define two mappings $R_{Y^X}:Y^X\times Y^X\to [H]$ and ${\lambda }_{Y^X}:Y^X\times Y^X\to H$ as follows: for each $(f,g)\in Y^X\times Y^X$,

$R_{Y^X}(f,g)=\bigvee \{h\in H:R_X(x,y)\wedge h\le R_Y(f(x),f(y)),\mathrm{for}\mathrm{each}(x,y)\in X\times X\}$ and

${\lambda }_{Y^X}(f,g)=\bigvee \{h\in H:{\lambda }_X(x,y)\wedge h\le {\lambda }_Y(f(x),f(y)),\mathrm{for}\mathrm{each}(x,y)\in X\times X\}.$ Then clearly, ${\mathcal{A}}_{Y^X}=<A_{Y^X},{\lambda }_{Y^X}>$ is a cubic H-relation in $Y^X$. Moreover, by the definitions of $R_{Y^X}$ and ${\lambda }_{Y^X}$,

$$R_X^{-}(x,y)\wedge R_{Y^X}^{-}(f,g)\le R_Y^{-}(f(x),f(y)),R_X^{+}(x,y)\wedge R_{Y^X}^{+}(f,g)\le R_Y^{-}(f(x),f(y))$$

and

$${\lambda }_X(x,y)\wedge {\lambda }_{Y^X}(f,g)\le {\lambda }_Y(f(x),f(y)),$$

for each $(x,y)\in X\times X$.

Let ${\mathbf{Y}}^{\mathbf{X}}=(Y^X,{\mathcal{R}}_{Y^X})$ and let us define a mapping $e_{X,Y}:X\times Y^X\to Y$ as follows: for each $(x,f)\in X\times Y^X$,

$$e_{X,Y}(x,f)=f(x).$$

Let $(x,f),(y,g)\in X\times Y^X.$ Then

$(R_X^{-}{\times }_P{R}_{Y^X}^{-})((x,f),(y,g))=R_X^{-}(x,y)\wedge R_{Y^X}^{-}(f,g)$

$\le R_Y^{-}(f(x),f(y))$

$=R_Y^{-}\circ e_{X,Y}^2((x,f),(y,g)),$

$[\mathrm{By}$ the definition of $e_{X,Y}$]

$(R_X^{+}{\times }_P{R}_{Y^X}^{+})((x,f),(y,g))=R_X^{+}(x,y)\wedge R_{Y^X}^{+}(f,g)$

$\le A_Y^{+}(f(x),f(y))$

$=A_Y^{+}\circ e_{X,Y}^2((x,f),(y,g))$ and

$({\lambda }_X{\times }_P{\lambda }_{Y^X})((x,f),(y,g))={\lambda }_X(x,y)\wedge {\lambda }_{Y^X}(f,g)$

$\le {\lambda }_Y(f(x),f(y))$

$={\lambda }_Y\circ e_{X,Y}^2((x,f),(y,g))$.

Thus, $e_{X,Y}:\mathbf{X}{\times }_P{\mathbf{Y}}^{\mathbf{X}}\to \mathbf{Y}$ is a ${\mathbf{CRel}}_P(H)$-mapping, where $\mathbf{X}{\times }_P{\mathbf{Y}}^{\mathbf{X}}=(X\times Y^X,<A_X{\times }_P{A}_{Y^X},{\lambda }_X{\times }_P{\lambda }_{Y^X}>)$.

For any cubic H-relational space $\mathbf{Z}=(Z,<A_Z,{\lambda }_Z>)$, let $k:\mathbf{X}{\times }_P\mathbf{Z}\to \mathbf{Y}$ be a ${\mathbf{CRel}}_P(H)$-mapping. We define a mapping $\overline{k}:Z\to Y^X$ as follows: for each $z\in Z$ and each $x\in X$,

$$[\overline{k}(z)](x)=k(x,z).$$

Then we can prove that $\overline{k}$ is a unique ${\mathbf{CRel}}_P(H)$-mapping such that $e_{X,Y}\circ (1_X\times \overline{k})=k$.

Now we define two mappings $R_{Y^X,R}:Y^X\times Y^X\to [H]$ and ${\lambda }_{Y^X,R}:Y^X\times Y^X\to H$ as follows: for each $(f,g)\in Y^X\times Y^X$ and each $x\in X$,

$$R_{Y^X,R}(f,g)=R_{Y^X,P}(f,g)$$

and

$${\lambda }_{Y^X,R}(f,g)=\bigwedge \{h\in H:{\lambda }_X(x,y)\vee h\ge {\lambda }_Y(f(x),f(y)),\mathrm{for}\mathrm{each}(x,y)\in X\times X\}.$$

Then clearly, ${\mathcal{R}}_{Y^X,R}=<R_{Y^X,R},{\lambda }_{Y^X,R}>$ is a cubic H-relation in $Y^X$. Moreover, by the definitions of $R_{Y^X,R}$ and ${\lambda }_{Y^X,R}$,

$$R_X(x,y)\wedge R_{Y^X,R}(f,g)\le R_Y(f(x),f(y))$$

and

$${\lambda }_X(x,y)\vee {\lambda }_{Y^X,R}(f,g)\ge {\lambda }_Y(f(x),f(y)),$$

for each $x\in X.$ Let ${\mathbf{Y}}^{\mathbf{X}}=(Y^X,{\mathcal{R}}_{Y^X,R})$ and let us define a mapping $e_{X,Y}:X\times Y^X\to Y$ as follows: for each $(x,f)\in X\times Y^X$,

$$e_{X,Y}(x,f)=f(x).$$

Let $(x,f),(y,g)\in X\times Y^X.$ Then by the definitions of $R_{Y^X,R}$ and ${\lambda }_{Y^X,R}$, we have the followings:

$$(R_X{\times }_R{A}_{Y^X,R})((x,f),(y,g))\le R_Y\circ e_{X,Y}^2((x,f),(y,g))$$

and

$$({\lambda }_X{\times }_R{\lambda }_{P,Y^X})((x,f),(y,g))\ge {\lambda }_Y\circ e_{X,Y}^2((x,f),(y,g)).$$

Thus, ${\mathcal{R}}_X{\times }_R{\mathcal{R}}_{Y^X,R}⋐{\mathcal{R}}_Y\circ e_{X,Y}^2.$ So $e_{X,Y}:\mathbf{X}{\times }_R{\mathbf{Y}}^{\mathbf{X}}\to \mathbf{Y}$ is a ${\mathbf{CRel}}_R(H)$-mapping, where $\mathbf{X}{\times }_R{\mathbf{Y}}^{\mathbf{X}}=(X\times Y^X,<R_X{\times }_R{R}_{Y^X,R},{\lambda }_X{\times }_R{\lambda }_{Y^X,R}>)$.

For any cubic H-relational space $\mathbf{Z}=(Z,<R_Z,{\lambda }_Z>)$, let $k:\mathbf{X}{\times }_R\mathbf{Z}\to \mathbf{Y}$ be a ${\mathbf{CRel}}_R(H)$-mapping. We define a mapping $\overline{k}:Z\to Y^X$ as follows: for each $z\in Z$ and each $x\in X$,

$$[\overline{k}(z)](x)=k(x,z).$$

Then we can prove that $\overline{k}$ is a unique ${\mathbf{CRel}}_R(H)$-mapping such that

$$e_{X,Y}\circ (1_X\times \overline{k})=k.$$

This completes the proof. □

Remark 1.

The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is not a topos (See [39] for its definition), since it has no subobject classifier.

Example 3.

Let $I=\{0,1\}$ be two points chain, respectively and let $X=\left\{a\right\}$. Let ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ be the cubic H-relations in X defined by:

$${\mathcal{R}}_1(a)=<\mathbf{0},0>and{\mathcal{R}}_2(a)=<\mathbf{1},1>.$$

Let $1_X:(X,{\mathcal{R}}_1)\to (X,{\mathcal{R}}_2)$ be the identity mapping. Then clearly, $1_X$ is both monomorphism and epimorphism in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$]. However, $1_X$ is not an isomorphism in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$]. Thus, $\mathbf{CRel}(H)$ has no subobject classifier.

4. The Categories ${\mathbf{CRel}}_{\mathit{P},\mathit{R}}(\mathit{H})$ and ${\mathbf{CRel}}_{\mathit{R},\mathit{R}}(\mathit{H})$

In this section, we obtain two subcategories ${\mathbf{CRel}}_{P,R}(H)$ and ${\mathbf{CRel}}_{R,R}(H)$ of ${\mathbf{CRel}}_P(H)$ and ${\mathbf{CRel}}_R(H)$, respectively which are topological universes over $\mathbf{Set}$.

It is interesting that final structures and exponential objects in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] are shown to be quite different from those in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$].

First of all, we list two well-known results.

Result 1 (Theorem 2.5 [25]). Let $\mathbf{A}$ be a well-powered and co(well-powered) topological category. Then the followings are equivalent:

(1)

$\mathbf{B}$ is bireflective in $\mathbf{A}$,

(2)

$\mathbf{B}$ is closed under the formation of initial sources, i.e., for any initial source ${(f_j:A\to A^j)}_{j\in J}$ in $\mathbf{A}$ with $A_j\in \mathbf{B}$ for each $j\in J$, then $A\in \mathbf{B}$.

Result 2 (Theorem 2.6 [25]). If $\mathbf{A}$ is a topological category and $\mathbf{B}$ is a bireflective subcategory of $\mathbf{A}$, then $\mathbf{B}$ is also a topological category. Moreover, every source in $\mathbf{B}$ which is initial in $\mathbf{A}$ is initial in $\mathbf{B}$.

Definition 8.

Let X be a nonempty set and let $\mathcal{R}=<R,\lambda >$ be a cubic H-relation in X. Then $\mathcal{R}$ is said to be reflexive, if R and λ are reflexive, i.e., $R(x,x)=\mathbf{1}$ and $\lambda (x,x)=1$, for each $x\in X$.

The class of all cubic H-reflexive relational spaces and ${\mathbf{CRel}}_P(H)$-mappings [resp. ${\mathbf{CRel}}_R(H)$-mappings between them forms a subcategory of ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] denoted by ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$].

The following is the immediate result of Definitions 1 and 8.

Lemma 4.

The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is properly fibered over $\mathbf{Set}$.

Lemma 5.

The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is closed under the formation of initial sources in The category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$]

Proof. 

Let $f_j:(X,{\mathcal{R}}_{X,P})\to (X_j,{\mathcal{R}}_j){)}_{j\in J}$ be an initial source in ${\mathbf{CRel}}_P(H)$ such that each $(X_j,{\mathcal{R}}_j)$ belongs to ${\mathbf{CRel}}_{P,R}(H)$, where $(X,{\mathcal{R}}_{X,P})=(X,<R_{X,P},{\lambda }_{X,P}>)$ and $(X_j,{\mathcal{R}}_j)=(X_j,<R_j,{\lambda }_j>)$. Let $x\in X$ and let $j\in J$. Since $R_j$ and ${\lambda }_j$ are reflexive, $R_j\circ f_j^2(x,x)=\mathbf{1}$ and ${\lambda }_j\circ f_j^2(x,x)=1$. Then

$$R_{X,P}(x,x)=\underset{j\in J}{\bigwedge }{R}_j\circ f_j^2(x,x)=\mathbf{1}\mathrm{and}{\lambda }_{X,P}(x,x)=\underset{j\in J}{\bigwedge }{\lambda }_j\circ f_j^2(x,x)=1.$$

Thus, ${\mathcal{R}}_{X,P}(x,x)=<\mathbf{1},1>$. So ${\mathcal{R}}_{X,P}$ is reflexive.

Now let $f_j:(X,{\mathcal{R}}_{X,R})\to (X_j,{\mathcal{R}}_j){)}_{j\in J}$ be an initial source in ${\mathbf{CRel}}_R(H)$ such that each $(X_j,{\mathcal{R}}_j)$ belongs to ${\mathbf{CRel}}_{R,R}(H)$. Then clearly, for each $x\in X$,

$$R_{X,R}(x,x)=R_{X,P}(x,x)=\mathbf{1}\mathrm{and}{\lambda }_{X,R}(x,x)=\underset{j\in J}{\bigvee }{\lambda }_j\circ f_j^2(x,x)=1.$$

Thus, ${\mathcal{R}}_{X,R}(x,x)=<\mathbf{1},1>$. So ${\mathcal{R}}_{X,R}$ is reflexive. This completes the proof. □

From Results 1, 2 and Lemma 5, we have the followings.

Proposition 3.

(1) The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is a bireflective subcategory of ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$].

(2) The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is topological over $\mathbf{Set}$.

It is well-known that a category $\mathbf{A}$ is topological if and only if it is cotopological. Then by (2) of the above Proposition, the category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is cotopological over $\mathbf{Set}$. However, we will prove that ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is cotopological over $\mathbf{Set}$, directly.

Lemma 6.

the category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] has final structure over $\mathbf{Set}$.

Proof. 

Let X be a nonempty set and let $((X_j,{\mathcal{R}}_j))=({(X_j,<R_j,{\lambda }_j>)}_{j\in J}$ be any family of cubic H-relational spaces indexed by a class J. We define two mappings $R_{X,P}:X\to [H]$ and ${\lambda }^{X,P}:X\to H$, respectively as below: for each $(x,y)\in X\times X$,

$$R_{X,P}(x,y)=\{\begin{array}{ll}{\bigvee }_{j\in J}{\bigvee }_{(x_j,y_j)\in f_j^{-2}(x,y)}{R}_j(x_j,y_j)\hfill & \mathrm{if}(x,y)\in (X\times X-{△}_X)\\ \mathbf{1}\hfill & \mathrm{if}(x,y)\in {△}_X\hfill \end{array}$$

and

$${\lambda }_{X,P}(x,y)=\left\{\begin{array}{ll}{\bigvee }_{j\in J}{\bigvee }_{(x_j,y_j)\in f_j^{-2}(x,y)}{\lambda }_j(x_j,y_j)\hfill & \hfill \mathrm{if}(x,y)\in (X\times X-{△}_X)\\ 1\hfill & \mathrm{if}(x,y)\in {△}_X,\hfill \end{array}\right.$$

where ${△}_X=\{(x,x):x\in X\}$. Then clearly, ${\mathcal{R}}_{X,P}$ is the cubic H-reflexive relation in X given by: for each $(x,y)\in X\times X$,

$${\mathcal{R}}_{X,P}(x,y)=\left\{\begin{array}{ll}{\bigsqcup }_{j\in J}{\bigsqcup }_{(x_j,y_j)\in f_j^{-2}(x,y)}{\mathcal{R}}_j(x_j,y_j)\hfill & if(x,y)\in (X\times X-{△}_X)\\ <\mathbf{1},1>\hfill & \mathrm{if}(x,y)\in {△}_X.\end{array}\right.$$

Moreover, we can easily check that $(X,{\mathcal{R}}_{X,P})=(X,<R_{X,P},{\lambda }_{X,P}>)$ is a final structure in ${\mathbf{CRel}}_{P,R}(H)$. Thus, ${(f_j:(X_j,{\mathcal{R}}_j)\to (X,{\mathcal{R}}_{X,P}))}_{j\in J}$ is a final sink in ${\mathbf{CRel}}_{P,R}(H)$.

Now we define two mappings $R_{X,R}:X\to [H]$ and ${\lambda }^{X,R}:X\to H$, respectively as follows: for each $(x,y)\in X\times X$,

$$R_{X,R}(x,y)=R_{X,P}(x,y)$$

and

$${\lambda }_{X,R}(x,y)=\left\{\begin{array}{ll}\underset{j\in J}{\bigwedge }\underset{(x_j,y_j)\in f_j^{-2}(x,y)}{\bigwedge }{\lambda }_j(x_j,y_j)\hfill & \mathrm{if}(x,y)\in (X\times X-{△}_X)\\ 1\hfill & \mathrm{if}(x,y)\in {△}_X.\end{array}\right.$$

Then clearly, ${\mathcal{R}}_{X,R}$ is the cubic H-reflexive relation in X given by: for each $(x,y)\in X\times X$,

$${\mathcal{R}}_{X,R}(x,y)=\left\{\begin{array}{ll}{⋓}_{j\in J}{⋓}_{(x_j,y_j)\in f_j^{-2}(x,y)}{\mathcal{R}}_j(x_j,y_j)\hfill & \mathrm{if}(x,y)\in (X\times X-{△}_X)\\ <\mathbf{1},1>\hfill & \mathrm{if}(x,y)\in {△}_X.\end{array}\right.$$

Moreover, we can easily show that ${(f_j:(X_j,{\mathcal{R}}_j)\to (X,{\mathcal{R}}_{X,R}))}_{j\in J}$ is a final sink in ${\mathbf{CRel}}_{R,R}(H)$. □

Lemma 7.

Final episinks in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] are preserved by pullbacks.

Proof. 

Let ${(g_j:(X_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_{Y,P}))}_{j\in J}$ be any final episink in ${\mathbf{CRel}}_{P,R}(H)$ and let $f:(W,{\mathcal{R}}_W)\to (Y,{\mathcal{R}}_{Y,P})$ be any ${\mathbf{CRel}}_P(H)$-mapping, where $(W,{\mathcal{R}}_W)$ is a cubic H-reflexive relational space. For each $j\in J$, let us take $U_j$, ${\mathcal{R}}_{U_j,P}$, $e_j$ and $p_j$ as in the first proof of Lemma 3. Then we can easily check that ${\mathbf{CRel}}_{P,R}(H)$ is closed under the formation of pullbacks in ${\mathbf{CRel}}_P(H)$. Thus, it is enough to prove that ${(e_j)}_{j\in J}$ is final.

Suppose ${\mathcal{R}}_W^{*}$ is the final cubic H-relation in W regarding ${(e_j)}_{j\in J}$ and let $(w,w^{{}^{\prime }})\in (W\times W-{△}_X)$. Then

${\mathcal{R}}_W(w,w^{{}^{\prime }})=<R_W(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})>$

$=<R_W(w,w^{{}^{\prime }})\wedge R_W(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_W(w,w^{{}^{\prime }})>$

${\le }_P<R_W(w,w^{{}^{\prime }})\wedge R_Y\circ f^2(w,w^{{}^{\prime }}),{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_Y\circ f^2(w,w^{{}^{\prime }})>$

$[\mathrm{Since}$$f:(W,{\mathcal{R}}_W)\to (Y,{\mathcal{R}}_Y)$ is a ${\mathbf{CRel}}_P(H)$-mapping]

$=<R_W(w,w^{{}^{\prime }})\wedge [{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}{R}_j(x_j,x_j^{{}^{\prime }})],$

${\lambda }_W(w,w^{{}^{\prime }})\wedge [{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}{\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$[\mathrm{Since}$${(g_j:(R_j,{\mathcal{R}}_j)\to (Y,{\mathcal{R}}_Y))}_{j\in J}$ is a final episink in ${\mathbf{CRel}}_P(H)$]

$=<{\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}[R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }})]],$

${\bigvee }_{j\in J}{\bigvee }_{(x_j,x_j^{{}^{\prime }})\in g_j^{-2}(f(w),f(w^{{}^{\prime }}))}[{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$=<{\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[R_W(w,w^{{}^{\prime }})\wedge R_j(x_j,x_j^{{}^{\prime }})]],$

${\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[{\lambda }_W(w,w^{{}^{\prime }})\wedge {\lambda }_j(x_j,x_j^{{}^{\prime }})]>$

$=<{\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[R_{U_j,P}((w,x_j,(w^{{}^{\prime }},x_j^{{}^{\prime }})],$

${\bigvee }_{j\in J}{\bigvee }_{((w,x_j),(w^{{}^{\prime }},x_j^{{}^{\prime }}))\in e_j^{-2}(w,w^{{}^{\prime }})}[{\lambda }_{U_j,P}((w,x_j,(w^{{}^{\prime }},x_j^{{}^{\prime }})]>$

$={\mathcal{R}}_W^{*}(w,w^{{}^{\prime }})$.

Thus, ${\mathcal{R}}_W⊏{\mathcal{R}}_W^{*}$. On the other hand, by a similar argument in the first proof of Lemma 3, ${\mathcal{R}}_W^{*}⊏{\mathcal{R}}_W$ on $W\times W-{△}_W$. So ${\mathcal{R}}_W^{*}={\mathcal{R}}_W$ on $W\times W-{△}_W$. Now let $(w,w)\in {△}_W$. Then clearly, ${\mathcal{R}}_W^{*}(w,w)=<\mathbf{1},1>={\mathcal{R}}_W(w,w)$. Thus, ${\mathcal{R}}_W^{*}={\mathcal{R}}_W$ on ${△}_W$. Hence ${\mathcal{R}}_W^{*}={\mathcal{R}}_W$ on W.

Now for each $j\in J$, let us ${\mathcal{R}}_{U_j,R}=<R_{U_j,R},{\lambda }_{U_j,R}>:U_j\to [H]\times H$ be the mapping as in the second proof of Lemma 3. Then we can similarly prove that final episinks in ${\mathbf{Rel}}_{R,R}(H)$ are preserved by pullbacks. This completes the proof. □

The following is the immediate result of Lemma 4, Proposition 3 (2) and Lemma 7.

Theorem 3.

The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is a topological universe over $\mathbf{Set}$. In particular, ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is Cartesian closed over $\mathbf{Set}$ (See [1]) and a concrete quasitopos(See [40]).

In [41], Noh obtained exponential objects in $\mathbf{Rel}(I)$, where $\mathbf{Rel}(I)$ denotes the category of fuzzy relations. By applying his construction of an exponential object in $\mathbf{Rel}(I)$ to the category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$], we have the following.

Proposition 4.

The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] has an exponential object.

Proof. 

For any $\mathbf{X}=(X,{\mathcal{R}}_X)=(X,<R_X,{\lambda }_X>,\mathbf{Y}=(Y,{\mathcal{R}}_Y)=(X,<R_Y,{\lambda }_Y>)\in \mathrm{Ob}({\mathbf{CRel}}_{P,R}(H))$ and let $Y^X=\mathrm{hom}(\mathbf{X},\mathbf{Y})$. For any $(f,g)\in Y^X\times Y^X$, let

$$D(f,g)=\{(x,y)\in X\times X:R_X(x,y)>R_Y(f(x),g(y)),{\lambda }_X(x,y)>{\lambda }_Y(f(x),g(y))\}.$$

We define a mapping ${\mathcal{R}}_{Y^X,P}=<R_{Y^X,P},{\lambda }_{Y^X,P}>:Y^X\times Y^X\to [H]\times H$ as follows: for each $(f,g)\in Y^X\times Y^X$,

$\begin{array}{ll}& {\mathcal{R}}_{Y^X,P}(f,g)\\ =& \left\{\begin{array}{c}<{\bigwedge }_{(x,y)\in D(f,g)}{R}_Y(f(x),f(y)),{\bigwedge }_{(x,y)\in D(f,g)}{\lambda }_Y(f(x),f(y))>\mathrm{if}D(f,g)\ne \varphi \hfill \\ <\mathbf{1},1>\mathrm{if}D(f,g)=\varphi .\hfill \end{array}\right.\end{array}$

Then by the definition of $D(f,g)$, $D(f,f)=\varphi$, for each $f\in Y^X$. Thus, ${\mathcal{R}}_{Y^X,P}(f,f)=<\mathbf{1},1>$, for each $f\in Y^X$. So ${\mathcal{R}}_{Y^X,P}$ is a cubic H-reflexive relation in $Y^X$.

Let ${\mathbf{Y}}^{\mathbf{X}}=(Y^X,{\mathcal{R}}_{Y^X,P})$ and we define the mapping $e_{X,Y}:\mathbf{X}{\times }_P{\mathbf{Y}}^{\mathbf{X}}\to \mathbf{Y}$ as follows: for each $(a,f)\in X\times Y^X$,

$$e_{X,Y}(a,f)=f(a).$$

Let $(a,f),(b,g)\in X\times Y^X$.

Case 1: Suppose $D(f,g)=\varphi$. Then

$({\mathcal{R}}_X{\times }_P{\mathcal{R}}_{Y^X,P})((a,f),(b,g))$

$=<R_X(a,b)\wedge R_{Y^X,P}(f,g),{\lambda }_X(a,b)\wedge {\lambda }_{Y^X,P}(f,g)>$

$=<R_X(a,b),{\lambda }_X(a,b)>$

$[\mathrm{By}$ the definition of $R_{Y^X,P}$, $R_{Y^X,P}(f,g)=\mathbf{1}$, ${\lambda }_{Y^X,P}(f,g)=1$]

${\le }_P<R_Y(f(x),g(y)),{\lambda }_Y(f(x),g(y))>$ [Since $D(f,g)=\varphi$]

$=<R_Y\circ e_{X,Y}^2((a,f),(b,g))$.

Case 2: Suppose $D(f,g)\ne \varphi$. Then

$({\mathcal{R}}_X{\times }_P{\mathcal{R}}_{Y^X,P})((a,f),(b,g))$

$=<R_X(a,b)\wedge [{\bigwedge }_{(x,y)\in D(f,g)}{R}_Y(f(x),f(y))],$

${\lambda }_X(a,b)\wedge [{\bigwedge }_{(x,y)\in D(f,g)}{\lambda }_Y(f(x),f(y))]>$

${\le }_P<R_Y(f(x),g(y)),{\lambda }_Y(f(x),g(y))>$

$=<R_Y\circ e_{X,Y}^2((a,f),(b,g))$.

Thus, in either case, ${\mathcal{R}}_X\times {\mathcal{R}}_{Y^X,P}⊏R_Y\circ e_{X,Y}^2$. So $e_{X,Y}$ is a ${\mathbf{CRel}}_P(H)$-mapping.

Let $\mathbf{Z}=(Z,{\mathcal{R}}_Z)=(Z,<R_Z,{\lambda }_Z>)$ be any cubic H-reflexive relational space and let $h:\mathbf{X}\times \mathbf{Z}\to \mathbf{Y}$ be any ${\mathbf{CRel}}_P(H)$-mapping. We define the mapping $\overline{h}:Z\to Y^X$ as follows: for each $c\in Z$ and each $a\in X$,

$$[\overline{h}(c)](a)=h(a,c).$$

Let $c\in Z$ and let $a,b\in X$. Then

${\mathcal{R}}_Y\circ {[\overline{h}(c)]}^2(a,b)$

$={\mathcal{R}}_Y([\overline{h}(c)](a),[\overline{h}(c)](b))$

$=<R_Y([\overline{h}(c)](a),[\overline{h}(c)](b)),{\lambda }_Y([\overline{h}(c)](a),[\overline{h}(c)](b))>$

$=<R_Y(h(a,c),h(b,c)),{\lambda }_Y(h(a,c),h(b,c))>$

$=<R_Y\circ h^2(h(a,c),h(b,c)),{\lambda }_Y\circ h^2(h(a,c),h(b,c))>$

$={\mathcal{R}}_Y\circ h^2((a,c),(b,c))$

${\ge }_P({\mathcal{R}}_X{\times }_P{\mathcal{R}}_Z)((a,c),(b,c))$

$=<(R_X{\times }_P{R}_Z)((a,c),(b,c)),({\lambda }_{X}time{s}_P{\lambda }_Z)((a,c),(b,c))>$

$=<R_X(a,b)\wedge R_Z(c,c),{\lambda }_X(a,b)\wedge {\lambda }_Z(c,c)>$

$=<R_X(a,b),{\lambda }_X(a,b)>$ [Since ${\mathcal{R}}_Z$ is reflexive]

$={\mathcal{R}}_X(a,b)$.

Thus, ${\mathcal{R}}_X⊏{\mathcal{R}}_Y\circ {[\overline{h}(c)]}^2$. So $\overline{h}(c):\mathbf{X}\to \mathbf{Y}$ is a ${\mathbf{CRel}}_P(H)$-mapping. Hence $\overline{h}$ is well-defined. Let $c,c^{{}^{\prime }}\in Z$.

Case 1: Suppose $D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))=\varphi$. Then

${\mathcal{R}}_{Y^X,P}\circ {\overline{h}}^2(c,c^{{}^{\prime }})={\mathcal{R}}_{Y^X,P}(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))$

$=<\mathbf{1},1>$ [By the definition of ${\mathcal{R}}_{Y^X,P}$]

${\ge }_P{\mathcal{R}}_Z(c,c^{{}^{\prime }})$.

Case 2: Suppose $D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))\ne \varphi$. Then

${\mathcal{R}}_{Y^X,P}(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))=<R_{Y^X,P}(\overline{h}(c),\overline{h}(c^{{}^{\prime }})),{\lambda }_{Y^X,P}(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))>$

$=<{\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}{R}_Y([\overline{h}(c)](a),[\overline{h}(c^{{}^{\prime }})](b)),$

${\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}{\lambda }_Y([\overline{h}(c)](a),[\overline{h}(c^{{}^{\prime }})](b))>$

$=<{\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}{R}_Y(h(a,c),h(b,c^{{}^{\prime }})),$

${\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}{\lambda }_Y(h(a,c),h(b,c^{{}^{\prime }}))>$

${\ge }_P<{\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}[R_X(a,b)\wedge R_Z(c,c^{{}^{\prime }})],$

${\bigwedge }_{(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))}[{\lambda }_X(a,b)\wedge {\lambda }_Z(c,c^{{}^{\prime }})]>$.

On one hand, for any $(a,b)\in D(\overline{h}(c),\overline{h}(c^{{}^{\prime }}))$,

$R_X(a,b)>R_Y([\overline{h}(c)](a),[\overline{h}(c^{{}^{\prime }})](b))$

$=R_Y(h(a,c),h(b,c^{{}^{\prime }}))$

$\ge R_X(a,b)\wedge R_Z(c,c^{{}^{\prime }})$.

Thus, $R_X(a,b)>R_Z(c,c^{{}^{\prime }})$. Similarly, we have ${\lambda }_X(a,b)>{\lambda }_Z(c,c^{{}^{\prime }})$. So

$${\mathcal{R}}_{Y^X,P}(\overline{h}(c),\overline{h}(c^{{}^{\prime }})){\ge }_P{\mathcal{R}}_Z(c,c^{{}^{\prime }}).$$

Hence in either cases, ${\mathcal{R}}_Z⊏{\mathcal{R}}_{Y^X,P}\circ {\overline{h}}^2$. Therefore $\overline{h}$ is a ${\mathbf{CRel}}_P(H)$-mapping. Furthermore, $\overline{h}$ is unique and $e_{X,Y}\circ (1_X\times \overline{h})=h$.

Now for any $\mathbf{X}=(X,{\mathcal{R}}_X)=(X,<R_X,{\lambda }_X>,\mathbf{Y}=(Y,{\mathcal{R}}_Y)=(X,<R_Y,{\lambda }_Y>)\in \mathrm{Ob}({\mathbf{CRel}}_{R,R}(H))$ and let $Y^X=\mathrm{hom}(\mathbf{X},\mathbf{Y})$. For any $(f,g)\in Y^X\times Y^X$, let

$$D^{{}^{\prime }}(f,g)=\{(x,y)\in X\times X:R_X(x,y)>R_Y(f(x),g(y)),{\lambda }_X(x,y)<{\lambda }_Y(f(x),g(y))\}.$$

We define a mapping ${\mathcal{R}}_{Y^X,R}=<R_{Y^X,R},{\lambda }_{Y^X,R}>:Y^X\times Y^X\to [H]\times H$ as follows: for each $(f,g)\in Y^X\times Y^X$,

$\begin{array}{l}{\mathcal{R}}_{Y^X,R}(f,g)\end{array}$

$=\left\{\begin{array}{c}<{\bigwedge }_{(x,y)\in D^{{}^{\prime }}(f,g)}{R}_Y(f(x),f(y)),{\bigvee }_{(x,y)\in D^{{}^{\prime }}(f,g)}{\lambda }_Y(f(x),f(y))>\mathrm{if}{D}^{{}^{\prime }}(f,g)\ne \varphi \hfill \\ <\mathbf{1},1>\mathrm{if}{D}^{{}^{\prime }}(f,g)=\varphi .\hfill \end{array}\right.$

Then we can easily check that ${\mathcal{R}}_{Y^X,R}$ is a cubic H-reflexive relation in $Y^X$. Moreover, by the similar argument of the above proof, we can show that ${\mathcal{R}}_{Y^X,R}$ is an exponential object in $Y^X$. This completes the proof. □

Remark 2.

(1) We can see that exponential objects in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] is quite different from those in ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] constructed in Theorem 1.

(2) The category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] has no subject classifier.

Example 4.

Let $H=\{0,1\}$ be the two points chain and let $X=\{a,b\}$. Let ${\mathcal{R}}_{1,P}=<R_{1,P},{\lambda }_{1,P}>$ and ${\mathcal{R}}_{2,P}=<R_{2,P},{\lambda }_{2,P}>$ be cubic H-reflexive relations in X given by:

$${\mathcal{R}}_{1,P}(a,a)={\mathcal{R}}_{1,P}(b,b)=<\mathbf{1},1>,{\mathcal{R}}_{1,P}(a,b)={\mathcal{R}}_{1,P}(b,a)=<\mathbf{0},0>$$

and

$${\mathcal{R}}_{2,P}(a,a)={\mathcal{R}}_{2,P}(b,b)=<\mathbf{1},1>,{\mathcal{R}}_{2,P}(a,b)={\mathcal{R}}_{2,P}(b,a)=<\mathbf{1},1>.$$

Let $1_X:(X,{\mathcal{R}}_{1,P})\to (X,{\mathcal{R}}_{2,P})$ be the identity mapping. Then clearly, $1_X$ is both monomorphism and epimorphism in ${\mathbf{CRel}}_P(H)$. However, $1_X$ is not an isomorphism in ${\mathbf{CRel}}_P(H)$.

5. Conclusions

We constructed the concrete category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] of cubic H-relational spaces and P-preserving [resp. R-preserving] mappings between them and studied it in the sense of a topological universe. In particular, we proved that it is Cartesian closed over $\mathbf{Set}$. Next, We introduced the category ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] of cubic H-reflexive relational spaces and P-preserving [resp. R-preserving] mappings between them and investigated it in a viewpoint of a topological universe. In particular, we obtained exponential objects in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$] quite different from those in ${\mathbf{CRel}}_{P,R}(H)$ [resp. ${\mathbf{CRel}}_{R,R}(H)$]. Also we proved that ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] is a topological universe but ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$] not a topological universe. In the future, we will expect one to study some full subcategories of the category ${\mathbf{CRel}}_P(H)$ [resp. ${\mathbf{CRel}}_R(H)$].