Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge
Abstract
1. Introduction
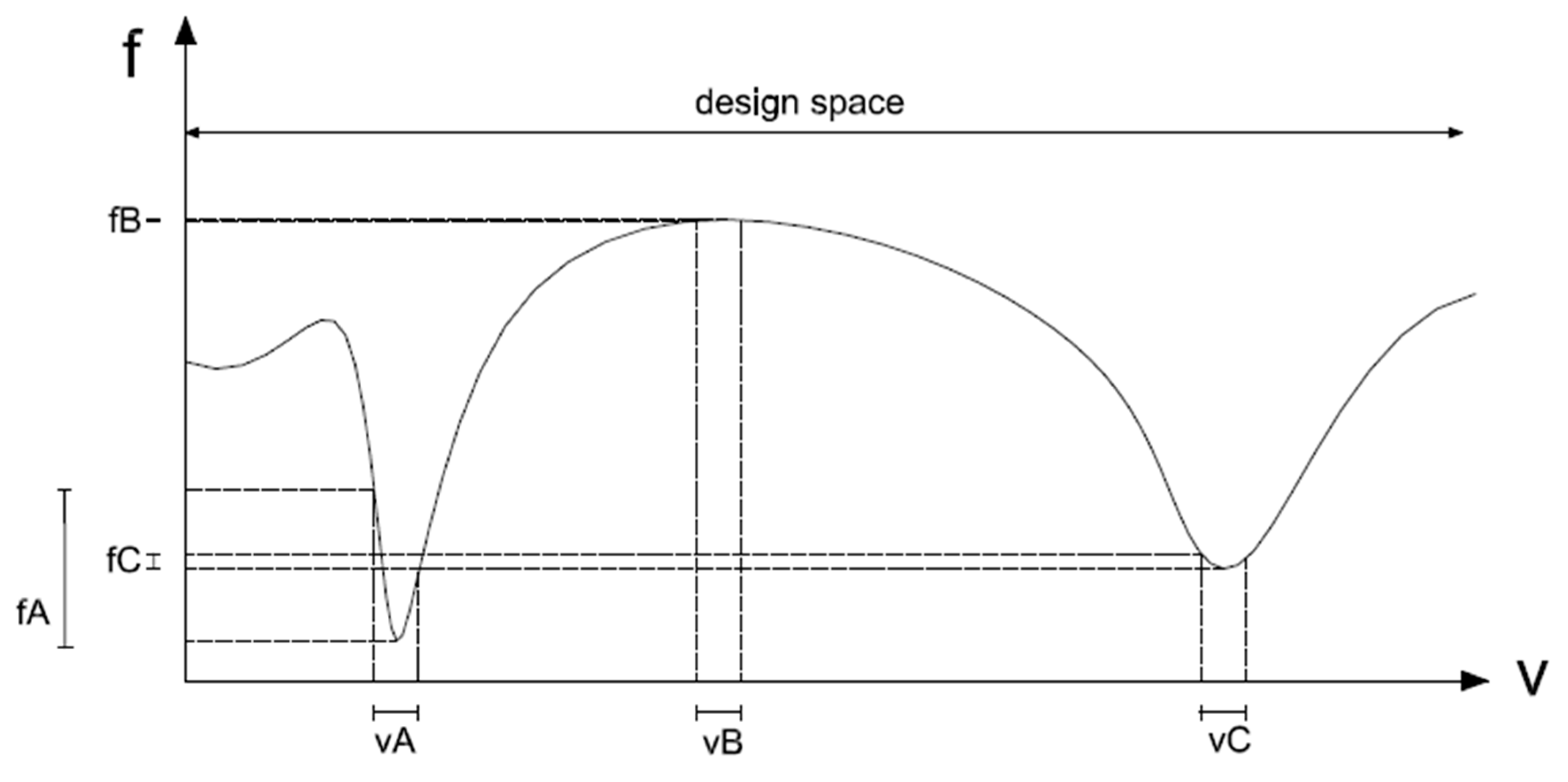
2. Robust Design Optimization
3. Robust Design Optimization Using Metamodels
3.1. Latin Hypercube Sampling
3.2. Kriging
3.3. The Fitted Model
3.4. Mean and Variance
3.5. Optimization
4. Problem Design
4.1. Description of the Box-Girder Footbridge
4.2. Description of the Robust Design Optimization Problem
5. Results
5.1. Variation of Modulus of Elasticity
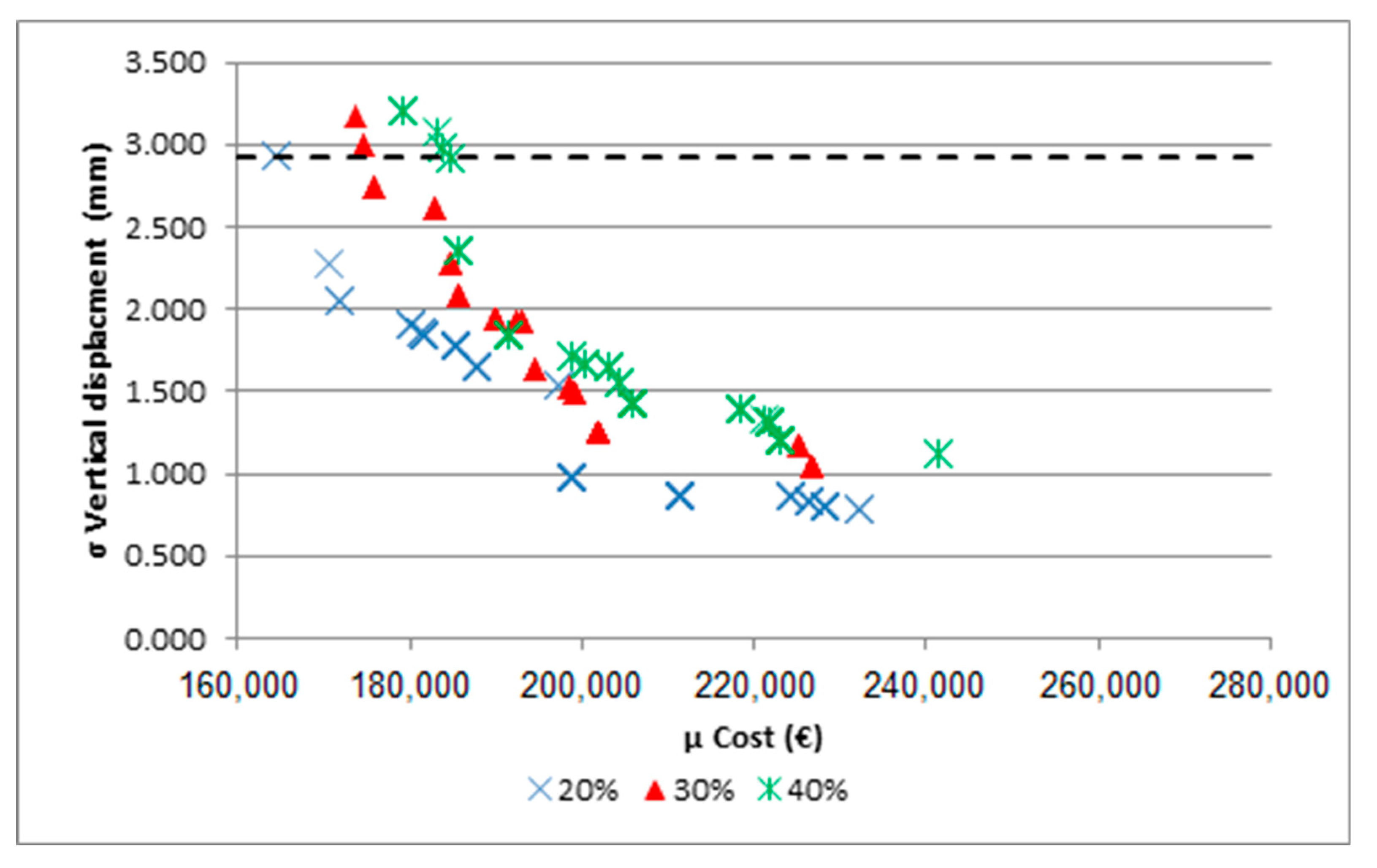
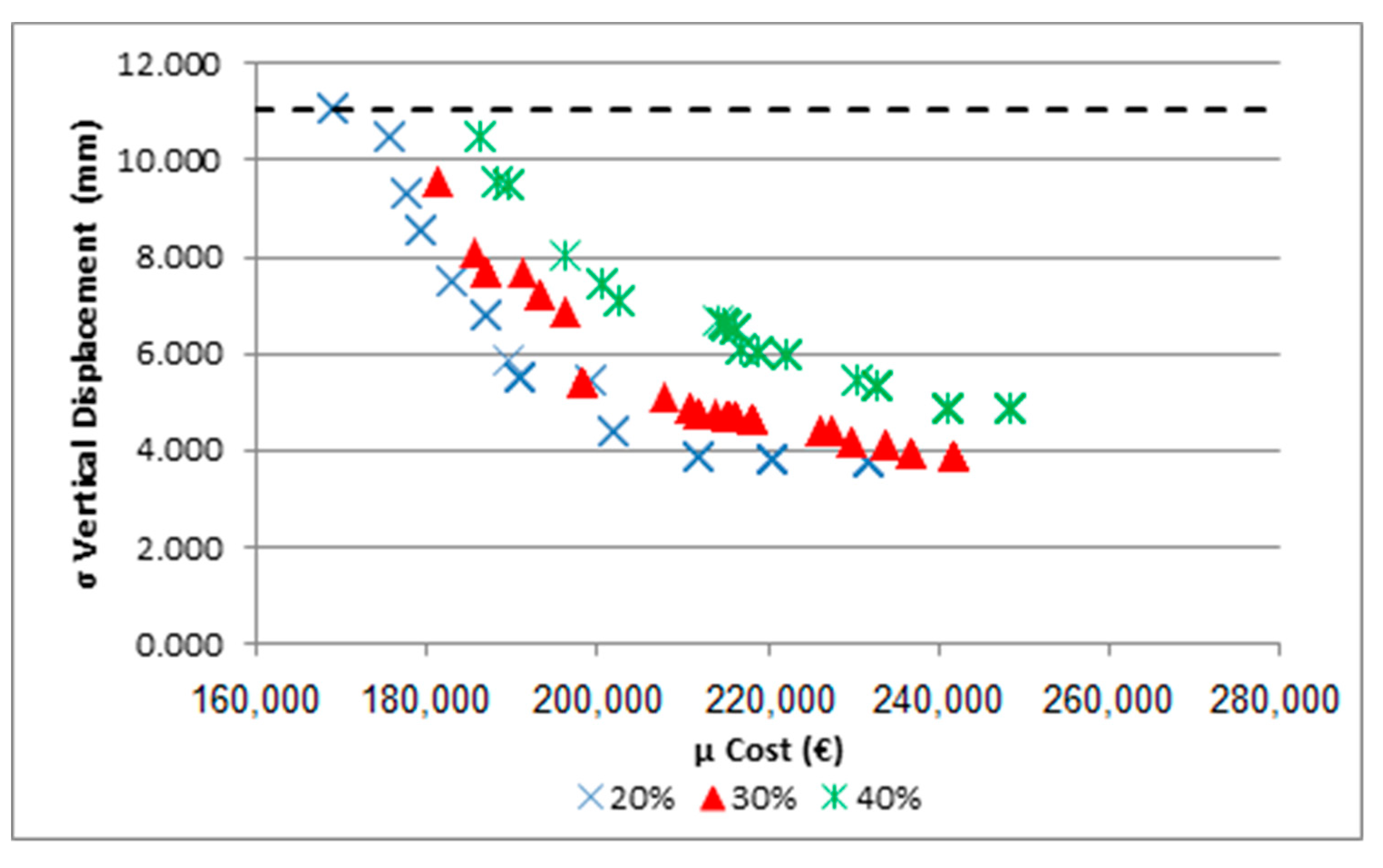
5.2. Variation of Loads: Overload and Prestressing Force
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taguchi, G. Introduction to Quality Engineering; Asian Productivity Organisation: Tokyo, Japan, 1986. [Google Scholar]
- Phadke, M.S.; Shridhar, M. Quality Engineering Using Robust Design; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Fowlkes, W.Y.; Creveling, C.M. Engineering Method for Robust Product Design; Addison-Wesley Publishing Company: Boston, MA, USA, 1995. [Google Scholar]
- Lee, K.-H.; Kang, D.-H. A robust optimization using the statistics based on kriging metamodel. J. Mech. Sci. Technol. 2006, 20, 1169–1182. [Google Scholar] [CrossRef]
- Carbonell, A.; González-Vidosa, F.; Yepes, V. Design of reinforced concrete road vaults by heuristic optimization. Adv. Eng. Softw. 2011, 42, 151–159. [Google Scholar] [CrossRef]
- Ahsan, R.; Rana, S.; Nurul Ghani, S. Cost optimum design of posttensioned I-girder bridge using global optimization algorithm. J. Struct. Eng. 2012, 138, 272–283. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Martí, J.V.; Alcalá, J. Optimization of concrete I-beams using a new hybrid glowworm swarm algorithm. Lat. Am. J. Solids Struct. 2014, 11, 1190–1205. [Google Scholar] [CrossRef]
- Pnevmatikos, N.G.; Thomos, G.T. Stochastic structural control under earthquake excitations. Struct. Control Health Monit. 2014, 21, 620–633. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V. Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- Martí, J.V.; García-Segura, T.; Yepes, V. Structural design of precast-prestressed concrete U-beam road bridges based on embodied energy. J. Clean. Prod. 2016, 120, 231–240. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T.; González-Vidosa, F. Heuristics in optimal detailed design of precast road bridges. Arch. Civ. Mech. Eng. 2017, 17, 738–749. [Google Scholar] [CrossRef]
- Sun, X.; Fu, H.; Zeng, J. Robust approximate optimality conditions for uncertain nonsmooth optimization with Infinite number of constraints. Mathematics 2018, 7, 12. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalez, P.T.; Rico-Ramirez, V.; Rico-Martinez, R.; Diwekar, U.M. A new approach to solving stochastic optimal control problems. Mathematics 2019, 7, 1207. [Google Scholar] [CrossRef]
- Moayyeri, N.; Gharehbaghi, S.; Plevris, V. Cost-based optimum design of reinforced concrete retaining walls considering different methods of bearing capacity computation. Mathematics 2019, 7, 1232. [Google Scholar] [CrossRef]
- Sierra, L.A.; Yepes, V.; García-Segura, T.; Pellicer, E. Bayesian network method for decision-making about the social sustainability of infrastructure projects. J. Clean. Prod. 2014, 176, 521–534. [Google Scholar] [CrossRef]
- Valdebenito, M.A.; Schuëller, G.I. A survey on approaches for reliability-based optimization. Struct. Multidiscip. Optim. 2010, 42, 645–663. [Google Scholar] [CrossRef]
- Doltsinis, I.; Kang, Z. Robust design of structures using optimization methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 2221–2237. [Google Scholar] [CrossRef]
- Simpson, T.W.; Booker, A.J.; Ghosh, D.; Giunta, A.A.; Koch, P.N.; Yang, R.-J. Approximation methods in multidisciplinary analysis and optimization: A panel discussion. Struct. Multidiscip. Optim. 2004, 27, 302–313. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Martí, P. Diseño óptimo robusto utilizando modelos Kriging: Aplicación al diseño óptimo robusto de estructuras articuladas. Rev. Int. Métodos Numéricos para Cálculo y Diseño Ing. 2014, 30, 97–105. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Martí-Vargas, J.R.; Ferri, F.J.; Yepes, V. Prediction of the transfer length of prestressing strands with neural networks. Comput. Concr. 2013, 12, 187–209. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueno, R. Emerging artificial intelligence methods in structural engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Jin, R.; Du, X.; Chen, W. The use of metamodeling techniques for optimization under uncertainty. Struct. Multidiscip. Optim. 2003, 25, 99–116. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Barton, R.R.; Meckesheimer, M. Metamodel-based simulation optimization. Handb. Oper. Res. Manag. Sci. 2006, 13, 535–574. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Chuang, C.H.; Yang, R.J.; Li, G.; Mallela, K.; Pothuraju, P. Multidisciplinary design optimization on vehicle tailor rolled blank design. Struct. Multidiscip. Optim. 2008, 35, 551–560. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Simpson, T.W.; Mauery, T.M.; Korte, J.; Mistree, F. Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Camp, C.V.; Huq, F. CO2 and cost optimization of reinforced concrete frames using a big bang-big crunch algorithm. Eng. Struct. 2013, 48, 363–372. [Google Scholar] [CrossRef]
- Martí, J.V.; González-Vidosa, F.; Yepes, V.; Alcalá, J. Design of prestressed concrete precast road bridges with hybrid simulated annealing. Eng. Struct. 2013, 48, 342–352. [Google Scholar] [CrossRef]
- Medina, J.R. Estimation of incident and reflected waves using simulated annealing. J. Watery Port Coast. Ocean Eng 2001, 127, 213–221. [Google Scholar] [CrossRef]
- Schlaich, J.; Scheef, H. Concrete Box-Girder Bridges; International Association for Bridge and Structural Engineering: Zürich, Switzerland, 1982. [Google Scholar]
- Ministerio de Fomento. EHE-08: Code on Structural Concrete; Ministerio de Fomento: Madrid, Spain, 2008. [Google Scholar]
- Ministerio de Fomento. IAP-11: Code on the Actions for the Design of Road Bridges; Ministerio de Fomento: Madrid, Spain, 2011.
- European Committee for Standardization. EN 1001-2: Eurocode 1: Actions on Structures-Part 2: Traffic Loads Bridges; European Committee for Standardization: Brussels, Belgium, 2003.
- European Committee for Standardisation. EN1992-2: Eurocode 2: Design of Concrete Structures-Part 2: Concrete Bridge-Design and Detailing Rules; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Catalonia Institute of Construction Technology. BEDEC PR/PCT ITEC Material Database; Catalonia Institute of Construction Technology: Barcelona, Spain, 2016. [Google Scholar]

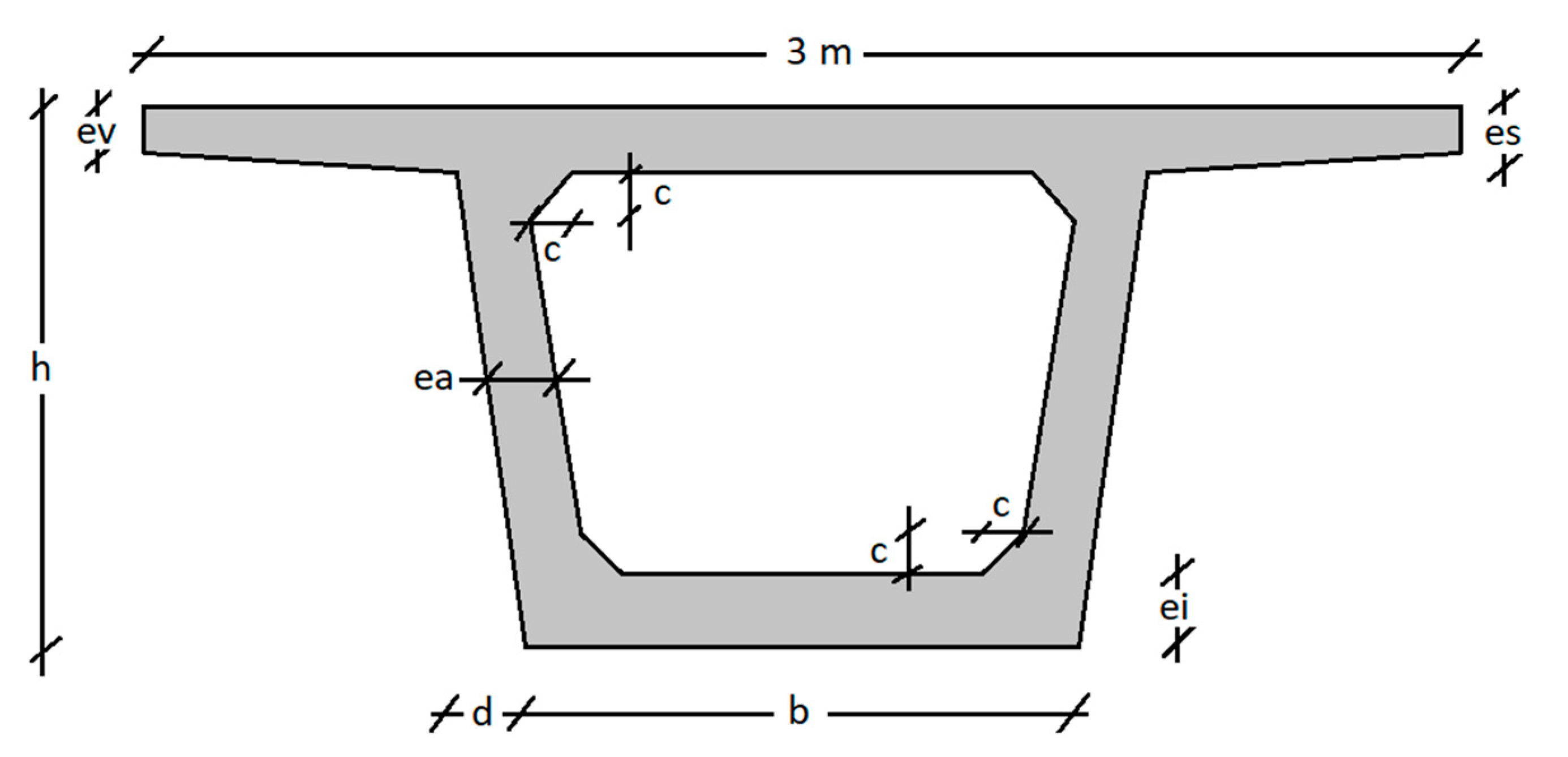

| Design Variable | Min. Value (m) | Max. Value (m) | Precision (m) |
|---|---|---|---|
| Depth (h) | 1.25 | 2.5 | 0.05 |
| Width (b) | 1.2 | 1.8 | 0.05 |
| Inclination width (d) | 0 | 0.4 | 0.05 |
| Top slab thickness (es) | 0.15 | 0.4 | 0.05 |
| External cantilever section thickness (ev) | 0.15 | 0.4 | 0.05 |
| Bottom slab thickness (ei) | 0.15 | 0.4 | 0.05 |
| Webs slab thickness (ea) | 0.3 | 0.6 | 0.05 |
| Unit Measurements | Cost (€) |
|---|---|
| m3 of scaffolding | 10.2 |
| m2 of formwork | 33.81 |
| m3 of lighting | 104.57 |
| kg of steel (B-500-S) | 1.16 |
| kg of post-tensioned steel (Y1860-S7) | 3.40 |
| m3 of concrete HP-35 | 104.57 |
| m3 of concrete HP-40 | 109.33 |
| m3 of concrete HP-45 | 114.10 |
| m3 of concrete HP-50 | 118.87 |
| m3 of concrete HP-55 | 123.64 |
| m3 of concrete HP-60 | 128.41 |
| m3 of concrete HP-70 | 137.95 |
| m3 of concrete HP-80 | 147.49 |
| m3 of concrete HP-90 | 157.02 |
| m3 of concrete HP-100 | 166.56 |
| Uncertainty of E (%) | 10 | 20 | 30 |
|---|---|---|---|
| μ Cost discrepancy | 1.21% | 1.28% | 1.07% |
| σ Displacement discrepancy | 4.63% | 4.75% | 4.03% |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S10 | 1200 | 1450 | 0 | 150 | 150 | 350 | 225 | 45 | 225 | 167,370.9 | 3.811 |
| S20 | 1200 | 1800 | 125 | 150 | 150 | 350 | 250 | 60 | 250 | 192,570.6 | 3.778 |
| S30 | 1200 | 1950 | 0 | 150 | 150 | 350 | 225 | 80 | 225 | 208,111.9 | 3.548 |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1200 | 1800 | 125 | 150 | 150 | 350 | 250 | 60 | 250 | 192,570.6 | 3.778 |
| B | 1200 | 1900 | 50 | 150 | 150 | 350 | 150 | 80 | 150 | 201,479.9 | 2.794 |
| C | 1800 | 2000 | 200 | 150 | 150 | 350 | 175 | 100 | 220 | 269,128.5 | 1.684 |
| Uncertainty of Overload (%) | 10 | 20 | 30 | 40 |
|---|---|---|---|---|
| μ Cost discrepancy | 1.32% | 1.19% | 1.17% | 1.28% |
| σ Displacement discrepancy | 38.61% | 15.78% | 11.53% | 15.18% |
| Uncertainty of P0 (%) | 10 | 20 | 30 | 40 |
|---|---|---|---|---|
| μ Cost discrepancy | 1.34% | 1.09% | 1.06% | 1.21% |
| σ Displacement discrepancy | 13.5% | 7.16% | 3.47% | 4% |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S20 | 1200 | 1250 | 0 | 150 | 150 | 350 | 200 | 60 | 200 | 164,594.2 | 2.924 |
| S30 | 1200 | 1250 | 200 | 150 | 150 | 350 | 175 | 70 | 175 | 174,467.1 | 2.991 |
| S40 | 1200 | 1700 | 25 | 175 | 175 | 350 | 250 | 50 | 250 | 184,821.6 | 2.917 |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1200 | 1350 | 100 | 150 | 150 | 350 | 175 | 80 | 175 | 180,240.5 | 1.913 |
| B | 1200 | 1850 | 200 | 175 | 175 | 350 | 225 | 60 | 225 | 198,687.3 | 0.971 |
| C | 1600 | 1800 | 150 | 275 | 275 | 350 | 225 | 70 | 225 | 238,573.8 | 0.753 |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S20 | 1200 | 1350 | 0 | 150 | 150 | 350 | 200 | 60 | 200 | 168,833.9 | 11.058 |
| S30 | 1200 | 1400 | 200 | 150 | 150 | 350 | 150 | 80 | 150 | 181,276.4 | 9.552 |
| S40 | 1200 | 1750 | 125 | 150 | 150 | 350 | 200 | 55 | 200 | 186,380.7 | 10.497 |
| b (mm) | h (mm) | d (mm) | ev (mm) | es (mm) | ea (mm) | ei (mm) | fck (MPa) | c (mm) | μcost (€) | σv,displacement (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1200 | 1350 | 0 | 150 | 150 | 350 | 200 | 60 | 200 | 168,833.9 | 11.058 |
| B | 1200 | 1650 | 0 | 150 | 150 | 350 | 175 | 80 | 175 | 190,734.7 | 5.510 |
| C | 1300 | 2000 | 0 | 225 | 300 | 350 | 275 | 80 | 275 | 231,832.0 | 3.772 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penadés-Plà, V.; García-Segura, T.; Yepes, V. Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge. Mathematics 2020, 8, 398. https://doi.org/10.3390/math8030398
Penadés-Plà V, García-Segura T, Yepes V. Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge. Mathematics. 2020; 8(3):398. https://doi.org/10.3390/math8030398
Chicago/Turabian StylePenadés-Plà, Vicent, Tatiana García-Segura, and Víctor Yepes. 2020. "Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge" Mathematics 8, no. 3: 398. https://doi.org/10.3390/math8030398
APA StylePenadés-Plà, V., García-Segura, T., & Yepes, V. (2020). Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge. Mathematics, 8(3), 398. https://doi.org/10.3390/math8030398







