Abstract
The framework of this paper is intertemporal choice and, more specifically, the so-called delay effect. Traditionally, this anomaly, also known as decreasing impatience, has been revealed when individuals reverse their preferences over monetary or non-monetary rewards. In this manuscript, we will analyze the delay effect by using preference relations and discount functions. The treatment of the delay effect with discount functions exhibits several scenarios for this paradox. Thus, the objective of this paper is to deduce the different expressions of the delay effect and their mathematical characterizations by using discount functions in stationary and dynamic settings. In this context, subadditivity will be derived as a particular case of decreasing impatience. Finally, we will introduce a new discount function, the so-called asymmetric exponential discount function, able to describe decreasing impatience.
1. Introduction
The Discounted Utility model, originally introduced by Samuelson [1], became one of the main paradigms of asset valuation when time is involved in the decision-making. The discount function which underlies the process of intertemporal choice is an exponential function that makes preferences consistent over time. However, from the 80s onwards, Thaler [2] opened a debate on the acceptance of Samuelson’s model, precisely due to the validation of the existence of time inconsistency in decision-making. This involved a large number of subsequent empirical studies which confirmed that, in effect, the discount ratios obtained in their empirical studies did not fit the theoretical basis of Samuelson’s model, and that these differences were due to a series of paradoxes, labeled as “anomalies” in intertemporal choice.
In the existing literature on this topic, a large number of these anomalies have been demonstrated, of which we can highlight [3] the following effects: delay effect, magnitude effect, sign effect, sequence effect, spread or dissemination effect, and delay-anticipation asymmetry effect, among others. That is why, over the last 30 years, several attempts have been made to find mathematical models able to cover the aforementioned deficiencies of the model proposed by Samuelson. Among them, we can find the hyperbolic discounting model [4,5] in which the discount rate decreases with the passage of time, thus solving the anomaly called “delay effect” or decreasing impatience, revealed for monetary [2,6] and non-monetary decisions [7].
This anomaly implies that, when the delay increases, the discount rate decreases, that is, there is an inverse relationship between the discount rate and time, which allows us to state that as time increases, impatience diminishes. This effect gives rise to time inconsistency, due to the change in preferences of the decision-maker since, starting from two equivalent rewards available at different times, the decision-maker is willing to wait to obtain a reward greater than the smaller outcome sooner.
This concept gives rise to subadditivity, investigated by Sholten and Read [8,9,10] and Cruz Rambaud and Muñoz Torrecillas [11]. We can say that a discount function is subadditive if the discount rate is greater when the interval is subdivided, that is, the discount in subintervals is greater than in the whole interval; in other words, the decision-maker prefers the earliest option when deciding in a subinterval, and the latest option in the entire interval. The opposite situation is superadditivity.
However, Cruz Rambaud and Muñoz Torrecillas [12] provided a new concept, the subadditivity of the second order, which is more general than subadditivity. Moreover, in the dynamic context, apart from the two former concepts, we have to distinguish between increasing discount ratios (delay effect) and decreasing discount rates (decreasing impatience), which are equivalent situations in a stationary context.
The objective of the paper is the mathematical treatment of the delay effect by using discount functions. This will allow us to derive several expressions of this anomaly and to deduce subadditivity as a particular case of decreasing impatience.
It is well known that intertemporal choice is a topic of great relevance in the field of finance, but not exclusively because it has been studied in a lot of disciplines, including medicine and psychology. In effect, several authors have shown the importance of applying discounting processes to health [13,14,15,16], as evidence has been found that people discount their future health status, particularly in certain addictive behaviors, such as smoking [17,18], gambling addiction, excessive alcohol consumption [19], and even in obesity-related behaviors [20,21]. In all these experiments, higher discount rates have been found in the closest decisions.
As described before, in a stationary context delay effect means that the discount rate decreases as the delay increases or, what is the same, the decision-maker discounts at a higher rate when the delay is shorter. Obviously, this definition is associated with the concept of impatience (the decision-maker prefers something which happens earlier than later) [22]. Consequently, we can say that, in the context of the delay effect, the decision-maker becomes more impatient when the reward is near the current moment. In this way, impulsivity and impatience are taken as analogous concepts by some researchers, such as Takahashi et al. [23] and specifically by Cruz Rambaud and Muñoz Torrecillas [24].
On the other hand, impatience gives rise to another concept, the so-called excessive discount [25], which occurs when the applied discount rates are excessively high. This phenomenon can be mainly associated with people with problems such as schizophrenia, obese people, drug addicts, and smokers, among others. Another related concept is subadditivity, also applied to health management [26], which implies that individuals with some addiction more readily relapse into addiction when there are several short abstinent periods than when there is only one period of major abstinence. The study of this concept is very important for designing a treatment to cure an addiction.
To describe the delay effect, Mazur [27] proposed the hyperbolic function as an alternative to the exponential discounting of Samuelson [1] since it better fits the empirical works carried out by numerous researchers. Cruz Rambaud, Muñoz Torrecillas, and Takahashi [28] also provided a discount function which better fits the decisions of people with addictions and, consequently, with excessive discount ratios, called the exponentiated hyperbolic discount function. This function exhibits a greater slope than the simple hyperbola presented by Mazur, reflecting the higher discount rates shown by decision-makers with problems of addiction.
In this manuscript, we are going to propose a novel dynamic discount function, the so-called asymmetric exponential discount function, which fits decreasing impatience better than the hyperbolic function of Mazur, since it exhibits the different types of delay effect presented in this work.
The structure of this paper is as follows. Section 2 presents the concept of subadditivity. In Section 3, we will define the concept of the delay effect by showing different alternatives derived from its treatment with discount functions. In particular, the concept of subadditivity will be derived from the general setting of the delay effect analyzed in this section. Section 4 provides a new discounting model that better fits the preferences of individuals, taking into account the different modalities of the delay effect. Finally, Section 5 summarizes and concludes.
2. Subadditivity
A concept closely related to the delay effect is the absence of additivity. Scholten and Read [8,9,10] studied subadditivity and superadditivity in intertemporal choices and, subsequently, Cruz Rambaud and Muñoz Torrecillas [11] investigated subadditivity and its relationship with the delay effect.
First, we are going to make a brief description of the additivity and subadditivity. To do this, we need the following definition.
Definition 1.
A (dynamic) discount function is a continuous real-valued function
where is the set of positive real numbers including zero, defined by:
such that and is strictly decreasing, for every t.
Observe that, in Definition 1, t and a represent the variable “time”, although t refers to a delay (a date or calendar time) and a refers to time as an interval. This distinction was already made by Scholten and Read [8,9,10] for whom delay refers to the time counted from 0, and interval is defined as the difference of two delays. Analogously, Cruz Rambaud and Muñoz Torrecillas [11] also made the same distinction, since they considered time as a point, that is to say, a date denoted by t, which refers to delay. On the other hand, the interval is considered as a period, for example, a week, a month, or a year, which is represented as a. Consequently, we can deduce that an interval can be considered as the difference between two delays.
Definition 2.
[29]. A discount function is said to be additive if its value in an interval is equal to the product of the values successively discounted by subintervals, that is to say:
for every t, and for every a and b greater than zero.
Figure 1 illustrates this concept graphically.
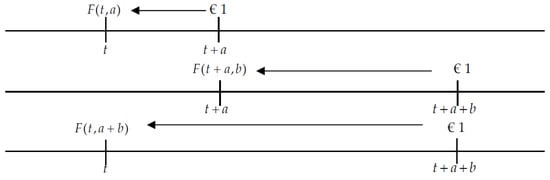
Figure 1.
Additivity. Source: Own elaboration.
Traditional discount functions follow the premise of additivity, that is to say, the effect of the discount on several small intervals or subintervals is identical to the discount on the total or undivided interval [29]. However, many empirical studies have detected the presence of subadditivity in discounting decisions (see, for example, [29,30,31,32]). In effect, these works have shown that the discount rates are higher when the intervals are divided, that is to say, the discount is greater by using smaller than larger intervals. Mathematically, it can be written as follows:
Definition 3.
A discount function is said to be subadditive if
for every t, and for every a and b greater than zero.
The following result characterizes subadditivity, but before we are going to introduce the following definition.
Definition 4.
Given two dated rewards
and
, and a stationary discount function
, we will say that
Obviously, ~ is an equivalence relation.
Theorem 1.
The following three conditions are equivalent:
- (i)
- is subadditive.
- (ii)
- For every t, and a and b greater than zero, if ~ and ~ then .
- (iii)
- For every t, a, and b greater than zero, there exists x, y, and z such that , but .
Proof.
(i) ⇔ (ii). Assume that F is subadditive. If ~ then . On the other hand, if ~ then . Consequently,
Therefore, . Reciprocally, consider the rewards , and . Obviously, the first reward is equivalent to the second one, and the second is equivalent to the third. By hypothesis, the third reward is preferred to the first from which subadditivity holds.
(ii) ⇔ (iii). The necessity follows by taking the rewards , and , for values of ε and δ small enough such that
The sufficiency is straightforward. □
Example 1.
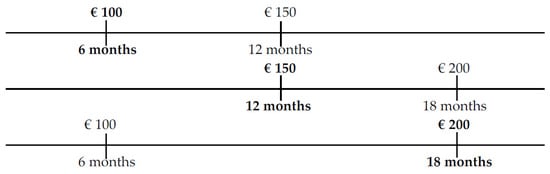
Assume the choice between €100 in 6 months and €150 in 12 (which is a 6-month subinterval), another choice between €150 at 12 and €200 at 18 (which is another subinterval of 6 months) and a last choice between €100 at 6 months and €200 at 18 (the interval here is 12-months length) (see Figure 2).

Figure 2.
Subadditivity. Source: Own elaboration.
In the former example, the discount would be subadditive when the decision-maker prefers €100 to €150 in the first subinterval (6 months), prefers €150 to €200 in the second subinterval (another period of 6 months), but prefers €200 to €100 in the 12-month interval, corresponding to the sum of the two previous periods, that is to say, the decision-maker prefers the earliest options in the subintervals and the latest choice in the undivided interval.
3. Delay Effect
3.1. Stationary Case
The delay effect has been one of the most studied anomalies. The first authors to analyze this effect were Prelec and Loewenstein [33], who, however, labeled it as the “common difference effect”.
The delay effect or common difference effect is the paradox in which the discount rate decreases as the delay increases or, said in other words, the discount rate is lower for intervals which start later.
Example 2.
A person may prefer receiving €50 in a month or receiving €75 in two months; however, this same person may prefer €75 within 13 months to €50 within 12 months. Observe that, between the two rewards, there is a difference of one month (from 1 to 2 and from 12 to 13); however, the preferences of the decision-maker have changed, resulting in a time inconsistency which is incompatible with the exponential discount function, since we have gone from preferring the €50 reward in a month to prefer the €75 reward in month 13 (in both cases, there has been an increase of the delay in 11 months).
In Example 2, we can see that the choice of the closest rewards becomes more important than the farthest rewards. This anomaly is called the delay effect. However, this effect can be confused with the immediacy effect, which refers to the decision-makers giving special importance to immediate results, that is, the decision-maker prefers the reward now to waiting. Therefore, to differentiate between these two effects, we must look at the moment of choosing the reward, that is to say, the left-hand endpoint of the interval.
Example 3.

If €50 is preferred today to €75 in a month, we would talk about the immediacy effect, while, if the interval does not start at the current moment, as in the given example, €50 in a month or €75 in two months, then we talk about the delay effect. The delay effect can be graphically represented in Figure 3.

Figure 3.
Delay effect (Example 2). Source: Own elaboration.
In Figure 3, we can observe time inconsistency because, when delaying the rewards, the individual prefers to wait longer to obtain a greater reward; however, in the first scenario, the individual prefers the small reward and not wait another month to obtain the later reward. The main problem of the situation described before is that, in the presence of time inconsistency, an individual could always prefer the first reward. Said, in other words, the former situation is not general to every couple of amounts. This could be the case of two rewards with similar amounts; for example, the individual could prefer €50 in one month and €50 in 12 months to €51 in two months and €51 in 13 months, respectively. This is why, to give a more accurate definition of the delay effect, we are going to start from an indifference relation instead of a preference. Mathematically, we can formalize this effect as follows:
where x and y () represent the rewards equivalent at instants s and t, respectively, and denotes the incremental delay (in Example 2, ε is 11 months) applied to each reward. On the other hand, the mathematical expression of the immediacy effect would remain in the following form [9]:
where x and y () represent the rewards equivalent at instants and t, respectively, and denotes the incremental delay.
To continue with the description of the delay effect, we are going to introduce the concept of the discount function in a stationary context.
Definition 5.
A (stationary) discount function is a continuous, strictly decreasing real-valued function
defined by:
such that .
The more general situation where the delay effect appears is the following: If , the discount ratio corresponding to interval is less than the discount ratio of the interval , that is to say:
or, equivalently,
Definition 6.
[12]. A discount function is said to be subadditive of the second order if it satisfies Equation (2).
Specifically, if , then
which is subadditivity. It can be shown that, if is differentiable, the following three conditions are equivalent [10]:
- is subadditive of the second order.
- is convex.
- The instantaneous discount rate, , is strictly decreasing.
This result could also be derived from the ambit of applied probability. In effect, in a stationary context, given a discount function , then is a distribution function. It is easy to see that the instantaneous discount rate of coincides with the failure (hazard) rate [34,35,36] of . Therefore, a decreasing instantaneous discount rate is the same as a decreasing failure rate. Chart 1 clarifies the involved implications:
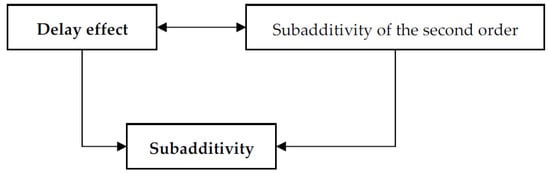
Chart 1.
Delay effect and subadditivity in a stationary context. Source: Own elaboration.
3.2. Dynamic Case
In a dynamic setting (see Definition 1), the most general situation where the delay effect appears is the following: If and , the discount ratio corresponding to interval is less than the discount ratio of the interval , for every (see Figure 4). That is to say:
or, equivalently,
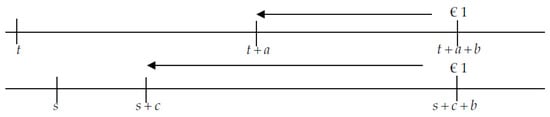
Figure 4.
Delay effect in a dynamic situation. Source: Own elaboration.
Definition 7.
[12]. A discount function is said to be subadditive of the second order in a dynamic context if it satisfies Equation (4).
If, in particular, in Equation (4) (which implies ), then:
which is subadditivity (see Figure 5).
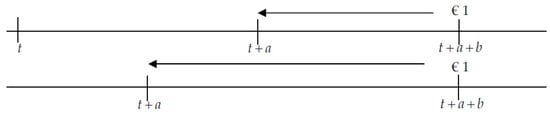
Figure 5.
Subadditivity in a dynamic situation. Source: Own elaboration.
In the rest of this section, we will assume that the discount function is differentiable with respect to their two variables. The following two results characterize subadditive discounting of the second order.
Theorem 2.
If a discount functionis subadditive of the second order, then the instantaneous discount rateis decreasing with respect to. Reciprocally, if the instantaneous discount rateis strictly decreasing with respect to, there exists a neighborhood of 0,, such thatis subadditive of the second order, for every a and b in.
Proof.
Taking natural logarithms in Inequality (3) and dividing by b, one has:
Finally, letting :
and so, as , the instantaneous discount rate is decreasing with respect to . The demonstration of the converse statement is obvious. □
Corollary 1.
If a discount functionis subadditive of the second order then, where is the directional derivative ofaccording to vector. Reciprocally, if, there exists a neighborhood of 0,, such thatis subadditive of the second order, for every a and b in.
Proof.
In effect, making the change of variable , by the Chain Rule of derivation, one has:
Observe that, by Theorem 2, the left-hand side of the former equation is negative and that the right-hand side is the directional derivative of according to vector . □
From now on, we will only enunciate necessary conditions. The following result characterizes the delay effect.
Corollary 2.
A necessary condition for a discount functionsatisfying the delay effect is that, for every t,is decreasing with respect to a.
Proof.
It is obvious taking into account Theorem 2 and that, in this case, t is constant. □
The following three results characterize subadditive discounting.
Corollary 3.
A necessary condition for a discount functionbeing subadditive is.
Proof.
It is obvious taking into account Theorem 2 and that, in this case, and . □
Theorem 3.
A necessary condition for a discount functionbeing subadditive is, where is the directional derivative ofaccording to vector.
Proof.
Taking natural logarithms in the following inequality:
and dividing by b, one has:
Observe that the right-hand side of the former inequality can be written as follows:
Finally, letting :
or, equivalently,
Corollary 4.
A necessary condition for a discount functionbeing subadditive is
Proof.
Observe that, according to Theorem 3,
or, equivalently,
Finally, letting :
Another case arises when comparing the values of the discount function for intervals and :
that is to say, the discount function is contractive (CONTR) (see [9]). Otherwise, the discount function is said to be expansive (EXP). A characterization of contractive discounting is provided by the following theorem.
Theorem 4.
A necessary condition for a discount functionbeing contractive is.
Chart 2 clarifies the involved implications:
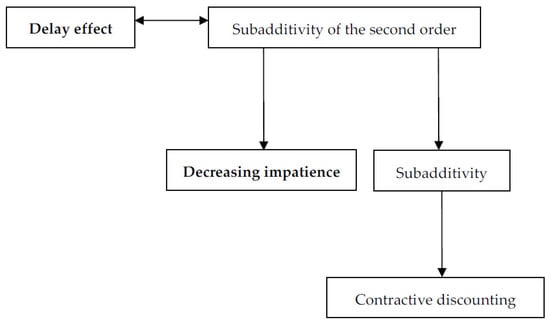
Chart 2.
Delay effect and subadditivity in a dynamic context. Source: Own elaboration.
4. Proposal of a New Discounting Function: The Asymmetric Exponential Discounting
Let us consider the following discount function:
where k, α, and β are strictly positive real numbers. To calculate the instantaneous discount rate, take into account that:
Thus,
Next, we are going to apply the sufficient conditions deduced in Section 3 to the new discount function proposed in this section. First, to analyze the subadditivity of the second order:
it is necessary to previously determine the partial derivative of with respect to t and with respect to a:
And
Therefore,
or, equivalently,
Consequently, if, and only if, the following inequality holds:
In particular, this inequality holds if or , and . Table 1 summarizes all possible cases according to the values of α and β, where SUB2 means subadditivity of the second order, and RSUB2 reverses superadditivity of the second order:

Table 1.
Delay effect according to the values of α and β. Source: Own elaboration.”
Now, to analyze the subadditivity, we will take into account the following sufficient condition:
it is necessary to take into account that:
Therefore,
or, equivalently,
On the other hand,
Consequently, if, and only if, .
Finally, the condition of contractiveness is satisfied by requiring:
holds if, and only if, .
Example 4.
Let us consider, for example, k = 0.1, t = 2, and a = 2 to calculate the subadditivity and superadditivity of the second order of the proposed model depending on the different values of α and β.
- Superadditivity of the second order:.
- Subadditivity of the second order: .

Table 2.
Example of the delay effect according to the values of α and β. Source: Own elaboration.
Example 5.

Let us consider, for example, k = 0.1, t = 2, and a = 2 to calculate the subadditivity of the proposed model depending on the different values of α and β. See Table 3.

Table 3.
Example of subadditivity according to the values of α and β. Source: Own elaboration.
This example confirms the conclusions obtained above.
Example 6.
If k = 0.1, t = 2, and a = 2, the condition of contractiveness is the following:
In Table 4, we can see that the condition of contractiveness holds if, and only if,

Table 4.
Example of contractiveness according to the values of α and β. Source: Own elaboration.
5. Conclusions
This paper has dealt with the topic of the delay effect and decreasing impatience in intertemporal choice, one of the most important anomalies of the Discounted Utility model. This paradox has been treated in a static framework, by using a stationary discount function, and in a dynamic setting with the use of a general discount function. The delay effect means a strong preference for small sooner rewards instead of larger later outcomes. In a stationary context, this is equivalent to requiring that the discount ratio corresponding to the underlying discount function is increasing with respect to the delay of a given interval.
In a dynamic framework, the delay effect can be analyzed following three methodologies:
- By comparing the discount ratios corresponding to two delayed intervals of the same length. This case gives rise to the concept of the subadditivity of the second order.
- By comparing the value of the discount function with the discount ratio corresponding to a delayed interval with the same amplitude. This is a condition weaker than the former one and gives rise to the concept of subadditivity.
- By comparing the values of the discount function in two intervals with the same amplitude. This situation gives rise to a contractive discount function.
This manuscript has presented mathematical characterizations of these three types of the delay effect, which will be useful in understanding the mode of decreasing impatience exhibited by a given discount function. Finally, we have provided a new function, the so-called asymmetric exponential discount function, which shows all types of decreasing impatience defined in this paper.
A further research line is to relate the delay effect with another very similar anomaly, the so-called interval effect, and analyze the adequacy of this novel discount function to explain both paradoxes.
Author Contributions
The individual contribution of each author has been as follows: writing, methodology, formal analysis and funding acquisition, S.C.R.; writing, conceptualization and supervision, P.O.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the Spanish Ministry of Economy and Competitiveness, grant number DER2016-76053R.
Acknowledgments
We are very grateful for the valuable comments and suggestions offered by three anonymous referees.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samuelson, P.A. A note on measurement of utility. Rev. Econ. Stud. 1937, 4, 155–161. [Google Scholar] [CrossRef]
- Thaler, R. Some empirical evidence on dynamic inconsistency. Econ. Lett. 1981, 8, 201–207. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. An analysis of the anomalies in traditional discounting models. Int. J. Psychol. Psychol. Ther. 2004, 4, 105–128. [Google Scholar]
- Ainslie, G. Specious reward: A behavioral theory of impulsiveness and impulse control. Psychol. Bull. 1975, 82, 463–496. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, G.; Prelec, D. Anomalies in intertemporal choice: Evidence and an interpretation. Q. J. Econ. 1992, 107, 573–597. [Google Scholar] [CrossRef]
- Benzion, U.; Rapoport, A.; Yagil, J. Discount rates inferred from decisions: An experimental study. Manag. Sci. 1989, 35, 270–284. [Google Scholar] [CrossRef]
- Christensen-Szalanski, J.J. Discount functions and the measurement of patients’ values: Women’s decisions during childbirth. Med. Decis. Mak. 1984, 4, 47–58. [Google Scholar] [CrossRef]
- Scholten, M.; Read, D. Interval effects: Superadditivity and subadditivity in intertemporal choice. Work. Pap. Lond. Sch. Econ. Political Sci. 2004. [Google Scholar]
- Scholten, M.; Read, D. Discounting by intervals: A generalized model of intertemporal choice. Manag. Sci. 2006, 52, 1424–1436. [Google Scholar] [CrossRef]
- Scholten, M.; Read, D. The psychology of intertemporal tradeoffs. Psychol. Rev. 2010, 117, 925. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. Delay and interval effects with subadditive discounting functions. In Preferences and Decisions: Models and Applications; Greco, S., Marques Pereira, R.A., Squillante, M., Yager, R.R., Eds.; Springer: Berlin, Germany, 2010; pp. 85–110. [Google Scholar]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. Some characterizations of (strongly) subadditive discounting functions. Appl. Math. Comput. 2014, 243, 368–378. [Google Scholar] [CrossRef]
- Chapman, G.B. Temporal discounting and utility for health and money. J. Exp. Psychol. Learn. Mem. Cogn. 1996, 22, 771–791. [Google Scholar] [CrossRef] [PubMed]
- Lazaro, A.; Barberan, R.; Rubio, E. Private and social time preferences for health and money: An empirical estimation. Health Econ. 2001, 10, 351–356. [Google Scholar] [CrossRef] [PubMed]
- Van der Pol, M.; Cairns, J. Valuing future private and social benefits: The discounted utility model versus hyperbolic discounting models. J. Econ. Psychol. 2000, 21, 191–205. [Google Scholar]
- Kirby, K.N.; Maraković, N.N. Modeling myopic decisions: Evidence for hyperbolic delay-discounting within subjects and amounts. Organ. Behav. Hum. Decis. Process. 1995, 64, 22–30. [Google Scholar] [CrossRef]
- Reynolds, B. Do high rates of cigarette consumption increase delay discounting? A cross-sectional comparison of adolescent smokers and young-adult smokers and nonsmokers. Behav. Process. 2004, 67, 545–549. [Google Scholar] [CrossRef] [PubMed]
- Harrison, G.W.; Lau, M.I.; Rutström, E.E. Individual discount rates and smoking: Evidence from a field experiment in Denmark. J. Health Econ. 2010, 29, 708–717. [Google Scholar] [CrossRef]
- Stea, J.N.; Hodgins, D.C.; Lambert, M.J. Relations between delay discounting and low to moderate gambling, cannabis, and alcohol problems among university students. Behav. Process. 2011, 88, 202–205. [Google Scholar] [CrossRef]
- Scharff, R.L. Obesity and hyperbolic discounting: Evidence and implications. J. Consum. Policy 2009, 32, 3–21. [Google Scholar] [CrossRef]
- Ikeda, S.; Kang, M.I.; Ohtake, F. Hyperbolic discounting, the sign effect, and the body mass index. J. Health Econ. 2010, 29, 268–284. [Google Scholar] [CrossRef]
- Prelec, D. Decreasing impatience: A criterion for non-stationary time preference and “hyperbolic” discounting. Scand. J. Econ. 2004, 106, 511–532. [Google Scholar] [CrossRef]
- Takahashi, T.; Oono, H.; Radford, M.H. Empirical estimation of consistency parameter in intertemporal choice based on Tsallis’ statistics. Phys. A Stat. Mech. Its Appl. 2007, 381, 338–342. [Google Scholar] [CrossRef]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J. Measuring impatience in intertemporal choice. PLoS ONE 2016, 11, e0149256. [Google Scholar] [CrossRef] [PubMed]
- Bickel, W.K.; Jarmolowicz, D.P.; Mueller, E.T.; Koffarnus, M.N.; Gatchalian, K.M. Excessive discounting of delayed reinforcers as a trans-disease process contributing to addiction and other disease-related vulnerabilities: Emerging evidence. Pharmacol. Ther. 2012, 134, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T. Time-estimation error following Weber–Fechner law may explain subadditive time-discounting. Med. Hypotheses 2006, 67, 1372–1374. [Google Scholar] [CrossRef] [PubMed]
- Mazur, J.E. An adjusting procedure for studying delayed reinforcement. In Quantitative Analyses of Behavior; Commons, M.L., Mazur, J.E., Nevin, J.A., Rachlin, H., Eds.; The effect of delay and of intervening events on reinforcement value; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 1987; Volume 5, pp. 55–73. [Google Scholar]
- Cruz Rambaud, S.; Muñoz Torrecillas, M.J.; Takahashi, T. Observed and normative discount functions in addiction and other diseases. Front. Pharmacol. 2017, 8, 416. [Google Scholar] [CrossRef]
- Read, D. Is time-discounting hyperbolic or subadditive? J. Risk Uncertain. 2001, 23, 5–32. [Google Scholar] [CrossRef]
- Baron, J. Can we use human judgments to determine the discount rate? Risk Anal. 2000, 20, 861–868. [Google Scholar] [CrossRef]
- Pender, J.L. Discount rates and credit markets: Theory and evidence from rural India. J. Dev. Econ. 1996, 50, 257–296. [Google Scholar] [CrossRef]
- Read, D.; Roelofsma, P.H. Subadditive versus hyperbolic discounting: A comparison of choice and matching. Organ. Behav. Hum. Decis. Process. 2003, 91, 140–153. [Google Scholar] [CrossRef]
- Prelec, D.; Loewenstein, G. Decision making over time and under uncertainty: A common approach. Manag. Sci. 1991, 37, 770–786. [Google Scholar] [CrossRef]
- Barlow, R.E.; Proschan, F. Mathematical Theory of Reliability; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Aven, T.; Jensen, U. Stochastic Models in Reliability; Springer: New York, NY, USA, 1999. [Google Scholar]
- Cruz Rambaud, S. A new argument in favor of hyperbolic discounting in very long term project appraisal. Int. J. Theor. Appl. Financ. 2014, 17, 1–17. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).