Optimal Shape and First Integrals for Inverted Compressed Column

Abstract

We study optimal shape of an inverted elastic column with concentrated force at the end and in the gravitational field. We generalize earlier results on this problem in two directions. First we prove a theorem on the bifurcation of nonlinear equilibrium equations for arbitrary cross-section column. Secondly we determine the cross-sectional area for the compressed column in the optimal way. Variational principle is constructed for the equations determining the optimal shape and two new first integrals are constructed that are used to check numerical integration. Next, we apply the Noether’s theorem and determine transformation groups that leave variational principle Gauge invariant. The classical Lagrange problem follows as a special case. Several numerical examples are presented.

1. Introduction

The first problem of optimization of elastic rods was formulated by Lagrange, [1]. The problem consists of finding the shape of an elastic rod of given volume that has largest value of the buckling force. The solution of the problem, with the simply supported boundary conditions, was obtained by Clausen in [2]. Various versions of the optimal shape of a column problem were treated in a number of publications, see [3,4,5,6,7,8,9,10].

In this work we propose to solve the problem of the strongest column in a constant gravity field for the case when the upper end is fixed, as in [10], and, additionally, loaded by a constant concentrated force at the top. Thus, we shall be able to reproduce both classical Clausen problem [2] as well as the problem of heavy inverted column, treated in [10]. Also we shall examine the bifurcation points of nonlinear equilibrium equations. Namely, we shall show that the lowest bifurcation point of linear and nonlinear problem coincide. This is important, since optimization will be performed at eigenvalues of the linearized problem. Also for differential equations describing the optimal shape of the column, a variational principle is formulated and two new first integrals are obtained. We also studied the invariance of the variational principle, by using the Noether’s theorem, see [11,12,13], where integer and fractional order systems are treated. We showed that one of two first integrals follow from the Absolute invariance of the Hamilton’s action integral and the other from so called Gauge invariance. Pontryagin’s principle and variational methods, including Noether’s theory, represent powerful methods for the study of mechanical and physical systems. Our results demonstrate this on an example where new results are obtained by using these methods. For recent contribution to a nontrivial extension of the Noether’s theory see [14]. In this work we will follow the notation of [11,15].

2. Formulation

In Figure 1 we show the column with inextensible axis of length $L.$ At upper end B the column is fixed with the possibility of sliding along the axis $x.$ A concentrated force of intensity F is applied at the end B. Equations describing behaviour of the column [15] are

$$\frac{dH}{dS}=q_{0}A;\frac{dV}{dS}=0;\frac{dM}{dS}=-Vcos\vartheta +Hsin\vartheta .$$

(1)

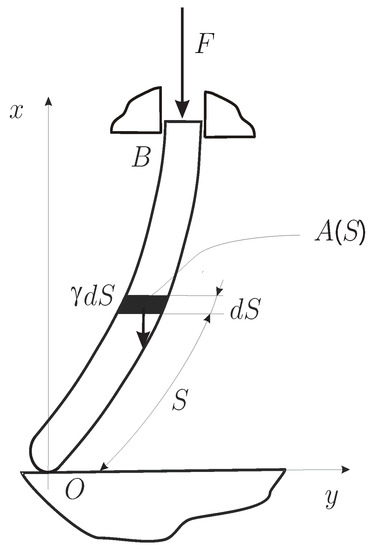
Figure 1. Coordinate system for the rod under self-weight and concentrated force.

Here H and V are components of cross-sectional force along x and y axes, M denotes the bending moment, $\vartheta$ denotes the angle between the tangent to the column axis and the x axis of a coordinate system $x-O-y.$ Also S denotes the arc-length of the column axis. We use the specific distributed force given as $q_0=\rho gA$ with $\rho$ being the mass density, g is the gravitational constant and $A>0$ is area of the rod at an specific point of the rod axis. In order to apply the Bernoulli–Euler bending theory we assume that $A\in C[0,L].$ Also

$$\frac{dx}{dS}=cos\vartheta ;\frac{dy}{dS}=sin\vartheta ,$$

(2)

express inextensibility of the axis. Constitutive equation of the classical Bernoulli–Euler theory reads

$$M=EI\frac{d\vartheta }{dS}.$$

(3)

In (2) and (3) x and y denote coordinates of an arbitrary point in system $x-O-y$. We use E to denote modulus of elasticity and I the second moment of the cross-section area. From Figure 1 we conclude that

$$y\left(0\right)=x\left(0\right)=0;M\left(0\right)=0;V\left(0\right)=0;\vartheta \left(L\right)=0;H\left(L\right)=-F,$$

(4)

so that

$$H\left(S\right)=-[{\int }_S^L{q}_{0}A(\xi )d\xi +F];V\left(S\right)=0.$$

(5)

The column has volume given by

$$W={\int }_0^{L}A\left(S\right)dS.$$

(6)

If the column cross-sections are similar and similarly oriented, then

$$I\left(S\right)=\alpha A^2\left(S\right),$$

(7)

with $\alpha$ being a constant, equal $\alpha =\frac{1}{4\pi }$ for circular cross-section. We introduce

$$t=\frac{S}{L};a=\frac{A}{L^2};{\lambda }_1=\frac{q_{0}L}{\alpha E};{\lambda }_2=\frac{F}{\alpha E{L}^2};u=\frac{x}{L};v=\frac{y}{L};w=\frac{W}{L^3},$$

(8)

so that (1)–(8) become

$${\left(a^2\dot{\vartheta }\right)}^{·}+[{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +{\lambda }_2]sin\vartheta =0;\dot{u}\begin{array}{c}=\end{array}cos\vartheta ;\dot{v}=sin\vartheta ,d(·)/dt=\stackrel{·}{(·)},$$

(9)

with

$$u\left(0\right)=0;v\left(0\right)=0;{\displaystyle \underset{t\to 0}{lim}}{a}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0.$$

(10)

The volume of the column now becomes

$$w=\underset{0}{\overset{1}{\int }}a\left(t\right)dt.$$

For (9) and (10) we find a trivial solution

$${\vartheta }_0=0;u_0=t;v_0=0,$$

valid for all values of ${\lambda }_1$ and ${\lambda }_2$ and for any $a>0.$ We examine the values of $({\lambda }_1,{\lambda }_2)=K\in {\mathbb{R}}^2$ that lead to a nontrivial solution of (9) and (10). First we write (9)${}_1$ in operator form as

$$M(K,\vartheta )={\left(a^2\dot{\vartheta }\right)}^{·}+[{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +{\lambda }_2]sin\vartheta ,\vartheta \in U,$$

with

$$U=\{\vartheta :\vartheta \in C^2(0,1);{\displaystyle \underset{t\to 0}{lim}}{a}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0\}.$$

Then (9)${}_1$ subject to (10)${}_{3,4}$ is equivalent to

$$M(K,\vartheta )=0.$$

(11)

The solution ${\vartheta }_0=0$ is trivial solution valid for all $K\in {\mathbb{R}}^2.$ The Fréchet derivative of $M(K,\vartheta )$ calculated at ${\vartheta }_0=0$ is

$$D{M}_{\vartheta }(K,0)\vartheta =B\left(K\right)\vartheta ={\left(a^2\dot{\vartheta }\right)}^{·}+[{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +{\lambda }_2]\vartheta .$$

We consider the linearized boundary value problem $B\left(K\right)\vartheta =0$, i.e.,

$${\left(a^2\dot{\vartheta }\right)}^{·}+[{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +{\lambda }_2]\vartheta =0.$$

It is known that the necessary condition for the existence of nontrivial solution of (9)${}_1$, (10)${}_{3,4}$ is that there is nontrivial solution of the linearized equation

$${\left(a^2\dot{\vartheta }\right)}^{·}+[{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +{\lambda }_2]\vartheta =0,$$

(12)

subject to

$${\displaystyle \underset{t\to 0}{lim}}{a}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0.$$

(13)

Suppose that $K=(\lambda ,{\lambda }_2)$ with ${\lambda }_1=\lambda >0$ fixed (gravitational force is not subject to changes) and ${\lambda }_2\in \mathbb{R}$ and ${\vartheta }_0$ is a solution to (12) and (13). Then with ${\lambda }_2$ as a bifurcation parameter, we have:

Proposition 1.

Given${\lambda }_1=\lambda$the boundary value problem (12) and (13) has only real eigenvalues, there are an infinite but countable number of them,${\lambda }_{2n}$,$n=1,2,\cdots$, and they can be ordered to satisfy

$$0<{\lambda }_{21}<{\lambda }_{22}<{\lambda }_{23}<\cdots$$

The number of zeros of the eigenfunction${\vartheta }_{2n}$in the interval (0,1) is$n-1.$Also,

$$\frac{{\lambda }_{2n}}{n^2}\to \frac{{\pi }^2}{{\left({\int }_0^1\frac{dt}{a\left(t\right)}\right)}^2}\mathrm{as}n\to \infty .$$

Proof of Proposition 1.

Note that with $a^2=p,{\lambda }_1\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi =q,w=1$ the conditions of the Theorem 4.3.1 of [16] are satisfied. The result follows from the application of this Theorem. ☐

The condition that guarantees that (9) and (10) have nontrivial solution is formulated next. Our interest is to show that at the lowest eigenvalue of (12) and (13), that is for $K=(\lambda ,{\lambda }_{21})$, the system (9) and (10) with arbitrary $a\left(t\right)>0$, $t\in (0,1)$, has a bifurcation point. We note that in the next Section $a\left(t\right)$ will be determined from the optimization procedure. We state this as:

Theorem 1.

Let${\lambda }_{21}=\Lambda$be the lowest eigenvalue of the system (12) and (13). The nonlinear boundary value problem (11) has a bifurcation point at$K=(\lambda ,\Lambda )$, i.e, there is continuously differentiable curve through$\left(\right(\lambda ,\Lambda ),0)$such that

$$\{((\lambda ,\Lambda \left(s\right)),\vartheta \left(s\right)),s\in (-\epsilon ,\epsilon ),((\lambda ,\Lambda \left(0\right)),\vartheta \left(0\right))=((\lambda ,\Lambda ),0)\},$$

(14)

and with

$$M(K=(\lambda ,\Lambda \left(s\right)),\vartheta \left(s\right))=0,s\in (-\epsilon ,\epsilon ).$$

(15)

Proof ofTheorem 1.

We use the Crandall–Rabinowitz theorem, see [17,18], p.15. Thus, let ${\vartheta }_0$ be eigenvector of (12) and (13) with given $\lambda$ and lowest eigenvalue $\Lambda$, i.e., $K(\lambda ,\Lambda ).$ We assume that ${\vartheta }_0$ is normalized, so that ${\int }_0^1{\left|{\vartheta }_0\right(t\left)\right|}^{2}dt=1.$ Note that

$${\left(a^2\dot{\vartheta }\right)}^{·}+[\lambda \underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +\Lambda ]\vartheta =0,$$

subject to

$${\displaystyle \underset{t\to 0}{lim}}{a}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0,$$

leads to unique eigenvector $\vartheta ={\vartheta }_0$. To prove that ${\vartheta }_0$ is unique, observe that $a\left(1\right)\ne 0.$ If $a\left(1\right)=0,$ from (3) we conclude that $M\left(1\right)=0.$ Then, the equilibrium equations for the rod lead to the conclusion that there is only trivial solution ${\vartheta }_0=0.$ Since $a\left(1\right)\ne 0$, the Theorem 5, p.73 of [19], implies that ${\vartheta }_0$ is unique. Next we determine $\frac{\partial B\left(K\right){\vartheta }_0}{\partial \Lambda }$ as

$$D^2{M}_{\vartheta ,\Lambda }(K,0){\vartheta }_0={\vartheta }_0.$$

Therefore it follows that $D^2{M}_{\vartheta ,\Lambda }(K,0){\vartheta }_0\notin$ Range $B(K=(\lambda ,\Lambda \left)\right).$ Thus, Theorem I.5.1 of [18] applies and (14) and (15) follow. ☐

Remark 1.

In principle the same results may be obtained if we treat both${\lambda }_1$and${\lambda }_2$as bifurcation parameters. In that case a generalization of the Crandall–Rabinowitz theorem given in [18], p.161, must be used. However, for our purposes the result presented here suffices since it shows that for any$a\left(t\right)>0$,$t\in (0,1)$, the bifurcation point of (12) and (13) leads to the bifurcation of (11).

The optimization problem is stated as: given $K_0=(\lambda ,\Lambda )$ find $a^{*}\left(t\right)$ in (12) and (13) so that a nontrivial solution exists and

$$w=\underset{0}{\overset{1}{\int }}{a}^{*}\left(t\right)dt$$

is minimal. This will represent the strongest compressed inverted column. We proceed with determining optimal $a^{*}\left(t\right).$

3. Minimization of w for Given Load Parameters $\lambda$ and $\Lambda$

We rewrite the system (12) and (13) as

$$\vartheta =x_1;a^2\dot{\vartheta }=x_2;x_3=\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi ,$$

(16)

so that (12) and (13) transforms to

$${\dot{x}}_1=\frac{x_2}{a^2};{\dot{x}}_2=-\lambda x_1{x}_3-\Lambda x_1;{\dot{x}}_3=-a,$$

(17)

and

$$x_1\left(1\right)=0;x_2\left(0\right)=0;x_3\left(1\right)=0.$$

(18)

The optimization problem now becomes: determine the control $a^{*}\left(t\right)\in U$ so that

$${\displaystyle \underset{a\in U}{min}}I={\displaystyle \underset{a\in U}{min}}\underset{0}{\overset{1}{\int }}a\left(t\right)dt=\underset{0}{\overset{1}{\int }}{a}^{*}\left(t\right)dt,$$

(19)

with differential constraints (17) and (18).

We take U as a set of continuous nonnegative functions, defined on the interval $[0,1]$, i.e., $U=\{u:u\in C^1([0,1],{\mathbb{R}}_{+});u\left(t\right)\ge 0\}.$

To solve the optimization problem we use the Pontryagin’s principle. For recent example of application of Pontryagin’s principle, see an example from biology [20]. Here the Pontryagin’s function $\mathcal{H}$ becomes (see [12])

$$\mathcal{H}=a+p_1\frac{x_2}{a^2}+p_2(-\lambda x_1{x}_3-\Lambda x_1)+p_3(-a),$$

where variables $p_i,i=1,2,3$, are determined from

$${\dot{p}}_1=-\frac{\partial \mathcal{H}}{\partial x_1}=p_2(\lambda x_3+\Lambda );{\dot{p}}_2=-\frac{\partial \mathcal{H}}{\partial x_2}=-\frac{p_1}{a^2};{\dot{p}}_3=-\frac{\partial \mathcal{H}}{\partial x_3}=\lambda x_1{p}_2,$$

(20)

and

$$p_1\left(0\right)=0;p_2\left(1\right)=0;p_3\left(0\right)=0.$$

(21)

From the condition ${\displaystyle \underset{a\in U}{min}}\mathcal{H}$ we obtain

$$\frac{\partial \mathcal{H}}{\partial a}=1-2p_1\frac{x_2}{a^3}-p_3=0,$$

(22)

or

$$a={\left(\frac{2p_1{x}_2}{1-p_3}\right)}^{1/3}.$$

(23)

We note that state variables $x_i,i=1,2$, and co-state variables $p_i,i=1,2$, have an important symmetry. Namely, by comparing

$$\begin{array}{cc}\hfill {\dot{x}}_1& =\frac{x_2}{a^2};{\dot{x}}_2=-x_1(\lambda x_3+\Lambda );x_1\left(1\right)=0;x_2\left(0\right)=0;\hfill \\ \hfill {\dot{p}}_1& =p_2(\lambda x_3+\Lambda );{\dot{p}}_2=-\frac{p_1}{a^2};p_1\left(0\right)=0;p_2\left(1\right)=0,\hfill \end{array}$$

we conclude that for any $c\ne 0$ the solution $x_1,x_2$ determines the co-state variables $p_1,p_2$ by

$$p_1=c{x}_2;p_2=-c{x}_1.$$

This type of identification was used in [9] and is applicable to both single and bi modal optimization of elastic rods. Since $a\ge 0$, we conclude from (23) that $c>0.$ We set $c=1$ so that

$$p_1=x_2;p_2=-x_1.$$

(24)

Thus, (23) becomes

$$a={\left(\frac{2x_2^2}{1-p_3}\right)}^{1/3}.$$

(25)

From (22) and (24) follows

$$\frac{{\partial }^2\mathcal{H}}{\partial a^2}=6\frac{x_2^2}{a^4}\ge 0.$$

(26)

Note that (26) is a necessary condition for ${\displaystyle \underset{a\in U}{min}}\mathcal{H}$. We comment now on the sufficient conditions for the minimality of (19). There are two main sufficiency theorems in optimal control theory. First one is the Mangasarian’s sufficiency theorem, see [21], which requires that the objective function and constraints are convex jointly in state and control variables for the minimization problems. The second condition, known as the Arrow’s theorem, is applied as follows, see [22]. The control variable (23) is substituted in Pontryagin’s function $\mathcal{H}$ to obtain

$$\mathcal{H}=2p_1\frac{x_2}{{\left(\frac{2x_2^2}{1-p_3}\right)}^{2/3}}+p_2(-\lambda x_1{x}_3-\Lambda x_1).$$

(27)

Now, the condition ${\displaystyle \underset{a\in U}{min}}\mathcal{H}$ is guaranteed if in expression (27) the function $\mathcal{H}$ is convex function with respect to $x_i,i=1,2,3$, when $p_i,i=1,2,3$, are fixed and positive. This is not the case here.

There are many other approaches to the problem of specifying the sufficient conditions for minimum of $\mathcal{H}.$ For example, in [23] the sufficient conditions involve Legendre–Clebsch condition and solution of an additional Riccati equation. Such a study is beyond the scope of our paper. Therefore, in the analysis that follow we will use only the necessary conditions for ${\displaystyle \underset{a\in U}{min}}\mathcal{H}$ given by (22).

Solving (20)${}_3$ and (21)${}_3$ for $p_3$ we obtain

$$p_3=-\lambda {\int }_0^t{x}_1^2\left(\xi \right)d\xi ,$$

(28)

so that (25) leads to

$$1+\lambda \underset{0}{\overset{t}{\int }}{\vartheta }^2\left(\xi \right)d\xi =2a{\dot{\vartheta }}^2.$$

(29)

Now, differentiating (29) it follows

$${(a{\dot{\vartheta }}^2)}^{·}-\frac{\lambda }{2}{\vartheta }^2=0.$$

(30)

Thus, the optimal compressed inverted column is determined from

$${\left(a^2\dot{\vartheta }\right)}^{·}+\lambda \vartheta \underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi +\Lambda \vartheta =0;{(a{\dot{\vartheta }}^2)}^{·}-\frac{\lambda }{2}{\vartheta }^2=0,$$

(31)

subject to

$${\displaystyle \underset{t\to 0}{lim}}{a}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0.$$

(32)

Our condition (31) and (32) reduces to condition presented in [24]. Also, the optimality conditions presented in [25,26] are equivalent to our conditions. We note that in [24,25,26] the results are obtained by methods different from ours. From (29) and (25) we obtain

$$a\left(0\right){\dot{\vartheta }}^2\left(0\right)=\frac{1}{2};a\left(0\right)=0.$$

4. Variational Principle and First Integrals for (31), (32)

Let

$$\dot{z}=-a\left(t\right),$$

(33)

with $z\left(1\right)=0.$ Then $z\left(t\right)$ is positive decreasing function. With (33) the system (31) becomes

$${({\dot{z}}^2\dot{\vartheta })}^{·}+\lambda \vartheta z+\Lambda \vartheta =0;{(\dot{z}{\dot{\vartheta }}^2)}^{·}+\frac{\lambda }{2}{\vartheta }^2=0,$$

(34)

subject to

$${\displaystyle \underset{t\to 0}{lim}}{\dot{z}}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0;w^{*}=z(0);z\left(1\right)=0.$$

(35)

Without loss of generality, we analyze (34) and (35) for $w^{*}=1$. With $w^{*}=1$ we have

$${\left({\dot{z}}^2\dot{\vartheta }\right)}^{·}+\lambda \vartheta z+\Lambda \vartheta =0;{(\dot{z}{\dot{\vartheta }}^2)}^{·}+\frac{\lambda }{2}{\vartheta }^2=0,$$

(36)

and

$${\displaystyle \underset{t\to 0}{lim}}{\dot{z}}^2\left(t\right)\dot{\vartheta }\left(t\right)=0;\vartheta \left(1\right)=0;z(0)=1;z\left(1\right)=0.$$

(37)

We state now our central result as:

Theorem 2.

For the solution to (36) and (37) we have:

1. 

($z,\vartheta$) gives stationary value

$$\delta J(z,\vartheta ,\Lambda )=0,$$

to the functional

$$J(Z,\Theta ,\Lambda )=\frac{1}{2}\underset{0}{\overset{1}{\int }}({\dot{Z}}^2{\dot{\Theta }}^2-\lambda {\Theta }^{2}Z-\Lambda {\Theta }^2)dt.$$

(38)

Here the functions$(Z,\Theta )$belong to the space$\mathcal{K}$defined as

$$\mathcal{K}=\{k:k=(Z,\Theta );Z\left(0\right)=1;Z\left(1\right)=0;{\displaystyle \underset{t\to 0}{lim}}{\dot{Z}}^2\left(t\right)\dot{\Theta }\left(t\right)=0;\Theta \left(1\right)=0\}.$$

2. 

The functional (38) on the solution of (36) and (37) has value equal to zero, i.e.,

$$J(z,\vartheta ,\Lambda )=\frac{1}{2}\underset{0}{\overset{1}{\int }}({\dot{z}}^2{\dot{\vartheta }}^2-\lambda {\vartheta }^{2}z-\Lambda {\vartheta }^2)dt=0.$$

(39)

3. 

The following first integrals of (36), (37) hold

$$\begin{array}{cc}\hfill \frac{3}{2}{\dot{z}}^2{\dot{\vartheta }}^2+\frac{1}{2}\lambda {\vartheta }^{2}z+\frac{1}{2}\Lambda {\vartheta }^2& =C,\hfill \\ \hfill 8\dot{z}{\dot{\vartheta }}^{2}z-5{\dot{z}}^2\dot{\vartheta }\vartheta +4+4\frac{\Lambda }{\lambda }[1+2\dot{z}{\dot{\vartheta }}^2]& =2Ct,\hfill \end{array}$$

(40)

where$C=\frac{3}{2}\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2$and is given as

$$C=\frac{1}{6}{[\sqrt{{\left(4\frac{\Lambda }{\lambda }\right)}^2+12(1+\frac{\Lambda }{\lambda })\frac{1}{\dot{\vartheta }{\left(1\right)}^2}}+4\frac{\Lambda }{\lambda }]}^2\dot{\vartheta }{\left(1\right)}^2.$$

Proof of Theorem 2.

Let

$$\mathcal{L}=\frac{1}{2}({\dot{Z}}^2{\dot{\Theta }}^2-\lambda {\Theta }^{2}Z-\Lambda {\Theta }^2).$$

(41)

Let $I(Z,\Theta )$ be a functional defined as

$$I(Z,\Theta )=\underset{0}{\overset{1}{\int }}\mathcal{L}dt,$$

and consider the problem of minimizing I when $(Z,\Theta )\in \mathcal{K}$. The necessary condition for optimality are the Euler–Lagrange equations

$$\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot{Z}}\right)-\frac{\partial \mathcal{L}}{\partial Z}=0;\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot{\Theta }}\right)-\frac{\partial \mathcal{L}}{\partial \Theta }=0,$$

which are equal to (36). Therefore

$$\delta J(z,\vartheta ,\Lambda )=0,$$

which is 1 in Theorem 1. Next by multiplying (36)${}_1$ by $\vartheta$ and integrating, we get

$$\underset{0}{\overset{1}{\int }}(-{\dot{z}}^2{\dot{\vartheta }}^2+\lambda {\vartheta }^{2}z+\Lambda {\vartheta }^2)dt=0,$$

that proves (39). Since $\mathcal{L}$ given by (41) does not have explicit dependance on t, we conclude that Hamiltonian $\mathcal{H}$ is a constant (i.e., $\mathcal{H}=\frac{\partial \mathcal{L}}{\partial \dot{z}}\dot{z}+\frac{\partial \mathcal{L}}{\partial \dot{\vartheta }}\dot{\vartheta }-\mathcal{L}=const.$). Thus, for (36) and (37) we have [12]

$$\frac{\partial \mathcal{L}}{\partial \dot{z}}\dot{z}+\frac{\partial \mathcal{L}}{\partial \dot{\vartheta }}\dot{\vartheta }-\mathcal{L}=\frac{3}{2}{\dot{z}}^2{\dot{\vartheta }}^2+\frac{\lambda }{2}{\vartheta }^{2}z+\frac{\Lambda }{2}{\vartheta }^2=const.$$

or

$$\frac{3}{2}{\dot{z}}^2{\dot{\vartheta }}^2+\frac{\lambda }{2}{\vartheta }^{2}z+\frac{\Lambda }{2}{\vartheta }^2=\frac{3}{2}{\dot{z}}^2\left(1\right){\dot{\vartheta }}^2\left(1\right).$$

(42)

To determine $\dot{z}$ in terms of $\dot{\vartheta }$ we multiply ${\left(36\right)}_1$ by $\vartheta$ and ${\left(36\right)}_2$ by $-2z$, add the result, integrate and use the boundary conditions to obtain

$$\underset{0}{\overset{1}{\int }}{\dot{z}}^2{\dot{\vartheta }}^{2}dt=1-\Lambda \underset{0}{\overset{1}{\int }}{\vartheta }^{2}dt.$$

(43)

Also from (29) we have

$$\underset{0}{\overset{1}{\int }}{\vartheta }^{2}dt=-\frac{1}{\lambda }[1+2\dot{z}\left(1\right)\dot{\vartheta }{\left(1\right)}^2].$$

(44)

By combining (43) and (44) and integrating (42) we obtain

$$\frac{3}{2}\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2-4\frac{\Lambda }{\lambda }\dot{z}\left(1\right)\dot{\vartheta }{\left(1\right)}^2-2(1+\frac{\Lambda }{\lambda })=0.$$

(45)

By solving (45) for $\dot{z}\left(1\right)$ and by using the result in (42) we obtain (40)${}_1$. Next we multiply (36)${}_1$ by $\vartheta$ and (36)${}_2$ by z and substitute in the resulting equations the term ${\dot{z}}^2{\dot{\vartheta }}^2$ from (42) to obtain

$$\begin{array}{cc}\hfill {\left({\dot{z}}^2\dot{\vartheta }\vartheta \right)}^{·}& =\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2-\frac{4}{3}[\lambda {\vartheta }^{2}z+\Lambda {\vartheta }^2],\hfill \\ \hfill {\left(z\dot{z}{\dot{\vartheta }}^2\right)}^{·}& =\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2-\frac{5}{6}\lambda {\vartheta }^{2}z-\frac{1}{3}\Lambda {\vartheta }^2.\hfill \end{array}$$

(46)

Using (42) and eliminating the term $\lambda {\vartheta }^{2}z$ from (46) we obtain

$$8{\left(z\dot{z}{\dot{\vartheta }}^2\right)}^{·}-5{\left({\dot{z}}^2\dot{\vartheta }\vartheta \right)}^{·}=3\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2+4\Lambda {\vartheta }^2.$$

Integrating the previous relation and using the boundary conditions it follows

$$8z\dot{z}{\dot{\vartheta }}^2-5{\dot{z}}^2\dot{\vartheta }\vartheta =3\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^{2}t-4+4\Lambda {\int }_0^t{\vartheta }^{2}d\xi .$$

Finally, by expressing ${\int }_0^t{\vartheta }^{2}d\xi$ from (29) and recalling that $3\dot{z}{\left(1\right)}^2\dot{\vartheta }{\left(1\right)}^2=2C$, we get

$$8\dot{z}{\dot{\vartheta }}^{2}z-5{\dot{z}}^2\dot{\vartheta }\vartheta =2Ct-4-4\frac{\Lambda }{\lambda }[1+2\dot{z}{\dot{\vartheta }}^2],$$

so that (40)${}_2$ holds. ☐

Remark 2.

In the special case$\Lambda =0$we have$C=2$, so that first integrals take the form

$$\begin{array}{cc}\hfill \frac{3}{2}{\dot{z}}^2{\dot{\vartheta }}^2+\frac{1}{2}\lambda {\vartheta }^{2}z& =2,\hfill \\ \hfill 5{\dot{z}}^2\dot{\vartheta }\vartheta -8\dot{z}{\dot{\vartheta }}^{2}z& =4(1-t),\hfill \end{array}$$

obtained in [10]. Also, by evaluating (40) at$t=0,$it follows$\vartheta \left(0\right)=\frac{2}{\sqrt{\lambda }}$.

5. Invariance Properties of the Integral (38)

Consider transformation of independent and dependent variables in (38) given by

$$\begin{array}{cc}\overline{z}\left(\overline{t}\right)& =z\left(t\right)+\epsilon F_z(t,z\left(t\right),\vartheta \left(t\right)),\hfill \\ \hfill \overline{\vartheta }\left(\overline{t}\right)& =\vartheta \left(t\right)+\epsilon F_{\vartheta }(t,z\left(t\right),\vartheta \left(t\right)),\hfill \\ \hfill \overline{t}& =t+\epsilon f(t,z(t),\vartheta (t\left)\right),\hfill \end{array}$$

(47)

where $F_z,F_{\vartheta }$ and f are generators of the infinitesimal transformation group and $\epsilon \ll 1.$ The case of multi-time transformation and corresponding version for Noether-type first integrals is presented in [14]. Here, it is assumed that $F_z,F_{\vartheta }$ and f are continuously differentiable with respect to all variables. If action integral (38) is invariant under the transformation (47), then Noether’s theorem guarantees the existence of a first integral to the Euler–Lagrange’s system of equations (34), see [12], p. 137. Using Noether’s theorem for the present case, we state:

Theorem 3.

If the generators of the infinitesimal transformation group$F_z$,$F_{\vartheta }$, f satisfy

$$\begin{array}{cc}\hfill & \frac{\partial \mathcal{L}}{\partial z}{F}_z+\frac{\partial \mathcal{L}}{\partial \vartheta }{F}_{\vartheta }+\frac{\partial \mathcal{L}}{\partial \dot{z}}({\dot{F}}_z-\dot{z}\dot{f})\hfill \\ \hfill & +\frac{\partial \mathcal{L}}{\partial \dot{\vartheta }}({\dot{F}}_{\vartheta }-\dot{\vartheta }\dot{f})+\frac{\partial \mathcal{L}}{\partial t}f+\mathcal{L}\dot{f}-\dot{P}\begin{array}{c}=\end{array}0,\hfill \end{array}$$

(48)

where$\mathcal{L}=\frac{1}{2}({\dot{z}}^2{\dot{\vartheta }}^2-\lambda {\vartheta }^{2}z-\Lambda {\vartheta }^2)$and$P=P(t,z,\vartheta )$is an arbitrary function continuously differentiable with respect to all variables (gauge function), then the system (34) has a first integral of the form

$$\frac{\partial \mathcal{L}}{\partial \dot{z}}(F_z-\dot{z}f)+\frac{\partial \mathcal{L}}{\partial \dot{\vartheta }}(F_{\vartheta }-\dot{\vartheta }f)+\mathcal{L}f-P=const.$$

(49)

We apply now the Theorem 3 to the Lagrangian (41). Thus, we calculate $\frac{\partial \mathcal{L}}{\partial z},\cdots ,\frac{\partial \mathcal{L}}{\partial \dot{\vartheta }}$ and substitute the result into (48). The invariance condition then becomes

$$\begin{array}{cc}\hfill & -\frac{1}{2}\lambda {\vartheta }^2{F}_z-(\lambda \vartheta z+\Lambda \vartheta )F_{\vartheta }+\dot{z}{\dot{\vartheta }}^2({\dot{F}}_z-\dot{z}\dot{f})\hfill \\ \hfill & +{\dot{z}}^2\dot{\vartheta }({\dot{F}}_{\vartheta }-\dot{\vartheta }\dot{f})+\frac{1}{2}({\dot{z}}^2{\dot{\vartheta }}^2-\lambda {\vartheta }^{2}z-\Lambda {\vartheta }^2)\dot{f}-\dot{P}\begin{array}{c}=\end{array}0.\hfill \end{array}$$

(50)

Consider two special cases generators of the infinitesimal transformation group $F_z,F_{\vartheta },f$ and gauge function P:

• Case 1: Suppose that $F_z=F_{\vartheta }=P=0,f=A,A=const.$ The condition (50) is satisfied and the first integral (49) is

  $$\frac{3}{2}{\dot{z}}^2{\dot{\vartheta }}^2+\frac{1}{2}\lambda {\vartheta }^{2}z+\frac{1}{2}\Lambda {\vartheta }^2=C,$$

  (51)

  given as (40)${}_1.$ Note that this first integral (51) may be writen as $2{\dot{z}}^2{\dot{\vartheta }}^2-\mathcal{L}=C.$
• Case 2: Suppose that $F_z=z,F_{\vartheta }=\frac{\vartheta }{2},f=0.$ We shall determine P so that (50) is satisfied. This leads to the condition

  $$\dot{P}=[\mathcal{L}+{\dot{z}}^2{\dot{\vartheta }}^2-\frac{\lambda }{2}{\vartheta }^{2}z],$$

  or

  $$\dot{P}=-C+3{\dot{z}}^2{\dot{\vartheta }}^2-\frac{1}{2}\lambda {\vartheta }^{2}z=C-\frac{3}{2}\lambda {\vartheta }^{2}z-\Lambda {\vartheta }^2.$$
  By using (46) to eliminate $\lambda {\vartheta }^{2}z$ we obtain

  $$\dot{P}=\frac{C}{4}+\frac{9}{8}{\left({\dot{z}}^2\dot{\vartheta }\vartheta \right)}^{·}-\frac{\Lambda }{2\lambda }{(1+2\dot{z}{\dot{\vartheta }}^2)}^{·}.$$
  Finally, from (29) we have ${\vartheta }^2=-\frac{{(1+2\dot{z}{\dot{\vartheta }}^2)}^{·}}{\lambda }$, so that substituting in the previous equation and integrating, we obtain

  $$P=\frac{C}{4}t+\frac{9}{8}{\dot{z}}^2\dot{\vartheta }\vartheta -\frac{\Lambda }{2\lambda }(1+2\dot{z}{\dot{\vartheta }}^2)+C_p,$$

  where $C_p$ is a constant. The first integral (49) now becomes

  $$8\dot{z}{\dot{\vartheta }}^{2}z-5{\dot{z}}^2\dot{\vartheta }\vartheta -2Ct+4\frac{\Lambda }{\lambda }[1+2\dot{z}{\dot{\vartheta }}^2]=const.$$

  which is equal to (40)${}_2$ when we specify the value of constant.

6. Results of Numerical Solution to (36), (37)

Using variables (16), $x_4=p_3$ and $x_5=\Lambda$ the system (17), (18), (25) and (28) transforms to

$$\begin{array}{cc}\hfill {\dot{x}}_1& =\frac{x_2}{{\left(\frac{2x_2^2}{1-x_4}\right)}^{2/3}};{\dot{x}}_2=-\lambda x_1{x}_3-x_5{x}_1;\hfill \\ \hfill {\dot{x}}_3& =-{\left(\frac{2x_2^2}{1-x_4}\right)}^{1/3};{\dot{x}}_4=-\lambda x_1^2;{\dot{x}}_5=0,\hfill \end{array}$$

(52)

with boundary conditions

$$x_1\left(1\right)=0;x_2\left(0\right)=0;x_3\left(1\right)=0;x_4\left(0\right)=0.$$

(53)

Thus, we have to choose $\Lambda =x_5$ in order to satisfy $x_3\left(1\right)=\left(\underset{t}{\overset{1}{\int }}a\left(\xi \right)d\xi \right){|}_{t=1}=0.$ Conservation laws (40) with $x_i,i=1,\cdots ,4$, become

$$\begin{array}{cc}\hfill & \frac{3}{2}\frac{{\left(x_2\left(t\right)\right)}^2}{{\left(\frac{2x_2{\left(t\right)}^2}{1-x_4\left(t\right)}\right)}^{2/3}}+\frac{\lambda }{2}{\left(x_1\left(t\right)\right)}^2{x}_3\left(t\right)+\frac{\Lambda }{2}{\left(x_1\left(t\right)\right)}^2=C,\hfill \\ \hfill & -4(1-x_4\left(t\right))x_3\left(t\right)-5x_1\left(t\right)x_2(t)+4+4\frac{\Lambda }{\lambda }{x}_4(t)=2Ct,t\in (0,1),\hfill \\ \hfill C& =\frac{1}{6}{[\sqrt{{\left(4\frac{\Lambda }{\lambda }\right)}^2+12(1+\frac{\Lambda }{\lambda })\frac{1}{\dot{\vartheta }{\left(1\right)}^2}}-4\frac{\Lambda }{\lambda }]}^2\dot{\vartheta }{\left(1\right)}^2,\dot{\vartheta }\left(1\right)=\frac{x_2\left(1\right)}{{\left(\frac{2x_2^2\left(1\right)}{1-x_4\left(1\right)}\right)}^{2/3}}.\hfill \end{array}$$

(54)

In solving (52), (53) we used (54) to monitor the accuracy of the integration. We solved (52) and (53) with $\lambda$ as a given parameter. The eigenvalue $\Lambda =x_5$ is determined so that $x_3\left(0\right)=1$, that is the volume of the column is given as $w=1$. In Table 1 the results of computation are presented.

Table 1. Critical values of the load parameter.

λ	0	1	2	3	3.5	3.893026
Λ	$3.289868$	$2.433148$	$1.583948$	$0.743068$	$0.326056$	0

For values of $\lambda$ shown in Table 1 the first integrals (54) are constants up to the order of ${10}^{-8}$. In numerical solution of (52), (53) and evaluation of the first integrals we used the computer package Mathcad 14.

In Figure 2 the optimal cross-sectional area is shown that corresponds to the following values of parameter $\lambda :{\lambda }_0=0,{\lambda }_1=1,{\lambda }_3=3,\lambda =3.893\dots$ The corresponding values of $\Lambda$ are taken from Table 1. We note that to ${\lambda }_0=0$ we have $\Lambda =3.289868133696451.$ This is a special case of optimally shaped light column, see [15] p.216, and the exact value is $\Lambda =\frac{{\pi }^2}{3}$. Our numerical result given in the Table 1 agrees with the exact value up to the order ${10}^{-10}$. Also for the light optimal rod, the analytical result is $a\left(1\right)=\frac{4}{3}$, while our numerical value is $a\left(1\right)=1.333435777857.$ Another special case presented in Figure 2 corresponds to the case $\lambda =3.893026$ and the compressive force is $\Lambda =0$. This shape is shown by curve ${\lambda }_{3.893\dots }$ in Figure 2.

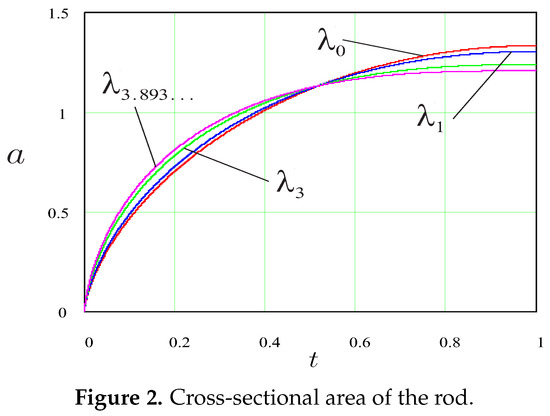
Figure 2. Cross-sectional area of the rod.

We present also the shape of the optimally designed column in the post-critical state. Thus, we solve the following system

$$\begin{array}{cc}\hfill \dot{X}& =cos\Theta ;X(0)=0;\dot{Y}=sin\Theta ;Y(0)=0;\dot{\Theta }=\frac{M}{{\left(a^{*}\right)}^2};\Theta (1)=0;\hfill \\ \hfill \dot{M}& =-[\lambda \underset{t}{\overset{1}{\int }}{a}^{*}\left(\xi \right)d\xi +\Lambda ]sin\Theta ;M(0)=0,\hfill \end{array}$$

(55)

where $a^{*}$ is given by (23). The solution for $X,Y$ of (55) is shown in Figure 3 for $\lambda ={\lambda }_{cr},\Lambda ={\Lambda }_{cr}+0.5,$ with $({\lambda }_{cr}=1,{\Lambda }_{cr}=2.433148).$ Also, in the same Figure 3 we show the shape of the rod $x,y$ according to linear theory.

Figure 3. Post-critical shape of optimally shaped rod X, Y and $x=t,y,$ where $\dot{y}=\vartheta$, and $\vartheta$ is the eigenfunction of (12) and (13).

7. Conclusions

We analysed the problem of finding the shape of the strongest compressed inverted column in a constant gravity field. The problem treated here, for the case when the column has constant cross-section, is analyzed in [27,28,29]. Our main results may be summarized as:

• We proved that the eigenvalues of the linearized problem are bifurcation points of the nonlinear equilibrium equations for arbitrary cross-sectional area, Theorem 1.
• We formulated optimality conditions in the form (31) and (32). The variational principle and two first integrals are determined.
• We determined transformation group that generates first integrals via Noether’s theorem. Those transformation groups leave the functional (38), absolutely in Case 1, and gauge invariant in Case 2.
• The shape of the column, as a function of arc-length, is determined for several values of parameters given in Table 1. The special case $\lambda =0$ corresponds to the known analytical solution of Lagrange problem.
• The post critical behaviour of the optimally shaped column is presented for one specific value of parameters.

The increase of the buckling force for optimally shaped column and the column with constant cross-section is between 12% for $\Lambda =0$, see [10], and 33%, for $\lambda =0$, see [3].