On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays
Abstract
1. Introduction
2. Preliminary Notes
- for , the functions are continuous, and the following relations hold:uniformly on .
- The functions are smooth enough on .
3. -Stability Results
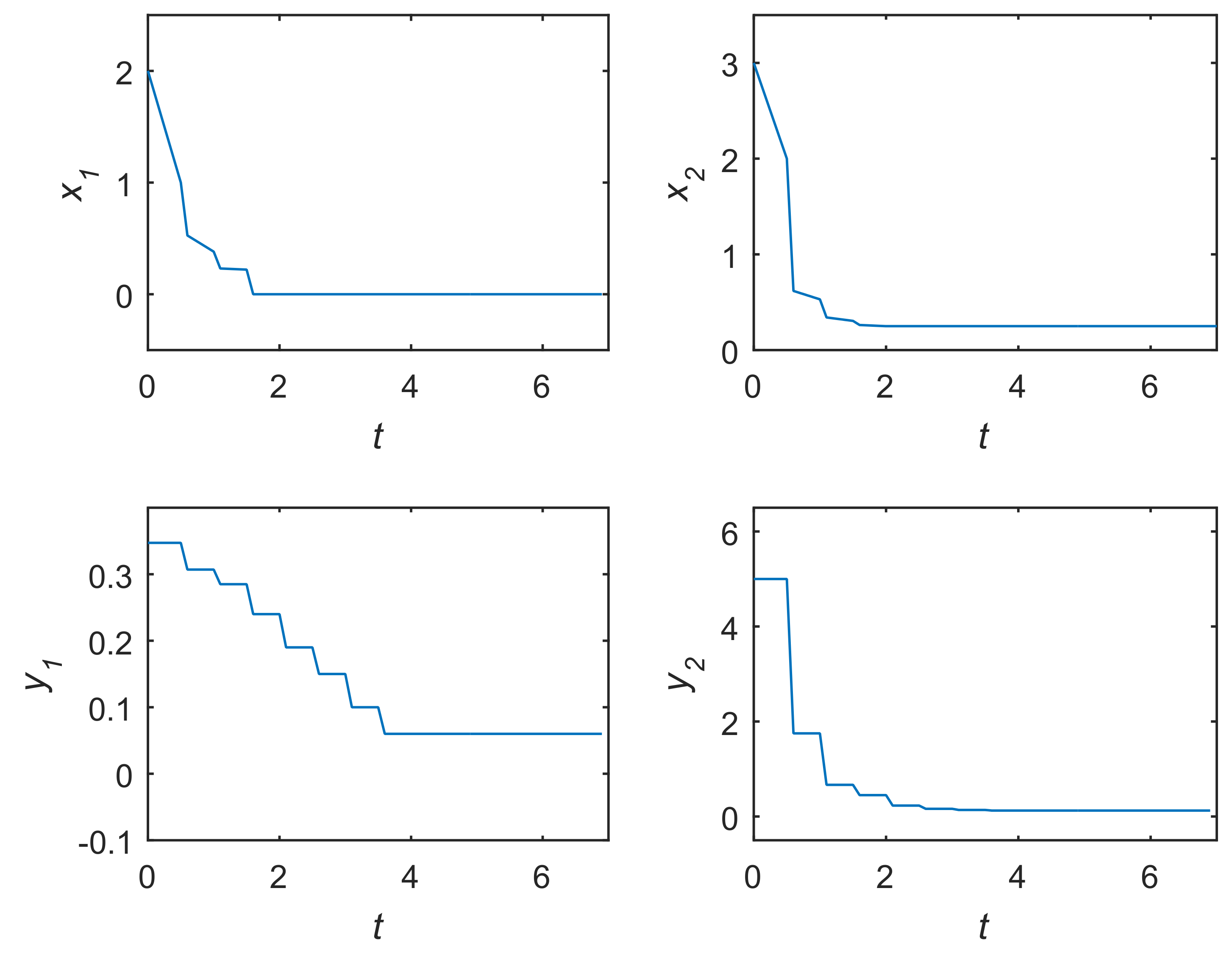
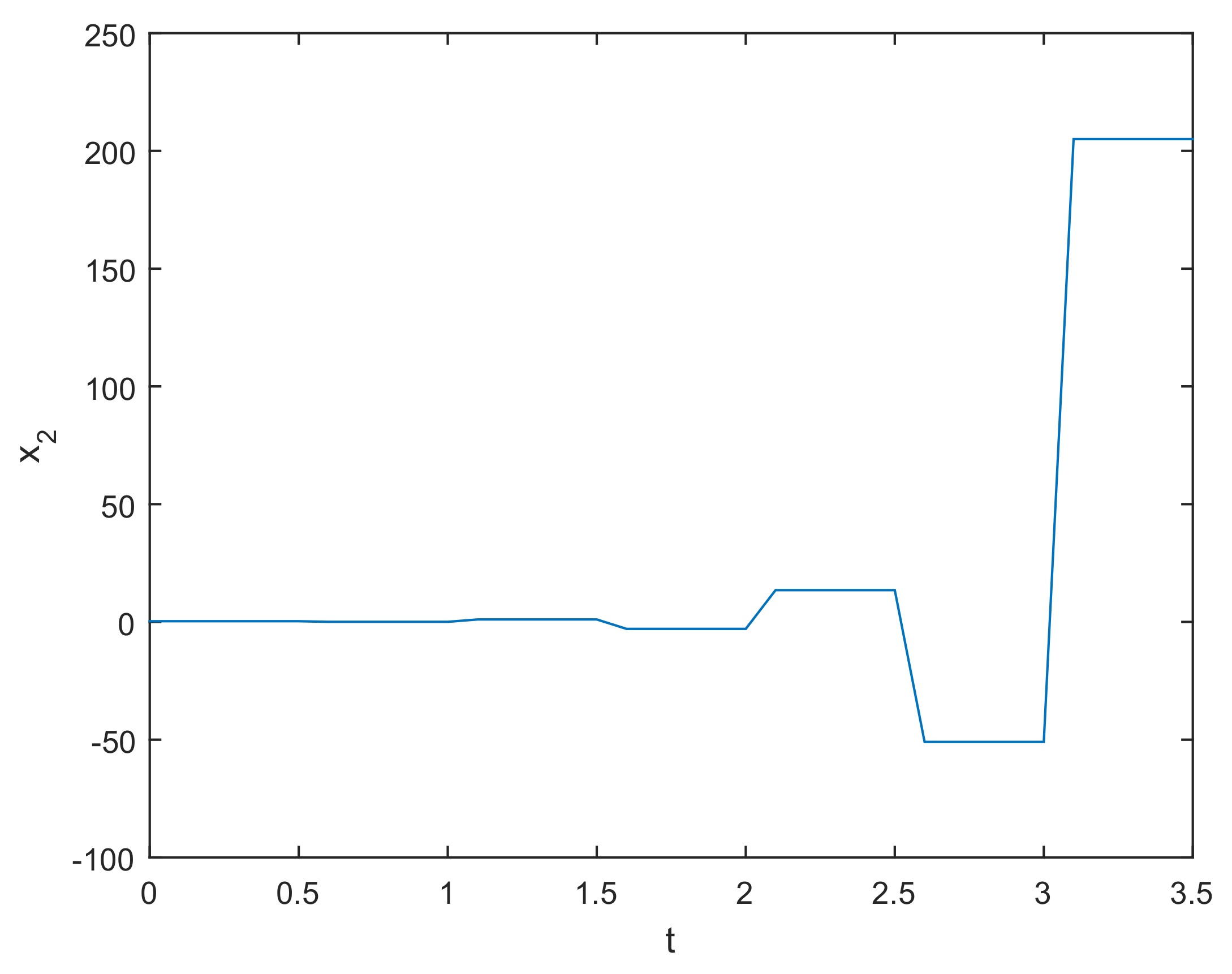
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cohen, M.A.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 1983, 13, 815–826. [Google Scholar] [CrossRef]
- Guo, S.; Huang, L. Stability analysis of Cohen–Grossberg neural networks. IEEE Trans. Neural Netw. 2006, 17, 106–117. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Huang, L.; Guo, Z.; Hu, Q. Stability analysis of Cohen–Grossberg neural networks with discontinuous neuron activations. Appl. Math. Model. 2010, 34, 358–365. [Google Scholar] [CrossRef]
- Wan, A.; Wang, M.; Peng, J.; Mao, W. Global exponential stability analysis of Cohen–Grossberg neural networks. Math. Appl. (Wuhan) 2006, 19, 381–387. [Google Scholar]
- Kosko, B. Adaptive bi-directional associative memories. Appl. Opt. 1987, 26, 4947–4960. [Google Scholar] [CrossRef]
- Kosko, B. Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18, 49–60. [Google Scholar] [CrossRef]
- Kosko, B. Neural Networks and Fuzzy Systems: A Dynamical System Approach to Machine Intelligence; Prentice-Hall: Englewood Cliffs, NJ, USA, 1992; ISBN1 0136114350. ISBN2 9780136114352. [Google Scholar]
- Wang, H.; Song, Q.; Duan, C. LMI criteria on exponential stability of BAM neural networks with both time-varying delays and general activation functions. Math. Comput. Simul. 2010, 81, 837–850. [Google Scholar] [CrossRef]
- Gan, Q. Adaptive synchronization of Cohen–Grossberg neural networks with unknown parameters and mixed time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3040–3049. [Google Scholar] [CrossRef]
- Song, Q.; Cao, J. Stability analysis of Cohen–Grossberg neural network with both time-varying and continuously distributed delays. Comput. Appl. Math. 2006, 197, 188–203. [Google Scholar] [CrossRef]
- Yuan, K.; Cao, J.; Li, H. Robust stability of switched Cohen–Grossberg neural networks with mixed time-varying delays. IEEE Trans. Syst. Man Cybern. 2006, 36, 1356–1363. [Google Scholar] [CrossRef]
- Arik, A. Global asymptotic stability of hybrid bidirectional associative memory neural networks with time delays. Phys. Lett. A 2006, 351, 85–91. [Google Scholar] [CrossRef]
- Cao, J.; Ho, D.W.C.; Huang, X. LMI-based criteria for global robust stability of bidirectional associative memory networks with time delay. Nonlinear Anal. 2007, 66, 1558–1572. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, B. Exponential stability of BAM neural networks with time-varying delays. J. Appl. Math. Comput. 2009, 30, 385–396. [Google Scholar] [CrossRef]
- Aouiti, C.; Assali, E.A. Nonlinear Lipschitz measure and adaptive control for stability and synchronization in delayed inertial Cohen–Grossberg-type neural networks. Int. J. Adapt. Control 2019, 33, 1457–1477. [Google Scholar] [CrossRef]
- Ozcan, N. Stability analysis of Cohen–Grossberg neural networks of neutral-type: Multiple delays case. Neural Netw. 2019, 113, 20–27. [Google Scholar] [CrossRef]
- Pratap, K.A.; Raja, R.; Cao, J.; Lim, C.P.; Bagdasar, O. Stability and pinning synchronization analysis of fractional order delayed Cohen–Grossberg neural networks with discontinuous activations. Appl. Math. Comput. 2019, 359, 241–260. [Google Scholar] [CrossRef]
- Zhao, Y.; Kurths, J.; Duan, L. Input-to-state stability analysis for memristive BAM neural networks with variable time delays. Phys. Lett. A 2019, 383, 1143–1150. [Google Scholar] [CrossRef]
- Ali, M.S.; Saravanan, S.; Rani, M.E.; Elakkia, S.; Cao, J.; Alsaedi, A.; Hayat, T. Asymptotic stability of Cohen–Grossberg BAM neutral type neural networks with distributed time varying delays. Neural Process. Lett. 2017, 46, 991–1007. [Google Scholar] [CrossRef]
- Cao, J.; Song, Q. Stability in Cohen–Grossberg type bidirectional associative memory neural networks with time-varying delays. Nonlinearity 2006, 19, 1601–1617. [Google Scholar] [CrossRef]
- Du, Y.; Zhong, S.; Zhou, N.; Shi, K.; Cheng, J. Exponential stability for stochastic Cohen–Grossberg BAM neural networks with discrete and distributed time-varying delays. Neurocomputing 2014, 127, 144–151. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Z.; Wang, L. Existence and global exponential stability of periodic solution to Cohen–Grossberg BAM neural networks with time-varying delays. Abstr. Appl. Anal. 2012, 2012, 805846. [Google Scholar] [CrossRef]
- Wang, J.; Tian, L.; Zhen, Z. Global Lagrange stability for Takagi-Sugeno fuzzy Cohen–Grossberg BAM neural networks with time-varying delays. Int. J. Control Autom. 2018, 16, 1603–1614. [Google Scholar] [CrossRef]
- Aouiti, C.; Ben Gharbia, I.; Cao, J.; M’hamdi, M.S.; Alsaedi, A. Existence and global exponential stability of pseudo almost periodic solution for neutral delay BAM neural networks with time-varying delay in leakage terms. Chaos Solitons Fractals 2018, 107, 111–127. [Google Scholar] [CrossRef]
- Benchohra, M.; Henderson, J.; Ntouyas, S. Impulsive Differential Equations and Inclusions; Hindawi Publishing Corporation: New York, NY, USA, 2006. [Google Scholar]
- Haddad, W.M.; Chellaboina, V.S.; Nersesov, S.G. Impulsive and Hybrid Dynamical Systems, Stability, Dissipativity, and Control, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2006; ISBN 9780691127156. [Google Scholar]
- Li, X.; Bohner, M.; Wang, C.K. Impulsive differential equations: Periodic solutions and applications. Autom. J. IFAC 2015, 52, 173–178. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K. Impulsive Systems on Hybrid Time Domains, 1st ed.; Springer: Cham, Switzerland, 2019; ISBN1 978-3-030-06211-8. ISBN2 978-3-030-06212-5. [Google Scholar]
- Stamova, I.M.; Stamov, G.T. Applied Impulsive Mathematical Models, 1st ed.; Springer: Cham, Switzerland, 2016; ISBN1 978-3-319-28060-8. ISBN2 978-3-319-28061-5. [Google Scholar]
- He, W.; Qian, F.; Cao, J. Pinning-controlled synchronization of delayed neural networks with distributed-delay coupling via impulsive control. Neural Netw. 2017, 85, 1–9. [Google Scholar] [CrossRef]
- Li, X.; Song, S. Stabilization of delay systems: Delay-dependent impulsive control. IEEE Trans. Autom. Control 2017, 62, 406–411. [Google Scholar] [CrossRef]
- Li, X.; Wu, J. Sufficient stability conditions of nonlinear differential systems under impulsive control with state-dependent delay. IEEE Trans. Autom. Control 2018, 63, 306–311. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Huang, T. Persistence of delayed cooperative models: Impulsive control method. Appl. Math. Comput. 2019, 342, 130–146. [Google Scholar] [CrossRef]
- Stamova, I.M. Impulsive control for stability of n-species Lotka-Volterra cooperation models with finite delays. Appl. Math. Lett. 2010, 23, 1003–1007. [Google Scholar] [CrossRef][Green Version]
- Stamova, I.M.; Stamov, A.G. Impulsive control on the asymptotic stability of the solutions of a Solow model with endogenous labor growth. J. Franklin Inst. 2012, 349, 2704–2716. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, G.T. Impulsive control on global asymptotic stability for a class of bidirectional associative memory neural networks with distributed delays. Math. Comput. Model. 2011, 53, 824–831. [Google Scholar] [CrossRef]
- Stamova, I.M.; Stamov, T.; Simeonova, N. Impulsive control on global exponential stability for cellular neural networks with supremums. J. Vib. Control 2013, 19, 483–490. [Google Scholar] [CrossRef]
- Yang, X.; Peng, D.; Lv, X.; Li, X. Recent progress in impulsive control systems. Math. Comput. Simul. 2019, 155, 244–268. [Google Scholar] [CrossRef]
- Bai, C. Stability analysis of Cohen–Grossberg BAM neural networks with delays and impulses. Chaos Solitons Fractals 2008, 35, 263–267. [Google Scholar] [CrossRef]
- Li, K.; Zeng, H. Stability in impulsive Cohen–Grossberg-type BAM neural networks with time-varying delays: A general analysis. Math. Comput. Simul. 2010, 80, 2329–2349. [Google Scholar] [CrossRef]
- Li, X. Exponential stability of Cohen–Grossberg-type BAM neural networks with time-varying delays via impulsive control. Neurocomputing 2009, 73, 525–530. [Google Scholar] [CrossRef]
- Li, X. Existence and global exponential stability of periodic solution for impulsive Cohen–Grossberg-type BAM neural networks with continuously distributed delays. Appl. Math. Comput. 2009, 215, 292–307. [Google Scholar] [CrossRef]
- Maharajan, C.; Raja, R.; Cao, J.; Rajchakit, G.; Alsaedi, A. Impulsive Cohen–Grossberg BAM neural networks with mixed time-delays: An exponential stability analysis issue. Neurocomputing 2018, 275, 2588–2602. [Google Scholar] [CrossRef]
- Zhou, Q.; Wan, L. Impulsive effects on stability of Cohen–Grossberg-type bidirectional associative memory neural networks with delays. Nonlinear Anal. Real World Appl. 2009, 10, 2531–2540. [Google Scholar] [CrossRef]
- Benchohra, M.; Henderson, J.; Ntouyas, S.K.; Ouahab, A. Impulsive functional differential equations with variable times. Comput. Math. Appl. 2004, 47, 1659–1665. [Google Scholar] [CrossRef]
- Song, Q.; Yang, X.; Li, C.; Huang, T.; Chen, X. Stability analysis of nonlinear fractional-order systems with variable-time impulses. J. Franklin Inst. 2017, 354, 2959–2978. [Google Scholar] [CrossRef]
- Stamov, G.T.; Stamova, I.M. Integral manifolds for uncertain impulsive differential–difference equations with variable impulsive perturbations. Chaos Solitons Fractals 2014, 65, 90–96. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Huang, T.; Chen, X. Mittag–Leffler stability analysis on variable-time impulsive fractional-order neural networks. Neurocomputing 2016, 207, 276–286. [Google Scholar] [CrossRef]
- Yilmaz, E. Almost periodic solutions of impulsive neural networks at non-prescribed moments of time. Neurocomputing 2014, 141, 148–152. [Google Scholar] [CrossRef]
- Bohner, M.; Stamov, G.T.; Stamova, I.M. Almost periodic solutions of Cohen–Grossberg neural networks with time-varying delay and variable impulsive perturbations. Commun. Nonlinear Sci. Numer. Simul. 2020, 80, 104952. [Google Scholar] [CrossRef]
- Bohner, M.; Stamova, I.; Stamov, G. Impulsive control functional differential systems of fractional order: Stability with respect to manifolds. Eur. Phys. J. Spec. Top. 2017, 226, 3591–3607. [Google Scholar] [CrossRef]
- Martynyuk, A.; Stamov, G.; Stamova, I. Practical stability analysis with respect to manifolds and boundedness of differential equations with fractional-like derivatives. Rocky Mt. J. Math. 2019, 49, 211–233. [Google Scholar] [CrossRef]
- Smale, S. Stable manifolds for differential equations and diffeomorphisms. Ann. Scuola Norm. Sup. Pisa 1963, 3, 97–116. [Google Scholar]
- Stamov, G.; Stamova, I.M. Impulsive delayed Lasota–Wazewska fractional models: Global stability of integral manifolds. Mathematics 2019, 7, 1025. [Google Scholar] [CrossRef]
- Martynyuk, A.A.; Stamov, G.T.; Stamova, I.M. Impulsive fractional-like differential equations: Practical stability and boundedness with respect to h-manifolds. Fractal Fract. 2019, 3, 50. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamov, G.; Stamova, I.; Simeonov, S.; Torlakov, I. On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays. Mathematics 2020, 8, 335. https://doi.org/10.3390/math8030335
Stamov G, Stamova I, Simeonov S, Torlakov I. On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays. Mathematics. 2020; 8(3):335. https://doi.org/10.3390/math8030335
Chicago/Turabian StyleStamov, Gani, Ivanka Stamova, Stanislav Simeonov, and Ivan Torlakov. 2020. "On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays" Mathematics 8, no. 3: 335. https://doi.org/10.3390/math8030335
APA StyleStamov, G., Stamova, I., Simeonov, S., & Torlakov, I. (2020). On the Stability with Respect to H-Manifolds for Cohen–Grossberg-Type Bidirectional Associative Memory Neural Networks with Variable Impulsive Perturbations and Time-Varying Delays. Mathematics, 8(3), 335. https://doi.org/10.3390/math8030335




