Abstract
This study is devoted to the description of the asymptotic expansions of solutions of linear ordinary differential equations with holomorphic coefficients in the neighborhood of an infinitely distant singular point. This is a classical problem of analytical theory of differential equations and an important particular case of the general Poincare problem on constructing the asymptotics of solutions of linear ordinary differential equations with holomorphic coefficients in the neighborhoods of irregular singular points. In this study we consider such equations for which the principal symbol of the differential operator has multiple roots. The asymptotics of a solution for the case of equations with simple roots of the principal symbol were constructed earlier.
1. Introduction
One of the fundamental problems of the analytic theory of ordinary differential equations with holomorphic coefficients is the problem of constructing the asymptotics of their solutions in the neighborhood of irregular singular points. This problem was formulated by Poincare in [1,2]. Poincare considered infinity as an irregular singular point. The problem of constructing the asymptotics of solutions in the neighborhood of an infinitely distant point was earlier considered by Thome in [3], where it was shown that in a particular case, the asymptotics of a solution of the considered problem can be represented in the form of an expression that contains a formal, generally speaking, divergent power series. Poincare has proved that the obtained divergent series are asymptotic and the idea was formulated that summation of the asymptotic series obtained can be performed by using an integral transform; in a particular case, it may be the Laplace transform. With the help of this integral transform, an attempt was made to construct uniform asymptotics of this problem. However, the integral Laplace transform is applicable only in some particular cases. Therefore, the problem of constructing the asymptotics of solutions for differential equations with holomorphic coefficients in the neighborhood of an infinitely distant point formulated by Poincare is still unsolved in the general case. Our study is devoted to solving this problem for a broad class of differential equations with holomorphic coefficients. The class of the considered equations is described below; it is quite broad and comprises all ordinary differential equations with holomorphic coefficients up to the 5th order inclusive. In this paper, the idea of using the integral transform for summation of the asymptotic series and, thus, for constructing an uniform asymptotics of a solution, is developed by applying the integral Laplace–Borel transform.
Namely, we consider the following equation with holomorphic coefficients:
The coefficients are the functions holomorphic at an infinitely distant point. This means that there is the exterior of a circle such that the function can be expanded in it into convergent power series . The goal of our study was constructing the asymptotics of a solution to Equation (1) at .
Generally speaking, infinity can be considered as an irregular singular point of Equation (1). In the particular case, where infinity is a regular singular point, the problem of constructing the asymptotics of solutions has already been solved. It is known that the asymptotics of solutions in the neighborhood of regular singular points are conormal (see, for instance, [4]). Namely, their form is , where , are some complex numbers. Here, k is some natural number. A more detailed consideration of asymptotics of linear differential equations in the neighborhood of regular and irregular singular points can be found, for example, in [5,6,7].
The resurgent analysis methods which we will use in this study are applied for finite irregular singular points. Therefore, by means of the substitution , we reduce the problem of constructing the asymptotics of a solution in the neighborhood of an infinitely distant point to the problem of constructing the asymptotics of the solution in the neighborhood of zero for the linear differential equations with a cuspidal singularity of the second order. Namely, Equation (1) can be rewritten in the form
where .
Let us consider the differential operator and put the function into correspondence with it; this function is called the symbol of the differential operator . The function is called the principal symbol of the differential operator .
Using this notation, we can introduce a classification of ordinary differential equations with holomorphic coefficients. This will be done below.
2. Review of Literature
The most studied class of equations is that for which the principal symbol has only simple roots. In some papers, including [1,2] written by Poincare and, further, in [8], the asymptotics of solutions to the equations belonging to this class in the neighborhood of an infinitely distant point are constructed.
Later, the case of simple roots for systems of linear differential equations was considered in many studies and was already included in classical textbooks [5,6,7].
In those papers, the asymptotic expansions of solutions to ordinary differential equations were obtained in the form of the sum of the products of the corresponding exponentials and asymptotic series; namely,
where are the roots of the polynomial ; and are some complex numbers. However, the question concerning interpretation of the obtained divergent series remained open; i.e., a systematic method for summing up these divergent series did not exist. Let us call such asymptotics the non-Fuchsian asymptotics.
In the case where the asymptotic expansion
contains at least two terms corresponding to the values and with different real components (to be more specific, let us assume that Re > Re ), a significant difficulty arises when interpreting the obtained expansion. The fact of the matter is that all the terms of the first element that correspond to the value (the dominant element) have a higher order at than any term of the second (recessive) element. Hence, for interpretation of expansion (4), it is necessary to sum up the series (generally speaking, divergent) that corresponds to the dominant element. In particular, it is important to consider the recessive components in the expansion of the solution u of Equation (1) to construct uniform asymptotics of solutions for the complex case, when the point r moves on the complex plane, since a recessive component in one of the sectors of the complex plane may become a dominant component in other sector and vice versa. In other words, a plane is conventionally divided into the sectors in which one of the components is dominant while another is recessive; when passing from one sector to another, a change in their leadership occurs (the recessive component becomes dominant and vice versa). However, in the neighborhood of these sectors’ boundaries of these sectors, several components are of equal order and no one of them can be neglected. This is the Stokes phenomenon.
This phenomenon occurs, for instance, when considering the Euler example (see [9]) and when constructing the asymptotics of solutions for problem (1) in the neighborhood of an infinitely distant point and for all the non-Fuchian asymptotics (3) in general. As a result, investigation of the asymptotic expansions of solutions to Equation (1) requires introduction of a regular method for summation of divergent series for constructing uniform asymptotics of solutions.
When introducing the method for summation of divergent series, we will obtain an algorithm of constructing the uniform asymptotics, which will make it possible to consider the recessive components without dividing the complex plane into sectors. This method for summation is described in detail in [9].
In the late 1980s, an appropriate technique for summing up such series was proposed. This technique is based on the Laplace–Borel transform and on the concept of the resurgent function which was introduced for the first time by J. Ecalle [10]. Later, this technique was actively applied in the B.-W. Schulze, B. Yu. Sternin, and V. E. Shatalov’s works to study the degenerating equations obtained when considering elliptic equations on the manifolds with cuspidal singularities, as well as for constructing the asymptotics of solutions to equations with a small parameter. In same cases in the weighted Sobolev spaces, they have succeeded in constructing the asymptotics of solutions to the equations with a parameter and to the equations with a cuspidal singularity [11,12,13].
However, later, one had to refuse consideration of asymptotics in the weighted Sobolev spaces. The main reason is related to the fact that it is unnatural to consider the Laplace–Borel transform, which is principal in resurgent analysis, in these spaces; therefore, the attempts to obtain significant results by using this approach resulted in some principal difficulties.
Later, another approach proposed by Shatalov and Sternin in [9] was chosen. In this book, they defined the Laplace–Borel transform that acts in the space of the functions of exponential growth.
The technique for interpreting and constructing the asymptotic expansions of the form (3) based on the Laplace–Borel transform is called resurgent analysis. The main idea of resurgent analysis consists in the fact that the formal Laplace–Borel transforms are the power series with respect to the dual variable p that converge in the vicinity of the points p = .
At that, the inverse Borel transform provides a regular technique for summation of series (3). To apply the resurgent analysis methods, it is necessary to prove the resurgence of the functions or, in other words, their infinite extendability along any path on the Riemann surface that does not pass through some discrete set depending on the function (an exact definition of the resurgence is given in [9]). As a rule, the process of proving this fact represented considerable difficulties. For ordinary differential equations with holomorphic coefficients and some types of equations with partial derivatives, the proof of resurgence of their solutions was obtained by M. Korovina [14,15]. Owing to this result, some problems of constructing uniform asymptotics of solutions for some ordinary differential equations with irregular points and for some classes of partial differential equations have been solved. For example, in [13,15], uniform asymptotics of solutions were constructed for the case when the principal symbol has simple roots. Therefore, this problem is already solved and we will consider in this study the equations for which the principal symbol has multiple roots. In addition, in [16], the problem of constructing the asymptotics of solutions for the Laplace equation on a manifold with a cuspidal singularity is also solved.
The case of the equations with multiple roots of the principal symbol has appeared to be significantly more complicated.
Recently, to solve the problem of multiple roots, the re-quantization method [17] was proposed. It is applied in the case when an integro-differential equation in the dual space cannot be solved by the method of successive approximations and, in its turn, can be reduced to an equation with cuspidal degeneracies. In this case, the theorem about the infinite extendability of its solution (this is proved for ordinary differential equations) is proved; the Laplace–Borel transform is applied one more time, and the asymptotics of a solution for the equation obtained are constructed; they allow finding the asymtotics of the initial equation. Nowadays, with the help of this method, some problems are solved for the equations with degeneracies in the case of multiple roots. This method will be used in our study to construct uniform asymtotics of solutions.
Earlier, the re-quantization method was used in [18,19]. In [18] a particular case of Equation (1), i.e., a model problem, was considered. For this particular case, the asymptotics of the solution of the model equation are constructed in the neighborhood of an infinitely distant point by the re-quantization method. Despite the fact that in this study we consider a significantly more general case that comprises a broad class of equations, including the model equation of [18], some stages of the proof for this model problem coincide with those presented in [18]. Therefore, we make references to [18] at the points where the proofs are identical. It is possible to read about the model problem below.
3. The Main Results
First, let us consider the case when the principal symbol of the differential operator has the only one root. Without loss of generality, we assume that this root is located at zero. In this case, the coefficients of Equation (2) can be represented in the form . Let the first coefficients of the power series be zero; i.e., the left-hand side of Equation (2) can be represented as a sum of the terms of the form and . Let us select among these terms those for which the number is minimal; in the corresponding power series, we designate the coefficient at the minimal power of r by .
Here, ; denotes the corresponding holomorphic functions. The numbers and j are chosen so that the inequality is fulfilled. Let us call the index of singularity of Equation (2). Let us call the terms of the form under the condition the lower-order terms of Equation (5). We subdivide the lower-order terms into two types. Let as attribute the terms for which to the first type; those for which , to the second type.
In [18], the model problem, which is Equation (5), was considered in the case when the index of singularity is , i.e., the case when . In this study, we generalize this result. Let us subdivide the equations with a multiple root of the principal symbol at zero into two types. We attribute to the first type the equations for which the inequality
is fulfilled for all the lower-order terms. It is obvious that the model equation considered in [18] is a particular case of the equation of the first type.
We attribute to the second type the equations for which there are the lower-order terms such that for them, this inequality is not fulfilled. In this paper we consider the equations of the first type. The goal of this study was constructing the asymptotics of solutions of the equations of the first type in the neighborhood of an infinitely distant point. For them, the following theorem is valid.
Theorem 1.
Let , then, the asymptotics of the solution to Equation (1) in the neighborhood of an infinitely distant point has the form
where are the roots of the polynomial ; , and are some numbers.
If , then the asymptotics of the solution will be conormal.
Proof.
We can subdivide the process of proving this theorem into several stages. At the first stage, we consider the case . It is evident that all the equations for which this inequality is fulfilled belong to the equations of the first type. In this case, it is shown that the singular point is regular, hence, the asymptotics are conormal. At the second stage, by using the Laplace–Borel transform, we transform the equation and determine the singular points of the solution of the transformed equation. At the third stage, using the re-quantization method, we construct the asymptotics of the solution in the neighborhood of the singular points and then perform the inverse Laplace–Borel transform of these asymptotics.
Let us prove this theorem for the case when the equation contains only one term of the first type and one term of the second type. Namely, the equation can be written in the form
where . Here, two last terms are the lower-order terms; one of them is of the first type, another is of the second type. In the general case, the proof is analogous to that presented below. If the degree of the differential equation is smaller or equal to the index of singularity, then, dividing this equation by we obtain the following equation
where
Here, denote the corresponding holomorphic functions. The latter equation is an equation of Fuchs type with a singularity at zero and, as is known, the asymptotics of its solution have a conormal form. Therefore, here and in what follows, we assume that the index on singularity of Equation (7) is smaller than n.
Let us search for the asymptotics of the solution of Equation (7) in the neighborhood of zero by the re-quantization method (see [17]).
Let us remind the definition of the Laplace–Borel transform.
Let us denote by the sector . We will say that the function f is of k-exponential growth, if f is analytical on and there are nonnegatie constants C and such that in the sector , the following inequality is valid:
Let us search for the solution to Equation (7) in the space of the functions holomorphic in the domain , and of k-exponential growth at zero.
Let us denote by the space of holomorphic functions in the domain
, and by the space of holomorphic functions with exponential growth.
Definition 1.
We will call k-transform of Laplace–Borel of the function the mapping
The inverse k-transform of Laplace–Borel is defined by the formula
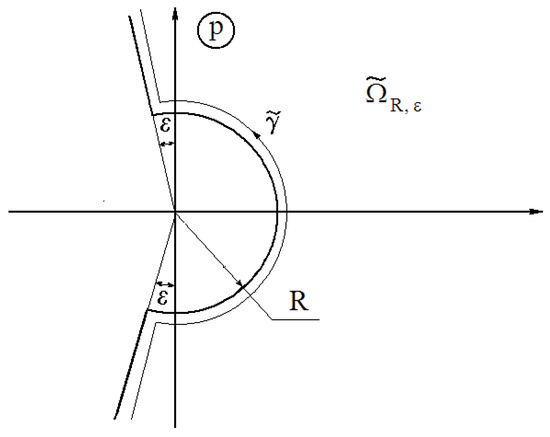
The contour is depicted in Figure 1. This contour was first described in the book [9].

Figure 1.
Integration contour.
The properties of the Laplace–Borel transform are as follows:
After performing the Laplace–Borel transform, we write Equation (7) in the form
Here, f denotes an arbitrary holomorphic function. Let us differentiate this equation k+m times, and multiplying the obtained equation by , transform Equation (8) to the form
We can easily demonstrate that Equation (9) can be reduced to the form
Here, denote the corresponding constants.
Let inequality (6) hold. It is equivalent to the inequality
By analogy with [18], we can demonstrate that if condition (11) is satisfied, the solution to Equation (10) is a resurgent function.
Let us introduce the following designation: . Let us assume that , otherwise, we zeroize it by the substitution .
The principal symbol of the operator in Equation (10) is . This polynomial has a multiple root at zero and nonzero simple roots , where . In the case where inequality (11) is fulfilled, Equation (10) is analogous to Equation (11) in [18], therefore, we will construct the asymptotics of the solutions to Equation (10) by analogy to that paper. First, let us construct the asymptotics of the solution to Equation (10) in the neighborhood of the point . Let us apply the re-quantization method to Equation (10). For that, we perform the Laplace–Borel transform of Equation (10):
Here, and , are the corresponding holomorphic functions. It is evident, that points are the points of holomorphy of the right-hand side of Equation (12) and each root is a singular point of the solution of this equation. Let us construct the asymptotics of the solution to Equation (12) at points . We rewrite Equation (12) in the form
Investigating this equation by the method of successive approximations as it was done in paper [18], we come to the following.
Lemma 1.
The asymptotics of function in the neighborhood of the point has the form
where , are holomorphic functions.
The proof of this lemma is identical to the proof of the corresponding lemma for Equation (13) from paper [18].
Now let us consider the singularity at zero. We have the equation
It should be noted that in the absence of the integral lower-order terms, differentiating this equation k times with respect to q, we can transform it to the equation with a conic singularity whose right-hand side has a conormal asymptotics. As is known, the solutions of such equations have conormal asymptotics. It would be reasonable to suppose that in the general case, i.e., in the presence of the lower-order terms, the solution will also have the form of a conormal asymptotics. Let us prove this. As was demonstrated in [18], the following equation holds:
Here, are some constants. Let us introduce the designation
Using this designation, we can rewrite Equation (15) in the form
To find the asymptotics of function at , we apply the method of successive approximations. Using this method, we can prove the following
Lemma 2.
The asymptotics of function at is conormal.
The proof of this lemma is performed using the successive approximation method, by substituting the absolute term of Equation (15), which at has a conormal asymptotics with no logarithms as multipliers, sequentially into all the integral operators of the right-hand side of Equation (15) and performing the corresponding estimations of the power series obtained. The proof of this lemma is identical to the proof of the similar lemma in [18].
As is known [20], the inverse transform of a conormal asymptotics is also a conormal asymptotics. Thus, the asymptotic term corresponding to the singular point is a conormal asymptotics. Now we have to construct the inverse transform of the asymptotic terms corresponding to the singular points .
Calculating the inverse Laplace–Borel transform of expression (14), we obtain
Here, is the corresponding number, and is an asymptotic series. In [21], the following theorem was proved.
Theorem 2.
The asymptotics of the function in the vicinity of zero have the form
Here, are the roots of the polynomial ; coefficients for , are some constants.
It follows from this theorem that
Finally, we have obtained that the asymptotics of the solution of Equation (5) in the neighborhood of an infinitely distant point have the form
where are the roots of the polynomial ; and are some numbers.
□
Earlier we supposed that the principal symbol of the differential operator has one root, now let it be not the case. Let the principal symbol have two roots, i.e.,
Here, are the corresponding numbers. In this case the equation has the form
Now we perform the Laplace–Borel transform
Let us find the asymptotics of solution of Equation (17) in the neighborhood of the point . With this purpose, let us rewrite Equation (17) in the form
Since the functions have no singularities at zero, the asymptotics of the solution of Equation (17) in the vicinity of the point is obtained by using the method of successive approximations as it was done for Equation (5). To find the asymptotics corresponding to the root , we must shift this root to zero. This can be done by substitution . Then we can find the asymptotics in the neighborhood of zero as it was done above.
Note that if , solution will not have a singularity at zero; if , then the asymptotics of this solution is conormal.
The results of Theorem 1 can be applied for some equations of mathematical physics.
The second-order differential equations with singular points are used in various domains of mechanics. For instance, Laplace operator written in spherical coordinate system has a singular point at zero. The second-order equation of this type is also used for solving the planar problem of finding the stress–strain state of a body of rectangular cross section with a cylindrical cavity along which an ideal incompressible fluid moves [22]. Papers [23,24,25] are also worth mentioning. In them, the asymptotic expansions of the solutions of the main boundary-value problems for the elasticity system and the biharmonic (polyharmonic) equation in the exterior of a compact set and in a half-space, including that in the form of a conormal asymptotics, were obtained.
Let us demonstrate the application of the result of Theorem 1 to constructing uniform asymptotics of solutions by an example of the boundary-value problem for the Klein–Gordon–Fock equation with holomorphic coefficients at . Namely, let us consider the following problem:
Here, are holomorphic functions in the neighborhood of an infinitely distant point, S – the smooth boundary of the domain.
Let us apply the method of separation of variables
We get the problem
and the equation
Let us designate by the eigenvalues of the Sturm–Liouville problem (18); by , the eigenfunction of this problem corresponding to this eigenvalue. Equation (19) is an equation of the first type; therefore, the asymptotics of its solution in the neighborhood of an infinitely distant point are determined by Theorem 1. Let us designate the asymptotics of the solution to this equation corresponding to the eigenvalue by . Then, the asymptotics of any solution of the boundary-value problem for the Klein–Gordon–Fock equation can be represented in the form .
It should be noted that in some studies, the asymptotics of solutions of linear differential equations at were constructed. For instance, equations similar to (19) with the condition were considered in [26,27]. In [28], an asymptotic formula for the eigenvalues of the second-order differential operators with continuous coefficients was obtained.
4. Conclusions
As a result of Theorem 1, we have constructed the uniform asymptotics of solutions of ordinary differential equations with holomorphic coefficients in the neighborhood of an infinitely distant point for the equations of the first type. It should be noted that there is quite a broad class of equations of the first type. For instance, all equations from the first to the fifth order inclusive are the equations of the first type. Therefore, the results of this study can be applied to constructing the asymptotics of solutions to equations with holomorphic coefficients in the neighborhood of an infinitely distant point for a broad class of ordinary differential equations, as well as for some equations of mathematical physics. For example, we have considered above the problem of constructing the uniform asymptotics of solutions by an example of the boundary value problem for the Klein–Gordon–Fock equation with holomorphic coefficients.
Analogously, the asymptotics of a solution for the boundary-value problem can be constructed for the wave equation at , for the Helmholtz equation at large values of the radius and for many other problems, as well as for some elliptic equations that are set on manifolds with singularities. An example of such a problem is constructing the asymptotics of the solution to the Laplace equation on a manifold with a cuspidal singularity in the neighborhood of the singular point of the manifold. This problem was solved in [16].
In our further investigations, we would like to construct the asymptotics of solutions for equations of the second type; i.e., to lift the constraint imposed by inequality (6) and definitely solve the problem formulated by Poincare—the problem of constructing the uniform asymptotics of solutions to ordinary differential equations in the neighborhood of an infinitely distant point. The ultimate goal of our investigations was solving the fundamental Poincare problem of constructing regular asymptotics of solutions of ordinary differential equations with holomorphic coefficients in the neighborhoods of irregular singular points.
Funding
This research received no external funding.
Acknowledgments
The author is grateful to V.E. Shatalov for constant discussions throughout the work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Poincaré, H. Sur les intégrales irrégulières des équations linéaires. Acta Math. 1886, 8, 295–344. [Google Scholar] [CrossRef]
- Poincare, H. Analysis of the mathematical and natural works of Henri Poincare. In Selected Works in Three Volumes. Volume 3. Mathematics. Theoretical Physics; “Nauka” Publishing House: Moscow, Russia, 1974. [Google Scholar]
- Thomé, L.W. Zur Theorie der linearen Differentialgleichungen. J. Für Die Reine Und Angew. Math. 1872, 74, 193–217. [Google Scholar] [CrossRef]
- Kondratév, V.A. Boundary-value problems for elliptic equations in conical regions. Sov. Math. Dokl. 1963, 4, 1600–1602. [Google Scholar]
- Olver, F.W.J. Asymptotics and Special Functions (AKP Classics); A K Peters/CRC Press: Wellesley, MA, USA, 1997. [Google Scholar]
- Cesari, L. Asymptotic Behavior and Stability Problems in Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- Coddington, E.; Levinson, N. Theory of Ordinary Differential Equations; Krieger Publishing Company: Malabar, FL, USA, 1958. [Google Scholar]
- Sternberg, W. Über die Asymptotische Integration von Differencialgleichungen. Math. Ann. 1920, 81, 119–186. [Google Scholar] [CrossRef]
- Sternin, B.; Shatalov, V. Borel–Laplace Transform and Asymptotic Theory. Introduction to Resurgent Analysis; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ecalle, J. Cinq Applications des Fonctions Résurgentes. In Prepublications Mathematiques; d’Orsay: Paris, France, 1984. [Google Scholar]
- Schulze, B.-W.; Sternin, B.; Shatalov, V. Asymptotic Solutions to Differential Equations on Manifolds with Cusps. In Preprint MPI/96-89, Max-Planck-Institut fur Mathematik; Max-Planck-Institut für Mathematik: Bonn, Germany, 1996; p. 45. [Google Scholar]
- Schulze, B.; Sternin, B.; Shatalov, V. An Operator Algebra on Manifolds with Cusp-Type Singularities. Ann. Glob. Anal. Geom. 1998, 16, 101–140. [Google Scholar] [CrossRef]
- Sternin, B.Y.; Shatalov, V.E. Differential Equations in Spaces with Asymptotics on Manifolds with Cusp Singularities. Differ. Equ. 2002, 38, 1764–1773. [Google Scholar] [CrossRef]
- Korovina, M.V. Existence of resurgent solutions for equations with higher-order degeneration. Differ. Equ. 2011, 47, 346–354. [Google Scholar] [CrossRef]
- Korovina, M.V. Asymptotics solutions of equations with higher-order degeneracies. Dokl. Math. 2011, 83, 182–184. [Google Scholar] [CrossRef]
- Korovina, M.V. Asymptotic solutions of second order equations with holomorphic coefficients with degeneracies and laplace’s equations on a manifold with a cuspidal singularity. Glob. J. Sci. Front. Res. GJSFR F Math. Decis. Sci. 2017, 17, 57–71. [Google Scholar]
- Korovina, M.V. Repeated quantization method and its applications to the construction of asymptotics of solutions of equations with degeneration. Differ. Equ. 2016, 52, 58–75. [Google Scholar] [CrossRef]
- Korovina, M.V. Application of the repeated quantization method to the problem of making asymptotic solutions of equations with holomorphic coefficients. Int. J. Open Inf. Technol. 2019, 7, 14–22. [Google Scholar]
- Korovina, M.V.; Smirnov, V.Y. Construction of Asymptotics of Solutions of Differential Equations with Cusp-Type Degeneration in the Coefficients in the Case of Multiple Roots of the Highest-Order Symbol. Differ. Equ. 2018, 54, 28–37. [Google Scholar] [CrossRef]
- Kats, D.S. Computation of the asymptotics of solutions for equations with polynomial degeneration of the coefficients. Differ. Equ. 2015, 51, 1589–1594. [Google Scholar] [CrossRef]
- Korovina, M.; Smirnov, I.; Smirnov, V. On a Problem Arising in Application of the Re-Quantization Method to Construct Asymptotics of Solutions to Linear Differential Equations with Holomorphic Coefficients at Infinity. Math. Comput. Appl. 2019, 24, 16. [Google Scholar] [CrossRef]
- Sciarra, G.; dell’Isola, F.; Hutter, K. Dilatational and compacting behavior around a cylindrical cavern leached out in a solid–fluid elastic rock salt. Int. J. Geomech. 2005, 5, 233–243. [Google Scholar] [CrossRef]
- Matevossian, O.A. Solutions of exterior boundary-value problems for the elasticity system in weighted spaces. Sb. Math. 2001, 192, 1763–1798. [Google Scholar] [CrossRef]
- Matevossian, H.A. On the Steklov-type biharmonic problem in unbounded domains. Russ. J. Math. Phys. 2018, 25, 271–276. [Google Scholar] [CrossRef]
- Matevossian, H.A. On the polyharmonic Neumann problem in weighted spaces. Complex Var. Elliptic Equ. 2019, 64, 1–7. [Google Scholar] [CrossRef]
- Shkalikov, A.A. Perturbations of selfadjoint and normal operators with a discrete spectrum. Russ. Math. Surv. 2016, 71, 907–964. [Google Scholar] [CrossRef]
- Savchuk, A.M.; Shkalikov, A.A. Sturm—Liouville operators with distribution potentials. Trans. Moscow Math. Soc. 2003, 64, 143–192. [Google Scholar]
- Kukushkin, M.V. On One Method of Studying Spectral Properties of Non-selfadjoint Operators. Abstr. Appl. Anal. 2020, 2020, 1461647. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).