Numerical Analysis for the Fractional Ambartsumian Equation via the Homotopy Herturbation Method

Abstract

The fractional calculus is useful in describing the natural phenomena with memory effect. This paper addresses the fractional form of Ambartsumian equation with a delay parameter. It may be a challenge to obtain accurate approximate solution of such kinds of fractional delay equations. In the literature, several attempts have been conducted to analyze the fractional Ambartsumian equation. However, the previous approaches in the literature led to approximate power series solutions which converge in subdomains. Such difficulties are solved in this paper via the Homotopy Perturbation Method (HPM). The present approximations are expressed in terms of the Mittag-Leffler functions which converge in the whole domain of the studied model. The convergence issue is also addressed. Several comparisons with the previous published results are discussed. In particular, while the computed solution in the literature is physical in short domains, with our approach it is physical in the whole domain. The results reveal that the HPM is an effective tool to analyzing the fractional Ambartsumian equation.

1. Introduction

Historically, the mathematical model describing the absorption of light by the interstellar matter was derived more than two decades earlier by Ambartsumian [1]. In the present time, the model is well known as Ambartsumian delay equation. The fractional generalization of this equation is called the fractional Ambartsumian equation (FAE) which takes the form:

$${}_0^C{D}_t^{\alpha }z\left(t\right)=-z\left(t\right)+\frac{1}{q}z\left(\frac{t}{q}\right),0<\alpha \le 1,q>1,$$

(1)

where q is a constant for the given model and $\alpha$ is the non-integer order of the fractional derivative. The FAE is subjected to

$$z\left(0\right)=\lambda ,$$

(2)

where $\lambda$ is also a constant. Equation (1) reduces to the classical model with ordinary derivative as $\alpha \to 1$. Although the classical Ambartsumian equation was physically derived by Ambartsumian [1], the derivation of the fractional form of this equation needs to introduce some materials about the physics of interstellar matter. However, the present work is focused on deriving accurate approximations of the fractional model (1–2) when compared with other approaches in the relevant literature.

In the literature [2,3,4,5,6], several analytical methods have been applied to solve/analyze the classical model. Patade and Bhalekar [2] obtained the solution of the ordinary model (as $\alpha \to 1$) as a power series. Additional results were also reported by Khaled et al. [7] for the Ambartsumian equation using the conformable derivative. However, the FAE has been investigated via the homotopy transform analysis method (HTAM) in Ref. [8] using the Caputo fractional derivative. Besides, Patade [9] obtained a closed-form power series solution for the present FAE using an iterative method. Such closed-form solution was obtained as a power series in terms of $t^{k\alpha }$ ($k=0,1,2,\cdots$), and it was proved for convergence for all $q>1$. The main observation of such closed-form solution [9] is that it is applicable in certain domains, i.e., it is not valid in the whole domain $t\in [0,\infty )$. So, we will show in this paper that the solution of the system (1–2) can be obtained in terms of the Mittag-Leffler functions which converge in the whole domain of the current model. The homotopy perturbation method (HPM) was used in references [10,11] to solve ordinary differential equations (ODEs) and also used for partial differential equations (PDEs) [12,13,14]. In this paper, the HPM is proposed to solve the current fractional model. Although several numerical approaches [15,16,17] were used to solve various fractional models, it will be declared that the HPM is an effective analytical tool to deal with the current fractional model. Several numerical comparisons will be presented to validate our results. The advantages of the HPM over the closed-form solution [9] will also be discussed.

2. Basic Concepts

The Caputo fractional derivative [18,19,20,21] of a function $z\left(t\right)$ is defined by

$${}_0^C{D}_t^{\alpha }z\left(t\right)=\frac{d^{\alpha }z\left(t\right)}{d{t}^{\alpha }}=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t{(t-\tau )}^{-\alpha }{z}^{\left(1\right)}\left(\tau \right)d\tau ,\hfill & \mathrm{if}0<\alpha <1,\hfill \\ \\ \frac{dz\left(t\right)}{dt},\hfill & \mathrm{if}\alpha =1.\hfill \end{array}\right.$$

(3)

The Laplace transform (LT) of the Caputo fractional derivative is given by

$$L\left[\frac{d^{\alpha }z\left(t\right)}{d{t}^{\alpha }}\right]=s^{\alpha }Z\left(s\right)-s^{\alpha -1}z\left(0\right).$$

(4)

The following relations are usually implemented to solve fractional differential equations by means of LT,

$$\begin{array}{ccc}& & L^{-1}\left[\frac{j!s^{\alpha -\beta }}{{(s^{\alpha }\mp a)}^{j+1}}\right]=t^{\alpha j+\beta -1}{E}_{\alpha ,\beta }^{\left(j\right)}(\pm a{t}^{\alpha }),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & L^{-1}\left[\frac{s^{\alpha -1}}{s^{\alpha }+a}\right]=E_{\alpha }(-a{t}^{\alpha }),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & L^{-1}\left[\frac{1}{s^{\alpha }+a}\right]=t^{\alpha -1}{E}_{\alpha ,\alpha }(-a{t}^{\alpha }),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& & L^{-1}\left[\frac{s^{-1}}{s^{\alpha }+a}\right]=t^{\alpha }{E}_{\alpha ,\alpha +1}(-a{t}^{\alpha }),\hfill \end{array}$$

(8)

where the Mittag-Leffler functions of one parameter $E_{\alpha }\left(t\right)$ and two parameters $E_{\alpha ,\beta }\left(t\right)$ are defined by

$$\begin{array}{ccc}& & E_{\alpha }\left(t\right)=\sum _{i=0}^{\infty }\frac{t^i}{\mathsf{\Gamma }(\alpha i+1)},\alpha >0,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & E_{\alpha ,\beta }\left(t\right)=\sum _{i=0}^{\infty }\frac{t^i}{\mathsf{\Gamma }(\alpha i+\beta )},(\alpha >0,\beta >0).\hfill \end{array}$$

(10)

Equations (9) and (10) lead to the following properties:

$$\begin{array}{ccc}& & E_{\alpha ,\beta }\left(t\right)=t{E}_{\alpha ,\alpha +\beta }\left(t\right)+\frac{1}{\mathsf{\Gamma }\left(\beta \right)},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & E_{\alpha }\left(t\right)=t{E}_{\alpha ,\alpha +1}\left(t\right)+1,E_{\alpha ,1}\left(t\right)=E_{\alpha }\left(t\right),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & E_{1,2}\left(t\right)=\left(e^t-1\right)/\left(t\right),\hfill \end{array}$$

(13)

and the integral formula:

$${\int }_0^t{\tau }^{\gamma -1}{E}_{\alpha ,\gamma }\left(a{\tau }^{\alpha }\right){\left(t-\tau \right)}^{\beta -1}{E}_{\alpha ,\beta }\left[b{\left(t-\tau \right)}^{\alpha }\right]d\tau =\frac{t^{\beta +\gamma -1}}{a-b}\left[a{E}_{\alpha ,\beta +\gamma }\left(a{t}^{\alpha }\right)-b{E}_{\alpha ,\beta +\gamma }\left(b{t}^{\alpha }\right)\right].$$

(14)

3. Application of the HPM

Before applying this method, we rewrite Equation (1) as

$$\frac{d^{\alpha }z\left(t\right)}{d{t}^{\alpha }}=-z\left(t\right)+\frac{p}{q}z\left(\frac{t}{q}\right),$$

(15)

where p is an auxiliary parameter such that the homotopy series solution is

$$z\left(t\right)=\sum _{n=0}^{\infty }{p}^n{z}_n\left(t\right).$$

(16)

Inserting Equation (16) into Equation (15), yields

$$\frac{d^{\alpha }{z}_0\left(t\right)}{d{t}^{\alpha }}+z_0\left(t\right)+\sum _{n=0}^{\infty }{p}^{n+1}\left(D_t^{\alpha }{z}_{n+1}\left(t\right)+z_{n+1}\left(t\right)-\frac{1}{q}{z}_n\left(\frac{t}{q}\right)\right)=0,$$

(17)

which leads to the following systems of initial value problems (IVPs):

$$\begin{array}{ccc}& & \frac{d^{\alpha }{z}_0\left(t\right)}{d{t}^{\alpha }}+z_0\left(t\right)=0,z_0\left(0\right)=\lambda ,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & \frac{d^{\alpha }{z}_n\left(t\right)}{d{t}^{\alpha }}+z_n\left(t\right)=\frac{1}{q}{z}_{n-1}\left(\frac{t}{q}\right),z_n\left(0\right)=0,n\ge 1.\hfill \end{array}$$

(19)

The solution of the zeroth-order IVP (18) is well known in fractional calculus and given by

$$z_0\left(t\right)=\lambda E_{\alpha }\left(-t^{\alpha }\right).$$

(20)

At $n=1$, the first-order IVP becomes

$$\frac{d^{\alpha }{z}_1\left(t\right)}{d{t}^{\alpha }}+z_1\left(t\right)=\frac{\lambda }{q}{E}_{\alpha }\left(-q^{-\alpha }{t}^{\alpha }\right),z_1\left(0\right)=0.$$

(21)

Applying the LT on Equation (21) gives

$$s^{\alpha }{Z}_1\left(s\right)-s^{\alpha -1}{z}_1\left(0\right)+Z_1\left(s\right)=L\left\{\frac{\lambda }{q}{E}_{\alpha }\left(-q^{-\alpha }{t}^{\alpha }\right)\right\}.$$

(22)

The LT of the r.h.s. is obtained by inserting the values $j=0$, $\beta =1$, and $a=q^{-\alpha }$ into Equation (5), note that $E_{\alpha ,1}\left(-q^{-\alpha }{t}^{\alpha }\right)=E_{\alpha }\left(-q^{-\alpha }{t}^{\alpha }\right)$. Accordingly, we obtain

$$(s^{\alpha }+1)Z_1\left(s\right)=\frac{\lambda s^{\alpha -1}}{q(s^{\alpha }+q^{-\alpha })},$$

(23)

and hence

$$Z_1\left(s\right)=\frac{\lambda s^{\alpha }}{qs(s^{\alpha }+1)(s^{\alpha }+q^{-\alpha })}.$$

(24)

However, $Z_1\left(s\right)$ can be factorized as

$$Z_1\left(s\right)=\frac{\lambda }{qs}\left[\frac{h_1}{s^{\alpha }+1}+\frac{h_2}{s^{\alpha }+q^{-\alpha }}\right],$$

(25)

where $h_1$ and $h_2$ are given by

$$h_1=\frac{1}{1-q^{-\alpha }},h_2=\frac{-q^{-\alpha }}{1-q^{-\alpha }}=-q^{-\alpha }{h}_1.$$

(26)

Inserting Equation (26) into Equation (25), yields

$$Z_1\left(s\right)=\frac{\lambda h_1}{q}\left[\frac{s^{-1}}{s^{\alpha }+1}-\frac{q^{-\alpha }{s}^{-1}}{s^{\alpha }+q^{-\alpha }}\right].$$

(27)

Applying the inverse LT, we obtain

$$z_1\left(t\right)=\frac{\lambda h_1}{q}\left[L^{-1}\left\{\frac{s^{-1}}{s^{\alpha }+1}\right\}-q^{-\alpha }{L}^{-1}\left\{\frac{s^{-1}}{s^{\alpha }+q^{-\alpha }}\right\}\right],$$

(28)

or

$$z_1\left(t\right)=\frac{\lambda h_1}{q}\left[t^{\alpha }{E}_{\alpha ,\alpha +1}\left(-t^{\alpha }\right)-q^{-\alpha }{t}^{\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)\right].$$

(29)

Inserting the value of $h_1$ into (29), we get $z_1\left(t\right)$ in the explicit form:

$$z_1\left(t\right)=\frac{\lambda q^{-1}}{1-q^{-\alpha }}{t}^{\alpha }.\left[E_{\alpha ,\alpha +1}\left(-t^{\alpha }\right)-q^{-\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)\right].$$

(30)

At $n=2$, we have the second-order IVP:

$$\frac{d^{\alpha }{z}_2\left(t\right)}{d{t}^{\alpha }}+z_2\left(t\right)=\frac{\lambda q^{-2-\alpha }}{1-q^{-\alpha }}{t}^{\alpha }.\left[E_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)-q^{-\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-2\alpha }{t}^{\alpha }\right)\right],z_2\left(0\right)=0.$$

(31)

Applying the LT, it then follows

$$\begin{array}{ccc}\hfill (s^{\alpha }+1)Z_2\left(s\right)& & =\frac{\lambda q^{-2-\alpha }}{1-q^{-\alpha }}\left[L\left\{t^{\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)\right\}-q^{-\alpha }L\left\{t^{\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-2\alpha }{t}^{\alpha }\right)\right\}\right],\hfill \\ & & =\frac{\lambda q^{-2-\alpha }}{1-q^{-\alpha }}\left[\frac{s^{-1}}{s^{\alpha }+q^{-\alpha }}-\frac{q^{-\alpha }{s}^{-1}}{s^{\alpha }+q^{-2\alpha }}\right],\hfill \end{array}$$

(32)

which can be simplified to obtain $Z_2\left(s\right)$ as

$$Z_2\left(s\right)=\frac{\lambda q^{-2-\alpha }{s}^{\alpha }}{s(s^{\alpha }+1)(s^{\alpha }+q^{-\alpha })(s^{\alpha }+q^{-2\alpha })}.$$

(33)

Implementing partial fractions, we have

$$Z_2\left(s\right)=\frac{\lambda q^{-2-\alpha }}{s}\left(\frac{h_3}{s^{\alpha }+1}+\frac{h_4}{s^{\alpha }+q^{-\alpha }}+\frac{h_5}{s^{\alpha }+q^{-2\alpha }}\right),$$

(34)

where

$$h_3=\frac{-1}{(1-q^{-\alpha })\left(1-q^{-2\alpha }\right)},h_4=\frac{1}{{\left(1-q^{-\alpha }\right)}^2},h_5=\frac{-q^{-\alpha }}{{\left(1-q^{-\alpha }\right)}^2(1+q^{-\alpha })}.$$

(35)

Hence,

$$Z_2\left(s\right)=\lambda q^{-2-\alpha }\left[\frac{h_3{s}^{-1}}{s^{\alpha }+1}+\frac{h_4{s}^{-1}}{s^{\alpha }+q^{-\alpha }}+\frac{h_5{s}^{-1}}{s^{\alpha }+q^{-2\alpha }}\right].$$

(36)

Applying the inverse LT again on $Z_2\left(s\right)$, we obtain

$$z_2\left(t\right)=\lambda q^{-2-\alpha }{t}^{\alpha }\left(h_3{E}_{\alpha ,\alpha +1}\left[-t^{\alpha }\right]+q^{-\alpha }{h}_4{E}_{\alpha ,\alpha +1}\left[-q^{-\alpha }{t}^{\alpha }\right]+q^{-2\alpha }{h}_5{E}_{\alpha ,\alpha +1}\left[-q^{-2\alpha }{t}^{\alpha }\right]\right),$$

(37)

where $h_3$, $h_4$, and $h_5$ are already obtained by Equation (35). The HPM gives the N-term approximate analytic solution ${\mathsf{\Psi }}_N\left(t\right)$ when $p\to 1$ as

$${\mathsf{\Psi }}_N\left(t\right)=\sum _{j=0}^{N-1}{z}_j\left(t\right).$$

(38)

Accordingly, the 3-term approximate solution is given by

$$\begin{array}{ccc}& & {\mathsf{\Psi }}_3\left(t\right)=\lambda E_{\alpha }\left(-t^{\alpha }\right)+\left(\frac{\lambda q^{-1}}{1-q^{-\alpha }}\right)t^{\alpha }.\left[E_{\alpha ,\alpha +1}\left(-t^{\alpha }\right)-q^{-\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)\right]+\hfill \\ & & \lambda q^{-2-\alpha }{t}^{\alpha }.\left[h_3{E}_{\alpha ,\alpha +1}\left(-t^{\alpha }\right)+q^{-\alpha }{h}_4{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)+q^{-2\alpha }{h}_5{E}_{\alpha ,\alpha +1}\left(-q^{-2\alpha }{t}^{\alpha }\right)\right].\hfill \end{array}$$

(39)

4. Unified Formula for $z_n\left(t\right),n\ge 1$

In this section we show that a unified formula for $z_n\left(t\right),\forall n\ge 1$ can be obtained. Hence, $z_n\left(t\right)$ can be calculated sequentially $\forall n\ge 1$. To do that, the LT is applied on the unified IVP (19) to give

$$s^{\alpha }{Z}_n\left(s\right)-s^{\alpha -1}{z}_n\left(0\right)+Z_n\left(s\right)=L\left\{\frac{1}{q}{z}_{n-1}\left(\frac{t}{q}\right)\right\}.$$

(40)

Since $z_n\left(0\right)=0,\forall n\ge 1$, we have

$$Z_n\left(s\right)=\frac{Z_{n-1}\left(qs\right)}{s^{\alpha }+1},$$

(41)

where $L\left\{\frac{1}{q}{z}_{n-1}\left(\frac{t}{q}\right)\right\}=Z_{n-1}\left(qs\right)$. Applying the inverse LT on the unified expression (41), yields

$$z_n\left(t\right)=L^{-1}\left\{\frac{1}{s^{\alpha }+1}\right\}\ast L^{-1}\left\{Z_{n-1}\left(qs\right)\right\},$$

(42)

or

$$z_n\left(t\right)=t^{\alpha -1}{E}_{\alpha ,\alpha }\left(-t^{\alpha }\right)\ast \left[\frac{1}{q}{z}_{n-1}\left(\frac{t}{q}\right)\right],$$

(43)

and the symbol $(\ast )$ describes the convolution operation. By this, we get

$$z_n\left(t\right)=\frac{1}{q}{\int }_0^t{(t-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{(t-\tau )}^{\alpha }\right)z_{n-1}\left(\frac{\tau }{q}\right)d\tau ,\forall n\ge 1.$$

(44)

To check this formula, we have at $n=1$ that

$$z_1\left(t\right)=\frac{1}{q}{\int }_0^t{(t-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{(t-\tau )}^{\alpha }\right)z_0\left(\frac{\tau }{q}\right)d\tau .$$

(45)

Since $z_0$ is already obtained by Equation (20), it then follows

$$z_1\left(t\right)=\frac{\lambda }{q}{\int }_0^t{(t-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{(t-\tau )}^{\alpha }\right)E_{\alpha }\left(-q^{-\alpha }{\tau }^{\alpha }\right)d\tau .$$

(46)

Evaluating this integral using the given Formula (14), we obtain

$$z_1\left(t\right)=\left(\frac{\lambda q^{-1}}{1-q^{-\alpha }}\right)t^{\alpha }\left[E_{\alpha ,\alpha +1}\left(-t^{\alpha }\right)-q^{-\alpha }{E}_{\alpha ,\alpha +1}\left(-q^{-\alpha }{t}^{\alpha }\right)\right],$$

(47)

which is the same obtained result in (30). By repeating this procedure, the higher-order components $z_n$ can be directly calculated via the unified Formula (44) with the help of the integration Formula (14). The advantage of this approach over the previous one in Section 2 is that each higher-order component $z_n$ can be evaluated by substituting the preceding obtained components $z_{n-1}$. In addition, the present unified integral formula may be better than solving several IVPs to derive the higher-order components $z_n$ in a separate manner. Furthermore, the unified Formula (44) is programmable by any software to reduce the time of calculations.

5. Results & Validation

5.1. As $\alpha \to 1$

At this point, the approximate solution (41) can be validated as $\alpha \to 1$. In this case, Equation (39) reduces to

$$\begin{array}{ccc}& & {\mathsf{\Psi }}_3\left(t\right)=\lambda E_1\left(-t\right)+\left(\frac{\lambda q^{-1}}{1-q^{-1}}\right)t.\left[E_{1,2}\left(-t\right)-q^{-1}{E}_{1,2}\left(-q^{-1}t\right)\right]+\hfill \\ & & \lambda q^{-3}t.\left[h_3{E}_{1,2}\left(-t\right)+q^{-1}{h}_4{E}_{1,2}\left(-q^{-1}t\right)+q^{-2}{h}_5{E}_{1,2}\left(-q^{-2}t\right)\right],\hfill \end{array}$$

(48)

where

$${\left[h_3\right]}_{\alpha \to 1}=\frac{-1}{(1-q^{-1})\left(1-q^{-2}\right)},{\left[h_4\right]}_{\alpha \to 1}=\frac{1}{{\left(1-q^{-1}\right)}^2},{\left[h_5\right]}_{\alpha \to 1}=\frac{-q^{-1}}{{\left(1-q^{-1}\right)}^2(1+q^{-1})}.$$

(49)

Inserting ${\left[h_3\right]}_{\alpha \to 1}$, ${\left[h_4\right]}_{\alpha \to 1}$, and ${\left[h_5\right]}_{\alpha \to 1}$ into Equation (48) and using the property (13) for simplifying the expression, we obtain

$${\mathsf{\Psi }}_3\left(t\right)=\lambda e^{-t}+\frac{\lambda }{q-1}\left(e^{-t/q}-e^{-t}\right)+\frac{\lambda }{\left(q-1\right)\left(q^2-1\right)}\left[q{e}^{-t/q^2}+e^{-t}-\left(q+1\right)e^{-t/q}\right],$$

(50)

which agrees with the 3-term approximate solution in the literature [4,6] and also agrees with Ref. [7] (see Equation (30)) for ordinary derivative ($\alpha \to 1$).

5.2. Convergence

The convergence of the HPM has been investigated in detail by Ayati and Biazar [11] for ordinary differential equations (ODEs) and by Touchent et al. [13] and Sene and Fall [14] for fractional partial differential equations (FPDEs). Moreover, it was proved in Ref. [11] that the homotopy series is convergent in the limit if $\exists (0\le {\mu }_i<1)$ such that ${\mu }_i=\frac{\parallel z_{i+1}\parallel }{\parallel z_i\parallel },\forall i\in \mathbb{N}$, with the norm defined in Banach space by $\parallel f\parallel ={\mathrm{Max}}_{0\le t\le 1}\left|f\left(t\right)\right|$ (see Ref. [11]). For such purpose, the values ${\mu }_1$, ${\mu }_2$, ${\mu }_3$, ⋯, ${\mu }_{10}$ are listed in Table 1 when $\lambda =1$ and $q=1.4$ at three different values of $\alpha$ including the fractional/ordinary derivative, i.e., $\alpha =0.5$, $\alpha =0.75$, and $\alpha =1$.

Table 1. List of the values of ${\mu }_i$ when $\lambda =1$ and $q=1.4$ at three different values of $\alpha$.

	${\mathit{\mu }}_{\mathit{j}}=\frac{\parallel {\mathit{z}}_{\mathit{i}+1}\parallel }{\parallel {\mathit{z}}_{\mathit{i}}\parallel }$
${\mathbf{\mu }}_{\mathbf{j}}$	$\mathbf{\alpha }=\mathbf{0.5}$	$\mathbf{\alpha }=\mathbf{0.75}$	$\mathbf{\alpha }=\mathbf{1}$
${\mu }_1$	0.214582	0.252230	0.308001
${\mu }_2$	0.479368	0.530858	0.604679
${\mu }_3$	0.563455	0.607480	0.668446
${\mu }_4$	0.607715	0.644733	0.693132
${\mu }_5$	0.635007	0.666278	0.704111
${\mu }_6$	0.653379	0.679961	0.709288
${\mu }_7$	0.666460	0.689178	0.711801
${\mu }_8$	0.676140	0.695606	0.713040
${\mu }_9$	0.683504	0.700277	0.713658
${\mu }_{10}$	0.689225	0.703657	0.713968

The calculations of the present results and graphs are deducted using the CAS Wolfram Mathematica. It can be seen from this table that the values of ${\mu }_i$ are all less than one which satisfy the requirement of convergence of the present approximate solutions. The convergence of the sequence $\left\{{\mathsf{\Psi }}_N\left(t\right)\right\}$ is also shown in Figure 1, where ${\mathsf{\Psi }}_4\left(t\right)$, ${\mathsf{\Psi }}_6\left(t\right)$, ${\mathsf{\Psi }}_8\left(t\right)$, ${\mathsf{\Psi }}_{10}\left(t\right)$, and ${\mathsf{\Psi }}_{12}\left(t\right)$ are depicted at $\lambda =1$, $q=1.5$, and $\alpha =0.5$. Figure 1 shows that the sequence of the approximations curves $\left\{{\mathsf{\Psi }}_N\left(t\right)\right\}$ converges to a certain function as the number of terms N increases. Hence, the convergence is achieved in the whole domain of t. Regarding the rate of convergence, it was shown in Ref. [11] that if $z_j$ and $z_j^{\prime }$ are obtained by two homotopy and ${\mu }_j<{\mu }_j^{\prime }$ for each $j\in \mathcal{N}$, then the rate of convergence of ${\sum }_{j=0}^{\infty }{z}_j$ is higher than ${\sum }_{j=0}^{\infty }{z}_j^{\prime }$.

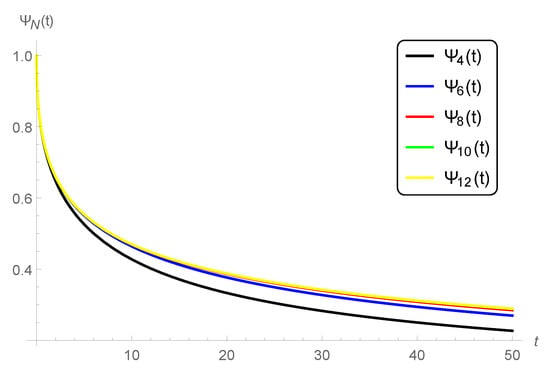
Figure 1. Convergence of the sequence of approximate solutions $\left\{{\mathsf{\Psi }}_N\right\}$ at $\lambda =1$, $q=1.5$, and $\alpha =0.5$.

5.3. Comparisons

In Ref. [9], Patade obtained the following closed-form power series solution for Equations (1) and (2) by applying an iterative method:

$$z\left(t\right)=\lambda \left[\sum _{k=0}^{\infty }\prod _{j=1}^k\left(q^{-(k-j)\alpha -1}-1\right)\frac{t^{k\alpha }}{\mathsf{\Gamma }(k\alpha +1)}\right].$$

(51)

The Solution (51) is convergent for all $q>1$, see [9] for detail. As a special case, $\lambda =1$, the Solution (51) can be recovered from the brilliant results obtained by Bhalekar and Patade [22] for the Pantograph equation. However, it will be shown here that the solution (51) converges in subdomains, i.e., it is not so in the whole domain $t\in [0,\infty )$. Furthermore, the advantages of our solution over the solution in the literature [9] is discussed here. For numerical purposes, the infinity in (51) is replaced by $M-1$ to give the M-term approximation as

$${\mathsf{\Phi }}_M\left(t\right)=\lambda \left[\sum _{k=0}^{M-1}\prod _{j=1}^k\left(q^{-(k-j)\alpha -1}-1\right)\frac{t^{k\alpha }}{\mathsf{\Gamma }(k\alpha +1)}\right].$$

(52)

From (38) and (52), we define the difference between our approximation (38) and the published one (52) (Ref. [9]) as $d_N\left(t\right)={\mathsf{\Psi }}_N\left(t\right)-{\mathsf{\Phi }}_N\left(t\right)$ when taking the same number of terms from both series, i.e., at $N=M$. In Table 2, the numerical values of the present ${\mathsf{\Psi }}_{10}\left(t\right)$ and ${\mathsf{\Phi }}_{10}\left(t\right)$ (Ref. [9]) are listed along with the obtained $d_N\left(t\right)$. The results declare that $d_N\left(t\right)$ is increased by increasing the domain of t. In addition, after a certain value of t the obtained values of $d_N\left(t\right)$ become significant and considerable. Moreover, it is noted from Table 2 that the truncated series solution ${\mathsf{\Phi }}_{10}\left(t\right)$ gives negative values for $t\ge 6$ which is not acceptable from the physical point of view. Accordingly, such truncated series solution [9] is physical in only subdomains while it is not so in the whole domain.

Table 2. Comparison between the present results and Picard iterative method [9] when $\lambda =1$, $q=1.4$ and $\alpha =1$.

	${\mathit{d}}_{\mathit{N}}\left(\mathit{t}\right)={\mathbf{\Psi }}_{\mathit{N}}\left(\mathit{t}\right)-{\mathbf{\Phi }}_{\mathit{N}}\left(\mathit{t}\right)$
$\mathit{t}$	${\mathsf{\Psi }}_{\mathbf{10}}$ (Present)	${\mathsf{\Phi }}_{\mathbf{10}}$ (Ref. [9])	${\mathbf{d}}_{\mathit{N}}\left(\mathbf{t}\right),\mathit{N}=\mathbf{10}$
0	1	1	0
1	0.77178479	0.77178478	1.0000 × 10−8
2	0.62270840	0.62269979	8.6100 × 10−6
3	0.51953974	0.51907862	4.6112 × 10−4
4	0.44464782	0.43701082	7.6370 × 10−3
5	0.38812397	0.32151337	6.6612 × 10−2
6	0.34409085	−0.04360569	3.8770 × 10−1
7	0.30888831	−1.39936299	0.1708 × 101
8	0.28013696	−5.86284892	0.6143 × 101
9	0.25623112	−18.66754017	0.1892 × 102
10	0.23605160	−51.37867472	0.5162 × 102

To confirm this point, a graphical comparison between the present 10-term approximate solution ${\mathsf{\Psi }}_{10}\left(t\right)$$(N=10)$ and the 30-term approximate solution ${\mathsf{\Phi }}_{30}\left(t\right)$$(M=30)$ (Ref. [9]) is displayed in Figure 2 at $\lambda =1$, $q=1.5$, and $\alpha =1$ (ordinary derivative). In addition, Figure 3 shows the comparison between the present ${\mathsf{\Psi }}_{10}\left(t\right)$ and ${\mathsf{\Phi }}_{40}\left(t\right)$ (Ref. [9]) at the same values of Figure 2, i.e., $\lambda =1$, $q=1.5$, and $\alpha =1$ (ordinary derivative).

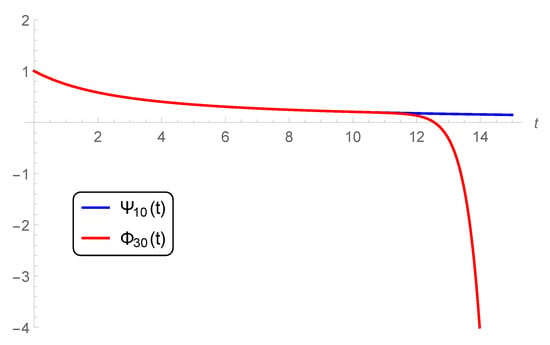
Figure 2. Comparison between ${\mathsf{\Psi }}_{10}$ (present) and ${\mathsf{\Phi }}_{30}$ (Ref. [9]) at $\lambda =1$, $q=1.5$, and $\alpha =1$ (ordinary derivative).

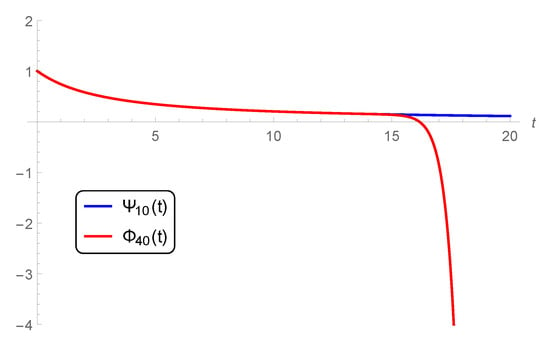
Figure 3. Comparison between ${\mathsf{\Psi }}_{10}$ (present) and ${\mathsf{\Phi }}_{40}$ (Ref. [9]) at $\lambda =1$, $q=1.5$, and $\alpha =1$ (ordinary derivative).

Besides, the comparison between ${\mathsf{\Psi }}_{10}\left(t\right)$ (present) and ${\mathsf{\Phi }}_{50}\left(t\right)$ at $\lambda =1$, $q=1.5$, and $\alpha =0.75$ (fractional derivative) is plotted in Figure 4. It is observed from these figures that the solution in the literature coincides with our approximate one in specified subdomains. After such subdomains, our solution goes smoothly unlike the corresponding one in [9]. In addition, the number of terms needed to be taken from (52) is multiples of the current number of terms. The effect of the delay parameter q on the difference $d_N$, defined above, is depicted in Figure 5 for $N=10$. The results reveal that $d_N$ is highly affected by increasing q. The preceding discussion shows the applicability and efficiency of the HPM in accurately solving the FAE.

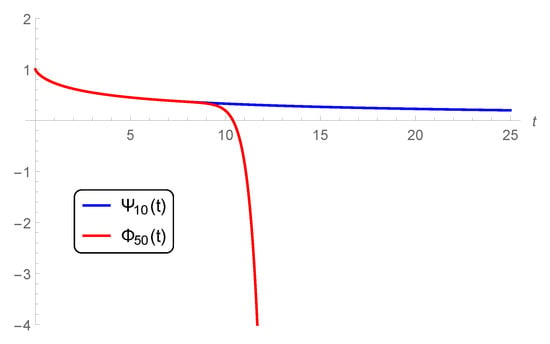
Figure 4. Comparison between ${\mathsf{\Psi }}_{10}$ (present) and ${\mathsf{\Phi }}_{50}$ (Ref. [9]) at $\lambda =1$, $q=1.5$, and $\alpha =0.75$ (fractional derivative).

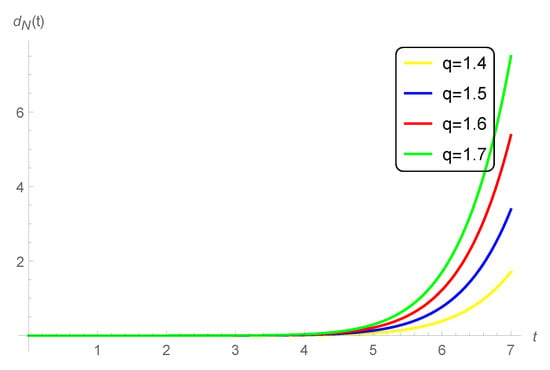
Figure 5. The effect of the delay parameter q on the difference $d_N\left(t\right)(N=10)$ at $\lambda =1$ and $\alpha =1$.

6. Conclusions

The HPM was applied successfully in this paper to approximate the FAE in view of the Caputo fractional derivative. The current approach was mainly based on applying the LT combined with the HPM. It may be the first time to introduce the approximate solutions of the FAE in terms of the Mittag-Leffler functions. The present approximate solution reduces to the corresponding one in the literature in the case of ordinary derivative. The convergence of the current approximate solutions were verified. It was shown in this paper that the obtained approximations in the relevant literature (power series solutions) converge in specified subdomains while our approximate ones converge in the whole domain. The obtained results were validated/supported via performing several comparisons between the current approach and the corresponding one in the literature. Finally, the obtained results were based on considering the Caputo fractional operator with a full memory (cf. left terminal in Equation (3) is 0). However, the present work can also be extended to explore the influence of short memory by following the approach developed by Wojciech and Voyiadjis [23], in this case the left-sided Caputo derivative is to be utilized.