Modernizing Archimedes’ Construction of π

Abstract

In his famous work, “Measurement of a Circle,” Archimedes described a procedure for measuring both the circumference of a circle and the area it bounds. Implicit in his work is the idea that his procedure defines these quantities. Modern approaches for defining $\pi$ eschew his method and instead use arguments that are easier to justify, but they involve ideas that are not elementary. This paper makes Archimedes’ measurement procedure rigorous from a modern perspective. In so doing, it brings a rigorous and geometric treatment of the differential properties of the trigonometric functions into the purview of an introductory calculus course.

1. Introduction

Archimedes’ estimate of the value of $\pi$ in “Measurement of a Circle” is one of his greatest achievements [1]. His approach anticipated foundational ideas of modern analysis as formulated in the 19th and early 20th centuries, making this work one of the first major analytical achievements. Archimedes implicitly defined the circumference of a unit circle axiomatically as a number always greater than the perimeters of approximating inscribed polygons and always less than the perimeters of approximating circumscribed polygons, where the approximating polygons are regular refinements of a regular hexagon. By calculating the perimeters of a regular inscribed and circumscribed polygon of 96 sides, he arrived at the famous estimate:

$$\begin{array}{c}\hfill \frac{223}{71}<\pi <\frac{22}{7}.\end{array}$$

He also found upper and lower bounds for the area of a disk, respectively given by the areas of regular refinements of circumscribed and inscribed squares. He showed that the area of the disk should be the area of a right triangle with one leg having a length equal to the circumference of the unit circle and the other having the length of the radius.

The fact that the approximation procedure for the circumference appears to depend both on the method of refinement and on the type of polygon used in the first stage of the approximation presents a difficulty from a modern point of view. The circumference should be intrinsic to the circle and independent of any specified approximation procedure. It is important to modernize Archimedes’ construction in a way that is maximally accessible to a contemporary of Archimedes for both aesthetic and practical reasons. A practical consequence is that such a modernization cleanly and efficiently resolves the principle difficulty that arises in developing the infinitesimal theory of the trigonometric functions, the calculation

$$\begin{array}{c}\hfill \underset{x\to 0}{lim}\frac{sin\left(x\right)}{x}=1.\end{array}$$

(1)

Gearhart and Schultz discuss in [2], the sinc function, its connection to a variety of topics, and some of its many applications that give important motivation for the independent study of (1). Unger notes in [3] some difficulties in the approaches to treating this limit that are common in differential calculus textbooks. Richman also points out in [4] some of these difficulties and directs the reader to the approach of Apostol [5], which avoids common logically circular arguments by using twice the area of a sector rather than arc length as the argument of the trigonometric functions. This is a natural point of view, especially when considering the direct analogy with the hyperbolic trigonometric functions. Although Apostol’s approach is compelling, it remains desirable to connect this nonstandard way of defining the trigonometric functions with the standard approach. Moreover, Apostol defines the area of a sector rather than deriving it from a limiting procedure using inscribed and circumscribed polygons, so there is still some work to be done to connect the viewpoints.

There are several approaches to computing (1) in the literature. Authors commonly use an analytical approach to solve the problem by defining the trigonometric functions as power series or as solutions to a system of differential equations. Some authors begin by defining the inverse of the tangent function as an integral. Unfortunately, these approaches lack geometric motivation. Cipra studied in [6] the derivatives of the sine and cosine functions by considering the properties of integrals of these functions. He then determined the circumference of the unit circle by using the formula for the length of an arc of a parameterized planar curve. However, the argument that he uses for the sine and cosine function is the arc length, so the length of an arc of a circle still requires a geometric definition independent of his approach.

In [7], Vietoris used the sum of angles formula for the trigonometric functions to prove (1) directly. The notion of an arbitrary fraction of a circle requires a group structure on the circle, and defining such a structure is certainly natural and unavoidable. The argument of the sine and cosine functions will be a multiple of the fraction of a circle that a particular arc represents. However, taking the multiple to be the length of an arc requires a definition of the length of an arc. Defining and computing the length of the arc is the primary difficulty. If one follows Vietoris, one must define $\pi$ in some way independent of it being the area of the unit circle, or half its circumference. If one uses the approach of Zeisel in [8] that follows Vietoris’—at least philosophically—then one can dispense with the alternate definition of $\pi$. Taking $\pi$ as the limit of the area given by regular circumscribed n-gons and taking the multiple of the fraction in the argument to be $2\pi$ will imply the limit (1). However, without some further work, even this elegant approach of Zeisel does not establish the meaning of the area and circumference of the unit circle or their relationship. In fact, one must still show that the limit of the areas he discusses actually exists.

The study of the properties of inscribed and circumscribed polygons and their generalizations are still of current interest, and Apostol and Mnatsakanian present in [9] some interesting results about circumgons, where the notion of a circumgon generalizes the notion of a circumscribed polygon. The novelty of the current study is our modernization of Archimedes’ approach to approximating the circle by inscribed and circumscribed polygons. Using only basic euclidean geometry, we prove our main technical result: for any arc $\mathcal{A}$ that is less than half of a circle, if n is greater than m and if ${\ell }_n$ and ${\ell }_m$ are the lengths of chords that respectively subtend arcs that are an $n\mathrm{th}$ and an $m\mathrm{th}$ of $\mathcal{A}$, then

$$\begin{array}{c}\hfill m{\ell }_n>n{\ell }_m.\end{array}$$

We prove an analogous but reverse inequality for lengths corresponding to edges of circumscribed polygons. These inequalities imply that the circle is a rectifiable curve. They, furthermore, give the classical relationship between the circumference of a circle and the area that it bounds in a way that is both rigorous and accessible to freshman calculus students. Using these inequalities, we show that $2\pi$ is the limiting value of any sequence of perimeters of approximating inscribed or circumscribed polygons. This approach is a simple modernization of the approach of Archimedes and makes rigorous the usual geometric arguments in calculus textbooks that prove (1). It is also elementary enough to be accessible, at least in principle, to a freshman calculus student.

2. Approximation by Regular ${\mathbf{2}}^{\mathbf{m}}\mathbf{n}$-Gons

Denote by $\mathcal{C}$ the unit circle centered at O. Unless otherwise specified, n will be in ${\mathbb{N}}_{\ge 3}$, the set of natural numbers greater than or equal to three, and m will be in ${\mathbb{N}}_0$, the natural numbers with zero. All sequences henceforth indexed by m will be indexed over the set ${\mathbb{N}}_0$.

2.1. Regular Inscribed and Circumscribed Polygons

Definition 1.

An inscribed polygon of $\mathcal{C}$ is a simple convex polygon all of whose vertices lie on $\mathcal{C}$. An inscribed polygon of $\mathcal{C}$ is regular if all of its edges are of equal length.

Definition 2.

A circumscribed polygon of $\mathcal{C}$ is a simple convex polygon all of whose edges intersect $\mathcal{C}$ tangentially. A circumscribed polygon of $\mathcal{C}$ is regular if each of its edges intersects $\mathcal{C}$ tangentially at its midpoint and all of its edges are of equal length.

Remark 1.

The assumption of convexity in the above definitions is redundant, as is the assumption in the case of circumscribed polygons that all edges have the same length. We leave the verification of these assertions to the reader as an exercise.

Denote respectively by $g(m,n)$ and $G(m,n)$ the regular inscribed and circumscribed polygons with $2^{m}n$ edges. Up to congruency, there is only one such inscribed and one such circumscribed polygon for each choice of m and n. Denote respectively by ${\ell }_n\left(m\right)$ and $L_n\left(m\right)$ the edge length of $g(m,n)$ and $G(m,n)$. The respective perimeters of $g(m,n)$ and $G(m,n)$ are $p_n\left(m\right)$ and $P_n\left(m\right)$, where

$$\begin{array}{c}\hfill p_n\left(m\right)=2^{m}n{\ell }_n\left(m\right)\mathrm{and}{P}_n\left(m\right)=2^{m}n{L}_n\left(m\right).\end{array}$$

Let P and Q be adjacent vertices of $g(m,n)$ and let A and B be adjacent vertices of $G(m,n)$. Denote respectively by ${\underline{\alpha }}_n\left(m\right)$ and ${\overline{\alpha }}_n\left(m\right)$ the areas of the triangles $▵POQ$ and $▵AOB$. The respective areas of $g(m,n)$ and $G(m,n)$ are $a_n\left(m\right)$ and $A_n\left(m\right)$, where

$$\begin{array}{c}\hfill a_n\left(m\right)=2^{m}n{\underline{\alpha }}_n\left(m\right)\mathrm{and}{A}_n\left(m\right)=2^{m}n{\overline{\alpha }}_n\left(m\right).\end{array}$$

The triangle inequality and the additivity of area together imply the following proposition.

Proposition 1.

For fixed n, the sequences $\left(p_n\left(m\right)\right)$ and $\left(a_n\left(m\right)\right)$ are both increasing and the sequences $\left(P_n\left(m\right)\right)$ and $\left(A_n\left(m\right)\right)$ are both decreasing.

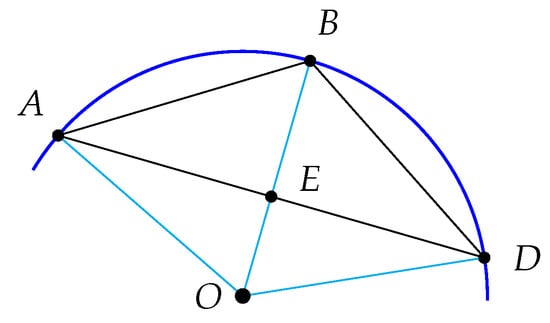
The parallel postulate implies the following useful lemma. Refer to Figure 1 to clarify the statement of the lemma.

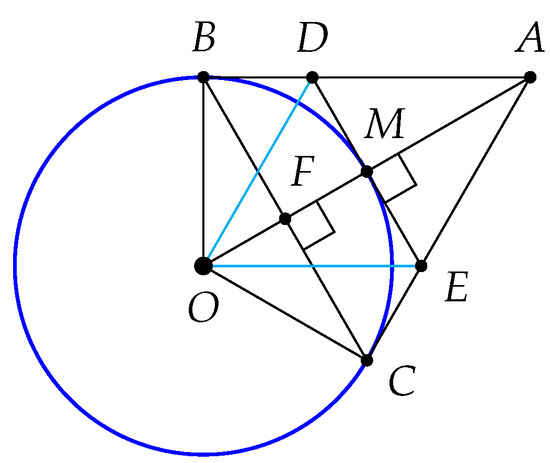
Figure 1. The intersection of adjacent edges of a circumscribed polygon and its refinement.

Lemma 1.

Suppose that C and B are points on $\mathcal{C}$ so that the counterclockwise oriented arc from C to B is less than half of $\mathcal{C}$. If $L_B$ and $L_C$ are lines tangent to $\mathcal{C}$ respectively at B and C, then $L_B$ and $L_C$ intersect at a point A and the right triangles $▵OAB$ and $▵OCA$ are congruent. If F is the point of intersection of $\overline{OA}$ with $\overline{BC}$, then $\angle AFB$ is a right angle. Let M be the point at which $\overline{OA}$ intersects $\mathcal{C}$ and $L_M$ be the line tangent to $\mathcal{C}$ at M. Denote by D the point at which the line $L_M$ intersects $\overline{BA}$ and denote by E the point at which $L_M$ intersects $\overline{CA}$. The angle $\angle AMD$ is congruent to $\angle EMA$ and both are right angles.

2.2. Area and Perimeter Bounds

While Proposition 1 guarantees for fixed n the strict monotonicity of $\left(p_n\left(m\right)\right)$, $\left(a_n\left(m\right)\right)$, $\left(P_n\left(m\right)\right)$ and $\left(A_n\left(m\right)\right)$, it does not guarantee that the sequences are bounded. The following proposition provides the desired bounds.

Proposition 2.

For each n and each m,

$$\begin{array}{c}\hfill p_n\left(m\right)<P_n\left(m\right)\mathrm{and}{a}_n\left(m\right)<A_n\left(m\right).\end{array}$$

Since $\left(p_n\left(m\right)\right)$ and $\left(a_n\left(m\right)\right)$ are increasing and bounded above by $P_n\left(0\right)$ and $A_n\left(0\right)$, and since $\left(P_n\left(m\right)\right)$ and $\left(A_n\left(m\right)\right)$ are decreasing and bounded below by $p_n\left(0\right)$ and $a_n\left(0\right)$, all four sequences are convergent, implying Proposition 3.

Proposition 3.

For each n, there are real numbers $p_n$, $P_n$, $a_n$, and $A_n$ such that

$$\begin{array}{c}\hfill p_n\left(m\right)\to p_n,P_n\left(m\right)\to P_n,a_n\left(m\right)\to a_n,\mathrm{and}{A}_n\left(m\right)\to A_n.\end{array}$$

2.3. Convergence of the Approximations

Proposition 3 gives for each fixed n respective limiting values for the areas and perimeters of regular refinements of regular inscribed and circumscribed polygons with n edges. It does not prove the equality of the respective limits.

Theorem 1

(Heron’s Theorem). If T is a triangle with side lengths $a,b,c$ and $A\left(T\right)$ is the area of T, then

$$\begin{array}{c}\hfill A\left(T\right)=\sqrt{s(s-a)(s-b)(s-c)}\mathrm{where}s=\frac{a+b+c}{2}.\end{array}$$

For any points A and B in the plane, denote by $\ell \left(\overline{AB}\right)$ the length of the line segment $\overline{AB}$. Denote by $h_n\left(m\right)$ the distance from a vertex of $G(m,n)$ to $\mathcal{C}$.

Proposition 4.

For each n,

$$\begin{array}{c}\hfill \left(i\right)a_n=\frac{1}{2}{p}_n,\left(ii\right)A_n=\frac{1}{2}{P}_n,\left(iii\right)P_n=p_n,\mathrm{and}\left(iv\right)A_n=a_n.\end{array}$$

(2)

Proof. 

Since the sequences $\left(p_n\left(m\right)\right)$ and $\left(P_n\left(m\right)\right)$ are both convergent and are respectively equal to $\left(2^{m}n{\ell }_n\left(m\right)\right)$ and $\left(2^{m}n{L}_n\left(m\right)\right)$, both ${\ell }_n\left(m\right)$ and $L_n\left(m\right)$ tend to zero as m tends to infinity. Heron’s theorem implies that

$$\begin{array}{c}\hfill {\underline{\alpha }}_n\left(m\right)=\sqrt{\left(1+\frac{1}{2}{\ell }_n\left(m\right)\right)\left(1-\frac{1}{2}{\ell }_n\left(m\right)\right){\left(\frac{1}{2}{\ell }_n\left(m\right)\right)}^2}=\frac{1}{2}{\ell }_n\left(m\right)\sqrt{1-\frac{1}{4}{\ell }_n{\left(m\right)}^2},\end{array}$$

and so

$$\begin{array}{c}\hfill a_n\left(m\right)=2^{m}n\frac{1}{2}{\ell }_n\left(m\right)\sqrt{1-\frac{1}{4}{\ell }_n{\left(m\right)}^2}=\frac{1}{2}{p}_n\left(m\right)\sqrt{1-\frac{1}{4}{\ell }_n{\left(m\right)}^2}\to \frac{1}{2}{p}_n.\end{array}$$

(3)

Since $\mathcal{C}$ is a unit circle, ${\overline{\alpha }}_n\left(m\right)$ is equal to $\frac{1}{2}{L}_n\left(m\right)$ and so

$$\begin{array}{c}\hfill A_n\left(m\right)=2^{m}n{\overline{\alpha }}_n\left(m\right)=2^{m-1}n{L}_n\left(m\right)=\frac{1}{2}{P}_n\left(m\right)\to \frac{1}{2}{P}_n.\end{array}$$

(4)

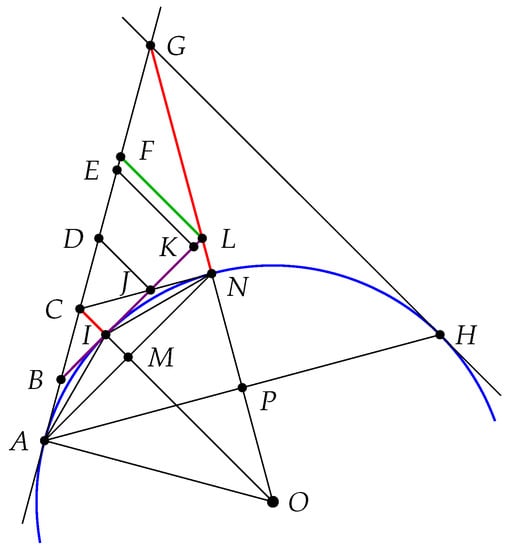
Suppose that G is a vertex of $G(m,n)$, that A and H are points on $\mathcal{C}$ where the edges of $G(m,n)$ with endpoint G are tangent to $\mathcal{C}$, and that $▵GAH$ is counterclockwise oriented (Figure 2). Line segments $\overline{AG}$ and $\overline{GH}$ are half edges of $G(m,n)$, so $\ell \left(\overline{AG}\right)$ is equal to $\frac{1}{2}{L}_n\left(m\right)$. Take N to be a point of $\mathcal{C}$ so that $\overline{AN}$ and $\overline{NH}$ are edges of $g(m+1,n)$. The intersection, C, of lines tangent to $\mathcal{C}$ at A and N is a vertex of $G(m+1,n)$. Take P to be the intersection of $\overline{AH}$ with $\overline{OP}$ and M to be the intersection of $\overline{AN}$ with $\overline{OC}$. Let I be the point of $\mathcal{C}$ that intersects $\overline{OC}$. Lemma 1 implies that $\angle GPA$ and $\angle CMA$ are right angles. Denote by B intersection of line tangent to $\mathcal{C}$ at A with line tangent to $\mathcal{C}$ at I. Denote by J the intersection of the line tangent to $\mathcal{C}$ at I with line tangent to $\mathcal{C}$ at N. The points B and J are adjacent vertices of $G(m+2,n)$. Angle $\angle GNA$ is obtuse because $\angle GNC$ is right; hence

$$\begin{array}{c}\hfill \frac{1}{2}{L}_n\left(m\right)>{\ell }_n(m+1).\end{array}$$

Figure 2. The sequence of heights $\left(h_n\left(m\right)\right)$ is a null sequence.

Extend $\overline{BJ}$ to meet $\overline{OG}$ at a point L. Lemma 1 implies that $\angle OMN$ and $\angle OIJ$ are both right angles and so $\overline{BJ}$ and $\overline{AN}$ are parallel. The point L therefore lies between N and G. The line segment $\overline{NG}$ has length $h_n\left(m\right)$ and $\ell \left(\overline{IC}\right)$ is equal to $h_n(m+1)$.

Line segments $\overline{BI}$, $\overline{IJ}$, and $\overline{JN}$ are congruent as half edges of $G(m+2,n)$. The hypotenuse of the right triangle $▵JNL$ is $\overline{JL}$, so $\ell \left(\overline{JL}\right)$ is greater than $\ell \left(\overline{BI}\right)$. Let K be a point on $\overline{JL}$ such that $\overline{JK}$ and $\overline{BI}$ are congruent. Furthermore, let E and F be points lying on $\overline{AG}$ such that $\overline{KE}$, $\overline{LF}$, and $\overline{IC}$ are parallel. The similarity of $▵BIC$, $▵BKE$, and $▵BLF$ and the equality of $\ell \left(\overline{BK}\right)$ and $3\ell \left(\overline{BI}\right)$ together imply that $\ell \left(\overline{KE}\right)$ is equal to $3\ell \left(\overline{IC}\right)$. Since $\angle OAC$ is right, $\angle OCG$ is obtuse and so $\angle LFG$ is as well, implying that $\ell \left(\overline{LG}\right)$ is greater than $\ell \left(\overline{LF}\right)$. Since $\ell \left(\overline{BL}\right)$ is greater than $\ell \left(\overline{BK}\right)$,

$$\begin{array}{c}\hfill h_n\left(m\right)=\ell \left(\overline{NG}\right)>\ell \left(\overline{LG}\right)>\ell \left(\overline{LF}\right)>\ell \left(\overline{KE}\right)=3\ell \left(\overline{IC}\right)=3h_n(m+1),\mathrm{so}{h}_n\left(m\right)<{\left(\frac{1}{3}\right)}^m{h}_n\left(0\right).\end{array}$$

The triangle inequality implies that $h_n\left(m\right)+{\ell }_n(m+1)$ is greater than $\frac{1}{2}{L}_n\left(m\right)$; hence

$$\begin{array}{c}\hfill 0<\frac{1}{2}{L}_n\left(m\right)-{\ell }_n(m+1)<h_n\left(m\right)<{\left(\frac{1}{3}\right)}^m{h}_n\left(0\right),\end{array}$$

and so

$$\begin{array}{c}\hfill 0<2^{m}n{L}_n\left(m\right)-2^{m+1}n{\ell }_n(m+1)=P_n\left(m\right)-p_n(m+1)<2n{\left(\frac{2}{3}\right)}^m{h}_n\left(0\right).\end{array}$$

(5)

The estimate (5) implies that

$$\begin{array}{cc}\hfill 0<P_n\left(m\right)-p_n\left(m\right)=(P_n\left(m\right)-p_n(m+1))+(p_n(m+1)-p_n\left(m\right))& \\ \hfill \phantom{0}<2n{\left(\frac{2}{3}\right)}^m{h}_n\left(0\right)+(p_n(m+1)-p_n\left(m\right))\to 0.\end{array}$$

The difference $P_n\left(m\right)-p_n\left(m\right)$ tends to zero as n tends to infinity; hence $P_n$ is equal to $p_n$. Of course, Proposition 4 part (iv) follows immediately from (3) and (4). □

3. Edge Length Comparison Theorems

Comparing the edge lengths of inscribed and circumscribed segments corresponding to different regular subdivisions of an arc is the key to proving that the definition of $\pi$ is independent of any approximation scheme. This section will present such a comparison.

Definition 3.

A(counter)clockwise oriented partition P of an arc $\mathcal{A}$ is a finite sequence of points of $\mathcal{A}$ that is (counter)clockwise ordered, and the first and last points of P are the endpoints of $\mathcal{A}$. Such a finite sequence is regular if all adjacent points of P are equidistant.

Temporarily ignore the previous restrictions on the natural numbers m and n and refer to Figure 3 for the discussion that follows.

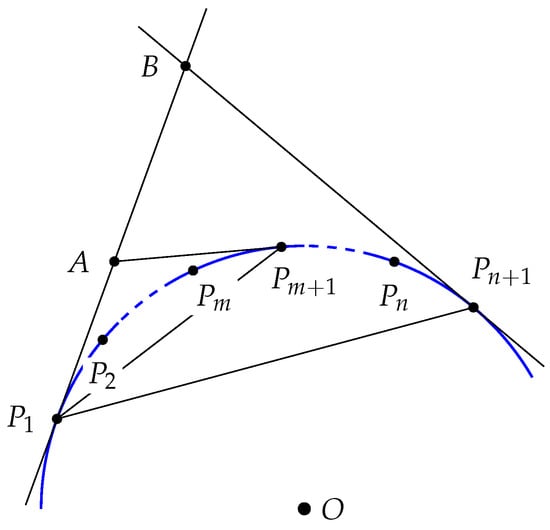
Figure 3. Comparing edge lengths associated to different numbers of congruent segments.

Suppose that m and n are natural numbers with n greater than m. Let $\mathcal{A}$ be an arc of $\mathcal{C}$ that is less than half of $\mathcal{C}$ and let $(P_1,\cdots ,P_{n+1})$ be a regular clockwise oriented partition of $\mathcal{A}$. Let B be the point of intersection of the lines tangent to $\mathcal{C}$ at $P_1$ and $P_{n+1}$ and let A be the point of intersection of the lines tangent to $\mathcal{C}$ at $P_1$ and $P_{M+1}$. Denote by ${\ell }_m$, ${\ell }_n$, $L_m$, and $L_n$ the respective lengths of $\overline{P_1{P}_{m+1}}$, $\overline{P_1{P}_{n+1}}$, $\overline{P_{1}B}$ and $\overline{P_{1}A}$. We will show that

$$\begin{array}{c}\hfill n{\ell }_m>m{\ell }_n\mathrm{and}n{L}_m<m{L}_n.\end{array}$$

3.1. General Symmetry Considerations for Polygonal Segments

Suppose that A, B, C, and D belong to a collection of points that form a regular partition of $\mathcal{A}$ (Figure 4), that A and B are adjacent, that C and D are adjacent, and that B and C lie on the same side of the line $\overline{AD}$ and opposite the side where O lies. Suppose furthermore that the quadruple $(A,B,C,D)$ forms a clockwise oriented partition of $\mathcal{A}$. Standard arguments using the SSS theorem imply Proposition 5, whose proof is left as an exercise.

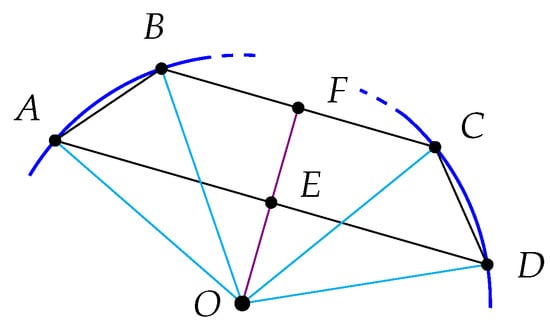
Figure 4. An inscribed isosceles trapezoid.

Proposition 5.

The quadrilateral $\square DCBA$(Figure 4) is an isosceles trapezoid and $\overline{AD}$ and $\overline{BC}$ are parallel. Furthermore, in the degenerate case (Figure 5) when B is equal to C, angles $\angle DAB$ and $\angle BDA$ are congruent and $\overline{BO}$ bisects $\overline{AD}$.

Figure 5. A degenerate inscribed isosceles trapezoid.

Refer to Figure 6. Suppose that $(A,B,C,D)$ is a clockwise ordered partition of an arc $\mathcal{A}$ of $\mathcal{C}$ and that $\overline{AB}$ has the same length as $\overline{CD}$. Let $L_A$, $L_B$, $L_C$ and $L_D$ be lines tangent to $\mathcal{A}$ that intersect A, B, C, and D respectively. Since $\mathcal{A}$ is less than half of a circle, Lemma 1 implies that $L_A$ and $L_D$ intersect at a point $P_{AD}$, $L_A$ and $L_C$ intersect at a point $P_{AC}$, $L_B$ and $L_D$ intersect at a point $P_{BD}$, and $L_B$ and $L_C$ intersect at a point $P_{BC}$. The SAS and SSS theorems along with Proposition 5 and Lemma 1 imply Proposition 6, whose proof is left to the reader as a standard exercise.

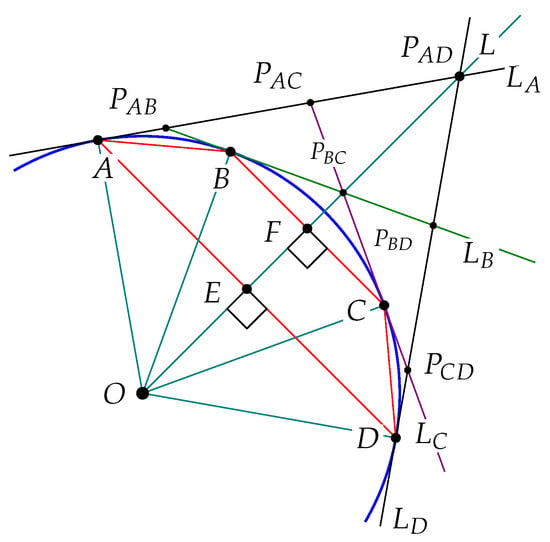
Figure 6. An isosceles trapezoid that defines a segment of a circumscribed polygon.

Proposition 6.

The line segment $\overline{P_{AD}{P}_{BC}}$ can be extended to a ray, L, that meets O and bisects and is perpendicular to $\overline{P_{AC}{P}_{BD}}$, $\overline{AD}$, and $\overline{BC}$. Furthermore, L bisects $\angle P_{AC}{P}_{AD}{P}_{BD}$. Finally, triangles $▵P_{AD}{P}_{AC}{P}_{BC}$ and $▵P_{AD}{P}_{BD}{P}_{BC}$ are congruent, as are $▵P_{AD}{P}_{BC}{P}_{AB}$ and $▵P_{AD}{P}_{BC}{P}_{CD}$.

Suppose that $\mathcal{A}$ is an arc of $\mathcal{C}$ that is less than half of $\mathcal{C}$ and suppose that $(P_1,\cdots ,P_n)$ is a regular clockwise orientated partition with n greater than 3 (Figure 7). For each natural number i in $[1,n]$, let $L_i$ be the line tangent to $\mathcal{A}$ and intersecting $P_i$. Since $\mathcal{A}$ is less than half of a circle, Lemma 1 implies that the lines $L_i$ and $L_j$ intersect for each i not equal to j; call this point of intersection $P_{i,j}$. Notice that $P_{i,j}$ is equal to $P_{j,i}$. The key theorem of the next section is to prove that

$$\begin{array}{c}\hfill j>i\mathrm{implies}\mathrm{that}\ell \left(\overline{P_{1,i}{P}_{1,i+1}}\right)<\ell \left(\overline{P_{1,j}{P}_{1,j+1}}\right).\end{array}$$

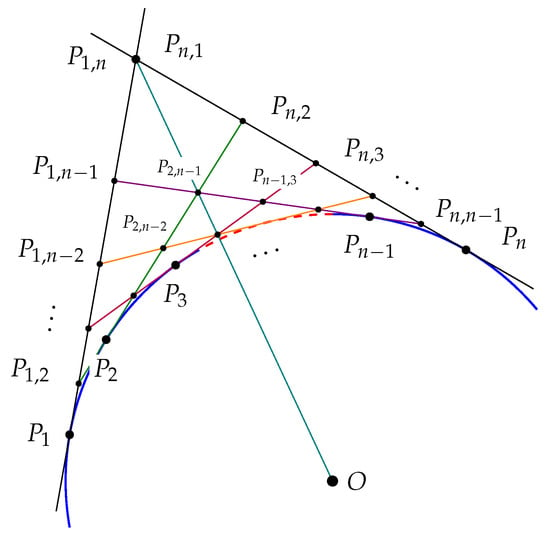
Figure 7. Line segments defined by refinements of a circumscribed polygon.

Denote by $m(\angle ABC)$ the degree measure of $\angle ABC$. Refer to Figure 7 for Proposition 7.

Proposition 7.

Suppose that n is in ${\mathbb{N}}_{\ge 3}$ and $(P_1,\cdots ,P_n)$ is a regular clockwise oriented partition of an arc $\mathcal{A}$ that is less than half of $\mathcal{C}$. If $m(\angle P_{i}O{P}_{i+1})$ is equal to ${\theta }^{\circ }$, then

(1) 

$m(\angle P_{1,n-1}{P}_{1,n}{P}_{n,2})={(180-n\theta )}^{\circ };$

(2) 

$m(\angle P_{2,n-1}{P}_{1,n-1}{P}_{1,n})=m(\angle P_{n,1}{P}_{n,2}{P}_{2,n-1})=(n-1){\theta }^{\circ }$;

(3) 

$m(\angle P_{n,2}{P}_{2,n-1}{P}_{1,n-1})={180}^{\circ }-(n-2){\theta }^{\circ }$.

Proof. 

Both $\angle P_{1,n}{P}_{n}O$ and $\angle O{P}_1{P}_{1,n}$ are right angles, implying that

$$\begin{array}{c}\hfill m(\angle P_{n}O{P}_1)+m(\angle P_1{P}_{1,n}{P}_n)={180}^{\circ }.\end{array}$$

Since $m(\angle P_{n}O{P}_1)$ is equal to $n{\theta }^{\circ }$, the fact that the sum of the interior angles of the quadrilateral formed by $P_1$, $P_n$, O and $P_{1,n}$ is ${360}^{\circ }$ implies (1). Since $P_1$, $P_{1,n-1}$ and $P_{1,n}$ lie on the same line, $\angle P_1{P}_{1,n-1}{P}_{2,n-1}$ and $\angle P_{2,n-1}{P}_{1,n-1}{P}_{1,n}$ are supplementary. By (1),

$$\begin{array}{c}\hfill m(\angle P_{1,1}{P}_{1,n-1}{P}_{2,n-1})={(180-(n-1)\theta )}^{\circ }\end{array}$$

and so

$$\begin{array}{c}\hfill m(\angle P_{1,n}{P}_{1,n-1}{P}_{2,n-1})=(n-1){\theta }^{\circ }.\end{array}$$

Of course, an analogous argument proves the same result for $\angle P_{2,n-1}{P}_{n,2}{P}_n$, implying (2), although another argument is not necessary in light of Proposition 6. Finally, since the sum of angles of a quadrilateral is ${360}^{\circ }$, (3) follows from (1) and (2). □

3.2. Length Estimates for Inscribed Polygonal Segments

Let $\mathcal{A}$ again be an arc of a unit circle that is less than half of the circle. Suppose that $(P_1,\cdots ,P_{n+1})$ is a regular clockwise oriented partition of $\mathcal{A}$ (Figure 8 and Figure 9). For each $P_i$ where i is a natural number in $[2,n]$, there is a line perpendicular to $\overline{P_1{P}_{n+1}}$ that intersects $P_i$ at a point $q_i$ on $\overline{P_1{P}_{n+1}}$.

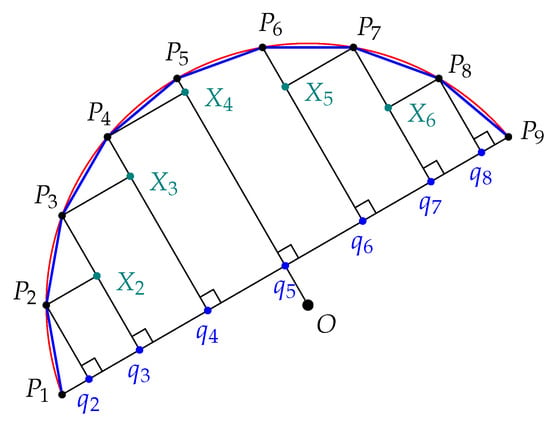
Figure 8. Inscribed length estimates for an odd number of points on an arc.

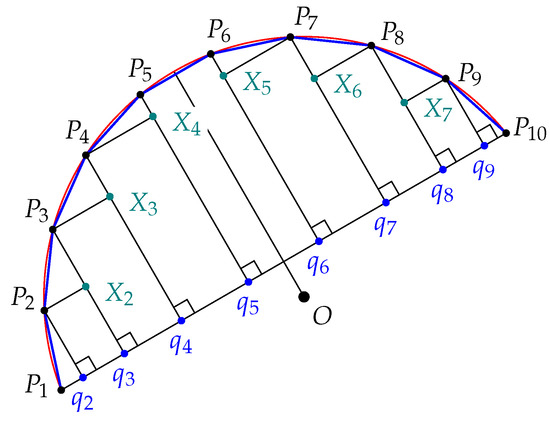
Figure 9. Inscribed length estimates for an even number of points on an arc.

Figure 8 shows an example where n is even and Figure 9 shows the qualitative difference in an odd example. Set $q_1$ to be equal to $P_1$ and let $q_{n+1}$ be equal to $P_{n+1}$. For each i between 1 and $n+1$, let $q_i$ be the point on $\overline{P_1{P}_{n+1}}$ so that $\overline{P_i{q}_i}$ is perpendicular to $\overline{P_1{P}_{n+1}}$.

Proposition 8.

If i and j are natural numbers in $\left[1,\frac{n+1}{2}\right]$ with i less than j, then

$$\begin{array}{c}\hfill \ell \left(\overline{q_i{q}_{i+1}}\right)<\ell \left(\overline{q_j{q}_{j+1}}\right)\mathrm{and}\ell \left(\overline{q_i{q}_{i+1}}\right)=\ell \left(\overline{q_{n+1-i}{q}_{n+2-i}}\right).\end{array}$$

Proof. 

Proposition 5 implies that each of the line segments $\overline{P_i{P}_{n+2-i}}$ is parallel to $\overline{P_1{P}_{n+1}}$. Since $\overline{P_i{q}_i}$ and $\overline{P_i{P}_{n+2-i}}$ are perpendicular for i in $\left[1,\frac{n}{2}\right]$,

$$\begin{array}{c}\hfill \ell \left(\overline{P_i{P}_{n+2-i}}\right)=\ell \left(\overline{q_i{q}_{n+2-i}}\right).\end{array}$$

Let $X_1$ be equal to $q_2$, and for each i in $\left[2,\frac{n}{2}\right]$, let $X_i$ be the point of intersection of $\overline{P_i{P}_{n+2-i}}$ and $\overline{P_{i+1}{q}_{i+1}}$. Let $X_{n-1}$ be equal to $q_n$, and for each i in $\left[\frac{n}{2}+1,n\right]$, let $X_i$ be the point of intersection of $\overline{P_{i+2}{P}_{n-i}}$ and $\overline{P_{i+1}{q}_{i+1}}$. For each i in $\left[1,\frac{n}{2}\right]$, Proposition 5 implies that $\ell \left(\overline{P_i{X}_i}\right)$ is equal to $\ell \left(\overline{X_{n-i}{P}_{n+2-i}}\right)$, which is equal to $\ell \left(\overline{q_i{q}_{i+1}}\right)$ and $\ell \left(\overline{q_{n+1-i}{q}_{n+2-i}}\right)$.

Let i and j be in $\left[1,\frac{n}{2}\right]$ with i less than j. To show that $\ell \left(P_i{X}_i\right)$ is less than $\ell \left(P_j{X}_j\right)$, it suffices to show that if i and $i+1$ are in $\left[1,\frac{n}{2}\right]$, then $\ell \left(P_i{X}_i\right)$ is less than $\ell \left(P_{i+1}{X}_{i+1}\right)$. Extend the line segment $\overline{P_i{P}_{i+1}}$ to a ray, $R_1$, originating at $P_i$. Extend the line segment $\overline{q_{i+2}{P}_{i+2}}$ to a ray, $R_2$, that meets $R_1$ at a point A. The ray $R_2$ passes through the point $X_{i+1}$ and $l\left(\overline{X_{i+1}A}\right)$ is greater than $l\left(\overline{X_{i+1}{P}_{i+2}}\right)$, while angles $\angle X_{i+1}{P}_{i+1}A$ and $\angle X_i{P}_i{P}_{i+1}$ are congruent, implying that $\angle X_i{P}_i{P}_{i+1}$ is greater than $\angle X_{i+1}{P}_{i+1}{P}_{i+2}$. Since $▵X_i{P}_i{P}_{i+1}$ and $▵X_{i+1}{P}_{i+1}{P}_{i+2}$ are both right triangles with hypotenuses that have the same length, $\angle P_i{P}_{i+1}{X}_i$ is greater than $\angle P_{i+1}{P}_{i+2}{X}_{i+1}$, implying that $\ell \left(\overline{P_i{X}_i}\right)$ is less than $\ell \left(\overline{P_{i+1}{X}_{i+1}}\right)$. Since i and j are integers, the statement of the proposition is different when n is odd and when n is even.

Note that if n is odd, then the above arguments show that $\overline{q_{\frac{n+1}{2}}{q}_{\frac{n+1}{2}+1}}$ is the longest of all of the segments $\overline{q_i{q}_{+1}}$. □

Since the lengths of the line segments $\overline{q_i{q}_{i+1}}$ are strictly increasing up to the midpoint of $\mathcal{A}$ for even n and the middle segment for odd n, the following corollary is immediate.

Corollary 1.

Let k be the largest integer less than or equal to $\frac{n}{2}$. If n is greater than 2 and s is a natural number in $(1,k]$, then

$$\begin{array}{c}\hfill \ell \left(\overline{q_1{q}_{s+1}}\right)<\frac{\ell \left(\overline{P_1{P}_{n+1}}\right)}{n}s.\end{array}$$

Remark 2.

The above corollary implies that the average length of a segment of $\overline{q_1{q}_{k+1}}$ is less than the average length of a segment of $\overline{q_1{q}_{n_1}}$ if the arc between $P_1$ and $P_{k+1}$ is less than half of $\mathcal{A}$.

From this corollary follows the following key theorem.

Theorem 2.

Suppose that $\mathcal{A}$ is an arc that is less than half of a circle and that $(P_1,\cdots ,P_{n+1})$ is a regular clockwise oriented partition of $\mathcal{A}$. Denote by ${\ell }_n$ the length of the line segment $\overline{P_1{P}_{n+1}}$, and by ${\ell }_m$ the length of $\overline{P_1{P}_{m+1}}$. If m is less than n, then

$$\begin{array}{c}\hfill n{\ell }_m>m{\ell }_n.\end{array}$$

Proof. 

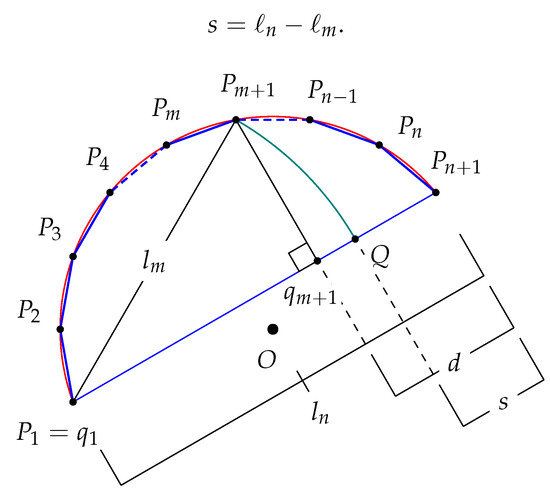
Assume first that $2m$ is greater than n and refer to Figure 10. Let Q be the point of intersection of the circle of radius ${\ell }_m$ centered at $P_1$ with the line segment $\overline{P_1{P}_{n+1}}$. The length of $\overline{P_{1}Q}$ is equal to ${\ell }_m$. If s the length of the line segment $\overline{Q{P}_{n+1}}$, then

$$\begin{array}{c}\hfill s={\ell }_n-{\ell }_m.\end{array}$$

Figure 10. Lengths of chords subtending arcs with different numbers of congruent segments.

There are n edges with vertices on the arc between $P_1$ and $P_{n+1}$. There are $m+1$ vertices of the regular subdivision between $P_1$ and $P_{m+1}$ on $\mathcal{A}$. Since $2m$ is greater than n, $P_{m+1}$ lies clockwise from the intersection, M, of a line bisecting $\overline{P_1{P}_{n+1}}$ and the circle. For the same reason, the point $P_{n-m}$ lies counterclockwise from M.

Proposition 8 implies that the average lengths of the segments $\overline{q_1{q}_2}$, $\overline{q_2{q}_3}$, ..., $\overline{q_{n-m}{q}_{n-m}}$ is the same as the average lengths of the segments $\overline{q_{n+1}{q}_n}$, $\overline{q_n{q}_{n-1}},\cdots ,\overline{q_{2+m}{q}_{1+m}}$. However, for any edge $\overline{P_i{P}_{i+1}}$ between the vertices $P_{n+1-m}$ and $P_{m+1}$, the projection of the edge, $\overline{q_i{q}_j}$ on the line $\overline{P_1{P}_{n+1}}$, is longer than the longest of the segments $\overline{q_j{q}_{j+1}}$ with j in $[1,n-m)\cup (m+1,n]$. Denote by d the length of the line segment $\overline{q_{m+1}{q}_{n+1}}$ to obtain the inequality

$$\begin{array}{c}\hfill d<{\displaystyle \frac{n-m}{n}}{\ell }_n.\end{array}$$

Since ${\ell }_m$ is the length of the hypotenuse of a triangle with a leg of length ${\ell }_n-d$ and ${\ell }_m$ is equal to ${\ell }_n-s$, the length s is less than d and so

$$\begin{array}{c}\hfill s<{\displaystyle \frac{n-m}{n}}{\ell }_n.\end{array}$$

Since, ${\ell }_m+s$ is equal to ${\ell }_n$,

$$\begin{array}{c}\hfill {\ell }_m+{\displaystyle \frac{n-m}{n}}{\ell }_n>{\ell }_n,\mathrm{and}\mathrm{so}n{\ell }_m>m{\ell }_m.\end{array}$$

Suppose that $2m$ is equal to n. Since the sum of the lengths of two sides of a non-degenerate triangle are greater than the length of the third, $2{\ell }_m$ is greater than ${\ell }_{2m}$, and so

$$\begin{array}{c}\hfill n{\ell }_m=2m{\ell }_m>m{\ell }_{2m}=m{\ell }_n.\end{array}$$

(6)

In the case when $2m$ is less than n, there is a natural number k with

$$\begin{array}{c}\hfill 2^{k}m<n\le 2^{k+1}m\end{array}$$

which together with (6) implies that

$$\begin{array}{c}\hfill n{\ell }_{2^{k}m}>2^{k}m{\ell }_n.\end{array}$$

The points $P_1$ and $P_{2^{k-1}m+1}$ have $2^{k-1}m$ segments between them as do the points $P_{2^{k-1}m+1}$ and $P_{2^{k}m+1}$. Thus,

$$\begin{array}{c}\hfill \ell \left(\overline{P_1{P}_{2^{k-1}m+1}}\right)=\ell \left(\overline{P_{2^{k-1}m+1}{P}_{2^{k}m+1}}\right)={\ell }_{2^{k-1}m}.\end{array}$$

Therefore, $2{\ell }_{2^{k-1}m}$ is equal to the sum of the lengths of two sides of $▵P_1{P}_{2^{k-1}m+1}{P}_{2^{k}m+1}$ and so is greater than ${\ell }_{2^{k}m}$. Therefore,

$$\begin{array}{c}\hfill 2n{\ell }_{2^{k-1}m}>n{\ell }_{2^{k}m}>2^{k}m{\ell }_n\mathrm{and}\mathrm{so}n{\ell }_{2^{k-1}m}>2^{k-1}m{\ell }_n>m{\ell }_n.\end{array}$$

The inequality

$$\begin{array}{c}\hfill n{\ell }_m>m{\ell }_n.\end{array}$$

follows from applying the above argument $k-1$ more times. □

3.3. Length Estimates for Circumscribed Polygonal Segments

Use the notation of Proposition 7 and refer to Figure 11 for the statement and proof of the proposition below.

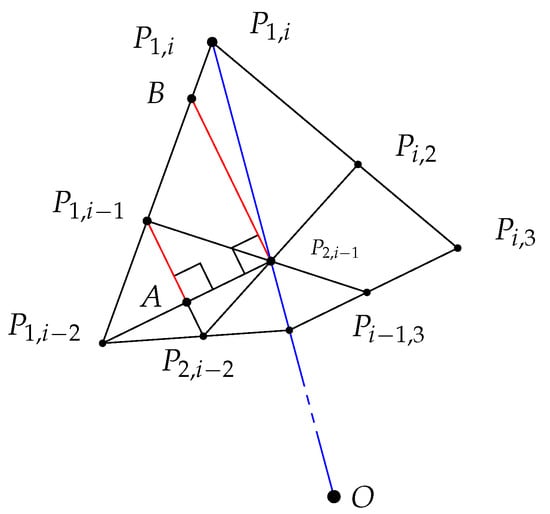
Figure 11. The apex of the intersection of circumscribed edges and their refinements.

Proposition 9.

If k and l are natural numbers, then

$$\begin{array}{c}\hfill 1\le k<l\le n-1\mathrm{implies}\mathrm{that}\ell \left(\overline{P_{1,k}{P}_{1,k+1}}\right)<\ell \left(\overline{P_{1,l}{P}_{1,l+1}}\right).\end{array}$$

Proof. 

Suppose that i is a natural number in $[3,n]$. Proposition 6 implies that the line $\overline{P_{1,i-1}{P}_{2,i-2}}$ is a perpendicular bisector of $\overline{P_{1,i-2}{P}_{2,i-1}}$. Denote by A this intersection. To prove the proposition, it suffices to show that $\angle P_{1,i}{P}_{2,i-1}{P}_{1,i-2}$ is greater than a right angle. In this case, there is a line that intersects $P_{2,i-1}$ and is perpendicular to $\overline{P_{1,i-2}{P}_{2,i-1}}$ that intersects $\overline{P_{1,i-2}{P}_{1,i}}$ at a point B. The triangles $▵P_{1,i-2}A{P}_{1,i-1}$ and $▵P_{1,i-2}{P}_{2,i-1}B$ are similar, but since $\overline{P_{1,i-2}{P}_{2,i-1}}$ is twice the length of $\overline{P_{1,i-2}A}$, $\overline{P_{1,i-2}B}$ is twice the length of $\overline{P_{1,i-2}{P}_{1,i-1}}$, and so

$$\begin{array}{c}\hfill \ell \left(\overline{P_{1,i-1}{P}_{1,i}}\right)>\ell \left(\overline{P_{1,i-1}B}\right)=\ell \left(\overline{P_{1,i-2}{P}_{1,i-1}}\right).\end{array}$$

Proposition 6 implies the congruency of the angles $\angle P_{1,i}{P}_{2,i-1}{P}_{1,i-1}$ and $\angle P_{i,2}{P}_{2,i-1}{P}_{1,i}$. Proposition 7 implies that

$$\begin{array}{c}\hfill m(\angle P_{1,i}{P}_{2,i-1}{P}_{1,i-1})={90}^{\circ }-\frac{i-2}{2}{\theta }^{\circ }.\end{array}$$

Proposition 6 implies that $\overline{P_{2,i-2}{P}_{1,i-1}}$ is perpendicular to $\overline{P_{1,i-2}{P}_{2,i-1}}$ and furthermore that $\overline{P_{2,i-2}{P}_{1,i-1}}$ bisects $\angle P_{2,i-1}{P}_{2,i-2}{P}_{1,i-2}$. Therefore, $\angle P_{1,i-2}{P}_{2,i-1}{P}_{2,i-2}$ and $\angle P_{2,i-2}{P}_{1,i-2}{P}_{2,i-1}$ are congruent. Proposition 7 implies that

$$\begin{array}{c}\hfill 2m(\angle P_{1,i-2}{P}_{2,i-1}{P}_{2,i-2})+{180}^{\circ }-(i-3){\theta }^{\circ }={180}^{\circ }.\end{array}$$

Therefore, $m(\angle P_{1,i-2}{P}_{2,i-1}{P}_{2,i-2})$ is equal to $\frac{i-3}{2}{\theta }^{\circ }$ and so

$$\begin{array}{cc}\hfill m(\angle P_{1,i}{P}_{2,i-1}{P}_{1,i-2})& =m(\angle P_{1,i}{P}_{2,i-1}{P}_{1,i-1})+m(\angle P_{1,i-1}{P}_{2,i-1}{P}_{1,i-2})\hfill \\ & ={90}^{\circ }-\frac{i-2}{2}{\theta }^{\circ }+\left((i-2){\theta }^{\circ }-\frac{i-3}{2}{\theta }^{\circ }\right)\hfill \\ & ={90}^{\circ }+{\frac{\theta }{2}}^{\circ }>{90}^{\circ }.\hfill \end{array}$$

Consider the case where i is 2 (Figure 12). As in the argument above, the key is to show that

$$\begin{array}{c}\hfill m(\angle P_{1,3}{P}_2{P}_1)>{90}^{\circ }.\end{array}$$

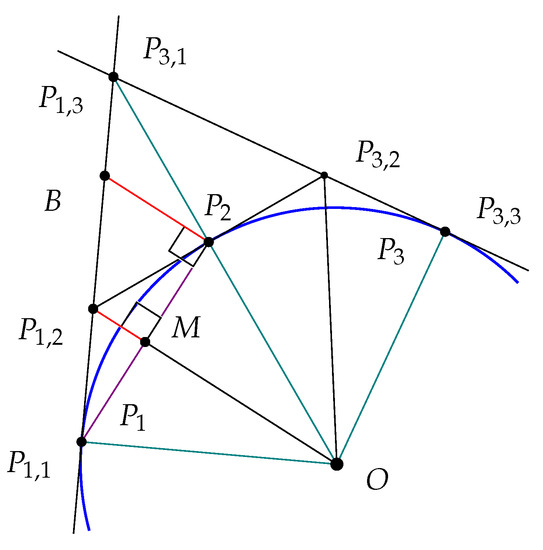
Figure 12. The intersection of circumscribed edges associated to an arc with two segments.

Proposition 6 implies that $\overline{P_{1,2}{P}_{3,2}}$ is tangent to $\mathcal{A}$, and hence perpendicular to $\overline{P_{1,3}{P}_2}$. It suffices to show that $m(\angle P_{1,2}{P}_2{P}_1)$ does not equal 0. Since

$$\begin{array}{c}\hfill m(\angle P_{2}O{P}_1)={\theta }^{\circ },\end{array}$$

$\angle P_1{P}_{1,2}{P}_2$ has measure ${(180-\theta )}^{\circ }$. Since the angles $\angle P_{1,2}{P}_1{P}_2$ and $\angle P_{1,2}{P}_2{P}_1$ are congruent, both have measure ${\frac{\theta }{2}}^{\circ }$, which is greater than 0. □

Theorem 3.

Suppose that n is a natural number greater than two and $(P_1,\cdots ,P_{n+1})$ is a regular clockwise orientated partition of an arc $\mathcal{A}$. If $L_n$ and $L_m$ respectively denote the length of the line segment $\overline{P_1{P}_{1,n+1}}$ and the length of the line segment $\overline{P_1{P}_{m+1}}$, then

$$\begin{array}{c}\hfill m<n\mathrm{implies}\mathrm{that}n{L}_m<m{L}_n.\end{array}$$

Proof. 

The lengths of the segments $\overline{P_{1,i}{P}_{1,i+1}}$ are increasing in i, so the average length of a segment of $L_n$ is larger than the average length of a segment of $L_m$. Therefore,

$$\begin{array}{c}\hfill \frac{L_n}{n}>\frac{L_m}{m},\end{array}$$

implying the desired result. □

4. Circumference and Area Are Intrinsic

Definition 4.

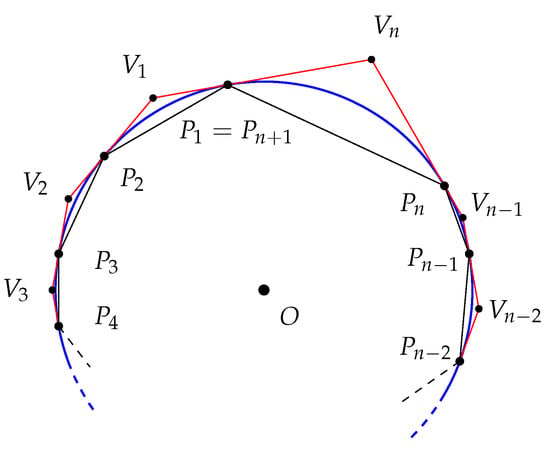
A circuit is a finite sequence of points $\left(P_1,\cdots ,P_{n+1}\right)$ on $\mathcal{C}$ that is counterclockwise ordered and with the property that $P_1$ is equal to $P_{n+1}$ (see Figure 13).

Figure 13. Inscribed and circumscribed polygons associated to a circuit.

Without loss in generality and in order to simplify the exposition, assume that the arc connecting adjacent points of a circuit is less than half of a circle.

Definition 5.

A refinement of a circuit ${\mathcal{S}}_1$ is a circuit ${\mathcal{S}}_2$ such that, as functions on finite sets, the range of ${\mathcal{S}}_1$ is a subset of the range of ${\mathcal{S}}_2$.

Denote by $S\left(\mathcal{C}\right)$ the set of all circuits on $\mathcal{C}$. Suppose that $\left(P_1,\cdots ,P_{n+1}\right)$ is in $S\left(\mathcal{C}\right)$. The inscribed polygon $g\left(P_1,\cdots ,P_{n+1}\right)$ is the polygon whose vertices are the points in the circuit and the circumscribed polygon $G\left(P_1,\cdots ,P_{n+1}\right)$ is the polygon whose vertices are the points given by the intersections of the lines tangent to $\mathcal{C}$ at adjacent points of the circuit.

Definition 6.

For any polygon P, denote by $\pi \left(P\right)$ the perimeter of P. Let $min\left(P_1,\cdots ,P_{n+1}\right)$ denote the minimum edge length of $g\left(P_1,\cdots ,P_{n+1}\right)$ and denote by $max\left(P_1,\cdots ,P_{n+1}\right)$ the maximal edge length of $g\left(P_1,\cdots ,P_{n+1}\right)$.

4.1. Approximation by Rational Circuits

Let the length ℓ be less than 2. Construct recursively a sequence of points and a corresponding piecewise linear path in the following way. Take $P_1$ to be a point on $\mathcal{C}$. Let $P_n$ be the $n^{\mathrm{th}}$ term in a sequence of points on $\mathcal{C}$ so that if $P_i$ and $P_{i+1}$ are adjacent points in the sequence, then $\ell \left(\overline{P_i{P}_{i+1}}\right)$ is equal to ℓ and the triangle $▵O{P}_i{P}_{i+1}$ is counterclockwise oriented. The circle ${\mathcal{C}}_{\ell ,n}$ of radius ℓ with center $P_n$ intersects $\mathcal{C}$ in exactly two places. Let $P_{n+1}$ be the first of these points counterclockwise from $P_n$. The line segment $\overline{P_n{P}_{n+1}}$ is of length ℓ. If the sequence has the property that for some k, $P_k$ is equal to $P_1$, then ℓ is a rational length and there is a first such k that is the numerator of ℓ, denoted by $\mathcal{N}\left(\ell \right)$. The closed piecewise linear path $\Gamma \left(\ell \right)$ is the finite sequence of edges

$$\begin{array}{c}\hfill \Gamma \left(\ell \right)=\left(\overline{P_1{P}_2},\cdots ,\overline{P_{\mathcal{N}\left(\ell \right)-1}{P}_{\mathcal{N}\left(\ell \right)}}\right).\end{array}$$

Let $\overline{O{P}_1}$ be the line from the origin to the point $P_1$. Denote by $\mathcal{D}\left(\ell \right)$, the denominator of ℓ, the number of times the lines $\overline{P_i{P}_{i+1}}$ intersect the line segment $\overline{O{P}_1}$, where i in $(1,\mathcal{N}(\ell \left)\right]$. The denominator counts how many times $\Gamma \left(\ell \right)$ wraps around the origin. A length ℓ is integral if $\mathcal{D}\left(\ell \right)$ is equal to 1, implying that ℓ is the edge length of a regular inscribed polygon. A circuit is said to be integral if all of its edge lengths are integral. A regular circuit is an integral circuit in which the distance between any two adjacent points in the circuit is the same. The counterclockwise ordered set of intersections of any circumscribed regular polygon with $\mathcal{C}$ is a regular circuit. Furthermore, any regular circuit is the set of intersections of a regular circumscribed polygon with $\mathcal{C}$.

Proposition 10.

Let ℓ and m be rational lengths. Let L and M denote the edge lengths of circumscribed edges corresponding to the inscribed edges ℓ and m respectively. If m is less than ℓ, then

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathcal{N}\left(\ell \right)}{\mathcal{D}\left(\ell \right)}}\ell <{\displaystyle \frac{\mathcal{N}\left(m\right)}{\mathcal{D}\left(m\right)}}m\mathrm{and}{\displaystyle \frac{\mathcal{N}\left(\ell \right)}{\mathcal{D}\left(\ell \right)}}L>{\displaystyle \frac{\mathcal{N}\left(m\right)}{\mathcal{D}\left(m\right)}}M.\end{array}$$

Remark 3.

If ℓ and m are integral lengths, then $\mathcal{D}\left(\ell \right)$ and $\mathcal{D}\left(m\right)$ are both equal to 1 and the proposition gives a comparison of the perimeters of the regular polygons of side lengths ℓ and m. In the rational but non-integral case, it is not reasonable to compare the lengths of the curves $\Gamma \left(\ell \right)$ and $\Gamma \left(m\right)$ because of the dissimilar wrapping of the curves $\Gamma \left(\ell \right)$ and $\Gamma \left(m\right)$ around the circle. Dividing the lengths of the above curves by their respective denominators gives a way to compare the average length of the curves on a single wrapping around the circle. It is this idea that will prove important in the next proposition.

Proof. 

Since length is invariant under rotation, assume that both paths $\Gamma \left(\ell \right)$ and $\Gamma \left(m\right)$ start with the same initial point. All the points on the paths $\Gamma \left(\ell \right)$ and $\Gamma \left(m\right)$ are points on the regular polygon with $\mathcal{N}\left(\ell \right)\mathcal{N}\left(m\right)$ sides containing the point $P_1$. Since ℓ may be realized as the edge length of a straight line segment traversing $\mathcal{D}\left(\ell \right)$ segments of a regular $\mathcal{N}\left(\ell \right)$-gon and m may be realized as the edge length of a straight line segment traversing $\mathcal{D}\left(m\right)$ segments of a regular $\mathcal{N}\left(m\right)$-gon, ℓ may also be realized as the edge length of a straight line segment traversing $\mathcal{D}\left(\ell \right)\mathcal{N}\left(m\right)$ segments of a regular $\mathcal{N}\left(\ell \right)\mathcal{N}\left(m\right)$-gon and m may also be realized as the edge length of a straight line segment traversing $\mathcal{D}\left(m\right)\mathcal{N}\left(\ell \right)$ segments of a regular $\mathcal{N}\left(m\right)$-gon. Since ℓ is larger than m,

$$\begin{array}{c}\hfill \mathcal{D}\left(\ell \right)\mathcal{N}\left(m\right)>\mathcal{D}\left(m\right)\mathcal{N}\left(\ell \right).\end{array}$$

By assumption, both lengths are less than a diameter. Theorem 2 therefore implies that

$$\begin{array}{c}\hfill \mathcal{D}\left(\ell \right)\mathcal{N}\left(m\right)m<\mathcal{D}\left(m\right)\mathcal{N}\left(\ell \right)\ell ,\end{array}$$

and this proves the proposition.

The case of circumscribed polygons is similar except that instead of comparing the lengths ℓ and m, compare the lengths L and M and appeal to Theorem 3 to obtain the reverse inequality. □

Proposition 11.

If $(P_1,\cdots ,P_{k+1})$ and $(Q_1,\cdots ,Q_{n+1})$ are two rational circuits, then

$$\begin{array}{c}\hfill min(P_1,\cdots ,P_{k+1})>max(Q_1,\cdots ,Q_{l+1})\end{array}$$

implies that

(1) 

$\pi \left(g(Q_1,\cdots ,Q_{l+1})\right)>\pi \left(g(P_1,\cdots ,P_{k+1})\right)$, and

(2) 

$\pi \left(G(Q_1,\cdots ,Q_{l+1})\right)<\pi \left(G(P_1,\cdots ,P_{k+1})\right)$.

Proof. 

Denote by ${\ell }_i$ and $m_i$ the lengths

$${\ell }_i=\ell \left(\overline{P_i{P}_{i+1}}\right)\mathrm{and}{m}_j=\ell \left(\overline{Q_j{Q}_{j+1}}\right).$$

Abuse notation and denote again by ${\ell }_i$ and $m_i$ the respective segments of length ${\ell }_i$ and $m_i$. There are k segments ${\ell }_1,\cdots ,{\ell }_k$ for $g\left(P_1,\cdots ,P_{k+1}\right)$ and n segments $m_1,\cdots ,m_n$ for $g\left(Q_1,\cdots ,Q_{n+1}\right)$. Let ${\ell }_1$ be the shortest of the segments of $g\left(P_1,\cdots ,P_{k+1}\right)$ and $m_n$ be the longest of the segments of $g\left(Q_1,\cdots ,Q_{n+1}\right)$. Take $\Lambda$ to be the product

$$\Lambda =\mathcal{N}\left({\ell }_1\right)\cdots \mathcal{N}\left({\ell }_k\right)\mathcal{N}\left(m_1\right)\cdots \mathcal{N}\left(m_n\right)$$

and take $\Lambda$ copies of both polygons. Compute the respective perimeters of these polygons to obtain

$$\begin{array}{cc}\hfill \Lambda \pi \left(g(P_1,\cdots ,P_{k+1})\right)& =\Lambda ({\ell }_1+{\ell }_2+\cdots +{\ell }_k)\hfill \\ & =\frac{\Lambda }{\mathcal{N}\left({\ell }_1\right)}\mathcal{N}\left({\ell }_1\right){\ell }_1+\cdots +\frac{\Lambda }{\mathcal{N}\left({\ell }_k\right)}\mathcal{N}\left({\ell }_k\right){\ell }_k\hfill \\ & =\mathcal{D}\left({\ell }_1\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_1\right)}\frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1+\cdots +\mathcal{D}\left({\ell }_k\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_k\right)}\frac{\mathcal{N}\left({\ell }_k\right)}{\mathcal{D}\left({\ell }_k\right)}{\ell }_k\hfill \\ & <\mathcal{D}\left({\ell }_1\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_1\right)}\frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1+\cdots +\mathcal{D}\left({\ell }_k\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_k\right)}\frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1\hfill \\ & =\left(\mathcal{D}\left({\ell }_1\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_1\right)}+\cdots +\mathcal{D}\left({\ell }_k\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_k\right)}\right)\frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1=\Lambda \frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1.\hfill \end{array}$$

The inequality follows from Theorem 2 since ${\ell }_1$ is the minimum length of the segments of $g(P_1,\cdots ,P_{k+1})$. The ultimate equality follows from the fact that

$$\begin{array}{c}\hfill \sum _{i=1}^k\mathcal{D}\left({\ell }_i\right)\frac{\Lambda }{\mathcal{N}\left({\ell }_i\right)}=\Lambda .\end{array}$$

To justify the last assertion, note that given $\Lambda$ copies of the polygon $g(P_1,\cdots ,P_{k+1})$, the segments in all of these copies form a path that wraps around $\mathcal{C}$ exactly $\Lambda$ times. However, this collection of polynomial contains $\Lambda$ copies of each segment ${\ell }_i$; hence, $\frac{\Lambda }{\mathcal{N}\left({\ell }_i\right)}$ copies each path $\Gamma \left({\ell }_i\right)$ which wraps around $\mathcal{C}$ exactly $\mathcal{D}\left({\ell }_i\right)$ times. Summing each of these $\frac{\Lambda }{\mathcal{N}\left({\ell }_i\right)}\mathcal{D}\left({\ell }_i\right)$ wrappings gives the total number of wrappings, $\Lambda$, implying the above formula for the sum.

Similarly, use the reverse inequality and make use of Proposition 10 to obtain the inequality

$$\begin{array}{c}\hfill \Lambda \pi \left(g(Q_1,\cdots ,Q_{n+1})\right)>\Lambda \frac{\mathcal{N}\left(m_n\right)}{\mathcal{D}\left(m_n\right)}{m}_n>\Lambda \frac{\mathcal{N}\left({\ell }_1\right)}{\mathcal{D}\left({\ell }_1\right)}{\ell }_1>\Lambda \pi \left(g(P_1,\cdots ,P_{k+1})\right).\end{array}$$

Dividing both sides of the inequality by $\Lambda$ finishes the proof for inscribed polygons.

The proof of the result for circumscribed polygons is done in the same way but appeals to the appropriate inequality in Proposition 10, reversing the inequalities analogous to those given above. □

Definition 7.

Following Archimedes, define $2\pi$ to be equal to $p_3$ (as defined in Proposition 3).

Denote by $\mathbb{Q}\left(\mathcal{C}\right)$ the set of all rational circuits on $\mathcal{C}$ and suppose that $\mathcal{P}$ is in $\mathbb{Q}\left(\mathcal{C}\right)$. Denote the maximal edge length of $\mathcal{P}$, the mesh of $\mathcal{P}$, by $\mu \left(\mathcal{P}\right)$.

Theorem 4.

For any positive real number ε there is a positive real number δ such that

$$\begin{array}{c}\hfill \mu \left(\mathcal{P}\right)<\delta \mathrm{implies}\mathrm{that}0<2\pi -\pi \left(g\right(\mathcal{P}\left)\right)<\epsilon \mathrm{and}0<\pi \left(G\right(\mathcal{P}\left)\right)-2\pi <\epsilon .\end{array}$$

Proof. 

Let $\epsilon$ be a positive real number. Both $\pi \left(g\right(m,3\left)\right)$ and $\pi \left(G\right(m,3\left)\right)$ tend to $2\pi$ as m tends to infinity, and so as long as $m^{\prime }$ is a large enough natural number,

$$\begin{array}{c}\hfill 0<2\pi -\pi \left(g(m^{\prime },3)\right)<\epsilon \mathrm{and}0<\pi \left(G(m^{\prime },3)\right)-2\pi <\epsilon .\end{array}$$

(7)

Let $\mathcal{P}$ be a rational circuit. Take $\delta$ to be a positive real number less than the side length of $g(m^{\prime },3)$, so that the maximum possible side length of $G\left(\mathcal{P}\right)$ is less than the side length of $G(m^{\prime },3)$ and the maximum possible side length of $g\left(\mathcal{P}\right)$ is less than the edge length of $g(m^{\prime },3)$. Since $\mu \left(\mathcal{P}\right)$ is less than $\delta$, Proposition 11 implies that

$$\begin{array}{c}\hfill \pi \left(g(m^{\prime },3)\right)<\pi \left(g\left(\mathcal{P}\right)\right)\mathrm{and}\pi \left(G(m^{\prime },3)\right)>\pi \left(G\left(\mathcal{P}\right)\right).\end{array}$$

(8)

Take $m^{\prime \prime }$ to be a large enough natural number so that the edge length of $\pi \left(g(m^{\prime \prime },3)\right)$ is smaller than the smallest edge length of $g\left(\mathcal{P}\right)$ and the edge length of $\pi \left(G(m^{\prime \prime },3)\right)$ is smaller than the smallest edge length of $G\left(\mathcal{P}\right)$. Such a choice of $m^{\prime \prime }$ is possible because the side lengths of both $\pi \left(g\right(m,3\left)\right)$ and $\pi \left(G\right(m,3\left)\right)$ tend to zero as m tends to infinity. Proposition 11 implies that

$$\begin{array}{c}\hfill \pi \left(g\left(\mathcal{P}\right)\right)<\pi \left(g(m^{\prime \prime },3)\right)<2\pi \mathrm{and}\pi \left(G\left(\mathcal{P}\right)\right)>\pi \left(G(m^{\prime \prime },3)\right)>2\pi .\end{array}$$

(9)

Inequalities (7)–(9) together imply the theorem. □

Denote by $\pi \left(n\right)$ the perimeter of a regular n-gon inscribed in $\mathcal{C}$ and denote by $\Pi \left(n\right)$ the perimeter of a regular circumscribed n-gon.

Corollary 2

(Corollary to Proposition 11). If n is greater than m and m is greater than 2, then

$$\begin{array}{c}\hfill \left(1\right)\pi \left(n\right)>\pi \left(m\right)\mathrm{and}\left(2\right)\Pi \left(n\right)<\Pi \left(m\right).\end{array}$$

Corollary 3

(Corollary to Theorem 4). For any natural numbers n and m larger than 2,

$$\begin{array}{c}\hfill p_m=p_n,P_m=P_n,a_m=a_n,\mathrm{and}{A}_m=A_n,\end{array}$$

where the notation follows Proposition 3.

Remark 4.

The next section presents results somewhat more general than those of the above theorem. Until this point we have only used the convergence of bounded monotone sequences, the axioms of Euclidean geometry, and the properties of the natural numbers. In this next section, we use a cardinality argument to show that not all edge lengths are rational lengths, and so this section relies on a consideration that is highly unlikely to have been considered by a contemporary of Archimedes, but is necessary from a modern perspective.

4.2. Approximation by General Circuits

Each rational length corresponds to a pair of two integers, a numerator and a denominator, making the set of rational lengths a countably infinite set. However, there are uncountably many possible edge lengths and so this necessitates a study of circuits that are not necessarily rational.

Proposition 12.

Given any circuit $(R_1,\cdots ,R_{n+1})$ and a positive real number ε, there is a rational circuit $(P_1,\cdots ,P_{n+1})$ such that

$$\begin{array}{c}\hfill |\pi \left(g(R_1,\cdots ,R_{n+1})\right)-\pi \left(g(P_1,\cdots ,P_{n+1})\right)|<\epsilon .\end{array}$$

Proof. 

Suppose that a circuit $\mathcal{R}$ has n distinct points and thus corresponds to a vertex set of an inscribed polygon with n sides. Let $\epsilon$ be a positive real number. There is a natural number m such that the edge length ℓ of $g(m,3)$ is smaller than $\frac{\epsilon }{2n}$. Take $R_1$ to be a point of $g(m,3)$. To each point $R_i$ of $\mathcal{R}$, take $P_i$ to be $R_i$ if $R_i$ is a vertex of $g(m,3)$. Otherwise, take $P_i$ to be the first vertex of $g(m,3)$ that is counterclockwise from $R_i$. With such a choice of $P_i$, the length $\ell \left(\overline{P_i{R}_i}\right)$ is less than ℓ. The circuit $\mathcal{P}$ that is equal to $(P_1,\cdots ,P_{n+1})$ is a rational circuit. Furthermore, for each natural number i in $[1,k+1]$,

$$\begin{array}{c}\hfill \left|\overline{\ell (P_i{P}_{i+1}})-\ell \left(\overline{R_i{R}_{i+1}}\right)\right|<2\ell <\frac{\epsilon }{n}\mathrm{and}\mathrm{so}|\pi \left(g\left(\mathcal{P}\right)\right)-\pi \left(g\left(\mathcal{R}\right)\right)|<\epsilon .\end{array}$$

□

Corollary 4.

For any circuits $(P_1,\cdots ,P_{k+1})$ and $(Q_1,\cdots ,Q_{l+1})$ on $\mathcal{C}$,

$$\begin{array}{c}\hfill min(P_1,\cdots ,P_{k+1})>max(Q_1,\cdots ,Q_{l+1})\Rightarrow \pi (Q_1,\cdots ,Q_{l+1})\ge \pi (P_1,\cdots ,P_{k+1}).\end{array}$$

Proof. 

Suppose that $\mathcal{P}$ is the circuit $(P_1,\cdots ,P_{k+1})$ and that $\mathcal{Q}$ is the circuit $(Q_1,\cdots ,Q_{l+1})$. Suppose further that $min(P_1,\cdots ,P_{k+1})$ is greater than $max(Q_1,\cdots ,Q_{l+1})$. For any positive real number $\epsilon$, there are rational circuits $\widehat{\mathcal{P}}$ and $\widehat{\mathcal{Q}}$ such that

$$\begin{array}{c}\hfill |\pi \left(g\left(\widehat{\mathcal{P}}\right)\right)-\pi \left(g\left(\mathcal{P}\right)\right)|<\frac{\epsilon }{2}\mathrm{and}|\pi \left(g\left(\widehat{\mathcal{Q}}\right)\right)-\pi \left(g\left(\mathcal{Q}\right)\right)|<\frac{\epsilon }{2}\end{array}$$

and furthermore such that

$$\begin{array}{c}\hfill min({\widehat{P}}_1,\cdots ,{\widehat{P}}_{k+1})>max({\widehat{Q}}_1,\cdots ,{\widehat{Q}}_{l+1}).\end{array}$$

We leave the straightforward details of the proof to the reader. Proposition 12 implies that $\pi \left(\widehat{\mathcal{Q}}\right)$ is greater than $\pi \left(\widehat{\mathcal{P}}\right)$, and so

$$\begin{array}{c}\hfill \pi \left(\mathcal{Q}\right)+\epsilon >\pi \left(\mathcal{P}\right).\end{array}$$

Since the above inequality holds for any positive $\epsilon$, $\pi \left(\mathcal{Q}\right)$ is greater than or equal to $\pi \left(\mathcal{P}\right).$ □

Given any two points on $\mathcal{C}$, there is an m large enough so that the arc between the two points contains two vertices of $g(m,3)$. The following lemma follows from this fact and the fact that rotations preserve the ordering of points on $\mathcal{C}$.

Lemma 2.

Given points P, Q, and R on $\mathcal{C}$ in counterclockwise order, there is a point S between Q and R such that $\ell \left(\overline{PS}\right)$ is a rational length.

Establish the following notation for the statements and proofs of Lemma 3 and Lemma 4. Suppose that A, B and C are points on $\mathcal{C}$ in counterclockwise order and the arc from A to C is less than half of $\mathcal{C}$. For any points X and Y on $\mathcal{C}$, denote by $P_{X,Y}$ the intersection of the lines tangent to $\mathcal{C}$ at X and Y (Figure 14 ).

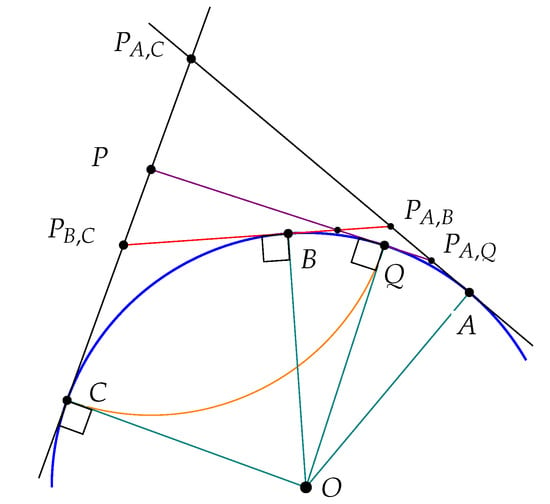
Figure 14. An order preserving bijection.

Lemma 3.

There is an order preserving bijection from the points on the line segment $\overline{P_{A,B}{P}_{A,C}}$ and the points on the arc between B and C.

Proof. 

Suppose P is a point on $\overline{P_{A,C}{P}_{B,C}}$. Let ${\mathcal{C}}_P$ be the circle of radius $\ell \left(\overline{CP}\right)$ centered at P. The circle ${\mathcal{C}}_p$ intersects $\mathcal{C}$ at precisely two points, at the point C and at a point Q that lies on the arc from A to B. Define the circles ${\mathcal{C}}_{P_{B,C}}$ and ${\mathcal{C}}_{P_{A,C}}$ in the same way as ${\mathcal{C}}_P$. The circles ${\mathcal{C}}_{P_{B,C}}$, ${\mathcal{C}}_P$, and ${\mathcal{C}}_{P_{A,C}}$ all intersect at C, and since they have different radii, they can meet at no more than two points. Since $\overline{OC}$ is tangent to all three circles, the three circles meet only at C. The radius of ${\mathcal{C}}_{P_{A,C}}$ is greater than the radius of ${\mathcal{C}}_P$, which is greater than the radius of ${\mathcal{C}}_{P_{B,C}}$, therefore

$$\begin{array}{c}\hfill \ell \left(\overline{BC}\right)<\ell \left(\overline{QC}\right)<\ell \left(\overline{AC}\right).\end{array}$$

Since all three points lie counterclockwise from A on an arc less that half of a circle, Q is clockwise from B and counterclockwise from A.

Suppose that Q is a point between A and B on the arc from A to B, that B is clockwise from C, and that the arc from A to C is less than half of a circle. Let L be the line tangent to $\mathcal{C}$ at Q. Since $\angle QOC$ is less than a straight line, L intersects the line tangent to $\mathcal{C}$ at C at a point P and the intersection occurs on the same side of C as $P_{A,C}$ and $P_{B,C}$. The point Q is between A and B, and so

$$\begin{array}{c}\hfill \ell \left(\overline{BC}\right)<\ell \left(\overline{QC}\right)<\ell \left(\overline{AC}\right),\mathrm{hence}m(\angle BOC)<m(\angle QOC)<m(\angle AOC).\end{array}$$

The line segments $\overline{BO}$, $\overline{QO}$, and $\overline{AO}$ are all radii, implying the equality of $\ell \left(\overline{BO}\right)$, $\ell \left(\overline{QO}\right)$, and $\ell \left(\overline{CO}\right)$, and therefore, the inequalities

$$\begin{array}{c}\hfill \ell \left(\overline{C{P}_{B,C}}\right)<\ell \left(\overline{CP}\right)<\ell \left(\overline{C{P}_{A,C}}\right).\end{array}$$

The point P therefore lies on the line segment $\overline{P_{A,C}{P}_{B,C}}$. Note that Lemma 1 implies that $\overline{PQ}$ and $\overline{CP}$ are congruent and so the map we initially constructed will map P to the point Q.

Let $\varphi$ be the map taking points on $\overline{P_{A,C}{P}_{B,C}}$ to points on the arc from A to B and let $\psi$ be the map taking points on the arc from A and B to point on $\overline{P_{A,C}{P}_{B,C}}$. These functions are inverses of each other, and so both are invertible, and hence bijective. □

Lemma 4.

Let ε be a positive real number. There is a Q on the arc from A to B such that Q is not equal to B and

$$\begin{array}{cc}\hfill & \left|\ell \left(\overline{A{P}_{A,B}}\right)+\ell \left(\overline{P_{A,B}B}\right)+\ell \left(\overline{B{P}_{B,C}}\right)+\ell \left(\overline{P_{B,C}C}\right)\right.\hfill \\ & \left.-\left(\ell \left(\overline{A{P}_{A,Q}}\right)+\ell \left(\overline{P_{A,Q}Q}\right)+\ell \left(\overline{Q{P}_{C,Q}}\right)+\ell \left(\overline{P_{C,Q}C}\right)\right)\right|<\epsilon .\hfill \end{array}$$

(10)

Furthermore, any point $Q^{\prime }$ on the arc from Q to B will also satisfy the above estimate where Q is replaced by $Q^{\prime }$.

Proof. 

Pick a point z on $\overline{A{P}_{A,B}}$ such that $\ell \left(\overline{z{P}_{A,B}}\right)$ is less than $\frac{\epsilon }{4}$. Lemma 3 guarantees the existence of a point Z on the arc between A and B such that z is the point of intersection of the line tangent to $\mathcal{C}$ at Z and the line segment $\overline{A{P}_{A,B}}$. Pick a point q on $\overline{z{P}_{A,B}}$ such that $\ell \left(\overline{q{P}_{A,B}}\right)$ is less than $\frac{\epsilon }{4}$. Lemma 3 guarantees the existence of a point Q on the arc from Z to B such that q is the point of intersection of the line tangent to $\mathcal{C}$ at Q and the line segment $\overline{A{P}_{A,B}}$. Using the established notation, q is the point $P_{A,Q}$, and furthermore, Q will satisfy the estimate (10). Since the bijection given in Lemma 3 is order preserving, if $Q^{\prime }$ is any point not equal to B in the arc from Q to B, then the point $Q^{\prime }$ will also satisfy the estimate (10). □

Proposition 13.

Suppose that $(P_1,\cdots ,P_{k+1})$ is a circuit with the property that the arc between any adjacent points is less than a fourth of a circle. Suppose ε is a positive real number. There is a rational circuit $(Q_1,\cdots ,Q_{l+1})$ such that

$$\begin{array}{c}\hfill |\pi \left(G(P_1,\cdots ,P_{k+1})\right)-\pi \left(G(Q_1,\cdots ,Q_{l+1})\right)|<\epsilon .\end{array}$$

Proof. 

Set $Q_1$ equal to $P_1$. Suppose that $(Q_1,Q_2,\cdots ,Q_i,P_{i+1},\cdots ,P_{k+1})$ is a sequence of points where each $Q_i$ lies on the arc between $P_i$ and $P_{i+1}$, each $Q_i$ lies on the same regular polygon, each edge is less than a quarter of the circle, and

$$\begin{array}{c}\hfill \left|\pi \left(G(P_1,P_2,\cdots ,P_i,P_{i+1},\cdots ,P_{k+1})\right)-\pi \left(G(Q_1,Q_2,\cdots ,Q_i,P_{i+1},\cdots ,P_{k+1})\right)\right|<\epsilon .\end{array}$$

Lemma 4 implies that there is a $Q_{i+1}$ not equal to $P_{i+1}$ but on the arc between $Q_{i+1}$ and $P_{i+2}$ such that for any Q on the arc between $Q_{i+1}$ and $P_{i+2}$,

$$\begin{array}{c}\hfill \left|\pi \left(G(P_1,P_2,\cdots ,P_i,P_{i+1},\cdots ,P_{k+1})\right)-\pi \left(G(Q_1,Q_2,\cdots ,Q_i,Q,P_{i+2},\cdots ,P_{k+1})\right)\right|<\epsilon .\end{array}$$

Take Q to be a vertex of a regular polygon on which $Q_1$ through $Q_i$ lie by choosing the regular polygon to be a sufficiently fine refinement of the regular polygon on which $Q_1$ through $Q_i$ are vertices. Recursively construct in this way a polygon $G(Q_1,\cdots ,Q_{k+1})$, with $Q_1$ and $Q_{k+1}$ both equal to $P_1$, which approximates $G(P_1,\cdots ,P_{k+1})$ in the sense that

$$\begin{array}{c}\hfill \left|\pi \left(G(P_1,\cdots ,P_{k+1})\right)-\pi \left(G(Q_1,\cdots ,Q_{k+1})\right)\right|<\epsilon .\end{array}$$

□

Corollary 5.

If $(P_1,\cdots ,P_{k+1})$ and $(Q_1,\cdots ,Q_{l+1})$ are two arbitrary sequences of points on C then

$$\begin{array}{c}\hfill min(P_1,\cdots ,P_{k+1})>max(Q_1,\cdots ,Q_{l+1})\end{array}$$

implies that

$$\begin{array}{c}\hfill \pi \left(G(Q_1,\cdots ,Q_{l+1})\right)\le \pi \left(G(P_1,\cdots ,P_{k+1})\right).\end{array}$$

Proof. 

The above corollary is proved exactly as the first corollary to Proposition 12 is proved above except that the inequalities are reversed because they are reversed in Proposition 11. □

Theorem 5.

Suppose that $\mathcal{P}$ is a general partition of $\mathcal{C}$. For any positive real number ε there is a positive real number δ such that

$$\begin{array}{c}\hfill \mu \left(\mathcal{P}\right)<\delta \mathrm{implies}\mathrm{that}0<2\pi -\pi \left(g\right(\mathcal{P}\left)\right)<\epsilon \mathrm{and}0<\pi \left(G\right(\mathcal{P}\left)\right)-2\pi <\epsilon .\end{array}$$

Proof. 

The theorem is proved in the same way as Theorem 4 but by appealing to Proposition 11 and the corollary to Proposition 13 rather than Proposition 11 and the corollary to Proposition 12. □

Let $\mathcal{P}$ be a general partition of $\mathcal{C}$. Denote by $\alpha \left(g\right(\mathcal{P}\left)\right)$ the area of the inscribed polygon $g\left(\mathcal{P}\right)$ and $\alpha \left(G\right(\mathcal{P}\left)\right)$ the area of the circumscribed polygon $G\left(\mathcal{P}\right)$.

Theorem 6.

For any positive real number ε there is a positive real number δ such that

$$\begin{array}{c}\hfill \mu \left(\mathcal{P}\right)<\delta \mathrm{implies}\mathrm{that}0<\pi -\alpha \left(g\right(\mathcal{P}\left)\right)<\epsilon \mathrm{and}0<\alpha \left(G\right(\mathcal{P}\left)\right)-\pi <\epsilon .\end{array}$$

Proof. 

Let $\epsilon$ be a positive real number. Theorem 5 implies that there is a positive real number $\delta$ so that if $\mathcal{P}$ is a circuit $(P_1,\cdots ,P_{n+1})$ with mesh less than $\delta$, then

$$\begin{array}{c}\hfill 0<2\pi -\pi \left(g\right(\mathcal{P}\left)\right)<\epsilon \mathrm{and}0<\pi \left(G\right(\mathcal{P}\left)\right)-2\pi <\epsilon .\end{array}$$

(11)

Restrict $\delta$ so that $\frac{\pi }{4}{\delta }^2$ is less than $\epsilon$. The equality

$$\begin{array}{c}\hfill \alpha \left(G\left(\mathcal{P}\right)\right)={\displaystyle \frac{1}{2}}\pi \left(G\left(\mathcal{P}\right)\right)\end{array}$$

together with (11) implies that

$$\begin{array}{c}\hfill 0<\alpha \left(G\left(\mathcal{P}\right)\right)-\pi ={\displaystyle \frac{1}{2}}\pi \left(G\left(\mathcal{P}\right)\right)-\pi <\pi +\frac{\epsilon }{2}-\pi =\frac{\epsilon }{2}.\end{array}$$

Denote by ${\ell }_i$ the length of the segment $\overline{P_i{P}_{i+1}}$. Heron’s Theorem implies that

$$\begin{array}{c}\hfill \alpha \left(g\left(\mathcal{P}\right)\right)=\sum _{i=1}^n{\displaystyle \frac{{\ell }_i}{2}}\sqrt{1-{\displaystyle \frac{{\ell }_i^2}{4}}}.\end{array}$$

For each i,

$$\begin{array}{c}\hfill {\displaystyle \frac{{\ell }_i}{2}}\left(1-{\displaystyle \frac{\mu {\left(\mathcal{P}\right)}^2}{4}}\right)\le {\displaystyle \frac{{\ell }_i}{2}}\left(1-{\displaystyle \frac{{\ell }_i^2}{4}}\right)\le {\displaystyle \frac{{\ell }_i}{2}}\sqrt{1-{\displaystyle \frac{{\ell }_i^2}{4}}}\le {\displaystyle \frac{{\ell }_i}{2}}.\end{array}$$

Since the sum of all of the ${\ell }_i$’s is the perimeter of an inscribed polygon and therefore less than $2\pi$, the bound on $\delta$ implies that

$$\begin{array}{c}\hfill {\displaystyle \frac{\pi \left(g\right(\mathcal{P}\left)\right)}{2}}-\frac{\epsilon }{2}<{\displaystyle \frac{\pi \left(g\right(\mathcal{P}\left)\right)}{2}}-{\displaystyle \frac{\mu {\left(\mathcal{P}\right)}^2}{8}}\sum _{i=1}^n{\ell }_i\le \alpha \left(g\left(\mathcal{P}\right)\right)\le {\displaystyle \frac{\pi \left(g\right(\mathcal{P}\left)\right)}{2}}.\end{array}$$

This proves the theorem. □

5. Application to the Circular Trigonometric Functions

5.1. Arclength of an Arc and Area of a Sector

Suppose that A and B are points on $\mathcal{C}$ and that $\mathcal{A}$ is the counterclockwise oriented arc from A to B. If the length $\ell \left(\overline{AB}\right)$ is a rational length, then for some natural number m, there is a regular inscribed n-gon $g(0,n)$ such that $\mathcal{A}$ has on it exactly $k+1$ vertices of $g(0,n)$ and both A and B are vertices of $g(0,n)$. Denote by ${\ell }_n$ the edge length of $g(0,n)$ to obtain the equality

$$\begin{array}{c}\hfill k{\ell }_n=\frac{k}{n}\pi \left(g(0,n)\right).\end{array}$$

The inscribed polygon $g(m,n)$ will have $2^{m}n+1$ vertices on $\mathcal{A}$. Denote by ${\pi }_{m,n}\left(\mathcal{A}\right)$ the approximation of the arc length of $\mathcal{A}$ given by

$$\begin{array}{c}\hfill {\pi }_{m,n}\left(\mathcal{A}\right)=2^{m}k{\ell }_n=\frac{2^{m}k}{2^{m}n}\pi \left(g(m,n)\right)=\frac{k}{n}\pi \left(g(m,n)\right)\to \frac{2\pi k}{n}\mathrm{as}m\to \infty .\end{array}$$

This approximation of the length of an arc of $\mathcal{C}$ depends only on the fraction of $\mathcal{C}$ that $\mathcal{A}$ represents and so defines the length of an arc for any arc whose endpoints form a rational length. Define similarly the area of a sector of $\mathcal{C}$, the area bounded by the lines $\overline{OA}$ and $\overline{OB}$ and the counterclockwise oriented arc $\mathcal{A}$, so that

$$\begin{array}{c}\hfill {\alpha }_{m,n}\left(\mathcal{A}\right)=\frac{k}{n}\alpha \left(g(m,n)\right)\to \frac{\pi k}{n}\mathrm{as}m\to \infty .\end{array}$$

If the length $\ell \left(\overline{AB}\right)$ is not a rational length, then there is a sequence of rational lengths that approximate it. In particular, take A to be a point on $g(0,n)$ for some n where n is a large enough natural number so that at least one vertex of $g(0,n)$ lies on $\mathcal{A}$ between A and B. For each m, choose the vertex $B_m$ of $g(m,n)$ that is closest to B. The counterclockwise oriented arc ${\mathcal{A}}_m$ from A to $B_m$ will have rational length $\ell \left(\overline{A{B}_m}\right)$ and will be a fraction $\varphi \left(A{B}_m\right)$ of a circle, where $\varphi \left(A{B}_m\right)$ is an increasing bounded above sequence with

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varphi \left(A{B}_m\right)=\varphi \left(AB\right),\end{array}$$

where $\varphi \left(AB\right)$ is an irrational number. m tends to infinity the limits

$$\begin{array}{c}\hfill {\pi }_{m,n}\left({\mathcal{A}}_m\right)=2\pi \varphi \left(A{B}_m\right)\to 2\pi \varphi \left(AB\right)\mathrm{and}{\alpha }_{m,n}\left({\mathcal{A}}_m\right)=\pi \varphi \left(A{B}_m\right)\to \pi \varphi \left(A{B}_m\right),\end{array}$$

where the limits are independent of the sequence $\left(B_m\right)$ that approximates B.

Using the notation above and given any counterclockwise arc $\mathcal{A}$ from a point X on $\mathcal{C}$ to a point Y on $\mathcal{C}$, define the angle measure $\theta \left(\mathcal{A}\right)$ by

$$\begin{array}{c}\hfill \theta \left(\mathcal{A}\right)=2\pi \varphi \left(XY\right).\end{array}$$

The length $\theta$ is the length of the arc $\mathcal{A}$. The area, $\alpha \left(\mathcal{A}\right)$, of the sector bounded by $\overline{OX}$, $\overline{OY}$, and the counterclockwise oriented arc $\mathcal{A}$ is given by

$$\begin{array}{c}\hfill \alpha \left(\mathcal{A}\right)=\frac{\theta \left(\mathcal{A}\right)}{2}.\end{array}$$

5.2. Limit of the Sine Function

The argument frequently given by authors of calculus texts for calculating the limit (1) is perfectly valid, although it does require some explanation since we have not yet introduced a coordinate system nor defined the trigonometric functions. View the unit circle as the subset $\mathcal{C}$ of the plane given by

$$\begin{array}{c}\hfill \mathcal{C}=\{(x,y):x^2+y^2=1\}.\end{array}$$

Define the trigonometric functions, as is customary, as functions of the argument $\theta$ in $[0,2\pi )$, so that the point $(cos(\theta ),sin(\theta \left)\right)$ is the point on the unit circle so that the counterclockwise oriented arc $\mathcal{A}$ from $(1,0)$ to $(cos(\theta ),sin(\theta \left)\right)$ has length $\theta$. The area of the sector defined by $\mathcal{A}$ is $\frac{\theta }{2}$. Take $\theta$ to be less that $\frac{\pi }{2}$. Bound the area of the sector above and below respectively by the areas of the triangles

$$▵(0,0)(1,0)\left(1,\frac{sin\left(\theta \right)}{cos\left(\theta \right)}\right)\mathrm{and}▵(0,0)(cos\left(\theta \right),0)(cos\left(\theta \right),sin\left(\theta \right))$$

to obtain the inequality

$$\begin{array}{c}\hfill \frac{1}{2}cos\left(\theta \right)sin\left(\theta \right)\le \frac{1}{2}\theta \le \frac{1}{2}\frac{sin\left(\theta \right)}{cos\left(\theta \right)}\mathrm{implying}\mathrm{that}1\le \frac{\theta }{sin\left(\theta \right)}\le \frac{1}{cos\left(\theta \right)}.\end{array}$$

Take limits and use the sandwich theorem to obtain the limit (1) as a one-sided limit. If $(x,y)$ is a point in the first quadrant so that the signed length of the arc from $(1,0)$ to $(x,y)$ is $\theta$, then define the signed length of the arc from $(1,0)$ to $(x,-y)$ to be $-\theta$. Given this signed argument, the sine function is an odd function of $\theta$ and the cosine function is even. Extending the definitions of the trigonometric functions in this way to negative signed arc lengths permits the limit (1) to be viewed as a two sided limit and the oddness of the sine function implies this two sided limit. While this is a standard approach to calculating the limit in many calculus texts—[10], for example—the approach is non-rigorous because these texts omit a discussion of the equivalence of $\pi$ defined as half the circumference of a unit circle and as the area of a unit circle, and so as well the relationship between the length of an arc and the area of the sector that the arc defines. Our current discussion closely follows Archimedes and remedies this shortcoming.