Coalgebras on Digital Images

Abstract

In this article, we investigate the fundamental properties of coalgebras with coalgebra comultiplications, counits, and coalgebra homomorphisms of coalgebras over a commutative ring R with identity $1_R$ based on digital images with adjacency relations. We also investigate a contravariant functor from the category of digital images and digital continuous functions to the category of coalgebras and coalgebra homomorphisms based on digital images via the category of unitary R-modules and R-module homomorphisms.

1. Introduction

1.1. Associative Algebra and Its Dual, Coalgebra

An associative algebra is an algebraic structure with compatible operations of additions, associative multiplications and scalar multiplications by elements in a module or a field. A counital coalgebra is one of the dual notions of the unital associative algebras; see [1] [page 197] and [2] [page 803]. Historically, coalgebras occur as the dual of algebras in [3,4] in the category theoretic approach to dynamical systems and automata. An automaton as a coalgebra was nicely presented and an early proof that the set of formal languages is a final coalgebra was described in [5]. A bisimulation as a notion of behavioural equivalence for concurrent processes and a notion of strong extensionality for the theory of non-well-founded sets were invented in [6,7,8]. The notion of bisimulation was generalized to the level of arbitrary coalgebras in [9]. As a consequence, coalgebra is one of the nice ingredients from mathematics and becomes an extensive field of research.

The axioms of unital associative algebras can be formulated in terms of commutative diagrams in the category-theoretic sense of reversing arrows. In general, it is well known that a coalgebra structure gives rise to an algebra structure. Classically, a coalgebra appears naturally in combinatorics, algebra, and algebraic topology as describing ways one can decompose objects into other objects of the same type. Moreover, a coalgebra occurs naturally in a number of contexts such as a universal enveloping algebra and a group scheme. There are also F-coalgebra structures with important applications in computer science; see [10,11].

One of the classical cohomology algebras is the singular (or simplicial) cohomology algebra whose multiplication is the usual cup product, and its unit is induced from the unique continuous function from a topological space to a one-point space. A graded singular homology module of a Hopf space becomes a graded algebra with a unit element. Moreover, it is well known that, if the homology modules of a Hopf space is free of a finite type, then it is a commutative and associative Hopf algebra over a principal ideal domain, and that the singular homology of a topological space with coefficients in a field has naturally the coalgebra structure whose coalgebra comultiplication and counit are induced by the diagonal map via the Künneth formula and by the unique continuous function from the topological space to a one-point space, respectively, as in the case of cohomology.

1.2. Homotopical Viewpoint for a Dual

In classical (or rational) homotopy theory, it is well known that the notion of a (pointed) Hopf space [12,13,14] is one of the Eckmann–Hilton dual concepts of a (pointed) co-Hopf space. Co-Hopf spaces were introduced in [15] and were used to determine whether a pointed CW-space has the same homotopy type of the suspension of another pointed CW-space or not [16] [Theorem A]; see also [17]. The second author has developed the structures of a wedge of (localized) spheres as the co-Hopf spaces with various homotopy comultiplications [18,19,20,21,22,23], and the suspension structure with the standard comultiplication in the sense of same homotopy n-types [24,25,26,27,28]; see also [29,30] for the topics which are related to the fundamental concepts of those CW-spaces, and [31] for the equivariant homotopy theoretic point of view with the behavior of the local cohomology spectral sequence.

1.3. Previous Results and Motivation

In the category of topological spaces and continuous maps, a pair $(Z,\omega )$ consisting of a space Z and a function $\omega :Z\to Z\vee Z$ is said to be a co-H-space if

$${\pi }_1\circ \omega \simeq 1_Z\simeq {\pi }_2\circ \omega :Z\to Z,$$

where ${\pi }_1,{\pi }_2:Z\vee Z\to Z$ are the first and second projections, respectively, and $1_Z$ is the identity map on Z. In this case, $\omega :Z\to Z\vee Z$ is called a topological comultiplication on the space Z.

Let $L_Z$ be the Quillen model of a rational co-Hopf space Z, i.e., a wedge of rational spheres up to homotopy, and let $L_Z\bigsqcup L_Z$ be the Quillen model of $Z\vee Z$. Then, there exists a bijection of sets between the set of all homotopy classes of topological comultiplications $\omega :Z\to Z\vee Z$ and the set of all homomorphisms $\psi :L_Z\to L_Z\bigsqcup L_Z$ such that

$${\pi }_1\circ \psi =1_{L_Z}={\pi }_2\circ \psi :L_Z\to L_Z,$$

where ${\pi }_1,{\pi }_2:L_Z\bigsqcup L_Z\to L_Z$ are the first and second projections; see [32] [Lemma 2.2].

Motivated from the above statements, we raise the following query: Are there any kinds of coalgebra structures based on a digital image to develop its fundamental properties in itself? To give an answer to this query, we try to investigate an R-module homomorphism

$$\phi :\underset{n\ge 0}{⨁}d{H}^n(X;R)\to \underset{n\ge 0}{⨁}d{H}^n(X;R){\otimes }_R\underset{n\ge 0}{⨁}d{H}^n(X;R)$$

of digital cohomology modules based on a $k_X$-connected digital image $(X,k_X)$ corresponding to the standard homomorphism $\psi :L_Z\to L_Z\bigsqcup L_Z$ and to the standard topological comultiplication $\omega :Z\to Z\vee Z$ via the bijection above. We can thus construct an R-coalgebra with an R-coalgebra comultiplication and an R-coalgebra counit. The coalgebra structure in this paper induces a familiar mathematical structure which is originated from a connected digital image, and offers a method for how to construct the standard coalgebra as the practical links between the algebraic approach and the analysis of digital images.

1.4. Digital Images and Our Goals

Digital topological spaces and digital images are highly related to combinatorial topology and computer science, and it mostly deals with the two-dimensional or three-dimensional digital images. Digital topology was first studied in the late 1960s by A. Rosenfeld, and digital surfaces (or digital manifolds) were also developed in the early 1980s and in 1990s by many authors. In particular, the formal and informal definitions of a lot of terms in homotopy and simplicial (co)homology theory based on a digital image on ${\mathbb{Z}}^2$ or ${\mathbb{Z}}^3$ with adjacency relations were nicely described in [33,34,35,36,37,38]; see also [22] for digital quasi co-Hopf space, and [39,40] for digital cohomology modules and cone metric spaces.

We need to develop another theory to study digital topological spaces (or digital images) out of classical cohomology theory and digital counterparts of those ideas in classical homology and cohomology theories. In the current paper, we study another consideration of the so-called algebraic approach from the classical cohomology groups. In fact, the current study deals with coalgebras, coalgebra comultiplications, counits, and coalgebra homomorphisms of coalgebras over a commutative ring R with identity $1_R$ based on digital images with adjacency relations. The functorial properties as one of the digital counterparts to classical cohomology theory originated from the algebraic invariants and their important properties of cohomology modules in classical cohomology theory will be discussed.

1.5. Organization

This paper is organized as follows: in Section 2, we briefly review the basic definitions of digital images with adjacency relations and digital continuous functions. We also examine the digital homology and cohomology modules over a commutative ring R with identity based on digital images with some adjacency relations. In Section 3, we consider coalgebras, coalgebra comultiplications, counits, and coalgebra homomorphisms of coalgebras over a commutative ring R with identity $1_R$ on digital images with adjacency relations, and find out the relationships between the category of digital images and digital continuous functions, the category of digital cohomology R-modules and R-module homomorphisms of digital cohomology R-modules, and the category of coalgebras and coalgebra homomorphisms based on digital images induced by the digital continuous functions between them.

2. Digital Images and Digital (Co)homology Modules

Let $\mathbb{Z}$ be the set of all integers, and let ${\mathbb{Z}}^n:=\underset{n-\mathrm{times}}{\underbrace{\mathbb{Z}\times \mathbb{Z}\times \cdots \times \mathbb{Z}}}.$ For a positive integer u with $1\le u\le n$, we define an adjacency relation in ${\mathbb{Z}}^n$ as follows:

Definition 1

([41]). Two different points $p=(p_1,p_2,\dots ,p_n)$ and $q=(q_1,q_2,\dots ,q_n)$ in ${\mathbb{Z}}^n$ are said to be $k(u,n)$-adjacent if

• there are at most u distinct indices i with the property$|p_i-q_i|=1$; and
• for each positive integer$i\le n$, if$|p_i-q_i|\ne 1$, then$p_i=q_i$.

Example 1

([39]).

(1) 

The set of$k(1,1)$-adjacent points of 0 in${\mathbb{Z}}^1$is the set consisting of$-1$and 1.

(2) 

The set of$k(1,2)$-adjacent points of$(0,0)$in${\mathbb{Z}}^2$is the set consisting of$(1,0)$,$(0,1)$,$(-1,0)$and$(0,-1)$.

(3) 

The set of$k(2,2)$-adjacent points of$(0,0)$in${\mathbb{Z}}^2$is the set consisting of$(1,0)$,$(1,1)$,$(0,1)$,$(-1,1)$,$(-1,0)$,$(-1,-1)$,$(0,-1)$, and$(1,-1)$.

We mostly denote a $k(u,n)$-adjacency relation on a digital image X (see below) by the $k_X$-adjacency relation for short unless we specifically state otherwise.

A digital image $(X,k_X)$ consists of a bounded and finite subset X of ${\mathbb{Z}}^n$ and an adjacency relation $k_X$ on X. A digital image $(X,k_X)$ in ${\mathbb{Z}}^n$ is said to be $k_X$-connected ([42,43]) if, for each set $\{x,y\}$ consisting of two distinct points x and y, there exists a subset

$$\begin{array}{c}\hfill P=\{x_0,x_1,\dots ,x_s\}\subseteq X\end{array}$$

(1)

consisting of $s+1$ distinct points such that

• $x=x_0$;
• $x_s=y$; and
• $x_i$ and $x_{i+1}$ are $k_X$-adjacent for $i=0,1,\dots ,s-1$.

Definition 2

([44]). A function

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(2)

of digital images $(X,k_X)$ and $(Y,k_Y)$ with $k_X$-adjacency and $k_Y$-adjacency relations, respectively, is said to be a $(k_X,k_Y)$-continuous function if the image of any $k_X$-connected subset of the digital image $(X,k_X)$ under the function f is a $k_Y$-connected subset of $(Y,k_Y)$; see also [43] [Definition 2.3].

Remark 1

([39]). We note that if $(X,k_X)$, $(Y,k_Y)$ and $(Z,k_Z)$ are digital images and if

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(3)

is a $(k_X,k_Y)$-continuous function and

$$\begin{array}{c}\hfill g:(Y,k_Y)\to (Z,k_Z)\end{array}$$

(4)

is a $(k_Y,k_Z)$-continuous function, then it can be shown that the composite

$$\begin{array}{c}\hfill g\circ f:(X,k_X)\to (Z,k_Z)\end{array}$$

(5)

is also a $(k_X,k_Z)$-continuous function. Therefore, it is possible for us to consider the category $\mathcal{D}$ of k-connected digital images and digital continuous functions; that is, the object classes of $\mathcal{D}$ are k-connected digital images and the morphism classes are digital continuous functions.

Let $e_0=(1,0,0,\dots ,0)$, $e_1=(0,1,0,\dots ,0)$, …, and $e_n=(0,0,\dots ,0,1)$ be elements of ${\mathbb{Z}}^{n+1}$, and let

$$\begin{array}{c}\hfill {\Delta }^n:=\{e_0,e_1,\dots ,e_n\}⊊{\mathbb{Z}}^{n+1}\end{array}$$

(6)

be the digital image in ${\mathbb{Z}}^{n+1}$ with the $k(2,n+1)$-adjacency relation. It can be seen that it is a $k(2,n+1)$-connected digital image.

Let R be a commutative ring with identity $1_R$ and let $(X,k_X)$ be a digital image with a $k_X$-adjacency relation. For each $n\ge 0$, we denote $d{C}_n(X;R)$ as the non-negatively graded free R-module with a basis consisting of all $(k_{{\Delta }^n},k_X)$-continuous functions

$$\begin{array}{c}\hfill \sigma :({\Delta }^n,k_{{\Delta }^n})\to (X,k_X),\end{array}$$

(7)

and define the so-called digital boundary operator

$$\begin{array}{c}\hfill {\partial }_n:d{C}_n(X;R)\to d{C}_{n-1}(X;R)\end{array}$$

(8)

by

$$\begin{array}{c}\hfill {\partial }_n\sigma =\left\{\begin{array}{cc}{\displaystyle \sum _{i=0}^n}{(-1)}^i\sigma \circ {ϵ}_i^n\hfill & \mathrm{if}n\ge 1;\hfill \\ 0\hfill & \mathrm{if}n=0,\hfill \end{array}\right.\end{array}$$

(9)

where ${ϵ}_i:{\Delta }^{n-1}\to {\Delta }^n$ is the i-th face function; see [45,46] for more details. It can be shown that

$$\begin{array}{c}\hfill {\partial }_n\circ {\partial }_{n+1}=0\end{array}$$

(10)

for all $n\ge 0$, and thus $\mathrm{Im}\left({\partial }_{n+1}\right)$ is automatically an R-submodule of $\mathrm{Ker}\left({\partial }_n\right)$ for each $n\ge 0$. The n-th digital homology module $d{H}_n(X;R)$ over R of a digital image $(X,k_X)$ with a $k_X$-adjacency relation is defined by

$$\begin{array}{c}\hfill d{H}_n(X;R)=\mathrm{Ker}\left({\partial }_n\right)/\mathrm{Im}\left({\partial }_{n+1}\right)\end{array}$$

(11)

for each $n\ge 0$ [45]; see also [36,47].

Definition 3

([39]). The n-th digital cohomology module $d{H}^n(X;R)$ over R of a digital image $(X,k_X)$ is defined to be the corresponding cohomology module over a commutative ring R with identity of the cochain complex obtained by the dual R-modules along with the dual R-module homomorphisms, i.e.,

$$\begin{array}{c}\hfill d{H}^n(X;R)=\mathrm{Ker}\left({\delta }^{n+1}\right)/\mathrm{Im}\left({\delta }^n\right)\end{array}$$

(12)

for all $n\ge 0$, where

$$\begin{array}{c}\hfill {\delta }^n=\mathrm{Hom}({\partial }_n,R):d{C}^{n-1}(X;R)\to d{C}^n(X;R)\end{array}$$

(13)

is the so-called digital coboundary operator which is the dual of the digital boundary operator ${\partial }_n:d{C}_n(X;R)\to d{C}_{n-1}(X;R)$ for each $n\ge 0$.

It can be seen in [39] that, for each digital image $(X,k_X)$, $d{H}^n(X;R)$ has the R-module structure whose scalar multiplication

$$\begin{array}{cc}\hfill \overline{s}=•:R\times d{H}^n(X;R)& ⟶d{H}^n(X;R)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill (r,[x\left]\right)& ⟼\overline{s}(r,\left[x\right])\hfill \end{array}$$

(15)

is given by

$$\begin{array}{c}\hfill \overline{s}(r,\left[x\right])=r•\left[x\right]=[r•x]=r•x+\mathrm{Im}\left({\delta }^n\right),\end{array}$$

(16)

where

• $r\in R$;
• $\left[x\right]=x+\mathrm{Im}\left({\delta }^n\right)\in d{H}^n(X;R)$ with $x\in \mathrm{Ker}\left({\delta }^{n+1}\right)$; and
• the second and third bullets ‘•’ in (16) are the scalar multiplications on $\mathrm{Ker}\left({\delta }^{n+1}\right)$ as an R-submodule of $d{C}^n(X;R)$.

Indeed, as a quotient R-module, $d{H}^n(X;R)$ has the unitary R-module structure because R is a commutative ring with identity; see [39] [Theorem 1] for further details.

Let A and B be R-modules. A function $h:A\to B$ is said to be an R-module homomorphism if

• $h\left(a_1{+}_A{a}_2\right)=h\left(a_1\right){+}_{B}h\left(a_2\right)$; and
• $h(r•a)=r•h\left(a\right)$,

for all $a_1,a_2,a\in A$ and $r\in R$, where

• ${+}_A:A\times A\to A$ is the binary operation on A;
• ${+}_B:B\times B\to B$ is the binary operation on B;
• the first bullet $•:R\times A\to A$ is the scalar multiplication on A; and
• the second bullet $•:R\times B\to B$ is the scalar multiplication on B.

Remark 2.

Let$\mathcal{D}$be the category of digital images and digital continuous functions as mentioned earlier in Remark 1, and let$Mo{d}_R$be the category of unitary R-modules and R-module homomorphisms. Then, it can be seen in [39] [Theorem 1] that the assignment

$$\begin{array}{c}\hfill d{H}^n(-;R):\mathcal{D}\to \mathcal{M}o{d}_R\end{array}$$

(17)

given by

$$\begin{array}{c}\hfill (X,k_X)⟼d{H}^n(X;R)\end{array}$$

(18)

is a contravariant functor for each$n\ge 0$.

3. Coalgebras, Counits, and Coalgebra Homomorphisms

In this section, two digital images $(X,k_X)$ and $(Y,k_Y)$ are always $k_X$-connected and $k_Y$-connected digital images, respectively, so that the 0-th digital cohomology modules of the digital images are just the coefficient rings; that is,

$$\begin{array}{c}\hfill d{H}^0(X;R)\cong R\cong d{H}^0(Y;R).\end{array}$$

(19)

Recall that a triple $(C,\phi ,ϵ)$ consisting of an R-module C and R-module homomorphisms

$$\begin{array}{c}\hfill \phi :C\to C{\otimes }_{R}C\end{array}$$

(20)

and

$$\begin{array}{c}\hfill ϵ:C\to R\end{array}$$

(21)

is said to be a coalgebra over a ring R (or an R-coalgebra) if the following diagrams

(22)

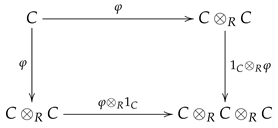and

(23)

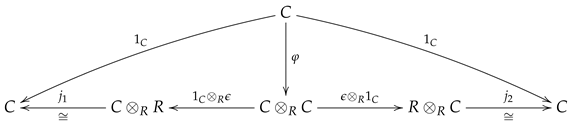are strictly commutative. Here,

• $1_C:C\to C$ is the identity automorphism;
• $j_1:C{\otimes }_{R}R\to C$ given by $j_1\left(c{\otimes }_{R}r\right)=c•r$ is an R-module isomorphism; and
• $j_2:R{\otimes }_{R}C\to C$ given by $j_2\left(r{\otimes }_{R}c\right)=r•c$ is an R-module isomorphism,

where the bullet multiplications above are coming from the right and left R-module structures on C with scalar multiplications

$$\begin{array}{c}\hfill •:C\times R\to C\end{array}$$

(24)

and

$$\begin{array}{c}\hfill •:R\times C\to C,\end{array}$$

(25)

respectively. The above R-module homomorphism

$$\begin{array}{c}\hfill \phi :C\to C{\otimes }_{R}C\end{array}$$

(26)

is said to be an R-coalgebra comultiplication on C, and the R-module homomorphism

$$\begin{array}{c}\hfill ϵ:C\to R\end{array}$$

(27)

is said to be an R-coalgebra counit.

A pointed digital Hopf space $Y:=(Y,y_0,k_Y,m_Y)$ consists of a pointed digital image $(Y,y_0)$ with an adjacency relation $k_Y$ and a $(k_{Y\times Y},k_Y)$-continuous function $m_Y:Y\times Y\to Y$ which is called a digital homotopy multiplication (or digital multiplication for short) such that the following diagrams

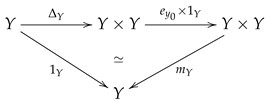and

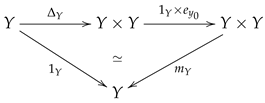commutate up to pointed digital homotopy, where ${\Delta }_Y:Y\to Y\times Y$ is the diagonal function; see [48,49] for more details.

Let $X:=(X,x_0,k_X,m_X)$ and $Y:=(Y,y_0,k_Y,m_Y)$ be pointed digital Hopf spaces with digital multiplications $m_X:X\times X\to X$ and $m_Y:Y\times Y\to Y$, respectively. A base point preserving $(k_X,k_Y)$-continuous function $f:(X,x_0)\to (Y,y_0)$ is said to be a digital Hopf function (compare with [50,51]) if $f\circ m_X$ and $m_Y\circ (f\times f)$ are pointed digital $(k_{X\times X},k_Y)$-homotopic in $(Y,y_0)$.

It can be shown that, if $(Y,y_0,k_Y,m_Y)$ is a pointed digital Hopf space with digital multiplication $m_Y:Y\times Y\to Y$, then the digital multiplication $m_Y$ provides the graded digital cohomology module $\left\{d{H}^n(Y;R)\right|n\ge 0\}$ with the structure of coalgebra over the commutative ring R with identity $1_R$.

Remark 3.

Since R is a commutative ring with identity$1_R$, we have the R-module structure of the tensor product$d{H}^n(X;R){\otimes }_{R}d{H}^n(X;R),n\ge 0$whose scalar multiplication

$$\begin{array}{c}\hfill •:R\times \left(d{H}^n(X;R){\otimes }_{R}d{H}^n(X;R)\right)\to d{H}^n(X;R){\otimes }_{R}d{H}^n(X;R)\end{array}$$

(28)

is given by

$$\begin{array}{c}\hfill r•\left(\left[x_1\right]{\otimes }_R\left[x_2\right]\right)=(r•\left[x_1\right]){\otimes }_R\left[x_2\right]=\left[x_1\right]{\otimes }_R(r•\left[x_2\right])\end{array}$$

(29)

for all$\left[x_1\right]{\otimes }_R\left[x_2\right]\in d{H}^n(X;R){\otimes }_{R}d{H}^n(X;R)$, where the second bullet in (29)

$$\begin{array}{c}\hfill •:R\times d{H}^n(X;R)\to d{H}^n(X;R)\end{array}$$

(30)

is the scalar multiplication on the R-module structure of$d{H}^n(X;R),n\ge 0$; see the Formula (16).

For a path connected Hopf space Y with a multiplication $m:Y\times Y\to Y$, it can be seen that the diagonal map $\Delta :Y\to Y\times Y$ and the multiplication $m:Y\times Y\to Y$ induce homomorphisms of classical homology and cohomology modules as follows:

• ${\widehat{\Delta }}_{*}:H_{*}(Y;R)\stackrel{{\Delta }_{*}}{\to }{H}_{*}(Y\times Y;R)\underset{\cong }{\overset{\times }{\to }}{H}_{*}(Y;R){\otimes }_R{H}_{*}(Y;R)$;
• ${\widehat{m}}_{*}:H_{*}(Y;R){\otimes }_R{H}_{*}(Y;R)\underset{\cong }{\overset{\times }{\to }}{H}_{*}(Y\times Y;R)\stackrel{m_{*}}{\to }{H}_{*}(Y;R)$;
• ${\widehat{m}}^{*}:H^{*}(Y;R)\stackrel{m^{*}}{\to }{H}^{*}(Y\times Y;R)\underset{\cong }{\overset{\times }{\to }}{H}^{*}(Y;R){\otimes }_R{H}^{*}(Y;R)$; and
• ${\widehat{\Delta }}^{*}:H^{*}(Y;R)\otimes H^{*}(Y;R)\underset{\cong }{\overset{\times }{\to }}{H}^{*}(Y\times Y;R)\stackrel{{\Delta }^{*}}{\to }{H}^{*}(Y;R)$,

where

• $H_{*}(Y;R):={⨁}_{n\ge 0}{H}_n(Y;R)$;
• $H^{*}(Y;R):={⨁}_{n\ge 0}{H}^n(Y;R)$;
• × is the homology and cohomology cross products; and
• the homology and cohomology modules are free modules of finite ranks.

It is well known in algebraic topology that $H_{*}(Y;R)$ has the structure of an R-algebra with ${\widehat{m}}_{*}$, and $H^{*}(Y:R)$ has the structure of an R-coalgebra with ${\widehat{m}}^{*}$. Similarly, the algebraic structure arising from the diagonal map $\Delta :Y\to Y\times Y$ has the coalgebra structure on homology and the algebra structure on cohomology together with the Künneth formula; see [52,53].

Let $Rcoal\left(C\right)$ be the set of all R-coalgebra comultiplications on an R-coalgebra C and let $\left|Rcoal\right(C\left)\right|$ be its cardinality. In general, there exist (infinitely) many types of R-algebra comultiplications on an R-coalgebra C; that is, $\left|Rcoal\right(C\left)\right|\le \infty$.

We now focus on the development of an R-coalgebra based on a $k_X$-connected digital image $(X,k_X)$. To do so, we define one of the R-coalgebra comultiplications on the direct sum ${⨁}_{n\ge 0}d{H}^n(X;R)$ of digital cohomology modules to construct the R-coalgebra structure on it as follows.

Definition 4.

Let $(X,k_X)$ be any $k_X$-connected digital image. Then, we define an R-module homomorphism

$$\begin{array}{c}\hfill \phi :\underset{n\ge 0}{⨁}d{H}^n(X;R)\to \underset{n\ge 0}{⨁}d{H}^n(X;R){\otimes }_R\underset{n\ge 0}{⨁}d{H}^n(X;R)\end{array}$$

(31)

by

$$\begin{array}{c}\hfill \phi \left(\left[x\right]\right)=\left\{\begin{array}{cc}\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right]\hfill & \mathrm{if} n\ge 1\hfill \\ 1_R{\otimes }_R{1}_R\hfill & \mathrm{if} n=0 \mathrm{and} \left[x\right]=1_R \mathrm{in} R\cong d{H}^0(X;R)\hfill \end{array}\right.\end{array}$$

(32)

for all $\left[x\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$, where $1_R$ is the identity element of the ground ring

$$\begin{array}{c}\hfill R\cong d{H}^0(X;R)\end{array}$$

(33)

corresponding to the unique element $1_R\otimes 1_R$ of $d{H}^0(X;R)\otimes d{H}^0(X;R)$; that is,

$$\begin{array}{cc}\hfill d{H}^0(X;R)\cong R& \cong d{H}^0(X;R)\otimes d{H}^0(X;R)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill 1_R& ⟷1_R\otimes 1_R.\hfill \end{array}$$

(35)

Indeed, by Remark 3, we can show that ‘$\phi$’ preserves the scalar multiplication and the addition as follows:

$$\begin{array}{c}\hfill \begin{array}{ccc}\phi (r•[x\left]\right)\hfill & =r•\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_{R}r•\left[x\right]\hfill & \mathrm{by} \left(32\right)\hfill \\ & =r•\left(\left[x\right]{\otimes }_R{1}_R\right)+r•\left(1_R{\otimes }_R\left[x\right]\right)\hfill & \mathrm{by} \left(29\right)\hfill \\ & =r•(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill & \mathrm{by} \mathrm{the} \mathrm{module} \mathrm{structure}\hfill \\ & =r•\phi \left(\right[x\left]\right)\hfill & \mathrm{by} \left(32\right)\hfill \end{array}\end{array}$$

(36)

for all $r\in R$ and $\left[x\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$ and

$$\begin{array}{c}\hfill \begin{array}{cc}\phi (\left[x_1\right]+\left[x_2\right])\hfill & =(\left[x_1\right]+\left[x_2\right]){\otimes }_R{1}_R+1_R{\otimes }_R(\left[x_1\right]+\left[x_2\right])\hfill \\ & =(\left[x_1\right]{\otimes }_R{1}_R+\left[x_2\right]{\otimes }_R{1}_R)+(1_R{\otimes }_R\left[x_1\right]+1_R{\otimes }_R\left[x_2\right])\hfill \\ & =(\left[x_1\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x_1\right])+(\left[x_2\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x_2\right])\hfill \\ & =\phi \left(\left[x_1\right]\right)+\phi \left(\left[x_2\right]\right)\hfill \end{array}\end{array}$$

(37)

for all $r\in R$ and $\left[x_1\right],\left[x_2\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$ and this is similar for the 0-dimensional digital cohomology case. Moreover, we can show that the R-module homomorphism $\phi$ is indeed an R-coalgebra comultiplication; that is, $\phi \in Rcoal\left({⨁}_{n\ge 0}d{H}^n(X;R)\right)$; see Theorem 1 below.

Remark 4.

We can also define another R-module homomorphism

$$\begin{array}{c}\hfill \psi :\underset{n\ge 0}{⨁}d{H}^n(X;R)\to \underset{n\ge 0}{⨁}d{H}^n(X;R){\otimes }_R\underset{n\ge 0}{⨁}d{H}^n(X;R)\end{array}$$

(38)

by

$$\begin{array}{c}\hfill \psi \left(\left[y_n\right]\right)=\left\{\begin{array}{cc}{\displaystyle \left[y_n\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[y_n\right]+\sum _{i+j=n}\left[y_i\right]\otimes \left[y_j\right]}\hfill & \mathrm{if} n\ge 1\hfill \\ 1_R{\otimes }_R{1}_R\hfill & \mathrm{if} n=0 \mathrm{and} \left[y_0\right]=1_R \mathrm{in} R\cong d{H}^0(X;R)\hfill \end{array}\right.\end{array}$$

(39)

for all$\left[y_s\right]\in {⨁}_{n\ge 0}d{H}^s(X;R),s=0,1,2,\dots$. The R-module homomorphism ψ is sometimes called a diagonal or coproduct in the sense of Hatcher [53] [page 283].

Let $\Delta :Z\to Z\times Z$ be the diagonal map. In classical homology and cohomology theories, an element z of $H_n(Z;R)$ is said to be a primitive homology class if

$$\begin{array}{c}\hfill {\Delta }_{*}\left(z\right)=z\otimes 1+1\otimes z\end{array}$$

(40)

in $H_n(Z;R){\otimes }_R{H}_n(Z;R)$. Similarly, if Y is a connected Hopf space with multiplication $m:Y\times Y\to Y$, then an element y of $H^n(Y;R)$ is said to be a primitive cohomology class if

$$\begin{array}{c}\hfill m^{*}\left(y\right)=y\otimes 1+1\otimes y\end{array}$$

(41)

in $H^n(Y;R){\otimes }_R{H}^n(Y;R)$. We note that the element $\left[x\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$ in Definition 4 looks like a primitive cohomology class.

Moreover, it can be seen that the R-module homomorphisms $\phi$ in Definition 4 and $\psi$ in Remark 4 are completely different from any types of the above homomorphisms ${\widehat{\Delta }}_{*}$ on homology and ${\widehat{\Delta }}^{*}$ on cohomology induced by the diagonal map $\Delta :Y\to Y\times Y$ on a topological space Y (or even a digital image $(X,k_X))$.

Definition 5.

We define an R-module homomorphism

$$\begin{array}{c}\hfill ϵ:\underset{n\ge 0}{⨁}d{H}^n(X;R)\to R\end{array}$$

(42)

by

$$\begin{array}{c}\hfill ϵ\left(\left[x\right]\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if} n\ge 1\hfill \\ 1_R\hfill & \mathrm{if} n=0 \mathrm{and} \left[x\right]=1_R \mathrm{in} R\cong d{H}^0(X;R)\hfill \end{array}\right.\end{array}$$

(43)

for$\left[x\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$.

Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}ϵ(r•[x\left]\right)\hfill & =ϵ\left(\right[r•x\left]\right)\hfill \\ & =\left\{\begin{array}{cc}0\hfill & \mathrm{if} n\ge 1\hfill \\ r\diamond 1_R=r\hfill & \mathrm{if} n=0 \mathrm{and} \left[x\right]=1_R \mathrm{in} R\cong d{H}^0(X;R)\hfill \end{array}\right.\hfill \\ & =\left\{\begin{array}{cc}r\diamond 0=0\hfill & \mathrm{if} n\ge 1\hfill \\ r\diamond 1_R=r\hfill & \mathrm{if} n=0 \mathrm{and} \left[x\right]=1_R \mathrm{in} R\cong d{H}^0(X;R)\hfill \end{array}\right.\hfill \\ & =r\diamond ϵ\left(\right[x\left]\right)\hfill \end{array}\end{array}$$

(44)

and

$$\begin{array}{c}\hfill \begin{array}{ccc}ϵ(1_R+1_R)\hfill & =ϵ(2\diamond 1_R)\hfill & \mathrm{by} \mathrm{the} \mathrm{ring} \mathrm{addition} \mathrm{on} R\hfill \\ & =2\diamond ϵ\left(1_R\right)\hfill & \mathrm{by} \left(44\right)\hfill \\ & =2\diamond 1_R\hfill & \mathrm{by} \mathrm{Definition} 5\hfill \\ & =1_R+1_R\hfill \\ & =ϵ\left(1_R\right)+ϵ\left(1_R\right)\hfill \end{array}\end{array}$$

(45)

for all $r\in R$ and $\left[x\right]\in {⨁}_{n\ge 0}d{H}^n(X;R)$, where ⋄ is the ring multiplication on R. By extending the linearity, we can see that ‘$ϵ$’ preserves the addition.

Convention. From now on, we make use of the notation $d{H}^{*}(X;R)$ to denote the direct sum ${⨁}_{n\ge 0}d{H}^n(X;R)$ of digital cohomology modules; that is, $d{H}^{*}(X;R):={⨁}_{n\ge 0}d{H}^n(X;R)$.

We now have the following.

Theorem 1.

Let$(X,k_X)$be a$k_X$-connected digital image, and let

$$\phi :d{H}^{*}(X;R)\to d{H}^{*}(X;R){\otimes }_{R}d{H}^{*}(X;R)$$

and

$$ϵ:d{H}^{*}(X;R)\to R$$

be the R-module homomorphisms in Definitions 4 and 5, respectively. Then, the triple

$$\begin{array}{c}\hfill (d{H}^{*}(X;R),\phi ,ϵ)\end{array}$$

(46)

is an R-coalgebra.

Proof. 

If $n\ge 1$, then we have

$$\begin{array}{c}\hfill \begin{array}{cc}\left(1_{d{H}^{*}(X;R)}{\otimes }_R\phi \right)\circ \phi \left(\left[x\right]\right)\hfill & =\left(1_{d{H}^{*}(X;R)}{\otimes }_R\phi \right)(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =\left[x\right]{\otimes }_R\left(1_R{\otimes }_R{1}_R\right)+1_R{\otimes }_R(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =\left[x\right]{\otimes }_R{1}_R{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R{1}_R{\otimes }_R\left[x\right]\hfill \\ & =(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right]){\otimes }_R{1}_R+1_R{\otimes }_R{1}_R{\otimes }_R\left[x\right]\hfill \\ & =\left(\phi {\otimes }_R{1}_{d{H}^{*}(X;R)}\right)(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =\left(\phi {\otimes }_R{1}_{d{H}^{*}(X;R)}\right)\circ \phi \left(\left[x\right]\right)\hfill \end{array}\end{array}$$

(47)

for all $\left[x\right]\in d{H}^{*}(X;R)$. If $n=0$, then we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}(1_{d{H}^0(X;R)}{\otimes }_R\phi )\circ \phi \left(1_R\right)\hfill & =(1_{d{H}^0(X;R)}{\otimes }_R\phi )\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =1_R{\otimes }_R\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =\left(1_R{\otimes }_R{1}_R\right){\otimes }_R{1}_R\hfill \\ & =(\phi {\otimes }_R{1}_{d{H}^0(X;R)})\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =(\phi {\otimes }_R{1}_{d{H}^0(X;R)})\circ \phi \left(1_R\right)\hfill \end{array}\end{array}$$

(48)

satisfying the condition in (22).

If $n\ge 1$, then we also obtain

$$\begin{array}{c}\hfill \begin{array}{cc}{j}_2\circ \left(ϵ{\otimes }_R{1}_{d{H}^{*}(X;R)}\right)\circ \phi \left(\left[x\right]\right)\hfill & =j_2\circ \left(ϵ{\otimes }_R{1}_{d{H}^{*}(X;R)}\right)(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =j_2(0{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =0•1_R+1_R•\left[x\right]\hfill \\ & =0+\left[x\right]\hfill \\ & =\left[x\right]\hfill \end{array}\end{array}$$

(49)

for all $\left[x\right]\in d{H}^{*}(X;R)$, where

$$\begin{array}{c}\hfill •:R\times d{H}^{*}(X;R)\to d{H}^{*}(X;R)\end{array}$$

(50)

is the scalar multiplication on a left unitary R-module $d{H}^{*}(X;R)$. The above Equation (49) shows that the triangle on the right-hand side of (23) is commutative. Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}{j}_1\circ \left(1_{d{H}^{*}(X;R)}{\otimes }_Rϵ\right)\circ \phi \left(\left[x\right]\right)\hfill & =j_1\circ \left(1_{d{H}^{*}(X;R)}{\otimes }_Rϵ\right)(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[x\right])\hfill \\ & =j_1(\left[x\right]{\otimes }_R{1}_R+1_R{\otimes }_{R}0)\hfill \\ & =\left[x\right]•1_R+1_R•0\hfill \\ & =\left[x\right]+0\hfill \\ & =\left[x\right]\hfill \end{array}\end{array}$$

(51)

for all $\left[x\right]\in d{H}^{*}(X;R)$, where

$$\begin{array}{c}\hfill •:d{H}^{*}(X;R)\times R\to d{H}^{*}(X;R)\end{array}$$

(52)

is the scalar multiplication on a right unitary R-module $d{H}^{*}(X;R)$ which is equal to the scalar multiplication on $d{H}^{*}(X;R)$ as a left unitary R-module in (50) by defining

$$\begin{array}{c}\hfill r•\left[x\right]=\left[x\right]•r.\end{array}$$

(53)

If $n=0$, then we have

$$\begin{array}{c}\hfill \begin{array}{cc}{j}_2\circ (ϵ{\otimes }_R{1}_{d{H}^0(X;R)})\circ \phi \left(1_R\right)\hfill & =j_2\circ (ϵ{\otimes }_R{1}_{d{H}^0(X;R)})\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =j_2\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =1_R•1_R\hfill \\ & =1_R\hfill \end{array}\end{array}$$

(54)

and

$$\begin{array}{c}\hfill \begin{array}{cc}{j}_1\circ (1_{d{H}^0(X;R)}{\otimes }_Rϵ)\circ \phi \left(1_R\right)\hfill & =j_1\circ (1_{d{H}^0(X;R)}{\otimes }_Rϵ)\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =j_1\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =1_R•1_R\hfill \\ & =1_R.\hfill \end{array}\end{array}$$

(55)

Indeed, it is possible for us to do so because the ground ring R is commutative. The above Equations (49), (51), (54), and (55) show that the two triangles in (23) are strictly commutative, as required. □

We now give an example of the digital cohomology modules of some digital images, and then present another example of an R-coalgebra based on the same digital images as follows.

Example 2.

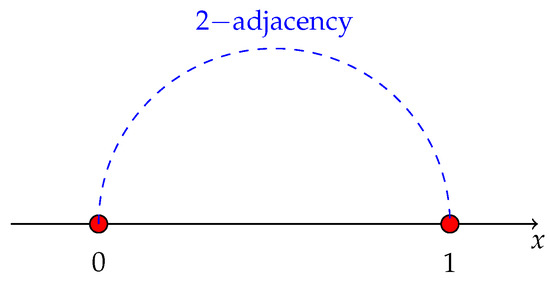
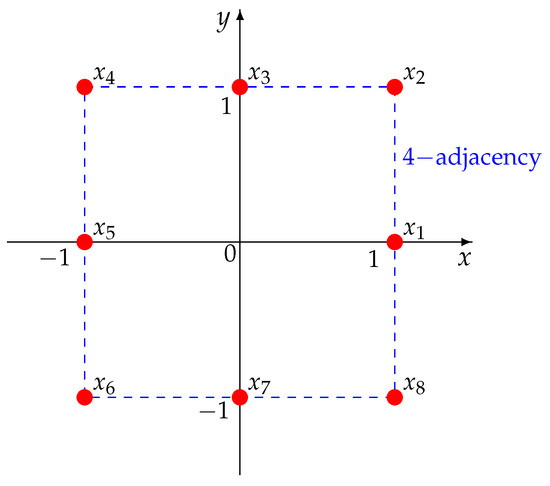
Let$X:=\{0,1\}$and$Y:=\left\{x_i\right|i=1,2,\dots ,8\}$be digital images in$\mathbb{Z}$and${\mathbb{Z}}^2$with 2-adjacency and 4-adjacency relations, respectively, where$x_1=(1,0),x_2=(1,1),x_3=(0,1),x_4=(-1,1)$,$x_5=(-1,0)$,$x_6=(-1,-1),x_7=(0,-1),x_8=(1,-1)$; see Figure 1 and Figure 2. Then, it can be shown that X and Y are 2-connected and 4-connected digital images, respectively. Moreover, we have

$$\begin{array}{c}\hfill d{H}^n(X;R)=\left\{\begin{array}{cc}R\hfill & \mathrm{if} n=0\hfill \\ 0\hfill & \mathrm{if} n\ge 1\hfill \end{array}\right.\end{array}$$

(56)

and

$$\begin{array}{c}\hfill d{H}^n(Y;R)=\left\{\begin{array}{cc}R\hfill & \mathrm{if} n=0,1\hfill \\ 0\hfill & \mathrm{if} n\ge 2.\hfill \end{array}\right.\end{array}$$

(57)

We note that

$$\begin{array}{c}\hfill d{H}^0(Y;R)=\mathrm{Ker}({\delta }^1:d{C}^0(Y;R)\to d{C}^1(Y;R))\end{array}$$

(58)

because there are no digital coboundaries in dimension 0; that is, the module of digital 0-coboundaries in$(Y,k_Y)$is trivial.

Figure 1. A digital image X with the 2-adjacency relation along with the dotted curve.

Figure 2. A digital image Y with the 4-adjacency relation along with the 8-dotted lines.

Example 3.

Let$X:=\{0,1\}$and$Y:=\left\{x_i\right|i=1,2,\dots ,8\}$be digital images in${\mathbb{Z}}^2$with 2-adjacency and 4-adjacency relations, respectively, in Example 2. We consider an R-coalgebra comultiplication

$${\phi }_{d{H}^{*}(Y;R)}:d{H}^{*}(Y;R)\to d{H}^{*}(Y;R){\otimes }_{R}d{H}^{*}(Y;R)$$

given by

$$\begin{array}{c}\hfill {\phi }_{d{H}^{*}(Y;R)}\left(\left[y\right]\right)=\left\{\begin{array}{cc}\left[y\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[y\right]\hfill & \mathrm{if} n\ge 1\hfill \\ 1_R{\otimes }_R{1}_R\hfill & \mathrm{if} n=0 \mathrm{and} \left[y\right]=1_R \mathrm{in} R\cong d{H}^0(Y;R)\hfill \end{array}\right.\end{array}$$

(59)

for all$\left[y\right]\in d{H}^{*}(Y;R)$in Definition 4. We also define an R-coalgebra counit

$${ϵ}_{d{H}^{*}(Y;R)}:d{H}^{*}(Y;R)\to R$$

to be the Formula (43) in Definition 5. Therefore, it can be seen that the triple

$$(d{H}^{*}(Y;R),{\phi }_{d{H}^{*}(Y;R)},{ϵ}_{d{H}^{*}(Y;R)})$$

has the R-coalgebra structure, and similarly for the digital image$(X,k_X)$, where$k_X=2$.

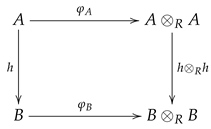
Definition 6.

Let$A:=(A,{\phi }_A,{ϵ}_A)$and$B:=(B,{\phi }_B,{ϵ}_B)$be coalgebras over a commutative ring R with identity. An R-module homomorphism

$$\begin{array}{c}\hfill h:A\to B\end{array}$$

(60)

is said to be an R-coalgebra homomorphism if the following diagrams

(61)

and

(62)

are strictly commutative.

For digital images $(X,k_X)$ and $(Y,k_Y)$, we let

$$\begin{array}{c}\hfill {\phi }_{d{H}^{*}(X;R)}:d{H}^{*}(X;R)\to d{H}^{*}(X;R){\otimes }_{R}d{H}^{*}(X;R)\end{array}$$

(63)

and

$$\begin{array}{c}\hfill {\phi }_{d{H}^{*}(Y;R)}:d{H}^{*}(Y;R)\to d{H}^{*}(Y;R){\otimes }_{R}d{H}^{*}(Y;R)\end{array}$$

(64)

be R-coalgebra comultiplications on $d{H}^{*}(X;R)$ and $d{H}^{*}(Y;R)$, respectively. Let

$$\begin{array}{c}\hfill {ϵ}_{d{H}^{*}(X;R)}:d{H}^{*}(X;R)\to R\end{array}$$

(65)

and

$$\begin{array}{c}\hfill {ϵ}_{d{H}^{*}(Y;R)}:d{H}^{*}(Y;R)\to R\end{array}$$

(66)

be R-coalgebra counits on $d{H}^{*}(X;R)$ and $d{H}^{*}(Y;R)$, respectively.

We note that if

$$\sigma :({\Delta }^n,k_{{\Delta }^n})\to (X,k_X)$$

is a $(k_{{\Delta }^n},k_X)$-continuous function and if

$$f:(X,k_X)\to (Y,k_Y)$$

is a $(k_X,k_Y)$-continuous function, then it can be shown that

$$f\circ \sigma :({\Delta }^n,k_{{\Delta }^n})\to (Y,k_Y)$$

is a $(k_{{\Delta }^n},k_Y)$-continuous function. Therefore, by using the linear property, we have an R-module homomorphism of R-modules

$$f_{♯}:d{C}_n(X;R)\to d{C}_n(Y;R)$$

defined by

$$f_{♯}(\sum r_{\sigma }•\sigma )=\sum r_{\sigma }•(f\circ \sigma ),$$

where $r_{\sigma }$ is an element of the commutative ring R with identity, and the bullets • are the scalar multiplications on the R-modules $d{C}_n(X;R)$ and $d{C}_n(Y;R)$ with the same notation.

Let

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(67)

be a $(k_X,k_Y)$-continuous function between digital images. Then, we define a map

$$\begin{array}{c}\hfill f^{♯}:d{C}^n(Y;R)\to d{C}^n(X;R)\end{array}$$

(68)

by

$$\begin{array}{c}\hfill f^{♯}\left(y\right)=y\circ f_{♯}\end{array}$$

(69)

for every $y\in d{C}^n(Y;R)$; that is, the following triangle

(70)

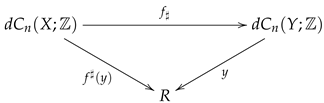is strictly commutative, where $\mathbb{Z}$ is the ring of integers.

Lemma 1.

Let

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(71)

be a$(k_X,k_Y)$-continuous function. Then, the map

$$\begin{array}{c}\hfill f^{*}=d{H}^n\left(f\right):d{H}^n(Y;R)\to d{H}^n(X;R)\end{array}$$

(72)

given by

$$\begin{array}{c}\hfill f^{*}\left(\left[y\right]\right)=[f^{♯}\left(y\right)]=[y\circ f_{♯}]\end{array}$$

(73)

is an R-module homomorphism, where

$$\begin{array}{c}\hfill \left[y\right]=y+Im\left({\delta }^n\right)\in d{H}^n(Y;R)\end{array}$$

(74)

and y is an element of the kernel of

$$\begin{array}{c}\hfill {\delta }^{n+1}:d{C}^n(Y;R)\to d{C}^{n+1}(Y;R).\end{array}$$

(75)

Proof. 

See [39] [Lemma 2] for further details. □

Theorem 2.

Let

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(76)

be a$(k_X,k_Y)$-continuous function between digital images. Then, the homomorphism

$$\begin{array}{c}\hfill f^{*}:(d{H}^{*}(Y;R),{\phi }_{d{H}^{*}(Y;R)},{ϵ}_{d{H}^{*}(Y;R)})\to (d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})\end{array}$$

(77)

induced by f is an R-coalgebra homomorphism.

Proof. 

It can be shown in [39] [Lemma 2] that

$$\begin{array}{c}\hfill f^{*}:d{H}^{*}(Y;R)\to d{H}^{*}(X;R)\end{array}$$

(78)

is an R-module homomorphism; that is, $f^{*}$ preserves the scalar multiplication and the addition as follows:

$$\begin{array}{c}\hfill f^{*}(r•\left[y\right])=r•f^{*}\left(\left[y\right]\right)\end{array}$$

(79)

and

$$\begin{array}{c}\hfill f^{*}(\left[y_1\right]+\left[y_2\right])=f^{*}\left(\left[y_1\right]\right)+f^{*}\left(\left[y_2\right]\right).\end{array}$$

(80)

all $r\in R$ and $\left[y\right],\left[y_1\right],\left[y_2\right]\in d{H}^{*}(Y;R)$.

If $n\ge 1$, then we have

$$\begin{array}{c}\hfill \begin{array}{cc}\left(f^{*}{\otimes }_R{f}^{*}\right)\circ {\phi }_{d{H}^{*}(Y;R)}\left(\left[y\right]\right)\hfill & =\left(f^{*}{\otimes }_R{f}^{*}\right)(\left[y\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[y\right])\hfill \\ & =\left(f^{*}\left(\left[y\right]\right){\otimes }_R{f}^{*}\left(1_R\right)\right)+\left(f^{*}\left(1_R\right){\otimes }_R{f}^{*}\left(\left[y\right]\right)\right)\hfill \\ & =\left(f^{*}\left(\left[y\right]\right){\otimes }_R{1}_R\right)+\left(1_R{\otimes }_R{f}^{*}\left(\left[y\right]\right)\right)\hfill \\ & ={\phi }_{d{H}^{*}(X;R)}\left(f^{*}\left(\left[y\right]\right)\right)\hfill \\ & ={\phi }_{d{H}^{*}(X;R)}\circ f^{*}\left(\left[y\right]\right)\hfill \end{array}\end{array}$$

(81)

for all $\left[y\right]\in d{H}^{*}(Y;R)$.

If $n=0$, then we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\left(f^{*}{\otimes }_R{f}^{*}\right)\circ {\phi }_{d{H}^0(Y;R)}\left(1_R\right)\hfill & =\left(f^{*}{\otimes }_R{f}^{*}\right)\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =f^{*}\left(1_R\right)\otimes f^{*}\left(1_R\right)\hfill \\ & =1_R{\otimes }_R{1}_R\hfill \\ & ={\phi }_{d{H}^0(X;R)}\left(1_R\right)\hfill \\ & ={\phi }_{d{H}^0(X;R)}\left(f^{*}\left(1_R\right)\right)\hfill \\ & ={\phi }_{d{H}^0(X;R)}\circ f^{*}\left(1_R\right),\hfill \end{array}\end{array}$$

(82)

where

$$\begin{array}{c}\hfill f^{*}:d{H}^0(Y;R)\to d{H}^0(X;R)\end{array}$$

(83)

is the identity automorphism on R.

For the R-coalgebra counits, if $n\ge 1$, then we have

$$\begin{array}{c}\hfill \begin{array}{ccc}{ϵ}_{d{H}^{*}(X;R)}\circ f^{*}\left(\left[y\right]\right)\hfill & ={ϵ}_{d{H}^{*}(X;R)}\left([y\circ f_{♯}]\right)\hfill & \mathrm{by} \mathrm{Lemma} 1\hfill \\ & =0\hfill & \mathrm{by} \left(43\right)\hfill \\ & ={ϵ}_{d{H}^{*}(Y;R)}\left(\left[y\right]\right)\hfill \end{array}\end{array}$$

(84)

for all $\left[y\right]\in d{H}^{*}(Y;R)$. Similarly, if $n=0$, then

$$\begin{array}{c}\hfill \begin{array}{ccc}{ϵ}_{d{H}^0(X;R)}\circ f^{*}\left(\left[1_R\right]\right)\hfill & ={ϵ}_{d{H}^0(X;R)}\left(\left[1_R\right]\right)\hfill & \mathrm{by} \left(43\right)\hfill \\ & =1_R\hfill \\ & ={ϵ}_{d{H}^0(Y;R)}\left(\left[1_R\right]\right),\hfill \end{array}\end{array}$$

(85)

where

$$\begin{array}{c}\hfill f^{*}:d{H}^0(Y;R)\to d{H}^0(X;R)\end{array}$$

(86)

is the identity automorphism on R, as required. □

Example 4.

Let$X:=\{0,1\}$and$Y:=\left\{x_i\right|i=1,2,\dots ,8\}$be digital images in$\mathbb{Z}$and${\mathbb{Z}}^2$with 2-adjacency and 4-adjacency relations, respectively, in Example 2. Let

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(87)

be any$(k_X,k_Y)$-continuous function between digital images. Then, it can seen that the map

$$\begin{array}{c}\hfill f^{*}:(d{H}^{*}(Y;R),{\phi }_{d{H}^{*}(Y;R)},{ϵ}_{d{H}^{*}(Y;R)})\to (d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})\end{array}$$

(88)

is an R-coalgebra homomorphism.

Indeed, if $n\ge 1$, then, by Example 2, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\left(f^{*}{\otimes }_R{f}^{*}\right)\circ {\phi }_{d{H}^{*}(Y;R)}\left(\left[y\right]\right)\hfill & =\left(f^{*}{\otimes }_R{f}^{*}\right)(\left[y\right]{\otimes }_R{1}_R+1_R{\otimes }_R\left[y\right])\hfill \\ & =0{\otimes }_R{1}_R+1_R{\otimes }_{R}0\hfill \\ & =0\hfill \\ & ={\phi }_{d{H}^{*}(X;R)}\left(0\right)\hfill \\ & ={\phi }_{d{H}^{*}(X;R)}\circ f^{*}\left(\left[y\right]\right)\hfill \end{array}\end{array}$$

(89)

for any element $\left[y\right]$ of $d{H}^{*}(Y;R)$. If $n=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\left(f^{*}{\otimes }_R{f}^{*}\right)\circ {\phi }_{d{H}^0(Y;R)}\left(1_R\right)\hfill & =\left(f^{*}{\otimes }_R{f}^{*}\right)\left(1_R{\otimes }_R{1}_R\right)\hfill \\ & =1_R{\otimes }_R{1}_R\hfill \\ & ={\phi }_{d{H}^0(X;R)}\left(1_R\right)\hfill \\ & ={\phi }_{d{H}^0(X;R)}\left(f^{*}\left(1_R\right)\right)\hfill \\ & ={\phi }_{d{H}^0(X;R)}\circ f^{*}\left(1_R\right).\hfill \end{array}\end{array}$$

(90)

Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}{ϵ}_{d{H}^{*}(X;R)}\circ f^{*}\left(\left[y\right]\right)\hfill & ={ϵ}_{d{H}^{*}(X;R)}\left([y\circ f_{♯}]\right)\hfill \\ & =\left\{\begin{array}{cc}0\hfill & \mathrm{if} n\ge 1\hfill \\ 1_R\hfill & \mathrm{if} n=0 \mathrm{and} [y\circ f_{♯}]=1_R=\left[y\right] \mathrm{in} d{H}^0(X;R)\cong R\cong d{H}^0(Y;R)\hfill \end{array}\right.\hfill \\ & ={ϵ}_{d{H}^{*}(Y;R)}\left(\left[y\right]\right),\hfill \end{array}\end{array}$$

(91)

as required.

Let $A:=(A,{\phi }_A,{ϵ}_A)$, $B:=(B,{\phi }_B,{ϵ}_B)$ and $C:=(C,{\phi }_C,{ϵ}_C)$ be coalgebras over a commutative ring R with identity $1_R$. If

$$\begin{array}{c}\hfill h_1:A\to B\end{array}$$

(92)

and

$$\begin{array}{c}\hfill h_2:B\to C\end{array}$$

(93)

are R-coalgebra homomorphisms, then it can be shown that

$$\begin{array}{c}\hfill h_2\circ h_1:A\to C\end{array}$$

(94)

is also an R-coalgebra homomorphism. Therefore, we can consider the category $Coal{g}_R$ of R-coalgebras and R-coalgebra homomorphisms of R-coalgebras; that is, the class of objects of the category $Coal{g}_R$ consists of R-coalgebras and the class of morphisms of $Coal{g}_R$ consists of R-coalgebra homomorphisms of R-coalgebras.

Corollary 1.

For each object class$(X,k_X)$in$\mathcal{D}$, the assignment

$$\begin{array}{c}\hfill E:\mathcal{D}\to Coal{g}_R\end{array}$$

(95)

given by

$$\begin{array}{c}\hfill (X,k_X)\mapsto (d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})\end{array}$$

(96)

is a contravariant functor.

Proof. 

Let $f:(X,k_X)\to (Y,k_Y)$ be any $(k_X,k_Y)$-continuous function. Then, by applying the contravariant functor

$$\begin{array}{c}\hfill d{H}^{*}(-,R):\mathcal{D}\to Mo{d}_R,\end{array}$$

(97)

we have an R-module homomorphism [39] [Theorem 1]

$$\begin{array}{c}\hfill d{H}^{*}(f;R)=f^{*}:d{H}^{*}(Y;R)\to d{H}^{*}(X;R).\end{array}$$

(98)

Let

$$\begin{array}{c}\hfill F:Mo{d}_R\to Coal{g}_R\end{array}$$

(99)

be the covariant functor assigning to each unitary R-module $d{H}^{*}(X;R)$ the R-coalgebra $(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})$. Then, by using Theorems 1 and 2, we have an R-coalgebra homomorphism

$$\begin{array}{c}\hfill f^{*}=F\left(f^{*}\right):F\left(d{H}^{*}(Y;R)\right)\to F\left(d{H}^{*}(X;R)\right)\end{array}$$

(100)

by putting the R-coalgebra comultiplications and the R-coalgebra counits into the digital cohomology modules (with the same notation $f^{*}=F\left(f^{*}\right)$), where

$$\begin{array}{c}\hfill F\left(d{H}^{*}(Y;R)\right)=(d{H}^{*}(Y;R),{\phi }_{d{H}^{*}(Y;R)},{ϵ}_{d{H}^{*}(Y;R)})\end{array}$$

(101)

and

$$\begin{array}{c}\hfill F\left(d{H}^{*}(X;R)\right)=(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)}).\end{array}$$

(102)

Therefore, it can be shown that, if

$$\begin{array}{c}\hfill 1_X:(X,k_X)\to (X,k_X)\end{array}$$

(103)

is the identity function on any digital image $(X,k_X)$, and if

$$\begin{array}{c}\hfill f:(X,k_X)\to (Y,k_Y)\end{array}$$

(104)

and

$$\begin{array}{c}\hfill g:(Y,k_Y)\to (Z,k_Z)\end{array}$$

(105)

are morphism classes in $\mathcal{D}$; that is, $(k_X,k_Y)$-continuous and $(k_Y,k_Z)$-continuous functions, respectively, then we have

$$\begin{array}{c}\hfill E\left(1_X\right)=1_{(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})}\end{array}$$

(106)

which is the identity morphism on $(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})$ as the unique morphism class of $Coal{g}_R$, and

$$\begin{array}{c}\hfill E(g\circ f)=E\left(f\right)\circ E\left(g\right):(d{H}^{*}(Z;R),{\phi }_{d{H}^{*}(Z;R)},{ϵ}_{d{H}^{*}(Z;R)})\to (d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)}),\end{array}$$

(107)

as required. □

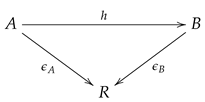
Remark 5.

Let

$$\begin{array}{c}\hfill F:Mo{d}_R\to Coal{g}_R\end{array}$$

(108)

be the covariant functor assigning to each unitary R-module$d{H}^{*}(X;R)$the R-coalgebra$(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})$as described in the proof of Corollary 1, and let

$$\begin{array}{c}\hfill G:Coal{g}_R\to Mo{d}_R\end{array}$$

(109)

be the forgetful functor, which assigns to each R-coalgebra$(d{H}^{*}(X;R),{\phi }_{d{H}^{*}(X;R)},{ϵ}_{d{H}^{*}(X;R)})$its underlying unitary R-module$d{H}^{*}(X;R)$(forgetting the R-coalgebra comultiplication and the R-coalgebra counit). Then, it can be shown that the following triangle

(110)

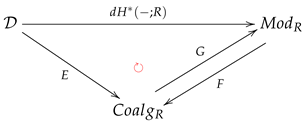is commutative as natural transformations; that is,

• $E=F\circ d{H}^{*}(-;R)$;
• $G\circ E=d{H}^{*}(-;R)$; and
• $G\circ F=1_{Mo{d}_R}$

of (covariant or contravariant) functors.

4. Conclusions and Applications

In applied mathematics or computer science, digital topology deals with features and properties of digital images in ${\mathbb{Z}}^n$, especially, the two-dimensional or three-dimensional digital images corresponding to the topological features and properties of object classes. In mathematics, coalgebras have the structures that are dual to unital associative algebras in the sense of category theory by reversing objects and arrows as objects classes and morphism classes, respectively.

In this paper, we have investigated some fundamental properties of the coalgebras, coalgebra comultiplications, counits, and coalgebra homomorphisms of coalgebras based on digital images with some adjacency relations. We have explored the functorial properties as one of the digital counterparts to classical cohomology theory originated from the algebraic invariants and their important properties of cohomology modules in classical cohomology theory. We have also developed the relationship between the category of digital images and digital continuous functions, the category of digital cohomology R-modules and R-module homomorphisms of digital cohomology R-modules, and the category of R-coalgebras and R-coalgebra homomorphisms induced by the digital continuous functions.

We have also constructed an R-module homomorphism $\phi :d{H}^{*}(X;R)\to d{H}^{*}(X;R){\otimes }_{R}d{H}^{*}(X;R)$ of digital cohomology modules based on a $k_X$-connected digital image $(X,k_X)$ as an R-coalgebra comultiplication to give $d{H}^{*}(X;R)$ the R-coalgebra structure on it. We do hope that our results will be applied to the world of Lie algebras and rational homotopy theory to develop the Lie algebra comultiplications based on graded vector spaces.