The G-Convexity and the G-Centroids of Composite Graphs

Abstract

The graph centroids defined through a topological property of a graph called g-convexity found its application in various fields. They have classified under the “facility location” problem. However, the g-centroid location for an arbitrary graph is $\mathcal{NP}$-hard. Thus, it is necessary to devise an approximation algorithm for general graphs and polynomial-time algorithms for some special classes of graphs. In this paper, we study the relationship between the g-centroids of composite graphs and their factors under various well-known graph operations such as graph Joins, Cartesian products, Prism, and the Corona. For the join of two graphs $G_1$ and $G_2$, the weight sequence of the composite graph does not depend on the weight sequences of its factors; rather it depends on the incident pattern of the maximum cliques of $G_1$ and $G_2$. We also characterize the structure of the g-centroid under various cases. For the Cartesian product of $G_1$ and $G_2$ and the prism of a graph, we establish the relationship between the g-centroid of a composite graph and its factors. Our results will facilitate the academic community to focus on the factor graphs while designing an approximate algorithm for a composite graph.

1. Introduction

Graph theory is a branch of mathematics that has applications in every other field including Arts, Humanities, Sociology, Anthropology, and Engineering. Whenever there is a pairwise relation existing among any entities, graphs are then used to model the system. This paper deals with finding a central structure. The problem of finding a central structure is an active research area. They are classified under facility location problems. Using discrete mathematical models, centrality can be defined in several different ways. One of them is using the eccentricity of vertices. This concept uses the traditional Euclidean distance metric applied to the underlying graph. Centrality can also be defined through the topological properties of graphs. This paper deals with geodesic-convexity (g-convexity for short). g-convexity in graphs have been studied by several different authors. A good review is presented in our earlier paper [1]. In [1], we define the g-convex weight sequences for graphs based on g-convexity and provided characterization for certain classes of graphs including trees.

A central structure called the g-centroid is defined through g-convexity. In another paper [2], the author demonstrated an application of g-convexity and g-centroids in Mobile Ad hoc Networks (MANET). They also find applications in other areas, including measuring dissimilarities in dynamical systems and dynamic search in graphs. In [3], Prakash constituted a first to a systematic study on the size of convex sets in graphs. Due to its application, the location of g-centroid for any arbitrary graphs as well as its characterization had gained importance. In [4], we have demonstrated that the g-centroid location problem is $\mathcal{NP}$-hard for disconnected graphs. In a later paper [2], Prakash closed the gap by proving $\mathcal{NP}$-hardness for connected graphs.

As there are no tractable solutions available to locate the g-centroid for arbitrary graphs, it is essential to design an approximate solution for the location problem. A graph is defined as a composite graph if it can be obtained from two or more graphs through well-defined graph operations. Currently, there is no work available in the literature that analyze the relation between the structure of the g-centroid of a graph and its factors. In this paper, we study the structure of g-centroid and the g-convex weight sequences (gcws) of composite graphs through some popular graph operations such as graph-joins, cartesian products, and corona. Through the derived properties, we may able to design efficient approximate algorithms to locate the g-centroid for composite graphs in the future.

In this paper, we make the following contributions.

• We present an application of g-convexity and g-centroids in MANET. This forms a strong motivation. We then present an overview of the $\mathcal{NP}$-hardness proof for the g-centroid location for arbitrary graphs.
• For the join of two graphs $G_1$ and $G_2$, the weight sequence of the composite graph does not depend on the weight sequences of its factors; rather it depends on the incident pattern of the maximum cliques of $G_1$ and $G_2$. We also characterize the structure of the g-centroid under various cases.
• For the Cartesian product of $G_1$ and $G_2$ and the prism of a graph, we establish the relationship between the composite graph and its factors.
• For Corona operations, we characterize the g-centroid based on its factors.

The rest of the paper is organized as follows.

In Section 2, we present preliminary definitions that are necessary for this paper. We also outline the $\mathcal{NP}$-hardness algorithm for the g-centroid location problem. In Section 3, we present our main results. We consider three important types of graph operations in this paper. They are Graph Joins, Cartesian Products, and Corona. As a special case of Cartesian products, we considered the prism of a graph. Section 4 deals with the Conclusion and Future direction. In this section, we present two important open problems.

2. Definitions and Preliminary Results

In this section, we present some of the important definitions that are needed to understand the rest of this paper. Standard graph-theoretic definitions that are not given here; the reader may refer to the work in [5]. We now present a recent application of the g-convexity. A Mobile Ad hoc Network (MANET) is a decentralized type of wireless network. It is ad hoc in nature because it does not rely on any preexisting infrastructure such as an Access Point (AP) or a router to route packets from a source to a destination node. The network is formed in fly and mobile nodes may join and leave the network as they wish. Thus, there is no admission or access control mechanism in a MANET. Due to this nature, MANETs are deployed during emergency response operations. Wireless nodes that are within each other’s radio range communicate directly like a point-to-point network. There is no switch to facilitate communication as a wired network. Nodes that are not within the radio range of each other can still communicate, provided that intermediate nodes act as a router to rely on their packets. Thus, the network is formed through cooperation from all other nodes in the network. Due to this cooperative process, nodes lose their energy on forwarding packets on behalf of other nodes. This is in addition to their transmission and reception. A mobile node spends more than 60% of its power on transmission and reception compared with its internal processing. Thus, energy conservation is one of the important problems in MANET. Therefore, every node needs to know how many pairs of nodes that require its help in forwarding a data packet. Several routing protocols designed for MANET uses some form of the shortest path algorithm to forward packets between a pair of nodes. Thus, if a mobile node z lies in the shortest path between two other nodes u and v, then z is expected to route packets for u and v.

The following is one of the important problems in MANETs.

For a mobile node u, locating the maximum set S of nodes that can communicate with each other without the help of u.

WiFi interface is known to be a primary energy consumption in mobile devices. The “idle listening” consumes more energy compared with transmission or reception. It is estimated that about 60% of the energy is wasted in idle listening. The only solution for reducing idle listening is to implement a sleep schedule. Thus, intuitively whenever the nodes in S are communicating, u can go to sleep mode to conserve its battery power from idle listening.

MANET can be modeled as a simple undirected graph. An edge between the mobile hosts u and v indicates that both u and v are within their radio ranges. To simplify our discussion, we assume that if u is within the transmission range of v, then v will be in the transmission range of u (i.e., the relation between the nodes are symmetric. This may not be true in general due to different factors like the transmission power of a node, geographical conditions, etc.; thus, the resulting graph is a directed graph). Thus, the resulting graph is undirected.

We formally define the g-convexity and various parameters that are defined through the g-convexity.

Definition 1.

A set $S\subseteq V$ is geodetic convex (g-convex for short) if for every pair of vertices $u,v\in S$, all vertices on any $u-v$ shortest path (also called a geodesic path) belong to S.

From the above definition, it easily follows that a singleton set, vertex pair of an edge, and the whole vertex set $V\left(G\right)$ are g-convex sets of G. We call them as trivial g-convex sets. Moreover, if S is a clique (S induces a complete subgraph of G), then S is a g-convex set of G.

A convex set is a set of vertices which is “closed” for the flow of information (routing, control, or data packets). This is in line with Mulder’s treatment of Interval functions in a graph [6]. For a connected graph G and two vertices u and v of G, the interval function $I(u,v)$ is defined as follows; $I(u,v)$ = {z:z lies on any $u-v$ geodesic path in G}. In our application terminology, $I(u,v)$ contains the set of all vertices that may be involved in communication between u and v. Based on his definition, a set $S\subseteq V\left(G\right)$ is g-convex if and only if $I(u,v)\subseteq S$ for every pair $u,v\in S$.

We define the cardinality of the maximum g-convex set not containing u as the g-weight of u, denoted by $w\left(u\right)$. We then turn our attention to the set of nodes having the least weight. Intuitively, these nodes participate in more routes than others. We now formally define these parameters:

Definition 2.

Let G = (V,E) be any connected graph. For $v\in V$, the g-weight $w\left(v\right)$ = max{$\mid S\mid$: S is a g-convex set of G not containing v}. Let $gc\left(G\right)$ = min{$w\left(v\right)$: $v\in V$}. Then $gc\left(G\right)$ is called the g-centroidal number of G and the vertices v for which $w\left(v\right)$ = $gc\left(G\right)$ are called the g-centroidal vertices. The g-centroid $C_g\left(G\right)$ is the set of all g-centroidal vertices of G (i.e., g-centroid is a set of vertices which satisfies the min-max relation).

For $v\in V\left(G\right)$, we denote by $S_v=S_v\left(G\right)$, any maximum g-convex set of G not containing v.

If the context is clear, we may call g-convexity and g-centroid by simply convexity and centroid.

Let G = (V, E) be a connected graph and $u\in V\left(G\right)$. Then, the eccentricity $e\left(u\right)$ is defined as $e\left(u\right)$ = max {$d(u,v):v\in V\left(G\right)\}$.

2.1. The G-Centroid Location Problem for Arbirtary Connected Graphs

The g-centroid location has several practical applications. One such application domain is MANET. It also has an application in measuring dissimilarities and information retrieval [5]. Due to its practical applications, it is thus necessary to devise an efficient algorithm to locate the g-centroid for an arbitrary graph. In this subsection, we outline the $\mathcal{NP}$-hardness of the g-centroid location algorithm. For the detailed proof, the readers may refer to our original paper [2].

If the context is clear, in what follows, by the term graph we always mean a connected graph.

The following proposition specifies the structure of a g-centroid and its convexity.

Proposition 1.

For any connected graph G, $C_g\left(G\right)$ is a g-convex set of G and $<C_g\left(G\right)>$ is connected.

Based on this proposition, we have the following results.

Proposition 2.

For a connected graph G, $C_g\left(G\right)$ lies in a block of G.

We now define the k-th neighborhood of a vertex u.

Let G = (V,E) be a connected graph and $u\in V\left(G\right)$. The k-th neighborhood of u, denoted by $N_k\left(u\right)$ consists of all vertices in G that are at a distance k from u, i.e., $N_k\left(u\right)$ = {$v\in V$: $d(u,v)=k$}.

The next result is obvious from the definition of the k-th neighborhood of a vertex and its maximal g-convex set realizing its weight.

Proposition 3.

Let G be a connected graph and u be a vertex of G. If $x,y\in N_k\left(u\right)\cap S_u$, then $d(x,y)<2k$.

The following corollary is immediate from Proposition 3.

Corollary 1.

Let $G=(V,E)$ be a connected graph. For every vertex u in G, $N_1\left(u\right)\cap S_u$ is either empty or induces a complete subgraph of G.

Note that for a vertex u of G, $N_1\left(u\right)\cap S_u$ may be empty. As a nice open problem it will be interesting to classify all graphs for which $N_1\left(u\right)\cap S_u\ne \varnothing$, for every vertex u and any arbitrary $S_u$. One such class is a tree.

We now outline the $\mathcal{NP}$-hardness of the g-centroid location algorithm. The proof is by polynomially reducing the “clique decision” problem to the g-centroid location problem. However, we could not establish the membership of the g-centroid location problem in $\mathcal{NP}$-class to establish the $\mathcal{NP}$-completeness. g-convexity is closely related to the clique incident pattern of the graph.

We recall the definition of the “clique decision problem”:

Given a connected graph G and an integer r with $2\le r\le n=\mid V\left(G\right)\mid$, does G has a clique of size r?

The clique decision problem is one of the classical $\mathcal{NP}$-complete problem in graph theory. Several graph-theoretic and optimization problems were proved to be $\mathcal{NP}$-complete or $\mathcal{NP}$-hard by reducing to the clique decision problem [7].

Definition 3.

For a given connected graph G and an integer r with $2\le r\le n$, we construct the graph $G_r$ from a copy of G, $K_{r-1}$ (the complete graph on $r-1$ vertices) and three new vertices a, b, and c as follows.

• $V\left(G_r\right)$ = $V\left(G\right)\cup \{a,b,c\}\cup V\left(K_{r-1}\right)$
• The edge set of $G_r$ consists of all the edges of G, $K_{r-1}$, and the following new edges.

  -

  Join a and b to all the vertices of G.

  -

  Join c to a and b and to some arbitrary vertex d of $K_{r-1}$.

For a given graph G, the graph $G_r$ will look as in Figure 1. Furthermore, it is easy to see that for a given graph G and a r, $2\le r\le n$, $G_r$ can be constructed in polynomial time. We explain this polynomial-time construction now:

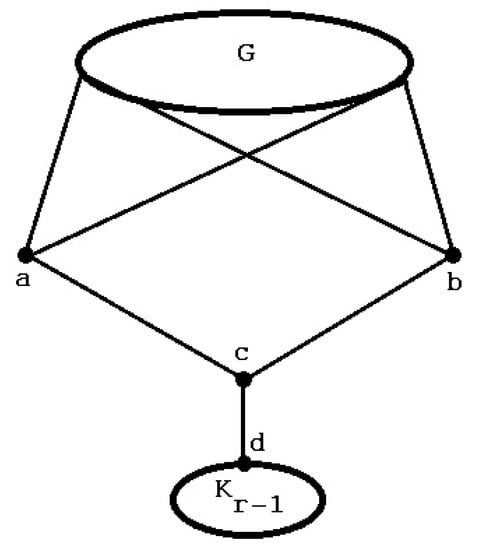
Figure 1. $G_r$ for a given graph G.

We may assume that the graph is stored as an “adjacency matrix”. To obtain $V\left(G_r\right)$, we need to add $r-1$ vertices that corresponds to $K_{r-1}$ and the three new vertices a, b, and c. This is done by adding $r+2$ rows and columns to the “adjacency matrix”. Creating adjacency entries that represents $K_{r-1}$ takes $O\left(r^2\right)$ time. Joining a to all the vertices of G is obtained by setting 1 for all columns that correspond to the vertices of G. This can be done in linear time. Similarly, joining b to all vertices of G can be done in linear time. Joining c to a and b and to some arbitrary vertex d of $K_{r-1}$ can be done in a constant time. Thus, the entire construction of $G_r$ from G takes polynomial time.

For an arbitrary connected graph G, we now analyze the structure of the g-centroid of $G_r$ for various values of r.

In what follows in this section, if the context is clear, we assume that the graph under consideration is $G_r$.

The following facts can easily be established.

Proposition 4.

Let G be a connected graph and $G_r$ be defined as in Definition 3. Let x be a vertex in the copy of $K_{r-1}$ of $G_r$, then $w\left(x\right)=\mid V\left(G_r\right)\mid -1=r+\mid V\left(G\right)\mid +1$.

The proof follows from the fact that $N_1\left(x\right)$ is complete and therefore $S_x=V\left(G_r\right)-\left\{x\right\}$.

Proposition 5.

Let G be a connected graph and $G_r$ be defined as in Definition 3. $w\left(d\right)=\mid V\left(G\right)\mid +3$.

The next proposition specifies the weight of the two vertices a and b based on the maximum clique size of G.

Proposition 6.

Let G be a connected graph and $G_r$ be defined as in Definition 3. $w\left(a\right)=w\left(b\right)=max\{w+1,r+1\}$, where $\omega \left(G\right)=w$ is the maximum clique size of G.

The following proposition determines the weight of the vertex c based on the chosen r and the maximum clique size of G.

Proposition 7.

Let G be a connected graph and $G_r$ be defined as in Definition 3. $w\left(c\right)$ = max {$w+1$, $r-1$}, where $w=\omega \left(G\right)$.

We now determine the weight of every vertex $u\in V\left(G\right)$. The weight of these vertices depends on the maximum clique incident pattern of G and the chosen r.

Proposition 8.

Let G be a connected graph and $G_r$ be defined as in Definition 3. Let $M_1,M_2,\cdots ,M_s$ be the maximum cliques of G, $M={\cap }_{i=1}^s{M}_i$, and $w=\omega \left(G\right)$. Then, the following hold.

• If $M=\varnothing$, then for every $u\in V\left(G\right)$, $w\left(u\right)$ = max {$w+1$,$r+1$}.
• If $M\ne \varnothing$, then for every $u\in M$, $w\left(u\right)$ = max {w,$r+1$}. For every $v\in V\left(G\right)-M$, $w\left(v\right)$ = max {$w+1$,$r+1$}.

From the above propositions, for a given connected graph G and an integer r with $2\le r\le \mid V\left(G\right)\mid$, we can find the weight of every vertex of $G_r$.

The following proposition analyze the structure of $C_g\left(G_r\right)$ for various values of r.

Proposition 9.

Let G be an arbitrary graph with the maximum clique size $\omega \left(G\right)$ = w. Let r be an integer such that $2\le r\le w-1$. Let $G_r$ be defined as in Definition 3. Then, the g-centroid of $G_r$, $C_g\left(G_r\right)$= $V\left(G\right)\cup \{a,b,c\}$ or M, depending upon whether the intersection of all the maximum cliques of G denoted by M is empty or not.

The following two propositions relate the chosen r and the maximum clique size of G.

Proposition 10.

Let G be a connected graph with the maximum clique size $\omega \left(G\right)$ = w and $G_r$ be defined as in Definition 3. Let $r\ge w+1$. Then, $C_g\left(G_r\right)$ = {c}.

Proposition 11.

Let G be a connected graph with the maximum clique size $\omega \left(G\right)$ = w and $G_r$ be defined as in Definition 3. Let $r=w$. Then, $C_g\left(G_r\right)$ = $V\left(G\right)\cup \{a,b,c\}$, irrespective of whether M is empty or not.

Combining all the results for $G_r$, we have the following theorem.

Theorem 1.

Let G be any connected graph and r be an integer such that $2\le r\le n=\mid V\left(G\right)\mid$. Let $G_r$ be defined as in Definition 3. Let $\omega \left(G\right)=w$ be the maximum clique size of G. If $r<w$, then $C_g\left(G_r\right)$ = M or $V\left(G\right)\cup \{a,b,c\}$ depending upon whether the intersection of all the maximum cliques of G denoted by M is non-empty or not. If $r=w$, $C_g\left(G_r\right)$ = $V\left(G\right)\cup \{a,b,c\}$, $r\ge w+1$, $C_g\left(G_r\right)$ = {c} irrespective of whether M is empty or not.

Based on Theorem 1, we can address the clique decision problem in polynomial time.

If $k\le \omega \left(G\right)-1$, then the g-centroid of $G_k$ is either $V\left(G\right)\cup \{a,b,c\}$ or M depending upon whether the intersection of all the maximum clique of G is empty of not. For $k=\omega \left(G\right)$, the g-centroid $C_g\left(G_k\right)$ = $V\left(G\right)\cup \{a,b,c\}$. For $k\ge \omega \left(G\right)+1$, $C_g\left(G_k\right)=\left\{c\right\}$. Thus, G has a clique of size k if and only if $C_g\left(G_k\right)=V\left(G\right)\cup \{a,b,c\}$ or M.

3. Graph Compositions

In Section 2.1 we outlined the $\mathcal{NP}$-hardness for a g-centroid location algorithm. It will be worth focusing on designing efficient approximation algorithms for the g-centroid location for a general graph or provide a polynomial-time algorithm for the g-centroid location for graphs with some special structure (such as chordal, interval, or unit disc graph). In this section, we analyze the structure of the g-centroid of composite graphs under some well-known graph operations. We now formally present some of the definitions of well-known graph operations:

Definition 4.

Let $G_1$ = ($V_1$, $E_1$) and $G_2$ = ($V_2$, $E_2$) be two graphs. Their join denoted by G = $G_1\vee G_2$ has the vertex set V = $V_1\cup V_2$ and the edge set E = $E_1\cup E_2\cup$ {$uv$: $u\in V_1,v\in V_2$}.

The Cartesian product G = $G_1\otimes G_2$ has the vertex set V = $V_1\times V_2$ and the edge set E is defined as follows; ($u_1$, $u_2$) and ($v_1$, $v_2$) are adjacent in G if and only if either $u_1$ = $v_1$ and $u_2{v}_2\in E\left(G_2\right)$ or $u_1{v}_1\in E\left(G_1\right)$ and $u_2$ = $v_2$.

As a special case of the cartesian product, we have the prism of a graph. The prism of a graph $G_1$ is G = $G_1\otimes K_2$, where $K_2$ is a complete graph on two vertices.

The corona of two graphs $G_1$ and $G_2$ of order $n_1$ and $n_2$ (where $n_1$ = $\mid V\left(G_1\right)\mid$ and $n_2$ = $\mid V\left(G_2\right)\mid$), denoted by G = $G_1\circ G_2$ is the graph obtained by taking one copy of $G_1$ and $n_1$ copies of $G_2$ and joining the i-th copy of $G_2$ to the i-th vertex of $G_1$, $1\le i\le n_1$.

Remark 1.

If G is a composition of $G_1$, $G_2$, ⋯, $G_r$, then we say that G is a composite graph and $G_1$, $G_2$, ⋯, $G_r$ are its factors.

We now analyze the g-centroids and gcws for composite graphs under the above-defined graph operations.

3.1. The Join of Graphs

In this subsection, we show that the weight sequence of G = $G_1\vee G_2$ does not depend on the weight sequence of $G_1$ and $G_2$, rather it depends on the incident pattern of the maximum cliques of $G_1$ and $G_2$.

If $G_1$ and $G_2$ are either complete or if both are incomplete, we give the weight sequence of G explicitly. If $G_1$ is complete and $G_2$ is incomplete, it is shown that for each $u\in V\left(G_2\right)$, $S_u\left(G\right)$ = $K\cup V\left(G_1\right)$, where K is a maximum g-convex set of $G_2$ not containing u.

The following Proposition is immediate from the definition of join of graphs.

Proposition 12.

Let $G_1$ and $G_2$ be two graphs and G = $G_1\vee G_2$. Then, the following holds.

• G has an induced subgraph isomorphic to $G_1$ as well as to $G_2$.
• G is complete if and only if both $G_1$ and $G_2$ are complete.

If both $G_1$ and $G_2$ are complete, then G is a complete graph on n = $\mid V\left(G_1\right)\mid$ + $\mid V\left(G_2\right)\mid$ vertices and the weight sequence of G is {${(n-1)}^n$} and $C_g\left(G\right)$ = $V\left(G\right)$.

Now consider the case when $G_1$ and $G_2$ are incomplete. The following proposition determines the structure of a g-convex sets when both $G_1$ and $G_2$ are incomplete.

Proposition 13.

Let $G_1$ and $G_2$ be two incomplete graphs and G = $G_1\vee G_2$. Then a proper subset S of $V\left(G\right)$ is a g-convex set of G if and only if $<S>$ is a complete subgraph of G.

Proof. 

Let S be a proper g-convex set of V. If possible, let u and v be two non adjacent vertices of G in S. From the construction of G, both u and v belong to either $G_1$ or $G_2$. Let u and v belong to $G_1$. Let z be any vertex of $G_2$. Then u,z,v is a geodesic joining u and v in G. As S is convex, $z\in S$. Thus $V\left(G_2\right)\subseteq S$ as z is arbitrary. As $G_2$ is incomplete, $G_2$ has a pair of non-adjacent vertices. Therefore by a similar argument, $V\left(G_1\right)\subseteq S$. Hence S = $V\left(G\right)$, which is a contradiction.

Proof of the sufficiency part follows trivially as cliques are always g-convex sets of G. □

Remark 2.

If M and N are the maximum cliques of $G_1$ and $G_2$, respectively, then $M\cup N$ is a maximum clique of G.

We now characterize the g-convex sequences of graph joins based on the incident pattern of the maximum cliques of their factor graphs.

Proposition 14.

Let $G_1$ and $G_2$ be two incomplete graphs and G = $G_1\vee G_2$. Let $M_1$, $M_2$, ⋯, $M_r$ and $N_1$, $N_2$, ⋯, $N_s$ be the maximum cliques of $G_1$ and $G_2$, respectively, of sizes ${\omega }_1$ and ${\omega }_2$. Let M = ${\cap }_{j=1}^r{M}_j$, N = ${\cap }_{j=1}^s{N}_j$, n = $\mid V\left(G\right)\mid$, $m_1$ = $\mid M\mid$ and $m_2$ = $\mid N\mid$.

• If $M\ne \varnothing$ and $N\ne \varnothing$, then the gcws of G is {${({\omega }_1+{\omega }_2-1)}^{m_1+m_2}$,${({\omega }_1+{\omega }_2)}^{n-(m_1+m_2)}$}
• If $M\ne \varnothing$ and $N=\varnothing$, then the gcws of G is {${({\omega }_1+{\omega }_2-1)}^{m_1}$, ${({\omega }_1+{\omega }_2)}^{n-m_1}$}
• If M and N are empty, then the gcws of G is {${({\omega }_1+{\omega }_2)}^n$}.

Let u be a vertex of G. Then, by Proposition 13, $S_u$ induces a complete subgraph of G.

(1) Let M,$N\ne \varnothing$. Let $x\in V\left(G_1\right)$ and $x\notin M$. Then there exists an i, $1\le i\le r$ such that $x\notin M_i$. Therefore $M_i\cup N_j$ ($1\le j\le s$) are maximum g-convex sets of G not containing x (as they are complete). Thus, $w\left(x\right)$ = ${\omega }_1+{\omega }_2$. Similarly, $w\left(x\right)$ = ${\omega }_1+{\omega }_2$ also if $x\in V\left(G_2\right)$ and $x\notin N$. If $x\in M$, then $(M_i-x)\cup N_j$, $1\le i\le r$ and $1\le j\le s$ are maximum g-convex sets of G not containing x, of cardinality ${\omega }_1+{\omega }_2-1$. Similarly if $x\in N$, then $w\left(x\right)$ = ${\omega }_1+{\omega }_2-1$. Therefore, the gcws of G is {${({\omega }_1+{\omega }_2-1)}^{m_1+m_2}$,${({\omega }_1+{\omega }_2)}^{n-(m_1+m_2)}$}.

Proofs of (2) and (3) are similar to the proof given above.

We now give the structure of $C_g\left(G\right)$ under the above cases. If the first case of Proposition 14 is arises, then $C_g\left(G\right)$ = $M\cup N$ and hence $C_g\left(G\right)$ is a clique of G. In the second case, $C_g\left(G\right)$ is either M or N depending upon whether N or M is empty. Thus in this case also $C_g\left(G\right)$ is a clique. In the third case, G is self centroidal. Thus, the following corollary is obvious.

Corollary 2.

If $G_1$ and $G_2$ are incomplete graphs and G = $G_1\vee G_2$, then $C_g\left(G\right)$ is either a clique of G or the entire vertex set of G.

We now discuss the case when $G_1$ is complete and $G_2$ is incomplete. Here, we show that $S_u\left(G\right)=K\cup V\left(G_1\right)$, where K is a maximum g-convex set in $G_2$ not containing u.

Proposition 15.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. Let $u\in V\left(G_1\right)$. Then $S_u\left(G\right)$ induces a complete subgraph of G.

The proof follows as in Proposition 13.

Proposition 16.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. Let $u\in V\left(G_2\right)$. Then $S_u\left(G\right)$ = $K\cup V\left(G_1\right)$, where K is a maximum g-convex set in $G_2$ not containing u.

Proof. 

Let $K^{\prime }$ be a maximum g-convex set of $G_2$ not containing u. We show that S = $V\left(G_1\right)\cup K^{\prime }$ is a g-convex set of G not containing u. Let x,y be a pair of non-adjacent vertices in S. Then, by our definition of G, x,$y\in K^{\prime }$. If $d_{G_2}(x,y)\ge 3$, then for any $z\in V\left(G_1\right)$, x,z,y is a geodesic joining x and y in G. Thus, in this case all $x-y$ geodesics lie in $<S>$ as $V\left(G_1\right)\subseteq S$. Suppose that $d_{G_2}(x,y)$ = 2. Let x,z,y be any $x-y$ geodesic in G. If $z\in V\left(G_1\right)$, then $z\in S$ as $V\left(G_1\right)\subseteq S$ otherwise $z\in K^{\prime }$, as $K^{\prime }$ is a g-convex set in $G_2$. Thus, in this case also, all $x-y$ geodesics lie in $<S>$. Therefore, S is a g-convex set of G. From the definition of g-weight, it follows that $w(u\mid G)\ge \mid S\mid$. To prove the equality, it is enough to show that for any $S_u\left(G\right)$, $S_u\left(G\right)\cap V\left(G_2\right)$ is a g-convex set of $G_2$ not containing u. Let K = $S_u\left(G\right)\cap V\left(G_2\right)$.

First, we show that K is non-empty. If K is empty, then $S_u\left(G\right)\subseteq V\left(G_1\right)$. As $G_2$ is incomplete, $\mid V\left(G_2\right)\mid \ge 3$. Let v be a vertex of $G_2$ different from u. Then S = $V\left(G_1\right)\cup \left\{v\right\}$ is a g-convex set of G, not containing u, properly containing $S_u\left(G\right)$. This is a contradiction.

Next we show that K is a g-convex set of $G_2$. If K is a clique, then K is trivially a g-convex set. Let $x,y\in K$ such that $d_{G_2}(x,y)$ = 2. Let x,z,y be a geodesic joining x and y in $G_2$. From the definition of G, $d_G(x,y)$ = 2 and x,z,y is a geodesic joining x and y in G. By the convexity of $S_u\left(G\right)$, $z\in S_u\left(G\right)$, and thus $z\in K$. Thus K is a g-convex set of $G_2$. □

Next we describe the structure of $C_g\left(G\right)$ when $G_1$ is complete and $G_2$ is incomplete.

Proposition 17.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. $V\left(G_1\right)\subseteq C_g\left(G\right)$.

Proof. 

Let $x\in V\left(G_1\right)$. Then, by Proposition 15, $S_x$ induces a complete subgraph of G. Thus, $w\left(x\right)$ = $n_1-1-\omega \left(G_2\right)$, where $n_1$ = $\mid V\left(G_1\right)\mid$. Let y be any vertex of $G_2$ and M be a maximum clique of $G_2$, not containing y. Then, $M\cup V\left(G_1\right)$ is a g-convex set of G not containing y and $\mid M\cup V\left(G_1\right)\mid$$\ge \omega \left(G_2\right)-1+n_1$ = $w\left(x\right)$. Thus, $w\left(y\right)\ge w\left(x\right)$. Since y is arbitrary, we have $V\left(G_1\right)\subseteq C_g\left(G\right)$. □

Corollary 3.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. Let $N_1$,$N_2$, ⋯, $N_s$ be the maximum cliques of $G_2$ and N = ${\cap }_{j=1}^s{N}_j$. If $N=\varnothing$, then $C_g\left(G\right)$ = $V\left(G_1\right)$.

Proof. 

If $x\in V\left(G_1\right)$, then by the proof of the above Proposition, $w\left(x\right)$ = $n_1+\omega \left(G_2\right)-1$. Let $y\in V\left(G_2\right)$. Since $N=\varnothing$, there exists an i, $1\le i\le s$ such that $y\notin N_i$. Then, $N_i\cup V\left(G_1\right)$ is a g-convex set of G not containing y with cardinality $\omega \left(G_2\right)+n_1$. Thus, $w\left(y\right)>w\left(x\right)$, and therefore $C_g\left(G\right)=V\left(G_1\right)$. □

Next, we describe the structure of $C_g\left(G\right)$ under this case.

Proposition 18.

Let G = $G_1\vee G_2$ with $G_1$ complete and $G_2$ incomplete. Then $C_g\left(G\right)$ induces a complete subgraph of G.

Proof. 

From Proposition 17, $V\left(G_1\right)\subseteq C_g\left(G\right)$. If $V\left(G_1\right)$ = $C_g\left(G\right)$, then $<C_g\left(G\right)>$ is complete. If $\mid C_g\left(G\right)\cap V\left(G_2\right)\mid$ = 1, then also $<C_g\left(G\right)>$ is complete. Let $\mid A=C_g\left(G\right)\cap V\left(G_2\right)\mid \ge 2$. Let $u,v\in A$. We now show that $uv\in E\left(G\right)$. As $w\left(x\right)$ = $\omega \left(G_2\right)+n_1-1$, for each vertex x of $G_1$, we have $w\left(u\right)$ = $w\left(v\right)$ = $\omega \left(G_2\right)+n_1-1$ (as $V\left(G_1\right)\subseteq C_g\left(G\right)$). If M is any maximum clique of $G_2$, then $u,v\in M$ (otherwise, $M\cup V\left(G_1\right)$ is a g-convex set of G not containing them of cardinality $\omega \left(G_2\right)+n_1$). As M is a clique, $uv\in E\left(G_2\right)$, and hence u and v are adjacent in G also. This proves that $<C_g\left(G\right)>$ is complete. □

The proof for the following corollary is immediate from Proposition 18.

Corollary 4.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. Let $N_1$,$N_2$, ⋯, $N_s$ be the maximum cliques of $G_2$. If $C_g\left(G\right)\cap V\left(G_2\right)\ne \varnothing$, then $C_g\left(G\right)\cap V\left(G_2\right)\subseteq {\cap }_{i=1}^s{N}_i$.

The containment can be proper. This is demonstrated in Figure 2.

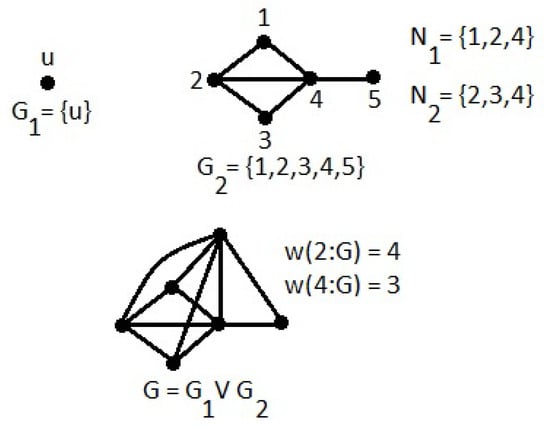
Figure 2. The proper containment: $C_g\left(G\right)\cap V\left(G_2\right)\subset {\cap }_{i=1}^s{N}_i$.

Proposition 19.

Let $G_1$ be a complete graph and $G_2$ be an incomplete graph and G = $G_1\vee G_2$. If $u\in C_g\left(G\right)\cap V\left(G_2\right)$, then $e_{G_2}\left(u\right)\le 3$.

Proof. 

From the above corollary, $u\in {\cap }_{i=1}^s{N}_i$. Thus all the maximum cliques of $G_2$ are contained in $N_{G_2}\left[u\right]$. Suppose that $e_{G_2}\left(u\right)\ge 4$. Let $x\in N_4(u:G_2)$. Then $(N_i-u)\cup \left\{x\right\}\cup V\left(G_1\right)$ is a convex set of G (as any $x-y$ geodesic path passes through only vertices from $V\left(G_1\right)\forall y\in (N_i-x)$), $x-y$ geodesic contains vertices only from $V\left(G_1\right)$ with cardinality $\omega \left(G_2\right)+n_1$. This is a contradiction. This proves that $e_{G_2}\left(u\right)\le 3$. □

3.2. Cartesian Product

In this section, we deal with the gcws of the cartesian product of two graphs. First, we prove that $S\subseteq V$ is a g-convex set in $G=G_1\otimes G_2$ if and only if $S=S_1\times S_2$, where $S_1$ and $S_2$ are g-convex sets of $G_1$ and $G_2$, respectively.

Proposition 20.

Let $G_1$ and $G_2$ be two connected graphs. Let G = $G_1\otimes G_2$. Then, $S\subseteq V\left(G\right)$ is a g-convex set of G iff S = $S_1\times S_2$, where $S_1$ and $S_2$ are g-convex sets of $G_1$ and $G_2$, respectively.

Proof. 

Let S be any g-convex set of G. Let $S_1$ = {u: (u,v) $\in S$} and $S_2$ = {v:(u,v) $\in S$} (i.e., the projection of S on $G_1$ and $G_2$). Then, clearly $S\subseteq S_1\times S_2$. First, we show that S = $S_1\times S_2$. Suppose (u,v) $\in S_1\times S_2$ and (u,v) $\notin S$. As $u\in S_1$ and $v\in S_2$, by the definition of $S_1$ and $S_2$, there exist x,y such that (u,x), (y,v) $\in S$. Let u = $u_1$,$u_2$, ⋯, $u_r=y$ be a $u-y$ geodesic in $G_1$ and $x=x_1$, $x_2$, ⋯, $x_s=v$ be a $x-v$ geodesic in $G_2$. Then $(u,x_1)$, $(u,x_2)$, ⋯, $(u,v=x_s)$, $(u_2,v)$, ⋯, $(u_r=y,v)$ is a geodesic joining $(u,x)$ and $(y,v)$ in G. Since S is convex, $(u,v)\in S$, a contradiction. This proves that $S=S_1\times S_2$.

Our next task is to show that $S_1$ and $S_2$ are convex sets of $G_1$ and $G_2$, respectively. Let $u,y\in S_1$ and u = $u_1$,$u_2$, ⋯, $u_r=y$ be any $u-y$ geodesic in $G_1$. Let x be any arbitrary vertex in $S_2$. Then $(u,x)$, $(v,x)\in S$. Now, $(u_1,x)$, $(u_2,x)$, ⋯, $(u_r,x)$ is a geodesic joining $(u,x)$ and $(y,x)$ in G. Since S is convex, $(u_i,x)\in S$ for $1\le i\le r$, and therefore $u_i\in S_1$. Thus, $S_1$ is a g-convex set of $G_1$. Similarly $S_2$ is a g-convex set of $G_2$.

The proof of the sufficiency part follows trivially. □

Corollary 5.

Let $G_1$ and $G_2$ be two connected graphs. Let G = $G_1\otimes G_2$. Let $S_1$ and $S_2$ be g-convex sets of $G_1$ and $G_2$ respectively, then $S_1\times V\left(G_2\right)$ and $V\left(G_1\right)\times S_2$ are g-convex sets of G.

The proof follows from the above proposition and the fact that $V\left(G_1\right)$ and $V\left(G_2\right)$ are g-convex sets of $G_1$ and $G_2$.

Proposition 21.

Let $G_1$ and $G_2$ be two connected graphs. Let G = $G_1\otimes G_2$. Let $(u,v)\in V\left(G\right)$. Then the weight of $(u,v)$ is

$$w(u,v)=max\{w(u:G_1)\times \mid V\left(G_2\right)\mid ,w(v:G_2)\times \mid V\left(G_1\right)\mid \}$$

Proof. 

Let S be a maximum g-convex set of G not containing $(u,v)$. Then, by Proposition 20, S = $S_1\times S_2$, where $S_1$ and $S_2$ are g-convex sets of $G_1$ and $G_2$, respectively. Since $(u,v)\notin S$, one of the following holds good.

• $u\notin S_1$ and $v\notin S_2$
• $u\in S_1$ and $v\notin S_2$
• $u\notin S_1$ and $v\in S_2$

By the maximality of S, if $u\notin S_1$, then $S_1$ is a maximum g-convex set of $G_1$ not containing u and similarly, if $v\notin S_2$, then $S_2$ is a maximum g-convex set of $G_2$ not containing v. Thus case (1) cannot happen (as $\mid S_u\left(G_1\right)\times V\left(G_2\right)\mid$ $>\mid S_1\times S_2\mid$. In case (2), $S_{(u,v)}$ = $V\left(G_1\right)\times S_v$ and in case (3), $S_{(u,v)}$ = $S_u\times V\left(G_2\right)$. Thus, we have

$$w(u,v)=max\{w(u:G_1)\times \mid V\left(G_2\right)\mid ,w(v:G_2)\times \mid V\left(G_1\right)\mid \}$$

 □

From the Proposition 21, we see that if $w(u:G_1)$ and $w(v:G_2)$ are known, then $w(u,v)$ can be computed.

We now relate the centroid of G to those of $G_1$ and $G_2$. We show that $C_g\left(G_1\right)\times C_g\left(G_2\right)\subseteq C_g\left(G\right)$ and the equality holds if $g_1{n}_2=g_2{n}_1$.

Proposition 22.

Let $G_1$ and $G_2$ be two connected graphs. Let G = $G_1\otimes G_2$. Let $g_1$ = $gc\left(G_1\right)$; $g_2$ = $gc\left(G_2\right)$; $n_1$ = $\mid V\left(G_1\right)\mid$ and $n_2$ = $\mid V\left(G_2\right)\mid$. If $g_1{n}_2$ = $g_2{n}_1$, then $C_g\left(G\right)$ = $C_g\left(G_1\right)\times C_g\left(G_2\right)$.

Proof. 

Let $(u,v)\in C_g\left(G_1\right)\mathrm{x}{C}_g\left(G_2\right)$. From Proposition 21, $w(u,v)$ = max {$g_1{n}_2$,$g_2{n}_1$}. Let $(x,y)\notin V\left(G\right)-C_g\left(G_1\right)\times C_g\left(G_2\right)$. Then, either $x\notin C_g\left(G_1\right)$ or $y\notin C_g\left(G_2\right)$ or both. In the first case $w(x,y)\ge \mid S_x\times V\left(G_2\right)\mid >g_1{n}_2$. (as $\mid S_x\mid >g_1$). Similarly, in all the other cases, we can show that $w(x,y)>w(u,v)$. Therefore, $C_g\left(G\right)$ = $C_g\left(G_1\right)\times C_g\left(G_2\right)$. □

Remark 3.

The converse of this proposition is not true. For, consider G = $K_2\otimes P_3$. Here, $g_1$ = 1, $n_1$ = 2, $g_2$ = 1, and $n_2$ = 3. Clearly $g_1{n}_2\ne g_2{n}_1$ but $C_g\left(G\right)$ = $C_g\left(K_2\right)\times C_g\left(P_3\right)$.

Proposition 23.

Let $G_1$ and $G_2$ be two connected graphs. Let G = $G_1\otimes G_2$. Let $g_1$ = $gc\left(G_1\right)$; $g_2$ = $gc\left(G_2\right)$; $n_1$ = $\mid V\left(G_1\right)\mid$ and $n_2$ = $\mid V\left(G_2\right)\mid$.

If $g_1{n}_2\ne g_2{n}_1$, then $C_g\left(G_1\right)\times C_g\left(G_2\right)\subseteq C_g\left(G\right)$.

Proof. 

Let $(u,v)\in C_g\left(G_1\right)\mathrm{x}{C}_g\left(G_2\right)$. From Proposition 10, $w(u,v)$ = max{$g_1{n}_2$,$g_2{n}_1$}. Without loss of generality, assume that $w(u,v)$ = $g_1{n}_2$. Let $(x,y)\in V\left(G\right)$. if $x\notin C_g\left(G_1\right)$ and $y\notin C_g\left(G_2\right)$, then $w(x,y)>g_1{n}_2$ (as $\mid S_x\mid >g_1$ and $S_x\mathrm{x}V\left(G_2\right)$ is a g-convex set of G not containing $(x,y)$). If $x\notin C_g\left(G_1\right)$ and $y\in C_g\left(G_2\right)$, then $w(x,y)\ge \mid S_x\mathrm{x}V\left(G_2\right)\mid >g_1{n}_2$ (as $g_1<\mid S_x$). Therefore in this case $(x,y)\notin C_g\left(G\right)$. If $x\in C_g\left(G_1\right)$, then $w(x,y)$ = max{$g_1{n}_2$,$w\left(y\right)\mathrm{x}{n}_1$} $\ge g_1{n}_2$ = $w(u,v)$. Thus for all $(x,y)$, $w(x,y)\ge w(u,v)$ for every $u\in C_g\left(G_1\right)$ and $v\in C_g\left(G_2\right)$. This proves that $C_g\left(G_1\right)\mathrm{x}{C}_g\left(G_2\right)\subseteq C_g\left(G\right)$. □

Remark 4.

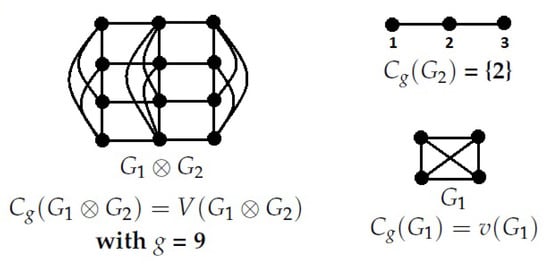
It can easily be seen that the containment can be proper. This is illustrated in Figure 3.

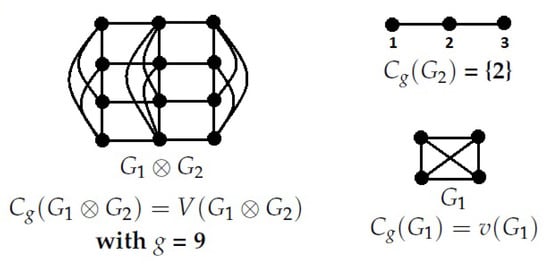
Figure 3. The proper containment of Proposition 23.

3.3. Prism of a Graph

As a special case of the cartesian product, we consider the prism of a graph. Let G be any connected graph. Take two copies of G, say $G\left(1\right)$ and $G\left(2\right)$. Label the vertices of the first copy with $u_{11}$,$u_{12}$,⋯,$u_{1n}$ and the second copy with $u_{21}$,$u_{22}$,⋯,$u_{2n}$ in the same order. Then, the prism of G denoted by $P\left(G\right)$ has the vertex set $V\left(G\right(1\left)\right)\cup V\left(G\right(2\left)\right)$ and the edge set defined as follows:

$$E\left(P\right(G\left)\right)=E\left(G\left(1\right)\right)\cup E\left(G\left(2\right)\right)\cup \{u_{1i}{u}_{2i}:1\le i\le n\}$$

Remark 5.

It is easy to see that the prism of a graph is the cartesican product of itself with $K_2$. That is, $P\left(G\right)$ = $G\otimes K_2$.

Proposition 24.

Let G be a connected graph and $u\in V\left(P\right(G\left)\right)$. Then, $w\left(u\right)$ = max { $\mid V\left(G\right)\mid$, $2\times w(u:G)$}.

The proof follows from the above remark and Proposition 21.

Proposition 25.

Let G be a connected graph and g = $gc\left(G\right)$. If $g\le n/2$, then $C_g\left(P\left(G\right)\right)$ = {$u_{ij}$, i = 1,2: $w(u_j:g)\le n/2$}; otherwise $C_g\left(P\left(G\right)\right)$ = $C_g\left(G\right)\otimes K_2$.

Proof. 

Let $g\le n/2$. Let $u_1\in C_g\left(G\right)$. Then, $w(u_i:G)\le n/2$. Therefore, from Proposition 24, $w\left(u_{1i}\right)$ = $w\left(u_{2i}\right)$ = n. Similarly if $u_j$ is any vertex of G with $w(u_j:g)\le n/2$, then also $w\left(u_{1j}\right)$ = $w\left(u_{2j}\right)$ = n. If $u_k$ is any vertex of G with $w(u_k:G)>n/2$, then $w\left(u_{ik}\right)$ = $2\times w\left(u_k\right)>n$. Thus, in this case, $C_g\left(P\left(G\right)\right)$ = {$u_{ij},i=1,2$: $w\left(u_j\right)\le n/2$}.

Proof of the other part follows similarly. □

3.4. The Corona

In this section, we deal with the corona of two graphs. Let G be the corona of $G_1$ with $G_2$. Then, we prove that $C_g\left(G\right)$ = $C_g\left(G_1\right)$.

Proposition 26.

Let G = $G_1\circ G_2$. Let $u\in V\left(G_1\right)$ and $v\in V(i,G_2)$. Then,

• $S_u\left(G\right)$ = $S_u\left(G_1\right)\cup \{V(i,G_2):i\in S_u\left(G_1\right)\}$ and
• $S_v\left(G\right)$ = $S\cup (V\left(G\right)-V(i,G_2))$, where S is a maximum g-convex set in $V(i,G_2)$ not containing v.

Proof. 

(1) Let $S^{\prime }$ be any maximum g-convex set of $G_1$ not containing u. i.e, $S^{\prime }$ = $S_u\left(G_1\right)$. We now show that S = $S^{\prime }\cup \{V(i,G_2):i\in S^{\prime }\}$ is a g-convex set of G.

If $x,y\in V\left(G_1\right)\cap S$, then $x,y\in S^{\prime }$ and all $x-y$ geodesics will lie in $<S>$ (as $S^{\prime }\subseteq S$).

Let $x,y\in V(i,G_2)$. In this case, if $d_{G_2}(x,y)\ge 3$, then $x,i,y$ is the only geodesic joining x and y in G, and by our definition of S, $i\in S$. If $d_{G_2}(x,y)=2$, then as before $i\in S$ and if $x,z,y$ is any other geodesic joining $x,y$ in G, then clearly $z\in V(i,G_2)\subseteq S$. Therefore, in all these cases, all $x-y$ geodesics lie in $<S>$.

Let $x\in V(i,G_2)$ and $y\in V(j,G_2)$ with $i,j\in S^{\prime }$. In this case it is easy to see that if P is a geodesic joining i and j in $G_1$, then $x\cup V\left(P\right)\cup y$ is a geodesic joining x and y in G and conversely. Since $i,j\in S^{\prime }$, all $i-j$ geodesics lie in $<S^{\prime }>$. Thus all $x-y$ geodesics lie in $<S>$.

Proof of the case when $x\in V(i,G_2)$ and $y\in V\left(G_1\right)$ is similar to that of the above case.

Thus the convexity of S is established. Obviously, S does not contain u. The reason that every such g-convex set S of G arises this way follows from the fact that $S^{\prime }$ = $S\cap V\left(G_1\right)$ is a g-convex set of $G_1$ not containing u and every $V(i,G_2)$ is a g-convex set of G. A maximum g-convex set of G not containing u is obtained by taking for $S^{\prime }$ a maximum g-convex set of $G_1$ not containing u; that is an $S_u\left(G_1\right)$. This establishes (1).

(2) Let $v\in V(i,G_2)$. Let $K^{\prime }$ be a maximum $g_2$-convex set in $G_2$ not containing v. Then as before by considering various cases, we can prove that $K^{\prime }\cup (V-V(i,G_2))$ is a g-convex set of G not containing v. If S is a maximum g-convex set of G not containing v, then trivially $S\cap V(i,G_2)$ is a $g_2$-convex set in $G_2$ not containing v. Therefore $S_v\left(G\right)$ = $S\cup (V\left(G\right)-V(i,G_2))$. □

In the case of the corona, we prove that the g-centroid of G and $G_1$ are the same.

Proposition 27.

Let $G_1$, $G_2$ be two connected graphs. Let G = $G_1\circ G_2$. Then, $C_g\left(G\right)=C_g\left(G_1\right)$.

Proof. 

Let $x\in V\left(G_1\right)$. Then $w(x:G_1)+n_2\mathrm{x}w(x:G_1)$ = $w(x:G)(1+n_2)$ (by (1) of the above proposition). If y is any vertex not in $C_g\left(G_1\right)$, then $w(y:G)>w(x:G)$ (as $w(y:G_1)>w(x:G_1)$). If $z\in V(i,G_2)$, then $V\left(G\right)-V(i,G_2)$ is a convex set of G not containing z with cardinality $n_1{n}_2+n_1-n_2$. Therefore $w(z:G)\ge n_1{n}_2+n_1-n_2$. For any $x\in C_g\left(G_1\right)$, $w(x:G)$ = $w(x:G_1)(1+n_2)\le$$(n_1-1)(1+n_2)$ = $n_1{n}_2-n_2+n_1-1$ $<w\left(z\right)$. Thus $w\left(z\right)>w\left(x\right)$. Therefore $C_g\left(G\right)=C_g\left(G_1\right)$. □

4. Conclusions and Future Directions

In this paper, we have considered the join of graphs and have shown that the gcws of G = $G_1\vee G_2$ depends on the intersection pattern of the maximum cliques of $G_1$ and $G_2$.

For cartesican products, we have proved that $S\subseteq V\left(G\right)$ is a convex set of G iff S = $S_1\times S_2$, where $S_1$ and $S_2$ are convex sets of $G_1$ and $G_2$, respectively, and deduced that $C_g\left(G_1\right)\times C_g\left(G_2\right)\subseteq C_g\left(G\right)$. As a special case of this, we have considered the prism of a graph.

Finally, we have dealt with the corona of a graph with another and shown that the centroid of the corona is that of the farmer graph.

There are several other important graph compositions such as wreath products, normal products (see [8]. Cf. 3), etc. Establishing the relation between the gcws and the g-centroid of the composite graph and its factor graphs under these graph operations is an interesting open problem in this area. It is also interesting to classify all classes of graphs such that for any arbitrary member graph G, $S_u\cap N\left(u\right)\ne \varnothing$ for all $u\in V\left(G\right)$. One such member class is trees.

The concept of convexity may be extended to directed graphs. It will be interesting to study the algorithmic complexity of g-centroid location algorithm for certain classes of directed graphs such as “strongly connected graphs”.