Abstract
This paper is devoted to establishing the most refined axiom for a digital covering space which remains open. The crucial step in making our approach is to simplify the notions of several types of earlier versions of local -isomorphisms and use the most simplified local -isomorphism. This approach is indeed a key step to make the axioms for a digital covering space very refined. In this paper, the most refined local -isomorphism is proved to be a -covering map, which implies that the earlier axioms for a digital covering space are significantly simplified with one axiom. This finding facilitates the calculations of digital fundamental groups of digital images using the unique lifting property and the homotopy lifting theorem. In addition, consider a simple closed -curve with five elements in , denoted by . After introducing the notion of digital topological imbedding, we investigate some properties of , where . Since is the minimal and simple closed k-curve with odd elements in which is not k-contractible, we strongly study some properties of it associated with generalized digital wedges from the viewpoint of fixed point theory. Finally, after introducing the notion of generalized digital wedge, we further address some issues which remain open. The present paper only deals with k-connected digital images.
Keywords:
local (k0,k1)-isomorphism; unique lifting property; homotopy lifting theorem; digital covering; digital topological imbedding; generalized digital wedge MSC:
54C08; 68R10; 05C40
1. Introduction
Since 2004 [1,2,3,4], the notion of digital covering space has been strongly used in digital topology and digital geometry. First of all, the unique path lifting (upl- for brevity) property [3] and the homotopy lifting theorem [2] among others [4,5,6] are key properties which can be used in calculating digital k-fundamental groups of digital images , classifying digital images using algebraic invariants [1,2,5], and their applications such as the winding number in a digital topological setting. Thus, there are many works using these properties including the papers [1,2,3,4,5,6,7] so that some results derived from these properties have been used in the fields of image analysis, pattern recognition, image processing, mathematical morphology and so forth.
Then, the following problems remain open:
(Q1) How to characterize several types of local -isomorphisms?
(Q2) What is the most simplified version of a local -isomorphism?
(Q3) What is the most refined axioms for a digital covering space?
Since is the minimal model satisfying the non-k-contractibility [3,8], we strongly need to investigate its digital topological properties.
(Q4) How to establish the notion of digital topological imbedding?
(Q5) What are digital topological properties of ?
(Q6) How to characterize the alignment of fixed point sets of and those of m-times of digital wedges of ?
Up to now, in literature, when studying an alignment of fixed point sets of , we have only studied it with the same k-adjacency of and . Assume two digital images and such that or . Then, after introducing a notion of generalized digital wedge, we may have the following queries.
(Q7) How can we establish a generalized digital wedge with a certain k-adjacency?
(Q8) How can we study an alignment of fixed point sets of a generalized digital wedge ?
For instance, given two digital images, and , how can we deal with the alignment of the fixed point sets of ?
In particular, regarding the issue referred to as (Q3), a recent paper [9] tried to establish certain relationships between a (strong) local -isomorphism [2] and a digital -map by using the notions of “conciliator” [9] and the upl-property for a -surjection [2,3]. However, this approach invokes certain redundant results because it took a detour for the work instead of a direct proof using the given hypothesis. Indeed, these properties are not necessary to address the query (Q3). Furthermore, some literature, including the paper [9], confused and misunderstood a rudimentary version of local -isomorphism in [1], a (strong) local -isomorphism [2], and certain relationships between the rudimentary version of a local -isomorphism and a digital -map. Hence we now need to make them more clarified in this paper and further, address the queries (Q1)–(Q8) above. In the present paper the notation “” is used for introducing a new terminology.
The paper is organized as follows. Section 2 investigates basic notions needed for the study in the present paper. Section 3 first proposes the notion of digital topological imbedding and studies some properties of it. In addition, it characterizes , where . Section 4 studies several types of local k-isomorphisms and some properties of them. Furthermore, it proposes the most simplified version of a local -isomorphism. Section 5 proposes the most refined axiom for a digital covering space using a very simplified version of a local -isomorphism. In Section 6, after mentioning some important features of which are associated with some digital homotopy properties of , we intensively study fixed point sets of and m-times of digital wedges of . Besides, using the notion of digital topological imbedding, we firstly introduce the notion of generalized digital wedge and further, study an alignment of fixed point sets of . Finally, Section 7 concludes the paper.
2. Preliminaries
Among many kinds of methods of studying digital images [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], motivated by the typical graph theory [26,27,28], the present paper will follow a graph theoretical approach to study digital images in [22,29]. Naively, a digital image can be considered to be a set with one of the k-adjacency of from (1) of the present paper (or a digital k-graph on [7]), where is the set of points in the Euclidean nD space with integer coordinates, and is the set of natural numbers.
Motivated by the digital k-connectivity for low dimensional digital images [22,29], as a generalization of this approach, the papers [1,3,30] firstly developed some k-adjacency relations for high dimensional digital images (see also (1) of the present paper). More precisely, the digital k-adjacency relations (or digital k-connectivity) for , were initially developed in [3] (see also [1,2,30]), as follows:
For a natural number t, , the distinct points and are -adjacent if at most t of their coordinates differ by and the others coincide.
According to this statement, the -adjacency relations of , are formulated [3] (see also [2,4,30]) as follows:
For instance, the following are obtained [2,30]:
Using these k-adjacency relations of in (1), , we will call the pair a digital image on , . Indeed, we should represent as a binary digital image , where the k-adjacency is concerned with the set and the -adjacency is associated with the set (see the paradox of digital k-connectivity in [18,22]). However, since this paper certainly approves this situation, for convenience, we only take the notation instead of .
Besides, these k-adjacency relations can be essential to studying digital products with normal adjacencies [3] and calculating digital k-fundamental groups of digital products [4,31]. For with , the set with 2-adjacency is called a digital interval [18,19].
Hereafter, is assumed in , with one of the k-adjacency of (1). The following terminology and notions [3,18,19,22,29,31] will be often used later. Two non-empty digital images and are said to be k-adjacent if and there are certain points and such that is k-adjacent to [18].
Consider a digital image in and a point which is the complement of X in . Then, the point y is said to be k-adjacent to if there is a point such that x is k-adjacent to y [19]. Equivalently, we may define that the point y is k-adjacent to if is k-adjacent to [19].
In a digital image , by a k-path, we mean a sequence such that and are k-adjacent if [19]. Besides, l is called a length of this k-path. Using this approach, we can also represent the concept of k-connectedness, as follows [19].
We say that is k-connected [19] if for any distinct points there is a k-path in X such that and (for more details see [31]). Besides, a singleton set is assumed to be k-connected (for more details see [31]).
By a simple k-path from x to y in , we mean a finite set as a sequence such that and are k-adjacent if and only if , where and [19]. Then, the length of this set is denoted by .
A simple closed k-curve (or simple k-cycle) with l elements in , denoted by [3,19], , is defined to be the set such that and are k-adjacent if and only if . Then, the number l of depends on both the dimension n of and the k-adjacency.
Given a digital image , the digital k-neighborhood of with radius is defined in X to be the following subset of X
where is the length of a shortest simple k-path from to x and .
Using the digital k-neighborhood of (2), we observe that a digital image can be a digital space [32]. To be precise, let us assume a certain relation on the set : We say that two distinct points x and y have a relation R, denoted by , if
Then, it is clear that the relation R in (3) is symmetric and non-reflexive so that the relation set is a digital space [31].
Since every point x of a digital image in always has an , the digital continuities of [22] can be represented as the following form which will be effectively used in addressing all of the questions posed in Section 1.
Proposition 1.
[3,4,7] Let and be digital images in and , respectively. A function is -continuous if and only if for every point , .
Owing to a digital k-graph theoretical feature of a digital image , we have often used a -isomorphism as in [7] instead of a -homeomorphism as in [8], as follows:
Definition 1.
[8] (see also [7]) For two digital images in and in , a map is called a -isomorphism if h is a -continuous bijection and further, : is -continuous. Then we use the notation . If and , then we call it a -isomorphism and use the notation .
3. Development of a Digital Topological Imbedding
plays an important role in digital topology because it is the minimal model for non-k-contractibility [3,8]. Thus, we need to explore digital topological properties of it. To characterize , where , we firstly develop a new notion of ‘digital topological imbedding’. Motivated by the topological imbedding [33], we now propose the following.
Definition 2.
Consider two digital images and such that there is an arbitrary -isomorphism . Then, is said to be a digital topological imbedding into with respect to the -isomorphism h.
In particular, in the case with the same k-adjacency of both X and , a digital topological imbedding is simply understood to be an inclusion .
Remark 1.
In Definition 2, we observe the following:
- (1)
- The dimension n need not be equal to .
- (2)
- The k-adjacency need not be equal to -adjacency.
- (3)
- Unlike the typical notion of a topological imbedding [33], the phrase “with respect to the -isomorphism h” is strongly required.
Definition 3.
In Definition 2, as to for X and for Y, if , then is said to be a strictly digital topological imbedding into with respect to the -isomorphism h.
Using these notions, we obtain the following:
Theorem 1.
is digital topologically imbedded into with respect to a -isomorphism, .
Proof.
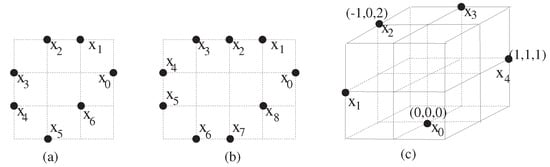
Let us take a certain set (see Figure 1c)

Figure 1.
Configuration of several types of : (a) [34], (b) [34], (c) . Here, , the underlying 3-dimensional lattice is shown as a dashed grid. The simple closed 26-curve consisting of 5 points appears as black dots labelled through . Indeed, there are several shapes of in .
Then, consider the map
defined by
where Y is the following set as an example
and .
Since the map h is a -isomorphism, the proof is completed. ☐
The map in (4) is just an example. Indeed, there are many types of -isomorphisms for supporting Theorem 1. It is clear that no exists, [34] and further, there is no , [34]. However, we obtain the following:
Corollary 1.
exists in if .
Proof.
After considering to be the set with respect to a certain -isomorphism which is similar to the map h in (4) for , which completes the proof. ☐
Example 1.
(1) is considered in . To be precise, since is equal to 64 (see the property (1)), consider the map defined by
where is the set referred to in the proof of Theorem 1 and Y is assumed to be the set.
Then the map is a -isomorphism supporting a digital topological imbedding of in with .
(2) is considered in . To be specific, since is equal to 80, assume the map in defined by
where is the set referred to in the proof of Theorem 1 and Z is assumed to be the following set.
Then, the map is a -isomorphism supporting a digital topological imbedding of in with .
Using methods similar to the digital topological imbeddings in Example 1, we obtain the following:
Corollary 2.
Given with , a digital topological imbedding of into exists if and , where .
In view of Theorem 1 and Corollary 1, and the notion of , according to the k-adjacency of as stated in (1), as to the number l of , we observe the following properties [34].
If , for , then it is clear that the number l of can be even or odd (see Figure 1a). Besides, if , then it is clear that the number l can be odd or even (see Figure 1c). More explicitly, for , the number l of can be assumed to be even or odd. For instance, consider , , , and (see Figure 1a,b). In general, and are considered according to the dimension , and . Regarding , we can sum up certain properties of l of , as follows:
Hereafter, regarding l of , we will follow the property (5) which is an improved version of (2) of [34].
4. Characterizations of Several Types of Local -Isomorphisms and Their Relationships with Both the -Continuity and a Surjection
In general and algebraic topology we define the notion of local homeomorphism as follows: For two topological spaces , we say that a map is a local homeomorphism if each point is contained in an open set such that is open in Y and the restriction is a homoeomorphism from to V [35]. Then, it turns out that not every local homeomorphic surjection is a covering map from the viewpoint of algebraic topology [35]. However, in digital topology, we have the query as referred to in Section 1.
This section initially compares several types of local k-isomorphisms such as a rudimentary version of a local -isomorphism (or a local -homeomorphism in [1]) and a (strong) local -isomorphism [2], which we can clarify a certain difference between them. Indeed, this approach is very important in making the axioms for a digital covering space refined. Motivated by Definition 1, as mentioned in the previous part, in the present paper we will call a pseudo local -isomorphism (see Definition 4) and a local -isomorphism (see Definitions 5 and 6) instead of a local -homeomorphism in [1,2].
Definition 4.
[1] (a rudimentary version of a local -isomorphism or a pseudo local -isomorphism) For two digital images in and in , a -continuous map is called a pseudo local -isomorphism if for every point , is -isomorphic with . If and , then the map h is called a pseudo local -isomorphism.
In Definition 4, we called the map h a pseudo local -isomorphism to avoid some confusion with the typical local -isomorphism in Definitions 5 and 6 below. Then, we consider the following example for Definition 4.
Example 2.
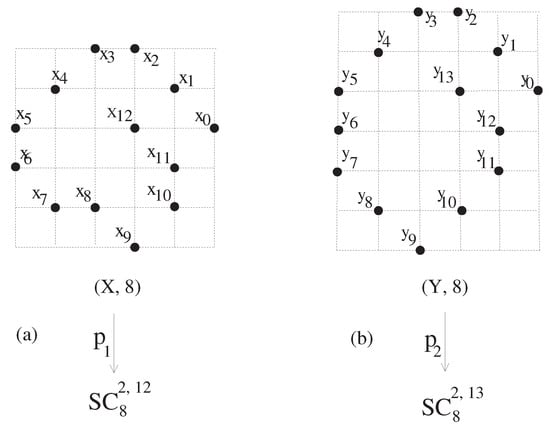
Let us consider the two maps and in Figure 2. Then, these maps are pseudo local 8-isomorphisms. More precisely, assume the set in Figure 2, where and and further, , where and .

Figure 2.
Configuration of local 8-isomorphisms of Definition 4 referred to in Example 2. (a) . (b) .
Then, consider the map defined by
Besides, consider the map defined by
Then, each maps and are pseudo local 8-isomorphisms.
As another version of a local -isomorphism, a paper [2] established the following notion which is stronger than a pseudo local -isomorphism.
Definition 5.
[2] For two digital images in and in , a -continuous map is called a local -isomorphism if for every , h maps -isomorphically onto . If and , then the map h is called a local -isomorphism.
Definition 5 can be certainly admissible in studying digital topology. However, regarding the questions (Q1)–(Q3) posed in Section 1, we now need to make Definition 5 more simplified and refined. Finally, we recognize that the condition “-continuous map ” is redundant for defining a “local -isomorphism” of Definition 5 because the condition “for every , h maps -isomorphically onto ” of Definition 5 implies the -continuity of the given map h, as follows:
Lemma 1.
For two digital images in and in , consider a map . Assume that the map h has the property that for every , h maps -isomorphically onto . Then h is a -continuous map. In particular, in the case and , the map h is a k-continuous map.
Proof.
With the hypothesis, for every and , h has the property
In other words, by Definitions 1 and 5, and (6), the restriction h to the set , i.e., , is a -isomorphism. Thus, using Proposition 1, since is a bijection, we obtain
By the hypothesis, for any point we have the property (7). Thus, by Proposition 1, we obtain the -continuity of h.
Indeed, we have
Naively, since is already determined by the given map h and , we certainly obtain
Conversely, for the sake of a contradiction, suppose there is a point .
Then, this assumtion invokes a contradicton to the -isomorphism of h. ☐
Owing to Lemma 1, we can make the local -isomorphism of Definition 5 simplified because the condition of the -continuity of the map h of Definition 5 is redundant for defining a local -isomorphism. Thus, after replacing the condition “a -continuous map ” by a just “map ”, we obtain the most refined version of a local -isomorphism, as follows:
Definition 6
(Refinement of a local -isomorphism of Definition 5). For two digital images in and in , consider a map . Then the map h is said to be a local -isomorphism if for every , h maps -isomorphically onto . If and , then the map h is called a local -isomorphism.
It is clear that a local -isomorphism of Definition 6 is stronger than a pseudo local -isomorphism of Definition 4. Hereafter, when studying digital images, we will follow a local -isomorphism in Definition 6 instead of Definition 5.
Remark 2.
(1) By Lemma 1 and Definition 6, a local -isomorphism is a -continuous map.
(2) A local -isomorphism need not be a -isomorphism. For instance, consider the map
defined by . Then, the map h is a local -isomorphism of Definition 6 which is not a -isomorphism.
Regarding (Q1)–(Q3), let us now examine if a local -isomorphism of Definition 6 is surjective.
Theorem 2.
A local -isomorphism is a surjection.
Before proving the assertion, we need to recall that all digital images in this paper are assumed to be k-connected. With the hypothesis, let us now prove the assertion.
Proof.
For the sake of a contradiction, suppose a local -isomorphism which is not surjective. With the hypothesis, since is clearly a -connected proper subset of , i.e., , we may take a point such that is -adjacent to because is assumed to be -connected. Then, there is a point which is -adjacent to . Let us now consider a point so that . Indeed, e need not be unique because of the local -isomorphism h. Then, take a certain point anyway. Owing to the hypothesis of a local -isomorphism of h, for the set , there is the following -isomorphism
Then, we have a contradiction to the property (8) because for the point , there is no point such that . ☐
Corollary 3.
(1) Given a digital image , the identity map of is a local k-isomorphism.
(2) Consider a digital topological imbedding from into with respect to a -isomorphism such that . Then, the map h is not a local -isomorphism.
(3) Given a digital image and its a proper subset , the inclusion map is not a k-local isomorphism.
Proof.
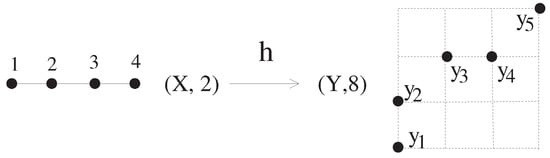
(1) For any element , since , the proof is completed.
(2) Assume a map such that is -isomorphic to and h is not surjective. Then, let us prove the assertion of (2) with a counterexample. Consider the sets and in Figure 3. Assume a map suggested in Figure 3, defined by
Then, consider the map defined by which is a -isomorphism. However, it is clear that is not a local -isomorphism because the point “” does not support a local -isomorphism of h. To be precise, it is clear that is a digital topologically imbedded into with respect to the -isomorphism . However, the map h is not a local -isomorphism because
so that is not -isomorphic to with respect to the given map h.
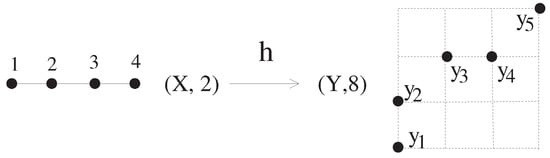
Figure 3.
Explanation of the map h referred to in the proof of Corollary 3, where is a portion of with 8-adjacency.
(3) As a special case of (2), the proof is completed. ☐
Example 3.
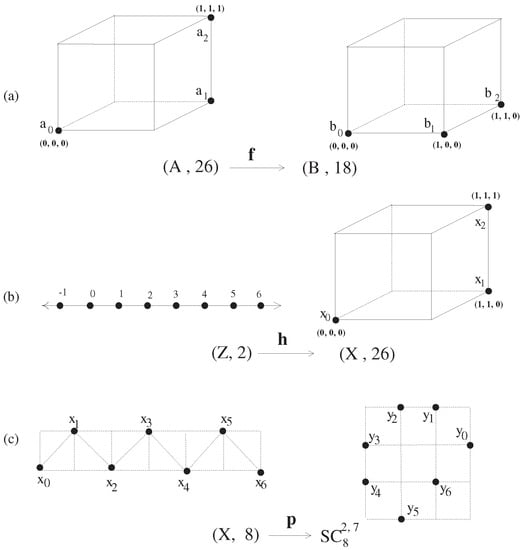
Given the three maps in Figure 4, we obtain the following:

Figure 4.
(a) Configuration of a -continuous surjection f which is a local -isomorphism mentioned in Example 3(1). (b) Configuration of a -continuous surjection which is not a local -isomorphism stated in Example 3(2). (c) Configuration of an -surjection which is not a local -isomorphism referred to in Example 3(3), where X consists of six elements.
- (1)
- In Figure 4a, the map defined by , is a local -isomorphism. However, if we replace above by the case with the map f above, the map f is not a local 18-isomorphism.
- (2)
- In Figure 4b, the map given by , is not a local -isomorphism. By contrary, suppose that the map h is a local -isomorphism. Then, take the digital 2-neighborhood of the point 0 with radius 1, . Then, we should have the -isomorphismHowever, the map in (9) is not a -isomorphism because the inverse map is not -continuous. More precisely, while every point has the property , some two points in are not 2-adjacent, , which invokes a contradiction to the -isomorphism in (9). More precisely, see the points “” which are not 2-adjacent, while their corresponding points which are 26-adjacent.
- (3)
- In Figure 4c, the map defined by , is not a local 8-isomorphism, where and . Indeed, we may call the set a finite fence set with 8-adjacency.
5. The Most Refined Axiom for a Digital Covering Space
It is well known that the notion of graph covering strongly contributed to the classification of graphs [28]. Similarly, the concept of covering space in algebraic topology has also been substantially used in classifying topological spaces [24,36]. However, investigating these covering structures [24,27,28], it turns out that digital covering spaces have their own features [1,2,3,4] and further, have some strong advantages of exploring various properties of digital images. Many properties derived from the notion of digital covering space have been often used in calculating digital fundamental groups [2,8,30] and classifying digital covering spaces [7,8]. Thus, the work making the earlier axioms for a digital covering space refined is really a hot issue (see (Q3)) in digital topology. Let us now recall the axioms of a digital covering space which are equivalent to the initial versions of a digital covering space in [3].
Definition 7.
[3] (see also [4]) Let and be digital images in and , respectively. Let be a (-continuous) surjection. Suppose, for any there exists such that
- (1)
- for some index set M, with ;
- (2)
- if and , then is an empty set; and
- (3)
- the restriction of p to from to is a -isomorphism for all .
Then the map p is called a -covering map, is said to be a -covering and is called a digital -covering space over .
The -neighborhood of Definition 7 is called an elementary -neighborhood of b with some radius [3]. The axioms for a digital covering space in Definition 7 are certainly acceptable because they are descriptive and constructive. Besides, the paper [4] established a slightly simpler form of the axioms of a digital covering space, as follows.
Remark 3.
(1) As for the axioms for a -covering of Definition 7, we can replace “-continuous surjection” with “surjection” because the surjection of p with the properties (1) and (3) of Definition 7 implies that p is -continuous [4].
(2) Given a surjection , if there is a certain such that the restriction map p to from to is a -isomorphism, then we say the map p is a radius ε local isomorphism [2]. In Definition 7, we may take [4]. However, to study some works such as the homotopy lifting theorem [2], since we need a radius 2 local -isomorphism, we may take as stated in Definition 7 (see Remark 1 of [4]).
(3) In view of (2) above, a digital -covering map is a obviously a radius 1 local -isomorphism [4] because a radius ε local -isomorphism implies a radius 1 local -isomorphism.
Remark 4.
A pseudo local -isomorphism need not imply a digital -map [1]. To be precise, consider the two maps and referred to in Example 2 (see also Figure 2) to be counterexamples instead of the misprinted counterexample in [1]. As already stated in Example 2, while each maps and are pseudo local 8-isomorphisms, they are not 8-covering maps. Naively, each and are neither 8-covering maps nor local 8-isomorphisms of Definition 6 (see the points or in Figure 2a and the points or in Figure 2b). Indeed, a pseudo local -isomorphism is quite different from the local -isomorphism of Definition 5 (see also Definition 6 in the present paper).
Let us now explore some properties of a local -isomorphism of Definition 6 which will be used in addressing the issue (Q3), as follows:
Proposition 2.
Consider a map such that every element has the property that
is -isomorphism, i.e., p is a local -isomorphism of Definition 6. Then, for any and some index set M, we obtain
Then, the following hold.
- (1)
- In (10), if and , then is an empty set;
- (2)
- In (10), for any , is -isomorphic to .
- (3)
- In (10), for any and , is not -adjacent to .
Proof.
(1) First of all, owing to the hypothesis of the map p, in (10), we prove the following:
By contrary, suppose is -adjacent to , which implies . Then, by the hypothesis, should be a -isomorphism. However, from (10), since we have so that the map is not injective, which invokes a contradiction to the -isomorphism of .
Next, in (10), we now prove that for any , the two sets and are disjoint. For the sake of a contradiction, for some and , suppose
Then, take a certain point
As proved above, since is not -adjacent to , we may take . Owing to the property (12), it is clear that the element is -adjacent to both the points and . Naively, with the property (11), we obtain
Owing to the hypothesis of a local -isomorphism of p and the property (10), the restriction p to , i.e.,
should be a -isomorphism. However, since , by the properties (10) and (13), the restriction map in (14) is not a -isomorphism because it is not injective, which invokes a contradiction to the property (14).
(2) Since a digital isomorphism clearly holds a composite, owing to the hypothesis of the local -isomorphism of p, the proof is completed because
(3) In (10), after recalling the fact already proved in (1), by contrary, in (10), suppose that there are certain with such that the sets is -adjacent to . Then, owing to the facts already proved in (1) and (2), there are at least two distinct points such that
Then, we have a simple -path such that . Let us now consider the sequence
Regarding the sequence in (15), since and , by the hypothesis, the -isomorphism
is also considered. Hence we have and further, is -adjacent to .
Similarly, by (10), we also obtain the following:
Besides, it is clear that is -connected. Hence the sequence is a -cycle with three points which is not simple. To be precise, since b is -adjacent to both and and further, is also -adjacent to , the sequence has a shape of a triangle with -adjacency and it is a subset of , where . This invokes a contradiction to the hypothesis of a local -isomorphism of p. More precisely, owing to the hypothesis, for each element , each restriction of p to ,
should be a -isomorphism so that the inverse map of , denoted by , should be a -isomorphism. However, it is clear that
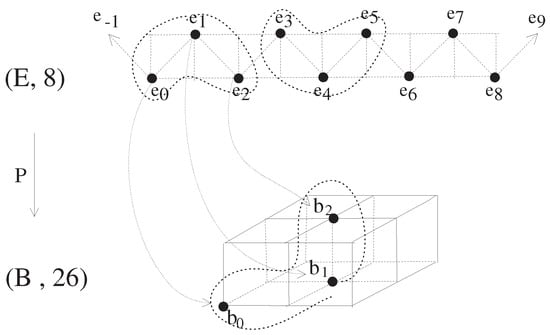
More explicitly, while is -adjacent to , the images by the map of the two points and are not -adjacent. To explain the situation related to (16), as an example, let us consider two digital images and in Figure 5, where
To support the above situation supposed in (15), assume the map defined by
Then we now show that the map p in (18) is not a local -isomorphism. To be precise, while the map p of (18) is a -continuous surjection supporting the property (15) and is 26-adjacent to , the element is not 8-adjacent to in . ☐

Figure 5.
Configuration of an -continuous surjection which is not a local -isomorphism referred to in (18), where E is a portion of an infinite set (or an infinite fence set with 8-adjacency) in (17).
Owing to Definition 7, Remark 2(1), Theorem 2, and Proposition 2, we obtain the following:
Corollary 4.
A local -isomorphism of Definition 6 is equivalent to a digital -covering map.
Before proving the assertion, by Remark 3(2), in Definition 7 we may assume to be 1 (see Remark 3(2) of the present paper or Remark 1 of [4]). With this setting, we prove the assertion.
Proof.
Since a digital -covering map implies a local -isomorphism (see Definition 7(3) and the surjection of Definition 7), it is sufficient to prove that a local -isomorphism of Definition 6 implies a digital -covering map. Based on the property (10), we observe the following:
- (1)
- By Remark 2(1), the given map is a -continuous map.
- (2)
- By Theorem 2, the given map is a surjection.
- (3)
- As mentioned in Remark 3(2), in Definition 7 we may take . Then, the properties from Proposition 2(1)–(2) with the hypothesis imply the axioms (2)–(3) of Definition 7. Naively, we obtain that and further, the restriction of p on , , is a -isomorphism. ☐
Owing to these properties, the proof is completed.
Based on Proposition 2 and Corollary 4, we now confirm the following:
Remark 5.
Let and be digital images in and , respectively. Let be a local -isomorphism. Then, for any , we obtain the following properties (see Remark 1 of [4]):
- (1)
- For some index set M, with ;
- (2)
- if and , then is an empty set; and
- (3)
- the restriction of p to from to is a -isomorphism for all .
Thus, the map p is a -covering map, is a -covering and is a digital -covering space over (see Remark 1 of [4]).
Motivated by Example 3(1) and Corollary 4, we obtain the following (see Figure 4a as an example):
Corollary 5.
Given a digital image and each point , if , then there are many -covering maps which need not be the identity map, where for any and is -isomorphic to .
Based on Corollary 4 and Remark 5, let us consider the upl-property and its related works. Given a digital image , take a certain point . Then, the pair is called a pointed digital image with the given k-adjacency. We say that a k-path on , begins at if [2]. If a -continuous map satisfies , then we say that f is a pointed -continuous map. Since the notion of digital lifting and the upl-property play important roles in digital covering theory, let us recall them.
Definition 8.
[2,3] (1) For digital images in , in , and in , let be a -continuous map and be a -continuous map. We say that a lifting of f (with respect to p) is a -continuous map such that . In particular, in the case be a -continuous map, the lifting of f denoted by is called a -path lifting (with respect to p).
(2) In (1), the map p has the upl-property if any two -paths are equal if = and .
Remark 6.
In Definition 8, we can replace the given map p by a certain -continuous surjection or a digital -covering map depending on the situation [2,3].
Since the upl-property plays a crucial role in digital covering theory, let us recall it as follows:
Theorem 3.
[3]([Unique path lifting property]) Let and be pointed digital images in and , respectively. Let be a -covering map such that . Then, any -path beginning at has a unique digital lifting to a -path in E beginning at .
Using Corollary 4, we can also simplify the upl-property using a local -isomorphism, as follows:
Proposition 3.
Let be a local -isomorphism of Definition 6. Then, the map p supports the upl-property.
Proof.
By Corollary 4, since a local -isomorphism implies a digital -covering map, by Theorem 3, the proof is completed. ☐
As mentioned above, the notion of local -isomorphism indeed plays an important role in digital curve theory. Based on this notion, the notion of radius local -isomorphism was developed [2] which is essential to developing the homotopy lifting theorem [3]. Without this theorem, we can neither calculate the digital fundamental groups of digital images nor study some local properties such as the (generalized) topological k-number [30]. Thus, based on the digital homotopy lifting theorem in [2] and Remark 3(2), we obtain the following:
Remark 7.
(1) Let be a radius 2 local -isomorphism such that . Namely, for any element , the restriction is a -isomorphism such that . Then, the map p supports the digital homotopy lifting theorem in [2] because a radius 2 local -isomorphism implies a local -isomorphism.
(2) When studying all properties related to a digital covering map, after replacing a digital covering map with a local -isomorphism of Definition 6, we can effectively study them. It turns out that this local -isomorphism facilitates the digital covering theory and related works.
In digital topology, there are several types of digital fundamental groups established by Kong [12], Malgouyres [20], Boxer [8] and so forth. The group proposed by Kong and Malgoure is different from that established by Boxer. In particular, when calculating the digital 4-fundamental group of , the two approachs appear quite differently. The latter is calculated by using some properties derived from digital covering theory such as the trivial extension [8], the upl-property [3] and the digital homotopy lifting theorem [2]. Eventually, if X is pointed k-contractible, then it turns out that the k-fundamental group of is a trivial group [8]. Regarding the homotopy lifting theorem [2] and the unique digital lifting theorem [3], we obtain the following properties of .
Remark 8.
(1) is the minimal model for a simple closed k-curve with an odd cardinality.
(2) is the minimal model which is not k-contractible.
(3) The map defined by is a local -isomorphism.
6. Generalized Digital Wedges and Alignments of Fixed Point Sets of , Where or
Given two digital images in and in , where and , this section explores a certain k-adjacency for a digital wedge of and . Using this approach, given two and , where or , we initially establish the digital wedge with a certain k-adjacency of , where and further, study some properties of an alignment of of fixed point sets of , where or , which remains open. Up to now, in the literature, there are only studies of alignments of fixed points sets of [34]. Thus, the study of an alignment of fixed point sets of the other cases remains open. Hence this section mainly deals with this study for the generalized digital wedges. As a generalization of a digital wedge in [3,34] and the compatible k-adjacency of a digital wedge in [30], using the notion of digital topological imbedding, we now establish the following:
Definition 9.
Given two digital images in and in , where and , take and . Then, we define a digital wedge of and in with a k-adjacency of , where , denoted by , as one point union of the certain digital images and in satisfying the following properties.
(W1) There are the following digital topological imbeddings,
such that the set is assumed with the k-adjacency and further,
(W2) is a singleton, say ,
(W3) and are not k-adjacent, and
(W4) as for the subsets , the following properties hold.
In view of this feature, we may consider to be which is one point union of and with k-adjacency.
Given two and , if and , then always exists in [34], where and .
Remark 9.
Given two and , if and , not every always exists with the k-adjacency of Definition 9.
Regarding Remark 9, we observe the following examples.
Example 4.
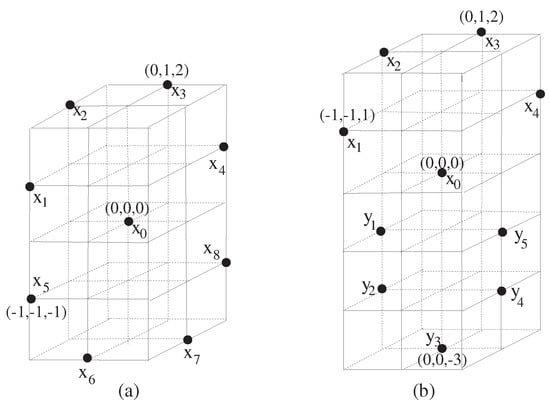
(1) Given and , no exists in for any .
(2) exists in with 26-adjacency (see Figure 6a). In general, exists in with -adjacency, .

Figure 6.
Configuration of digital wedges of two simple closed k-curves, , and . (a) . Here, , the underlying 3-dimensional lattice is shown as a dashed grid. The digital wedge generated by the two simple closed 26-curve consisting of 5 points appears as black dots labelled through with . (b) . Here, , the underlying 3-dimensional lattice is shown as a dashed grid. The digital wedge generated by both the simple closed 26-curve and the simple closed 18- or 8-curve appears as black dots labelled through and through with
(3) exists in (see Figure 6b).
(4) is obtained in (see Figure 6b).
(5) Consider , , and .
While exists in , no exists in for any k-adjacency of .
Recent papers [34,37] studied some alignments of fixed point sets of digital image with the notation, as follows:
where , the notation means the cardinality of the given set X, and
Besides, the set of (19) means the set of all cardinalities of fixed point sets of every k-continuous self-maps of . Then, based on the set in (19), we define the following:
Definition 10.
[34] Given , as a digital image is said to be an alignment of fixed point sets of k-continuous self-maps of .
Definition 11.
[34] Given , if , then (or for brevity) is said to be perfect.
Lemma 2.
[34] Given (see the property (2)), depending on the number l which is odd or even, we obtain the following:
- (1)
- if [34].
- (2)
- if [37].
Theorem 4.
(1) if .
(2) if .
Proof.
Given and , according to Definition 9, the generalized digital wedge is obtain in with 26-adjacency. Among many kinds of 26-continuous self-maps f of , regarding , it is sufficient to consider only the maps f such that
- (a)
- ; or
- (b)
- ; or
- (c)
- and ; or
- (d)
- f does not have any fixed point of it, where means the restriction function f to the given set X.
Firstly, from (a), since has the cardinality , by Lemma 2(1)), we have
Secondly, from (b), by Lemma 2(1), we obtain
Thirdly, from (c)–(d), we have
After comparing the three numbers in (20)–(22), we conclude that if .
(2) Based on Lemma 2(2), using methods similar to (20)–(22), we complete the proof. ☐
Example 5.
.
(2) .
Theorem 5.
, where and .
Proof.
By using the approach similar to (a)–(d) of the proof of Theorem 4, we initially obtain
where . Since , we complete the proof. ☐
Corollary 6.
(1) is perfect, where P is a simple k-path with length 1.
(2) is perfect.
Proof.
(1) First of all, we find that the difference between and is equal to 2. Secondly, join a simple k-path with length 1 onto the set to establish the digital wedge . Thirdly, using the approaches similar to (a)–(d) of the proof of Theorem 4, we complete the proof.
(2) First of all, we find that and the difference between and is equal to 2. After joining onto the set to establish the digital wedge and further, using the approaches similar to (a)–(d) of the proof of Theorem 4, we complete the proof. ☐
The paper [38] proposed the fixed point property of the infinite M-sphere (see Theorem 2 of [38]). More precisely, let [39] be the Alexandroff one point compactification of the Marcus-Wyse topological plane and be the set of all self-continuous maps of . Then, we obtain the following:
Theorem 6.
[38] does not have the fixed point property in .
This theorem is correct. However, the paper [38] has a misprinted part related to the map g in (9) and Figure 1 of [38]. Thus, we would improve them related to the proof of Theorem 2 of [38], as follows:
Proof.
Although there are many examples replacing the map (9) and Figure 1 in [38], we will take the following [39]. Let (for more details, see the map g below and Figure 3 in [39]).
With , consider the self-map g of defined by [39]
Then, we obtain
While the map g is continuous, does not have any point such that , where . ☐
7. Conclusions
It turns out that the simplified version of a local -isomorphism gives us very strong advantages of making the earlier version of axioms for a digital covering space most simplified. Besides, this approach is a key step in addressing the hot issue which was an unsolved problem during the last 20 years. Finally, it appears that the most refined local -isomorphism of Definition 6 implies the earlier version of axioms for a digital covering space. Thanks to the most refined version of the local -isomorphism, we can replace axioms for a digital covering space in all literature with the local -isomorphism of Definition 6 as just one axiom with some properties, which facilitates the study of digital covering theory. Furthermore, owing to the new notion of digital topological imbedding, we proposed a suitable k-adjacency for the digital wedge , where or . This work also plays an important role in digital topology and digital geometry. Since a digita image can be considered to be a digital metric space, using the work [40], we can further expand the obtained works.
Funding
The author was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology(2019R1I1A3A03059103).
Conflicts of Interest
The author declares no conflict of interest.
References
- Han, S.-E. Digital (k0, k1)-covering map and its properties. Honam Math. J. 2004, 26, 107–117. [Google Scholar]
- Han, S.-E. Digital coverings and their applications. J. Appl. Math. Comput. 2005, 18, 487–495. [Google Scholar]
- Han, S.-E. Non-product property of the digital fundamental group. Inf. Sci. 2005, 171, 73–91. [Google Scholar] [CrossRef]
- Han, S.-E. Discrete Homotopy of a Closed k-Surface. In LNCS 4040; Springer: Berlin, Germany, 2006; pp. 214–225. [Google Scholar]
- Boxer, L.; Karaca, I. The classification of digital covering spaces. J. Math. Imaging Vis. 2008, 32, 23–29. [Google Scholar] [CrossRef]
- Boxer, L.; Karaca, I. Some properties of digital covering spaces. J. Math. Imaging Vis. 2010, 37, 17–26. [Google Scholar] [CrossRef][Green Version]
- Han, S.-E. On the simplicial complex stemmed from a digital graph. Honam Math. J. 2005, 27, 115–129. [Google Scholar]
- Boxer, L. A classical construction for the digital fundamental group. J. Math. Imaging Vis. 1999, 10, 51–62. [Google Scholar] [CrossRef]
- Pakdaman, A.; Zakki, M. Equivalent conditions for digital covering maps. arXiv 2020, arXiv:1805.03041v4. [Google Scholar]
- Han, S.-E.; Jafari, S.; Kang, J.M. Topologies on ℤn which are not homeomorphic to the n-dimensional Khalimsky topological space. Mathematics 2019, 7, 1072. [Google Scholar] [CrossRef]
- Johnstone, P.T. Stone Spaces; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Khalimsky, E. Motion, Deformation, and Homotopy in Finite Spaces. In Proceedings of the IEEE International Conferences on Systems, Man, and Cybernetics, Alexandria, Egypt, 20–23 October 1987; pp. 227–234. [Google Scholar]
- Khalimsky, E. Pattern Analysis of n-Dimensional Digital Images. In Proceedings of the IEEE International Conferences on Systems, Man, and Cybernetics, Atlanta, GA, USA, 14 October 1986; pp. 1562–1599. [Google Scholar]
- Khalimsky, E. Topological structures in computer sciences. J. Appl. Math. Simul. 1987, 1, 25–40. [Google Scholar] [CrossRef]
- Khalimsky, E.; Kopperman, R.; Meyer, P.R. Boundaries in digital planes. J. Appl. Math. Stoch. Anal. 1990, 3, 27–55. [Google Scholar] [CrossRef]
- Kong, T.Y. A digtal fundamental group. Comput. Graph. 1989, 13, 159–1663. [Google Scholar] [CrossRef]
- Kong, T.Y.; Roscoe, A.W. Continuous analogs of aximatized digital surfaces. Comput. Vision Graph. Image Process. 1985, 29, 60–85. [Google Scholar] [CrossRef]
- Kong, T.Y.; Rosenfeld, A. Digital topology: Introduction and survey. Comput. Vision Graph. Image Process 1989, 48, 357–393. [Google Scholar] [CrossRef]
- Kong, T.Y.; Rosenfeld, A. Topological Algorithms for the Digital Image Processing; Elsevier Science: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Magouryes, R. Homotopy in 2-dimensional digital images. Theor. Comput. Sci. 2000, 230, 221–233. [Google Scholar]
- Kovalevsky, V. Finite topology as applied to image analysis. Comput. Vis. Graph. Image Process. 1989, 46, 141–161. [Google Scholar] [CrossRef]
- Rosenfeld, A. Digital topology. Am. Math. Mon. 1979, 86, 76–87. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Klette, R. Digital geometry. Inf. Sci. 2003, 148, 123–127. [Google Scholar] [CrossRef]
- Šlapal, J. Topological structuring of the digital plane. Discret. Math. Theor. Comput. Sci. 2013, 15, 165–176. [Google Scholar]
- Wyse, F.; Marcus, D. Solution to problem 5712. Am. Math. Mon. 1970, 77, 1119. [Google Scholar]
- Berge, C. Graphs and Hypergraphs, 2nd ed.; North-Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Boldi, P.; Vigna, S. Fibrations of graphs. Discrete Math. 2002, 243, 21–66. [Google Scholar] [CrossRef]
- Gross, J.L.; Tucker, T.W. Topological Graph Theory; John Wiley and Sons: New York, NY, USA, 1987. [Google Scholar]
- Rosenfeld, A. Continuous functions on digital pictures. Pattern Recognit. Lett. 1986, 4, 177–184. [Google Scholar] [CrossRef]
- Han, S.-E. Estimation of the complexity of a digital image form the viewpoint of fixed point theory. Appl. Math. Comput. 2019, 347, 236–248. [Google Scholar]
- Han, S.-E. Digital k-Contractibility of an n-times Iterated Connected Sum of Simple Closed k-Surfaces and Almost Fixed Point Property. Mathematics 2020, 8, 345. [Google Scholar] [CrossRef]
- Herman, G.T. Oriented surfaces in digital spaces. CVGIP Graph. Model. Image Process. 1993, 55, 381–396. [Google Scholar] [CrossRef]
- Munkres, J.R. Topology A First Course; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1975. [Google Scholar]
- Han, S.-E. Fixed point sets of k-continuous self-maps of m-iterated digital wedges. Mathematics 2020, 8, 1617. [Google Scholar] [CrossRef]
- Spanier, E.H. Algebraic Topology; McGraw-Hill Inc.: New York, NY, USA, 1966. [Google Scholar]
- Massey, W.S. Algebraic Topology; Springer: New York, NY, USA, 1977. [Google Scholar]
- Boxer, L.; Staecker, P.C. Fixed point sets in digital topology, 1. Appl. Gen. Topol. 2020, 21, 87–110. [Google Scholar] [CrossRef]
- Han, S.-E.; Ózçağ, S. The fixed point property of the infinite M-sphere. Mathematics 2020, 8, 599. [Google Scholar] [CrossRef]
- Han, S.-E. The fixed point property of the infinite K-sphere in the set Con★((ℤ2)*). Filomat 2020, in press. [Google Scholar]
- Mitrović, Z.D.; Radenović, S.; Reich, S.; Zaslavski, A.J. Iterating nonlinear contrative mapoing in Banach spaces. Carpatian J. Math. CJM 2020, 36, 287–294. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).