Abstract
The main focus of this study was to develop a numerical scheme with new expressions for interface flux approximations based on the upwind approach in the finite volume method. Our new proposed numerical scheme is unconditionally stable with second-order accuracy in both space and time. The method is based on the second-order formulation for the temporal approximation, and an upwind approach of the finite volume method is used for spatial interface approximation. Some numerical experiments have been conducted to illustrate the performance of the new numerical scheme for a convection–diffusion problem. For the phenomena of convection dominance and diffusion dominance, we developed a comparative study of this new upwind finite volume method with an existing upwind form and central difference scheme of the finite volume method. The modified numerical scheme shows highly accurate results as compared to both numerical schemes.
Keywords:
finite volume method; second-order; convection–diffusion problem; stability; convergence order MSC:
26A33; 35R11; 65M12
1. Introduction
Partial differential equations (PDEs) have a vital role in describing different phenomena in real life. Such applications appear in many fields—in industry, biology, agriculture, petro-chemistry, heat transfer in draining films, the spread of solutes in liquid flowing through a tube, flow in porous media, meteorology and electric discharge [1,2,3,4,5,6]. Fluid dynamics is an important scientific area where governing equations are most often differential equations, and any analytical solutions for these equations are only possible for a restricted and limited number of cases. Due to this, several numerical techniques have been developed for the numerical approximations of convection–diffusion problems [7,8,9,10,11,12,13,14,15,16,17,18]. The most common numerical techniques are based on the finite difference method, the finite volume method and the finite element method. The comparison of finite difference and finite volume method for the numerical approximation of the convection–diffusion equation was studied in the papers [19,20,21,22]. The finite volume method is a special kind of numerical approach which is widely used for solving convection–diffusion problems in computational fluid dynamics [23,24,25,26,27] and also to simulate advection-diffusion problems with convection dominated processes [28,29,30]. The numerical simulation and the error estimate of steady-state convection–dominated diffusion problem was investigated in [31] using a cell-vertex finite volume approximation, whereas [32] used cell-centered finite difference approximations for a steady-state convection–diffusion problem to get second-order convergence that fulfilled the discrete maximum principle with discrete Sobolev spaces. By looking at the work in [33] a singular perturbed convection–diffusion problem was discretized with the help of the upwind finite volume scheme with uniform point-wise convergence over layer-adapted meshes. The authors [34] discussed the numerical solution of the unsteady-state advection-diffusion problem in two dimensions using the upwind finite volume method and an alternating-implicit, upwind finite volume method. Numerical simulations of non-Newtonian fluids were investigated using the finite volume formulation [35], where the approximation of the convection process is managed by using the QUICK differences scheme. A two-dimensional, incompressible in-viscid-free surface was simulated in [36] and they used the level set method for capturing the interface. A numerical solution of the convection–diffusion problem with variable coefficients over the nonstandard control volume grid was analyzed in [37] using the weighted upwind finite volume method. In the [38] finite volume method combined with the Lattice–Boltzmann method was studied for discretizing the convection operator over different regions, whereas [39] discussed the error estimation of the non-linear advection operator using the upwind finite volume method over a geometric corrector. In the meantime, the convergence analysis for the general initial and boundary condition with linear transport problems over the regularity property was solved in [40] using the upwind finite volume method.
Since in flow simulations it is imperative to satisfy conservation laws at all levels [41], by avoiding generation and consumption of mass, energy and momentum due to artificial terms inside the control volume, this is not guaranteed in finite difference and finite element methods. The control volume integration is a key step in the finite volume method, which ensures the conservation of relevant properties at each finite control cell level. This control volume integration gives a semi–discretize conservation law which involves fluxes at the interfaces of control volumes. The most popular forms of the finite volume method discretization are cell-centered, vertex-centered and face-centered [42]. The important contributions of the finite volume method are that it can also be formulated in the physical space on unstructured meshes and it is relatively easy to implement a variety of boundary conditions in a non-invasive manner [43].
The numerical schemes for time-dependent problems are known as explicit, implicit and fully implicit based on the chosen temporal approximation. One of the most common and widely used techniques for temporal approximation is the Crank–Nicolson method [44,45]. This technique forms a second-order implicit scheme in time. John Crank and Phyllis Nicolson constructed this well-known numerical technique in the mid 20th century [44,46,47,48,49,50,51]. In the past, based on spatial interface approximations, several finite volume numerical schemes were developed to solve the convection–diffusion problem.
In this study, based on the upwind approach, new expressions were obtained for spatial approximation at the interface. Crank–Nicolson formulation is used for the approximation along the temporal direction, and using these new interface approximations, a numerical scheme was developed for the numerical approximation of convection–diffusion problem. This newly developed scheme is unconditionally stable and gives second-order accuracy. Some numerical experiments have been carried out to validate our newly developed theoretical algorithm for the upwind approach, and we have compared the numerical results of our modified upwind approach with the central differences scheme and the most common upwind approach [4,21], and the numerical approximation of the unsteady convection–diffusion problem.
The paper is organized as follows: we have introduced preliminary remarks and definitions in Section 2. We have also shown the discretized and formulated form of our problem in Section 3, and in Section 4, the numerical scheme is treated and analyzed with the boundary condition. In addition, our stability and convergence order analysis are discussed using the von Neumann–Fourier method in Section 5. In Section 6, numerical experiments are shown to verify our theoretical study and the conclusions are presented in Section 7.
2. Preliminary Remarks
Definition 1.
The finite volume method is an integration-based numerical method, where after integration, we need to approximate the variables at interfaces and different choices of interface approximations give rise to different numerical schemes. The existing and most common techniques for interface approximation are central difference approximation (piece-wise linear profile assumption) and upwind approach approximation (stepwise profile assumption). Interface approximation using central difference approach are given as
Definition 2.
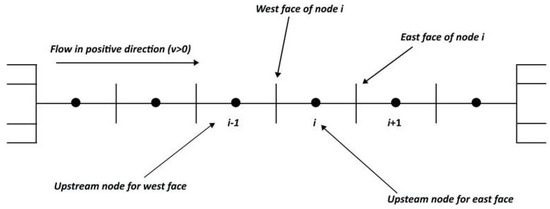
The upwind or donor cell approach takes into account the flow direction. This approach makes the interface approximation in terms of the upstream node, which means the stronger influencing node at the interface (see Figure 1). In the positive directional flow, the upstream node for west and east faces are respectively

Figure 1.
Upstream and downstream nodes for a flow in positive direction.
And for downwind or negative directional flow, the upstream nodes for interfaces are defined as
Definition 3.
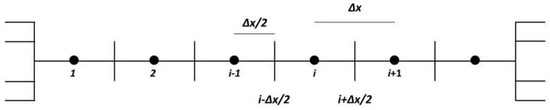
In the theory of finite volume method, interface Γ is the common boundary of adjacent control volumes; it can be divided into two classes, internal faces (between two control volumes) and boundary faces (which coincide with the boundaries of the physical domain). Let the computational domain Ω be divided into sub-domains also called control volumes as
The boundary of the control volume is express as:
where denotes the number of faces or edges of a control volume. In our one dimensional study, each control volume has two edges, i.e., = 2 (see Figure 2), whereas, for triangular and quadrilateral cells, there are 3 and 4 respectively. On a uniform and structured mesh, cells centers or computational nodes are indexed by subscript i or (i,j) for one and two-dimensional domains respectively. For an interface between the cell i and the useful subscript notation is (see in Figure 2).

Figure 2.
Node and face generation in a uniform discretization of finite volume method.
Remark 1.
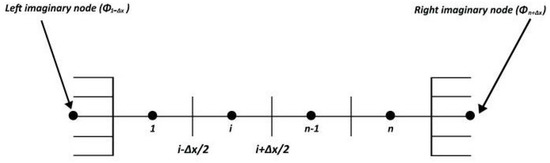
In our study, by taking the transportiveness of the property or flow direction under consideration, we have obtained new expressions for the interface approximation, and for the treatment of boundary nodes we have adjusted imaginary or mirror nodes and at a distance of outside the left and right boundaries of computational domain shown (indicated in Figure 3) which are approximated by:

Figure 3.
Indication of imaginary nodes for the treatment of boundary nodes.
Lemma 1
([40,52,53]). Let be a bounded smooth domain and let T > 0; then the transportive linear equation with initial and boundary conditions
with being constant coefficients, has a finite and unique solution.
3. Discretization and Formulation of the Problem
The convection–diffusion equation can be either convection or diffusion dominated; it depends on the rate of convection and the rate of diffusion. The impact of convection on the transport of physical quantity is measured by Reynold number or the local Peclet number . For the discretization we have used the domains and . Consider the one-dimensional convection–diffusion equation with constant coefficients:
with initial condition
and boundary condition
where represent the convective velocity and diffusion coefficient respectively, whereas is the variable convected in x-direction. and are called convective (sometimes advective) and diffusive (sometimes viscous) terms respectively. For easy implementation of the new upwind approach of the finite volume method, we do not consider the source/sink term in our discretization of the Equation (1). The term convection means the movement of molecules within the fluid. In contrast, diffusion describes the spread of particles through the random motion from the region of high concentration to lower concentration region. In problems in which fluid flow plays important roles, we must consider the effects of convection dominance. A uniform discretization of the finite volume method is shown in Figure 2.
By integrating the problem over the control volume, around the nodal point i.
Here, the first term will be approximated by using trapezoidal rule for numerical integration
Here we need to make an approximation of variable and its gradients at the interface, as gradients will be approximated using central difference approximation as
Remark 2.
One of the major inadequacies of the central difference scheme is its inability to identify the flow direction while approximating these interface fluxes. This scheme treats equally (taking the average value) both neighbor nodes of any interface when approximating the variable at interface, whereas the existing and commonly used upwind approach considers the flow direction with the first-order accuracy. In the current study a numerical scheme based on upwind approach is proposed with second-order accuracy.
For an upwind approach, The upstream or high influential node for each interface of ith control volume is indicated in Figure 1. In the case of the upwind approach () the flow is coming from the left side and approximates at its east face in terms of its upstream node will be:
Here can be approximated by using the central difference approximation between the nodes and as follows:
This Equation (6), shows our expression for east interface approximation based on the upwind approach (). Now for the upwind approach () the west face will be approximated by its upstream node :
Here can be approximated by central difference scheme approximation between the node and as follows:
Substitute this approximation into (7) and it becomes:
This Equation (8) shows our approximation at the west interface of the ith control volume when (). Now substitute the approximations given in Equations (3), (4), (6) and (8) in above semi-discretized Equation (2); we get:
After some simplification we get:
After some rearrangements, the above expression becomes:
Here method is used to evaluate the temporal integration:
where
For the Crank–Nicolson scheme = and also divide by
Let the coefficients be
This Equation (13) shows our numerical scheme based on the upwind approach of the finite volume method, and it is valid for interior nodes from node 3 to with the convergence of second-order in both space and time. For and this scheme gives , and which we do not have in our computational domain; such cells are called ghost cells and values for these cells are called ghost values. For the special treatment of these boundary nodes (see in Section 4), our modified scheme holds the property of boundedness and also ensures the conservation of the variable using the consistent and same approximation expressions for a common interface of the two adjacent control volumes.
Remark 3.
For a downwind approach also we have define the upstream nodes (see Definition 2) and in the case of the downwind approach, i.e., , our interface approximations will be
With these interface approximations for the downwind approach the numerical scheme will be
4. The Formulation of the Problem within the Analysis of Boundary Conditions
The boundary nodes 1, 2 and n need special treatment for the discretization of a governing equation over these nodes.
For node 1 the wet face is known because it coincides with the left boundary of the physical domain.
The east face of node 1 can be approximate from Equation (6) by taking . For the approximation of east face of node 1 we have adjusted an imaginary node outside the boundary of the domain at a distance (see in Remark 1 and Figure 3). For east face of node 1, Equation (6) becomes
Here is our left imaginary node; substitute its approximated value (see Remark 1) in Equation (15)
This expression (16) shows the east face approximation of node 1. By substituting the approximations in expression (14) and (16) into Equation (2), the discretized equation for node 1 will be
This is the discretized equation for node 1. As the uniqueness and major advantage of the finite volume method is to ensure the conservation of variable by using the consistent expression for a common interface between two adjacent control volumes, the west face of node 2 and east face of node 1 must have same approximation expression:
The east face of node 2 can be approximated from expression (6) by taking .
Using the expressions (18) and (19) for west and east face approximations of node 2 respectively, the expression (2) after some simplification and applying the method gives the discretized equation for node 2 as
This is the final discretized equation for node 2. The upstream node for east face is node n and can by approximated form expression (6) by taking :
is our right side imaginary node (see Figure 3); put the approximation of imaginary node (see Remark 1) in Equation (21) and it becomes
is known because it lies over the right boundary of physical domain. The west face can be approximated using Equation (8) by taking :
5. Theoretical Aspects and Analysis of the Numerical Scheme
5.1. Stability Analysis
In this section, our objective is to find the stability region for the modified scheme of the finite volume method. The von Neumann technique based on Fourier mode analysis is used. Now the the stability of a scheme actually requires .
Theorem 1.
Let be the numerical approximation of the exact solution ; then scheme (13) is unconditionally stable over a finite domain and .
Proof of Theorem 1.
In Fourier analysis the amplification factor of error is represented by where is a time dependent variable, s represents and is wave number with associated wavelength . When we apply this factor to our scheme (13), its error equation becomes
Simplification and collecting like-terms:
Then, we can find the factor at time-level as:
By further simplification we get:
After simplification of coefficients, expression (25) can be expressed in a simple form:
and are complex numbers in where :
As we know, for two complex numbers we have the inequality
This implies
Using this inequality, expression (27) becomes
From the Expression (29) it is clear that the magnitude is bounded, which indicates that the numerical scheme is unconditionally stable, as we expected. It means that there are no restrictions on the spatial and temporal step sizes and respectively, but we should choose and in such a way that the accuracy order of the scheme should not be degraded. □
5.2. Convergence Analysis of the Scheme
Theorem 2.
Proof of Theorem 2.
The numerical approximation gives an error at each grid point defined as where and ; we have from our numerical scheme (13),
if :
if
where and c is a positive constant which is independent of and .
We can use the mathematical induction to prove the Theorem 2. Let and assume
Suppose that if ; hold and assume ; let
which completes the proof. □
6. Numerical Experiments
1. Let be the property transported by means of convection and diffusion processes through one dimensional domain. Using equally spaced cells with the modified scheme of the finite volume method for the convection–diffusion equation, calculate the distribution of . The analytical solution of the problem given in [15] by is considered on the finite domain . The initial and boundary values are calculated from the exact solution by taking and , respectively.
For time step and spatial step size the convection–diffusion problem is solved using a modified upwind approach of the finite volume method, obtaining numerical solution and maximum are shown in Figure 4.
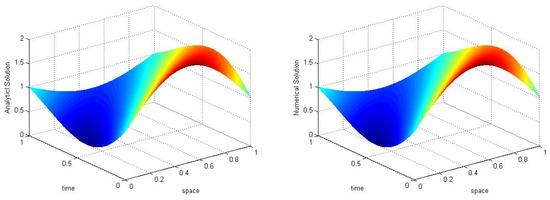
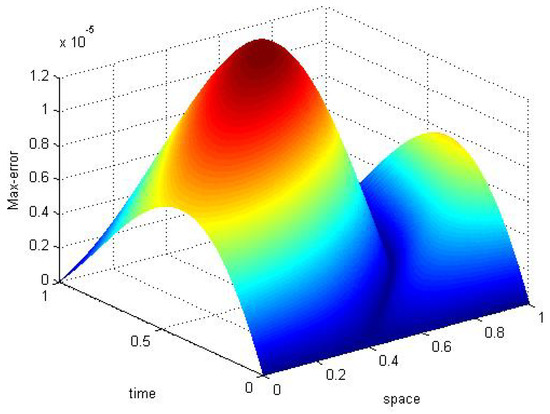
Figure 4.
Analytical solution with numerical solution and Max-error are shown for convection -diffusion problem taking gives for numerical example 1.
The spatial and temporal convergence order of the newly constructed scheme are displayed in Table 1 and Table 2, respectively. In Table 1 spatial convergence has been proved for temporal step sizes and , whereas spatial step size taken as and . In Table 2 results for the temporal convergence order have been shown. Temporal convergence order is proved for spatial step size () taken as and ,;the temporal step size () is or . The obtained spatial and temporal convergence order mentioned in Table 1 and Table 2 supports our theoretical approach about the convergence order of our scheme (see Section 3 and Section 5.2).

Table 1.
Spatial convergence order taking fixed temporal step size with and

Table 2.
Temporal convergence order taking fixed spatial step size with and
2. Consider a homogeneous one dimensional convection–diffusion problem over a computational domain, ; its exact solution is given in [16] as: with as the convection velocity to the direction and as the diffusion coefficient. Now, we can find the transported property for two different cases of convection dominance and diffusion dominance respectively, using the modified upwind finite volume method with equally spaced cells. The initial and boundary values are calculated from an exact solution by taking and , respectively.
In Figure 5 numerical results for the convection dominant case () are expressed. The left figures show the numerical approximation and maximum error of the modified upwind finite volume method. In contrast, figures on the right side represent the numerical solution and maximum error using an existing upwind finite volume method for the convection–diffusion problem. In this case, the numerical value of maximum error produced by the new upwind scheme was 3.1930 ×, but for the existing upwind scheme, the maximum error was . This indicates new upwind scheme has the ability to deal with a dominant convection problem numerically as compared to the existing upwind scheme, and this shows consistency with our theoretical approach.
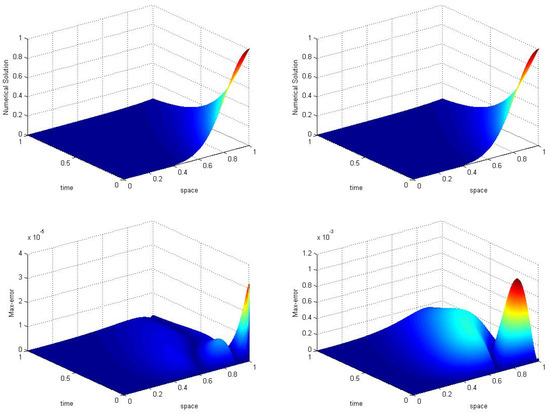
Figure 5.
Numerical solution and max-error of modified FVM (left) and existing upwind FVM (right) for convection dominant phenomenon taking ( for numerical example 2).
Table 3 and Table 4 respectively show the maximum errors with spatial convergence order and temporal convergence order respectively, for the new scheme and existing upwind scheme of finite volume method. The spatial order of convergence in the case of convection dominance (k = 0.4 and v = 1) has been proven for temporal step sizes 1/5000 and 1/10,000. For temporal convergence order, spatial discretization width is taken as and . The results shown in both tables support to our theoretical algorithm.

Table 3.
Spatial convergence order of new upwind FVM and existing upwind approach of FVM taking in the case of convection dominance.

Table 4.
Temporal convergence order of new upwind FVM and existing upwind approach of FVM taking in the case of convection dominance.
In Figure 6 numerical results for the diffusion dominant case are expressed. Left figures show the numerical approximation and maximum error of the modified upwind finite volume method. In contrast, figures at the right side represent the numerical solution and maximum error using an existing upwind finite volume method for the convection–diffusion problem. In this case, the numerical value of maximum error produced by the new upwind scheme is , but for the existing upwind scheme, it is . This implies that for a dominant diffusion problem, the new upwind scheme gives a higher accuracy solution than the existing upwind FVM.
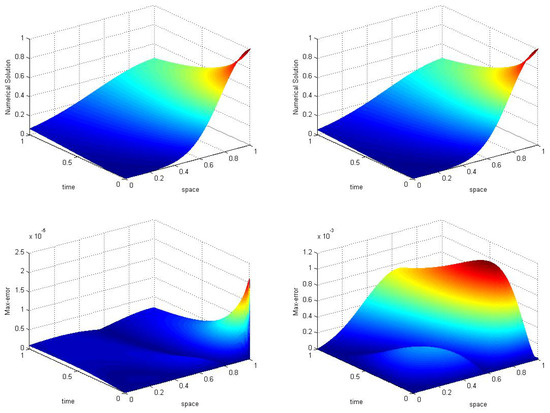
Figure 6.
Numerical solution and max-error of modified FVM (left) and existing upwind FVM (right) for diffusion dominant phenomenon taking ( = 1/320 , for numerical example 2).
Table 5 and Table 6 respectively show the maximum error with spatial convergence order and temporal convergence order for the new numerical scheme and existing upwind scheme of finite volume method in the case of diffusion dominance. To prove the spatial and temporal convergence order in case of diffusion dominance, coefficients are taken as and . For temporal convergence, the numbers of spatial nodes are taken as and 400. For spatial convergence, time level is fixed at and 10,000. The results shown in both tables support to our theoretical algorithm. From both tables it is clear that the new upwind scheme gives less maximum error; this implies that the numerical approximation is highly accurate as compared to the existing numerical scheme.

Table 5.
Spatial convergence order of new upwind FVM and existing upwind approach of FVM taking in case of diffusion dominance.

Table 6.
Temporal convergence order of new upwind FVM and existing upwind approach of FVM taking in case of convection dominance.
Figure 7 shows the numerical approximation (for numerical example 2) of the convection–diffusion problem using the modified upwind finite volume method with different time levels. Numerically, we have tested the modified scheme for convection dominance (see left of Figure 7) and for diffusion dominance (see right of Figure 7). Both figures indicate that the increase of the time level for a numerical solution using our proposed numerical scheme get closeness to an exact solution.
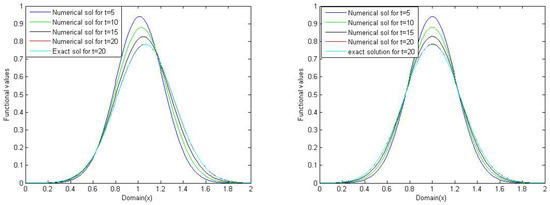
Figure 7.
Numerical approximation for convection dominance (at (left) with ) and diffusion dominance (at (right) with ) taking for numerical example 2.
3. Consider a homogeneous one dimensional convection–diffusion problem over a computational domain, where its exact solution is given in [16] as: with is the convection velocity to the direction and is the diffusion coefficient. Now, we can find the transported property for two different cases of convection dominance using new upwind finite volume method with equally spaced cells. The initial and boundary values are calculated from the exact solution by taking and , respectively. We took time step and spatial step size . This numerical experiment also shows a numerical comparison of the modified finite volume method and the most common form (central difference scheme) of finite volume method for the approximation of the convection–diffusion problem.
In Figure 8 and Figure 9 numerical approximations using new form of finite volume method and the most central difference scheme of FVM are compared for different cases of convection dominance. When we compare the max-errors of both numerical schemes, in the first case (when and ) the max-errors produced by new FVM scheme and central (FVM) scheme are and respectively. For the second convection dominance case () the new scheme gives max-error and the central scheme gives . This implies that, for both cases, this newly constructed FVM scheme gives highly accurate results and it has the good capability to deal with convection dominance as compared to the central scheme of finite volume method.
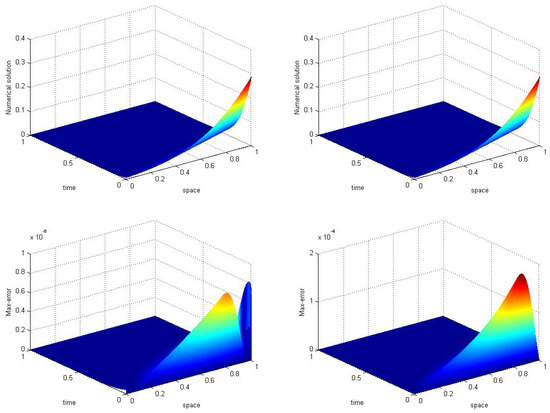
Figure 8.
Numerical solution and max-error using modified FVM (Left) and central scheme of FVM (right) for convection dominance taking for numerical example 3).
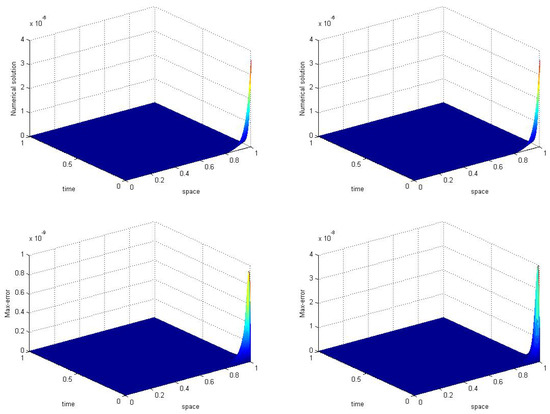
Figure 9.
Numerical solution and max-error using modified FVM (Left) and central scheme of FVM (right) for right for convection dominance taking ( for numerical example 3).
Figure 10 shows the numerical behavior of both numerical schemes for different values of the Peclet number (). Figure 10 left and right express the results for and respectively. From both figures, it is clear that the central difference scheme produces a solution that appears to oscillate about the exact solution. These oscillations are often called “wiggles” in the literature. The consistency with the analytical solution is weak as compared to the modified scheme of finite volume method.
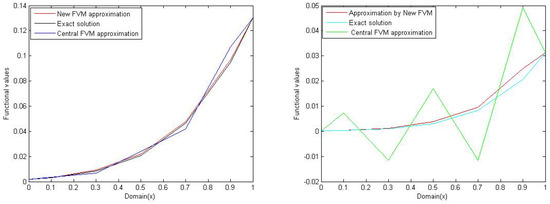
Figure 10.
Comparison of numerical approximation with exact solution taking for numerical example 3.
7. Conclusions
In this article, an upwind approach of finite volume method is proposed to treat the convection–diffusion equation numerically with the Dirichlet-type boundary condition. With the consideration of convection dominance or flow direction, new expressions for interface approximations have been obtained for the directional flow phenomenon, and using those approximations a numerical scheme was developed with second-order accuracy in both space and time. The stability of this modified method has been discussed and it was shown that it is unconditionally stable; it has been numerically proven too. The convection diffusion equations for different values of convective velocity and diffusion coefficient have been numerically solved by this newly developed upwind approach, and also we have displayed the numerical results of convergence order for space and time which are consistent with our modified theoretical algorithm. The performance of this current numerical scheme for the convection–diffusion problem has been studied by measuring the maximum error and convergence order for convection and diffusion dominance phenomena. We showed a numerical comparison of our modified upwind approach of the finite volume method with an existing upwind approach of the finite volume method and an upwind approach of the finite difference method. The numerical results produced by these numerical methods indicate that our proposed numerical scheme gives numerical results which are highly accurate and near to the exact solution, so this approach is a good alternative to some existing ones for solving physical problems.
Author Contributions
The authors equally contributed. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Key Research (grant number 2017YFB0305601) and Development Program of China (grant number 2017YFB0701700).
Acknowledgments
The authors are thankful to the editor and the anonymous reviewers for their meaningful comments to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 6. [Google Scholar]
- Hrvoje, J. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows; Imperial College: London, UK, 1996. [Google Scholar]
- Lemos, E.M.; Secchi, A.R.; Biscaia, E.C., Jr. Development of high-order finite volume method with multiblock partition technique. Braz. J. Chem. Eng. 2012, 29, 183–201. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: Edinburgh, UK, 2007. [Google Scholar]
- Fuhrmann, J.; Ohlberger, M.; Rohde, C. Finite Volumes for Complex Applications VII: Methods and Theoretical Aspects; Springer; FVCA: Berlin, Germany, 2014; Volume 77. [Google Scholar]
- Arminjon, P.; Smith, L. Upwind finite volume schemes with anti—Diffusion for the numerical study of electric discharges in gas-filled cavities. Comput. Methods Appl. Mech. Eng. 1992, 100, 149–168. [Google Scholar] [CrossRef]
- Causona, D.; Mingham, C.; Qia, L. Introductory Finite Volume Methods for PDEs; Manchester Metropolitan University: Manchester, UK, 2011. [Google Scholar]
- Karahan, H. Solution of weighted finite difference techniques with the advection—Diffusion equation using spreadsheets. Comput. Appl. Eng. Edu. 2008, 16, 147–156. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, C.; Zhang, J. Relaxation method for unsteady convection—Diffusion equations. Comput. Math. Appl. 2011, 61, 908–920. [Google Scholar] [CrossRef][Green Version]
- Dehghan, M. On the numerical solution of the one-dimensional convection—Diffusion equation. Math. Probl. Eng. 2005, 2005, 456730. [Google Scholar] [CrossRef]
- Wei, T.; Xu, M. An integral equation approach to the unsteady convection—Diffusion equations. Appl. Math. Comput. 2016, 274, 55–64. [Google Scholar] [CrossRef]
- Mohammadi, R. Exponential B—Spline solution of convection—Diffusion equations. Appl. Math. 2013, 4, 933–944. [Google Scholar] [CrossRef]
- Tian, Z.F.; Yu, P.X. A high-order exponential scheme for solving 1D unsteady convection–diffusion equations. J. Comput. Appl. Math. 2011, 235, 2477–2491. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Gresho, P.M.; Griffiths, D.F. The stability of explicit Euler time-integration for certain finite difference approximations of the multi-dimensional advection—Diffusion equation. Int. J. Numer. Methods Fluids 1984, 4, 853–897. [Google Scholar] [CrossRef]
- Peng, H.F.; Yang, K.; Cui, M.; Gao, X.W. Radial integration boundary element method for solving two-dimensional unsteady convection–diffusion problem. Eng. Anal. Bound. Elem. 2019, 102, 39–50. [Google Scholar] [CrossRef]
- Mohammadi, A.; Manteghian, M.; Mohammadi, A. Numerical solution of the one-dimensional advection-diffusion equation using simultaneously temporal and spatial weighted parameters. Aust. J. Basic Appl. Sci. 2011, 6, 1536–1543. [Google Scholar]
- Lazarov, R.D.; Mishev, I.D.; Vassilevski, P.S. Finite volume methods for convection-diffusion problems. SIAM J. Numer. Anal. 1996, 33, 31–55. [Google Scholar] [CrossRef]
- Anley, E.F.; Zheng, Z. Finite difference approximation method for a space fractional convection—Diffusion equation with variable coefficients. Symmetry 2020, 12, 485. [Google Scholar] [CrossRef]
- Shukla, A.; Singh, A.K.; Singh, P.; Shukla, A.; Singh, A.K.; Singh, P.A. comparative study of finite volume method and finite difference method for convection-diffusion problem. Am. J. Comput. Appl. Math. 2011, 1, 67–73. [Google Scholar] [CrossRef]
- Liu, R.; Wang, D.; Zhang, X.; Li, W.; Yu, B. Comparison Study on the Performances of Finite Volume Method and Finite Difference Method. J. Appl. Math. 2013, 2013, 596218. [Google Scholar] [CrossRef]
- Botte, G.G.; Ritter, J.A.; White, R.E. Comparison of finite difference and control volume methods for solving differential equations. Comput. Chem. Eng. 2000, 24, 2633–2654. [Google Scholar] [CrossRef]
- Mazumder, S. Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods; Academic Press: London, UK, 2015. [Google Scholar]
- Zhang, T.; Zheng, L. A finite volume method for Stokes problems on quadrilateral meshes. Comput. Math. Appl. 2019, 77, 1091–1106. [Google Scholar] [CrossRef]
- ten Thije Boonkkamp, J.H.M.; Anthonissen, M.J.H. The finite volume-complete flux scheme for advection-diffusion-reaction equations. J. Sci. Comput. 2011, 46, 47–70. [Google Scholar] [CrossRef]
- Xu, M. A modified finite volume method for convection-diffusion-reaction Problems. Int. J. Heat Mass Transf. 2018, 117, 658–668. [Google Scholar] [CrossRef]
- Cordero, E.; De Biase, L.; Pennati, V. A new finite volume method for the solution of convection–diffusion equations: Analysis of stability and convergence. Commun. Numer. Methods Eng. 1997, 13, 923–940. [Google Scholar] [CrossRef]
- Anley, E.F. Numerical solutions of elliptic partial differential equations by using finite volume method. Pure Appl. Math. J. 2015, 5, 120–129. [Google Scholar] [CrossRef]
- Kinney, R.B.; Mahdi, H.S. A new finite-volume approach with adaptive upwind convection. Int. J. Numer. Methods Eng. 1988, 26, 1325–1343. [Google Scholar] [CrossRef]
- Pan, D.; Chang, C.H. Upwind finite-volume method for natural and forced convection. Numer. Heat Transf. Part B Fundam. 1994, 25, 177–191. [Google Scholar] [CrossRef]
- Manzini, G.; Russo, A. A finite volume method for advection–diffusion problems in convection-dominated regimes. Comput. Methods Appl. Mech. Eng. 2008, 197, 1242–1261. [Google Scholar] [CrossRef]
- Morton, K.; Stynes, M.; Suli, E. Analysis of a cell-vertex finite volume method for convection-diffusion problems. Math. Comput. 1997, 66, 1389–1406. [Google Scholar] [CrossRef]
- Lararov, R.D.; Mishev, I.D.; Vassilevski, P.S. Finite volume methods with local refinement for convection-diffusion problems. Computing 1994, 53, 33–57. [Google Scholar] [CrossRef]
- Linss, T. Uniform point-wise convergence of an upwind finite volume method on layer-adapted meshes. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. Appl. Math. Mech. 2002, 82, 247–254. [Google Scholar]
- Wang, H.; Zhao, W. An upwind finite volume scheme and its maximum-principle-preserving ADI splitting for unsteady-state advection-diffusion equations. Numer. Methods Partial Differ. Equ. Int. J. 2003, 19, 211–226. [Google Scholar] [CrossRef]
- Neofytou, P. A third order upwind finite volume method for generalized Newtonian fluid flows. Adv. Eng. Softw. 2005, 36, 664–680. [Google Scholar] [CrossRef]
- Yang, A.; Chen, S.; Yang, L.; Yang, X. An upwind finite volume method for incompressible inviscid free surface flows. Comput. Fluids 2014, 101, 170–182. [Google Scholar] [CrossRef]
- Liang, D.; Zhao, W. The Weighted upwinding finite volume method for the convection—Diffusion problem on a nonstandard covolume grid. Appl. Numer. Anal. Comp. Math. 2004, 1, 180–194. [Google Scholar] [CrossRef]
- Stiebler, M.; Tolke, J.; Krafczyk, M. An upwind discretization scheme for the finite volume lattice Boltzmann method. Comput. Fluids 2006, 35, 814–819. [Google Scholar] [CrossRef]
- Bouche, D.; Ghidaglia, J.; Pascal, F.P. Error estimate for the upwind finite volume method for the nonlinear scalar conservation law. J. Comput. Appl. Math. 2011, 235, 5394–5410. [Google Scholar] [CrossRef][Green Version]
- Boyer, F. Analysis of the upwind finite volume method for general initial-and boundary-value transport problems. IMA J. Numer. Anal. 2012, 32, 1404–1439. [Google Scholar] [CrossRef]
- Lin, S.Y.; Chin, Y.S. An upwind finite-volume scheme with a triangular mesh for conservation laws. J. Comput. Phys. 1990, 107, 324–337. [Google Scholar] [CrossRef]
- Vieira, L.M.; Giacomini, M.; Sevilla, R.; Huerta, A. A second-order face-centred finite volume method for elliptic problems. Comput. Methods Appl. Mech. Eng. 2020, 358, 112655. [Google Scholar] [CrossRef]
- Pan, D.; Cheng, J.-C. A second-order upwind finite-volume method for the Euler solution on unstructured triangular meshes. Int. J. Numer. Meth. Fluids 1993, 16, 1079–1098. [Google Scholar] [CrossRef]
- Piskarev, S.; Zwart, H. Crank-Nicolson scheme for abstract linear system. Numer. Funct. Anal. Optim. 2007, 26, 717–736. [Google Scholar] [CrossRef]
- Gu, W.; Wang, P. A Crank Nicolson difference scheme for solving a type of variable coefficient delay partial differential equations. J. Appl. Math. 2014, 2014, 560567. [Google Scholar] [CrossRef]
- Siddque, M. Smoothing of Crank–Nicolson scheme for the two-dimensional diffusion with an integral condition. Appl. Math. Comput. 2009, 214, 512–522. [Google Scholar] [CrossRef]
- Luskin, M.; Rannacher, R.; Wendland, W. On the smoothing property of the crank-nicolson scheme. Appl. Anal. 1982, 14, 117–135. [Google Scholar] [CrossRef]
- Oishi, C.M.; Yuan, J.Y.; Cuminato, J.A.; Stewart, D.E. Stability analysis of Crank–Nicolson and Euler schemes for time-dependent diffusion equations. BIT Numer. Math. 2015, 55, 487–513. [Google Scholar] [CrossRef]
- Nassif, N.R. Numerical solution of parabolic problems by the generalized Crank-Nicolson schemme. Calcolo 1975, 12, 51–61. [Google Scholar] [CrossRef]
- Van, C.J.A. On the Crank-Nicolson scheme once again. J. Evol. Equ. 2011, 11, 457–476. [Google Scholar]
- Kadalbajoo, M.K.; Awasthi, A. A numerical method based on Crank-Nicolson scheme for Burgers’ equation. Appl. Math. Comput. 2006, 182, 1430–1442. [Google Scholar] [CrossRef]
- Anderson, J.R. Local existence and uniqueness of solutions of degenerate parabolic equations. Comm. Partial. Differ. Equ. 1991, 16, 105–143. [Google Scholar] [CrossRef]
- Gilding, B.H.; Kersner, R. The characterization of reaction-convection-diffusion processes by travelling waves. J. Differ. Equ. 1996, 124, 27–79. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).