Unpredictable Solutions of Linear Impulsive Systems

Abstract

We consider a new type of oscillations of discontinuous unpredictable solutions for linear impulsive nonhomogeneous systems. The models under investigation are with unpredictable perturbations. The definition of a piecewise continuous unpredictable function is provided. The moments of impulses constitute a newly determined unpredictable discrete set. Theoretical results on the existence, uniqueness, and stability of discontinuous unpredictable solutions for linear impulsive differential equations are provided. We benefit from the B-topology in the space of discontinuous functions on the purpose of proving the presence of unpredictable solutions. For constructive definitions of unpredictable components in examples, randomly determined unpredictable sequences are newly utilized. Namely, the construction of a discontinuous unpredictable function is based on an unpredictable sequence determined by a discrete random process, and the set of discontinuity moments is realized by the logistic map. Examples with numerical simulations are presented to illustrate the theoretical results.

1. Introduction

A new type of oscillation, called an unpredictable trajectory, was introduced in the paper [1]. An unpredictable trajectory is necessarily positively Poisson stable, and one of its distinctive features is the emergence of chaos in the corresponding quasi-minimal set. The type of chaos based on the presence of an unpredictable trajectory is called Poincaré chaos [1]. Symbolic dynamics, logistic map, and Hénon map are some examples that possess unpredictable motions [1,2]. Instead of interaction of several motions, which is a requirement in other chaos types [3,4,5], it is enough to check the existence of a single unpredictable motion to verify Poincaré chaos. Thus, the connection of unpredictable oscillations with Poincaré chaos is based on Poisson stable motions. The basics of the Poisson stable motion can be seen in [6]. In the theory of differential equations, the class of Poisson stable solutions has been intensively studied [7,8,9,10].

The theoretical basics of the present research lies in the theory of dynamical systems, which was founded H. Poincaré and G. Birkhoff [6,11]. It was the French genius, who learned that underneath of chaotic dynamics is the Poisson stable motion. The line of different types of oscillations was maintained by the notion of an unpredictable point in paper [1]. Let $(X,d)$ be a metric space and $\pi :{\mathbb{R}}_{+}\times X\to X$, where ${\mathbb{R}}_{+}$ is the set of non-negative real numbers, be a semiflow on X. A point $x\in X$ and the trajectory through it are unpredictable if there exists a positive number ${ϵ}_0$ and sequences $t_n,s_n$ both of which diverge to infinity, such that ${\displaystyle \underset{x\to \infty }{lim}\pi \left(t_n,x\right)=x}$ and $d(\pi \left(t_n+s_n,x\right),\pi \left(t_n,x\right))\ge {ϵ}_0$ for each $n\in \mathbb{N}$. In paper [1], it was proved that a Poisson stable motion equipped with the unpredictability property determines sensitivity in the quasi-minimal set. It is usual that dynamical properties generate functional ones. For example, recurrent or almost periodic motions allow us to define recurrent and almost periodic functions, respectively. Similarly, issuing from the unpredictable point introduced in [1], in paper [12] the unpredictable function was defined as a point of the Bebutov dynamics, where the state space is a set of functions. In the present research we replace the metrical state space of the dynamics with the B-topology [13], where a convergence of piecewise continuous functions on compact subsets of the real axis is utilized. This makes our suggestions more universal and effective in applications, since constructive verifiable conditions are proposed. In this study it is applied for linear impulsive systems.

Unpredictable points and unpredictable functions are becoming increasingly applicable in the study of chaos theory. For instance, some topological properties of Poincaré chaos were considered by Miller [14], and Thakur and Das [15]. Various types of differential equations with unpredictable solutions were considered in the papers [2,12,16,17,18] and in the book [19]. Recently it is proved in paper [20] that unpredictable motions take place also in random processes.

Alongside the theory of chaos, impulsive differential equations have also played an essential role from both theoretical and practical points of view over the past few decades [13,21,22,23,24,25,26,27,28,29,30]. Such differential equations describe dynamics of real world phenomena in which abrupt interruptions of continuous processes are present, and they play a crucial role in various fields such as mechanics, electronics, medicine, neural networks, communication systems, and population dynamics [31,32,33,34,35,36,37,38]. Chaos in the sense of Li-Yorke and the presence of period-doubling route to chaos in impulsive systems were investigated in the studies [39,40] by means of the replication of chaos technique.

In the present study, we show that unpredictable perturbations can lead to the presence of discontinuous unpredictable motions in the dynamics of linear impulsive systems. In the absence of the perturbation term, the linear system under investigation has a simple dynamics such that it admits an asymptotically stable regular solution. However, our results reveal that the presence of an unpredictable term dominates the behavior of the resulting dynamics and a discontinuous unpredictable solution occurs. In the present study, we also investigate the case of the presence of unpredictability in the impulsive moments. Due to the nature of impulsive systems, the concept of B-topology [13] is required for the theoretical investigation of discontinuous unpredictable solutions.

We have already obtained the essential results for ordinary linear and quasilinear systems, as well as discrete equations [17,18]. One of the main contributions of the present study is the presentation of the novel definitions of discontinuous unpredictable function and unpredictable discrete set. Another main contribution is the demonstration of the existence and uniqueness of unpredictable solutions for linear impulsive systems. Systems with both non-unpredictable and unpredictable impulsive actions are under investigation.

Benefiting from the techniques introduced in [2,12,16,19] and results on the theory of impulsive differential equations [13,21], the existence, uniqueness, and stability of discontinuous unpredictable solutions of linear impulsive systems are investigated in this study. To construct an unpredictable function, an unpredictable sequence resulting from a randomly defined discrete Bernoulli process [20] is utilized.

2. Preliminaries

Throughout the paper, $\mathbb{R}$, $\mathbb{N}$, and $\mathbb{Z}$ respectively stand for the sets of real numbers, natural numbers, and integers. Moreover, we make use of the usual Euclidean norm for vectors and the spectral norm for square matrices [41].

It is known that solutions of an impulsive system are piecewise continuous functions, which have discontinuities of the first kind. A difficulty of investigation of impulsive system is that, in general, discontinuity moments of distinct solutions do not coincide. For that reason the concept of B-topology is required in our investigations [13].

Denote by $\mathcal{R}$ the set of all functions defined on the real axis. They are continuous except countable sets of points. At the points the, functions admit one-sided limits. The sets of points do not necessarily coincide, if functions are different. The sets of points do not have finite accumulation points and are unbounded on both sides.

Two functions $F\left(t\right)$ and $G\left(t\right)$ from $\mathcal{R}$, are said to be $ϵ$-equivalent on an interval $J\subseteq \mathbb{R}$ if the points of discontinuity of the functions $F\left(t\right)$ and $G\left(t\right)$ in J can be respectively numerated ${\theta }_i^F$ and ${\theta }_i^G$, $i=1,2,\dots ,k$, such that $|{\theta }_i^F-{\theta }_i^G|<ϵ$ for each $i=1,2,\dots ,k$, and $\left|\right|F\left(t\right)-G\left(t\right)\left|\right|<ϵ$ for each $t\in J$, except those between ${\theta }_i^F$ and ${\theta }_i^G$ for each i. In the case that F and G are $ϵ$-equivalent on J, we also say that the functions are in $ϵ$-neighborhoods of each other. The topology defined with the aid of such neighborhoods is called the B-topology.

In what follows we will denote by $\left[\widehat{a_1,a_2}\right],a_1,a_2\in \mathbb{R}$, the interval $[a_1,a_2]$, if $a_1<a_2$ and the interval $[a_2,a_1]$, if $a_2<a_1$.

Let ${\theta }_i$, $i\in \mathbb{Z}$, be a sequence of real numbers such that $\underline{\theta }\le {\theta }_{i+1}-{\theta }_i\le \overline{\theta }$ for some positive numbers $\underline{\theta }$, $\overline{\theta }$, and $\left|{\theta }_i\right|\to \infty$ as $\left|i\right|\to \infty$.

Definition 1.

A piecewise continuous and bounded function $\phi \left(t\right):\mathbb{R}\to {\mathbb{R}}^p$ with the set of discontinuity points ${\theta }_i$, $i\in \mathbb{Z}$, satisfying $\phi ({\theta }_i-)=\phi \left({\theta }_i\right)$ for each $i\in \mathbb{Z}$ is called discontinuous unpredictable function (d.u.f.) if there exist positive numbers ${ϵ}_0$, σ, sequences $t_n,s_n$ of real numbers and sequences $l_n,m_n$ of integers all of which diverge to infinity such that

(a) 

$\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|\to 0$ as $n\to \infty$ on each bounded interval of integers and $\left|{\theta }_{m_n+l_n}-t_n-{\theta }_{m_n}\right|\ge {ϵ}_0$ for each natural number n;

(b) 

for every positive number ϵ, there exists a positive number δ such that $∥\phi \left({\rho }_1\right)-\phi \left({\rho }_2\right)∥<ϵ$ whenever the points ${\rho }_1$ and ${\rho }_2$ belong to the same interval of continuity and $\left|{\rho }_1-{\rho }_2\right|<\delta$;

(c) 

$\phi (t+t_n)\to \phi \left(t\right)$ as $n\to \infty$ in B-topology on each bounded interval;

(d) 

for each natural number n there exists an interval $[s_n-\sigma ,s_n+\sigma ]\subseteq [\widehat{{\theta }_{m_n},({\theta }_{m_n+l_n}}-t_n)]$ which does not contain any point of discontinuity of $\phi \left(t\right)$ and $\phi (t+t_n)$, and $\parallel \phi (t+t_n)-\phi \left(t\right)\parallel \ge {ϵ}_0$ for each $t\in [s_n-\sigma ,s_n+\sigma ]$.

In Definition 1, we call the property $\left(b\right)$conditional uniform continuity of $\phi$, the property $\left(c\right)$Poisson stability of $\phi$, and the property $\left(d\right)$unpredictability of $\phi$.

Definition 2.

Suppose that $\omega \left(t\right):\mathbb{R}\to {\mathbb{R}}^p$ is a piecewise continuous and bounded function with the set of discontinuity points ${\theta }_i$, $i\in \mathbb{Z}$, satisfying $\omega ({\theta }_i-)=\omega \left({\theta }_i\right)$ and ${\Gamma }_i$, $i\in \mathbb{Z}$, is a bounded sequence in ${\mathbb{R}}^p$. The couple $\left(\omega \left(t\right),{\Gamma }_i\right)$ is called unpredictable if there exist positive numbers ${ϵ}_0$, σ, sequences $t_n,s_n$ of real numbers and sequences $l_n,m_n$ of integers all of which diverge to infinity such that

(a) 

$\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|\to 0$ as $n\to \infty$ on each bounded interval of integers and $\left|{\theta }_{m_n+l_n}-t_n-{\theta }_{m_n}\right|\ge {ϵ}_0$ for each natural number n;

(b) 

for every positive number ϵ there exists a positive number δ such that $∥\omega \left({\rho }_1\right)-\omega \left({\rho }_2\right)∥<ϵ$ whenever the points ${\rho }_1$ and ${\rho }_2$ belong to the same interval of continuity and $\left|{\rho }_1-{\rho }_2\right|<\delta$;

(c) 

$\omega (t+t_n)\to \omega \left(t\right)$ as $n\to \infty$ in B-topology on each bounded interval;

(d) 

for each natural number n there exists an interval $[s_n-\sigma ,s_n+\sigma ]\subseteq [\widehat{{\theta }_{m_n},({\theta }_{m_n+l_n}}-t_n)]$ which does not contain any point of discontinuity of $\omega \left(t\right)$ and $\omega (t+t_n)$, and $\parallel \omega (t+t_n)-\omega \left(t\right)\parallel \ge {ϵ}_0$ for each $t\in [s_n-\sigma ,s_n+\sigma ]$;

(e) 

$\left|{\Gamma }_{i+l_n}-{\Gamma }_i\right|\to 0$ as $n\to \infty$ for each i in bounded intervals of integers and $\left|{\Gamma }_{m_n+l_n}-{\Gamma }_{m_n}\right|\ge {ϵ}_0$ for each natural number n.

Similarly to Definition 1, in Definition 2 we call the property $\left(b\right)$conditional uniform continuity of $\omega$, the property $\left(c\right)$Poisson stability of $\omega$, and the property $\left(d\right)$unpredictability of $\omega$.

The sequence ${\theta }_i,i\in \mathbb{Z}$, is said to be an unpredictable discrete set if the condition $\left(a\right)$ is satisfied.

It is clear that if the couple $\left(\omega \left(t\right),{\Gamma }_i\right)$ is unpredictable in the sense of Definition 2, then $\omega \left(t\right)$ is a discontinuous unpredictable function in the sense of Definition 1.

Obviously, Definition 1 does not follow from the Definition 2, since one cannot obtain the former just by diminishing the terms ${\Gamma }_i$. The sequence of zeros is not an unpredictable sequence. Consequently, both definitions are needed in the paper.

The definition of the unpredictable sequence is as follows.

Definition 3

([16]). A bounded sequence ${\kappa }_i,i\in \mathbb{Z}$, in ${\mathbb{R}}^p$ is called unpredictable if there exist a positive number ${\epsilon }_0$ and sequences ${\zeta }_n$, ${\eta }_n$, $n\in \mathbb{N}$, of positive integers both of which diverge to infinity such that $\parallel {\kappa }_{i+{\zeta }_n}-{\kappa }_i\parallel \to 0$ as $n\to \infty$ for each i in bounded intervals of integers and $\parallel {\kappa }_{{\zeta }_n+{\eta }_n}-{\kappa }_{{\eta }_n}\parallel \ge {\epsilon }_0$ for each $n\in \mathbb{N}$.

According to the purpose of the present study, we specify the discontinuity moments of the impulsive systems that will be investigated as

$$\begin{array}{c}\hfill {\theta }_i=iT+{\gamma }_i,i\in \mathbb{Z},\end{array}$$

(1)

where ${\gamma }_i$, $i\in \mathbb{Z}$, is a sequence of real numbers which is unpredictable in the sense of Definition 3 and $T\ge 4$ is a number such that ${\displaystyle \underset{i\in \mathbb{Z}}{sup}\left|{\gamma }_i\right|<T/h}$ for some number $h\ge 3$.

Since ${\gamma }_i,$$i\in \mathbb{Z}$, is an unpredictable sequence, there exists a positive number ${ϵ}_0$ and sequences ${\zeta }_n$, ${\eta }_n$, both of which diverge to infinity such that $|{\gamma }_{i+{\zeta }_n}-{\gamma }_i|\to 0$ as $n\to \infty$ for each i in bounded intervals of integers and $|{\gamma }_{{\zeta }_n+{\eta }_n}-{\gamma }_{{\eta }_n}|\ge {ϵ}_0$ for each natural number $n.$

Let us show that the sequence ${\theta }_i$, $i\in \mathbb{Z}$, is unpredictable discrete set. More precisely, we will demonstrate that property $\left(a\right)$ mentioned in Definition 1 is valid for ${\theta }_i$, $i\in \mathbb{Z}$, with $t_n=T{\zeta }_n$, $l_n={\zeta }_n$, and $m_n={\eta }_n$ for each natural number n. By these choices of the sequences $t_n,l_n$, and $m_n$, we have that

$$\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|=\left|(i+{\zeta }_n)T+{\gamma }_{i+{\zeta }_n}-{\zeta }_{n}T-iT-{\gamma }_i\right|=\left|{\gamma }_{i+{\zeta }_n}-{\gamma }_i\right|.$$

Therefore, $\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|\to 0$ as $n\to \infty$ for each i in bounded intervals of integers. On the other hand,

$$\left|{\theta }_{m_n+l_n}-t_n-{\theta }_{m_n}\right|=\left|({\eta }_n+{\zeta }_n)T+{\gamma }_{{\eta }_n+{\zeta }_n}-{\zeta }_{n}T-{\eta }_{n}T-{\gamma }_{{\eta }_n}\right|=\left|{\gamma }_{{\eta }_n+{\zeta }_n}-{\gamma }_{{\eta }_n}\right|\ge {ϵ}_0$$

for each natural number $n.$

Additionally, one can confirm that ${\theta }_i$, $i\in \mathbb{Z}$, defined by (1) satisfies the inequality $\underline{\theta }\le {\theta }_{i+1}-{\theta }_i\le \overline{\theta }$ with ${\displaystyle \underline{\theta }=T-\frac{2T}{h}}$ and ${\displaystyle \overline{\theta }=T+\frac{2T}{h}}$.

3. Linear Systems with Non-Unpredictable Impulses

The main object of the present section linear impulsive system,

$$\begin{array}{ccc}\hfill & & x^{\prime }\left(t\right)=Ax\left(t\right)+f\left(t\right),t\ne {\theta }_i,\hfill \\ & & {\Delta x|}_{t={\theta }_i}=Bx\left({\theta }_i\right),\hfill \end{array}$$

(2)

where $t\in \mathbb{R}$, the matrices $A\in {\mathbb{R}}^{p\times p}$ and $B\in {\mathbb{R}}^{p\times p}$ commute, the sequence ${\theta }_i$, $i\in \mathbb{Z}$, of discontinuity moments is defined by Equation (1), and $f\left(t\right):\mathbb{R}\to {\mathbb{R}}^p$ is a d.u.f. in the sense of Definition 1. We suppose that $det(I+B)\ne 0$, where I is the $p\times p$ identity matrix.

Let us denote by $X(t,u)$ the Cauchy matrix of the following linear impulsive system associated with (2),

$$\begin{array}{ccc}\hfill & & x^{\prime }\left(t\right)=Ax\left(t\right),t\ne {\theta }_i,\hfill \\ & & {\Delta x|}_{t={\theta }_i}=Bx\left({\theta }_i\right).\hfill \end{array}$$

(3)

Since the matrices A and B commute, we have for $t>u$ that

$$\begin{array}{c}\hfill X(t,u)=e^{A(t-u)}{\left(I+B\right)}^{i\left(\right[u,t\left)\right)},\end{array}$$

(4)

where $i\left(\right[u,t\left)\right)$ denotes the number of the terms of the sequence ${\theta }_i$, $i\in \mathbb{Z}$, which belong to the interval $[u,t)$, and $X(u,u)=I$ [21].

Let us denote by ${\lambda }_j$, $j=1,2,\dots ,p$, the eigenvalues of the matrix ${\displaystyle A+\frac{1}{T}\mathrm{Ln}(I+B)}$.

The following condition on the system (2) is required.

$\left(C\right)$

${\displaystyle \underset{j}{max}\Re e{\lambda }_j=\lambda <0}$, where $\Re e{\lambda }_j$ is the real part of ${\lambda }_j$ for each $j=1,2,\dots ,p$.

In consequence of (4), under the condition $\left(C\right)$, there exist numbers $K\ge 1$ and $0<\alpha <-\lambda$ such that

$$\begin{array}{c}\hfill ∥X(t,u)∥\le K{e}^{-\alpha (t-u)}\end{array}$$

(5)

for $t\ge u$ [13,21].

Let us prove the following auxiliary assertion.

Lemma 1.

Assume that the condition $\left(C\right)$ is fulfilled, then the following inequality

$$\begin{array}{c}\hfill ∥X(t+t_n,u+t_n)-X(t,u)∥\le K_0{e}^{-\alpha (t-u)}\end{array}$$

(6)

holds, where ${\displaystyle K_0=Kmax\left(1,∥B∥\right)}$.

Proof. 

By using (4) and (5), we can show that

$$\begin{array}{ccc}\hfill ∥X(t+t_n,u+t_n)-X(t,u)∥& \le & ∥e^{A(t-u)}{\left(I+B\right)}^{i\left([u+t_n,t+t_n)\right)}-e^{A(t-u)}{\left(I+B\right)}^{i\left(\right[u,t\left)\right)}∥\hfill \\ & \le & ∥e^{A(t-u)}{\left(I+B\right)}^{i\left(\right[u,t\left)\right)}∥∥{\left(I+B\right)}^{|i\left([u+t_n,t+t_n)\right)-i\left([u,t)\right)|}-I∥\hfill \\ & \le & {\displaystyle Kmax\left(1,∥B∥\right)e^{-\alpha (t-u)}.}\hfill \end{array}$$

for $t\ge u$. □

The following theorem is concerned with the discontinuous unpredictable solution of system (2).

Theorem 1.

Suppose that the condition $\left(C\right)$ is valid. If $f\left(t\right)$ is a d.u.f. in the sense of Definition 1, then system (2) possesses a unique asymptotically stable discontinuous unpredictable solution.

Proof. 

As it is known from the theory of impulsive differential equations [13,21], according to the boundedness of the function $f\left(t\right)$, system (2) admits a unique solution $\phi \left(t\right)$ which is bounded on the real axis and satisfies the equation

$$\begin{array}{c}\hfill \phi \left(t\right)=\underset{-\infty }{\overset{t}{\int }}X(t,u)f\left(u\right)du,t\in \mathbb{R}.\end{array}$$

(7)

One can verify for points of continuity that

$$\begin{array}{ccc}\hfill & & ∥\frac{d\phi \left(t\right)}{dt}∥\le ∥A∥\underset{-\infty }{\overset{t}{\int }}∥X(t,u)∥∥f\left(u\right)∥du+∥f\left(t\right)∥=\frac{∥A∥M_{f}K}{\alpha }+M_f,\hfill \end{array}$$

(8)

where ${\displaystyle M_f=\underset{t\in \mathbb{R}}{sup}\parallel f\left(t\right)\parallel }$. Therefore, $\phi \left(t\right)$ is a conditional uniform continuous function. The asymptotic stability of $\phi \left(t\right)$ can be verified in a very similar way to the stability of a bounded solution mentioned in [13].

Since $f\left(t\right)$ is a d.u.f., there exist positive numbers ${ϵ}_0$, $\sigma$, sequences $t_n,s_n$ of real numbers and sequences $l_n,m_n$ of integers all of which diverges to infinity such that the properties $\left(c\right)$ and $\left(d\right)$ in Definition 1 hold for $f\left(t\right)$, i.e., when $\phi$ is replaced by f.

Let us continue with the verification of the Poisson stability of $\phi \left(t\right)$, i.e., property (c) in Definition 1.

Fix an arbitrary positive number $ϵ$ and an arbitrary compact interval $[a,b]$, where $b>a$. We will show for sufficiently large n that the inequality $\parallel \phi (t+t_n)-\phi \left(t\right)\parallel <ϵ$ is satisfied for each t in $[a,b].$ Choose numbers $c<a$ and $\xi >0$ such that

$$\begin{array}{c}\hfill \frac{M_f(K_0+2K)}{\alpha }{e}^{-\alpha (a-c)}<\frac{ϵ}{3},\end{array}$$

(9)

$$\begin{array}{c}\hfill \frac{M_f(K_0+2K)\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}<\frac{ϵ}{3},\end{array}$$

(10)

and

$$\begin{array}{c}\hfill \frac{K\xi }{\alpha }<\frac{ϵ}{3}.\end{array}$$

(11)

Let n be a sufficiently large natural number such that $\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|<\xi$ for ${\theta }_i\in [c,b]$, $i\in \mathbb{Z}$, and $\left|\right|f(t+t_n)-f\left(t\right)\left|\right|<\xi$ for $t\in [c,b]$. We assume without loss of generality that ${\theta }_i\le {\theta }_{i+l_n}$. Additionally, suppose that

$$\begin{array}{c}\hfill {\theta }_{m-1}\le c\le {\theta }_m<\cdots <{\theta }_q\le t\le {\theta }_{q+1}\end{array}$$

for $m,q\in \mathbb{Z}$.

If $t\in [a,b]$, then we have

$$\begin{array}{ccc}& & ∥\phi (t+t_n)-\phi \left(t\right)∥\le \underset{-\infty }{\overset{c}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du\hfill \\ & & +\underset{c}{\overset{t}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du+\underset{-\infty }{\overset{c}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du\hfill \\ & & +\underset{c}{\overset{t}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du.\hfill \end{array}$$

Using the inequality (6), one can obtain

$$\begin{array}{ccc}& & \underset{-\infty }{\overset{c}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du\le \underset{-\infty }{\overset{c}{\int }}{M}_f{K}_0{e}^{-\alpha (t-u)}du<\frac{M_f{K}_0}{\alpha }{e}^{-\alpha (a-c)}.\hfill \end{array}$$

Moreover, we have

$$\begin{array}{ccc}& & {\displaystyle \underset{c}{\overset{t}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du\le \sum _{i=m}^q\underset{{\theta }_i}{\overset{{\theta }_{i+l_n}-t_n}{\int }}{M}_f{K}_0{e}^{-\alpha (t-u)}du}\hfill \\ & & {\displaystyle \le \sum _{i=m}^q\frac{M_f{K}_0}{\alpha }{e}^{-\alpha t}\left(e^{\alpha ({\theta }_{i+l_n}-t_n)}-e^{\alpha {\theta }_i}\right)\le \sum _{i=m}^q\frac{M_f{K}_0}{\alpha }{e}^{-\alpha (t-{\theta }_i)}\left(e^{\alpha \xi }-1\right)}\hfill \\ & & {\displaystyle <\frac{M_f{K}_0}{\alpha }\left(e^{\alpha \xi }-1\right)e^{-\alpha (t-{\theta }_q)}\sum _{i=m}^q{e}^{-\alpha ({\theta }_q-{\theta }_i)}<\frac{M_f{K}_0\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}.}\hfill \end{array}$$

In a similar way to the last inequality, one can deduce that

$$\begin{array}{ccc}\hfill & & \underset{-\infty }{\overset{c}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du+\underset{c}{\overset{t}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du\hfill \\ & & {\displaystyle \le \underset{-\infty }{\overset{c}{\int }}2M_{f}K{e}^{-\alpha (t-u)}du+\underset{c}{\overset{t}{\int }}K\xi e^{-\alpha (t-u)}du+\sum _{i=m}^q\underset{{\theta }_i}{\overset{{\theta }_{i+l_n}-t_n}{\int }}2M_{f}K{e}^{-\alpha (t-u)}du}\hfill \\ & & <\frac{2M_{f}K}{\alpha }{e}^{-\alpha (a-c)}+\frac{K\xi }{\alpha }+\frac{2M_{f}K\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}.\hfill \end{array}$$

The inequalities (9)–(11) imply that $∥\phi (t+t_n)-\phi \left(t\right)∥<ϵ$ for $t\in [a,b]$, and therefore, $\phi (t+t_n)\to \phi \left(t\right)$ uniformly on each compact interval in B-topology.

Next, we will show the existence of a sequence $r_n$, which diverges to infinity, and positive numbers ${ϵ}_1$, $\sigma$ such that $∥\phi (t+t_n)-\phi \left(t\right)∥\ge {ϵ}_1$ for $t\in [r_n-\sigma ,r_n+\sigma ]$.

Corresponding to the Definition 1 for the d.u.f. $f\left(t\right)$, the interval $[s_n-\sigma ,s_n+\sigma ]\subseteq [\widehat{{\theta }_{m_n},({\theta }_{m_n+l_n}}-t_n)]$, does not admit any points of discontinuity of $f\left(t\right)$ and $f(t+t_n)$. For that reason, the following discussion ignores the presence of a discontinuity moment.

There exists a positive number ${\sigma }_1<\sigma$ such that the inequalities

$$\begin{array}{c}\hfill ∥f(t+t_n)-f(t_n+s_n)∥\le \frac{{ϵ}_0}{4\sqrt{p}}\end{array}$$

and

$$\begin{array}{c}\hfill ∥f\left(t\right)-f\left(s_n\right)∥\le \frac{{ϵ}_0}{4\sqrt{p}},\end{array}$$

are valid for every $t\in [s_n-{\sigma }_1,s_n+{\sigma }_1]$ and natural number n.

Let us fix an arbitrary natural number n, and suppose that $f\left(t\right)=(f_1\left(t\right),f_2\left(t\right),\dots ,f_p\left(t\right))$, where each $f_k\left(t\right)$, $k=1,2,\dots ,p$, is a real valued function. One can confirm that there exists an integer $j_n$, $1\le j_n\le p$, such that

$$\begin{array}{c}\hfill \left|f_{j_n}(t_n+s_n)-f_{j_n}\left(s_n\right)\right|\ge \frac{{ϵ}_0}{\sqrt{p}}.\end{array}$$

Therefore, the inequality

$$\begin{array}{ccc}\hfill \left|f_{j_n}(t+t_n)-f_{j_n}\left(t\right)\right|& & \ge \left|f_{j_n}(t_n+s_n)-f_{j_n}\left(s_n\right)\right|-\left|f_{j_n}(t+t_n)-f_{j_n}(t_n+s_n)\right|\hfill \\ & & -\left|f_{j_n}\left(t\right)-f_{j_n}\left(s_n\right)\right|\hfill \\ & & \ge \frac{{ϵ}_0}{2\sqrt{p}}\hfill \end{array}$$

(12)

is valid for $t\in [s_n-{\sigma }_1,s_n+{\sigma }_1]$.

There exist numbers $u_1^n,u_2^n,\dots ,u_p^n$ in the interval $[s_n-{\sigma }_1,s_n+{\sigma }_1]$ such that

$$\begin{array}{c}\hfill ∥\underset{s_n-{\sigma }_1}{\overset{s_n+{\sigma }_1}{\int }}\left(f(u+t_n)-f\left(u\right)\right)du∥=2{\sigma }_1{\left[{\displaystyle \sum _{k=1}^p{\left(f_i(u_i^n+t_n)-f_i\left(u_i^n\right)\right)}^2}\right]}^{1/2}.\end{array}$$

It can be verified by utilizing the inequality (12) that

$$\begin{array}{c}\hfill ∥\underset{s_n-{\sigma }_1}{\overset{s_n+{\sigma }_1}{\int }}\left(f(u+t_n)-f\left(u\right)\right)du∥\ge 2{\sigma }_1\left|f_{j_n}(u_{j_n}^n+t_n)-f_{j_n}\left(u_{j_n}^n\right)\right|\ge \frac{{\sigma }_1{ϵ}_0}{\sqrt{p}}.\end{array}$$

Additionally, using the equation

$$\begin{array}{ccc}\hfill \phi (t_n+s_n+{\sigma }_1)-\phi (s_n+{\sigma }_1)& =& \phi (t_n+s_n-{\sigma }_1)-\phi (s_n-{\sigma }_1)+\underset{s_n-{\sigma }_1}{\overset{s_n+{\sigma }_1}{\int }}A\left(\phi (u+t_n)-\phi \left(u\right)\right)du\hfill \\ & & +\underset{s_n-{\sigma }_1}{\overset{s_n+{\sigma }_1}{\int }}\left(f(u+t_n)-f\left(u\right)\right)du,\hfill \end{array}$$

we deduce that

$$\begin{array}{c}\hfill {\displaystyle ∥\phi (t_n+s_n+{\sigma }_1)-\phi (s_n+{\sigma }_1)∥\ge \frac{{\sigma }_1{ϵ}_0}{\sqrt{p}}-(1+2{\sigma }_1\left|\right|A\left|\right|)\underset{t\in [s_n-{\sigma }_1,s_n+{\sigma }_1]}{sup}∥\phi (t+t_n)-\phi \left(t\right)∥.}\end{array}$$

Hence, the inequality

$$\begin{array}{c}\hfill {\displaystyle \underset{t\in [s_n-{\sigma }_1,s_n+{\sigma }_1]}{sup}∥\phi (t+t_n)-\phi \left(t\right)∥\ge \frac{{\sigma }_1{ϵ}_0}{2(1+{\sigma }_1\left|\right|A\left|\right|)\sqrt{p}}}\end{array}$$

holds.

Suppose that ${\displaystyle \underset{t\in [s_n-{\sigma }_1,s_n+{\sigma }_1]}{sup}∥\phi (t+t_n)-\phi \left(t\right)∥=\left|\right|\phi (t_n+r_n)-\phi \left(r_n\right)\left|\right|}$ for some number $r_n\in [s_n-{\sigma }_1,s_n+{\sigma }_1]$. Let us denote

$$\begin{array}{c}\hfill {ϵ}_1=\frac{{\sigma }_1{ϵ}_0}{4(1+{\sigma }_1\left|\right|A\left|\right|)\sqrt{p}}\end{array}$$

and

$$\begin{array}{c}\hfill \tilde{\sigma }=\frac{{\sigma }_1\alpha {ϵ}_0}{8M_f(1+{\sigma }_1\left|\right|A\left|\right|\left)\right(\alpha +2K\left|\right|A\left|\right|)\sqrt{p}}.\end{array}$$

Let us choose $\overline{\sigma }$ such that

$$\begin{array}{c}\hfill {\displaystyle \overline{\sigma }<min\left(\tilde{\sigma },\sigma -{\sigma }_1\right).}\end{array}$$

(13)

Then, for $t\in [r_n-\overline{\sigma },r_n+\overline{\sigma }]$, we have that

$$\begin{array}{ccc}\hfill ∥\phi (t+t_n)-\phi \left(t\right)∥& \ge & ∥\phi (t_n+r_n)-\phi \left(r_n\right)∥-\left|\underset{r_n}{\overset{t}{\int }}\left|\right|A\left|\right|∥\phi (u+t_n)-\phi \left(u\right)∥du\right|\hfill \\ & -& \left|\underset{r_n}{\overset{t}{\int }}∥f(u+t_n)-f\left(u\right)∥du\right|\hfill \\ & \ge & \frac{{\sigma }_1{ϵ}_0}{2(1+{\sigma }_1\left|\right|A\left|\right|)\sqrt{p}}-\frac{4\overline{\sigma }{M}_{f}K\left|\right|A\left|\right|}{\alpha }-2\overline{\sigma }{M}_f\hfill \\ & =& {ϵ}_1.\hfill \end{array}$$

Thus, $∥\phi (t+t_n)-\phi \left(t\right)∥\ge {ϵ}_1$ for each t from the intervals $[r_n-\overline{\sigma },r_n+\overline{\sigma }]\subseteq [\widehat{{\theta }_{m_n},({\theta }_{m_n+l_n}}-t_n)]$, $n\in \mathbb{N}$. It is clear that the sequence $r_n$ diverges to infinity. Consequently, $\phi \left(t\right)$ is the unique discontinuous unpredictable solution of system (2). □

4. Linear Systems with Unpredictable Impulses

Consider the following linear impulsive system,

$$\begin{array}{ccc}\hfill & & x^{\prime }\left(t\right)=Ax\left(t\right)+f\left(t\right),t\ne {\theta }_i,\hfill \\ & & {\Delta x|}_{t={\theta }_i}=Bx\left({\theta }_i\right)+I_i,\hfill \end{array}$$

(14)

where $t\in \mathbb{R}$, the matrices $A\in {\mathbb{R}}^{p\times p}$ and $B\in {\mathbb{R}}^{p\times p}$ commute, the sequence ${\theta }_i$, $i\in \mathbb{Z}$, of discontinuity moments is defined by Equation (1), and $(f\left(t\right),I_i)$ is an unpredictable couple in the sense of Definition 2. Additionally, $det(I+B)\ne 0$, where I is the $p\times p$ identity matrix.

It is worth noting that (14) is a linear impulsive system with unpredictable impulses, and it is not a particular case of system (2). Indeed, to introduce the perturbations $I_i$ in the impulsive part, one must not only consider the sequence to be unpredictable but also assume that the sequences $t_n$ and $s_n$ proper for the unperturbed system have to be consistent with the new terms.

In the proof of the following theorem, we will again use the notations ${\displaystyle K_0=Kmax\left(1,∥B∥\right)}$ and ${\displaystyle M_f=\underset{t\in \mathbb{R}}{sup}\parallel f\left(t\right)\parallel }$ as mentioned in the proof of Theorem 1. Moreover, we set ${\displaystyle M_I=\underset{i\in \mathbb{Z}}{sup}\parallel I_i\parallel }$.

Theorem 2.

Suppose that the condition $\left(C\right)$ is valid. If the couple $\left(f\left(t\right),I_i\right)$ is unpredictable in the sense of Definition 2, then system (14) possesses a unique asymptotically stable discontinuous unpredictable solution.

Proof. 

According to the results of [13,21], system (14) possesses a unique solution $\omega \left(t\right)$ which is bounded on the whole real axis. Moreover, $\omega \left(t\right)$ satisfies the equation

$$\begin{array}{c}\hfill {\displaystyle \omega \left(t\right)=\underset{-\infty }{\overset{t}{\int }}X(t,u)f\left(u\right)du+\sum _{{\theta }_i<t}X(t,{\theta }_i+)I_i}\end{array}$$

(15)

for $t\in \mathbb{R}$. If t is not one of the discontinuity moments ${\theta }_i$, then

$$\begin{array}{ccc}\hfill ∥\frac{d\omega \left(t\right)}{dt}∥& \le & ∥A∥\underset{-\infty }{\overset{t}{\int }}∥X(t,u)∥∥f\left(u\right)∥du+∥f\left(t\right)∥\hfill \\ & \le & ∥A∥\underset{-\infty }{\overset{t}{\int }}{M}_{f}K{e}^{-\alpha (t-u)}du+M_f\hfill \\ & =& ∥A∥\frac{M_{f}K}{\alpha }+M_f.\hfill \end{array}$$

The last inequality yields the conditional uniform continuity of $\omega \left(t\right)$. Moreover, the asymptotic stability of $\omega \left(t\right)$ can be verified using the results mentioned in the books [13,21].

The asymptotic stability of the solution $\omega \left(t\right)$ can be verified as stability of a bounded solution in [13].

Since the couple $\left(f\left(t\right),I_i\right)$ is unpredictable, there exist positive numbers ${ϵ}_0$, $\sigma$, sequences $t_n,s_n$ of real numbers and sequences $l_n,m_n$ of integers all of which diverges to infinity such that the properties $\left(c\right)$, $\left(d\right)$, and $\left(e\right)$ in Definition 2 hold for the function $f\left(t\right)$ and the sequence $I_i$, i.e., when $\omega$ and ${\Gamma }_i$ are respectively replaced by f and $I_i$.

Next, we focus on the Poisson stability of $\omega \left(t\right)$. Fix an arbitrary positive number $ϵ$ and a compact interval $[a,b]$ with $b>a$. We will show that for sufficiently large n the inequality $\parallel \omega (t+t_n)-\omega \left(t\right)\parallel <ϵ$ holds for each $t\in [a,b].$

Let us fix numbers $c<a$ and $\xi >0$ satisfying the inequalities

$$\begin{array}{c}\hfill \frac{M_f(K_0+2K)}{\alpha }{e}^{-\alpha (a-c)}<\frac{ϵ}{5},\end{array}$$

(16)

$$\begin{array}{c}\hfill \frac{4M_{I}K}{1-e^{-\alpha \underline{\theta }}}{e}^{-\alpha (a-c)}<\frac{ϵ}{5},\end{array}$$

(17)

$$\begin{array}{c}\hfill \frac{M_f\left(K_0+2K\right)\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}<\frac{ϵ}{5},\end{array}$$

(18)

$$\begin{array}{c}\hfill \frac{K\xi \left(M_I+1\right)}{1-e^{-\alpha \underline{\theta }}}<\frac{ϵ}{5},\end{array}$$

(19)

and

$$\begin{array}{c}\hfill \frac{K\xi }{\alpha }<\frac{ϵ}{5}.\end{array}$$

(20)

One can check that if n is a sufficiently large natural number, then the equation

$$\begin{array}{c}\hfill {\displaystyle \sum _{{\theta }_i<t+t_n}X(t+t_n,{\theta }_i+)I_i=\sum _{{\theta }_i<t}X(t+t_n,{\theta }_{i+l_n}+)I_{i+l_n}}\end{array}$$

is valid.

Fix a sufficiently large natural number n such that $\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|<\xi$, $∥I_{i+l_n}-I_i∥<\xi$ whenever ${\theta }_i\in [c,b]$ and $\left|\right|f(t+t_n)-f\left(t\right)\left|\right|<\xi$ for $t\in [c,b]$. Assume without loss of generality that ${\theta }_i\le {\theta }_{i+l_n}$. For all $t\in [a,b]$, we have

$$\begin{array}{ccc}& & ∥\omega (t+t_n)-\omega \left(t\right)∥\hfill \\ & & {\displaystyle \le \underset{-\infty }{\overset{c}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du+\sum _{{\theta }_i<c}∥X(t+t_n,{\theta }_{i+l_n}+)-X(t,{\theta }_i+)∥∥I_{i+l_n}∥}\hfill \\ & & {\displaystyle +\underset{c}{\overset{t}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du+\sum _{c\le {\theta }_i<t}∥X(t+t_n,{\theta }_{i+l_n}+)-X(t,{\theta }_i+)∥∥I_{i+l_n}∥}\hfill \\ & & {\displaystyle +\underset{-\infty }{\overset{c}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du+\sum _{{\theta }_i<c}∥X(t,{\theta }_i+)∥∥I_{i+l_n}-I_i∥}\hfill \\ & & {\displaystyle +\underset{c}{\overset{t}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥+\sum _{c\le {\theta }_i<t}∥X(t,{\theta }_i+)∥∥I_{i+l_n}-I_i∥du.}\hfill \end{array}$$

Using the inequality (6), it can be verified that

$$\begin{array}{ccc}& & {\displaystyle \underset{-\infty }{\overset{c}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du+\sum _{{\theta }_i<c}∥X(t+t_n,{\theta }_{i+l_n}+)-X(t,{\theta }_i+)∥∥I_{i+l_n}∥}\hfill \\ & & {\displaystyle \le \underset{-\infty }{\overset{c}{\int }}{M}_f{K}_0{e}^{-\alpha (t-u)}du+\sum _{i=-\infty }^{m-1}{M}_{I}K{e}^{-\alpha (t+t_n-{\theta }_{i+l_n})}+\sum _{i=-\infty }^{m-1}{M}_{I}K{e}^{-\alpha (t-{\theta }_i)}}\hfill \\ & & <\left(\frac{M_f{K}_0}{\alpha }+\frac{2M_{I}K}{1-e^{-\alpha \underline{\theta }}}\right)e^{-\alpha (a-c)}.\hfill \end{array}$$

On the other hand, one can obtain that

$$\begin{array}{ccc}& & {\displaystyle \underset{c}{\overset{t}{\int }}∥X(t+t_n,u+t_n)-X(t,u)∥∥f(u+t_n)∥du+\sum _{c\le {\theta }_i<t}∥X(t+t_n,{\theta }_{i+l_n}+)-X(t,{\theta }_i+)∥∥I_{i+l_n}∥}\hfill \\ & & {\displaystyle \le \sum _{i=m}^q\underset{{\theta }_i}{\overset{{\theta }_{i+l_n}-t_n}{\int }}{M}_f{K}_0{e}^{-\alpha (t-u)}du+\sum _{i=m}^q{M}_{I}K\xi e^{-\alpha (t-{\theta }_i)}<\frac{M_f{K}_0\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}+\frac{M_{I}K\xi }{1-e^{-\alpha \underline{\theta }}}.}\hfill \end{array}$$

Additionally, the inequality

$$\begin{array}{ccc}& & {\displaystyle \underset{-\infty }{\overset{c}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥du+\sum _{{\theta }_i<c}∥X(t,{\theta }_i+)∥∥I_{i+l_n}-I_i∥}\hfill \\ & & {\displaystyle \le \underset{-\infty }{\overset{c}{\int }}2M_{f}K{e}^{-\alpha (t-u)}du+\sum _{i=-\infty }^{m-1}2M_{I}K{e}^{-\alpha (t-{\theta }_i)}<\left(\frac{2M_{f}K}{\alpha }+\frac{2M_{I}K}{1-e^{-\alpha \underline{\theta }}}\right)e^{-\alpha (a-c)}}\hfill \end{array}$$

holds for $t\in [a,b]$. Furthermore, we have

$$\begin{array}{ccc}& & {\displaystyle \underset{c}{\overset{t}{\int }}∥X(t,u)∥∥f(u+t_n)-f\left(u\right)∥+\sum _{c\le {\theta }_i<t}∥X(t,{\theta }_i+)∥∥I_{i+l_n}-I_i∥du}\hfill \\ & & {\displaystyle \le \underset{c}{\overset{t}{\int }}K\xi e^{-\alpha (t-u)}du+\sum _{i=m}^q\underset{{\theta }_i}{\overset{{\theta }_{i+l_n}-t_n}{\int }}2M_{f}K{e}^{-\alpha (t-u)}du+\sum _{i=m}^{q}K\xi e^{-\alpha (t-{\theta }_i)}}\hfill \\ & & <\frac{K\xi }{\alpha }+\frac{2M_{f}K\left(e^{\alpha \xi }-1\right)}{\alpha \left(1-e^{-\alpha \underline{\theta }}\right)}+\frac{K\xi }{1-e^{-\alpha \underline{\theta }}}.\hfill \end{array}$$

Thus, $∥\omega (t+t_n)-\omega \left(t\right)∥<ϵ$ for $t\in [a,b]$ in accordance with the inequalities (16)–(20). Therefore, $\omega (t+t_n)\to \omega \left(t\right)$ uniformly in B-topology on each compact interval.

The unpredictability of solution $\omega \left(t\right)$ can be proved identically to that for solution $\phi \left(t\right)$ of system (2). □

5. Examples

Example 1.

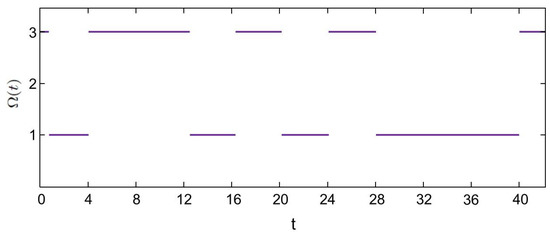
In this example, we will construct a discontinuous unpredictable function by means of an unpredictable orbit of the logistic map and a randomly determined unpredictable sequence [20].

In the paper [2], it was proved that for each $\mu \in [3+{(2/3)}^{1/2},4]$, the logistic map

$$\begin{array}{c}\hfill {\nu }_{i+1}=\mu {\nu }_i(1-{\nu }_i),i\in \mathbb{Z}.\end{array}$$

(21)

possesses an unpredictable solution ${\gamma }_i,i\in \mathbb{Z}$, in the interval $[0,1]$. There exists a positive number ${ϵ}_0$ and sequences ${\zeta }_n,$${\eta }_n$, both of which diverge to infinity such that $\left|{\gamma }_{i+{\zeta }_n}-{\gamma }_i\right|\to 0$ as $n\to \infty ,$ for each i in bounded intervals of integers and $\left|{\gamma }_{{\eta }_n+{\zeta }_n}-{\gamma }_{{\eta }_n}\right|\ge {ϵ}_0$ for each $n\in \mathbb{N}$.

Consider the sequence ${\theta }_i,i\in \mathbb{Z}$ defined by

$$\begin{array}{c}\hfill {\theta }_i=4i+{\gamma }_i,i\in \mathbb{Z}.\end{array}$$

(22)

Since the sequence (22), is of the form (1), with $T=4$, there exists a positive number ${ϵ}_0$, a sequence $t_n=4{\zeta }_n$ of real numbers and sequences $l_n={\zeta }_n,$$m_n={\eta }_n$ of integers all of which diverge to infinity such that $\left|{\theta }_{i+l_n}-t_n-{\theta }_i\right|\to 0$ as $n\to \infty$ for each i in bounded intervals of integers and $\left|{\theta }_{m_n+l_n}-t_n-{\theta }_{m_n}\right|\ge {ϵ}_0$ for each natural number n. That is, the sequence is an unpredictable discrete set.

In this example, we utilize a realization of the Bernoulli process, for construction of a discontinuous unpredictable function by considering it as infinite sequences of two integers 1 and 3 with equal probability $1/2$ such that according to (Theorem 1, [20]). Then, there exists an unpredictable sequence ${\tau }_i$, ${\tau }_i=1,3,i\in \mathbb{Z}$, and there exist sequences ${\zeta }_n$, ${\eta }_n$, $n\in \mathbb{N}$, of positive integers both of which diverge to infinity as $n\to \infty$ such that ${\tau }_{i+{\zeta }_n}={\tau }_i$ for each i in bounded intervals of integers and $|{\tau }_{{\zeta }_n+{\eta }_n}-{\tau }_{{\eta }_n}|\ge {\epsilon }_0=|1-3|=2$ for each natural number n.

Let $\mathsf{\Omega }\left(t\right):\mathbb{R}\to \mathbb{R}$ be the function defined through the equation $\mathsf{\Omega }\left(t\right)={\tau }_i$ for $t\in [{\theta }_i,{\theta }_{i+1})$, $i\in \mathbb{Z}$. We will show that $\mathsf{\Omega }\left(t\right)$ is a discontinuous unpredictable function in the sense of Definition 1.

One can show that if $t\in [{\theta }_i,{\theta }_{i+1})$, $i\in \mathbb{Z}$, then $t+t_n\in [{\theta }_{i+{\zeta }_n},{\theta }_{i+1+{\zeta }_n})$, $i\in \mathbb{Z}$. For $t\in [{\theta }_i^{\prime },{\theta }_{i+1}^{\prime })$, $i\in \mathbb{Z}$, it can be verified that ${\theta }_i^{\prime }\le t<{\theta }_{i+1}^{\prime },$ and ${\theta }_i^{\prime }+t_n\le t+t_n<{\theta }_{i+1}^{\prime }+t_n,$ then ${\theta }_{i+{\zeta }_n}^{\prime }\le t+t_n<{\theta }_{i+1+{\zeta }_n}^{\prime }.$ That is, the discontinuity points of $\mathsf{\Omega }(t+t_n)$ are that ones for $\mathsf{\Omega }\left(t\right)$. Let us denote them ${\theta }_i^{\prime }={\theta }_{i+{\zeta }_n}-t_n$. Accordingly, for each $i\in \mathbb{Z},n\in \mathbb{N}$ the value of function $\mathsf{\Omega }(t+t_n)$ is equal to ${\tau }_{i+{\zeta }_n}$. Hence, by using the unpredictability ${\tau }_i$, we have that $\mathsf{\Omega }(t+t_n)\to \mathsf{\Omega }\left(t\right)$ as $n\to \infty$ in B-topology on each bounded interval. Moreover, the values of functions $\mathsf{\Omega }\left(t\right)$ and $\mathsf{\Omega }(t+t_n)$, on the corresponding intervals $[{\theta }_{{\eta }_n},{\theta }_{{\eta }_n+1})$, and $[{\theta }_{{\eta }_n+{\zeta }_n},{\theta }_{{\eta }_n+1+{\zeta }_n})$, for fixed n, are respectively equal to ${\tau }_{{\eta }_n}$ and ${\tau }_{{\eta }_n+{\zeta }_n}$. Consequently, we have that $\left|\mathsf{\Omega }(t+t_n)-\mathsf{\Omega }\left(t\right)\right|=\left|{\tau }_{{\eta }_n+{\zeta }_n}-{\tau }_{{\eta }_n}\right|\ge {ϵ}_0=2$.

Thus, $\mathsf{\Omega }\left(t\right)$ is a discontinuous unpredictable function with positive numbers ${ϵ}_0=2,\sigma =\frac{3}{2}$ and sequences $t_n=4{\zeta }_n,s_n=\frac{{\theta }_{{\eta }_n}+{\theta }_{{\eta }_n+1}}{2}$. The graph of the function $\mathsf{\Omega }\left(t\right)$ is represented in Figure 1.

Figure 1. The graph of discontinuous unpredictable function $\mathsf{\Omega }\left(t\right)$.

Example 2.

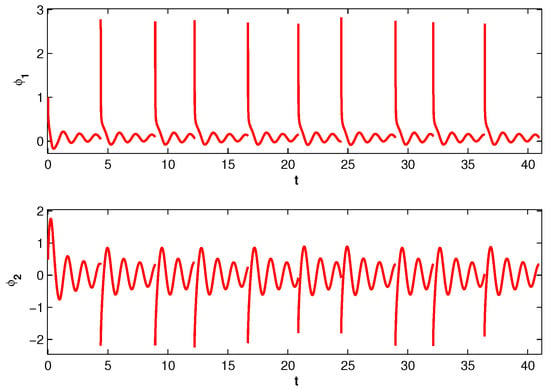
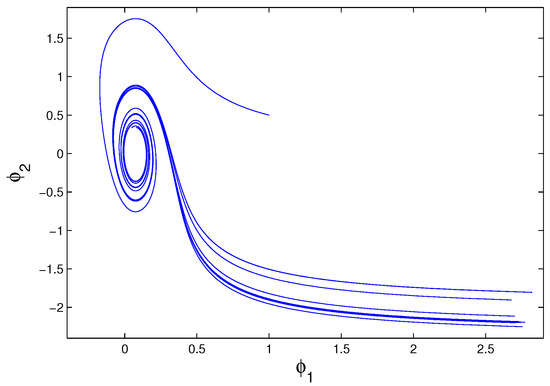
Let us consider the impulsive system,

$$\begin{array}{ccc}\hfill & & x_1^{\prime }=-x_2+2{\mathsf{\Omega }}^3\left(t\right),t\ne {\theta }_i,\hfill \\ & & x_2^{\prime }=x_1-7\mathsf{\Omega }\left(t\right),t\ne {\theta }_i,\hfill \\ & & \Delta x_1{|}_{t={\theta }_i}=-\frac{15}{16}{x}_1+3{\gamma }_i,\hfill \\ & & \Delta x_2{|}_{t={\theta }_i}=-\frac{15}{16}{x}_2-2{\gamma }_i,\hfill \end{array}$$

(23)

where $\mathsf{\Omega }\left(t\right)$ is the d.u.f. from Example 1, and

$$\begin{array}{c}\hfill A=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right),B=\left(\begin{array}{cc}-\frac{15}{16}& 0\\ 0& -\frac{15}{16}\end{array}\right).\end{array}$$

The couple $\left(f\left(t\right),I_i\right)=\left(\left(\begin{array}{c}2{\left(\mathsf{\Omega }\left(t\right)\right)}^3\\ -7\mathsf{\Omega }\left(t\right)\end{array}\right),\left(\begin{array}{c}3{\gamma }_i\\ -2{\gamma }_i\end{array}\right)\right)$ is unpredictable in the sense of Definition 2 according to (Lemmas 1.4 and 1.5 [17]).

The matrices A and B commute, and the matrix

$$\begin{array}{c}\hfill A+\frac{1}{T}ln(I+B)=\left(\begin{array}{cc}-ln2& -1\\ 1& -ln2\end{array}\right),\end{array}$$

has the eigenvalues ${\lambda }_{1,2}=-ln2\pm i$. One can show that

$$\begin{array}{c}\hfill X(t,u)=P\left(\begin{array}{cc}cos(t-u)& -sin(t-u)\\ sin(t-u)& cos(t-u)\end{array}\right)P^{-1}{(I+B)}^{i(u,t)},\end{array}$$

where $P=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$. Inequality (5) is satisfied for system (23) with $\alpha =0.5$ and $K=2$. According to Theorem 2, there exists the unique asymptotically stable discontinuous unpredictable solution of system (23).

It is worth noting that the simulation of an unpredictable function is not possible, since the initial value is not known. That is why, we will simulate a solution $\varphi \left(t\right)=({\varphi }_1\left(t\right),{\varphi }_2\left(t\right))$ which approaches to the unpredictable solution $x\left(t\right)$ as time increases. Instead of the curve describing the unpredictable solution, one can take the graph of $\varphi \left(t\right)$. We depict in Figure 2 the graph of the solution with initial values ${\varphi }_1\left(0\right)=1,{\varphi }_2\left(0\right)=0.5$. Moreover, Figure 3 presents the orbit of the solution $\varphi \left(t\right)$.

Figure 2. The time series of the coordinates ${\varphi }_1$, ${\varphi }_2$ of the solution of system (23) with the initial conditions ${\varphi }_1\left(0\right)=1.0$, ${\varphi }_2\left(0\right)=0.5$.

Figure 3. The trajectory of the solution $\varphi \left(t\right)$, which approximates the discontinuous unpredictable solution $x\left(t\right)$.

6. Conclusions

In this study, we present sufficient conditions for the existence and uniqueness of asymptotically stable discontinuous unpredictable solutions. To determine the presence of unpredictability at discontinuity moments of the solutions, we introduced the concepts of unpredictable discrete set and discontinuous unpredictable function. Our approach can be applied in studies of the unpredictability of various types of impulsive differential equations.