On BV-Algebras

Abstract

In this paper, we introduce the notion of a $BV$-algebra, and we show that a $BV$-algebra is logically equivalent to several algebras, i.e., $BM$-algebras, $BT$-algebras, $BO$-algebras and 0-commutative B-algebras. Moreover, we show that a $BV$-algebra with $\left(F\right)$ is logically equivalent to several algebras, and we show some relationships between a $BV$-algebra with $\left(F\right)$ and several related algebras.

1. Introduction

The notion of $BCK$-algebras was formulated by $\mathrm{Is}\acute{\mathrm{e}}\mathrm{ki}$. The motivation of this notion is based on both set theory and propositional calculus (see [1]). As a generalization of this notion, $BCI$-, $BCH$-, $BCH$-, $BCC$-algebras have been developed by many researchers (see [2,3,4]). Jun et al. [5] introduced the notion of a $BH$-algebra, which is a generalization of $BCK/BCI/B$-algebras. The concept of B-algebras was introduced by Neggers and Kim [6]. Kim and Kim [7] defined the notion of a $BM$-algebra. They showed that a $BM$-algebra is equivalent to a 0-commutative B-algebra. Kim and Kim [8] introduced the notion of a $BO$-algebra, and proved that every $BO$-algebra is 0-commutative, and obtained several algebras which are logically equivalent to the $BO$-algebra. Walendziak [9] introduced a $BF$-algebra, which is a generalization of a B-algebra, and investigated some properties of (normal) ideals in $BF$-algebras. Kim and Kim [10] defined the notion of a $BN$-algebra, and showed that an algebra A is a $BN$-algebra if and only if it is a 0-commutative $BF$-algebra. Kim et al. [11] introduced the notions of (pre-)Coxeter algebras in the Smarandache setting, and Kim and Kim [12] discussed some relations between (pre-)Coxeter algebras and its related topics.

In this paper, we introduce the notion of a $BV$-algebra consisting of 3 simple axioms, and we show it is logically equivalent to several known algebras. In particular, we investigate the role of the axiom $\left(BV\right)$ for proving the logically (non-) equivalence to several algebras. Moreover, we show that a $BV$-algebra with $\left(F\right)$ is logically equivalent to several algebras, and we show some relationships between a $BV$-algebra with $\left(F\right)$ and several related algebras.

2. Preliminaries

A B-algebra [6] is a non-empty set A with a constant 0 and a binary operation ‘*’ satisfying the following axioms:

(A1)

$x\ast x=0$,

(A2)

$x\ast 0=x$,

(B)

$(x\ast y)\ast z=x\ast [z\ast (0\ast y\left)\right]$

for any $x,y,z\in A$

Proposition 1.

[6] If $(A,\ast ,0)$ is a B-algebra, then $x=0\ast (0\ast x)$ for all $x\in A$.

An algebra $(A,\ast ,0)$ is called a $BH$-algebra [5] if it satisfies $\left(A1\right),\left(A2\right)$ and $\left(BH\right)$, where

(BH)

$x\ast y=0$ and $y\ast x=0$ imply $x=y$.

Kim and Kim [7] defined a $BM$-algebra satisfying $\left(A2\right)$ and $\left(BM\right)$, where

(BM)

$(z\ast x)\ast (z\ast y)=y\ast x$

for any $x,y,z\in A$. Walendziak [9] introduced a $BF$-algebra as an algebra $(A,\ast ,0)$ satisfying $\left(A1\right),\left(A2\right)$ and $\left(BF\right)$, where

(BF)

$0\ast (x\ast y)=y\ast x$

for any $x,y\in A$. An algebra $(A,\ast ,0)$ is called a $BO$-algebra [8] if it satisfies $\left(A1\right),\left(A2\right)$ and $\left(BO\right)$, where

(BO)

$(x\ast y)\ast (0\ast z)=x\ast (y\ast z)$

for any $x,y,z\in A$. An algebra $(A,\ast ,0)$ is said to be 0-commutative [13] if $x\ast (0\ast y)=y\ast (0\ast x)$ for any $x,y\in A$. Cho and Kim [13] discussed B-algebras and quasigroups using the notion of the 0-commutativity.

Proposition 2.

[8] An algebra $(A,\ast ,0)$ is a $BO$-algebra if and only if it is a 0-commutative B-algebra.

An algebra $(A,\ast ,0)$ is called a Coxeter algebra if it satisfies $\left(A1\right),\left(A2\right)$ and $\left(D\right)$, where

(D)

$(x\ast y)\ast z=x\ast (y\ast z)$

for all $x,y,z\in A$. It is known that a Coxeter algebra is a special type of abelian groups, i.e., a Boolean group (see [11,12]). An algebra $(A,\ast ,0)$ is called a pre-Coxeter algebra if it satisfies $\left(A1\right),\left(A2\right)$ and

(E1)

if $x\ast y=0=y\ast x$, then $x=y$,

(E2)

$x\ast y=y\ast x$

for all $x,y\in A$. It was proved that every Coxeter algebra is a pre-Coxeter algebra, but the converse need not be true in general (see [11,12]).

3. $\mathit{BV}$-Algebras

In this section, we define a notion of a $BV$-algebra, and we investigate some relations between $BV$-algebras and other algebras, i.e., B-algebras, 0-commutative B-algebras, $BF$-algebras, $BH$-algebras, $BM$-algebras, $BN$-algebras, $BO$-algebras, $BT$-algebras and Coxeter-algebras.

Definition 1.

An algebra $(A,\ast ,0)$ is said to be a $BV$-algebra if it satisfies $\left(A1\right),\left(A2\right)$ and $\left(BV\right)$, where

(BV)

$(x\ast y)\ast z=(0\ast y)\ast (z\ast x)$

for all $x,y,z\in A$.

Example 1.

Let $A:=\{0,1,2,3,4\}$ be a set with the following table:

*	0	1	2	3	4
0	0	2	1	4	3
1	1	0	3	2	4
2	2	4	0	3	1
3	3	1	4	0	2
4	4	3	2	1	0

Then it is easy to see that $(A,\ast ,0)$ is a $BV$-algebra.

Proposition 3.

If $(A,\ast ,0)$ is a $BV$-algebra, then the followings hold:

(i) 

$x\ast y=(0\ast y)\ast (0\ast x)$,

(ii) 

$0\ast (0\ast x)=x$,

(iii) 

$x\ast z=0\ast (z\ast x)$,

(iv) 

$(x\ast y)\ast x=0\ast y$,

(v) 

$x\ast (0\ast y)=y\ast (0\ast x)$,

(vi) 

$(x\ast z)\ast y=(x\ast y)\ast z$,

(vii) 

$x\ast y=0⟹x=y$

(viii) 

$0\ast x=0\ast y⟹x=y$,

(ix) 

$(x\ast (0\ast x\left)\right)\ast x=x$,

(x) 

$x\ast y=x\ast z⟹y=z$,

(xi) 

$x\ast y=z\ast y⟹x=z$,

for any $x,y,z\in A$.

Proof. 

(i). If we let $z:=0$ in $\left(BV\right)$, then $x\ast y=(x\ast y)\ast 0=(0\ast y)\ast (0\ast x)$ by $\left(A2\right)$. (ii). If we let $y:=0$ in (i), then, by $\left(A2\right)$ and $\left(A1\right)$, we obtain $x=x\ast 0=(0\ast 0)\ast (0\ast x)=0\ast (0\ast x)$. (iii). If we let $y:=0$ in $\left(BV\right)$, then $(x\ast 0)\ast z=(0\ast 0)\ast (z\ast x)$, and hence $x\ast z=0\ast (z\ast x)$. (iv). If we let $z:=x$ in $\left(BV\right)$, then $(x\ast y)\ast x=(0\ast y)\ast (x\ast x)=(0\ast y)\ast 0=0\ast y$. (v). If we let $y:=0\ast y$ in (i), then $x\ast (0\ast y)=(0\ast (0\ast y\left)\right)\ast (0\ast x)$. By applying (ii), we obtain $x\ast (0\ast y)=y\ast (0\ast x)$. (vi). If we let $y:=z,z:=y$ in $\left(BV\right)$, then, by applying (iii) and (i), we have $(x\ast z)\ast y=(0\ast z)\ast (y\ast x)=(0\ast z)\ast (0\ast (x\ast y\left)\right)=(x\ast y)\ast z$. (vii). If $x\ast y=0$ in (iv), then $0\ast x=0\ast y$, which implies $0\ast (0\ast x)=0\ast (0\ast y)$. It follows that $x=y$ by (ii). (viii). If $0\ast x=0\ast y$, then $0\ast (0\ast x)=0\ast (0\ast y)$ and hence $x=y$ by (ii). (ix). If we let $y:=0\ast x$ in (iv), then $(x\ast (0\ast x\left)\right)\ast x=0\ast (0\ast x)$. By applying (ii), we obtain $(x\ast (0\ast x\left)\right)\ast x=x$. (x). Assume $x\ast y=x\ast z$. Then, by applying (iv), we have

$$\begin{array}{ccc}\hfill 0\ast y& =& (x\ast y)\ast x\hfill \\ & =& (x\ast z)\ast x\hfill \\ & =& 0\ast z.\hfill \end{array}$$

By applying (viii), we obtain $y=z$. (xi). If we assume $x\ast y=z\ast y$, then, by (iii), we obtain $0\ast (y\ast x)=0\ast (y\ast z)$. By applying (viii), we have $y\ast x=y\ast z$. By (x), we obtain $x=z$. □

By applying (iii) and (vii) of Proposition 3, we obtain the following theorem:

Theorem 1.

Let $(A,\ast ,0)$ be a $BV$-algebra. Then

(i) 

it is a $BF$-algebra,

(ii) 

it is a $BH$-algebra.

Remark 1.

The converse of Theorem 1(i) does not hold in general.

Example 2.

Let $A:=\{0,1,2,3,4\}$ be a set. Define a binary operation “*” on A as follows:

*	0	1	2	3	4
0	0	1	2	4	3
1	1	0	4	1	4
2	2	3	0	3	4
3	3	1	4	0	0
4	4	3	3	0	0

Then $(A,\ast ,0)$ is a $BF$-algebra, but not a $BV$-algebra, since $(0\ast 3)\ast (4\ast 1)=0\ne 4=(1\ast 3)\ast 4$.

Theorem 2.

If $(A,\ast ,0)$ is a Coxeter algebra, then it is a $BV$-algebra.

Proof. 

Let $(A,\ast ,0)$ be a Coxeter algebra. Since A satisfies the conditions $\left(A1\right)$ and $\left(A2\right)$, it is enough to show the condition $\left(BV\right)$. Given $x,y,z\in A$, we have

$$\begin{array}{ccc}\hfill (0\ast y)\ast (z\ast x)& =& y\ast (z\ast x)\hfill \\ & =& y\ast (x\ast z)\hfill \\ & =& (y\ast x)\ast z\hfill \\ & =& (x\ast y)\ast z.\hfill \end{array}$$

Hence A is a $BV$-algebra. □

Remark 2.

The converse of Theorem 2 does not hold in general.

Example 3.

Let $(A,\ast ,0)$ be a $BV$-algebra as in Example 1. Then it is not a Coxeter algebra, since $(1\ast 2)\ast 3=0\ne 2=1\ast 3=1\ast (2\ast 3)$.

Lemma 1.

If $(A,\ast ,0)$ is a $BV$-algebra, then it is a 0-commutative.

Proof. 

It follows immediately from Proposition 3(v). □

Theorem 3.

If $(A,\ast ,0)$ is a $BV$-algebra, then it is a B-algebra.

Proof. 

Let A be a $BV$-algebra. Since A satisfies the conditions $\left(A1\right)$ and $\left(A2\right)$, it is enough to show the condition $\left(A3\right)$. If $x,y$ and z be any elements of A, then

$$\begin{array}{cccc}\hfill x\ast [z\ast (0\ast y\left)\right]& =[0\ast (0\ast x\left)\right]\ast [z\ast (0\ast y\left)\right]\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{ii}\right)]\hfill \\ & =\left[\right(0\ast y)\ast (0\ast x\left)\right]\ast z\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =(x\ast y)\ast z.\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{i}\right)]\hfill \end{array}$$

Hence A is a B-algebra. □

Remark 3.

The converse of this theorem does not hold.

Example 4.

Let A be the set of all real numbers except for a negative integer $-n$. Define a binary operation “*” on A as follows:

$$\begin{array}{c}\hfill x\ast y:=\frac{n(x-y)}{n+y}\end{array}$$

for any $x,y\in A$. Then $(A,\ast ,0)$ is a B-algebra [6], but it is not a $BV$-algebra, since $(2\ast 0)\ast 1=\frac{n}{n+1}\ne \frac{n}{2}=(0\ast 0)\ast (1\ast 2)$.

By using Lemma 1 and Theorem 3, we obtain the following:

Corollary 1.

If $(A,\ast ,0)$ is a $BV$-algebra, then it is a 0-commutative B-algebra.

Theorem 4.

If $(A,\ast ,0)$ is a 0-commutative B-algebra, then it is a $BV$-algebra.

Proof. 

Let $(A,\ast ,0)$ be a 0-commutative B-algebra. Then

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =(0\ast y)\ast [z\ast (0\ast (0\ast x)\left)\right]\hfill & & [\because \mathrm{Proposition}1]\hfill \\ & =\left[\right(0\ast y)\ast (0\ast x\left)\right]\ast z\hfill & & [\because \left(\mathrm{B}\right)]\hfill \\ & =(x\ast y)\ast z.\hfill & & [\because 0-\mathrm{commutative}]\hfill \end{array}$$

for all $x,y,z\in A$. Hence $(A,\ast ,0)$ is a $BV$-algebra. □

By Corollary 1 and Theorem 4, we obtain the following corollary:

Corollary 2.

An algebra $(A,\ast ,0)$ is a $BV$-algebra if and only if it is a 0-commutative B-algebra.

An algebra $(A,\ast ,0)$ is called a $BT$-algebra if the conditions $\left(A1\right),\left(A2\right)$ and $\left(BT\right)$ hold, where

(BT)

$[x\ast (0\ast y\left)\right]\ast z=y\ast (z\ast x)$

for all $x,y,z\in A$

Theorem 5.

An algebra $(A,\ast ,0)$ is a $BV$-algebra if and only if it is a $BT$-algebra.

Proof. 

Assume that $(A,\ast ,0)$ is a $BV$-algebra. We show the condition $\left(BT\right)$. Given $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill [x\ast (0\ast y\left)\right]\ast z& =[0\ast (0\ast y\left)\right]\ast (z\ast x)\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =y\ast (z\ast x).\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{ii}\right)]\hfill \end{array}$$

for all $x,y,z\in A$. Hence A is a $BT$-algebra.

Conversely, assume that A is a $BT$-algebra. If we let $y=z=0$ in $\left(BT\right)$, then, by (A1) and (A2), we have $x=[x\ast (0\ast 0\left)\right]\ast 0=0\ast (0\ast x)$ for all $x\in X$. To show that A is a $BV$-algebra, we show that the condition $\left(BV\right)$ holds. In fact, we have

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =[x\ast (0\ast (0\ast y)\left)\right]\ast z\hfill & & [\because \left(\mathrm{BT}\right)]\hfill \\ & =(x\ast y)\ast z\hfill & & \hfill \end{array}$$

for all $x,y,z\in A$. Hence A is a $BV$-algebra. □

Kim and Kim defined the notion of a $BN$-algebra. An algebra $(A,\ast ,0)$ is said to be a $BN$-algebra [10] if it satisfies the conditions $\left(A1\right)$, $\left(A2\right)$ and $\left(BN\right)$, where

(BN)

$(0\ast z)\ast (y\ast x)=(x\ast y)\ast z$

for all $x,y,z\in A$. It was proved that $BN$-algebras are equivalent to 0-commutative $BF$-algebras [10].

Theorem 6.

If $(A,\ast ,0)$ is a $BV$-algebra, then it is a $BN$-algebra.

Proof. 

Let A be a $BV$-algebra. Then A satisfies the conditions $\left(A1\right)$ and $\left(A2\right)$. We show that the condition $\left(BN\right)$ holds.

$$\begin{array}{cccc}\hfill (0\ast z)\ast (y\ast x)& =(x\ast z)\ast y\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =(x\ast y)\ast z\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{vi}\right)]\hfill \end{array}$$

for all $x,y,z\in A$. Hence A is a $BN$-algebra. □

Remark 4.

The converse of Theorem 6 does not hold in general.

Example 5.

Let $A:=\{0,1,2,3,4\}$ be a set with the following table:

*	0	1	2	3
0	0	1	2	3
1	1	0	1	1
2	2	1	0	1
3	3	1	1	0

Then $(A,\ast ,0)$ is a $BN$-algebra, but not a $BV$-algebra, since $(0\ast 3)\ast (2\ast 3)=1\ne 2=(3\ast 3)\ast 2$.

By Corollary 2, Theorem 5 and Proposition 2, we obtain the interesting result below:

Theorem 7.

The following statements are logically equivalent:

(1) 

A is a $BV$-algebra,

(2) 

A is a 0-commutative B-algebra,

(3) 

A is a $BO$-algebra,

(4) 

A is a $BT$-algebra,

(5) 

A is a $BM$-algebra.

We summarize the above discussion, and we give a diagram describing some relations between $BV$-algebras and its related algebras as follows:

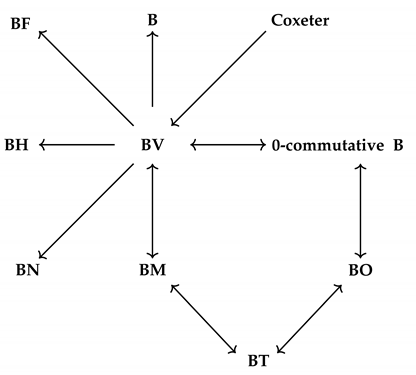
4. $\mathit{BV}$-Algebras with Some Conditions

In this section, we investigate some relationships between several general algebraic structures and $BV$-algebras with special conditions as follows:

(D)

$(x\ast y)\ast z=x\ast (z\ast y)$

(F)

$0\ast x=x$

for all $x,y,z\in A$. Note that Boolean groups and the Klein four group are $BV$-algebras with $\left(F\right)$.

Theorem 8.

If $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$, then it is a pre-Coxeter algebra.

Proof. 

Let $(A,\ast ,0)$ be a $BV$-algebra with $\left(F\right)$. If $x\ast y=0=y\ast x$, then $x=y$ by Proposition 3(vii). On the other hand, by Proposition 3(iii), we obtain $x\ast y=0\ast (y\ast x)=y\ast x$. Hence A is a pre-Coxeter algebra. □

Remark 5.

The converse of Theorem 8 does not hold in general.

Example 6.

Let $A:=\{0,1,2,3,4,5,6,7,8,9\}$ be a set with the following table:

*	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	0	3	2	5	4	7	6	9	8
2	2	3	0	1	6	8	4	9	5	7
3	3	2	1	0	9	7	8	5	6	4
4	4	5	6	9	0	1	2	8	7	3
5	5	4	8	7	1	0	9	3	2	6
6	6	7	4	8	2	9	0	1	3	5
7	7	6	9	5	8	3	1	0	4	2
8	8	9	5	6	7	2	3	4	0	1
9	9	8	7	4	3	6	5	2	1	0

Then $(A,\ast ,0)$ is a pre-Coxeter algebra, but it is not a $BV$-algebra with $\left(F\right)$, since $(3\ast 4)\ast 5=6\ne 8=(0\ast 4)\ast (5\ast 3)$.

Theorem 9.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a Coxeter algebra.

Proof. 

Assume that $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$. Then A satisfies the conditions $\left(A1\right)$ and $\left(A2\right)$. Given $x,y,z\in X$, we obtain

$$\begin{array}{cccc}\hfill (x\ast y)\ast z& =(0\ast y)\ast (z\ast x)\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =y\ast (z\ast x)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =0\ast \left[\right(z\ast x)\ast y]\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{iii}\right)]\hfill \\ & =0\ast \left[\right(z\ast y)\ast x]\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{vi}\right)]\hfill \\ & =x\ast (y\ast z).\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{iii}\right)]\hfill \end{array}$$

This shows that A is a Coxeter algebra.

Conversely, assume that $(A,\ast ,0)$ is a Coxeter algebra. Then A satisfies the conditions $\left(A1\right)$ and $\left(A2\right)$. Given $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =\left[\right(0\ast y)\ast z]\ast x\hfill & & [\because \mathrm{associativity}]\hfill \\ & =(y\ast z)\ast x\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =x\ast (y\ast z)\hfill & & [\because \mathrm{commutativity}]\hfill \\ & =(x\ast y)\ast z\hfill & & [\because \mathrm{associativity}]\hfill \end{array}$$

Hence $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$. □

Note that the $BV$-algebra $(A,\ast ,0)$ in Example 1 does not satisfy the condition $\left(F\right)$, and hence it is not a Coxeter algebra.

Lemma 2.

Let $(A,\ast ,0)$ be a $BV$-algebra. Then the followings are equivalent: for any $x,y,z\in A$,

(i) 

$0\ast x=x$,

(ii) 

$(x\ast y)\ast z=x\ast (z\ast y)$.

Proof. 

(i) ⇒ (ii). Suppose the condition (i) holds. Then, for any $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill x\ast (z\ast y)& =(0\ast x)\ast (z\ast y)\hfill & & [\because \left(\mathrm{i}\right)]\hfill \\ & =(y\ast x)\ast z\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =(0\ast (x\ast y\left)\right)\ast z\hfill & & [\because \mathrm{Proposition}3\left(\mathrm{iii}\right)]\hfill \\ & =(x\ast y)\ast z\hfill & & [\because \left(\mathrm{i}\right)]\hfill \end{array}$$

(ii) ⇒ (i). Suppose the condition (ii) holds. If we let $x=z=0$ in (ii), then, by (A2) and Proposition 3(ii), we obtain $0\ast y=(0\ast y)\ast 0=0\ast (0\ast y)=y$ for any $y\in A$. □

Example 7.

In Example 1, we see that $0\ast 2=1\ne 2$ and hence the condition $(x\ast y)\ast z=x\ast (z\ast y)$ does not hold for some $x,y,z\in A$. In fact, $(3\ast 4)\ast 1=4\ne 2=3\ast (1\ast 4)$.

Lemma 3.

If $(A,\ast ,0)$ is a B-algebra with $\left(F\right)$, then $x\ast y=y\ast x$ for any $x,y\in A$.

Proof. 

Since A is a B-algebra with $\left(F\right)$, if we let $x:=0$ in $\left(B\right)$, then $y\ast z=(0\ast y)\ast z=0\ast [z\ast (0\ast y\left)\right]=z\ast y$ for all $y,z\in A$. □

Example 8.

In Example 4, we see that $0\ast y=\frac{-y}{n+y}\ne y$ and hence the condition $x\ast y=y\ast x$ does not hold for some $x,y\in A$. In fact, $3\ast 4=\frac{-n}{n+4}\ne \frac{n}{n+3}=4\ast 3$.

Theorem 10.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a B-algebra with $\left(F\right)$.

Proof. 

Let $(A,\ast ,0)$ be a $BV$-algebra with the condition $\left(F\right)$. Then, for any $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill x\ast [z\ast (0\ast y\left)\right]& =x\ast (z\ast y)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(y\ast z)\ast x\hfill & & [\because \mathrm{Lemma}2]\hfill \end{array}$$

Hence $(A,\ast ,0)$ is a B-algebra with $\left(F\right)$.

Conversely, let A be a B-algebra with $\left(F\right)$. Then

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =y\ast [z\ast (0\ast x\left)\right]\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(y\ast x)\ast z\hfill & & [\because \left(\mathrm{B}\right)]\hfill \\ & =(x\ast y)\ast z\hfill & & [\because \mathrm{Lemma}3]\hfill \end{array}$$

for any $x,y,z\in A$. Hence A is a $BV$-algebra with $\left(F\right)$. □

Lemma 4.

If $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$, then $x\ast y=y\ast x$ for any $x,y\in A$.

Proof. 

Since $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$, by Proposition 3(iii) and $\left(F\right)$, we have $x\ast y=0\ast (y\ast x)=y\ast x$ for any $x,y\in A$. □

Lemma 5.

If $(A,\ast ,0)$ is a $BF$-algebra with $\left(D\right)$, then

(i) 

$0\ast x=x$,

(ii) 

$x\ast y=y\ast x$.

for any $x,y\in A$.

Proof. 

(i). Let A be a $BF$-algebra with $\left(D\right)$. If we let $y:=x,z:=x$ in $\left(D\right)$, then $(x\ast x)\ast x=x\ast (x\ast x)$ and hence $0\ast x=x\ast 0=x$ for all $x\in A$.

(ii). If we let $x:=0$ in $\left(D\right)$, then $y\ast z=(0\ast y)\ast z=0\ast (z\ast y)=z\ast y$ by (i) for any $y,z\in A$. □

Theorem 11.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a $BF$-algebra with $\left(D\right)$.

Proof. 

Assume that A is a $BV$-algebra with $\left(F\right)$. Then A satisfies the conditions (A1) and (A2). By Proposition 3(iii), A satisfies the condition $\left(BF\right)$. Let $x,y$ and z be any elements of A. Then

$$\begin{array}{cccc}\hfill (x\ast y)\ast z& =(y\ast x)\ast z\hfill & & [\because \mathrm{Lemma}4]\hfill \\ & =(0\ast x)\ast (z\ast y)\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =x\ast (z\ast y).\hfill & & [\because \left(\mathrm{F}\right)]\hfill \end{array}$$

Hence A is a $BF$-algebra with $\left(D\right)$.

Conversely, assume that A is a $BF$-algebra with $\left(D\right)$. Then A satisfies the conditions (A1) and (A2). By Lemma 5(i), A satisfies the condition $\left(F\right)$. Let $x,y$ and z be any elements of A. Then

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =y\ast (z\ast x)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(y\ast x)\ast z\hfill & & [\because \left(\mathrm{D}\right)]\hfill \\ & =(x\ast y)\ast z.\hfill & & [\because \mathrm{Lemma}5\left(\mathrm{ii}\right)]\hfill \end{array}$$

Hence A is a $BV$-algebra with $\left(F\right)$. □

Lemma 6.

Let $(A,\ast ,0)$ be a $BN$-algebra with $\left(D\right)$. Then

(i) 

$0\ast (x\ast y)=y\ast x$,

(ii) 

$0\ast (0\ast x)=x$,

(iii) 

$0\ast x=x$,

(iv) 

$x\ast y=y\ast x$,

for any $x,y\in A$.

Proof. 

Let A be a $BN$-algebra with $\left(D\right)$. (i). If we let $z:=0$ in $\left(BN\right)$, then $(0\ast 0)\ast (y\ast x)=(x\ast y)\ast 0$. By applying $\left(A1\right)$ and $\left(A2\right)$, we obtain $0\ast (y\ast x)=x\ast y$.

(ii). If we let $y:=0,z:=0$ in $\left(BN\right)$, then $(0\ast 0)\ast (0\ast x)=(x\ast 0)\ast 0$. By applying $\left(A1\right)$ and $\left(A2\right)$, we obtain $0\ast (0\ast x)=x$.

(iii). Let $x:=0,z:=0$ in $\left(D\right)$. Then $(0\ast y)\ast 0=0\ast (0\ast y)$. By applying (ii) and $\left(A2\right)$, we obtain $y=0\ast (0\ast y)=(0\ast y)\ast 0=0\ast y$ for all $y\in A$.

(iv). If we let $x:=0$ in $\left(BN\right)$, then $(0\ast z)\ast (y\ast 0)=(0\ast y)\ast z$. By applying (iii) and $\left(A2\right)$, we obtain $z\ast y=y\ast z$ for all $y,z\in A$. □

Theorem 12.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a $BN$-algebra with $\left(D\right)$.

Proof. 

Let $(A,\ast ,0)$ be a $BV$-algebra with $\left(F\right)$. Then A satisfies the conditions (A1) and (A2). By Lemma 2, A satisfies the condition $\left(D\right)$. By applying Proposition 3(vi), we obtain $(0\ast z)\ast (y\ast x)=(x\ast z)\ast y=(x\ast y)\ast z$ for all $x,y,z\in A$, which shows that the condition $\left(BN\right)$ holds. Hence $(A,\ast ,0)$ is a $BN$-algebra with $\left(D\right)$.

Conversely, let A be a $BN$-algebra with $\left(D\right)$. Then A satisfies the condition (A1) and (A2). By Lemma 6(iii), A satisfies the condition $\left(F\right)$. Given $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill (0\ast y)\ast (z\ast x)& =y\ast (z\ast x)\hfill & & [\because \mathrm{Lemma}6\left(\mathrm{iii}\right)]\hfill \\ & =(y\ast x)\ast z\hfill & & [\because \left(\mathrm{D}\right)]\hfill \\ & =(x\ast y)\ast z.\hfill & & [\because \mathrm{Lemma}6\left(\mathrm{iv}\right)]\hfill \end{array}$$

Hence A is a $BV$-algebra with $\left(F\right)$. □

From Lemma 2, we have the following corollary:

Corollary 3.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a $BV$-algebra with $\left(D\right)$.

Theorem 13.

Let $(A,\ast ,0)$ be a B-algebra. Then the followings are equivalent: for any $x,y,z\in A$,

(i) 

$0\ast x=x$,

(ii) 

$(x\ast y)\ast z=x\ast (z\ast y)$.

Proof. 

(i) ⇒ (ii). Let A be a B-algebra. Assume A satisfies the condition (i). Then

$$\begin{array}{cccc}\hfill (x\ast y)\ast z& =x\ast [z\ast (0\ast y\left)\right]\hfill & & [\because \left(\mathrm{B}\right)]\hfill \\ & =x\ast (z\ast y)\hfill & & [\because \left(\mathrm{i}\right)]\hfill \end{array}$$

for any $x,y,z\in A$.

(ii) ⇒ (i). Assume A satisfies the condition (ii). Then

$$\begin{array}{cccc}\hfill x& =0\ast (0\ast x)\hfill & & [\because \mathrm{Proposition}1]\hfill \\ & =(0\ast x)\ast 0\hfill & & [\because \left(\mathrm{ii}\right)]\hfill \\ & =0\ast x\hfill & & [\because \left(\mathrm{A}2\right)]\hfill \end{array}$$

for any $x\in A$. □

Lemma 7.

Let $(A,\ast ,0)$ be a $BO$-algebra with $\left(F\right)$. Then, for any $x,y,z\in A$, we have

(i) 

$(x\ast y)\ast z=x\ast (y\ast z)$,

(ii) 

$x\ast y=y\ast x$.

Proof. 

(i). Since A is a $BO$-algebra with $\left(F\right)$, we have

$$\begin{array}{cccc}\hfill (x\ast y)\ast z& =(x\ast y)\ast (0\ast z)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =x\ast (y\ast z)\hfill & & [\because \left(\mathrm{BO}\right)]\hfill \end{array}$$

for any $x,y,z\in A$.

(ii). By (i), $(A,\ast ,0)$ is a Coxeter algebra, and hence $x\ast y=y\ast x$ for all $x,y\in A$. □

By Theorem 7, we know that a $BV$-algebra is logically equivalent to a $BO$-algebra, but there is no direct proof of its equivalence. Using the condition $\left(F\right)$, we describe its relationship as below:

Theorem 14.

An algebra $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$ if and only if it is a $BO$-algebra with $\left(F\right)$.

Proof. 

Let $(A,\ast ,0)$ be a $BV$-algebra with $\left(F\right)$. We show that the condition $\left(B\right)$ holds. If we take $x,y$ and z in A, then

$$\begin{array}{cccc}\hfill (x\ast y)\ast (0\ast z)& =(x\ast y)\ast z\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =z\ast (y\ast x)\hfill & & [\because \mathrm{Theorem}8]\hfill \\ & =(0\ast z)\ast (y\ast x)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(x\ast z)\ast y\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =y\ast (x\ast z)\hfill & & [\because \mathrm{Theorem}8]\hfill \\ & =(0\ast y)\ast (x\ast z)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(z\ast y)\ast x\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =x\ast (y\ast z).\hfill & & [\because \mathrm{Theorem}8]\hfill \end{array}$$

Hence A is a $BO$-algebra with $\left(F\right)$.

Conversely, assume that A is a $BO$-algebra with $\left(F\right)$. We show the condition $\left(BV\right)$. Given $x,y,z\in A$, by using Lemma 7(i) and $\left(F\right)$, we obtain:

$$\begin{array}{ccc}\hfill (0\ast y)\ast (z\ast x)& =& y\ast (z\ast x)\hfill \\ & =& (y\ast z)\ast x\hfill \\ & =& x\ast (y\ast z)\hfill \\ & =& (x\ast y)\ast z.\hfill \end{array}$$

Hence A is a $BV$-algebra with $\left(F\right)$. □

Theorem 15.

If $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$, then it is a $BN$-algebra with $\left(F\right)$.

Proof. 

Assume that $(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$. We prove the condition $\left(BN\right)$. Given $x,y,z\in A$, we have

$$\begin{array}{cccc}\hfill (0\ast z)\ast (y\ast x)& =(x\ast z)\ast y\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \\ & =y\ast (z\ast x)\hfill & & [\because \mathrm{Theorem}8]\hfill \\ & =(0\ast y)\ast (z\ast x)\hfill & & [\because \left(\mathrm{F}\right)]\hfill \\ & =(x\ast y)\ast z.\hfill & & [\because \left(\mathrm{BV}\right)]\hfill \end{array}$$

Hence A is a $BN$-algebra with $\left(F\right)$. □

Remark 6.

The converse of Theorem 15 does not hold in general.

Example 9.

Let $A:=\{0,1,2\}$ be a set with the following table:

*	0	1	2
0	0	1	2
1	1	0	1
2	2	1	0

Then it is easy to see that A is a $BN$-algebra with $\left(F\right)$, but not a $BV$-algebra with $\left(F\right)$, since $(1\ast 2)\ast 1=1\ast 1=0\ne 2=2\ast 0=(0\ast 2)\ast (1\ast 1)$.

From the above theorems, we obtain the following equivalent statements:

Corollary 4.

The followings are equivalent:

(i) 

$(A,\ast ,0)$ is a $BV$-algebra with $\left(F\right)$,

(ii) 

$(A,\ast ,0)$ is a B-algebra with $\left(F\right)$,

(iii) 

$(A,\ast ,0)$ is a $BO$-algebra with $\left(F\right)$,

(iv) 

$(A,\ast ,0)$ is a $BF$-algebra with $\left(D\right)$,

(v) 

$(A,\ast ,0)$ is a $BN$-algebra with $\left(D\right)$,

(vi) 

$(A,\ast ,0)$ is a $BV$-algebra with $\left(D\right)$,

(vii) 

$(A,\ast ,0)$ is a Coxeter algebra,

(viii) 

$(A,\ast ,0)$ is a Boolean group.

We provide a diagram describing some relations between $BV$-algebras with $\left(F\right)$ and its related algebras as follows:

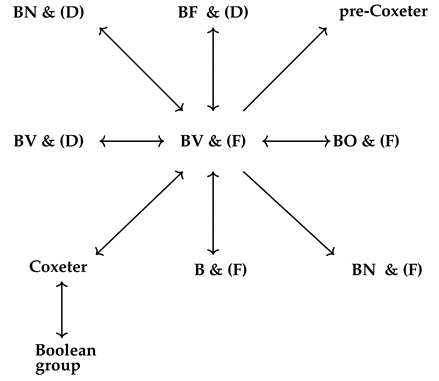
5. Conclusions and Future Works

We introduced the notion of a $BV$-algebra, and investigated some relations between $BV$-algebras and their related topics. Moreover, by using some additional axioms, we discussed some relations between $BV$-algebras with $\left(F\right)$ and several algebraic structures with additional axioms. In particular, we have focussed on the axiom $\left(BV\right)$, and investigated some relations with several other axioms which are discussed in various different algebraic structures. We found that the role of the axiom $\left(BV\right)$ is important in studying general algebraic structures.

We will discuss several ideal theories, isomorphism theorems in $BV$-algebras, and some applications to fuzzy theory, soft set theory and neutrosophic theory in the sequel. Moreover, we will investigate the axiom $\left(BT\right)$ for further development of general algebraic structures.