Estimating the Parameters of the Two-Parameter Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Data with Competing Risks
Abstract
1. Introduction
1.1. Two-Parameter Rayleigh Distribution
1.2. Adaptive Type II Progressive Hybrid Censoring

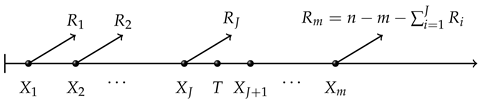
1.3. Competing Risks
2. Maximum Likelihood Estimation
3. Bayesian Estimation
3.1. Prior Distribution
3.2. Loss Functions
3.3. Lindley Method
4. Simulation
| Algorithm 1: Generating adaptive Type II progressive hybrid censored data with two competing risks from the two-parameter Rayleigh distribution. |
|
5. Data Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dey, S.; Dey, T.; Kundu, D. Two-Parameter Rayleigh Distribution: Different Methods of Estimation. Am. J. Math. Manag. Sci. 2014, 33, 55–74. [Google Scholar] [CrossRef]
- Dey, T.; Dey, S.; Kundu, D. On Progressively Type-II Censored Two-parameter Rayleigh Distribution. Commun. Stat. Simul. Comput. 2014, 45, 438–455. [Google Scholar] [CrossRef]
- Seo, J.I.; Jeon, J.W.; Kang, S.B. Exact Interval Inference for the Two-Parameter Rayleigh Distribution Based on the Upper Record Values. J. Probab. Stat. 2016, 2016, 8246390. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Fernández, A.; Abdi, M. Confidence sets for the two-parameter Rayleigh distribution under progressive censoring. Appl. Math. Model. 2017, 47, 656–667. [Google Scholar] [CrossRef]
- Khan, H.M.R.; Provost, S.B.; Singh, A. Predictive Inference from a Two-Parameter Rayleigh Life Model Given a Doubly Censored Sample. Commun. Stat. Theory Methods 2010, 39, 1237–1246. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Kundu, D.; Chan, P.S. Statistical analysis of exponential lifetimes under an adaptive Type-II progressive censoring scheme. Nav. Res. Logist. 2009, 56, 687–698. [Google Scholar] [CrossRef]
- Hemmati, F.; Khorram, E. Statistical Analysis of the Log-Normal Distribution under Type-II Progressive Hybrid Censoring Schemes. Commun. Stat. Simul. Comput. 2013, 42, 52–75. [Google Scholar] [CrossRef]
- Panahi, H.; Moradi, N. Estimation of the inverted exponentiated Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Sample. J. Comput. Appl. Math. 2020, 364, 112345. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O. Estimation of the inverse Weibull parameters under adaptive type-II progressive hybrid censoring scheme. J. Comput. Appl. Math. 2017, 315, 228–239. [Google Scholar] [CrossRef]
- Sobhi, M.M.A.; Soliman, A.A. Estimation for the exponentiated Weibull model with adaptive Type-II progressive censored schemes. Appl. Math. Model. 2016, 40, 1180–1192. [Google Scholar] [CrossRef]
- Nassar, M.; Abo-Kasem, O.; Zhang, C.; Dey, S. Analysis of Weibull Distribution Under Adaptive Type-II Progressive Hybrid Censoring Scheme. J. Indian Soc. Probab. Stat. 2018, 19, 25–65. [Google Scholar] [CrossRef]
- Liao, H.; Gui, W. Statistical Inference of the Rayleigh Distribution Based on Progressively Type II Censored Competing Risks Data. Symmetry 2019, 11, 898. [Google Scholar] [CrossRef]
- Shi, Y.; Jin, L.; Wei, C.; Yue, H. Constant-Stress Accelerated Life Test with Competing Risks under Progressive Type-II Hybrid Censoring. Adv. Mater. Res. 2013, 712–715, 2080–2083. [Google Scholar] [CrossRef]
- Wang, L. Inference for Weibull Competing Risks Data Under Generalized Progressive Hybrid Censoring. IEEE Trans. Reliab. 2018, 67, 998–1007. [Google Scholar] [CrossRef]
- Lindley, D.V. Approximate Bayesian methods. Trab. Estadística Investig. Oper. 1980, 31, 223–245. [Google Scholar] [CrossRef]
- Howlader, H.A.; Hossain, A.M. Bayesian survival estimation of Pareto distribution of the second kind based on failure-censored data. Comput. Stat. Data Anal. 2002, 38, 301–314. [Google Scholar] [CrossRef]
- Nie, J.; Gui, W. Parameter Estimation of Lindley Distribution Based on Progressive Type-II Censored Competing Risks Data with Binomial Removals. Mathematics 2019, 7, 646. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data. 2011. Available online: http://www.ru.ac.bd/wp-content/uploads/sites/25/2019/03/403_02_Lawless_Statistical-Models-and-Methods-for-Lifetime-Data-Second-Edition.pdf (accessed on 5 May 2020).

| (n,m,T) | Sch | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | ||
| Non-Informative | Informative | Non-Informative | Informative | Non-Informative | Informative | ||||||||||
| (30,25,4) | I | 0.0843 | 0.0417 | 0.0396 | 0.0299 | −0.0569 | 0.1299 | 0.0281 | 0.025 | −0.0352 | 0.0043 | 0.0034 | 0.023 | −0.0334 | 0.0066 |
| II | 0.0822 | 0.0343 | 0.0366 | 0.0245 | −0.0459 | 0.015 | 0.0252 | 0.021 | −0.0361 | 0.0045 | 0.0002 | 0.0191 | −0.0348 | 0.0066 | |
| (30,25,2) | I | 0.0749 | 0.0332 | 0.032 | 0.0243 | −0.0423 | 0.0085 | 0.0219 | 0.0211 | −0.0349 | 0.0041 | −0.0025 | 0.0207 | −0.0364 | 0.0069 |
| II | 0.0771 | 0.0317 | 0.0315 | 0.0226 | −0.0422 | 0.0092 | 0.021 | 0.0197 | −0.0356 | 0.004 | −0.004 | 0.018 | −0.0364 | 0.0066 | |
| (30,20,2) | I | 0.0894 | 0.0494 | 0.0376 | 0.0349 | −0.088 | 0.0857 | 0.0236 | 0.0288 | −0.0566 | 0.0065 | −0.0039 | 0.0268 | −0.0472 | 0.0074 |
| II | 0.1018 | 0.0529 | 0.0434 | 0.0357 | −0.111 | 0.1742 | 0.0283 | 0.0291 | −0.0672 | 0.0125 | 0.001 | 0.0266 | −0.0503 | 0.0143 | |
| (50,40,4) | I | 0.0416 | 0.0141 | 0.0131 | 0.0111 | −0.0077 | 0.0037 | 0.008 | 0.0104 | −0.0104 | 0.0039 | −0.0093 | 0.0099 | −0.0217 | 0.0054 |
| II | 0.0505 | 0.0171 | 0.0208 | 0.0134 | −0.0056 | 0.0038 | 0.0154 | 0.0123 | −0.0074 | 0.004 | −0.0016 | 0.0118 | −0.0182 | 0.0056 | |
| (50,40,2) | I | 0.0433 | 0.0139 | 0.0149 | 0.0109 | −0.0063 | 0.0036 | 0.0097 | 0.0102 | −0.0092 | 0.0038 | −0.0078 | 0.0097 | −0.021 | 0.0053 |
| II | 0.0448 | 0.0142 | 0.0161 | 0.0112 | −0.0054 | 0.0037 | 0.0109 | 0.0105 | −0.0083 | 0.0038 | −0.0066 | 0.0099 | −0.02 | 0.0053 | |
| (50,30,2) | I | 0.0575 | 0.0221 | 0.0228 | 0.0169 | −0.0176 | 0.005 | 0.0156 | 0.0152 | −0.0175 | 0.0038 | −0.0051 | 0.0142 | −0.0264 | 0.0061 |
| II | 0.0578 | 0.0238 | 0.0122 | 0.0658 | −0.0342 | 0.1274 | 0.0098 | 0.0197 | −0.0254 | 0.0093 | −0.0091 | 0.0152 | −0.0311 | 0.0069 | |
| (80,70,4) | I | 0.025 | 0.0072 | 0.0068 | 0.0061 | 0.0004 | 0.0038 | 0.0042 | 0.0059 | −0.0018 | 0.0037 | −0.0066 | 0.0057 | −0.0114 | 0.0041 |
| II | 0.0268 | 0.0072 | 0.0089 | 0.0063 | 0.0024 | 0.0043 | 0.0065 | 0.0064 | −0.0006 | 0.0037 | −0.009 | 0.0224 | −0.0107 | 0.0042 | |
| (80,70,2) | I | 0.0208 | 0.0065 | 0.0092 | 0.0475 | 0.0035 | 0.0428 | 0.0002 | 0.0053 | −0.0049 | 0.0034 | −0.0108 | 0.0054 | −0.0149 | 0.0039 |
| II | 0.0291 | 0.0068 | 0.0104 | 0.0057 | 0.0033 | 0.0035 | 0.0077 | 0.0055 | 0.001 | 0.0034 | −0.0032 | 0.0052 | −0.0086 | 0.0037 | |
| (80,60,2) | I | 0.0289 | 0.0077 | 0.0085 | 0.0065 | 0.0004 | 0.0037 | 0.0055 | 0.0062 | −0.0021 | 0.0037 | −0.0065 | 0.006 | −0.0124 | 0.0041 |
| II | 0.0288 | 0.0078 | 0.0083 | 0.0065 | 0.0001 | 0.0037 | 0.0052 | 0.0062 | −0.0026 | 0.0036 | −0.007 | 0.006 | −0.0131 | 0.0041 | |
| (n,m,T) | Sch | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | ||
| Non-Informative | Informative | Non-Informative | Informative | Non-Informative | Informative | ||||||||||
| (30,25,4) | I | 0.0860 | 0.0422 | −0.0252 | 0.0436 | −0.0398 | 0.0257 | −0.0319 | 0.0447 | −0.0446 | 0.0282 | −0.0344 | 0.0435 | −0.0503 | 0.0324 |
| II | 0.0895 | 0.0436 | −0.0222 | 0.0457 | −0.0356 | 0.0262 | −0.0278 | 0.0460 | −0.0405 | 0.0286 | −0.0310 | 0.0435 | −0.0464 | 0.0328 | |
| (30,25,2) | I | 0.0751 | 0.0492 | −0.0341 | 0.0455 | −0.0488 | 0.0484 | −0.0380 | 0.0399 | −0.0535 | 0.0424 | −0.0473 | 0.0544 | −0.0634 | 0.0963 |
| II | 0.0895 | 0.0382 | −0.0225 | 0.0379 | −0.0338 | 0.0232 | −0.0286 | 0.0388 | −0.0390 | 0.0254 | −0.0319 | 0.0387 | −0.0447 | 0.0288 | |
| (30,20,2) | I | 0.0818 | 0.0452 | −0.0384 | 0.0481 | −0.0536 | 0.0249 | −0.0445 | 0.0499 | −0.0578 | 0.0281 | −0.0465 | 0.0456 | −0.0633 | 0.0325 |
| II | 0.0976 | 0.0492 | −0.0246 | 0.0489 | −0.0497 | 0.0619 | −0.0278 | 0.0472 | −0.0485 | 0.0376 | −0.0295 | 0.0464 | −0.0485 | 0.0288 | |
| (50,40,4) | I | 0.0509 | 0.0193 | −0.0222 | 0.0197 | −0.0253 | 0.0150 | −0.0271 | 0.0205 | −0.0298 | 0.0157 | −0.0319 | 0.0209 | −0.0361 | 0.0176 |
| II | 0.0642 | 0.0224 | −0.0073 | 0.0205 | −0.0144 | 0.0171 | −0.0102 | 0.0225 | −0.0178 | 0.0170 | −0.0173 | 0.0224 | −0.0193 | 0.0258 | |
| (50,40,2) | I | 0.0629 | 0.0208 | −0.0098 | 0.0190 | −0.0143 | 0.0146 | −0.0146 | 0.0194 | −0.0187 | 0.0153 | −0.0194 | 0.0202 | −0.0239 | 0.0165 |
| II | 0.0548 | 0.0200 | −0.0171 | 0.0195 | −0.0214 | 0.0151 | −0.0218 | 0.0201 | −0.0258 | 0.0159 | −0.0267 | 0.0210 | −0.0311 | 0.0174 | |
| (50,30,2) | I | 0.0626 | 0.0241 | −0.0163 | 0.0216 | −0.0251 | 0.0217 | −0.0190 | 0.0232 | −0.0286 | 0.0197 | −0.0247 | 0.0222 | −0.0322 | 0.0180 |
| II | 0.0535 | 0.0213 | −0.0333 | 0.0472 | −0.0403 | 0.0707 | −0.0342 | 0.0266 | −0.0390 | 0.0215 | −0.0373 | 0.0246 | −0.0426 | 0.0195 | |
| (80,70,4) | I | 0.0336 | 0.0113 | −0.0142 | 0.0112 | −0.0155 | 0.0097 | −0.0174 | 0.0115 | −0.0186 | 0.0100 | −0.0213 | 0.0119 | −0.0227 | 0.0107 |
| II | 0.0362 | 0.0113 | −0.0101 | 0.0109 | −0.0111 | 0.0111 | −0.0129 | 0.0110 | −0.0153 | 0.0095 | −0.0192 | 0.0130 | −0.0218 | 0.0165 | |
| (80,70,2) | I | 0.0337 | 0.0105 | 0.0014 | 0.2513 | 0.0001 | 0.2365 | −0.0173 | 0.0103 | −0.0181 | 0.0092 | −0.0163 | 0.0420 | −0.0225 | 0.0103 |
| II | 0.0400 | 0.0115 | −0.0075 | 0.0108 | −0.0095 | 0.0094 | −0.0105 | 0.0110 | −0.0124 | 0.0096 | −0.0142 | 0.0113 | −0.0162 | 0.0101 | |
| (80,60,2) | I | 0.0391 | 0.0112 | −0.0120 | 0.0112 | −0.0136 | 0.0096 | −0.0151 | 0.0113 | −0.0166 | 0.0097 | −0.0187 | 0.0115 | −0.0204 | 0.0102 |
| II | 0.0363 | 0.0104 | −0.0132 | 0.0100 | −0.0150 | 0.0086 | −0.0163 | 0.0102 | −0.0180 | 0.0089 | −0.0200 | 0.0107 | −0.0218 | 0.0094 | |
| (n,m,T) | Sch | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | ||
| Non-Informative | Informative | Non-Informative | Informative | Non-Informative | Informative | ||||||||||
| (30,25,4) | I | 0.1202 | 0.0779 | 0.06 | 0.0576 | −0.0062 | 0.0132 | 0.0365 | 0.0469 | −0.0121 | 0.0156 | 0.0065 | 0.0456 | −0.0292 | 0.0219 |
| II | 0.1131 | 0.0703 | 0.0516 | 0.05 | −0.0067 | 0.013 | 0.0302 | 0.0413 | −0.0134 | 0.0147 | 0.0015 | 0.0412 | −0.0299 | 0.0202 | |
| (30,25,2) | I | 0.1256 | 0.0813 | 0.0647 | 0.0588 | −0.0063 | 0.0246 | 0.0401 | 0.0468 | −0.0092 | 0.0151 | 0.0117 | 0.0455 | −0.0251 | 0.0207 |
| II | 0.1432 | 0.095 | 0.0808 | 0.0696 | 0.0022 | 0.0154 | 0.0564 | 0.0561 | 0.0002 | 0.017 | 0.0277 | 0.0535 | −0.0141 | 0.0231 | |
| (30,20,2) | I | 0.168 | 0.124 | 0.0922 | 0.0852 | −0.0343 | 0.0281 | 0.0591 | 0.0649 | −0.0225 | 0.0146 | 0.0265 | 0.0625 | −0.0309 | 0.0229 |
| II | 0.1621 | 0.1266 | 0.0835 | 0.088 | −0.0349 | 0.0295 | 0.0517 | 0.0685 | −0.0236 | 0.0172 | 0.0207 | 0.0672 | −0.0336 | 0.0253 | |
| (50,40,4) | I | 0.0813 | 0.0379 | 0.0414 | 0.0291 | 0.0188 | 0.0148 | 0.0292 | 0.0258 | 0.0098 | 0.0144 | 0.0083 | 0.0245 | −0.0072 | 0.0158 |
| II | 0.0827 | 0.0363 | 0.0427 | 0.0281 | 0.0213 | 0.0155 | 0.0304 | 0.025 | 0.0118 | 0.0147 | 0.0093 | 0.024 | −0.0057 | 0.0162 | |
| (50,40,2) | I | 0.0831 | 0.0378 | 0.0433 | 0.0291 | 0.0212 | 0.0155 | 0.0312 | 0.026 | 0.012 | 0.0149 | 0.0102 | 0.0246 | −0.0052 | 0.0161 |
| II | 0.0621 | 0.0291 | 0.0233 | 0.0232 | 0.0069 | 0.0132 | 0.0121 | 0.021 | −0.0022 | 0.0128 | −0.0085 | 0.0205 | −0.02 | 0.0142 | |
| (50,30,2) | I | 0.1101 | 0.0663 | 0.0599 | 0.0503 | 0.0125 | 0.0184 | 0.0417 | 0.0423 | 0.0054 | 0.0176 | 0.0159 | 0.0404 | −0.0119 | 0.021 |
| II | 0.0863 | 0.0514 | 0.0326 | 0.0383 | −0.0032 | 0.0157 | 0.0159 | 0.0335 | −0.0131 | 0.0162 | −0.0093 | 0.0326 | −0.0311 | 0.0199 | |
| (80,70,4) | I | 0.0405 | 0.0153 | 0.0155 | 0.0129 | 0.01 | 0.0099 | 0.0096 | 0.0122 | 0.0046 | 0.0096 | −0.0033 | 0.0119 | −0.0077 | 0.0097 |
| II | 0.0458 | 0.0151 | 0.0217 | 0.0133 | 0.016 | 0.0109 | 0.0149 | 0.0117 | 0.0094 | 0.0092 | 0.0011 | 0.0122 | −0.0036 | 0.0099 | |
| (80,70,2) | I | 0.0407 | 0.0148 | 0.0155 | 0.0124 | 0.0101 | 0.0097 | 0.0097 | 0.0117 | 0.0047 | 0.0093 | −0.0031 | 0.0114 | −0.0074 | 0.0094 |
| II | 0.0494 | 0.0157 | 0.024 | 0.0129 | 0.0179 | 0.01 | 0.0181 | 0.0122 | 0.0124 | 0.0096 | 0.0053 | 0.0117 | 0.0003 | 0.0095 | |
| (80,60,2) | I | 0.0574 | 0.0198 | 0.0291 | 0.0159 | 0.0198 | 0.0112 | 0.0218 | 0.0147 | 0.0133 | 0.0106 | 0.0068 | 0.0139 | −0.0004 | 0.0107 |
| II | 0.0529 | 0.0182 | 0.0243 | 0.0146 | 0.0163 | 0.0107 | 0.0173 | 0.0136 | 0.0099 | 0.0102 | 0.0027 | 0.0131 | −0.0036 | 0.0103 | |
| (n,m,T) | Sch | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | ||
| Non-Informative | Informative | Non-Informative | Informative | Non-Informative | Informative | ||||||||||
| (30,25,4) | I | 0.0771 | 0.0302 | −0.0019 | 0.0273 | −0.011 | 0.0209 | −0.0077 | 0.0268 | −0.0158 | 0.0214 | −0.012 | 0.0284 | −0.0202 | 0.0237 |
| II | 0.0642 | 0.0234 | −0.0131 | 0.0208 | −0.0214 | 0.0168 | −0.018 | 0.021 | −0.025 | 0.0172 | −0.0215 | 0.0229 | −0.0283 | 0.0195 | |
| (30,25,2) | I | 0.0762 | 0.0265 | −0.0034 | 0.0224 | −0.0131 | 0.0175 | −0.0085 | 0.0227 | −0.0172 | 0.0183 | −0.0117 | 0.0232 | −0.0203 | 0.0191 |
| II | 0.0771 | 0.0261 | 0.0005 | 0.0228 | −0.0094 | 0.0173 | −0.0039 | 0.0231 | −0.013 | 0.0181 | −0.0068 | 0.0235 | −0.0159 | 0.0189 | |
| (30,20,2) | I | 0.0926 | 0.0326 | 0.002 | 0.0256 | −0.0143 | 0.0183 | −0.0032 | 0.0259 | −0.0179 | 0.0194 | −0.0064 | 0.0263 | −0.0206 | 0.0204 |
| II | 0.0739 | 0.024 | −0.0104 | 0.0214 | −0.0215 | 0.016 | −0.0145 | 0.0217 | −0.0247 | 0.0167 | −0.017 | 0.0221 | −0.0271 | 0.0175 | |
| (50,40,4) | I | 0.0538 | 0.0141 | 0.0002 | 0.0117 | −0.0036 | 0.0102 | −0.0031 | 0.0118 | −0.0068 | 0.0104 | −0.0059 | 0.0121 | −0.0094 | 0.0107 |
| II | 0.0492 | 0.013 | 0.0008 | 0.0152 | −0.0032 | 0.0119 | −0.0042 | 0.011 | −0.0074 | 0.0098 | −0.0075 | 0.0123 | −0.0107 | 0.0111 | |
| (50,40,2) | I | 0.0552 | 0.0148 | 0.0018 | 0.0123 | −0.002 | 0.0106 | −0.0016 | 0.0125 | −0.0052 | 0.0108 | −0.0043 | 0.0127 | −0.0079 | 0.0113 |
| II | 0.045 | 0.0113 | −0.0067 | 0.0101 | −0.009 | 0.0089 | −0.0097 | 0.0102 | −0.012 | 0.0091 | −0.0122 | 0.0104 | −0.0144 | 0.0093 | |
| (50,30,2) | I | 0.067 | 0.0206 | 0.0037 | 0.0166 | −0.0032 | 0.0136 | −0.0003 | 0.0167 | −0.0067 | 0.0138 | −0.0033 | 0.017 | −0.0095 | 0.0142 |
| II | 0.0432 | 0.012 | −0.0155 | 0.0119 | −0.0184 | 0.0097 | −0.0184 | 0.0121 | −0.0212 | 0.0101 | −0.0206 | 0.0123 | −0.0236 | 0.0105 | |
| (80,70,4) | I | 0.0332 | 0.0073 | −0.002 | 0.0064 | −0.003 | 0.006 | −0.0042 | 0.0064 | −0.0051 | 0.006 | −0.006 | 0.0065 | −0.0069 | 0.0061 |
| II | 0.0329 | 0.0069 | 0.0002 | 0.007 | −0.0007 | 0.0069 | −0.0027 | 0.006 | −0.0038 | 0.0057 | −0.0087 | 0.0247 | −0.0085 | 0.0152 | |
| (80,70,2) | I | 0.0326 | 0.0074 | −0.0027 | 0.0066 | −0.0037 | 0.0061 | −0.005 | 0.0066 | −0.0059 | 0.0062 | −0.0066 | 0.0067 | −0.0075 | 0.0063 |
| II | 0.0335 | 0.0068 | −0.0003 | 0.0059 | −0.0015 | 0.0055 | −0.0022 | 0.006 | −0.0034 | 0.0056 | −0.0039 | 0.006 | −0.0051 | 0.0057 | |
| (80,60,2) | I | 0.0395 | 0.0085 | 0.001 | 0.0072 | −0.001 | 0.0066 | −0.0014 | 0.0072 | −0.0033 | 0.0067 | −0.0034 | 0.0073 | −0.0052 | 0.0068 |
| II | 0.0314 | 0.0063 | −0.0042 | 0.0057 | −0.0056 | 0.0053 | −0.0061 | 0.0058 | −0.0075 | 0.0054 | −0.0078 | 0.0059 | −0.0091 | 0.0055 | |
| Sch | Data and Corresponding Risk Causes | |
|---|---|---|
| (37, 30, 0.5) | I | (1.2710, 2), (1.4269, 2), (1.6713, 2), (1.7853, 2), (1.8117, 2), (1.9275, 2), (1.9867, 2), (2.0263, 1), |
| (2.0905, 2), (2.1303, 1), (2.1612, 1), (2.1711, 2), (2.1778, 1), (2.1824, 2), (2.1911, 1), (2.1923, 1), | ||
| (2.1926, 1), (2.2031, 2), (2.2038, 2), (2.2141, 1), (2.2295, 2), (2.2313, 1), (2.2351, 1), (2.2424, 1), | ||
| (2.2618, 1), (2.3101, 1), (2.4010, 1) | ||
| II | (1.2710, 2), (1.4269, 2), (1.4758, 2), (1.6713, 2), (1.7853, 2), (1.9275, 2), (1.9867, 2), (2.0073, 2), | |
| (2.0263, 1), (2.0905, 2), (2.1303, 1), (2.1374, 1), (2.1711, 2), (2.1778, 1), (2.1824, 2), (2.1842, 1), | ||
| (2.1911, 1), (2.1923, 1), (2.1926, 1), (2.2038, 2), (2.2085, 2), (2.2141, 1), (2.2295, 2), (2.2313, 1), | ||
| (2.2351, 1), (2.2424, 1), (2.2601, 1) |
| Data I | MLE | S | L | E |
| 13.2035 | 11.4226 | 10.7848 | 10.7186 | |
| 2.0062 | 1.9863 | 1.9863 | 1.9863 | |
| 0.5235 | 0.4487 | 0.4362 | 0.4146 | |
| 1.1631 | 1.0766 | 1.0755 | 1.0751 | |
| Data II | MLE | S | L | E |
| 13.9304 | 12.2914 | 11.4543 | 11.4838 | |
| 2.0109 | 1.9957 | 1.9957 | 1.9957 | |
| 0.6213 | 0.5051 | 0.4894 | 0.4722 | |
| 1.1719 | 1.0750 | 1.0750 | 1.0754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Gui, W. Estimating the Parameters of the Two-Parameter Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Data with Competing Risks. Mathematics 2020, 8, 1783. https://doi.org/10.3390/math8101783
Liu S, Gui W. Estimating the Parameters of the Two-Parameter Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Data with Competing Risks. Mathematics. 2020; 8(10):1783. https://doi.org/10.3390/math8101783
Chicago/Turabian StyleLiu, Shuhan, and Wenhao Gui. 2020. "Estimating the Parameters of the Two-Parameter Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Data with Competing Risks" Mathematics 8, no. 10: 1783. https://doi.org/10.3390/math8101783
APA StyleLiu, S., & Gui, W. (2020). Estimating the Parameters of the Two-Parameter Rayleigh Distribution Based on Adaptive Type II Progressive Hybrid Censored Data with Competing Risks. Mathematics, 8(10), 1783. https://doi.org/10.3390/math8101783






