Abstract
We show how a small subgroup confinement-like attack may be mounted on the Bitcoin addresses generation protocol, by inspecting a special subgroup of the group associated to point multiplication. This approach does not undermine the system security but highlights the importance of using fair random sources during the private key selection.
1. Introduction
Since its appearance in 2008 [1], Bitcoin (BTC) has been attracting a considerable attention from many communities, embracing several different fields, such as cryptography, computer science, and finance [2]. Although it has seen the light as a decentralized digital currency, its underlying blockchain structure has been rapidly adopted for diverse purposes [3,4]. Instances of its use, beyond modern cryptocurrencies, are smart contracts [5], financial services [6], supply chain monitoring [7], and digital notarization [8].
The security of these distributed ledgers has been widely studied and usually relies on a mixture of cryptographic and consensus-reaching algorithms [9]. In the renowned case of BTC, the consensus is reached via a hashcash proof of work [10], while public (asymmetric) cryptography is employed to ensure transactions legitimacy. In a nutshell, apart from some special cases, the owner of a bitcoin is any person who can prove (following the BTC protocol) to own the private key associated to the public address where that bitcoin has been previously sent.
Thus, it is crucial for such a cryptosystem to generate private keys that do not allow their recovering from public information. In the BTC case, this depends on the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP) and the preimage resistance of some hash functions. However, if the keys are not uniformly distributed, there may be a (relatively) small portion of the keyspace where they can be easily found (see, e.g., Reference [11]).
In this short note, we pursue the latter idea. In 2017, we conjectured that the key generation algorithms used by some BTC wallets to select private keys were flawed, that is, there was a non-negligible probability that some of the private keys would lie inside a small keyspace with prescribed algebraic properties, which can be entirely inspected. To be more precise, given the size q of the BTC curve, in 2018, we scanned a reasonably small subgroup of the multiplicative group , actually finding (against all odds) a few public addresses corresponding to elements of such group. Immediately after that, we devised a method to warn the anonymous bitcoin’s holders of this problem. Then, we followed a prudent responsible disclosure behavior, not mentioning the current note publicly until 2020 [12].
This paper is organized as follows: we begin by recalling, in Section 2, the mathematical notions employed for BTC address generation, while, in Section 3, the aforementioned group of weak private keys is determined and analyzed. The method effectiveness and further possible work directions are finally discussed in Section 4.
2. Preliminaries
2.1. Elliptic Curve Discrete Logarithm Problem
In this section, we recall some basic notions and facts about elliptic curves and their related discrete logarithm problem. For a more detailed discussion of these topics, we refer to Reference [13,14].
Since we are here interested only in cryptographic applications of elliptic curves, we present this celebrated mathematical object in its simplest version (as the short Weierstrass form of a non-singular planar cubic). In the same spirit, in this short note the underlying field may always be considered finite [15]. Given a prime integer p, we will denote the prime field with p elements by .
Definition 1
(Elliptic curve).Let be a field of characteristic different from 2 and 3 and be elements such that . The elliptic curve defined by over is the set
where is called the point at infinity.
It is well-known that on an elliptic curve E one may define the chord-tangent point-addition law
which makes E into an abelian group with as the identity element, and with the inverses given by
This operation reflects the following geometric construction: given two points , the point is the inverse of Q, the third point of intersection of the curve with line connecting and . When the underlying field is finite, this construction still holds with a toric identification of , as in Figure 1.
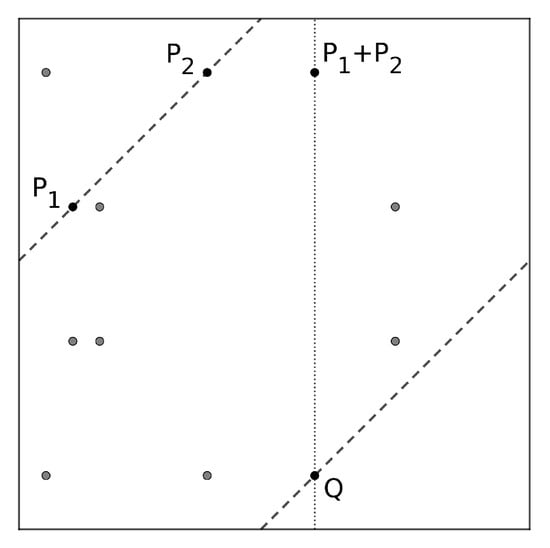
Figure 1.
Chord-tangent sum over finite fields.
The point at infinity is a formal point that may be considered to be vertically aligned with every pair of inverse curve points.
The iterated sum of a given point naturally defines an action of on E, as follows.
Definition 2
(Scalar multiplication). Let k be a positive integer and let P be a point on an elliptic curve.
We define as
If , we set , while, when , we define .
Given a point , we denote by the subgroup generated by P in E, i.e., all the points of E that may be written as for some .
Problem 1
(ECDLP). Let E be an elliptic curve defined over a finite field , and let be one of its points, called the base-point. Finding the discrete logarithm of any amounts to finding an integer such that .
While computing a point-multiple is computationally easy, solving the discrete logarithm problem is considered hard, except for few special cases [13]. For this reason, scalar multiplication over elliptic curves is considered a valid one-way function, on which cryptographic protocols may be designed. These objects own many other cryptographically desirable properties, for which we refer to Reference [16].
In practical implementations, curves of large and prime size are considered. The point groups of such curves are cyclic, so that each non-zero element is a proper generator and a valid base-point.
2.2. The Bitcoin Address Generation
The BTC system is based on public key encryption: in short, addresses are generated by public keys, which are originated from private ones, withheld by users. All these steps are performed through one-way functions, which are considered impossible to reverse in a feasible time.
2.2.1. Public Key Generation
In the BTC system, both private and public keys depend on an elliptic curve , known as Secp256k1, which belongs to the Standards for Efficient Cryptography Group [17]. The parameters of are
i.e., its affine points form the zero set of
The base-point is defined as , where
It may be verified that this curve is a cyclic group, of prime order
thus, is isomorphic to via the mapping .
A private key is any integer , so that the key space may be identified with .
The corresponding public key is the point of .
This curve may be visualized as a set of scattered points inside the plane with a prescribed base-point P, in which multiples generate the whole curve, as in the small example of Figure 2.
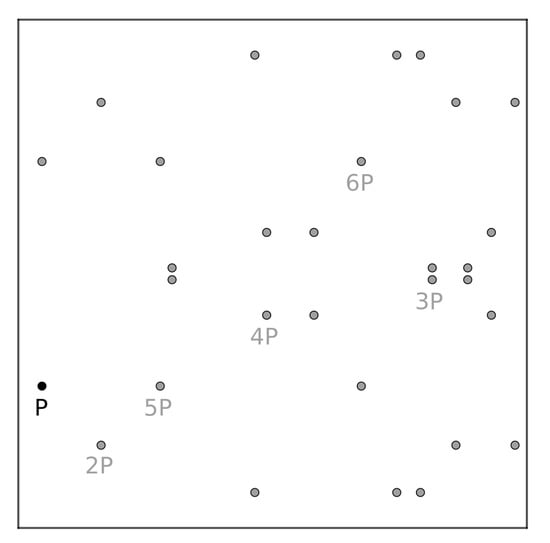
Figure 2.
with some multiples of the distinguished point .
2.2.2. Address Generation
Given any public key , the corresponding address may be computed by first applying two hash functions consecutively, SHA-256 [18] and RIPEMD-160 [19], then adding an initial byte and four final checksum bytes, and finally encoding the result to Base58 [20]. To sum up, the BTC address is obtained from any public key (we are omitting a few details) by performing
where means string concatenation, and c is a prescribed constant.
For the following discussion, it is important to notice that SHA-256 turns any input element into a 256-bit string, while RIPEMD-160 squeezes it into a 160-bit string. Therefore, even if the final address is 200-bit long, there may be, at most, distinct BTC addresses.
3. A Small Subgroup Attack
3.1. Subgroup Detection
Since private keys are elements of , a straight brute force attack to the Bitcoin system seems infeasible, as inverting the map
would imply solving an ECDLP instance.
However, there are few small subgroups that may be inspected, for which an exhaustive computation of all the possible keys and corresponding addresses may be carried out. This way one may compute the inverse of the restricted map
Since the keys are supposed to be uniformly distributed, there is no probabilistic argument suggesting their presence in specific small subgroups. However, assuming that this is the case, we need to choose a suitable subgroup. In this view, by considering the factorization of into prime integers
it is not difficult to test that the maximal subgroup of moderate size (i.e. that can today be checked with an average computer) contains N elements, where
Such a group may be easily produced by considering any primitive element t of , such as , and considering the element , which generates the subgroup
Indeed, we summarize in the following theorem two well-known results.
Theorem 1.
Let be a field. Then, any finite subgroup is cyclic. Moreover, for every positive integer M dividing , there is a unique subgroup such that .
3.2. Subgroup Inspection
The group H as previously defined has less than 20 millions elements; therefore, we were able to straightforwardly construct, in a few days, the BTC addresses originated by all private keys and to check whether they have appeared in the BTC blockchain since its creation until 2018.
We recall that an address appears in the blockchain whenever it receives any amount of bitcoin. Note that the number of addresses in the BTC blockchain does not correspond to the number of actual BTC users, as modern wallets handle many different addresses for each user.
With this procedure, we found 4 BTC addresses, in which private keys belong to H:
- 1PSRcasBNEwPC2TWUB68wvQZHwXy4yqPQ3,
- 1B5USZh6fc2hvw2yW9YaVF75sJLcLQ4wCt,
- 1EHNa6Q4Jz2uvNExL497mE43ikXhwF6kZm,
- 1JPbzbsAx1HyaDQoLMapWGoqf9pD5uha5m.
Two of them, (3) and (4), came from the trivial keys 1 and , and they might have been generated on purpose, but the remaining two addresses appear to be legit. In particular, a blockchain inspection (Reference [21], 2018) suggests that one of them (2) has been used as temporary address for moving a small amount of bitcoins, while the other (1) has probably been used as a personal address, since its owner has stored some bitcoins there for 4 years.
To show that the private key of address (1) was really recovered, we used three of our addresses
- A.
- 1FCuka8PYyfMULbZ7fWu5GWVYiU88KAU9W,
- B.
- 1NChjA8s5cwPgjWZjD9uu12A5sNfoRHhbA,
- C.
- 1695755gMv3fJxYVCDitMGaxGu7naSXYmv,
and we performed tiny transactions from each of them, as shown in Figure 3.
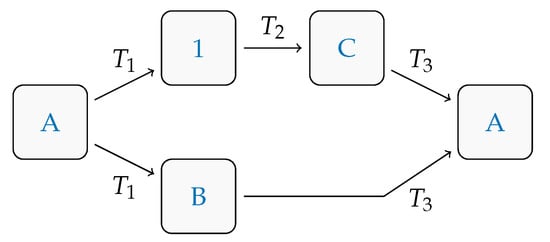
Figure 3.
Transactions summary.
These operations may be easily verified through any blockchain explorer, such as Reference [21], by searching for their transaction IDs:
- T1.
- 69ad7033376cea2bbea01e7ef76cc8d7bc028325e9179b2231ca1076468c1a1e,
- T2.
- 1dd5c256a1acc81ea4808a405fd83586ea03d8b58e29a081ebf3d0d95e77bf63,
- T3.
- b722c77dcdd13c3616bf0c4437f2eb63d96346f74f4eeb7a1e24c1a9711fc101.
4. Discussion and Conclusions
Although our approach has found only few addresses that may be generated by secret keys in the considered subgroup, it is worth noting that this outcome is still unexpected. At the time of our analysis (June 2018), there were about
BTC addresses that have appeared in the blockchain [21]. We have inspected
addresses of those generated from the secret keys in H. As we have already noticed in Section 2.2, the number of possible distinct addresses is, at most,
which we may assume to be all existent under the assumption of uniform distribution of the considered hash functions (SHA-256 and RIPEMD-160). Therefore, the expected probability of finding at least a BTC address in the blockchain from a random sampling performed N times was
We conclude that, if the BTC private keys had been generated in a random manner, we would not have found any addresses.
There may be many reasons why such an unlikely event has occurred. Probably it depends on the pseudo-random algorithms (or their implementations) used by wallets to generate user’s addresses. Our 2017 conjecture started from this obvious fact from group theory: if , then for all a. Therefore, if private keys are obtained via iterated powers, once the wallet gets a key inside a subgroup, all the other keys will be in the same.
As for future research lines, it might be interesting to realize such an approach on different cryptocurrencies, or to examine other algebraic structures that may be associated to the private key space, such as special cosets of H.
Author Contributions
Conceptualization, M.S.; Investigation, D.S. and D.T.; Methodology, D.S. and D.T.; Project administration, D.T.; Supervision, M.S.; Writing-original draft, D.S. and D.T.; Writing-review and editing, M.S. and D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This note has been supported in part by the European Union’s H2020 Programme under grant agreement number ERC-669891.
Acknowledgments
We thank Roberto La Scala, for supporting the current short note and supervising the second author’s MSC thesis. For interesting discussions and comments, the authors would like to thank Marco Amadori, Michele Elia, and Andrea Visconti. This note was first informally presented in Reference [12].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 5 May 2020).
- Narayanan, A.; Bonneau, J.; Felten, E.; Miller, A.; Goldfeder, S. Bitcoin and Cryptocurrency Technologies: A Comprehensive Introduction; Princeton University Press: Princeton, NJ, USA, 2016; Available online: https://press.princeton.edu/books/hardcover/9780691171692/bitcoin-and-cryptocurrency-technologies (accessed on 5 May 2020).
- Chen, W.; Xu, Z.; Shi, S.; Zhao, Y.; Zhao, J. A Survey of Blockchain Applications in Different Domains. In Proceedings of the 2018 International Conference on Blockchain Technology and Application ICBTA 2018, Xi’an China, 10–12 December 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 17–21. [Google Scholar] [CrossRef]
- Blockchains: The Great Chain of Being Sure about Things. The Economist. 2015. Available online: https://www.economist.com/briefing/2015/10/31/the-great-chain-of-being-sure-about-things (accessed on 5 July 2020).
- Alharby, M.; Aldweesh, A.; van Moorsel, A. Blockchain-based Smart Contracts: A Systematic Mapping Study of Academic Research. In Proceedings of the 2018 International Conference on Cloud Computing, Big Data and Blockchain (ICCBB) 2018, Fuzhou, China, 15–17 November 2018. [Google Scholar] [CrossRef]
- Eyal, I. Blockchain Technology: Transforming Libertarian Cryptocurrency Dreams to Finance and Banking Realities; IEEE: Piscataway, NJ, USA, 2017; pp. 38–49. [Google Scholar] [CrossRef]
- Foodchain. Available online: https://food-chain.it/ (accessed on 5 June 2020).
- Chowdhury, M.J.M.; Colman, A.; Kabir, M.A.; Han, J.; Sarda, P. Blockchain as a Notarization Service for Data Sharing with Personal Data Store. In Proceedings of the 2018 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/12th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018. [Google Scholar] [CrossRef]
- Lin, I.C.; Liao, T.C. A Survey of Blockchain Security Issues and Challenges. Netw. Secur. 2017, 19, 653–659. [Google Scholar] [CrossRef]
- Meneghetti, A.; Sala, M.; Taufer, D. A Survey on PoW-based Consensus. Ann. Emerg. Technol. Comput. AETiC 2020, 4, 8–18. [Google Scholar] [CrossRef]
- Lim, C.H.; Lee, P.J. A Key Recovery Attack on Discrete Log-Based Schemes Using a Prime Order Subgroup. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1998; pp. 249–263. [Google Scholar] [CrossRef]
- Sogiorno, D. Una Famiglia di Chiavi Deboli Nel Bitcoin, CRYPTANALYSIS: A Key Tool in Securing and Breaking Ciphers. 2020. Available online: http://www.decifris.it/2020/crittanalisi2020.html (accessed on 5 May 2020).
- Galbraith, S.D.; Gaudry, P. Recent progress on the elliptic curve discrete logarithm problem. Des. Codes Cryptogr. 2016, 78, 51–72. [Google Scholar] [CrossRef]
- Silverman, J.H. The Arithmetic of Elliptic Curves; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Lidl, R.; Niederreiter, H. Finite Fields; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Vo, S.C. A Survey of Elliptic Curve Cryptosystems, Part I: Introductory. In NASA Advanced Supercomputing Division; NAS Technical Report—NAS-03-012; 2003. Available online: https://www.nas.nasa.gov/assets/pdf/techreports/2003/nas-03-012.pdf (accessed on 18 May 2020).
- Certicom Research. SEC 2: Recommended Elliptic Curve Domain Parameters. 2000. Available online: http://www.secg.org/sec2-v2.pdf (accessed on 18 May 2020).
- Penard, W.; van Werkhoven, T. On the Secure Hash Algorithm Family, Cryptography in Context. Chapter 1. 2007. Available online: https://www.staff.science.uu.nl/~tel00101/liter/Books/CrypCont.pdf (accessed on 18 May 2020).
- Dobbertin, H.; Bosselaers, A.; Preneel, B. RIPEMD-160: A Strengthened Version of RIPEMD. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 1996; pp. 71–82. [Google Scholar] [CrossRef]
- Antonopoulos, A.M. Base58 and Base58Check Encoding. In Mastering Bitcoin; O’Reilly: Sevastopol, CA, USA, 2015; Available online: https://www.oreilly.com/library/view/mastering-bitcoin-2nd/9781491954379/ch04.html#base58 (accessed on 20 May 2020).
- Blockchain.com. Available online: https://www.blockchain.com/explorer?view=btc (accessed on 20 May 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).