On Cocyclic Hadamard Matrices over Goethals-Seidel Loops

Abstract

About twenty-five years ago, Horadam and de Launey introduced the cocyclic development of designs, from which the notion of cocyclic Hadamard matrices developed over a group was readily derived. Much more recently, it has been proved that this notion may naturally be extended to define cocyclic Hadamard matrices developed over a loop. This paper delves into this last topic by introducing the concepts of coboundary, pseudocoboundary and pseudococycle over a quasigroup, and also the notion of the pseudococyclic Hadamard matrix. Furthermore, Goethals-Seidel loops are introduced as a family of Moufang loops so that every Hadamard matrix of Goethals-Seidel type (which is known not to be cocyclically developed over any group) is actually pseudococyclically developed over them. Finally, we also prove that, no matter if they are pseudococyclic matrices, the usual cocyclic Hadamard test is unexpectedly applicable.

1. Introduction

A (binary) Hadamard matrix is a square matrix H with entries $\pm 1$ whose row (equivalently, column) vectors are pairwise orthogonal. It may be readily checked that every Hadamard matrix must have order 1, 2 or a multiple of 4, as soon as three rows must be pairwise orthogonal. Surprisingly, no other restrictions on the order of a Hadamard matrix are known. Actually, it is conjectured that a Hadamard matrix exists for every order multiple of 4. This is the century-old Hadamard Conjecture.

About twenty-five years ago, the use of cocycles and cocyclic matrices was introduced by Horadam and de Launey as a part of a theory of development of designs [1]. Furthermore, they showed [2] that the cocyclic framework could provide a structural approach in order to resolve the Hadamard Conjecture. This idea is currently supported by the fact that many known constructions of Hadamard matrix families have been shown to be cocyclic, as, for instance, Sylvester matrices, Paley matrices, Williamson matrices or Ito’s type Q matrices (see, for instance, [3,4,5,6,7,8]). On the other hand, two of the most prolific of these families have actually been shown to fail to be cocyclic [6]. Namely, the family of two-circulant core Hadamard matrices [9] and the so-called Goethals-Seidel arrays [10], which are related in turn with supplementary difference sets [11]. This paper figures out a new approach to deal with a cocyclic development of Goethals-Seidel arrays, not over a group, but over a certain family of Moufang loops, for positive integers $t\ge 1$. This is a particular case of the more general theory, which has recently been proved. That is, the notion of cocyclic matrix may naturally be extended to cover quasigroups [12].

While the study of quasigroups may be dated back at least to Euler’s work on orthogonal Latin squares, as the years went by, the theory of quasigroups was somehow banished by the development of the theory of groups. It is worthwhile noting, in particular, that a well-established cohomology theory for groups exists from the mid-1940s, by means of the seminal works of Eilenberg and Mac Lane [13,14,15]. Yet, surprisingly, no such theory has been fully developed for quasigroups. However, there are some remarkable papers on cohomology for loops (see [16,17,18] and the references therein) and a few for quasigroups [19,20]. For a brief survey on prospective applications of quasigroups and loops, and a panoramic of the state of the art, the interested reader is referred to [21,22,23].

The paper is organized as follows. Some background notions on Hadamard matrices, quasigroups and cocyclic matrices developed over quasigroups are introduced in Section 2. In Section 3, we introduce the notion of coboundary over a quasigroup and we prove that certain triples of elements of a quasigroup over which a Hadamard matrix is cocyclic have to be associative in order to obtain cocyclic elementary coboundaries. This last fact leads us to introduce both concepts of pseudocoboundary and pseudococycle over a quasigroup, and also the notion of pseudococyclic Hadamard matrices. In particular, the existence of pseudococyclic Hadamard matrices over quasigroups that are not loops is illustrated. Finally, in Section 4, we describe Goethals-Seidel arrays as pseudococyclic Hadamard matrices. Moreover, even if the cocyclic Hadamard test is shown to be no longer available for pseudococyclic matrices in general, it is proved that the usual cocyclic Hadamard test actually still applies on Goethals-Seidel arrays.

2. Preliminaries

Let us review some basic concepts and results on Hadamard matrices, quasigroups and cocyclic matrices over quasigroups that are used throughout the paper. We refer the reader to [12,24,25] for more details about these topics.

2.1. Hadamard Matrices

Two matrices with entries $\pm 1$ are Hadamard equivalent if they are equal up to permutations or negation of their rows and columns. This is an equivalence relation among Hadamard matrices, which we denote ${\sim }_H$.

One of the most prolific methods for constructing Hadamard matrices is via the so-called Goethals-Seidel arrays [10], which consist of $4t\times 4t$-block matrices of the type

$$\left(\begin{array}{cccc}\hfill A& \hfill BR& \hfill CR& \hfill DR\\ \hfill BR& \hfill -A& \hfill RD& \hfill -RC\\ \hfill CR& \hfill -RD& \hfill -A& \hfill RB\\ \hfill DR& \hfill RC& \hfill -RB& \hfill -A\end{array}\right),$$

(1)

for A, B, C and D being $t\times t$-circulant matrices and R being the back circulant permutation matrix having $(0,\dots ,0,1)$ as its first row. This matrix is Hadamard if

$$A{A}^T+B{B}^T+C{C}^T+D{D}^T=4t{I}_t,$$

(2)

where $X^T$ denotes the transpose of $X\in \{A,B,C,D\}$ and $I_t$ denotes the $t\times t$-identity matrix with ones in its main diagonal, and zeros elsewhere.

Goethals-Seidel arrays are related to certain supplementary difference sets consisting of four subsets, as soon as one attends to the positions in which negative entries occur at the first row, in every $t\times t$ block. More concretely, given a finite abelian group $(G,·)$ of order t, four subsets $X_1,X_2,X_3,X_4\subset G$ form a supplementary difference set of parameters $(t;k_1,k_2,k_3,k_4;\lambda )$, for $k_i=\left|X_i\right|$, if, for every $g\in G\backslash \left\{1\right\}$, there are exactly $\lambda$ different ordered pairs $(h,j)\in {\displaystyle \bigcup _{i=1}^4}{X}_i\times X_i$ such that $h{j}^{-1}=g$. Consequently, it must be

$$\sum _{i=1}^4{k}_i(k_i-1)=\lambda (t-1).$$

(3)

Furthermore, assuming Equation (3), Equation (2) is equivalent to

$$\sum _{i=1}^4{k}_i=\lambda +t.$$

(4)

In particular, taking $G={\mathbf{Z}}_t$, such a supplementary difference set leads readily to a Goethals-Seidel array. To this end, the first rows of the matrices A, B, C and D are defined from the subsets $X_0$, $X_1$, $X_2$ and $X_3$ in such a way that the i-th entry of the first row of A (respectively, B, C or D) is $-1$ if and only if $i-1$ belongs to $X_0$ (respectively, $X_1$, $X_2$ or $X_3$).

There exist several methods for constructing Hadamard matrices of Goethals-Seidel type of a given order $4t$ from suitable supplementary difference sets. Thus, for instance:

• Spence [26] proved their existence for $t=1+q+q^2$, with q being a prime power, whenever there exists a cyclic projective plane of order $q^2$ and two supplementary difference sets in a cyclic group of order t.
• Whiteman [27] proved their existence for $t=2p+1$, with p being a prime and $2p-1$ a prime power.
• Ðoković [28,29,30,31,32] made use of supplementary difference sets in order to construct Hadamard matrices of Goethals-Seidel type, for all $t\in \{39,47,49,61,65,81,93,103,109,121,127,129,133,145,$$151,169,217,219,247,267,463\}$. Together with other authors [33,34], he also dealt with examples for $t\in \{239,251,331,631\}$.

In any case, there is still much to do on the subject (see [11] for recent details about this concern).

In general, Goethals-Seidel arrays fail to be cocyclic over a group, as was pointed out in [6]. Recall in this regard that a matrix with entries $\pm 1$ is cocyclic over a group $(G,·)$ if there exists a map $\psi :G\times G\to \{\pm 1\}$ obeying the cocycle equation

$$\psi (i,j)\psi (i·j,k)\psi (i,j·k)\psi (j,k)=1,$$

(5)

for all $i,j,k\in G$, so that the matrix under consideration is Hadamard equivalent to the cocyclic matrix $M_{\psi }:={\left(\psi (i,j)\right)}_{i,j\in G}$. The map $\psi$ is called a cocycle [1,2] over the group.

This notion is somehow more relaxing than those originally termed in [2], where cocyclically developed matrices of the form $\left(\psi \right(g,h\left)\varphi \right(gh\left)\right)$ and pure cocyclic matrices of the form $\left(\psi \right(g,h\left)\right)$ were distinguished for $\psi$ being a two-cocycle and $\varphi$ being an arbitrary function. Notice that a cocyclically developed matrix is Hadamard equivalent to a pure cocyclic matrix.

In the context of Hadamard matrices, the main advantage of cocyclic matrices is that there is a faster way to check whether they are Hadamard or not, the cocyclic Hadamard test [2]. This method consists of checking whether the summation of each row of the matrix is zero, except for the first one if the matrix is normalized (that is, both its first row and first column consist all of ones).

Two matrices with entries $\pm 1$ are cocyclically equivalent if they are, respectively, cocyclic with respect to a pair of cocycles $\psi$ and $\varphi$ over a group $(G,·)$, and there exists a map $\partial :G\to \{\pm 1\}$ such that

$$\varphi (i,j)=\partial \left(i\right)\partial \left(j\right)\partial (i·j)\psi (i,j),\mathrm{for}\mathrm{all}i,j\in G.$$

This constitutes an equivalence relation among cocyclic Hadamard matrices, which we denote ${\sim }_c$. No known relation exists between ${\sim }_c$ and ${\sim }_H$. In fact, lying in the same ${\sim }_c$-class, one may easily find cocyclic matrices $M_{\psi }{\sim }_c{M}_{\varphi }$ such that the former is Hadamard and the latter is not [2].

Progressing on the ideas and techniques of [3,35,36], a full classification of cocyclic Hadamard matrices up to order 36 was performed in [37], from which we next reproduce in Table 1 the proportion ${\sim }_{H+c}$ of ${\sim }_H$-classes which have a cocyclic representative over some group. In particular the exact number of nonequivalent Hadamard matrices of order 32 that was calculated in [38,39] is found.

Table 1. Proportion ${\sim }_{H+c}$ of ${\sim }_H$-classes with a cocyclic representative over some group.

order	2	4	8	12	16	20	24	28	32	36
${\sim }_H$	1	1	1	1	5	3	60	487	13710027	$\ge 3\times {10}^6$
${\sim }_{H+c}$	1	1	1	1	5	3	16	6	100	35

As highlighted in bold, the proportion decreases significantly from order 24, which suggests that cocyclic matrices developed over groups fail to cover a wide amount of nonequivalent Hadamard matrices. Actually, this is the main motivation of this paper, which deals with the quasigroup development theory, expecting that the proportion of ${\sim }_H$-classes having a cocyclic representative over some quasigroup is significantly greater than that over groups.

2.2. Quasigroups

A quasigroup [40] of order n is a pair $(Q,·)$ formed by a finite set Q of n elements that is endowed with a multiplication · defined so that any two of the three elements $i,j,k\in Q$ in the equation $i·j=k$ determine in a unique way the third element. From here on, the multiplication sign · is removed from equations whenever there is no risk of confusion. Notice that the multiplication table of every quasigroup of order n constitutes a Latin square of the same order; that is, an $n\times n$ array filled with n different symbols so that each symbol occurs exactly once in each row and exactly once in each column. Conversely, every Latin square of order n can be taken as the multiplication table of a quasigroup.

A loop is a quasigroup $(Q,·)$ with unit element e; that is, such that $ie=ei=i$, for all $i\in Q$. Every associative loop is a group. A Moufang loop is a loop satisfying any one of the following equivalent identities:

$$\begin{array}{c}\hfill \left(ij\right)\left(ki\right)=i\left(\right(jk\left)i\right),\\ \hfill \left(\right(ij\left)i\right)k=i\left(j\right(ik\left)\right),\\ \hfill i\left(j\right(kj\left)\right)=\left(\right(ij\left)k\right)j.\end{array}$$

(6)

Every Moufang loop $(Q,·)$ with unit element e satisfies the inverse property; that is, for each element $i\in Q$, there exists just one element $i^{-1}\in Q$ such that $i^{-1}i=i{i}^{-1}=e$ and $i^{-1}\left(ij\right)=\left(ji\right)i^{-1}=j$, for all $j\in Q$. In particular, ${\left(ij\right)}^{-1}=j^{-1}{i}^{-1}$ for all $i,j\in Q$.

2.3. Cocyclic Matrices Over Quasigroups

As introduced in [12], a (two-dimensional, binary) cocycle $\psi$ over a quasigroup $(Q,·)$ of order $4t$ is a map $\psi :Q\times Q\to \{\pm 1\}$ satisfying the cocycle Equation (5), for all $i,j,k\in Q$. Once an indexing of the elements of Q is chosen, the cocycle $\psi$ is uniquely represented by the cocyclic matrix $M_{\psi }:={\left(\psi (i,j)\right)}_{i,j\in Q}$. If the matrix $M_{\psi }$ is Hadamard, then the quasigroup $(Q,·)$ must indeed be a loop (see [12], theorem 28). The cocyclic Hadamard test also holds in this case (see [12],Theorem 29).

3. Coboundaries and Pseudocoboundaries Over Quasigroups

In the conclusion section of [12], it was briefly commented that the notion of coboundary of groups cannot be generalized in a natural way for non-associative loops, except for the trivial normalized coboundary. We start this section by showing that such an assessment was not accurate.

Firstly, similarly to the classical notion over groups [1,2], we introduce here the notion of coboundary over quasigroups. A cocycle $\psi$ over a quasigroup $(Q,·)$ is called a coboundary if there exists a map $\partial :Q\to \{\pm 1\}$ such that

$$\psi (i,j)=\partial \left(i\right)\partial \left(j\right)\partial \left(ij\right),\mathrm{for}\mathrm{all}i,j\in Q.$$

Notice that, from the cocycle equation

$$\partial \left(i\right(jk\left)\right)=\partial \left(\right(ij\left)k\right)\mathrm{must}\mathrm{hold}\mathrm{for}\mathrm{all}i,j,k\in Q.$$

Even if this last condition is trivial in case of dealing with groups, this is not so for non-associative quasigroups. Nevertheless, unlike it was indicated in [12], such a condition does not require the map ∂ to be the trivial normalized function. The following example illustrates this fact.

Example 1.

It is known [12] that the following Latin square of order eight constitutes the multiplication table of a non-associative loop $(Q,·)$ over which a cocyclic Hadamard matrix exists.

$$\begin{array}{|cccccccc|}\hline 1& 2& 3& 4& 5& 6& 7& 8\\ 2& 1& 4& 3& 6& 5& 8& 7\\ 3& 4& 1& 2& 7& 8& 5& 6\\ 4& 3& 2& 1& 8& 7& 6& 5\\ 5& 6& 8& 7& 3& 4& 2& 1\\ 6& 5& 7& 8& 4& 3& 1& 2\\ 7& 8& 6& 5& 1& 2& 4& 3\\ 8& 7& 5& 6& 2& 1& 3& 4\\ \hline\end{array}$$

It can readily be checked that the associative property $\left(ij\right)k=i\left(jk\right)$ does not hold in this loop in case of being $\{i,j,k\}\subset \{5,6,7,8\}$, but it is satisfied in any other case. Moreover, it can also be checked that, given three elements $i,j,k\in \{5,6,7,8\}$, then the set $\left\{\right(ij)k,i(jk\left)\right\}$ coincides exactly with either $\{5,6\}$ or $\{7,8\}$. Due to this, every map $\partial :Q\to \{\pm 1\}$ associated to a coboundary over the loop under consideration must satisfy that $\partial \left(5\right)=\partial \left(6\right)$ and $\partial \left(7\right)=\partial \left(8\right)$.

Thus, for instance, the following matrix is cocyclic over our non-associative loop, by means of the coboundary associated to the map $\partial :Q\to \{\pm 1\}$ described by $\partial \left(i\right)=1$, for all $i\in \{1,2,3,5,6\}$, and $-1$, otherwise.

$$\left(\begin{array}{cccccccc}+& +& +& +& +& +& +& +\\ +& +& -& -& +& +& +& +\\ +& -& +& -& -& -& -& -\\ +& -& -& +& +& +& +& +\\ +& +& -& +& +& -& -& -\\ +& +& -& +& -& +& -& -\\ +& +& -& +& -& -& -& +\\ +& +& -& +& -& -& +& -\end{array}\right),$$

where, from here on, the signs + and $-$ represent, respectively, the entries 1 and $-1$. Notice, however, that this matrix is not Hadamard. Indeed, from an exhaustive study of cases, it can readily be checked that, whatever the map ∂ is, there does not exist any coboundary over the loop $(Q,·)$ determining a cocyclic Hadamard matrix.

Let $(Q,·)$ be a quasigroup and let $h\in Q$. From here on, let ${\partial }_h:Q\to \{\pm 1\}$ be the map defined as ${\partial }_h\left(i\right)=-1$, if $i=h$, and 1, otherwise; and let ${\psi }_h:Q\times Q\to \{\pm 1\}$ be the map defined as

$${\psi }_h(i,j):={\partial }_h\left(i\right){\partial }_h\left(j\right){\partial }_h\left(ij\right).$$

(7)

We say that a coboundary $\psi$ over a quasigroup $(Q,·)$ is elementary if there exists an element $h\in Q$ such that $\psi ={\psi }_h$. If this is the case, then the cocycle equation implies that

$$i\left(jk\right)=h\iff \left(ij\right)k=h,\mathrm{for}\mathrm{all}i,j,k\in Q.$$

(8)

As such, Equation (8) discriminates among potential coboundaries ${\psi }_h$. In order to illustrate this fact, observe that the map ${\psi }_h$ constitutes an elementary coboundary over the non-associative loop described in Example 1 if and only if $h\in \{1,2,3,4\}$.

Those maps ${\psi }_h$ for which Equation (8) does not hold are also of interest in the quasigroup development theory (see Section 3). Due to this, we term pseudocoboundaries to such maps. By extension, we call pseudococycle to any map $\psi =\left({\prod }_{h\in H}{\psi }_h\right)\varphi$ that is obtained as the product of some pseudocoboundaries ${\psi }_h$, with $h\in H\subseteq Q$, and a cocycle $\varphi$, all of them over a given quasigroup $(Q,·)$. It is represented by the pseudococyclic matrix $M_{\psi }:={\left(\psi (i,j)\right)}_{i,j\in Q}$. Finally, we call pseudococyclic Hadamard matrix to any matrix that is Hadamard equivalent to that one defined by any such pseudococycle. The following example illustrates all these concepts.

Example 2.

By definition, the map ${\psi }_h$ is a pseudocoboundary over the non-associative loop described in Example 1, for all $h\in \{5,6,7,8\}$. If we denote ϕ the coboundary associated to the map ∂ described in such an example, then the map $\psi ={\psi }_5{\psi }_7\varphi$ constitutes a pseudococycle over the mentioned loop. It is represented by the pseudococyclic matrix

$$\left(\begin{array}{cccccccc}+& +& +& +& +& +& +& +\\ +& +& -& -& -& -& -& -\\ +& -& +& -& -& -& -& -\\ +& -& -& +& -& -& -& -\\ +& -& +& +& +& +& -& +\\ +& -& +& +& +& +& +& -\\ +& -& +& +& -& +& -& -\\ +& -& +& +& +& -& -& -\end{array}\right).$$

In order to illustrate that the map ψ does not satisfy the cocycle equation in general, notice, for example, that

$$\psi (5,6)\psi (5·6,7)\psi (5,6·7)\psi (6,7)=\psi (4,7)\psi (5,1)=-1.$$

Unlike the cocyclic framework, the following example illustrates the existence of pseudococyclic Hadamard matrices over quasigroups that are not loops.

Example 3.

Let us consider the following Latin square and Hadamard matrix of order four.

$$\begin{array}{|cccc|}\hline 1& 3& 2& 4\\ 2& 1& 4& 3\\ 3& 4& 1& 2\\ 4& 2& 3& 1\\ \hline\end{array}and\left(\begin{array}{cccc}+& -& -& +\\ +& +& -& -\\ +& -& +& -\\ +& +& +& +\end{array}\right).$$

The latter is pseudococyclic over the non-associative quasigroup having the former as as multiplication table, by means of the pseudococycle ${\psi }_2$. Notice in this regard that the map ${\partial }_2$ constitutes an elementary pseudocoboundary over such a quasigroup, because we have, for instance, that $(1·1)·3=2\ne 3=1·(1·3)$.

Further, the following two examples illustrate that the cocyclic Hadamard test is no longer available for pseudococyclic matrices.

Example 4.

Let us consider the following Latin square and binary matrix of order eight.

$$\begin{array}{|cccccccc|}\hline 1& 2& 3& 4& 5& 6& 7& 8\\ 2& 1& 5& 6& 3& 4& 8& 7\\ 3& 6& 1& 7& 8& 2& 4& 5\\ 4& 5& 8& 1& 2& 7& 6& 3\\ 5& 4& 2& 8& 7& 1& 3& 6\\ 6& 3& 7& 2& 1& 8& 5& 4\\ 7& 8& 6& 3& 4& 5& 2& 1\\ 8& 7& 4& 5& 6& 3& 1& 2\\ \hline\end{array}and\left(\begin{array}{cccccccc}+& +& +& +& +& +& +& +\\ +& +& -& -& -& -& -& -\\ +& -& -& +& +& +& -& -\\ +& -& +& -& +& +& -& -\\ +& -& +& +& +& -& -& -\\ +& -& +& +& -& +& -& -\\ +& -& -& -& -& -& -& +\\ +& -& -& -& -& -& +& -\end{array}\right).$$

The latter is cocyclic over the non-associative loop having the former as multiplication table, by means of a cocycle ϕ. Further, it is readily checked that the maps ${\psi }_2$, ${\psi }_3$ and ${\psi }_7$ constitute pseudocoboundaries over such a loop, because we have, for instance, that $(5·8)·4=2\ne 7=5·(8·4)$ and $(2·6)·8=3\ne 6=2·(6·8)$.

In general, there is no relation between the usual cocyclic Hadamard test and the Hadamard character of a pseudococyclic matrix. In order to illustrate this fact, notice that the pseudococyclic matrix

$$M_{{\psi }_2{\psi }_3{\psi }_7\varphi }=\left(\begin{array}{cccccccc}+& +& +& +& +& +& +& +\\ +& +& -& +& -& +& -& -\\ +& -& -& +& -& +& -& +\\ +& +& -& -& -& -& +& +\\ +& +& +& +& -& -& -& -\\ +& -& +& -& -& +& +& -\\ +& -& -& -& +& +& +& -\\ +& -& +& -& -& +& -& +\end{array}\right)$$

satisfies the cocyclic Hadamard test, but it is not Hadamard. On the other hand, the pseudococyclic matrix $M_{\varphi {\psi }_2}$ satisfies the cocyclic Hadamard test and it is Hadamard.

The following result holds instead of the classical cocyclic Hadamard test.

Lemma 1.

Let $M_{\psi }={\left(\psi (i,j)\right)}_{i,j\in Q}$ be the pseudococylic matrix related to a pseudococycle $\psi =\left({\prod }_{h\in H}{\psi }_h\right)\varphi$ over a quasigroup $(Q,·)$. If $i,j\in Q$, then the $\left(ij\right)$$\mathrm{th}$ and j$\mathrm{th}$ rows in the matrix $M_{\psi }$ are orthogonal if and only if

$$\sum _{k\in Q}\psi (i,jk)\prod _{h\in H}{\partial }_h\left(i\left(jk\right)\right){\partial }_h\left(\left(ij\right)k\right)=0.$$

(9)

Proof. 

Let $i,j\in Q$. In order to study if ${\sum }_{k\in Q}\psi (ij,k)\psi (j,k)=0$, notice that, for each $k\in Q$,

$$\begin{array}{cc}\hfill \psi (ij,k)\psi (j,k)& =\left(\prod _{h\in H}{\partial }_h\left(ij\right){\partial }_h\left(k\right){\partial }_h\left(\left(ij\right)k\right){\partial }_h\left(j\right){\partial }_h\left(k\right){\partial }_h\left(jk\right)\right)\varphi (ij,k)\varphi (j,k)\hfill \\ \hfill & =\left(\prod _{h\in H}{\partial }_h\left(ij\right){\partial }_h\left(\left(ij\right)k\right){\partial }_h\left(j\right){\partial }_h\left(jk\right)\right)\varphi (ij,k)\varphi (j,k).\hfill \end{array}$$

Now, from the cocycle equation, since $\varphi$ is a cocycle over the quasigroup $(Q,·)$, we have that $\varphi (ij,k)\varphi (j,k)=\varphi (i,j)\varphi (i,jk)$. Further,

$$\begin{array}{cc}\hfill \psi (i,j)\psi (i,jk)& =\left(\prod _{h\in H}{\partial }_h\left(i\right){\partial }_h\left(j\right){\partial }_h\left(ij\right){\partial }_h\left(i\right){\partial }_h\left(jk\right){\partial }_h\left(i\left(jk\right)\right)\right)\varphi (i,j)\varphi (i,jk)\hfill \\ \hfill & =\left(\prod _{h\in H}{\partial }_h\left(j\right){\partial }_h\left(ij\right){\partial }_h\left(jk\right){\partial }_h\left(i\left(jk\right)\right)\right)\varphi (i,j)\varphi (i,jk).\hfill \end{array}$$

Then, the result follows readily from the fact of being

$$\psi (ij,k)\psi (j,k)=\psi (i,j)\psi (i,jk)\prod _{h\in H}{\partial }_h\left(i\left(jk\right)\right){\partial }_h\left(\left(ij\right)k\right).$$

□

Let us remark that Equation (9) is not necessarily related to the summation of row i in $M_{\psi }$, as it is the case in the usual cocyclic framework.

4. An Infinite Family of Pseudococyclic Hadamard Matrices Over Loops: Goethals-Seidel Arrays

In this section, we prove the existence of an infinite family of Moufang loops over which the family of Goethals-Seidel arrays are pseudococyclic. To this end, for each positive integer $t\ge 1$, let us consider the finite ordered set of elements

$$G{S}_{4t}:=\{e,a,a^2,\dots ,a^{t-1},b,a^{t-1}b,\dots ,a^{2}b,ab,c,a^{t-1}c,\dots ,a^{2}c,ac,d,a^{t-1}d,\dots ,a^{2}d,ad\}.$$

Next, let us endow the set $G{S}_{4t}$ with the multiplication · that is described by the $4t\times 4t$-block matrix

$$\left(\begin{array}{cccc}\hfill {A_t}_{\leftarrow }& \hfill {B_t}_{\to }& \hfill {C_t}_{\to }& \hfill {D_t}_{\to }\\ \hfill {B_t}_{\leftarrow }& \hfill {A_t}_{\to }& \hfill {\overline{D_t}}_{\leftarrow }& \hfill {\overline{C_t}}_{\leftarrow }\\ \hfill {C_t}_{\leftarrow }& \hfill {\overline{D_t}}_{\leftarrow }& \hfill {A_t}_{\to }& \hfill {\overline{B_t}}_{\leftarrow }\\ \hfill {D_t}_{\leftarrow }& \hfill {\overline{C_t}}_{\leftarrow }& \hfill {\overline{B_t}}_{\leftarrow }& \hfill {A_t}_{\to }\end{array}\right),$$

(10)

where

• $A_t$, $B_t$, $C_t$ and $D_t$ are the t-tuples identities:

  $$\begin{array}{cc}\hfill A_t:=& (e,a,a^2,\dots ,a^{t-1}),\hfill \end{array}$$

  (11)

  $$\begin{array}{cc}\hfill B_t:=& (b,a^{t-1}b,\dots ,a^{2}b,ab),\hfill \end{array}$$

  (12)

  $$\begin{array}{cc}\hfill C_t:=& (c,a^{t-1}c,\dots ,a^{2}c,ac),\hfill \end{array}$$

  (13)

  $$\begin{array}{cc}\hfill D_t:=& (d,a^{t-1}d,\dots ,a^{2}d,ad);\hfill \end{array}$$

  (14)
• $\overline{X}=(x_{t-1},\dots ,x_1,x_t)$, for every t-tuple $X=(x_1,\dots ,x_t)\in \{B_t,C_t,D_t\}$; and
• $X_{\to }$ and $X_{\leftarrow }$ denote, respectively, the circulant and back-circulant matrices derived from the corresponding t-tuple $X\in \{A_t,B_t,C_t,D_t,\overline{B_t},\overline{C_t},\overline{D_t}\}$ as first row vector.

It is readily verified that the block matrix so defined is a Latin square of order $4t$ (see Example 5, which illustrates the case $t=3$), where the elements of both its first row and its first column, respectively, index the rows and columns of the array. Hence, the pair $(G{S}_{4t},·)$ is a loop having the element e as unit element. Let us prove that it is indeed a Moufang loop.

Proposition 1.

The pair $(G{S}_{4t},·)$ is a Moufang loop, for all positive integer $t\ge 1$.

Proof. 

Notice that every element $x\in G{S}_{4t}$ is of the form $a^m\alpha$, where $m\in {\mathbb{Z}}_t:=\{0,1,\dots ,t-1\}$ and $\alpha \in \{e,b,c,d\}$. Here, we are considering $x^0=e$ and, of course, $ex=xe=x$, for all $x\in G{S}_{4t}$. Then, the following identities hold from Matrix (10). In all of them, the sum of exponents refers to the addition within the usual cyclic group $({\mathbb{Z}}_t,+)$.

$$a^m·\left(a^n\alpha \right)=a^{m+n}\alpha ,\mathrm{for}\mathrm{all}\alpha \in \{e,b,c,d\}\mathrm{and}m,n\in {\mathbb{Z}}_t.$$

(15)

$$\left(a^m\alpha \right)·a^n=a^{m-n}\alpha ,\mathrm{for}\mathrm{all}\alpha \in \{b,c,d\}\mathrm{and}m,n\in {\mathbb{Z}}_t.$$

(16)

$$\left(a^m\alpha \right)·\left(a^n\alpha \right)=a^{m-n},\mathrm{for}\mathrm{all}\alpha \in \{b,c,d\},\mathrm{and}m,n\in {\mathbb{Z}}_t.$$

(17)

$$\left(a^m\alpha \right)·\left(a^n\beta \right)=a^{2-m-n}\gamma ,\mathrm{where}\{\alpha ,\beta ,\gamma \}=\{b,c,d\}\mathrm{and}m,n\in {\mathbb{Z}}_t.$$

(18)

A simple study of cases based on the Equations (15)–(18) enables one to ensure that the loop $(G{S}_{4t},·)$ satisfies all the three Equation (6). In order to illustrate this fact, we show here a pair of cases:

• If $i=a^m$, $j=a^{n}b$ and $k=a^{s}c$, then
  • $\left\{\begin{array}{c}\begin{array}{cc}\left(ij\right)\left(ki\right)\hfill & =(a^m·a^{n}b)(a^{s}c·a^m)=a^{m+n}b·a^{s-m}c=a^{2-n-s}d.\hfill \end{array}\hfill \\ \begin{array}{cc}i\left(\right(jk\left)i\right)\hfill & =a^m\left((a^{n}b·a^{s}c)a^m\right)=a^m(a^{2-n-s}d·a^m)=a^m·a^{2-n-s-m}d=a^{2-n-s}d.\hfill \end{array}\hfill \end{array}\right.$
  • $\left\{\begin{array}{c}\begin{array}{cc}\left(\right(ij\left)i\right)k\hfill & =(a^m·a^{n}b)a^m)a^{s}c=(a^{m+n}b·a^m)a^{s}c=a^{n}b·a^{s}c=a^{2-n-s}d.\hfill \end{array}\hfill \\ \begin{array}{cc}i\left(j\right(ik\left)\right)\hfill & =a^m\left(a^{n}b(a^m·a^{s}c)\right)=a^m(a^{n}b·a^{m+s}c)=a^m·a^{2-n-m-s}d=a^{2-n-s}d.\hfill \end{array}\hfill \end{array}\right.$
  • $\left\{\begin{array}{c}\begin{array}{cc}i\left(j\right(kj\left)\right)\hfill & =a^m\left(a^{n}b(a^{s}c·a^{n}b)\right)=a^m(a^{n}b·a^{2-s-n}d)=a^m·a^{s}c=a^{m+s}c.\hfill \end{array}\hfill \\ \begin{array}{cc}\left(\right(ij\left)k\right)j\hfill & =\left((a^m·a^{n}b)a^{s}c\right)a^{n}b=(a^{m+n}b·a^{s}c)a^{n}b=a^{2-m-n-s}d·a^{n}b=a^{m+s}c.\hfill \end{array}\hfill \end{array}\right.$
• If $i=a^{m}b$, $j=a^{n}b$ and $k=a^{s}c$, then
  • $\left\{\begin{array}{c}\begin{array}{cc}\left(ij\right)\left(ki\right)\hfill & =(a^{m}b·a^{n}b)(a^{s}c·a^{m}b)=a^{m-n}·a^{2-s-m}d=a^{2-n-s}d.\hfill \end{array}\hfill \\ \begin{array}{cc}i\left(\right(jk\left)i\right)\hfill & =a^{m}b\left((a^{n}b·a^{s}c)a^{m}b\right)=a^{m}b(a^{2-n-s}d·a^{m}b)=a^{m}b·a^{n+s-m}c=a^{2-n-s}d.\hfill \end{array}\hfill \end{array}\right.$
  • $\left\{\begin{array}{c}\begin{array}{cc}\left(\right(ij\left)i\right)k\hfill & =\left((a^{m}b·a^{n}b)a^{m}b\right)a^{s}c=(a^{m-n}·a^{m}b)a^{s}c=a^{2m-n}b·a^{s}c=a^{2-2m+n-s}d.\hfill \end{array}\hfill \\ \begin{array}{cc}i\left(j\right(ik\left)\right)\hfill & =a^{m}b\left(a^{n}b(a^{m}b·a^{s}c)\right)=a^{m}b(a^{n}b·a^{2-m-s}d)=a^{m}b·a^{m+s-n}c=a^{2-2m+n-s}d.\hfill \end{array}\hfill \end{array}\right.$
  • $\left\{\begin{array}{c}\begin{array}{cc}i\left(j\right(kj\left)\right)\hfill & =a^{m}b\left(a^{n}b(a^{s}c·a^{n}b)\right)=a^{m}b(a^{n}b·a^{2-s-n}d)=a^{m}b·a^{s}c=a^{2-m-s}d.\hfill \end{array}\hfill \\ \begin{array}{cc}\left(\right(ij\left)k\right)j\hfill & =\left((a^{m}b·a^{n}b)a^{s}c\right)a^{n}b=(a^{m-n}·a^{s}c)a^{n}b=a^{m-n+s}c·a^{n}b=a^{2-m-s}d.\hfill \end{array}\hfill \end{array}\right.$

□

Remark 1.

In light of Equations (15)–(18), notice that the structure beneath the $t\times t$-blocks of Matrix (10) is that of the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

It is readily verified that the Moufang loop $(G{S}_{4t},·)$ is a group when $t\in \{1,2\}$. Nevertheless, this is not true for $t>2$, in which case the loop $(G{S}_{4t},·)$ is non-associative. Thus, observe for instance that

$$a·(b·\left(a^{1-m}c\right))=a^{2+m}d\ne a^{m}d=(a·b)·\left(a^{1-m}c\right),$$

(19)

for any $m\in {\mathbb{Z}}_t$. The following result enables one to ensure that the case $t>2$ is, however, worthy to be analyzed. In fact, due to this result, we term the Goethals-Seidel loop to the Moufang loop $(G{S}_{4t},·)$ when $t>2$.

Proposition 2.

The Goethals-Seidel array of order $4t$ is pseudococyclic over $(G{S}_{4t},·)$, for all $t>2$.

Proof. 

Let us prove that, even Goethals-Seidel arrays are not themselves pure pseudococylic, they are Hadamard equivalent to some pure pseudococyclic matrices. To this end, we first prove that, for every $h\in G{S}_{4t}\backslash \left\{e\right\}$, the map ${\psi }_h$ defines a pseudocoboundary over the Moufang loop $(G{S}_{4t},·)$, with the only exception of those maps related to $h=a^m$ when t is even. Actually, for even t and $h=a^m$, a straightforward calculation from Equations (15)–(18) shows that ${\psi }_h$ satisfies Equation (8). Consequently, it defines a genuine cocycle over $(G{S}_{4t},·)$. We may, therefore, suppose that t is odd or $h\ne a^m$. Under such assumptions, let us show a triplet of elements $i,j,k\in G{S}_{4t}$ for which Equation (8) fails to hold.

• If $h=a^m$ (and consequently t may be assumed odd), for some $m\in {\mathbb{Z}}_t\backslash \left\{0\right\}$, then

  $$b·(a^{m+1}c·ad)=a^{-m}\ne a^m=(b·a^{m+1}c)·ad.$$
• If $h=a^{m}b$, for some $m\in {\mathbb{Z}}_t$, then

  $$a·(c·a^{1-m}d)=a^{m+2}b\ne a^{m}b=(a·c)·a^{1-m}d.$$
• If $h=a^{m}c$, for some $m\in {\mathbb{Z}}_t$, then

  $$a·(b·a^{1-m}d)=a^{m+2}c\ne a^{m}c=(a·b)·a^{1-m}d.$$
• If $h=a^{m}d$, for some $m\in {\mathbb{Z}}_t$, then

  $$a·(b·a^{1-m}c)=a^{m+2}d\ne a^{m}d=(a·b)·a^{1-m}c.$$

Secondly, let us see how the just mentioned pseudocoboundaries are components of a pseudococycle whose pseudococyclic matrix is the Goethals-Seidel array of order $4t$. To this end, let $M_{\overline{h}}$ be the matrix that is obtained by negating both the row and column of the matrix ${\left({\psi }_h(i,j)\right)}_{i,j\in G{S}_{4t}}$ that are indexed by h. From here on, we denote such row and column as h-row and h-column, respectively.

From Equation (7), the matrix $M_{\overline{h}}$ is of the form of Matrix (10). Moreover, every row i (and column j) in $M_{\overline{h}}$ consists of exactly one negative entry, which is located at position $(i,j)$, for $ij=h$. Thus, in particular, the negative entry in the first row of $M_{\overline{h}}$ appears at the h-column.

As a consequence, from the formal point of view of the symbols $A_t,B_t,C_t,D_t$ (up to sign of the $t\times t$-blocks of Matrix (1), by the moment), Matrix (1) may formally be obtained from the element-wise product of some matrices $M_{\overline{h}}$, just by permuting the $a^m$- and the $a^{t-m}$-rows, for $m\in {\mathbb{Z}}_t\backslash \left\{0\right\}$. We term H to the set of indexes h of such matrices, which is determined by the positions of the $-1$ s in the first row of Matrix (1).

Now, let us consider the following $4t\times 4t$-matrix with entries $\pm 1$ that is formed of $t\times t$-blocks of constant signs.

$$S_{4t}:=\left(\begin{array}{cccc}{+}_t& {+}_t& {+}_t& {+}_t\\ {+}_t& {-}_t& {+}_t& {-}_t\\ {+}_t& {-}_t& {-}_t& {+}_t\\ {+}_t& {+}_t& {-}_t& {-}_t\end{array}\right).$$

Because of the block structure of both $S_{4t}$ and the multiplication table of the Moufang loop $(G{S}_{4t},·)$ (as we pointed out in Remark 1), checking whether the former is cocyclic over the latter reduces to check whether the $4\times 4$ matrix

$$\left(\begin{array}{cccc}+& +& +& +\\ +& -& +& -\\ +& -& -& +\\ +& +& -& -\end{array}\right)$$

is cocyclic over ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$, which is actually the case (see [2] for instance). Furthermore, it remains unchanged under the permutation of any $a^m$- and $a^{t-m}$ rows, with $m\ne 0$. Thus, the matrix $S_{4t}$ is cocyclic by means of some cocycle ${\varphi }_{4t}$ over $G{S}_{4t}$.

Since we have just considered operations involving both the negation of rows and columns and the permutation of rows, every Goethals-Seidel array is pseudococylic over the Moufang loop. This is due to the fact that it is Hadamard equivalent to the pseudococyclic matrix generated by the pseudococycle $\psi :G{S}_{4t}\times G{S}_{4t}\to \{\pm 1\}$, which is defined as

$$\psi :=\left(\prod _{h\in H}{\psi }_h\right){\varphi }_{4t}.$$

(20)

Here, the elements of the subset $H\subseteq G{S}_{4t}$ index those columns of the Goethals-Seidel array whose first entry is negative, as commented before. □

The remainder of this section is devoted to prove that, even if we have just shown that the Goethals-Seidel arrays are Hadamard equivalent to the pseudococyclic (but not cocyclic) matrices $M_{\psi }$ of Equation (20), the usual cocyclic Hadamard test actually still applies on these matrices. For the sake of clarity and a better understanding, we next include a broad sketch of the proof:

• In Lemma 1, we have already shown that checking orthogonality of rows $ij$ and j in the pseudococyclic matrix $M_{\psi }$, for $\psi$ as described in Equation (20), reduces to check whether

  $$\sum _{k\in G{S}_{4t}}{\sigma }_k(i,j)\psi (i,jk)=0,$$

  (21)

  for

  $${\sigma }_k(i,j):=\prod _{h\in H}{\partial }_h\left(i\left(jk\right)\right){\partial }_h\left(\left(ij\right)k\right),$$

  (22)

  where the subset $H\subseteq G{S}_{4t}$ is determined by the indices of those pseudocoboundaries $\partial {\psi }_h$ defining $\psi$.
• In particular, those indices $k\in G{S}_{4t}$ satisfying that ${\sigma }_k(i,j)=-1$ are of interest, since they make the difference to readily meet the summation of row i in $M_{\psi }$. In Lemma 2, we show that ${\sigma }_k(i,j)=-1$ if and only if precisely one element among $i\left(jk\right)$ and $\left(ij\right)k$ is in H.
• In Lemma 4, we show that these indices are in one to one correspondence with the ends of certain sequences $(h_0,\dots ,h_r)$ in H (described as maximal $(i,j)$-walks in Definition 1) so that either $i\left(jk\right)=h_0$ or $\left(ij\right)k=h_r$.
• In Proposition 4, we show that these sequences $(h_0,\dots ,h_r)$ are preserved by the left action of $i^{-1}$ in such a way that, for each $\ell \in \{0,\dots ,r-1\}$, both $i^{-1}{h}_{\ell }$ and $i^{-1}{h}_{\ell +1}$ are consecutive components of another sequence in $G{S}_{4t}$.
• Two cases arise, depending on whether $\psi (i,jk)=-\psi (i,j{k}^{\prime })$ (developed in Lemma 5) or $\psi (i,jk)=\psi (i,j{k}^{\prime })$ (developed through Lemmas 8, 9, and 10). Whichever is the case, every index $k\in G{S}_{4t}$ with ${\sigma }_k(i,j)=-1$ is shown to have a uniquely related index $k^{\prime }\in G{S}_{4t}$ with ${\sigma }_{k^{\prime }}(i,j)=-1$ and $\psi (i,jk)=-\psi (i,j{k}^{\prime })$.
• As a result, we show in Lemma 12 that Equation (21) is satisfied if and only if the summation of row i in $M_{\psi }$ is zero, from which Theorem 1 readily follows.

Let us detail separately each one of the previous stages.

Lemma 2.

Let $i,j,k\in G{S}_{4t}$. Then, ${\sigma }_k(i,j)=-1$ if and only if precisely one element among $i\left(jk\right)$ and $\left(ij\right)k$ is in H.

Proof. 

This is a straightforward consequence from the definition of ${\sigma }_k$ in Equation (22). □

Lemma 2 leads us to introduce the notion of $(i,j)$-path in a subset of a quasigroup, which is extremely useful for our purposes. In this regard, let $(Q,·)$ be a quasigroup and let $i,j\in Q$. From here on, for each element $h\in Q$, let ${\kappa }_1^{i,j,h}$ and ${\kappa }_2^{i,j,h}$, respectively, denote the unique elements (non necessarily distinct) in Q such that

$$i\left(j{\kappa }_1^{i,j,h}\right)=h=\left(ij\right){\kappa }_2^{i,j,h}.$$

They are well-defined because of being $(Q,·)$ a quasigroup. From Equation (8), the map ${\psi }_h$ is an elementary coboundary over the quasigroup $(Q,·)$ if and only if ${\kappa }_1^{i,j,h}={\kappa }_2^{i,j,h}$, for all $i,j\in Q$. This always holds when the quasigroup is associative (that is, a group). From here on, we refer to these two elements as ${\kappa }_1^h$ and ${\kappa }_2^h$, respectively, whenever there is no risk of confusion about both elements $i,j\in Q$.

Definition 1.

Let $(Q,·)$ be a quasigroup and let $i,j\in Q$. Then, an $(i,j)$-path in a subset $H\subseteq Q$ is a sequence $(h_0,\dots ,h_r)$, where $h_{\ell }\in H$, for all $\ell \in \{0,\dots ,r\}$, and such that ${\kappa }_2^{h_{\ell }}={\kappa }_1^{h_{\ell +1}}$ (equivalently, $j{\kappa }_2^{h_{\ell }}=i^{-1}{h}_{\ell +1})$, for all non-negative integer $\ell <r$. Each one of these components $h_{\ell }$ is called a link of the $(i,j)$ path.

For the convenience of the reader, even if they may be readily derived from the definition above, we explicitly give the relation among consecutive links in a path.

Lemma 3.

Let $(Q,·)$ be a quasigroup and let $i,j\in Q$. Given an element h in a subset $H\subseteq Q$, the potential links $h_{-}$ and $h_{+}$ in any $(i,j)$-path $(\dots ,h_{-},h,h_{+},\dots )$ in H are

$$h_{-}:=\left(ij\right)\left(j^{-1}\left(i^{-1}h\right)\right)\mathrm{and}{h}_{+}:=i\left(j\left({\left(ij\right)}^{-1}h\right)\right).$$

Eventually, it may be of interest noting the length n of an $(i,j)$-path. In such a case, we use the notation $(i,j)$-n-path. Further, paraphrasing the usual notation in Graph Theory, we say that an $(i,j)$-path is an $(i,j)$-cycle when it is closed (that is, ${\kappa }_2^{h_r}={\kappa }_1^{h_0}$). Otherwise, we call it an $(i,j)$-walk. Finally, we say that an $(i,j)$-path is maximal if there is no way to extend such a sequence neither to the left nor to the right. Notice that every subset $H\subseteq Q$ may be partitioned into disjoint maximal $(i,j)$-paths. Moreover, the set Q may be partitioned into disjoint $(i,j)$-cycles. Further, in case of dealing with a group, all the $(i,j)$-cycles are of length one, for all $i,j\in Q$. In this last regard, one may consider the computation of $(i,j)$-cycles as a way to measure how far a quasigroup is from being a group.

The following example illustrates how $(i,j)$-cycles may be explicitly constructed.

Example 5.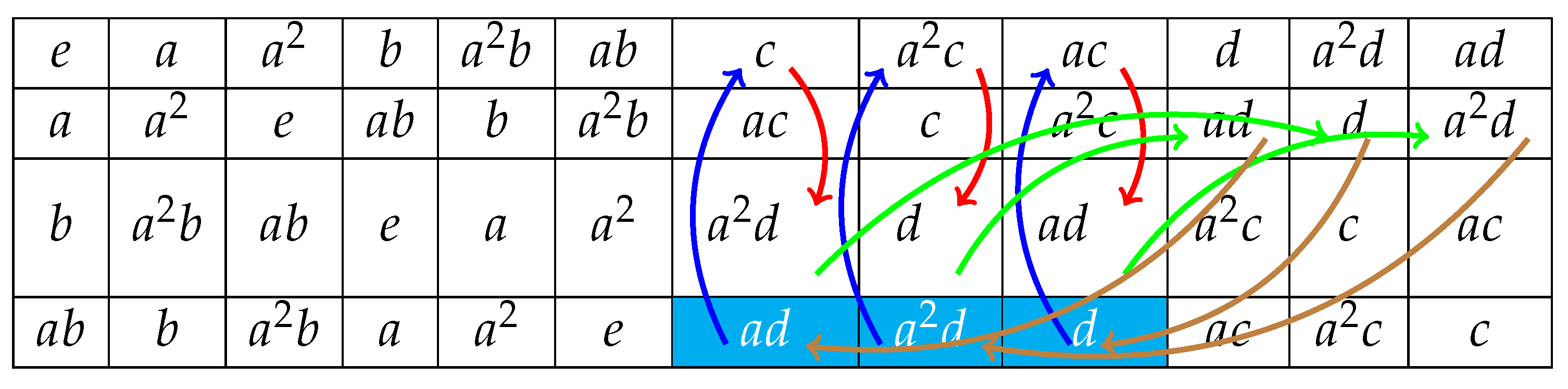

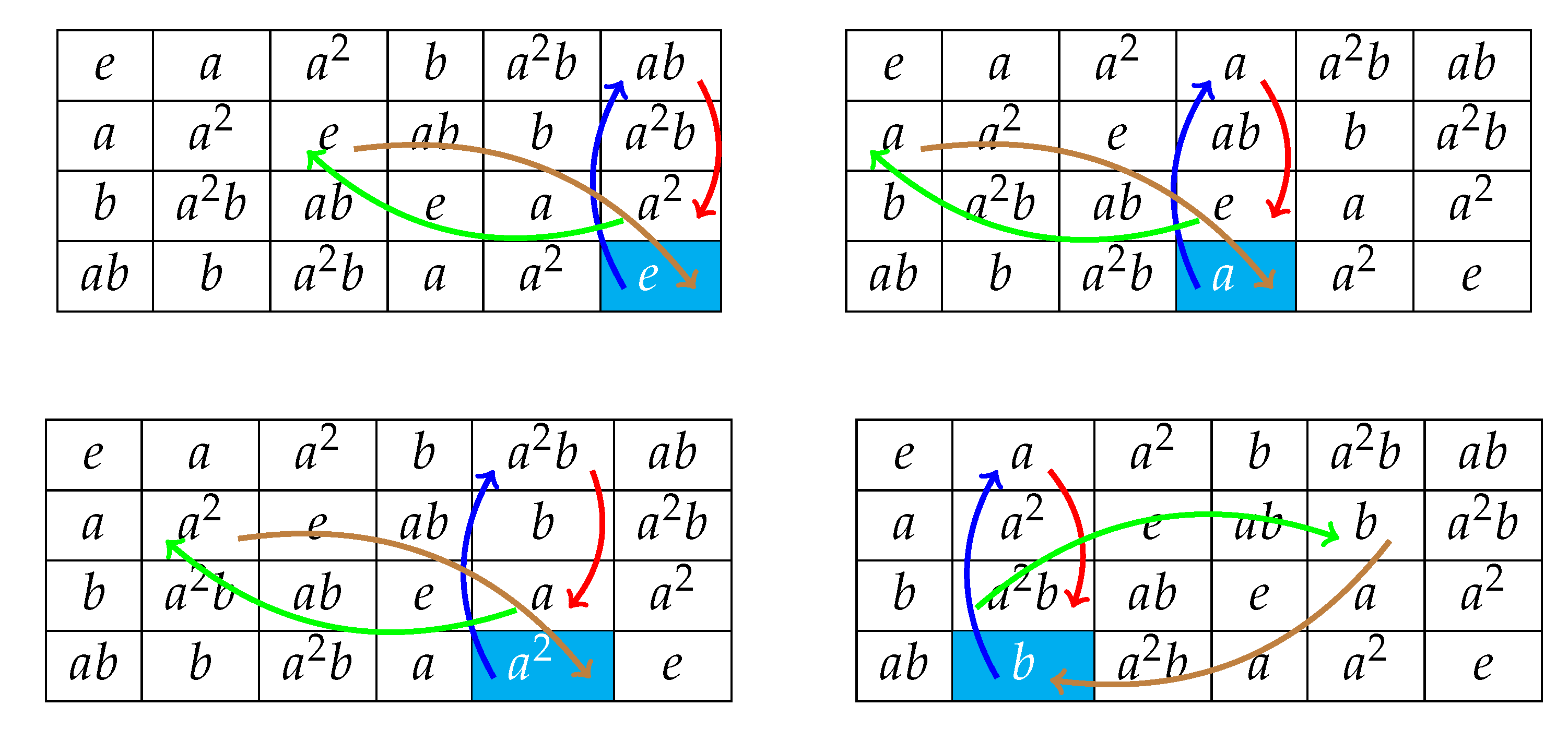
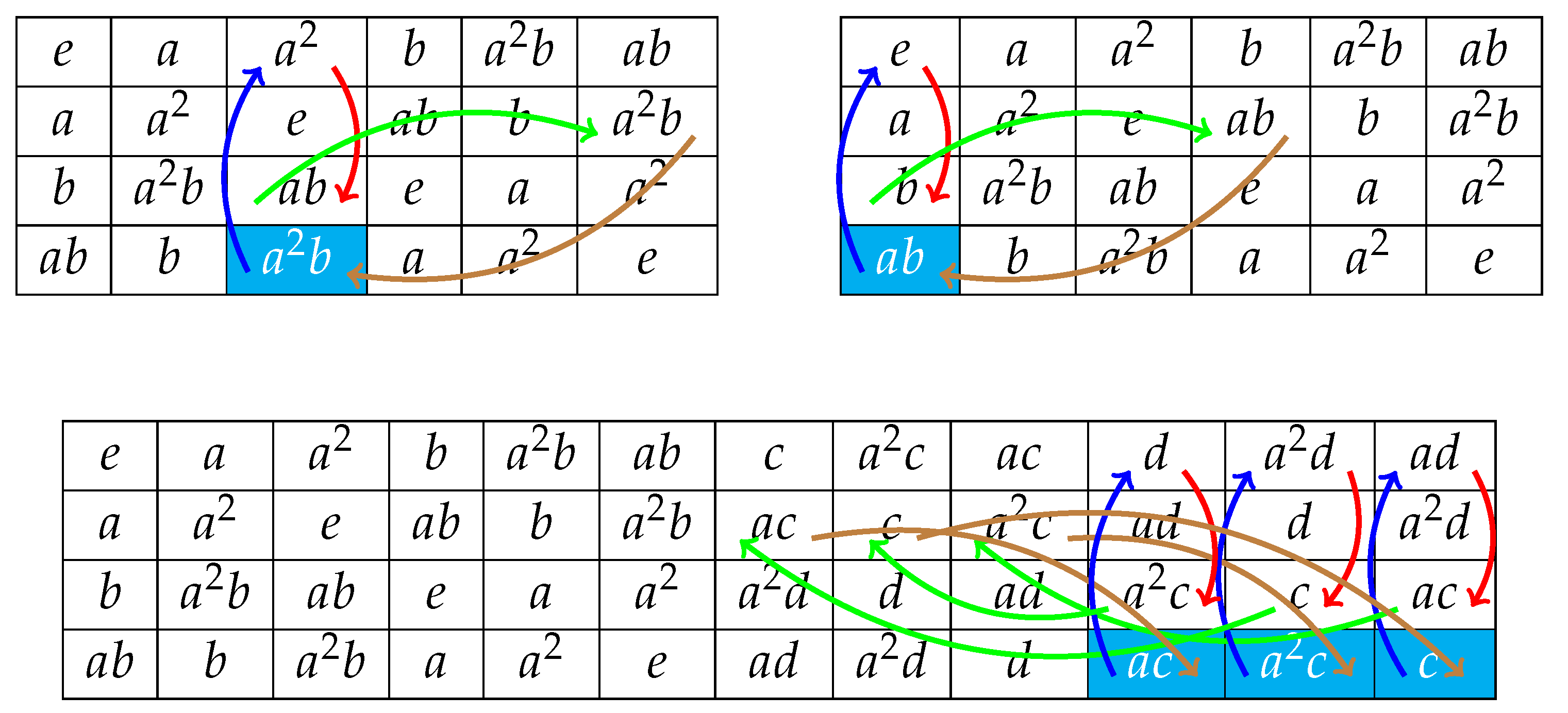
Let us consider the Goethals-Seidel loop $(G{S}_{12},·)$, whose multiplication table is the Latin square

$$\begin{array}{|cccccccccccc|}\hline e& a& a^2& b& a^{2}b& ab& c& a^{2}c& ac& d& a^{2}d& ad\\ a& a^2& e& ab& b& a^{2}b& ac& c& a^{2}c& ad& d& a^{2}d\\ a^2& e& a& a^{2}b& ab& b& a^{2}c& ac& c& a^{2}d& ad& d\\ b& a^{2}b& ab& e& a& a^2& a^{2}d& d& ad& a^{2}c& c& ac\\ a^{2}b& ab& b& a^2& e& a& d& ad& a^{2}d& c& ac& a^{2}c\\ ab& b& a^{2}b& a& a^2& e& ad& a^{2}d& d& ac& a^{2}c& c\\ c& a^{2}c& ac& a^{2}d& d& ad& e& a& a^2& a^{2}b& b& ab\\ a^{2}c& ac& c& d& ad& a^{2}d& a^2& e& a& b& ab& a^{2}b\\ ac& c& a^{2}c& ad& a^{2}d& d& a& a^2& e& ab& a^{2}b& b\\ d& a^{2}d& ad& a^{2}c& c& ac& a^{2}b& b& ab& e& a& a^2\\ a^{2}d& ad& d& c& ac& a^{2}c& b& ab& a^{2}b& a^2& e& a\\ ad& d& a^{2}d& ac& a^{2}c& c& ab& a^{2}b& b& a& a^2& e\\ \hline\end{array}.$$

Let us illustrate the computation of all the $(a,b)$-cycles in $G{S}_{12}$. In order to make it more visual for the reader, we describe all the steps for computing each $(a,b)$-cycle $(h_0,\dots ,h_r)$ in $G{S}_{12}$ by means of a coloured directed cycle connecting certain cells of the e-, a-, b- and $ab$-rows. This directed cycle is defined as follows:

• Firstly, notice that each symbol $h_{\ell }\in G{S}_{12}$ within the $ab$-row is always placed in the same column as the symbol ${\kappa }_2^{h_{\ell }}$ within the e-row, because $\left(ab\right)·{\kappa }_2^{h_{\ell }}=h_{\ell }$. We represent this relationship in our coloured directed cycle as a blue arrow from the former to the latter.
• Secondly, since $h_{\ell +1}=a\left(b{\kappa }_2^{h_{\ell }}\right)$ (and hence, ${\kappa }_1^{h_{\ell +1}}={\kappa }_2^{h_{\ell }}$), we add a red arrow from the cell containing the symbol ${\kappa }_2^{h_{\ell }}$ within the e-row to the cell within the b-row that is placed in the same column as the former. This last cell contains the symbol $b{\kappa }_2^{h_{\ell }}$. Next, we add a green arrow from this last cell to the intersection between the a-row and the $b{\kappa }_2^{h_{\ell }}$-column. This last cell contains the symbol $h_{\ell +1}$.
• Finally, we add a brown arrow from this last cell to that one within the $ab$-row containing the symbol $h_{\ell +1}$.

Due to the Latin square condition and the finiteness of the loop, the output of this procedure is our coloured directed cycle. Its related $(a,b)$-cycle is the sequence of symbols in the $ab$-row appearing in the same order as they do in the coloured directed cycle. In order to identify such symbols, we colour in cyan the background of the corresponding cells. Thus, for instance, the $(a,b)$-cycle containing the element $d\in G{S}_{12}$ is identified with the coloured directed cycle that is shown in the following array.

More specifically, if $h_0=d$, then the non-associative product described in Equation (19) implies that ${\kappa }_2^d=ac$. Now,

$$a\left(b{\kappa }_2^d\right)=a·ad=a^{2}d=h_1.$$

In particular, ${\kappa }_1^{a^{2}d}=ac$. From the multiplication table, we have that ${\kappa }_2^{a^{2}d}=a^{2}c$, and hence,

$$a\left(b{\kappa }_2^{a^{2}d}\right)=a·d=ad=h_2.$$

In particular, ${\kappa }_1^{ad}=a^{2}c$. From the multiplication table, we have that ${\kappa }_2^{ad}=c$, and hence,

$$a\left(b{\kappa }_2^{ad}\right)=a·a^{2}d=d=h_0.$$

Hence, the $(a,b)$-cycle in $G{S}_{12}$ containing the element d is the sequence $(d,a^{2}d,ad)$.In a similar way, we obtain that the set $G{S}_{12}$ may be partitioned into eight $(a,b)$-cycles: The already mentioned sequence $(d,a^{2}d,ad)$ and the seven sequences

$$\left(e\right),\left(a\right),\left(a^2\right),\left(b\right),\left(a^{2}b\right),\left(ab\right)\mathrm{and}(c,a^{2}c,ac).$$

The seven coloured directed cycles related to these last $(a,b)$-cycles are represented in the following arrays.

Depending on a given subset $H\subseteq G{S}_{12}$, these $(a,b)$-cycles might split onto different maximal $(a,b)$-walks. For instance, taking $H=\{a,c,ac,d\}\subset G{S}_{12}$, one gets three maximal $(a,b)$-paths, namely the $(a,b)$-1-cycle $\left(a\right)$ and the maximal $(a,b)$-walks $(ac,c)$ and $\left(d\right)$.

We now persevere in the analysis of Equation (21). As pointed out in Lemma 2, we focus on the addends corresponding to those indices $k\in G{S}_{4t}$ such that ${\sigma }_k(i,j)=-1$.

Lemma 4.

Let $M_{\psi }$ be a Goethals-Seidel pseudococyclic matrix, for $\psi :G{S}_{4t}\times G{S}_{4t}\to \{\pm 1\}$ as described in Equation (20), and let $i,j\in G{S}_{4t}$. Then, the set of indices $k\in G{S}_{4t}$ such that ${\sigma }_k(i,jk)=-1$ are in one to one correspondence with the ends of the maximal $(i,j)$-walks $(h_0,\dots ,h_r)$ in H, so that either $i\left(jk\right)=h_0$ or $\left(ij\right)k=h_r$.

Proof. 

In what follows, we refer the reader to Lemma 3 for the notations $h_{-}$ and $h_{+}$. From Lemma 2, every index $k\in G{S}_{4t}$ such that ${\sigma }_k(i,j)=-1$ holds precisely one of the following two assertions.

• $i\left(jk\right)\in H$ and $\left(ij\right)k\notin H$. In this case, if we denote $h=i\left(jk\right)\in H$, then $h_{-}=\left(ij\right)k\notin H$ and hence, h constitutes the bottom end of a maximal $(i,j)$-walk in H.
• $i\left(jk\right)\notin H$ and $\left(ij\right)k\in H$. In this case, if we denote $h=\left(ij\right)k\in H$, then $h_{+}=i\left(jk\right)\notin H$ and hence, h constitutes the upper end of a maximal $(i,j)$-walk in H.

Notice that the argument works in both directions. □

Therefore, the study of Equation (21) may be organized in terms of maximal $(i,j)$-walks $(h_0,\dots ,h_r)$, depending on whether $\psi (i,j{\kappa }_1^{h_0})\psi (i,j{\kappa }_2^{h_r})$ is equal to 1 or $-1$. The following result deals with the second case.

Lemma 5.

Under the assumptions of Lemma 4, let $(h_0,\dots ,h_r)$ be a maximal $(i,j)$-walk in H such that $\psi (i,j{\kappa }_1^{h_0})\psi (i,j{\kappa }_2^{h_r})=-1$. Then, the ends $h_0$ and $h_r$ contribute to Equation (21) with two addends such that ${\sigma }_{{\kappa }_1^{h_0}}(i,j)\psi (i,j{\kappa }_1^{h_0})=-{\sigma }_{{\kappa }_2^{h_r}}(i,j)\psi (i,j{\kappa }_2^{h_r})$.

Proof. 

This is a straightforward consequence from the fact that the ends of a maximal walk provide negative signs ${\sigma }_k$, as Lemma 4 indicates. □

The case in which the ends of the $(i,j)$-walk provide a relation $\psi (i,j{\kappa }_1^{h_0})\psi (i,j{\kappa }_2^{h_r})=1$ needs a more careful study.

Lemma 6.

Under the assumptions of Lemma 4, let $(h_0,\dots ,h_r)$ be a maximal $(i,j)$-walk in H such that $\psi (i,j{\kappa }_1^{h_0})\psi (i,j{\kappa }_2^{h_r})=1$. Then, precisely one element between $j{\kappa }_1^{h_0}$ and $j{\kappa }_2^{h_r}$ is in H. Moreover, it determines uniquely a new maximal $(i,j)$-walk in H by means of the left action of $i^{-1}$.

Proof. 

Firstly, notice that any two consecutive links h and $h_{+}=i\left(j\left({\left(ij\right)}^{-1}h\right)\right)$ (as introduced in Lemma 3) in any $(i,j)$-walk in H share a common value ${\phi }_{4t}(i,i^{-1}h)={\phi }_{4t}(i,i^{-1}{h}_{+})$, because the matrix $S_{4t}$ is formed by $t\times t$ blocks of constant signs (this fact is somehow generalized in Proposition 3).

Secondly, in our case, since the $(i,j)$-walk $(h_0,\dots ,h_r)$ is maximal in H, we have that ${\left(h_r\right)}_{+}=i\left(j{\kappa }_2^{h_r}\right)\notin H$. However, $i\left(j{\kappa }_1^{h_0}\right)=h_0\in H$. Then, it is readily evident from Equation (20) that

$${\partial }_H\left(j{\kappa }_1^{h_0}\right){\partial }_H\left(j{\kappa }_2^{h_r}\right)=-1,$$

where ${\partial }_H\left(z\right)=-1$, if $z\in H$, and 1, otherwise. As a consequence, precisely one of the two elements $i^{-1}{h}_0=j{\kappa }_1^{h_0}$ and $i^{-1}{\left(h_r\right)}_{+}=j{\kappa }_2^{h_r}$ belongs to H, and hence, a new maximal $(i,j)$-walk in H containing such an element is uniquely determined. □

Remark 2.

Lemma 6 introduces a way to determine a new maximal $(i,j)$-walk in H from a given maximal $(i,j)$-walk $(h_0,\dots ,h_r)$ in H, with $\psi (i,j{\kappa }_1^{h_0})\psi (i,j{\kappa }_2^{h_r})=1$, by means of the left action of $i^{-1}$, so that just one of the ends of the initial $(i,j)$-walk is projected to the new one. From now on and for simplicity on the exposition, we say that the $(i,j)$-walk $(h_0,\dots ,h_r)$ is of type $\stackrel{i^{-1}}{\to }[\dots )$ (respectively, $\stackrel{i^{-1}}{\to }(\dots ]$) if it is the bottom end $h_0$ (respectively, the upper end $h_r$), the one that is projected on the new maximal $(i,j)$-walk in H. Furthermore, since this left action of $i^{-1}$ may indeed be applied on any maximal $(i,j)$-walk in H, we also say that the latter is of type $\stackrel{i^{-1}}{\to }(\dots )$ (respectively, $\stackrel{i^{-1}}{\to }[\dots ]$) if none of its ends is projected (respectively, its both ends are projected) on the new maximal $(i,j)$-walk in H.

In order to show how the procedure of determining new maximal $(i,j)$-walks by means of the left action of $i^{-1}$ might be iterated, Proposition 4 describes explicitly such an action on any $(i,j)$-path of $G{S}_{4t}$. To this end, some preliminary results are required. Notice in this regard that, for any $h\in G{S}_{12}$ appearing in Example 5, both elements ${\kappa }_1^h$ and ${\kappa }_2^h$ are components of the same triple within the set $\{A_t,B_t,C_t,D_t\}$ described in Equations (11)–(14). The same happens for all the components of any given $(a,b)$-walk in the mentioned example. Furthermore, notice that the left action of $a^{-1}=a^2$ somehow preserves these walks. Thus, for instance, since $a^{-1}\left(ac\right)=c$ and $a^{-1}c=a^{2}c$, one has that the $(a,b)$-walk $(ac,c)$ is projected on the $(a,b)$-walk $(c,a^{2}c)$ by means of such an action. The following results show how these facts may readily be generalized for every Goethals-Seidel loop.

Lemma 7.

If $i,j,h\in G{S}_{4t}$, then there exists an integer $m\in {\mathbb{Z}}_t$ such that ${\kappa }_2^{i,j,h}=a^m{\kappa }_1^{i,j,h}$.

Proof. 

Notice that the product at the level of $t\times t$-blocks within Matrix (10) is that of the group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ (and hence, associative), as we pointed out in Remark 1. As a consequence, both elements ${\kappa }_1^{i,j,h}$ and ${\kappa }_2^{i,j,h}$ appear in the same $t\times t$-block. Then, the result follows readily from Equations (15)–(18). □

Proposition 3.

Let $i,j\in G{S}_{4t}$ and let $(h_0,\dots ,h_r)$ be an $(i,j)$-path in a subset of $G{S}_{4t}$. Let $h,h^{\prime }\in \{h_0,\dots ,h_r\}$ and $s,s^{\prime }\in \{1,2\}$. Then, there exist a pair of integers $m,m^{\prime }\in {\mathbb{Z}}_t$ such that $h^{\prime }=a^{m}h$ and ${\kappa }_s^h=a^{m^{\prime }}{\kappa }_{s^{\prime }}^{h^{\prime }}$.

Proof. 

It follows readily from Lemma 7 and the notion of path in a subset of a given quasigroup. □

Proposition 4.

Let $(h_0,\dots ,h_r)$ be an $(i,j)$-path in a subset of $G{S}_{4t}$, with $i,j\in G{S}_{4t}$. Let $\alpha ,\beta ,\gamma \in \{b,c,d\}$ be pairwise distinct and let $m,n,s\in \{0,\dots ,t-1\}$. Then, the following assertions hold.

1. 

If $(i,j,h_0)=(a^m,a^n\alpha ,a^s\beta )$, with $m\ne 0$, then the sequence $(i^{-1}{h}_0,\dots ,i^{-1}{h}_r)$ also is an $(i,j)$-path in a subset of $G{S}_{4t}$.

2. 

If $(i,j)=(a^m\alpha ,a^n\beta )$ and exactly one of the following four cases holds, then $r=1$ and both sequences $(h_0,h_1)$ and $(i^{-1}{h}_0,i^{-1}{h}_1)$ are $(i,j)$-2-cycles in $G{S}_{4t}$.

(a) 

$h_0=a^s$, with $s\ne 0$.

(b) 

$h_0=a^s\alpha$, with $s\ne m$.

(c) 

$h_0=a^s\beta$, with $s\ne n$.

(d) 

$h_0=a^s\gamma$, with $s\ne 2-m-n$.

3. 

If $(i,h_0)=(a^m\alpha ,a^s\beta )$, then the sequence $(i^{-1}{h}_r,\dots ,i^{-1}{h}_0)$ also is an $(i,j)$-path in a subset of $G{S}_{4t}$, whenever

(a) 

$j=a^n$, with $n\ne 0$; or

(b) 

$j=a^n\alpha$, with $n\ne m$.

Moreover, every $(i,j)$-path in a subset of $G{S}_{4t}$ satisfying none of the previous cases coincides indeed with an $(i,j)$-1-cycle.

Proof. 

Under the assumptions of the first two assertions, one can ensure from Equations (15)–(18) that $\left(ij\right)i=j$. Then, since $(G{S}_{4t},·)$ is a Moufang loop, we have from Equation (6) that ${\kappa }_1^{i^{-1}h}=i{\kappa }_1^h$, for all $h\in G_{4t}$, because

$$i\left(j\left(i{\kappa }_1^h\right)\right)=\left(\left(ij\right)i\right){\kappa }_1^h=j{\kappa }_1^h=i^{-1}h.$$

Thus, in order to prove each one of the first two assertions, it is enough to check that ${\kappa }_2^{i^{-1}{h}_{\ell }}=i{\kappa }_2^{h_{\ell }}$, for all $0\le \ell <r$. To this end, we focus on the case $\ell =0$. The remaining cases follow similarly, because, from Proposition 3, every $h_{\ell }$ has the same form (that is, $a^{s^{\prime }}$, $a^{s^{\prime }}\alpha$, $a^{s^{\prime }}\beta$ or $a^{s^{\prime }}\gamma$, with $s^{\prime }\in \{0,\dots ,t-1\}$) than $h_0$.

Concerning the first assertion, we have that ${\kappa }_2^{h_0}=a^{2-m-n-s}\gamma$ and hence,

$$\left(ij\right)\left(i{\kappa }_2^{h_0}\right)=(a^m·a^n\alpha )(a^m·a^{2-m-n-s}\gamma )=a^{m+n}\alpha ·a^{2-n-s}\gamma =a^{s-m}\beta =a^{-m}·a^s\beta =i^{-1}{h}_0.$$

Now, concerning the second assertion, we prove separately each one of the four Cases (2a)–(2d).

• In (2a), we have that ${\kappa }_2^{h_0}=a^{2-m-n-s}\gamma$ and hence,

  $$\left(ij\right)\left(i{\kappa }_2^{h_0}\right)=(a^m\alpha ·a^n\beta )(a^m\alpha ·a^{2-m-n-s}\gamma )=a^{2-m-n}\gamma ·a^{n+s}\beta =a^{m-s}\alpha =a^m\alpha ·a^s=i^{-1}{h}_0.$$
  Further, since ${\kappa }_1^{h_1}={\kappa }_2^{h_0}$, we have that

  $$h_1=i\left(j{\kappa }_1^{h_1}\right)=i\left(j{\kappa }_2^{h_0}\right)=a^m\alpha (a^n\beta ·a^{2-m-n-s}\gamma )=a^{-s}\alpha .$$
  Notice that $h_1\ne h_0$ if and only if $s\ne 0$. In any case, it holds analogously that $h_2=h_0$ and hence, both sequences $(h_0,h_1)$ and $(i^{-1}{h}_0,i^{-1}{h}_1)$ are $(i,j)$-2-cycles, whenever $s\ne 0$.
• In (2b), we have that ${\kappa }_2^{h_0}=a^{m+n-s}\beta$ and hence,

  $$\left(ij\right)\left(i{\kappa }_2^{h_0}\right)=(a^m\alpha ·a^n\beta )(a^m\alpha ·a^{m+n-s}\beta )=a^{2-m-n}\gamma ·a^{2-2m-n+s}\gamma =a^{m-s}=a^m\alpha ·a^s\alpha =i^{-1}{h}_0.$$
  Further,

  $$h_1=a^m\alpha (a^n\beta ·a^{m+n-s}\beta )=a^{2m-s}\alpha .$$
  Thus, $h_1\ne h_0$ if and only if $s\ne m$. In any case, $h_2=h_0$ and thus, both sequences $(h_0,h_1)$ and $(i^{-1}{h}_0,i^{-1}{h}_1)$ are $(i,j)$-2-cycles, whenever $s\ne m$.
• In (2c), we have that ${\kappa }_2^{h_0}=a^{m+n-s}\alpha$ and hence,

  $$\left(ij\right)\left(i{\kappa }_2^{h_0}\right)=(a^m\alpha ·a^n\alpha )(a^m\alpha ·a^{m+n-s}\alpha )=a^{2-m-n}\gamma ·a^{-n+s}=a^{2-m-s}\gamma =a^m\alpha ·a^s\beta =i^{-1}{h}_0.$$
  Further,

  $$h_1=a^m\alpha (a^n\beta ·a^{m+n-s}\alpha )=a^{2n-s}\beta .$$
  As a consequence, $h_1\ne h_0$ if and only if $s\ne n$. In any case, $h_2=h_0$ and thus, both sequences $(h_0,h_1)$ and $(i^{-1}{h}_0,i^{-1}{h}_1)$ are $(i,j)$-2-cycles, whenever $s\ne n$.
• Finally, in (2d), we have that ${\kappa }_2^{h_0}=a^{2-m-n-s}$ and hence,

  $$\left(ij\right)\left(i{\kappa }_2^{h_0}\right)=(a^m\alpha ·a^n\alpha )(a^m\alpha ·a^{2-m-n-s})=a^{2-m-n}\gamma ·a^{2m+n+s-2}\alpha =a^{2-m-s}\beta =a^m\alpha ·a^s\gamma =i^{-1}{h}_0.$$
  Further,

  $$h_1=a^m\alpha (a^n\beta ·a^{2-m-n-s})=a^{4-2m-2n-s}\gamma .$$
  As a consequence, $h_1\ne h_0$ if and only if $s\ne 2-m-n$. In any case, $h_2=h_0$ and thus, both sequences $(h_0,h_1)$ and $(i^{-1}{h}_0,i^{-1}{h}_1)$ are $(i,j)$-2-cycles, whenever $s\ne 2-m-n$.

Let us focus now on the proof of each one of the two Cases (3a) and (3b) of the third assertion.

• In (3a), we have that ${\kappa }_2^{h_0}=a^{2-m+n-s}\gamma$ and hence,

  $$h_1=a^m\alpha (a^n·a^{2-m+n-s}\gamma )=a^{s-2n}\beta .$$
  Thus, $h_1\ne h_0$ if and only if $n\ne 0$. If this is the case, we have for each $\ell \in \{0,\dots ,r\}$ that

  $$h_{\ell }=a^{s-2\ell n}\beta ,{\kappa }_1^{h_{\ell }}=a^{2-m-s+(2\ell -1)n}\gamma \mathrm{and}{\kappa }_2^{h_{\ell }}=a^{2-m-s+(2\ell +1)n}\gamma .$$
  In particular, ${\kappa }_1^{h_{\ell }}={\kappa }_2^{h_{\ell -1}}$, for all $\ell \in \{1,\dots ,r\}$. Further, we also have for each $\ell \in \{0,\dots ,r\}$ that

  $$i^{-1}{h}_{\ell }=a^{2-m-s+2\ell n}\gamma ,{\kappa }_1^{i^{-1}{h}_{\ell }}=a^{s-(2\ell +1)n}\beta \mathrm{and}{\kappa }_2^{i^{-1}{h}_{\ell }}=a^{s-(2\ell -1)n}\beta .$$
  Thus, ${\kappa }_2^{i^{-1}{h}_{\ell }}={\kappa }_1^{i^{-1}{h}_{\ell -1}}$, for all $\ell \in \{1,\dots ,r\}$, and hence, the sequence $(i^{-1}{h}_r,\dots ,i^{-1}{h}_0)$ is an $(i,j)$-path of a subset of $G{S}_{4t}$.
• In (3b), we have that ${\kappa }_2^{h_0}=a^{s-m+n}\beta$ and hence,

  $$h_1=a^m\alpha (a^n\alpha ·a^{s-m+n}\beta )=a^{s-2(m-n)}\beta .$$
  Thus, $h_1\ne h_0$ if and only if $n\ne m$. If this is the case, we have for each $\ell \in \{0,\dots ,r\}$ that

  $$h_{\ell }=a^{s-2\ell (m-n)}\beta ,{\kappa }_1^{h_{\ell }}=a^{s-(2\ell -1)(m-n)}\beta \mathrm{and}{\kappa }_2^{h_{\ell }}=a^{s-(2\ell +1)(m-n)}\beta .$$
  In particular, ${\kappa }_1^{h_{\ell }}={\kappa }_2^{h_{\ell -1}}$, for all $\ell \in \{1,\dots ,r\}$. Further, we also have for each $\ell \in \{0,\dots ,r\}$ that

  $$i^{-1}{h}_{\ell }=a^{2-s-m+2\ell (m-n)}\gamma ,{\kappa }_1^{i^{-1}{h}_{\ell }}=a^{2-s-n+2\ell (m-n)}\gamma \mathrm{and}{\kappa }_2^{i^{-1}{h}_{\ell }}=a^{2-s-n+2(\ell -1)(m-n)}\gamma .$$
  Thus, ${\kappa }_2^{i^{-1}{h}_{\ell }}={\kappa }_1^{i^{-1}{h}_{\ell -1}}$, for all $\ell \in \{1,\dots ,r\}$, and hence, the sequence $(i^{-1}{h}_r,\dots ,i^{-1}{h}_0)$ is an $(i,j)$-path of a subset of $G{S}_{4t}$.

Finally, in order to finish the proof of the last statement of the proposition, it is enough to observe that, for each one of the cases that have not still been considered in the current proof, we have that $h_{\ell }=i\left(j{\kappa }_2^{h_{\ell }}\right)=\left(ij\right){\kappa }_2^{h_{\ell }}=\left(ij\right){\kappa }_1^{h_{\ell +1}}=h_{\ell +1}$, for all $\ell \in \{0,\dots ,r-1\}$. □

We are now in conditions to complete the study of Equation (21). To this end, we aim to prove that, under the assumptions of Lemma 6, the pair of ends $({\kappa }_1^{h_0},{\kappa }_2^{h_r})$ is uniquely related to another pair of different ends $({\kappa }_1^{h_0^{\prime }},{\kappa }_2^{h_s^{\prime }})$ delimiting a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ in H such that

$$\psi (i,j{\kappa }_1^{h_0^{\prime }})=\psi (i,j{\kappa }_2^{h_s^{\prime }})=-\psi (i,j{\kappa }_1^{h_0})=-\psi (i,j{\kappa }_2^{h_r}).$$

(23)

This new $(i,j)$-walk is obtained from the initial one after a finite number of projections by means of the left action of $i^{-1}$. As commented in Remark 2, for the sake of reading, we make use of brackets and parenthesis for noting which one of the ends of the initial $(i,j)$-walk are projected onto the new $(i,j)$-walk by means of the action of $i^{-1}$.

As a final remark, it is convenient to recall that the map $\psi$ of Equation (20) is described as the product of some pseudocoboundaries ${\psi }_h$ (those ones that are indexed by the set H) and a cocycle ${\phi }_{4t}$ (whose matrix representation is $S_{4t}$, consisting of $t\times t$-blocks of constant signs). Therefore, checking Equation (23) might eventually require calculating the value of each one of these factors.

In light of Proposition 4, we may distinguish three different cases, depending on the values of the triple $(i,j,h)$. These cases are studied separately in Lemmas 8–10.

Lemma 8.

Under the assumptions of Lemma 6 and Proposition 4 list 1, a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ in H exists such that Equation (23) holds.

Proof. 

Two subcases arise depending on the type ($\stackrel{i^{-1}}{\to }[\dots )$ or $\stackrel{i^{-1}}{\to }(\dots ]$) of the initial $(i,j)$-walk.

1.

If the $(i,j)$-walk $(h_0,\dots ,h_r)$ is of type $\stackrel{i^{-1}}{\to }[\dots )$, then its projected maximal $(i,j)$-walk by means of the left action of $i^{-1}$ must be of type either $\stackrel{i^{-1}}{\to }(\dots ]$ or $\stackrel{i^{-1}}{\to }[\dots ]$. This is due to the fact that $i^{-1}\left(i^{-1}h\right)=h_{+}$, for all $h\in G{S}_{4t}$, because $i=a^m$, with $m\ne 0$.

In the particular case in which the bottom end is projected (that is, in case of dealing with the type $\stackrel{i^{-1}}{\to }[\dots ]$), it constitutes a foothold to keep on applying once more time the action of $i^{-1}$. This procedure may be iterated until a projection is achieved providing a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ of type $\stackrel{i^{-1}}{\to }(\dots ]$.

2.

Similarly, if the $(i,j)$-walk $(h_0,\dots ,h_r)$ is of type $\stackrel{i^{-1}}{\to }(\dots ]$, then its projected maximal $(i,j)$-walk by means of the left action of $i^{-1}$ is necessarily of type either $\stackrel{i^{-1}}{\to }[\dots )$ or $\stackrel{i^{-1}}{\to }[\dots ]$ .

In the particular case in which the upper end is projected (that is, in case of dealing with the type $\stackrel{i^{-1}}{\to }[\dots ]$), it constitutes a foothold to keep on applying the action of $i^{-1}$. This process may be iterated until a projection is achieved providing a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ of the type $\stackrel{i^{-1}}{\to }[\dots )$.

In both subcases, the iterative procedure finishes, because the subset H is finite and all the resulting $(i,j)$-walks are uniquely determined by Lemma 6. Whichever is the case, a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ in H exists, which preserves the complementary end as compared with the initial projected walk. This implies that

$$\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0)=-\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0^{\prime }).$$

Since $i=a^m$, it must be ${\phi }_{4t}(i,i^{-1}{h}_0)={\phi }_{4t}(i,i^{-1}{h}_0^{\prime })$, and hence, Equation (23) holds. □

Lemma 9.

Under the assumptions of Lemma 6 and Proposition 4 list 2, a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ in H exists such that Equation (23) holds.

Proof. 

Attending to Proposition 4, we start from a maximal $(i,j)$-1-walk $\left(h_0\right)$. Furthermore, no matter which among the bottom or the upper end is projected, the projected walk $\left(h_0^{\prime }\right)=\left(i^{-1}{h}_0\right)$ is of the same type as the initial one. Hence,

$$\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0)=\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0^{\prime }).$$

However, taking into account the possible values for $(i,h)$, we have that ${\phi }_{4t}(i,i^{-1}{h}_0)=-{\phi }_{4t}(i,i^{-1}{h}_0^{\prime })$, and hence, Equation (23) holds. □

Lemma 10.

Under the assumptions of Lemma 6 and Proposition 4 list 3, a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ in H exists such that Equation (23) holds.

Proof. 

This case follows analogously to that of Lemma 8. In particular, once again, two subcases arise depending on whether the bottom or the upper end is projected. No matter $\stackrel{i^{-1}}{\to }[\dots )$ or $\stackrel{i^{-1}}{\to }(\dots ]$ is the case, it is readily checked that under a new action of $i^{-1}$, any of the $(i,j)$-walks in Proposition 4 list 3 projects to another maximal $(i,j)$-walk that preserves the opposite end. This is due to the reverse property described in such a proposition.

If the other end is eventually preserved as well, it constitutes a foothold to keep on applying once more time the left action of $i^{-1}$. This procedure may be iterated until a projection is achieved providing a maximal $(i,j)$-walk $(h_0^{\prime },\dots ,h_s^{\prime })$ for which precisely one end is projected by the action of $i^{-1}$.

The iterative procedure finishes because of being H finite. Furthermore, depending on the parity of the number n of developed projections, one of the following two assertions hold.

• Either $h_0^{\prime }=a^m{h}_0$ and the walks preserve different ends; which implies that

  $${\phi }_{4t}(i,i^{-1}{h}_0)={\phi }_{4t}(i,i^{-1}{h}_0^{\prime })$$

  and

  $$\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0)=-\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0^{\prime }).$$
• Or $h_0^{\prime }=a^m\left(i^{-1}{h}_0\right)$ and the walks preserve the same ends; which implies that

  $${\phi }_{4t}(i,i^{-1}{h}_0)=-{\phi }_{4t}(i,i^{-1}{h}_0^{\prime })$$

  and

  $$\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0)=\prod _{h\in H}{\psi }_h(i,i^{-1}{h}_0^{\prime }).$$

In any case, Equation (23) holds. □

The following result is a straightforward consequence of Lemmas 5 and 8–10.

Lemma 11.

Under the assumptions of Lemma 6, and attending to Equation (21), the set of indices $d\in G{S}_{4t}$ such that ${\sigma }_d(i,j)=-1$ may be organized into pairs $(k,k^{\prime })$ uniquely determined such that $\psi (i,jk)\psi (i,j{k}^{\prime })=-1$.

Finally, the following lemma supports the sufficient condition of the cocyclic test over Goethals-Seidel arrays, which we show in Theorem 1.

Lemma 12.

Under the assumptions of Lemma 6, Equation (21) holds if and only if the summation of row i in the pseudococyclic matrix $M_{\psi }$ is 0.

Proof. 

In order to prove that

$$\sum _{k\in G{S}_{4t}}\psi (i,jk){\sigma }_k(i,j)=\sum _{k\in G{S}_{4t}}\psi (i,k),$$

(24)

it suffices to show that both expressions share the same amount of positive and negative addends. Observe in this regard that, if $k\in G{S}_{4t}$ is such that ${\sigma }_k(i,j)=1$, then the corresponding addends at both sides of Equation (24) are obviously equal. Hence, we can focus on those elements $k\in G{S}_{4t}$ such that ${\sigma }_k(i,j)=-1$. However, Lemma 11 guarantees that such addends come by pairs, which provide summands having opposite signs. □

We are ready to prove that the usual cocyclic test still applies over Goethals-Seidel arrays.

Theorem 1.

Let us consider a positive integer $t>2$. The Goethals-Seidel array of order $4t$ is Hadamard if and only if the underlying pseudococyclic matrix $M_{\psi }$ of Equation (20) over the Goethals-Seidel loop $(G{S}_{4t},·)$ satisfies the cocyclic Hadamard test.

Proof. 

In the proof of Proposition 2, we noticed that the Goethals-Seidel array of order $4t$ is Hadamard equivalent to the matrix $M_{\psi }$. Since the latter is normalized, a necessary condition for $M_{\psi }$ being Hadamard is that the summation of all the elements of its rows (but the first one) is zero, which gives rise to the “only if” condition of the hypothesis. On the other hand, Lemma 12 supports the sufficient condition. □

Example 6.

The pseudococycle $\psi ={\psi }_2{\psi }_5{\psi }_8{S}_{12}$ gives rise to the following pseudococyclic matrix $M_{\psi }$ over $G{S}_{12}$,

$$M_{\psi }=\left(\begin{array}{cccccccccccc}+& +& +& +& +& +& +& +& +& +& +& +\\ +& +& -& -& +& +& -& +& +& -& -& -\\ +& -& -& -& -& +& -& -& +& +& +& +\\ +& +& +& -& -& -& +& -& +& +& -& -\\ +& +& -& +& -& -& -& +& -& +& +& -\\ +& -& -& +& +& -& +& -& +& -& +& -\\ +& +& +& -& +& -& -& -& -& -& +& +\\ +& +& -& +& -& +& +& -& -& -& -& +\\ +& -& -& -& +& -& +& +& -& +& -& +\\ +& -& +& -& -& +& +& +& -& -& +& -\\ +& -& +& +& -& -& -& +& +& -& -& +\\ +& -& +& +& +& +& -& -& -& +& -& -\end{array}\right).$$

Since every row (but the first) sums zero, the matrix $M_{\psi }$ is Hadamard.

Remark 3.

The fact that the summation of every row (up to the first) equals zero in the pseudococyclic matrix $M_{\psi }$ is equivalent to Equation (4), for $G={\mathbb{Z}}_t$. To this end, one takes into account that, for each $i\in G{S}_{4t}\backslash \left\{e\right\}$, the i-row of any pseudocoboundary matrix $M_{{\psi }_h}$ consists of two negative entries, which are located precisely at the h- and the $i^{-1}h$-columns (except for the h-row, which consists all of $-1$ s, up to entries at the 1- and h-columns).

5. Conclusions and Further Work

Beyond the work of some of the authors in [12], this paper progresses on the idea of extending the theory of cocyclic matrices over groups, focusing on quasigroups. More specifically, we introduce here the concepts of pseudocoboundary and pseudococycle over a quasigroup, and also the notion of the pseudococyclic Hadamard matrix.

We have also provided some general structures that might be used for studying pseudococyclic matrices over quasigroups. This is the case of $(i,j)$-walks.

In particular, Goethals-Seidel arrays have been shown to be pseudococyclically developed over Goethals-Seidel loops. Furthermore, no matter if they are pseudococyclic matrices, the usual cocyclic Hadamard test has been shown to be unexpectedly applicable. Notice that this is an unusual fact, as Example 4 shows.

It is an open question whether some assumption may be imposed in order to generalize this behavior to other families of loops (either Moufang as well or not).

The door to promising new tools for looking for (pseudo)cocyclic Hadamard matrices over loops is open. In particular, the following major problems might be considered.

• Show whether these new (pseudo)cocyclic structures strictly extend the usual cocyclic framework, in the sense that some Hadamard equivalence classes which are known not to be cocyclic over groups are actually (pseudo)cocyclic over some loops.
• Construct some new Hadamard matrices (pseudo)cocyclically developed over loops of orders for which no (cocyclic) Hadamard matrix is still known to exist.

This will be the concern of our future work.