Characterizations of the Beta Kumaraswamy Exponential Distribution

Abstract

In this article, the five-parameter beta Kumaraswamy exponential distribution (BKw-E) is introduced, and some characterizations of this distribution are obtained. The shape of the hazard function and some other important properties—such as median, mode, quantile function, and mean—are studied. In addition, the moments, skewness, and kurtosis are found. Furthermore, important measures such as Rényi entropy and order statistics are obtained; these have applications in many fields. An example of a real data set is discussed.

1. Introduction

The Kumaraswamy distribution was originally called the double-bounded distribution. It was introduced by [1]. This distribution has a closed-form cumulative distribution function (cdf). It has been found that the Kumaraswamy distribution fits hydrological data in simulations (see [1]) and is more computationally tractable (see [2]). Reference [3] proposed a new procedure for building a new distribution known as the Kumaraswamy-H distribution (Kw-H). The Kw-H can be constructed for any continuous baseline cumulative function H(x), with the cdf given by

$$G\left(x\right)=1-{\{1-{\left[H\left(x\right)\right]}^a\}}^b,$$

(1)

where $a,b>0$ are the shape parameters.

Putting the cdf of exponential distribution ($H\left(x\right)=1-e^{-\lambda x}$) in Equation (1), we obtain the Kumaraswamy exponential (Kw-E) distribution, whose cdf is given by

$$G\left(x\right)=1-{\{1-{(1-e^{-\lambda x})}^a\}}^b,x>0,$$

(2)

where $a,b>0$ are the shape parameters and $\lambda >0$ is the scale parameter.

In recent years, there were several studies about generalized Kumaraswamy distribution and its generalizations. Reference [4] derived a simple representation for the Kw-H density function as a linear combination of exponentiated-H distributions. They obtained its mathematical properties. In addition, they proposed some new distributions as sub-models. Moreover, they discussed the estimation of maximum likelihood and applied the model to a real data set. Reference [5] considered an exponentiated Kumaraswamy distribution. They discussed its properties. In addition, they proposed the log-exponentiated Kumaraswamy distribution and obtained the maximum likelihood estimators of the log-exponentiated Kumaraswamy distribution. Reference [6] introduced the Kumaraswamy linear exponential distribution with four parameters and obtained some of its mathematical properties. In addition, the estimations of the unknown parameters were derived by using the maximum likelihood estimation. Reference [7] introduced the the maximum likelihood of the unknown parameters for Kumaraswamy exponential distribution. In addition, they obtained the information matrix and applied the model to a real data set. Reference [8] introduced the exponentiated Kumaraswamy exponential distribution (Expk-E). They considered its characterization and properties. In addition, they obtained the estimation of the parameters by applying the maximum likelihood estimation; the application showed that the model proposed can be very useful in fitting real data. Reference [9] introduced the estimation of the parameters for Kumaraswamy exponential distribution under progressive type-II censored samples. In addition, the estimators of the parameters were obtained using maximum likelihood and Bayes estimates under different loss functions. Furthermore, the Monte Carlo simulation was applied for numerical comparison between various estimates.

On the other hand, Reference [10] proposed a class of generalized distributions as follows:

$$F\left(x\right)=\frac{1}{B(l,m)}{\int }_0^{G\left(x\right)}{w}^{l-1}{(1-w)}^{m-1}dw,$$

(3)

where $l,m>0$ are the shape parameters. The cdf G(x) could represent any baseline cumulative function, while F(x) is named the beta-G(x) distribution.

Many authors have studied the generalized beta distribution and its generalizations. Reference [10] proposed a general class of distributions generated from the beta distribution with two extra parameters. They introduced the beta-normal distribution as a special model. They obtained moments and discussed the estimation of the maximum likelihood estimators. Furthermore, Reference [11] considered the beta exponential distribution. They studied some of its properties and derived the first four moments, the moment-generating function, and the extreme order statistics. In addition, they obtained the maximum likelihood estimation. Reference [12] proposed the beta generalized exponential distribution. They provided a comprehensive mathematical treatment for the distribution and derived the moment-generating function, including the densities of the order statistic. They discussed the estimation of the parameters by maximum likelihood and provided the information matrix. In addition, they applied the model to a real data set. Furthermore, Reference [13] considered the beta generalized inverted exponential distribution. Various properties of the distribution were obtained. In addition, the Fisher information matrix, the maximum likelihood estimators, and the confidence interval were found. Furthermore, they discussed the Monte Carlo simulation, and applications with real data were provided. Reference [14] proposed the beta-generated Kumaraswamy-G family. They obtained some of its properties; the order statistics, probability weighted moments, moment-generating function, and Rényi entropy were also derived. Moreover, two methods of estimation were discussed. Reference [15] continued some studies on the beta generated Kumaraswamy-G family by proposing the beta generated Kumaraswamy Burr type X distribution. Some properties of the distribution were provided; the maximum likelihood estimation was also obtained, and the model was applied to a real data set.

In this article, a new distribution is introduced by taking the cdf of the Kw-E distribution as the baseline of the beta distribution. We refer to the new distribution as the beta Kumaraswamy exponential (BKw-E) distribution. This model is a generalization of the Kw-E distribution. In the further sections, we first present our model BKw-E distribution, as well as the reliability and the hazard functions in Section 2. The properties of the distribution—such as moments, quntile function, median, and other important properties—are studied in Section 3. The Rényi entropy is discussed in Section 4. Order statistics are discussed in Section 5, and an application on a real data set is provided in Section 6. Finally, conclusions are presented in Section 7.

2. The BKw-E Distribution

In this section, we introduce the five-parameter beta Kumaraswamy exponential (BKw-E) distribution. By subtitling Equation (2) as a baseline cumulative function in Equation (3), the cdf of BKw-E is obtained as follows:

$$F\left(x\right)=\frac{1}{B(l,m)}{\int }_0^{1-{\{1-{(1-e^{-\lambda x})}^a\}}^b}{w}^{l-1}{(1-w)}^{m-1}dw,x>0,l,m,a,b,\lambda >0,$$

(4)

and the corresponding probability density function (pdf) of the BKw-E takes the form

$$\begin{array}{c}f\left(x\right)=\frac{a\lambda b}{B(l,m)}{e}^{-\lambda x}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{mb-1}{\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{l-1},\\ x>0,a,b,\lambda ,l,m>0.\end{array}$$

(5)

Equation (5) can be rewritten as an infinite power series in the form

$$\begin{array}{c}f\left(x\right)=a\lambda b\sum _{k=0}^{\infty }\frac{{(-1)}^k{e}^{-\lambda x}}{lB(k+1,l-k)B(l,m)}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b(m+k)-1},x>0,a,b,\lambda ,l,m>0,\end{array}$$

(6)

or it can be rewritten as a mixture of exponential distribution, which has the form

$$f\left(x\right)=\lambda \sum _{i=0}^{\infty }(i+1){\psi }_i{e}^{-\lambda (i+1)x},x>0,l,m,a,b,\lambda >0,$$

(7)

where

$$\begin{array}{c}{\psi }_i=\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{{(-1)}^{k+j+i}}{l(m+k)(j+1)B(k+1,l-k)B(l,m)B\left(b\right(m+k)-j,j+1)(i+1)B\left(a\right(j+1)-i,i+1)}.\end{array}$$

(8)

From Equation (6), the corresponding cdf is given as

$$\begin{array}{c}F\left(x\right)=\sum _{k=0}^{\infty }\frac{{(-1)}^k}{l(m+k)B(k+1,l-k)B(l,m)}\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b(m+k)}\right],x>0,a,b,\lambda ,l,m>0.\end{array}$$

(9)

From the pdf in Equation (7), the cdf can be written in the form

$$F\left(x\right)=\sum _{i=0}^{\infty }{\psi }_i\left[1-e^{-\lambda (i+1)x}\right],x>0,l,m,a,b,\lambda >0,$$

(10)

where ${\psi }_i$ is defined in Equation (8).

We can get the pdf of the Kw-E distribution as a special case from the BKw-E distribution, when $l=m=1$ in Equation (5) as follow:

$$f\left(x\right)=a\lambda b{e}^{-\lambda x}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b-1},x>0,a,b,\lambda >0.$$

(11)

In addition, we can assume that all of the properties of ExpK-E by [8] still hold when $m=1$ in Equation (5), and the pdf is given by

$$\begin{array}{c}f\left(x\right)=\left(la\lambda b\right)e^{-\lambda x}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b-1}{\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{l-1},x>0,a,b,\lambda ,l>0.\end{array}$$

(12)

Furthermore, the exponential (Exp) distribution can be found when $m=l=b=a=1$.

$$f\left(x\right)=\lambda e^{-\lambda x},x>0,\lambda >0.$$

(13)

There are many sub-models that we can generate from the BKw-E, such as the beta generalized exponential distribution which was proposed by [12] or the Beta exponential distribution. The proposed model shows diversity and flexibility, which can be useful for goodness of fit tests and applications of real data, as we will discuss in Section 6.

Figure 1 shows that the shape of the probability density function is uni-modal and is positively skewed for different values of the parameters.

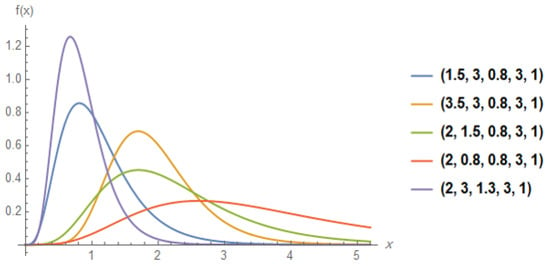
Figure 1. The probability density function (pdf) curves of the beta Kumaraswamy exponential distribution (BKw-E) with $(a,b,\lambda ,l,m)$.

The Hazard and Reliability Functions

The hazard function is the instant rate of failure at a given time t, while the reliability function is the probability of the non-failure occurring before time t. The reliability function of the BKw-E distribution is given by:

$$\begin{array}{c}R\left(x\right)=1-\sum _{k=0}^{\infty }\frac{{(-1)}^k}{l(k+m)B(k+1,l-k)B(l,m)}\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b(m+k)}\right],x>0,a,b,\lambda ,l,m>0,\end{array}$$

(14)

and the corresponding hazard function of the BKw-E distribution takes the form

$$h\left(x\right)=\frac{a\lambda b{\sum }_{k=0}^{\infty }\frac{{(-1)}^k{e}^{-\lambda x}}{lB(k+1,l-k)B(l,m)}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b(m+k)-1}}{1-{\sum }_{k=0}^{\infty }\frac{{(-1)}^k}{l(k+m)B(k+1l-k)B(l,m)}\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^{b(m+k)}\right]},x>0,a,b,\lambda ,l,m>0.$$

(15)

Figure 2 shows the reliability curves for different values of the parameters for the BKw-E distribution, while Figure 3 shows that the hazard function of the BKw-E distribution increases for different values of $(a,b,\lambda ,l,m)$. The BKw-E distribution shows good statistical behavior based on these two functions.

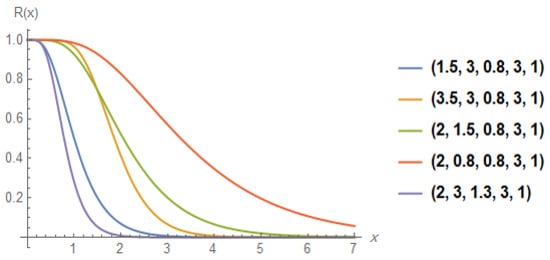
Figure 2. The reliability curves of the BKw-E distribution with $(a,b,\lambda ,l,m)$.

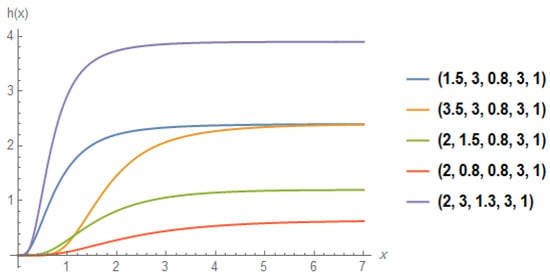
Figure 3. The hazard curves of the BKw-E distribution with $(a,b,\lambda ,l,m)$.

3. Statistical Properties

3.1. Moments

The rth moment of the BKw-E distribution random variable X is given by

$$E\left(X^r\right)={\int }_0^{\infty }{x}^r\frac{a\lambda b}{B(l,m)}{e}^{-\lambda x}{(1-e^{-\lambda x})}^{a-1}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{mb-1}{\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{l-1}dx.$$

By using the pdf in Equation (7)

$$E\left(X^r\right)=\lambda \sum _{i=0}^{\infty }(i+1){\psi }_i{\int }_0^{\infty }{x}^r{e}^{-\lambda (i+1)x},$$

(16)

the closed form for the moment is given by

$${\mu }_r^{{}^{\prime }}=\sum _{i=0}^{\infty }{\psi }_i\frac{r!}{{\lambda }^r{(i+1)}^r},$$

(17)

and for $r=1$, we obtain the mean:

$$\mu =\sum _{i=0}^{\infty }{\psi }_i\frac{1}{\lambda (i+1)}·$$

(18)

3.2. Quantile Function

Let $u=F\left(x\right)$ where U follows uniform $(0,1)$. By using the transformation method, we consider the random variable X of Bkw-E as follows:

$$x=Q\left(u\right)=-\frac{1}{\lambda }log\left[1-{\left[1-{\left[1-I_u^{-1}(l,m)\right]}^{\frac{1}{\theta }}\right]}^{\frac{1}{a}}\right],$$

(19)

where $I_u^{-1}(l,m)$ is the inverted incomplete beta function with parameters l and m. The quantile function in Equation (19) is an important function in the simulation study for generating random numbers from the Bkw-E distribution.

3.3. Median

The median $\left(med\right)$ of the BKw-E distribution can be found using the cdf in Equation (9). Substituting $l=1$ in Equation (9), we have

$$\left[1-{\left[1-{(1-e^{-\lambda med})}^a\right]}^{b(m+k)}\right]=\frac{1}{2}·$$

(20)

After solving Equation (20), the median is given by

$$med=-\frac{1}{\lambda }log\left[1-{\left[1-{(0.5)}^{\frac{1}{bm}}\right]}^{\frac{1}{\alpha }}\right]·$$

(21)

3.4. Mode

The mode of the BKw-E distribution can be found by solving the following equation:

$$\frac{df\left(x\right)}{dx}=0·$$

Using Equation (5), we have

$$\begin{array}{c}f\left(x\right)\left[\lambda \right[-1+e^{-\lambda x}{(1-e^{-\lambda x})}^{-1}[(a-1)-a{(1-e^{-\lambda x})}^a{\left[1-{(1-e^{-\lambda x})}^a\right]}^{-1}\times \\ \left[(mb-1)-b(a-1){\left[1-{(1-e^{-\lambda x})}^a\right]}^b{\left[{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{-1}\right]\left]\right]]=0.\end{array}$$

(22)

Since $f\left(x\right)>0$, the mode is the solution of the following equation:

$$\begin{array}{c}\lambda [-1+e^{-\lambda x}{(1-e^{-\lambda x})}^{-1}[(a-1)-a{(1-e^{-\lambda x})}^a{\left[1-{(1-e^{-\lambda x})}^a\right]}^{-1}\\ \times \left[(mb-1)-b(a-1){\left[1-{(1-e^{-\lambda x})}^a\right]}^b{\left[{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{-1}\right]\left]\right]=0.\end{array}$$

(23)

Equation (23) is a nonlinear equation, and its solution cannot be found analytically. Furthermore, it can be found numerically by using Newton–Raphson method.

3.5. Skewness and Kurtosis

By using quantiles, the skewness and kurtosis of the BKw-E can be calculated. Bowley’s skewness is based on quartiles (see [16]), and it takes the form

$$B=\frac{Q(3/4)-2Q(1/2)+Q(1/4)}{Q(3/4)-Q(1/4)}.$$

Moors’ kurtosis (see [17]) is based on octiles, and could be written as

$$M=\frac{Q(7/8)-Q(5/8)+Q(3/8)-Q(1/8)}{Q(6/8)-Q(2/8)},$$

where Q(.) is the quantile function defined in Equation (19).

The behavior of the BKw-E distribution can be studied in Table 1 and Figure 1. The curve of the distribution approaches the normal shape when the value of a increases, which explains why the value of the skewness is near to zero. On the other hand, the curve of the distribution is positively skewed as the value of b decreases. By increasing b, the mean, mode, and median decrease. Further, by increasing the scale parameter $\lambda$, the values of kurtosis and skewness remain constant, although the mode, median, and mean decrease. In addition, as we increase the value of l, the values of the mode, median, kurtosis, and skewness remain constant while the mean increases. Moreover, the mean, mode, and median decrease with the increase of the value of m.

Table 1. The mean, mode, median, skewness, and kurtosis for different values of the parameters.

a	b	$\mathit{\lambda }$	l	m	Mean	Mode	Median	Skewness	Kurtosis
1.5	3	0.8	3	1	1.101	0.474	0.536	0.186	1.263
3.5	3	0.8	3	1	1.950	1.784	1.267	0.106	1.245
4	3	0.8	3	1	2.095	2.007	1.401	0.099	1.245
2	0.5	0.8	3	1	1.860	2.728	2.513	0.217	1.304
2	0.8	0.8	3	1	2.964	1.999	1.791	0.197	1.289
2	1.5	0.8	3	1	2.376	1.346	1.172	0.172	1.269
2	3	0.9	3	1	1.219	0.791	0.673	0.1496	1.251
2	3	1.3	3	1	0.844	0.546	0.466	0.1496	1.251
2	3	2	3	1	0.549	0.356	0.303	0.1496	1.251
2	3	0.8	4	1	1.505	0.8896	0.757	0.1496	1.251
2	3	0.8	5	1	1.608	0.8896	0.757	0.1496	1.251
2	3	0.8	3	0.2	2.785	1.631	2.198	0.1496	1.251
2	3	0.8	3	2	0.970	0.650	0.501	0.1496	1.251

3.6. The Mean Deviation

The mean deviation is a measure of dispersion derived by computing the mean of the absolute values of the differences between the observed values of a variable and the mean or the median of the variable. The mean deviation about the mean and the median are, respectively, defined by:

$$D\left(\mu \right)=E\left(\right|x-\mu \left|\right)$$

and

$$D\left(m\right)=E\left(\right|x-m\left|\right),$$

where $\mu =E\left(X\right)$ and $m=Q\left(\frac{1}{2}\right)$.

The mean deviation about the mean can be obtained from the following theorem:

Theorem 1.

The mean deviation about the mean of the BKw-E distribution is in the form

$$D\left(\mu \right)=2\sum _{i=0}^{\infty }{\psi }_i\left[\mu -\frac{1}{\lambda (i+1)}(1-e^{-\mu \lambda (i+1)})\right].$$

Proof. 

The mean deviation about the mean can be defined as

$$\begin{array}{cc}D\left(\mu \right)\hfill & =E\left(\right|x-\mu \left|\right)={\int }_0^{\infty }|x-\mu |f\left(x\right)dx\hfill \\ \hfill & ={\int }_0^{\mu }(\mu -x)f\left(x\right)dx+{\int }_{\mu }^{\infty }(x-\mu )f\left(x\right)\hfill \\ \hfill & =2{\int }_0^{\mu }(\mu -x)f\left(x\right)dx\hfill \\ \hfill & =2\mu F\left(\mu \right)-2{\int }_0^{\mu }xF\left(x\right)dx\hfill \\ \hfill & =2{\int }_0^{\mu }F\left(x\right)dx·\hfill \end{array}$$

(24)

By using the cdf in Equation (10), the mean deviation of the BKw-E distribution can be derived as:

$$D\left(\mu \right)=2\sum _{i=0}^{\infty }{\psi }_i{\int }_0^{\mu }\left[1-e^{-\lambda (i+1)x}\right]dx$$

$$\begin{array}{cc}=& 2\sum _{i=0}^{\infty }{\psi }_i\times \left[{\int }_0^{\mu }dx-{\int }_0^{\mu }{e}^{-\lambda (i+1)x}dx\right].\hfill \end{array}$$

Then, the mean deviation about the mean is given by:

$$D\left(\mu \right)=2\sum _{i=0}^{\infty }{\psi }_i\left[\mu -\frac{1}{\lambda (i+1)}(1-e^{-\mu \lambda (i+1)})\right]·$$

(25)

Hence, the theorem is proved. □

Next, the mean deviation about the median can be obtained from the following theorem:

Theorem 2.

The mean deviation about the median of BKw-E distribution is given by

$$D\left(med\right)=\mu -med+2\sum _{i=0}^{\infty }{\psi }_i\left[med-\frac{1}{\lambda (i+1)}(1-e^{-med\lambda (i+1)})\right].$$

Proof. 

The mean deviation from the median can be defined as

$$\begin{array}{ccc}\hfill D\left(med\right)& =& E\left(\right|x-med\left|\right)={\int }_0^{\infty }|x-med|f\left(x\right)dx\hfill \\ & =& 2{\int }_0^{med}(med-x)f\left(x\right)dx-{\int }_0^{med}(med-x)f\left(x\right)dx+{\int }_{med}^{\infty }(x-med)f\left(x\right)dx\hfill \\ & =& 2{\int }_0^{med}(med-x)f\left(x\right)dx+{\int }_0^{\infty }(x-med)f\left(x\right)dx\hfill \\ & =& \mu -2\left[medF\left(x\right)-{\int }_0^{med}F\left(x\right)dx\right]\hfill \\ & =& \mu -med+2{\int }_0^{med}F\left(x\right)dx.\hfill \end{array}$$

By using the cdf in Equation (10), we obtain

$$D\left(med\right)=\mu -med+2\sum _{i=0}^{\infty }{\psi }_i{\int }_0^{med}\left[1-e^{-\lambda (i+1)x}\right]dx·$$

(26)

The third term in Equation (26) is the same as that in Equation (24), with upper limit $med$ instead of $\mu$. Hence, the mean deviation about the median of BKw-E distribution can be obtained as the following:

$$D\left(med\right)=\mu -med+2\sum _{i=0}^{\infty }{\psi }_i\left[med-\frac{1}{\lambda (i+1)}(1-e^{-med\lambda (i+1)})\right].$$

(27)

Hence, the theorem is proved. □

4. Rényi Entropy

The Rényi entropy was introduced by [18], and is one of the several generalizations of Shannon’s entropy [19]. The entropy of a random variable is a measure of uncertainty or randomness of a system. In addition, the theory of entropy has been successfully used in various of applications such as in information theory, engineering, and physics [20]. It is useful in describing a nonlinear dynamical or disordered system [21], and in statistics for testing hypotheses in parametric models and lifetime distributions (see [18,22]).

Theorem 3.

The Rényi entropy of order β for the BKw-E distribution is in the form

$$\begin{array}{c}{R}_{\beta }\left(X\right)=\frac{1}{1-\beta }log\left[{\frac{a\lambda b}{B(l,m)}}^{\beta }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right)\times \left(\genfrac{}{}{0pt}{}{bk+\beta (mb-1)}{j}\right)\left(\genfrac{}{}{0pt}{}{aj+\beta (a-1)}{i}\right)\frac{{(-1)}^{k+j+i}}{\lambda (i+\beta )}\right].\end{array}$$

(28)

Proof. 

For the density function $f\left(x\right)$, the Rényi entropy is defined as:

$$R_{\beta }\left(X\right)=\frac{1}{1-\beta }log\left[J\left(\beta \right)\right],$$

(29)

where $J\left(\beta \right)={\int }_0^{\infty }{f}^{\beta }\left(x\right)dx$, $\beta >0$ and $\beta \ne 1$. By using the pdf in Equation (5), we have

$$\begin{array}{c}J\left(\beta \right)={\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }{\int }_0^{\infty }{e}^{-\beta \lambda x}{(1-e^{-\lambda x})}^{\beta (a-1)}{\left[1-{(1-e^{-\lambda x})}^a\right]}^{\beta (mb-1)}{\left[1-{\left[1-{(1-e^{-\lambda x})}^a\right]}^b\right]}^{\beta (l-1)}dx.\end{array}$$

Now, by applying the binomial expansion, we get

$$\begin{array}{c}J\left(\beta \right)={\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right){(-1)}^k\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right){\int }_0^{\infty }{e}^{-\beta \lambda x}{(1-e^{-\lambda x})}^{\beta (a-1)}\\ \times {\left[1-{(1-e^{-\lambda x})}^a\right]}^{bk+\beta (mb-1)}dx.\end{array}$$

Using the binomial expansion again, we have

$$\begin{array}{c}J\left(\beta \right)={\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right)\left(\genfrac{}{}{0pt}{}{bk+\beta (mb-1)}{j}\right)\left(\genfrac{}{}{0pt}{}{aj+\beta (a-1)}{i}\right){(-1)}^{k+j+i}{\int }_0^{\infty }{e}^{-\lambda (I+\beta )x}dx.\end{array}$$

After integrating, we get

$$J\left(\beta \right)={\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right)\left(\genfrac{}{}{0pt}{}{bk+\beta (mb-1)}{j}\right)\left(\genfrac{}{}{0pt}{}{aj+\beta (a-1)}{i}\right)\frac{{(-1)}^{k+j+i}}{\lambda (i+\beta )}.$$

Then, by taking the logarithm, we have

$$\begin{array}{c}log\left[J\left(\beta \right)\right]=log\left[{\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right)\left(\genfrac{}{}{0pt}{}{bk+\beta (mb-1)}{j}\right)\left(\genfrac{}{}{0pt}{}{aj+\beta (a-1)}{i}\right)\frac{{(-1)}^{k+j+i}}{\lambda (i+\beta )}\right].\end{array}$$

(30)

Substituting Equation (30) into (29), we get the Rényi entropy for BKw-E as

$$R_{\beta }\left(X\right)=\frac{1}{1-\beta }log\left[{\left(\frac{a\lambda b}{B(l,m)}\right)}^{\beta }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{\beta (l-1)}{k}\right)\left(\genfrac{}{}{0pt}{}{bk+\beta (mb-1)}{j}\right)\left(\genfrac{}{}{0pt}{}{\alpha j+\beta (a-1)}{i}\right)\frac{{(-1)}^{k+j+i}}{\lambda (i+\beta )}\right].$$

Hence, the theorem is proved. □

5. Order Statistics

Considering that $x_{\left(1\right)}\le x_{\left(2\right)}\le x_{\left(3\right)}\le \dots \le x_{\left(n\right)}$ denotes the order statistic of a random sample $X_1,X_2,X_3,\dots ,X_n$ from the BKw-E distribution with cdf $F\left(x\right)$ and pdf $f\left(x\right)$, the pdf of $X_{\left(r\right)}$ can be written as (see [23])

$$f_r\left(x_{\left(r\right)}\right)=\frac{n!}{(r-1)!(n-r)!}f\left(x\right){\left[F\left(x\right)\right]}^{r-1}{\left[1-F\left(x\right)\right]}^{n-r}.$$

(31)

By using the pdf in Equation (7) and the cdf in the Equation (10), we get

$$\begin{array}{cc}\begin{array}{c}{f}_r\left(x_{\left(r\right)}\right)=\frac{n!}{(r-1)!(n-r)!}\lambda \sum _{i=0}^{\infty }(i+1){\psi }_i{e}^{-\lambda (i+1)x_{\left(r\right)}}{\left[\sum _{i=0}^{\infty }{\psi }_i\left[1-e^{-\lambda (i+1)x_{\left(r\right)}}\right]\right]}^{r-1}\\ \times {\left[1-\left[\sum _{i=0}^{\infty }{\psi }_i\left[1-e^{-\lambda (i+1)x_{\left(r\right)}}\right]\right]\right]}^{n-r},\end{array}& x_{\left(r\right)}>0.\end{array}$$

(32)

The pdf of the largest order statistic $X_{\left(n\right)}$ is given by

$$f_n\left(x_{\left(r\right)}\right)=n\lambda \sum _{i=0}^{\infty }(i+1){\psi }_i{e}^{-\lambda (i+1)x_{\left(n\right)}}{\left[\sum _{i=0}^{\infty }{\psi }_i\left[1-e^{-\lambda (i+1)x_{\left(n\right)}}\right]\right]}^{n-1},x_{\left(n\right)}>0.$$

(33)

The pdf of the smallest order statistic $X_{\left(1\right)}$ is

$$f_1\left(x_{\left(1\right)}\right)=n\lambda \sum _{i=0}^{\infty }(i+1){\psi }_i{e}^{-\lambda (i+1)x_{\left(1\right)}}{\left[1-\left[\sum _{i=0}^{\infty }{\psi }_i\left[1-e^{-\lambda (i+1)x_{\left(1\right)}}\right]\right]\right]}^{n-1},x_{\left(1\right)}>0.$$

(34)

6. Application with a Real Data Set

In this section, we present an example of a real data set. A comparison between the presented model (BKw-E) distribution and other sub-models is provided, using the maximum likelihood method of estimation (MLEs) to estimate the parameters. To establish that our model could be superior, we compared the models employing the Akaike information criterion (AIC), corrected Akaike information criterion (CAIC), Hannan–Quinn information criterion (HQIC) (see, [13]), and the negative log-likelihood function under the considered models. The data set we considered (see [24]) represents 40 patients suffering from blood cancer (Leukemia) from one Ministry of Health hospital in Saudi Arabia and the order values in years.

Table 2 shows the estimates of the MLEs for the parameters of the presented models along with their (-2logl, AIC, CAIC, HQIC) values. According to the criteria used for the goodness of fit, the proposed model (BKw-E) fits such data better because it has the smallest values of (AIC, CAIC, HQIC). Furthermore, the cdfs of the fitted models with the cumulative frequency of observed data in Figure 4 indicate that the BKw-E distribution provides a closer fit to the observed data set.

Table 2. The MLEs for the parameters of the models, log-likelihood, Akaike information criterion (AIC), corrected Akaike information criterion (CAIC), and Hannan–Quinn information criterion (HQIC) of patients suffering from blood cancer.

Model	MLEs		−2logL	AIC	CAIC	HQIC
Exp	$\widehat{\lambda }$ = 0.321		170.917	172.917	173.022	173.528
ExpK-E	$\widehat{a}$ = 0.0250	$\widehat{b}$ = 0.227	145.405	153.405	154.548	155.847
	$\widehat{\lambda }$ = 3.005	$\widehat{l}$ = 11.125
Kw-E	$\widehat{a}$ = 2.959	$\widehat{b}$ = 5.619	142.758	148.758	149.414	150.58
	$\widehat{\lambda }$ = 0.227
BKw-E	$\widehat{a}$ = 10.138	$\widehat{b}$ = 4.420	132.04	142.04	143.804	145.093
	$\widehat{l}$ = 0.224	$\widehat{m}$ = 32.859
	$\widehat{\lambda }$ = 0.189

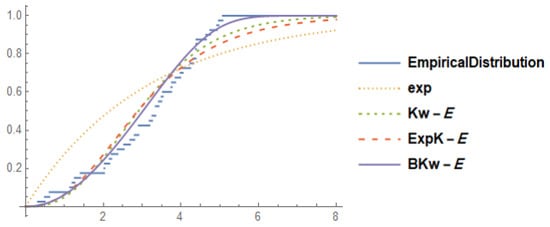
Figure 4. Plot of the cdf for Exp, Kumaraswamy exponential distribution (Kw-E), exponentiated Kumaraswamy exponential distribution (ExpK-E), BKw-E, and the empirical distribution.

7. Conclusions

We introduced the five-parameter beta Kumaraswamy exponential (BKw-E) distribution, which generalizes the beta generalized exponential distribution proposed by [12] and the beta exponential distribution which was discussed by [11]. In addition, the BKw-E distribution has sub-models, such as the Kumaraswamy exponential introduced by [8] and the exponentiated Kumaraswamy exponential discussed by [9]. For our study, we provided the pdf, the cdf, and the shape of the hazard function. The shape of the pdf of the BKw-E distribution is uni-modal and positively skewed, while the hazard function of the BKw-E distribution is increasing. In addition, some important properties of the Bkw-E—such as the moments, mode, and median—are proven. The order statistics were provided, as well as the Rényi entropy, which is suitable in many applications. Finally, a real data set was presented using the maximum likelihood estimation; we can show that the proposed model is a good fit for lifetime data.