Abstract
The aim of this work is to completely solve the reversibility problem for symmetric linear cellular automata with radius and null boundary conditions. The main result obtained is the explicit computation of the local transition functions of the inverse cellular automata. This allows introduction of possible and interesting applications in digital image encryption.
1. Introduction and Preliminaries
The notion of cellular automaton was originated by Von Neumann and S. Ulam [1], and it can be defined as a simple computational model capable of simulating complex phenomena. This concept was popularized in the seventies by M. Gardner with John Conway’s Game of Life [2], and was brought into academic fashion by S. Wolfram [3] in the eighties. Since then, cellular automata have been extensively analyzed, and not only from a theoretical perspective [4,5]; they have also been used to simulate different phenomena [6,7,8].
One can find different definitions of cellular automaton depending on the perspective [9]. J. Kari defines them as ultradiscrete dynamical systems that consist of a finite collection of state automata (called cells) that are endowed with a state at every time step and these states change according to a local transition function. The variables of this function are the states at the previous step of time of the cell itself and its neighborhood.
More precisely, a cellular automaton over the finite field is given by a 3-uplet , such that is the cellular space, f is the local transition function, and is the neighborhood. Specifically, is formed by n cells that are arranged uniformly in a one-dimensional lattice. Each of them is endowed with a state from that changes at every step of time according to a local transition function f. Specifically, if stands for the state of the i-th cell at time t, then
where , and represent the neighborhood of the i-th cell. As the cellular space is constituted by n cells (the cellular space is finite), some type of boundary conditions must be stated in order to define the dynamics of the system in a proper way. This work deals with null boundary conditions, that is, for each t when .
The cellular automaton is linear when its local transition function f is linear. Moreover, a linear cellular automaton is said to be symmetric of radius r if . Consequently, its local transition function is
This cellular automaton will be denoted by . Note that we are dealing with 1D boolean cellular automata.
If is the global configuration of at step of time t, the local transition function leads to global transition function F, such that
The graphical illustration of the global evolution of a CA can be obtained using the simple evolution diagram and the global state transition diagram. The evolution diagram is a two-dimensional grid, where the rows represent the configurations of the cellular automaton (that are sequentially computed from the initial configuration) such that the color of each site is black for state 1 or white for state 0. On the other hand, the global state transition diagram can be defined as a directed graph whose nodes represent the configurations of the cellular automaton and whose edges represent transformations .
If the global transition function F is bijective, the cellular automaton is said to be reversible. Thus, the evolution backwards can be computed by means of the inverse cellular automaton whose global transition function is [10,11]. Reversibility is probably the most studied property of cellular automata; not only have several theoretical works appeared (see, for example, works by the authors of [12,13,14,15,16]), but different applications based on this property have also been proposed (see, for example, work by the authors of [17,18,19,20]).
The reversibility problem for symmetric linear cellular automata endowed with periodic boundary conditions has been tackled in several works [21,22,23,24] and completely solved by I. Siap, H. Akin, and M.E. Koroglu [25] and the explicit expressions for the inverse of a reversible cellular automaton with -cyclic rule are given in the work by the authors of [23]. On the other hand, in the case of null boundary conditions, the cases and have been tackled in works by the authors of [26,27]; moreover, in the work by the authors of [28], it is shown that the symmetric linear cellular automaton of radius r, whose cellular space is formed by cells, is reversible.
The main objective of this work is to completely solve the reversibility problem for the symmetric linear cellular automaton with n cells and radius , which is denoted by . Specifically, the explicit expressions of the local transition matrices of the inverse cellular automata are computed, and an illustrative application of this result to the encryption of digital images is proposed.
The rest of the paper is organized as follows. Section 2 is devoted to introduce the particular characteristics of symmetric cellular automata with radius and endowed with null boundary conditions; the reversibility problem is tackled in Section 3. In Section 4, some potential applications in the field of digital image encryption are shown. Finally, the conclusions are presented in Section 5.
2. The Symmetric Linear Cellular Automata with
The explicit expression of the local transition function of the symmetric cellular automaton with radius and n cells, , is as follows.
If , is the global configuration of the cellular automaton at step of time t, then its global evolution is given by
where is the local transition matrix. If null boundary conditions are considered, then is a band matrix of order n with bandwidth whose coefficients inside the band are all equal to 1, that is,
In Figure 1a, the evolution state diagram of the cellular automaton is shown when the initial configuration is given by . Furthermore, in Figure 1b, the evolution state diagram associated to is introduced when the initial configuration is randomly defined.

Figure 1.
(a) Evolution diagram of when . (b) Evolution diagram of when the initial configuration is selected at random.
3. The Reversibility Problem
Taking into account the notion of reversibility and the interpretation of the dynamics of in terms of linear algebra, this cellular automaton is said to be reversible when its local transition matrix is nonsingular, and consequently its inverse is the local transition matrix of the inverse cellular automaton. Consequently, in this case, the order and characteristics of the transition matrix determine the reversibility of the cellular automata. For example, and are reversible, whereas is not. In Figure 2 and Figure 3, the global state transition diagrams of and are shown; note that as they are reversible, each configuration has a unique predecessor. In this case, each configuration is represented by the number . Conversely, is not reversible, and some configurations in the global state transition diagram have more than one predecessor (see Figure 4).

Figure 2.
Global state transition diagram of .

Figure 3.
Global state transition diagram of .
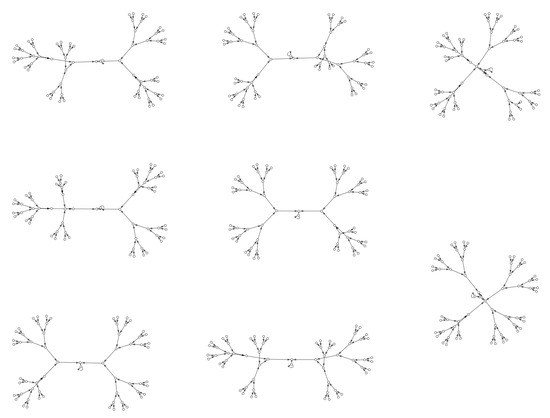
Figure 4.
Global state transition diagram of .
Specifically, the following result holds.
Theorem 1.
The symmetric linear cellular automaton with , , is reversible if and only if or , with .
Proof.
Assume that the arithmetic is performed in and set the transition matrix of . From Lemma (2) of the work by the authors of [28], it is . Consequently, if with and , then . A simple computation shows that
Consequently,
thus finishing, taking . □
Furthermore, it is possible to compute in an explicit way the expression of the inverse cellular automata as follows.
Theorem 2.
(1) The local transition matrix of the inverse cellular automaton when is
where
(2) The local transition matrix of the inverse cellular automaton when is
where
Proof.
(1) For the sake of simplicity, we can suppose that where is defined as follows.
On the other hand, set
the local transition matrix of the CA , such that
with
Then we have to proof that .
First of all, suppose that such that , then
Now, we can distinguish five cases depending on the values of subindices i and j:
- (a)
- (b)
- Suppose that (the coefficients of the first upper diagonal of ), then from Equations (16) and (18) we obtain
- (c)
- If (the coefficients of the first lower diagonal of ), then, using Equations (16) and (18), the following result holds.
- (d)
- Now we will compute the coefficients with and corresponding to the entries below the first lower diagonal. In this case
- (e)
- Finally consider the coefficients above the first upper diagonal, with and . A similar calculus shows that
Consequently,
thus . In a similar way, one can check that .
(2) First of all, note that the local transition matrix of the inverse cellular automaton can be expressed in terms of a block matrix, as follows.
where . On the other hand, it is also easy to check that
where
To finish the proof, we have to prove that Note that
Now, by recurrence over k it is easy to check that
thus finishing. A similar argument shows that . □
4. A Potential Application to Image Encryption
This section introduces a possible application for image encryption of the theoretical results shown in Section 3. J. Fridrich proposed a methodology to design cryptographic protocols for digital images consisting of the successive application of two phases: the confusion phase and the diffusion phase [29]. In the confusion phase, all pixels of the digital image are permuted without changing its numerical color code (that is the histogram of the image remains constant), whereas, in the diffusion phase, the color code of each pixel is modified according to different mathematical techniques. This paradigm has been considered in the great majority of digital image encryption protocols proposed in the scientific literature (see, for example, works by the authors of [30,31]).
A gray-scale digital image can be interpreted as an matrix , where the coefficient represents the numeric value of the gray level assigned to pixel . On the other hand, an RGB color digital image is defined by means of an array of dimension , such that . In this case, the coordinates of denote the intensity of each color (red, green, and blue, respectively) as an integer between 0 and 255.
The reversibility of (whose global transition function is denoted by ) shown in the last section allows defining a byte-level transformation that could be used as a part of the diffusion phase of an encryption algorithm for both gray-scale and RGB color digital images. It is defined as follows.
- (a)
- If stands for the matrix associated to a gray-scale image, then the transformed image is defined by the matrix , is the decimal expression associated to , is the binary expression (one byte) associated to , and .
- (b)
- If is the array representing an RGB color digital image, then determines the transformed digital image, such that withwhere and are the binary expressions of , and , and , respectively.
In Figure 5 and Figure 6, two illustrative examples of this technique are shown. As the global state transition diagram of exhibits 16 cycles of length 14, four cycles of length 7, and four time-invariant configurations (see Figure 3), is a periodic transformation of period 14. As a consequence, the original image is recovered after 14 iterations.
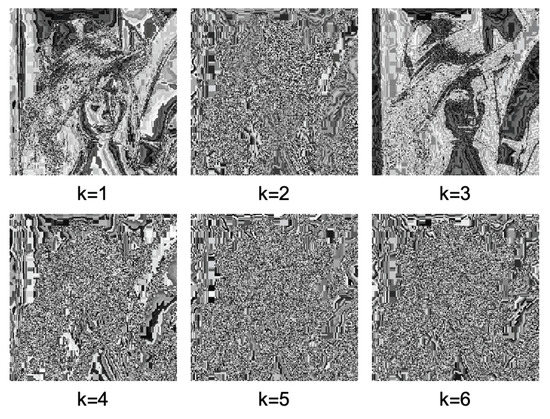

Figure 5.
Gray-scale images obtained by applying .


Figure 6.
Color images obtained by applying .
It is important to note that this transformation by itself is not secure against cryptanalysis (see, for example, the homogeneous patterns exhibited by some transformed images in the examples). In this sense, it is necessary to include it as a part of a more complex algorithm.
5. Conclusions
In this work, the reversibility problem for symmetric linear cellular automata with n cells, radius , and state set has been completely solved. Specifically, it is shown that these 1D boolean cellular automata are reversible when or with , and, in these cases, the explicit expressions of the inverse cellular automata are derived in terms of the local transition matrices.
Furthermore, a potential application to Cryptography has been presented. Specifically, these reversible cellular automata can be used as additional transformations to be applied in the diffusion phase of a digital image encryption algorithm.
Future work aims at exploring other applications of reversible cellular automata, such as voting systems, data compression, etc.
Author Contributions
A.M.d.R., R.C.V., and D.H.S. conceived and designed the study and A.M.d.R. performed the computational implementations. The paper has been written, edited, and revised by all authors.
Funding
This research was funded by Ministerio de Ciencia, Innovación y Universidades (MCIU, Spain), Agencia Estatal de Investigación (AEI, Spain), and Fondo Europeo de Desarrollo Regional (FEDER, UE) under project TIN2017-84844-C2-2-R (MAGERAN) and project SA054G18 supported by Consejería de Educación (Junta de Castilla y León, Spain).
Acknowledgments
The authors want to thank the anonymous referees for their valuable suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Von Neumann, J.; Burks, A.W. Theory of Self-Reproducing Automata; University of Illinois Press: Urbana, IL, USA; London, UK, 1966. [Google Scholar]
- Gardner, M. Mathematical games—The fantastic combinations of John Conway’s new solitaire game “life”. Sci. Am. 1970, 223, 120–123. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular Automata and Complexity: Collected Papers; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Ilachinski, A. Cellular Automata: A Discrete Universe; World Scientific: Singapore, 2001. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media Inc.: Champaign, IL, USA, 2002. [Google Scholar]
- Chopard, B.; Droz, M. Cellular Automata Modeling of Physical Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gutowitz, H. (Ed.) Cellular Automata: Theory and Experiment; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Sarkar, P. A brief history of cellular automata. ACM Comput. Surv. 2000, 32, 80–107. [Google Scholar] [CrossRef]
- Bhattacharjee, K.; Naskar, N.; Roy, S.; Das, S. A survey of cellular automata: Types, dynamics, non-uniformity and applications. Nat. Comput. 2018, 1–29. [Google Scholar] [CrossRef]
- Toffoli, M.; Margolus, N. Invertible cellular automata: A review. Phys. D 1990, 45, 229–253. [Google Scholar] [CrossRef]
- Morita, K. Reversible computing and cellular automata—A survey. Theor. Comput. Sci. 2008, 395, 101–131. [Google Scholar] [CrossRef]
- Seck-Tuoh-Mora, J.C.; Medina-Marin, J.; Hernandez-Romero, N.; Martinez, G.J.; Barragan-Vite, I. Welch sets for random generation and representation of reversible one-dimensional cellular automata. Inform. Sci. 2017, 382–383, 81–95. [Google Scholar] [CrossRef]
- Di Lena, P.; Margara, L. Nondeterministic Cellular Automata. Inform. Sci. 2014, 287, 13–25. [Google Scholar] [CrossRef]
- Gajardo, A.; Kari, J.; Moreira, A. On time-symmetry in cellular automata. J. Comput. Syst. Sci. 2012, 78, 1115–1126. [Google Scholar] [CrossRef]
- Kari, J. Reversible Cellular Automata: From Fundamental Classical Results to Recent Developments. New Gener. Comput. 2018, 36, 145–172. [Google Scholar] [CrossRef]
- MacLean, S.; Montalva-Medel, M.; Goles, E. Block invariance and reversibility of one dimensional cellular automata. Adv. Appl. Math. 2019, 105, 83–101. [Google Scholar] [CrossRef]
- Uguz, S.; Akin, H.; Siap, I.; Sahin, U. On the irreversibility of Moore cellular automata over the ternary field and image application. Appl. Math. Model. 2016, 17–18, 8017–8032. [Google Scholar] [CrossRef]
- Temiz, F.; Sah, F.; Akin, H. Reversibility of a Family of 2D Cellular Automata Hybridized by Diamond and Cross Rules Over Finite Fields and an Application to Visual Cryptography. J. Cell. Autom. 2019, 14, 241–262. [Google Scholar]
- Su, Y.R.; Wo, Y.; Han, G.Q. Reversible cellular automata image encryption for similarity search. Signal Process. Image Commun. 2019, 72, 134–147. [Google Scholar] [CrossRef]
- Martín del Rey, A. A multi-secret sharing scheme for 3D solid objects. Expert Syst. Appl. 2015, 42, 2114–2120. [Google Scholar]
- Chang, C.-H.; Chang, H. On the Bernoulli automorphism of reversible linear cellular automata. Inform. Sci. 2016, 345, 217–225. [Google Scholar] [CrossRef]
- Cinkir, Z.; Akin, H.; Siap, I. Reversibility of 1D Cellular Automata with Periodic Boundary over Finite Fields . J. Stat. Phys. 2011, 143, 807–823. [Google Scholar] [CrossRef]
- Hernández Serrano, D.; Martín del Rey, A. A closed formula for the inverse of a reversible cellular automaton with (2R + 1)-cyclic rule. Appl. Math. Comput. 2019, 357, 23–34. [Google Scholar]
- Hernández Encinas, L.; Martín del Rey, A. Inverse rules of ECA with rule number 150. Appl. Math. Comput. 2007, 189, 1782–1786. [Google Scholar]
- Siap, I.; Akin, H.; Koroglu, M.E. The reversibility of (2r + 1)-cyclic rule cellular automata. TWMS J. Pure Appl. Math. 2013, 4, 215–225. [Google Scholar]
- Martín del Rey, A.; Rodríguez Sánchez, G. On the reversibility of 150 Wolfram cellular automata. Int. J. Mod. Phys. C 2006, 17, 975–984. [Google Scholar]
- Martín del Rey, A.; Rodríguez Sánchez, G. Reversibility of linear cellular automata. Appl. Math. Comput. 2011, 217, 8360–8366. [Google Scholar]
- Martín del Rey, A.; Rodríguez Sánchez, G. Reversibility of a symmetric linear cellular automata. Int. J. Mod. Phys. C 2009, 20, 1081–1086. [Google Scholar]
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. A Comprehensive Review on Image Encryption Techniques. Arch. Comput. Methods Eng. 2018. [Google Scholar] [CrossRef]
- Ghadirli, H.M.; Nodehi, A.; Enayatifar, R. An overwiew of encryption algorithms in color images. Signal Process. 2019, 164, 163–185. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).