New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions

Abstract

The generalized time fractional Kolmogorov-Petrovsky-Piskunov equation (FKPP), $D_t^{\alpha }\omega (x,t)=a(x,t)$ $D_{xx}\omega (x,t)+F\left(\omega (x,t)\right)$, which plays an important role in engineering, chemical reaction problem is proposed by Caputo fractional order derivative sense. In this paper, we develop a framework wavelet, including shift Chebyshev polynomial of the first kind as a mother wavelet, and also construct some operational matrices that represent Caputo fractional derivative to obtain analytical solutions for FKPP equation with three different types of Initial Boundary conditions (Dirichlet, Dirichlet-Neumann, and Neumann-Robin). Our results shown that the Chebyshev wavelet is a powerful method, due to its simplicity, efficiency in analytical approximations, and its fast convergence. The comparison of the Chebyshev wavelet results indicates that the proposed method not only gives satisfactory results but also do not need large amount of CPU times.

1. Introduction

A generalization of differentiation and integration with arbitrary (non-integer) order which is called fractional calculus has gained considerable popularity and during the past almost three decades, mainly due to its attractive applications in numerous diverse and widespread fields of sciences and engineering [1,2,3]. The concepts of fractional derivatives are to incorporate nonlocal and systematic memory effects through fractional order space and time derivatives, which are powerful features that allow modeling of phenomena across multiple time and space scales without having to partition the problem into smaller compartment [4]. Operators of fractional differentiation and integration have been used in the hydraulics of dam, diffusion problems, and waves in liquids and gasses. Many systems can be described more accurately and more conveniently by fractional differential equations. The main advantage of the fractional calculus is that the fractional derivative provides an excellent instrument for the description of memory and hereditary properties of various materials and processes.

Fractional derivatives have been widely used in mathematical modeling of reaction-diffusion systems, which explain how the concentration of one or more substances distributed in space changes under the influence of two processes: local chemical reactions in which the substances are transformed into each other and diffusion which causes the substances to spread out over a surface in space.

Analytical and approximate series solutions for the nonlinear fractional differential equations are fundamental importance for seeking solutions of the most complex phenomena that are modeled. There are many methods that have also been proposing for solving analytical and approximate series solutions: the transform methods, including Laplace, Fourier, and Mellin transforms [5]; the Tau method [6]; the Adomian decomposition method [7]; the variational iteration method [7,8]; the Sumudu decomposition method [9]; the blockpulse functions [10]; shifted Chebyshev polynomials [11]; shifted Legendre polynomials [12]; Chebyshev wavelets [13,14]; and Legendre wavelets [15].

The Chebyshev wavelet method is one powerful tool by employing the fundamental concept of wavelets and shifted Chebyshev polynomials. Approximations through Chebyshev wavelet effectively handle singularities in the problem. It is fast convergence and not undergo from the instability problems related to other numerical methods. Y. Chen et al. proposed The Chebyshev wavelet method by solving fractional integral and differential equations of Bratu-type [13]. A.K. Gupta and S.S. Ray studied the solution of fractional fifth-order Sawada-Kotera equation using second kind Chebyshev wavelet method [14] and many others [16,17,18,19].

In this paper an efficient mathematical tool the Chebyshev wavelet collocation method, introduced by some operational matrices for fractional derivative and integration is successfully applied to obtain the analytical solution of the generalize time fractional Kolmogorov-Petrovsky-Piskunov equation (FKPP) of a volume chemical reaction:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=a(x,t)\frac{{\partial }^2\omega }{\partial x^2}+F\left(\omega \right),$$

(1)

subjected to the initial condition

$$\omega (x,0)=f\left(x\right),$$

(2)

and three types of boundary conditions:

$$\begin{array}{ccc}\hfill \mathrm{Dirichlet}& :& \omega (0,t)=g_1\left(t\right),\omega (L,t)=g_2\left(t\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \mathrm{Dirichlet}-\mathrm{Neumann}& :& D_t^{\alpha }\omega (0,t)=h_1\left(t\right),D_t^{\alpha }\omega (L,t)=h_2\left(t\right)\left(t\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \mathrm{Neumann}-\mathrm{Robin}& :& D_t^{\alpha }\omega (0,t)=h_1\left(t\right),D_t^{\alpha }\omega (L,t)+a\omega (L,t)=h_3\left(t\right)\left(t\right),\hfill \end{array}$$

(5)

where $\omega (x,t)$ represents the concentration of one substance, $a(x,t)$ is diffusion coefficients and several types of a rate, $F\left(\omega \right)$, of a volume chemical reactions such as power–law nonlinearities, $\left(d\omega \right(1-\omega \left)\right)$; exponential nonlinearities, $(b+d{e}^{-\lambda \omega })$; or logarithmic nonlinearities, $(dln(\omega +b\left)\right)$ [20].

2. Preliminaries

2.1. Fractional Calculus

In this section we introduce some necessary definitions, notations, and mathematical preliminaries of fractional calculus [21].

Definition 1.

The Riemann-Liouville fractional integral operator $I^{\alpha }$ of a function $f\left(t\right)$ and of order $\alpha >0$ is defined as

$$I_a^{\alpha }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_a^t{(t-\tau )}^{\alpha -1}f\left(\tau \right)d\tau ,\alpha >0and\alpha \in {\mathcal{R}}^{+},$$

(6)

where some properties of the operator $I^{\alpha }$ are provided as follows:

$$I^{\alpha }{I}^{\beta }f\left(t\right)=I^{\alpha +\beta }f\left(t\right),(\alpha >0,\beta >0),$$

(7)

$$I_a^{\alpha }{t}^{\gamma }=\frac{\mathsf{\Gamma }(1-\gamma )}{\mathsf{\Gamma }(1+\gamma +\alpha )}{t}^{\alpha +\gamma },(\gamma >-1).$$

(8)

Definition 2.

The Caputo fractional derivative operator $D_t^{\alpha }$ of a function $f\left(t\right)$ and of order $\alpha >0$ is defined as

$$\begin{array}{c}\hfill D_a^{\alpha }f\left(t\right)=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_a^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau ,n-1<\alpha <n.\end{array}$$

(9)

Some properties of Caputo fractional derivatives:

$$\begin{array}{ccc}\hfill D_a^{\alpha }C& =& 0,C\mathrm{is}\mathrm{a}\mathrm{constant}\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill D_a^{\alpha }{t}^{\beta }& =& \left\{\begin{array}{cc}0,\hfill & \beta <\lceil \alpha \rceil ,\hfill \\ \frac{\mathsf{\Gamma }(\beta +1)}{\mathsf{\Gamma }(\beta +1-\alpha )}{t}^{\beta -\alpha },\hfill & \beta \ge \lceil \alpha \rceil ,\hfill \end{array}\right.\hfill \end{array}$$

(11)

where $\beta \in \mathbb{N}\cup 0$, $\lfloor \alpha \rfloor$ denotes the largest integer less than or equal to $\alpha$ and $\lceil \alpha \rceil$ is the smallest integer greater than or equal to $\alpha$ and

$$I_a^{\alpha }\left(D_a^{\alpha }f\left(t\right)\right)=f\left(t\right)-\sum _{j=1}^n{\left[D_a^{\alpha -j}f\left(t\right)\right]}_{t=a}\frac{{(t-a)}^{\alpha -j}}{\mathsf{\Gamma }(\alpha -j+1)}.$$

(12)

2.2. Chebyshev Wavelet Method

By a definition, Chebyshev wavelets consist of a family of functions that are coming from dilation and translation of a Chebyshev function named a mother wavelet, which n as a dilation parameter and m as translation parameter vary continuously. The following family of continuous Chebyshev wavelets may be obtained [22] and defined on the interval $[0,1)$ by

$$\begin{array}{c}\hfill {\psi }_{n,m}\left(t\right)=\left\{\begin{array}{c}{2}^{k/2}{\overline{T}}_m(2^{k}t-2n+1),\frac{n-1}{2^{k-1}}\le t<\frac{n}{2^{k-1}},\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(13)

where k can be determined as any positive integer and ${\overline{T}}_m\left(t\right)=\sqrt{\frac{2}{\pi }}{T}_m\left(t\right)$, $T_m\left(t\right),m=0,1,2,\dots ,M$ are the first kind Chebyshev polynomials of degree m defined on the interval $[-1,1]$ and satisfy the following recursive formula.

$$\begin{array}{ccc}\hfill T_0\left(t\right)& =& 1,\hfill \\ \hfill T_1\left(t\right)& =& 2t,\hfill \\ \hfill T_{m+1}\left(t\right)& =& 2t{T}_m\left(t\right)-T_{m-1}\left(t\right),m=1,2,3,\dots ,\hfill \end{array}$$

which are orthogonal with respect to the weight function $w\left(t\right)=\frac{1}{\sqrt{1-t^2}}$.

2.3. The Kronecker Product

The matrices A and B are given by

$$\begin{array}{c}\hfill A={\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]}_{m\times n},B={\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1q}\\ b_{21}& b_{22}& \cdots & b_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ b_{p1}& b_{p2}& \cdots & b_{pq}\end{array}\right]}_{p\times q}.\end{array}$$

The Kronecker product $A\otimes B$ is the $mp\times nq$ matrix and defined as [23,24]

$$\begin{array}{c}\hfill A\otimes B=\left[\begin{array}{cccc}{a}_{11}B& a_{12}B& \cdots & a_{1n}B\\ a_{21}B& a_{22}B& \cdots & a_{2n}B\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}B& a_{m2}B& \cdots & a_{mn}B\end{array}\right],\end{array}$$

where some Kronecker product properties are provided by

• $A\otimes \left(\alpha B\right)=\alpha (A\otimes B),$ where $\alpha$ is a scalar.
• $(A+B)\otimes C=(A\otimes C)+(B\otimes C)$.
• $A\otimes (B+C)=(A\otimes B)+(A\otimes C)$.
• $A\otimes (B\otimes C)=(A\otimes B)\otimes C$.
• $(A\otimes B)(C\otimes D)=AC\otimes BD$.
• $\overline{A\otimes B}=\overline{A}\otimes \overline{B}$.
• ${(A\otimes B)}^T=A^T\otimes B^T$,
  ${(A\otimes B)}^{\ast }=A^{\ast }\otimes B^{\ast }$ (${}^{\ast }$ denotes conjugate transpose).

2.4. Hadamard Product

Definition 3.

For two $m\times n$ matrices A and B,

$$\begin{array}{c}\hfill A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right],B=\left[\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right].\end{array}$$

The Hadamard product [25] $A\circ B$ is a matrix of the same dimension as the operands, with elements given by

$$\begin{array}{c}\hfill A\circ B=\left[\begin{array}{cccc}{a}_{11}{b}_{11}& a_{12}{b}_{12}& \cdots & a_{1n}{b}_{1n}\\ a_{21}{b}_{21}& a_{22}{b}_{22}& \cdots & a_{2n}{b}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{m1}& a_{m2}{b}_{m2}& \cdots & a_{mn}{b}_{mn}\end{array}\right],\end{array}$$

where some important properties are given by

1. 

$A\circ B=B\circ A$.

2. 

$A^T\circ B^T={(A\circ B)}^T$.

3. 

$(A\circ B){(C\circ D)}^T=A{C}^T\circ B{D}^T=A{D}^T\circ B{C}^T$.

4. 

$C\circ (A+B)=(C\circ A)+(C\circ B)$.

5. 

$\alpha (A\circ B)=\left(\alpha A\right)\circ B=A\circ \left(\alpha B\right)$.

3. Chebyshev Wavelets Approximation

An arbitrary function of two variables $\omega (x,t)\in L^2(\mathcal{R}\times \mathcal{R})$ defined over $[0,1)\times [0,1)$, can be approximated by Chebyshev wavelets basis as

$$\begin{array}{ccc}\hfill \omega (x,t)& \approx & \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}\sum _{n^{\prime }=1}^{2^{k-1}}\sum _{m^{\prime }=0}^{M-1}{a}_{nm{n}^{\prime }{m}^{\prime }}{\psi }_{nm}\left(x\right){\psi }_{n^{\prime }{m}^{\prime }}\left(t\right),\hfill \end{array}$$

(14)

where the Chebyshev wavelet ${\psi }_{n,m}(·)$ in (13). In the other hand, the function $\omega (x,t)$ in (14) can be rewritten a finite sum of entries of the spatial matrix as

$$\begin{array}{ccc}\hfill \omega (x,t)& =& \sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\xi }_{ij}(x,t),\hfill \end{array}$$

(15)

where ${\xi }_{ij}(x,t)$ are entries of the Hadamard-Kronecker product matrix $\mathbf{A}\circ \left(\mathsf{\Psi }\left(x\right)\otimes \mathsf{\Psi }\left(t\right)\right)$ and

$$\begin{array}{c}\hfill \mathbf{A}=\left[\begin{array}{cccc}{a}_{1010}& a_{1011}& \cdots & a_{1(M-1)1(M-1)}\\ a_{1020}& a_{1021}& \cdots & a_{1(M-1)2(M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ a_{2^{k-1}{02}^{k-1}0}& a_{2^{k-1}{02}^{k-1}1}& \cdots & a_{2^{k-1}(M-1)2^{k-1}(M-1)}\end{array}\right],\end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathsf{\Psi }\left(x\right)\otimes \mathsf{\Psi }\left(t\right)& =& \left[\begin{array}{cccc}{\psi }_{10}\left(x\right)\mathsf{\Psi }\left(t\right)& {\psi }_{11}\left(x\right)\mathsf{\Psi }\left(t\right)& \dots & {\psi }_{1(M-1)}\left(x\right)\mathsf{\Psi }\left(t\right)\\ {\psi }_{20}\left(x\right)\mathsf{\Psi }\left(t\right)& {\psi }_{21}\left(x\right)\mathsf{\Psi }\left(t\right)& \dots & {\psi }_{2(M-1)}\left(x\right)\mathsf{\Psi }\left(t\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\psi }_{2^{k-1}0}\left(x\right)\mathsf{\Psi }\left(t\right)& {\psi }_{2^{k-1}1}\left(x\right)\mathsf{\Psi }\left(t\right)& \cdots & {\psi }_{2^{k-1}(M-1)}\left(x\right)\mathsf{\Psi }\left(t\right)\end{array}\right],\hfill \end{array}$$

(17)

where

$$\begin{array}{c}\hfill \mathsf{\Psi }(·)={\left[\begin{array}{cccc}{\psi }_{10}(·)& {\psi }_{11}(·)& \dots & {\psi }_{1(M-1)}(·)\\ {\psi }_{20}(·)& {\psi }_{21}(·)& \dots & {\psi }_{2(M-1)}(·)\\ ⋮& ⋮& \ddots & ⋮\\ {\psi }_{2^{k-1}0}(·)& {\psi }_{2^{k-1}1}(·)& \cdots & {\psi }_{2^{k-1}(M-1)}(·)\end{array}\right]}_{2^{k-1}\times M}.\end{array}$$

(18)

The h-times integration of ${\psi }_{n,m}\left(t\right)$ in (13) can be expressed as follows

$$\begin{array}{c}\hfill I_0^h{\psi }_{n,m}\left(t\right)=\left\{\begin{array}{c}{2}^{k/2}\underset{h}{\underbrace{{\int }_0^t\cdots {\int }_0^t}}{\overline{T}}_m(2^k\tau -2n+1)d\tau \cdots d\tau ,\hfill \\ \frac{n-1}{2^{k-1}}\le \tau <\frac{n}{2^{k-1}},\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(19)

$h=1,2,3,\dots$, where h-times integration of Chebyshev wavelets matrix is obtained by

$$\begin{array}{c}\hfill P^h\left(\mathsf{\Psi }(·)\right)=\left[\begin{array}{cccc}{I}_0^h{\psi }_{10}(·)& I_0^h{\psi }_{11}(·)& \dots & I_0^h{\psi }_{1M-1}(·)\\ I_0^h{\psi }_{20}(·)& I_0^h{\psi }_{21}(·)& \dots & I_0^h{\psi }_{2M-1}(·)\\ ⋮& ⋮& \ddots & ⋮\\ I_0^h{\psi }_{2^{k-1}0}(·)& I_0^h{\psi }_{2^{k-1}1}(·)& \cdots & I_0^h{\psi }_{2^{k-1}M-1}(·)\end{array}\right]\end{array}$$

(20)

Riemann-Liouville fractional integration order $\alpha$ of ${\psi }_{n,m}\left(t\right)$ in (13) can be expressed as follows

$$\begin{array}{c}\hfill I_a^{\alpha }{\psi }_{n,m}\left(t\right)=\left\{\begin{array}{c}{2}^{k/2}{I}_a^{\alpha }{\overline{T}}_m(2^{k}t-2n+1),\frac{n-1}{2^{k-1}}\le t<\frac{n}{2^{k-1}},\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(21)

so fractional integration with order $\alpha$ of Chebyshev wavelets matrix becomes

$$\begin{array}{c}\hfill P^{\alpha }\left(\mathsf{\Psi }(·)\right)=\left[\begin{array}{cccc}{I}_a^{\alpha }{\psi }_{10}(·)& I_a^{\alpha }{\psi }_{11}(·)& \dots & I_a^{\alpha }{\psi }_{1M-1}(·)\\ I_a^{\alpha }{\psi }_{20}(·)& I_a^{\alpha }{\psi }_{21}(·)& \dots & I_a^{\alpha }{\psi }_{2M-1}(·)\\ ⋮& ⋮& \ddots & ⋮\\ I_a^{\alpha }{\psi }_{2^{k-1}0}(·)& I_a^{\alpha }{\psi }_{2^{k-1}1}(·)& \cdots & I_a^{\alpha }{\psi }_{2^{k-1}M-1}(·)\end{array}\right].\end{array}$$

(22)

The h-times differentiation of Chebyshev wavelets matrix is obtained by

$$\begin{array}{c}\hfill D^h\left(\mathsf{\Psi }(·)\right)=\left[\begin{array}{cccc}{D}^h{\psi }_{10}(·)& D^h{\psi }_{11}(·)& \dots & D^h{\psi }_{1M-1}(·)\\ D^h{\psi }_{20}(·)& D^h{\psi }_{21}(·)& \dots & D^h{\psi }_{2M-1}(·)\\ ⋮& ⋮& \ddots & ⋮\\ D^h{\psi }_{2^{k-1}0}(·)& D^h{\psi }_{2^{k-1}1}(·)& \cdots & D^h{\psi }_{2^{k-1}M-1}(·)\end{array}\right]\end{array}$$

(23)

and the fractional differentiation with order $\alpha$ of Chebyshev wavelets matrix is given by

$$\begin{array}{c}\hfill D^{\alpha }\left(\mathsf{\Psi }(·)\right)=\left[\begin{array}{cccc}{D}_a^{\left(\alpha \right)}{\psi }_{10}(·)& D_a^{\left(\alpha \right)}{\psi }_{11}(·)& \dots & D_a^{\left(\alpha \right)}{\psi }_{1M-1}(·)\\ D_a^{\left(\alpha \right)}{\psi }_{20}(·)& D_a^{\left(\alpha \right)}{\psi }_{21}(·)& \dots & D_a^{\left(\alpha \right)}{\psi }_{2M-1}(·)\\ ⋮& ⋮& \ddots & ⋮\\ D_a^{\left(\alpha \right)}{\psi }_{2^{k-1}0}(·)& D_a^{\left(\alpha \right)}{\psi }_{2^{k-1}1}(·)& \cdots & D_a^{\left(\alpha \right)}{\psi }_{2^{k-1}M-1}(·)\end{array}\right].\end{array}$$

(24)

4. Description of the Proposed Method

In this section, we applied a fundamental solution of the Chebyshev wavelet method for generalized time fractional Kolmogorov-Petrovsky-Piskunov equation (FKPP) with the initial condition and three types of boundary conditions.

Case 1: the time fractional KPP equation with Dirichlet boundary conditions:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=a(x,t)\frac{{\partial }^2\omega }{\partial x^2}+F\left(\omega \right),$$

(25)

subjected to the initial and boundary conditions

$$\begin{array}{ccc}\hfill \omega (x,0)& =& f\left(x\right),\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill \omega (0,t)& =& g_1\left(t\right),\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill \omega (1,t)& =& g_2\left(t\right),\hfill \end{array}$$

(28)

where $\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}$ denotes the Caputo fractional derivative of the function $\omega (x,t)$. The function $f\left(x\right)$, $g_1\left(t\right)$ and $g_2\left(t\right)$ are continuous on $[0,1]$. Now, by performing Chebyshev wavelets method on (25).

Let $\omega (x,t)={\sum }_{i=1}^{2^{2k-2}}{\sum }_{j=1}^{M^2}{\mathsf{\Omega }}_{ij}(x,t)$ be a solution of (25), where ${\mathsf{\Omega }}_{ij}(x,t)$ are entries of the $2^{2k-2}\times M^2$ the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$. To determine the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$, we first assume that

$$\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left(\frac{{\partial }^2\overline{\mathsf{\Omega }}(x,t)}{\partial x^2}\right)=\mathbf{A}\circ \left(\mathsf{\Psi }\left(x\right)\otimes \mathsf{\Psi }\left(t\right)\right),$$

(29)

where the unknown coefficient matrix $\mathbf{A}={\left[a_{nm{n}^{\prime }{m}^{\prime }}\right]}_{2^{2k-2}\times M^2}$ can be determined and the matrix $\mathsf{\Psi }(·)$ is defined by (18). By Caputo fractional integration (12), integrating of (29) with respect to t from 0 to t and using condition (26), we obtain

$$\begin{array}{ccc}\frac{{\partial }^2\overline{\mathsf{\Omega }}(x,t)}{\partial x^2}\hfill & =\hfill & \mathbf{A}\circ \left(\mathsf{\Psi }\left(x\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)+\frac{{\partial }^2\overline{\mathsf{\Omega }}(x,0)}{\partial x^2}\mathsf{\Phi }\hfill \\ & =\hfill & \mathbf{A}\circ \left(\mathsf{\Psi }\left(x\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)+f^{″}\left(x\right)\mathsf{\Phi },\hfill \end{array}$$

(30)

where the matrix $\mathsf{\Phi }$ is

$$\begin{array}{c}\hfill \mathsf{\Phi }={\left[\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 0\end{array}\right]}_{2^{2k-2}\times M^2}.\end{array}$$

Next integrating of (29) with respect to x twice from 0 to x, we obtain

$$\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}=\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)+x\left(\frac{\partial }{\partial x}{\left.\left(\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\right)\right|}_{x=0}\right)\mathsf{\Phi }+\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(0,t)}{\partial t^{\alpha }}\mathsf{\Phi }.$$

(31)

Evaluating $x=1$ in (31), we have:

$$\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(1,t)}{\partial t^{\alpha }}=\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)+\frac{\partial }{\partial x}{\left.\left(\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\right)\right|}_{x=0}\mathsf{\Phi }+\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(0,t)}{\partial t^{\alpha }}\mathsf{\Phi },$$

so

$$\frac{\partial }{\partial x}{\left.\left(\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\right)\right|}_{x=0}\mathsf{\Phi }=\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(1,t)}{\partial t^{\alpha }}-\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)-\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(0,t)}{\partial t^{\alpha }}\mathsf{\Phi },$$

(32)

then substituting (32) into (31), we have

$$\begin{array}{ccc}\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\hfill & =\hfill & \mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)+x\left(\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(1,t)}{\partial t^{\alpha }}-\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)\right.\hfill \\ \hfill & \hfill & \left.-\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(0,t)}{\partial t^{\alpha }}\mathsf{\Phi }\right)+{\left.\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\right|}_{x=0}\mathsf{\Phi },\hfill \end{array}$$

(33)

substituting boundary conditions (27) and (28), then we get

$$\begin{array}{ccc}\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\hfill & =\hfill & \mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)-x\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)\hfill \\ \hfill & \hfill & +x\left(D_0^{\alpha }{g}_2\left(t\right)-D_0^{\alpha }{g}_1\left(t\right)\right)\mathsf{\Phi }+D_0^{\alpha }{g}_1\left(t\right)\mathsf{\Phi }.\hfill \end{array}$$

(34)

Taking Riemann-Liouville fractional integrating of (34), so the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$ is given by

$$\begin{array}{c}\overline{\mathsf{\Omega }}(x,t)=\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)-x\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)\hfill \\ +\left\{x\left[g_2\left(t\right)-g_1\left(t\right)-g_2\left(0\right)+g_1\left(0\right)\right]+g_1\left(t\right)-g_1\left(0\right)+f\left(x\right)\right\}\mathsf{\Phi }.\hfill \end{array}$$

(35)

The collocation points of time and space are defined by

$$t_i=\frac{2i-1}{2m},x_i=\frac{2i-1}{2m},i=1,2,\dots ,2^{k-1}M.$$

(36)

Substituting (30), (34), (35), and (36) into (25), we have the system that can be solved the coefficient matrix $\mathbf{A}$:

$$\begin{array}{c}\mathbf{A}\circ \left[P^2\left(\mathsf{\Psi }\left(x_i\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)-a\mathsf{\Psi }\left(x_i\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t_i\right)\right)\right]-x_i\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)\right)\hfill \\ +\left\{x_i\left(D_0^{\alpha }{g}_2\left(t_i\right)-D_0^{\alpha }{g}_1\left(t_i\right)\right)+D_0^{\alpha }{g}_1\left(t_i\right)-a{f}^{″}\left(x_i\right)-F\left(\overline{\mathsf{\Omega }}(x_i,t_i)\right)\right\}\mathsf{\Phi }=\overline{\mathbf{0}},\hfill \end{array}$$

(37)

where $P^2\left(\mathsf{\Psi }(·)\right)$ and $P^{\alpha }\left(\mathsf{\Psi }(·)\right)$ in (20) and (22), respectively, $\overline{\mathbf{0}}$ is a zero $2^{2k-2}\times M^2$ matrix, and then substituting the coefficient matrix $\mathbf{A}$ into (35), therefore the solution

$$\omega (x,t)=\sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\mathsf{\Omega }}_{ij}(x,t)$$

of FKPP (25) with Dirichlet boundary conditions, where ${\mathsf{\Omega }}_{ij}(x,t)$ are entries of the matrix $\overline{\mathsf{\Omega }}(x,t)$ in (35).

Remark 1.

For fractional order $\alpha =1$, from (35) the matrix $P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)$ is replaced by the matrix $P^1\left(\mathsf{\Psi }\left(t\right)\right)$ so the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$ is given by

$$\begin{array}{c}\overline{\mathsf{\Omega }}(x,t)=\mathit{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes P^1\left(\mathsf{\Psi }\left(t\right)\right)\right)-x\mathit{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes P^1\left(\mathsf{\Psi }\left(t\right)\right)\right)\hfill \\ +\left\{x\left[g_2\left(t\right)-g_1\left(t\right)-g_2\left(0\right)+g_1\left(0\right)\right]+g_1\left(t\right)-g_1\left(0\right)+f\left(x\right)\right\}\mathsf{\Phi }.\hfill \end{array}$$

(38)

Case 2: The time fractional KPP equation with Dirichlet-Neumann boundary conditions:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=a(x,t)\frac{{\partial }^2\omega }{\partial x^2}+F\left(\omega \right),$$

(39)

subjected to the initial and boundary conditions

$$\begin{array}{ccc}\hfill \omega (x,0)& =& f\left(x\right),\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill D^{\alpha }\omega (0,t)& =& h_1\left(t\right),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill D^{\alpha }\omega (1,t)& =& h_2\left(t\right).\hfill \end{array}$$

(42)

From (33) and the Dirichlet-Neumann boundary conditions in (41) and (42), we have

$$\begin{array}{ccc}\frac{{\partial }^{\alpha }\overline{\mathsf{\Omega }}(x,t)}{\partial t^{\alpha }}\hfill & =\hfill & \mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)-x\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t\right)\right)\hfill \\ \hfill & \hfill & +\left\{x\left(h_2\left(t\right)-h_1\left(t\right)\right)+h_1\left(t\right)\right\}\mathsf{\Phi }.\hfill \end{array}$$

(43)

Taking Riemann-Liouville fractional integrating from 0 to t of (43),

$$\begin{array}{ccc}\overline{\mathsf{\Omega }}(x,t)\hfill & =\hfill & \mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)-x\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)\hfill \\ \hfill & \hfill & +\left\{x{I}_0^{\alpha }\left[h_2\left(t\right)-h_1\left(t\right)\right]+I_0^{\alpha }\left(h_1\left(t\right)\right)+f\left(x\right)\right\}\mathsf{\Phi }.\hfill \end{array}$$

(44)

Substituting (30), (43), (44), and (36) into (25), coefficient matrix A can solve from the system

$$\begin{array}{c}\mathbf{A}\circ \left[P^2\left(\mathsf{\Psi }\left(x_i\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)-a\mathsf{\Psi }\left(x_i\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t_i\right)\right)\right]-x_i\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)\right)\hfill \\ +\left\{x_i\left(h_2\left(t_i\right)-h_1\left(t_i\right)\right)+h_1\left(t_i\right)-a{f}^{″}\left(x_i\right)-F\left(\overline{\mathsf{\Omega }}(x_i,t_i)\right)\right\}\mathsf{\Phi }=\overline{\mathbf{0}}.\hfill \end{array}$$

(45)

Finally, substituting the known coefficient matrix $\mathbf{A}$ into (44), so the solution of FKPP is given by

$${\displaystyle \omega (x,t)=\sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\mathsf{\Omega }}_{ij}(x,t),}$$

where ${\mathsf{\Omega }}_{ij}(x,t)$ are entries of the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$.

Case 3: the time fractional KPP equation with Neumann-Robin boundary conditions:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=a(x,t)\frac{{\partial }^2\omega }{\partial x^2}+F\left(\omega \right),$$

(46)

subjected to the initial and boundary conditions

$$\begin{array}{ccc}\hfill \omega (x,0)& =& f\left(x\right),\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill D^{\alpha }\omega (0,t)& =& h_1\left(t\right),\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill D^{\alpha }\omega (1,t)+a\omega (1,t)& =& h_3\left(t\right).\hfill \end{array}$$

(49)

Applying Neumann-Robin boundary conditions in (48) and (49) to (43), similar to (44), we have

$$\begin{array}{ccc}\overline{\mathsf{\Omega }}(x,t)\hfill & =\hfill & \mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(x\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)-x\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t\right)\right)\right)\hfill \\ \hfill & \hfill & +\left\{x{I}^{\alpha }\left[h_3\left(t\right)-a\overline{\mathsf{\Omega }}(1,t)-h_1\left(t\right)\right]+I^{\alpha }\left(h_1\left(t\right)\right)+f\left(x\right)\right\}\mathsf{\Phi }.\hfill \end{array}$$

(50)

Now, substituting (30), (50), and (36) into (25), the coefficient matrix A can solve from the system

$$\begin{array}{c}\mathbf{A}\circ \left[P^2\left(\mathsf{\Psi }\left(x_i\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)-a\mathsf{\Psi }\left(x_i\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t_i\right)\right)\right]-x_i\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)\right)\hfill \\ +\left\{x_i\left(h_3\left(t_i\right)-a\overline{\mathsf{\Omega }}(1,t_i)-h_1\left(t_i\right)\right)+h_1\left(t_i\right)-a{f}^{″}\left(x_i\right)-F\left(\overline{\mathsf{\Omega }}(x_i,t_i)\right)\right\}\mathsf{\Phi }=\overline{\mathbf{0}}.\hfill \end{array}$$

(51)

Finally, substituting the known coefficient matrix $\mathbf{A}$ into (50), so the solution of FKPP is given by

$${\displaystyle \omega (x,t)=\sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\mathsf{\Omega }}_{ij}(x,t),}$$

where ${\mathsf{\Omega }}_{ij}(x,t)$ are entries of the Hadamard-Kronecker product matrix $\overline{\mathsf{\Omega }}(x,t)$.

5. Convergence and Error Analysis of the Chebyshev Wavelet

We next investigate convergence and error analysis for Chebyshev wavelets approximation

Theorem 1.

If the Chebyshav wavelets solution $\omega (x,t)\in C\left([0,1]\times [0,1]\right)$ where

$$\begin{array}{ccc}\hfill \omega (x,t)& =& \sum _{n=1}^{\infty }\sum _{m=0}^{\infty }\sum _{n^{\prime }=1}^{\infty }\sum _{m^{\prime }=0}^{\infty }{a}_{nm{n}^{\prime }{m}^{\prime }}{\psi }_{nm}\left(x\right){\psi }_{n^{\prime }{m}^{\prime }}\left(t\right).\hfill \end{array}$$

(52)

of the fractional KPP equation in (25) has a bounded second-order of partial derivatives $\left|\frac{{\partial }^2\omega (x,t)}{\partial x^2}\right|\le N_1$, $\left|\frac{\partial \omega (x,t)}{\partial x}\right|\le N_2$, then the Chebyshev wavelet solution converges uniformly with

$$\begin{array}{c}\hfill \left|a_{nm{n}^{\prime }{m}^{\prime }}\right|\le \left\{\begin{array}{c}\frac{2\pi N_1}{{\left(2n^{\prime }\right)}^{\frac{1}{2}}{\left(2n\right)}^{\frac{5}{2}}(m^2-1)};m>1\hfill \\ \frac{2{\pi }^2{N}_2}{{\left(2n^{\prime }\right)}^{\frac{1}{2}}{\left(2n\right)}^{\frac{3}{2}}};m=1.\hfill \end{array}\right.\end{array}$$

Our proof is similar to the proof in the work by the authors of [26].

Theorem 2.

If the Chebyshav wavelets solution $\omega (x,t)\in C\left([0,1]\times [0,1]\right)$ where

$$\begin{array}{ccc}\hfill \omega (x,t)& =& \sum _{n=1}^{\infty }\sum _{m=0}^{\infty }\sum _{n^{\prime }=1}^{\infty }\sum _{m^{\prime }=0}^{\infty }{a}_{nm{n}^{\prime }{m}^{\prime }}{\psi }_{nm}\left(x\right){\psi }_{n^{\prime }{m}^{\prime }}\left(t\right)\hfill \end{array}$$

(53)

of the fractional KPP equation in (25) has a bounded second-order of partial derivatives $\left|\frac{{\partial }^2\omega (x,t)}{\partial x^2}\right|\le N_1$, $\left|\frac{\partial \omega (x,t)}{\partial x}\right|\le N_2$, and the Chebyshev wavelet approximate solution of the fractional KPP equation in (25) given by

$$\sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\xi }_{ij}(x,t)$$

(54)

where ${\xi }_{ij}(x,t)$ are entries of the Hadamard-Kronecker product matrix $\mathbf{A}\circ \left(\mathsf{\Psi }\left(x\right)\otimes \mathsf{\Psi }\left(t\right)\right)$, $\mathbf{A}$ in (16) and $\mathsf{\Psi }\left(x\right)\otimes \mathsf{\Psi }\left(t\right)$ in (17) then the absolute error is defined by

$$\begin{array}{c}\hfill \left|\omega (x,t)-\sum _{i=1}^{2^{2k-2}}\sum _{j=1}^{M^2}{\xi }_{ij}\right|\le \left\{\begin{array}{c}\sqrt{{\sum }_{i=2^{2k-2}}^{\infty }{\sum }_{n^{\prime }=2^k}^{\infty }\frac{4{\pi }^2{N}_1^2}{{\left(2n\right)}^5\left(2n^{\prime }\right){(m^2-1)}^2}};m>1,\hfill \\ \sqrt{{\sum }_{i=2^{2k-2}}^{\infty }{\sum }_{n^{\prime }=2^k}^{\infty }\frac{4{\pi }^4{N}_2^2}{{\left(2n\right)}^3\left(2n^{\prime }\right)}};m=1.\hfill \end{array}\right.\end{array}$$

This proof is similar to the proof in the work by the authors of [27].

6. Chebyshev Wavelet Solutions for the Time Fractional Kpp Equations

In this section, the efficiency and reliability of Chebyshev wavelet method are shown in some examples.

Example 1.

Consider the KPP equation (Fisher equation) with power–law nonlinearities chemical reaction:

$$\frac{\partial \omega }{\partial t}=\frac{{\partial }^2\omega }{\partial x^2}+6\omega (1-\omega ),0\le x\le 1,0\le t\le 0,$$

(55)

subject to the initial condition

$$\omega (x,0)=\frac{1}{{(1+e^x)}^2},0\le x\le 1,$$

(56)

Case 1: Dirichlet boundary conditions

$$\begin{array}{ccc}\hfill \omega (0,t)& =& \frac{1}{{(1+e^{-5t})}^2},0\le t\le 1,\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill \omega (1,t)& =& \frac{1}{{(1+e^{1-5t})}^2},0\le t\le 1.\hfill \end{array}$$

(58)

The exact solution of this problem is $\omega (x,t)=\frac{1}{{(1+e^{x-5t})}^2}.$

In Chebyshev wavelets process, given $k=2,M=3$ and the collocation points in (36) are given by

$$t=\left[\frac{1}{12}\frac{3}{12}\frac{5}{12}\dots \frac{11}{12}\right],x=\left[\frac{1}{12}\frac{3}{12}\frac{5}{12}\dots \frac{11}{12}\right].$$

Using the system from (37) and the Maple program (Maple 17) for solving the coefficient matrix $\mathbf{A}$ as

$$\begin{array}{c}\mathbf{A}\circ \left[P^2\left(\mathsf{\Psi }\left(x_i\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)-a\mathsf{\Psi }\left(x_i\right)\otimes P^{\alpha }\left(\mathsf{\Psi }\left(t_i\right)\right)\right]-x_i\mathbf{A}\circ \left(P^2\left(\mathsf{\Psi }\left(1\right)\right)\otimes \mathsf{\Psi }\left(t_i\right)\right)\hfill \\ +\left\{x_i\left(D_0^{\alpha }{g}_2\left(t_i\right)-D_0^{\alpha }{g}_1\left(t_i\right)\right)+D_0^{\alpha }{g}_1\left(t_i\right)-a{f}^{″}\left(x_i\right)-F\left(\overline{\mathsf{\Omega }}(x_i,t_i)\right)\right\}\mathsf{\Phi }=\overline{\mathbf{0}},\hfill \end{array}$$

(59)

which gives the matrix $\mathbf{A}$ as

$$\begin{array}{ccc}\hfill \mathbf{A}& =& \begin{array}{c}\hfill \left[\begin{array}{ccccc}-0.1873& 0.3707& 0.3357& \dots & -0.0030\\ 0.0980& -0.0453& -0.0564& \dots & -0.0006\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0.1235& -0.0076& -0.0518& \dots & 0.0020\end{array}\right].\end{array}\hfill \end{array}$$

Therefore, the Chebyshev wavelet solution of KPP equation ($k=2,M=3$) is given by

$$\begin{array}{ccc}\hfill \omega (x,t)& =& -0.3746\frac{x^{2}t}{\pi }+0.7414\frac{x^2\sqrt{2}\left(2t^2-t\right)}{\pi }+0.6715x^2\sqrt{2}\left(\frac{32}{3}{t}^3-8t^2+t\right){\pi }^{-1}\hfill \\ & & +0.3524\left(2/3x^3-1/2x^2\right)\left(\frac{32}{3}{t}^3-8t^2+t\right){\pi }^{-1}-0.7414\frac{x\sqrt{2}\left(2t^2-t\right)}{\pi }\hfill \\ & & +0.0308\frac{\sqrt{2}\left(8/3x^4-8/3x^3+1/2x^2\right)t}{\pi }-0.0496\frac{\left(8/3x^4-8/3x^3+1/2x^2\right)\left(2t^2-t\right)}{\pi }\hfill \\ & & -0.0243\left(8/3x^4-8/3x^3+1/2x^2\right)\left(\frac{32}{3}{t}^3-8t^2+t\right){\pi }^{-1}+0.3746\frac{xt}{\pi }+\cdots \hfill \\ & & -\frac{0.0465x}{\pi }(\frac{32}{3}{t}^3-8t^2+t)+x\left(\frac{1}{{\left(1+e^{1-5t}\right)}^2}-\frac{1}{{\left(1+e\right)}^2}-\frac{1}{{\left(1+e^{-5t}\right)}^2}+\frac{1}{4}\right)\hfill \\ & & +\frac{1}{{\left(1+e^{-5t}\right)}^2}-\frac{1}{4}.\hfill \end{array}$$

We show the accuracy of this method by comparing between the Chebyshev wavelet solutions ($k=1,M=6$ and $k=2,M=3$) and the exact solution with absolute errors, $|{\omega }_{exact}(x,t)-\omega (x,t)|$ that numerical results have shown in Table 1.

Table 1. Numerical results and absolute error.

t	x	${\mathit{\omega }}_{\mathit{exact}}$	$\mathit{k}=1,\mathit{M}=6$	Abs. Error	$\mathit{k}=2,\mathit{M}=3$	Abs. Error
	$x=0.1$	0.35842	0.35797	$4.510\times {10}^{-4}$	0.35828	$1.455\times {10}^{-4}$
	$x=0.3$	0.30231	0.30112	$1.196\times {10}^{-3}$	0.30189	$4.273\times {10}^{-4}$
$t=0.1$	$x=0.5$	0.25000	0.24850	$1.497\times {10}^{-3}$	0.24930	$6.977\times {10}^{-4}$
	$x=0.7$	0.20264	0.20142	$1.224\times {10}^{-3}$	0.20257	$8.574\times {10}^{-5}$
	$x=0.9$	0.16105	0.16057	$4.725\times {10}^{-4}$	0.16101	$5.482\times {10}^{-4}$
	$x=0.1$	0.64349	0.64348	$1.595\times {10}^{-5}$	0.64346	$3.517\times {10}^{-5}$
	$x=0.3$	0.59063	0.59059	$3.849\times {10}^{-5}$	0.59042	$2.064\times {10}^{-5}$
$t=0.3$	$x=0.5$	0.53444	0.53439	$5.132\times {10}^{-5}$	0.53404	$4.017\times {10}^{-5}$
	$x=0.7$	0.47606	0.47601	$4.803\times {10}^{-5}$	0.47627	$5.059\times {10}^{-5}$
	$x=0.9$	0.41687	0.41685	$2.122\times {10}^{-5}$	0.41690	$3.253\times {10}^{-5}$
	$x=0.1$	0.84057	0.84057	$6.583\times {10}^{-6}$	0.84031	$2.543\times {10}^{-5}$
	$x=0.3$	0.81044	0.81047	$2.127\times {10}^{-5}$	0.80999	$4.555\times {10}^{-5}$
$t=0.5$	$x=0.5$	0.77580	0.77584	$4.035\times {10}^{-5}$	0.77555	$2.468\times {10}^{-5}$
	$x=0.7$	0.73641	0.73647	$5.109\times {10}^{-5}$	0.73610	$3.123\times {10}^{-5}$
	$x=0.9$	0.69225	0.69228	$2.957\times {10}^{-5}$	0.69226	$8.097\times {10}^{-6}$
	$x=0.1$	0.93645	0.93643	$2.082\times {10}^{-5}$	0.93650	$5.305\times {10}^{-5}$
	$x=0.3$	0.92320	0.92313	$7.030\times {10}^{-5}$	0.92331	$1.103\times {10}^{-5}$
$t=0.7$	$x=0.5$	0.90739	0.90727	$1.219\times {10}^{-4}$	0.90749	$9.328\times {10}^{-5}$
	$x=0.7$	0.88863	0.88849	$1.408\times {10}^{-4}$	0.88867	$3.626\times {10}^{-5}$
	$x=0.9$	0.86650	0.86642	$7.645\times {10}^{-4}$	0.86650	$2.782\times {10}^{-6}$
	$x=0.1$	0.97589	0.97594	$5.102\times {10}^{-4}$	0.97581	$7.752\times {10}^{-5}$
	$x=0.3$	0.97067	0.97086	$1.940\times {10}^{-4}$	0.97047	$1.904\times {10}^{-5}$
$t=0.9$	$x=0.5$	0.96435	0.96471	$3.611\times {10}^{-4}$	0.96410	$8.439\times {10}^{-6}$
	$x=0.7$	0.95671	0.95714	$4.306\times {10}^{-4}$	0.95667	$4.561\times {10}^{-5}$
	$x=0.9$	0.94751	0.94774	$2.330\times {10}^{-4}$	0.94749	$2.069\times {10}^{-5}$

Case 2: Dirichlet-Neumann boundary conditions

$$\begin{array}{ccc}\hfill \frac{d\omega (0,t)}{dt}& =& \frac{10e^{-5t}}{{(1+e^{-5t})}^3},0\le t\le 1,\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill \frac{d\omega (1,t)}{dt}& =& \frac{10e^{1-5t}}{{(1+e^{1-5t})}^3},0\le t\le 1.\hfill \end{array}$$

(61)

By using Equation (45), the Chebyshev wavelet solution of KPP with Dirichlet-Neumann boundary condition ($k=1,M=8$) is given by

$$\begin{array}{ccc}\hfill \omega (x,t)& =& -0.378\frac{x\sqrt{2}\left(t^2-t\right)}{\pi }-0.007\frac{x\sqrt{2}\left(8/3t^3-4t^2+t\right)}{\pi }+0.361\frac{x\sqrt{2}\left(8t^4-16t^3+9t^2-t\right)}{\pi }\hfill \\ & & -0.127x\sqrt{2}\left(\frac{128}{5}{t}^5-64t^4+\frac{160}{3}{t}^3-16t^2+t\right){\pi }^{-1}\hfill \\ & & -0.054x\sqrt{2}\left(\frac{256}{3}{t}^6-256t^5+280t^4-\frac{400}{3}{t}^3+25t^2-t\right){\pi }^{-1}\hfill \\ & & +0.093x\sqrt{2}\left(t-1024t^6+\frac{2048}{7}{t}^7+280t^3+\frac{6912}{5}{t}^5-896t^4-36t^2\right){\pi }^{-1}\hfill \\ & & -0.028x\sqrt{2}\left(-t+\frac{19712}{3}{t}^6-4096t^7+102t^8-\frac{1568}{3}{t}^3-5376t^5+2352t^4+49t^2\right){\pi }^{-1}\hfill \\ & & -0.090\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\sqrt{2}t}{\pi }-0.069\frac{\left(8/5x^5-4x^4+3x^3-1/2x^2\right)\sqrt{2}t}{\pi }\hfill \\ & & +\cdots +x\left(\frac{1}{{\left(1+e^{1-5t}\right)}^2}-\frac{1}{{\left(1+e\right)}^2}-\frac{1}{{\left(1+e^{-5t}\right)}^2}+\frac{1}{4}\right)+\frac{1}{{\left(1+e^{-5t}\right)}^2}-\frac{1}{4}.\hfill \end{array}$$

The graph of Chebyshev wavelet solution is shown in Figure 1 and the graph of the absolute errors is shown in Figure 2.

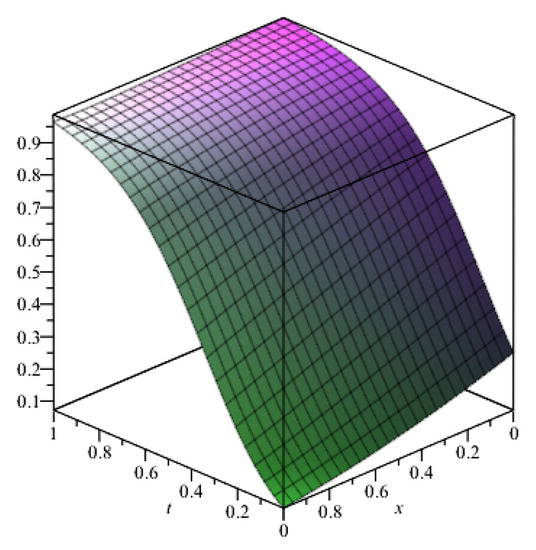
Figure 1. Graph of Chebyshev wavelet solutions with $k=1,M=8$.

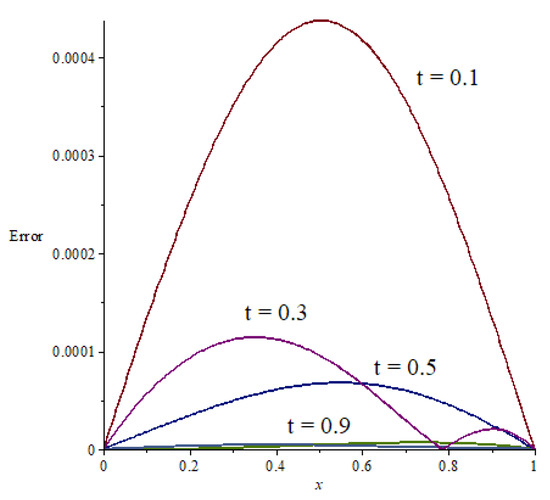
Figure 2. Graph of absolute errors with $k=1,M=8$.

Case 3: Neumann-Robin boundary conditions

$$\begin{array}{ccc}\hfill \frac{d\omega (0,t)}{dt}& =& \frac{10e^{-5t}}{{(1+e^{-5t})}^3},0\le t\le 1,\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill \frac{d\omega (1,t)}{dt}+\omega (1,t)& =& \frac{1+11e^{1-5t}}{{(1+e^{1-5t})}^3},0\le t\le 1.\hfill \end{array}$$

(63)

By using Equation (51) the analytical Chebyshev wavelet solution of KPP with Neumann-Robin boundary conditions ($k=1$, $M=3$, 4, 5, and 7) is given by

$$\begin{array}{ccc}\hfill \omega (x,t)& =& -0.279\frac{x\sqrt{2}\left(t^2-t\right)}{\pi }+0.031\frac{x\sqrt{2}\left(8/3t^3-4t^2+t\right)}{\pi }+0.456\frac{x\sqrt{2}\left(8t^4-16t^3+9t^2-t\right)}{\pi }\hfill \\ & & +0.260\frac{\left(1/3x^3-1/2x^2\right)\sqrt{2}t}{\pi }+0.074\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\sqrt{2}t}{\pi }\hfill \\ & & +0.078\frac{\left(8/5x^5-4x^4+3x^3-1/2x^2\right)\sqrt{2}t}{\pi }+0.194\frac{x\left(8/3t^3-4t^2+t\right)}{\pi }\hfill \\ & & +0.007\left(\frac{64}{15}{x}^6-\frac{64}{5}{x}^5+\frac{40}{3}{x}^4-16/3x^3+1/2x^2\right)\sqrt{2}t{\pi }^{-1}+\cdots \hfill \\ & & +x\left(\frac{1}{{\left(1+e^{1-5t}\right)}^2}-\frac{1}{{\left(1+e\right)}^2}-\frac{1}{{\left(1+e^{-5t}\right)}^2}+\frac{1}{4}\right)+\frac{1}{{\left(1+e^{-5t}\right)}^2}-\frac{1}{4},\hfill \end{array}$$

and graphs of absolute errors for $k=1$ when $M=3,4,5$ and 7 are shown in Figure 3 and Figure 4.

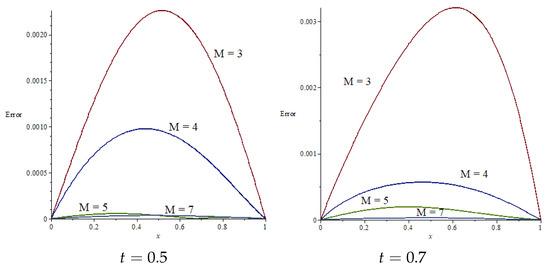
Figure 3. Graphs of absolute errors for Fisher equation at $t=0.5$ and $t=0.7$.

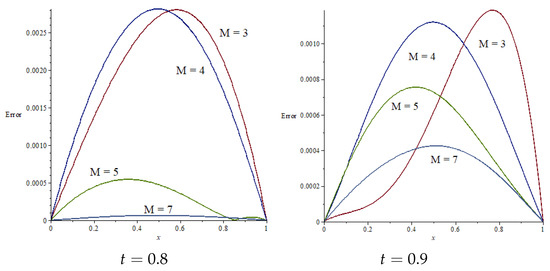
Figure 4. Graphs of absolute errors for Fisher equation at $t=0.8$ and $t=0.9$.

Example 2.

Consider the Fractional Kolmogorov-Petrovsky-Piskunov equation with exponential nonlinearities chemical reaction:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=\frac{{\partial }^2\omega }{\partial x^2}+2e^{\omega }+3,0\le x\le 1,0\le t\le 1,$$

(64)

subject to the initial condition

$$\omega (x,0)=4x(1-x),0\le x\le 1,$$

(65)

Case 1: Dirichlet boundary conditions

$$\begin{array}{ccc}\hfill \omega (0,t)& =& 0,0\le t\le 1,\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill \omega (1,t)& =& 0.0\le t\le 1.\hfill \end{array}$$

(67)

Computing by Chebyshev method (37) the solution with $\alpha =1$ is given by

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =1}& =& \frac{46.2673xt}{\pi }-\frac{1.0296x}{\pi }\left(\frac{246}{7}{t}^6-137t^5+321t^4-\frac{429}{4}{t}^3+17t^2-t\right)\hfill \\ & & +\cdots -\frac{22.3115\sqrt{2}{x}^2}{\pi }\left(t^2-t\right).\hfill \end{array}$$

We compare the Chebyshev wavelet solution with numerical solution of finite difference method in Table 2.

Table 2. Numerical results for $\alpha =1$ and compare with finite difference method from the MAPLE program.

t	x	CW ($\mathit{k}=1,\mathit{M}=10$)	FD sol.	Abs. Error
	$x=0.1$	0.15311	0.15375	$5.324\times {10}^{-4}$
	$x=0.3$	0.37476	0.37435	$3.531\times {10}^{-4}$
$t=0.1$	$x=0.5$	0.45356	0.04532	$4.625\times {10}^{-4}$
	$x=0.7$	0.37476	0.37435	$3.557\times {10}^{-4}$
	$x=0.9$	0.15311	0.15375	$5.323\times {10}^{-4}$
	$x=0.1$	0.03334	0.03385	$8.223\times {10}^{-4}$
	$x=0.3$	0.08441	0.08409	$6.001\times {10}^{-5}$
$t=0.3$	$x=0.5$	0.10264	0.10275	$5.121\times {10}^{-5}$
	$x=0.7$	0.08441	0.08409	$6.372\times {10}^{-5}$
	$x=0.9$	0.03334	0.03385	$8.216\times {10}^{-4}$
	$x=0.1$	0.04432	0.04405	$7.062\times {10}^{-4}$
	$x=0.3$	0.09821	0.09820	$1.305\times {10}^{-4}$
$t=0.5$	$x=0.5$	0.11448	0.14424	$1.751\times {10}^{-4}$
	$x=0.7$	0.09821	0.09820	$1.345\times {10}^{-4}$
	$x=0.9$	0.04432	0.04405	$7.064\times {10}^{-4}$
	$x=0.1$	0.03388	0.03336	$1.159\times {10}^{-4}$
	$x=0.3$	0.08258	0.02868	$2.118\times {10}^{-4}$
$t=0.7$	$x=0.5$	0.09984	0.09978	$3.645\times {10}^{-4}$
	$x=0.7$	0.08258	0.02868	$2.102\times {10}^{-4}$
	$x=0.9$	0.03388	0.03336	$1.101\times {10}^{-4}$
	$x=0.1$	0.03467	0.03477	$1.511\times {10}^{-4}$
	$x=0.3$	0.07426	0.07454	$9.014\times {10}^{-5}$
$t=0.9$	$x=0.5$	0.08511	0.08536	$3.715\times {10}^{-4}$
	$x=0.7$	0.07426	0.07454	$9.297\times {10}^{-5}$
	$x=0.9$	0.03467	0.03477	$1.563\times {10}^{-4}$

Case 2: Dirichlet-Neumann boundary conditions

$$\begin{array}{ccc}\hfill \frac{d^{\alpha }\omega (0,t)}{d{t}^{\alpha }}& =& 0,0\le t\le 1,\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill \frac{d^{\alpha }\omega (1,t)}{d{t}^{\alpha }}& =& 0.0\le t\le 1.\hfill \end{array}$$

(69)

In this case, the Chebyshev wavelet solutions for $\alpha =0.3,0.5,0.7,0.9$ and 1 can be computed using the Chebyshev wavelet method in (45):

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =0.3}& =& \frac{0.007(13-20t)}{\sqrt{\pi }}\left(\frac{64}{15}{x}^6-\frac{64}{5}{x}^5+\frac{40}{3}{x}^4-\frac{16}{3}{x}^3+\frac{1}{2}{x}^2\right)t^{\frac{3}{10}}\hfill \\ & & +\cdots -\frac{6.2709\sqrt{2}x}{\sqrt{\pi }}{t}^{\frac{3}{10}}+\frac{0.0150x}{\sqrt{\pi }}(13-20t)t^{\frac{3}{10}},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =0.5}& =& \frac{0.004x}{\sqrt{\pi }}\left(35-420t+896t^2-512t^3\right)\sqrt{t}+\frac{0.036x}{\sqrt{\pi }}\left(15-80t+64t^2\right)\sqrt{t}\hfill \\ & & +\cdots -\frac{7.4675\sqrt{2}{x}^2}{\pi }\sqrt{t},\hfill \\ \hfill \omega {(x,t)}_{\alpha =0.7}& =& -\frac{0.012(17-20t)}{\sqrt{\pi }}\left(\frac{64}{15}{x}^6-\frac{64}{5}{x}^5+\frac{40}{3}{x}^4-\frac{16}{3}{x}^3+\frac{1}{2}{x}^2\right)t^{\frac{7}{10}}\hfill \\ & & +\cdots +\frac{0.0128x}{\sqrt{\pi }}\left(17-20t\right)t^{\frac{7}{10}}-\frac{0.0038x}{\sqrt{\pi }}\left(459-2160t+1600t^2\right)t^{\frac{7}{10}},\hfill \\ \hfill \omega {(x,t)}_{\alpha =0.9}& =& -\frac{0.086(19-20t)}{\sqrt{\pi }}\left(\frac{64}{15}{x}^6-\frac{64}{5}{x}^5+\frac{40}{3}{x}^4-\frac{16}{3}{x}^3+\frac{1}{2}{x}^2\right)t^{\frac{9}{10}}\hfill \\ & & +\cdots +\frac{12.458x\sqrt{2}}{\sqrt{\pi }}{t}^{\frac{9}{10}}-\frac{0.0095x}{\sqrt{\pi }}\left(551-2320t+1600t^2\right)t^{\frac{9}{10}},\hfill \\ \hfill \omega {(x,t)}_{\alpha =1}& =& \frac{4.40\sqrt{2}{x}^{2}t}{\sqrt{\pi }}-\frac{20.90\sqrt{2}(1.12t^2-1.12t)}{\sqrt{\pi }}+\frac{4.44\sqrt{2}{x}^2(3.00t^3-4.51t^2+1.12t)}{\sqrt{\pi }}\hfill \\ & & +\cdots -\frac{4.43x(1.12t^2-1.12t)}{\sqrt{\pi }}.\hfill \end{array}$$

Numerical solutions for $\alpha =0.3,0.5,0.7,0.9$, and 1 are reported in Table 3.

Table 3. Numerical results of the fractional Kolmogorov-Petrovsky-Piskunov (FKPP) equation with difference values of $\alpha$.

t	x	$\mathit{\alpha }=0.3$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.7$	$\mathit{\alpha }=0.9$	$\mathit{\alpha }=1$
	$x=0.1$	0.07964	0.09655	0.11655	0.13990	0.15307
	$x=0.3$	0.19225	0.23413	0.28375	0.34183	0.37473
$t=0.1$	$x=0.5$	0.23141	0.28223	0.34248	0.41306	0.45307
	$x=0.7$	0.19225	0.23413	0.28375	0.34183	0.37473
	$x=0.9$	0.07964	0.09655	0.11655	0.13990	0.15307
	$x=0.1$	0.05989	0.05687	0.05059	0.04035	0.03379
	$x=0.3$	0.14423	0.13762	0.12318	0.09935	0.08414
$t=0.3$	$x=0.5$	0.17349	0.16578	0.14867	0.12034	0.10226
	$x=0.7$	0.14423	0.13762	0.12318	0.09935	0.08414
	$x=0.9$	0.05989	0.05687	0.05059	0.04035	0.03379
	$x=0.1$	0.06147	0.06109	0.05848	0.05137	0.04484
	$x=0.3$	0.14675	0.14496	0.13691	0.11652	0.09822
$t=0.5$	$x=0.5$	0.17602	0.17353	0.16317	0.13738	0.11439
	$x=0.7$	0.14675	0.14496	0.13691	0.11652	0.09822
	$x=0.9$	0.06147	0.06109	0.05848	0.05137	0.04484
	$x=0.1$	0.05586	0.05096	0.04473	0.03777	0.03398
	$x=0.3$	0.13349	0.12173	0.10709	0.09125	0.08278
$t=0.7$	$x=0.5$	0.16017	0.14604	0.12857	0.10987	0.09994
	$x=0.7$	0.13349	0.12173	0.10709	0.09125	0.08278
	$x=0.9$	0.05586	0.05096	0.04473	0.03777	0.03398
	$x=0.1$	0.05763	0.05470	0.04928	0.04032	0.03497
	$x=0.3$	0.13694	0.12854	0.11323	0.08846	0.07403
$t=0.9$	$x=0.5$	0.16400	0.15339	0.13410	0.10309	0.08513
	$x=0.7$	0.13694	0.12854	0.11323	0.08846	0.07403
	$x=0.9$	0.05763	0.05470	0.04928	0.04032	0.03497

Case 3: Neumann-Robin boundary conditions

$$\begin{array}{ccc}\hfill \frac{d^{\alpha }\omega (0,t)}{d{t}^{\alpha }}& =& 0,0\le t\le 1,\hfill \end{array}$$

(70)

$$\begin{array}{ccc}\hfill \frac{d^{\alpha }\omega (1,t)}{d{t}^{\alpha }}+\omega (1,t)& =& 0,0\le t\le 1.\hfill \end{array}$$

(71)

The graphs of Chebyshev wavelet solutions for $\alpha =0.3,0.5,0.7$ and 1 from Chebyshev wavelet method (51) which satisfy Neumann-Robin boundary conditions can be shown in Figure 5 and Figure 6.

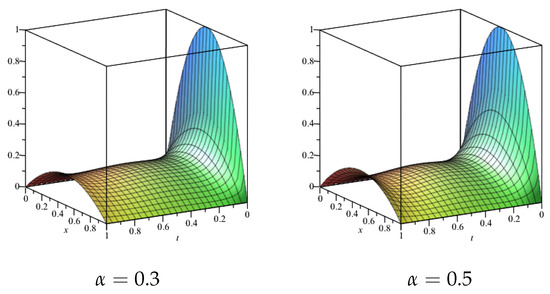
Figure 5. Graphs of solutions for order $\alpha =0.3$ and $0.5$.

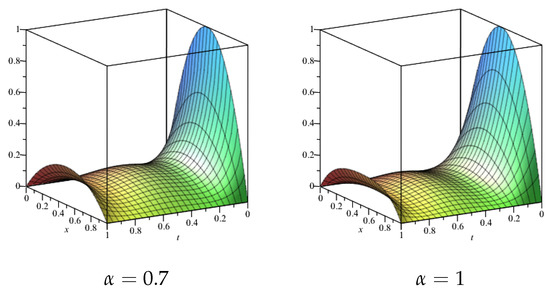
Figure 6. Graphs of solutions for order $\alpha =0.7$ and 1.

Example 3.

Consider the fractional Kolmogorov-Petrovsky-Piskunov equation with logarithmic nonlinearities chemical reaction:

$$\frac{{\partial }^{\alpha }\omega }{\partial t^{\alpha }}=\frac{{\partial }^2\omega }{\partial x^2}+5ln(\omega +1),0\le x\le 1,0\le t\le 1,$$

(72)

subject to the initial condition

$$\omega (x,0)=x-x^2,0\le x\le 1,$$

(73)

Case 1: Dirichlet boundary condition

$$\begin{array}{ccc}\hfill \omega (0,t)& =& t-t^2,0\le t\le 1,\hfill \\ \hfill \omega (1,t)& =& t-t^2,0\le t\le 1,\hfill \end{array}$$

Case 2: Dirichlet-Neumann boundary condition

$$\begin{array}{ccc}\hfill D^{\left(0.8\right)}\omega (0,t)& =& 1.0891t^{1/5}-1.8152t^{6/5},0\le t\le 1,\hfill \\ \hfill D^{\left(0.8\right)}\omega (1,t)& =& 1.0891t^{1/5}-1.8152t^{6/5},0\le t\le 1,\hfill \end{array}$$

Case 3: Neumann-Robin boundary condition

$$\begin{array}{ccc}\hfill D^{\left(0.5\right)}\omega (0,t)& =& 1.1283\sqrt{t}-1.5045t^{3/2},0\le t\le 1,\hfill \\ \hfill D^{\left(0.5\right)}\omega (1,t)+\omega (1,t)& =& t-t^2+1.1283\sqrt{t}-1.5045t^{3/2},0\le t\le 1.\hfill \end{array}$$

The Chebyshev wavelet solution for $\alpha =1$ with Dirichlet boundary condition (Case 1), is given by

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =1}& =& x+t-3.814\frac{x\sqrt{2}t}{\sqrt{\pi }}-0.312\frac{x\sqrt{2}\left(-1.128t+1.128t^2\right)}{\sqrt{\pi }}\hfill \\ & & +0.784\frac{x\sqrt{2}\left(-1.128t+10.155t^2-18.054t^3+9.027t^4\right)}{\sqrt{\pi }}\hfill \\ & & -3.164\frac{x\sqrt{2}\left(28.886t^5-72.216t^4+60.18t^3-18.054t^2+1.128t\right)}{\sqrt{\pi }}\hfill \\ & & -3.835\times {10}^{-7}\left(\frac{256}{21}{x}^7-\frac{128}{3}{x}^6+56x^5-\frac{100}{3}{x}^4+\frac{25}{3}{x}^3-1/2x^2\right)t\frac{1}{\sqrt{\pi }}\hfill \\ & & +\cdots +4.489\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\left(-1.128t+1.128t^2\right)}{\sqrt{\pi }}.\hfill \end{array}$$

The Chebyshev wavelet solution for $\alpha =0.8$ with Dirichlet-Neumann boundary condition (Case 2), is given by

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =0.8}& =& 2.251\frac{\sqrt{2}{x}^2{t}^{4/5}}{\sqrt{\pi }}-3.023\times {10}^{-9}\frac{\left(1/3x^3-1/2x^2\right)\left(9.0-10.0t\right)t^{4/5}}{\sqrt{\pi }}\hfill \\ & & +3.98\times {10}^{-10}\frac{\left(1/3x^3-1/2x^2\right)t^{4/5}\left(63.0-280.0t+200.0t^2\right)}{\sqrt{\pi }}\hfill \\ & & -5.165\times {10}^{-11}\frac{\left(1/3x^3-1/2x^2\right)\left(399.0-3990.0t+7600.0t^2-4000.0t^3\right)t^{4/5}}{\sqrt{\pi }}\hfill \\ & & +0.100\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)t^{4/5}\left(63.0-280.0t+200.0t^2\right)}{\sqrt{\pi }}\hfill \\ & & -2.675\times {10}^{-9}\frac{\left(8/5x^5-4x^4+3x^3-1/2x^2\right)\left(9.0-10.0t\right)t^{4/5}}{\sqrt{\pi }}\hfill \\ & & +x+t+1.598\times {10}^{-5}\frac{\left(1/3x^3-1/2x^2\right)t^{4/5}}{\sqrt{\pi }}+4.01\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)t^{4/5}}{\sqrt{\pi }}\hfill \\ & & +\cdots +1.03\times {10}^{-4}\frac{x\left(399.0-3990.0t+7600.0t^2-4000.0t^3\right)t^{4/5}}{\sqrt{\pi }}.\hfill \end{array}$$

The Chebyshev wavelet solution for $\alpha =0.5$ with Neumann-Robin boundary condition (Case 3), is given by

$$\begin{array}{ccc}\hfill \omega {(x,t)}_{\alpha =0.5}& =& 1.356\frac{\sqrt{2}{x}^2\sqrt{t}}{\sqrt{\pi }}-1.039\times {10}^{-10}\frac{\left(1/3x^3-1/2x^2\right)\left(3.0-4.0t\right)\sqrt{t}}{\sqrt{\pi }}\hfill \\ & & +5.314\times {10}^{-11}\frac{\left(1/3x^3-1/2x^2\right)\sqrt{t}\left(15.0-80.0t+64.0t^2\right)}{\sqrt{\pi }}\hfill \\ & & -2.67\times {10}^{-11}\frac{\left(1/3x^3-1/2x^2\right)\left(35.0-420.0t+896.0t^2-512.0t^3\right)\sqrt{t}}{\sqrt{\pi }}\hfill \\ & & +0.186\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\left(3.0-4.0t\right)\sqrt{t}}{\sqrt{\pi }}\hfill \\ & & +0.069\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\sqrt{t}\left(15.0-80.0t+64.0t^2\right)}{\sqrt{\pi }}\hfill \\ & & +0.009\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\left(35.0-420.0t+896.0t^2-512.0t^3\right)\sqrt{t}}{\sqrt{\pi }}\hfill \\ & & +1.976\times {10}^{-6}\frac{\left(8/5x^5-4x^4+3x^3-1/2x^2\right)\sqrt{t}}{\sqrt{\pi }}+x+t+\cdots \hfill \\ & & +1.260\frac{\left(2/3x^4-4/3x^3+1/2x^2\right)\sqrt{t}}{\sqrt{\pi }}-0.364\frac{x\sqrt{2}\left(3.0-4.0t\right)\sqrt{t}}{\sqrt{\pi }}.\hfill \end{array}$$

The graphs of Chebyshev wavelet solutions for $\alpha =1,0.8$, and $0.5$ are shown in Figure 7.

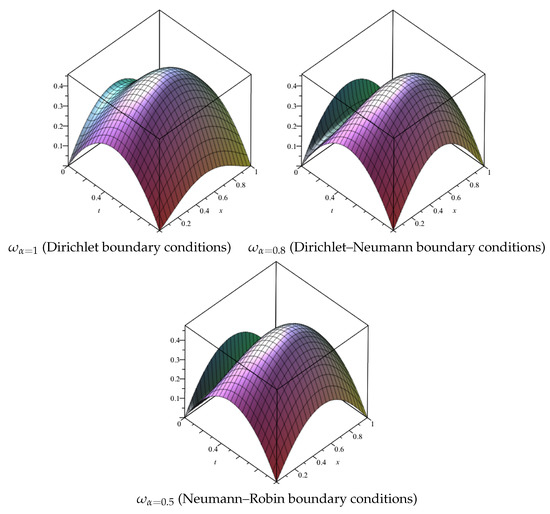
Figure 7. Graphs of solutions for order $\alpha =1,0.8$, and $0.5$.

7. Conclusions

The proposed method uses a technique for computation of Caputo fractional differential equation by constructing their operational matrices that represent Caputo fractional integration and differentiation. This approach provide the suitable analytical solutions of FKKP equation in Caputo fractional derivative sense, which is able to determine for initial condition, Dirichlet boundary, Dirichlet-Neumann boundary, and Neumann-Robin boundary conditions, respectively. The validity, accuracy and applicability of Chebyshev wavelet method have been illustrated through several examples by comparing with analytical results and exact solutions in Table 1, numerical solutions of finite difference method in Table 2. The execution of Chebyshev wavelet method shows that it is very simple and very efficient as an analytical result; the comparisons show that the Chebyshev wavelet method gives good accuracy and more rapidly convergent when increasing dilation ($2^{k-1}$) and translation (M) parameters. The Chebyshev wavelet method can solve some analytical solutions of FKPP Dirichlet boundary problem with various fractional orders $\alpha$. Furthermore, useful applications form the proposed method can be applied to solve solutions for various fractional order derivatives or other fractional partial equations.