New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Calculus
2.2. Chebyshev Wavelet Method
2.3. The Kronecker Product
- where is a scalar.
- .
- .
- .
- .
- .
- ,( denotes conjugate transpose).
2.4. Hadamard Product
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
- 5.
- .
3. Chebyshev Wavelets Approximation
4. Description of the Proposed Method
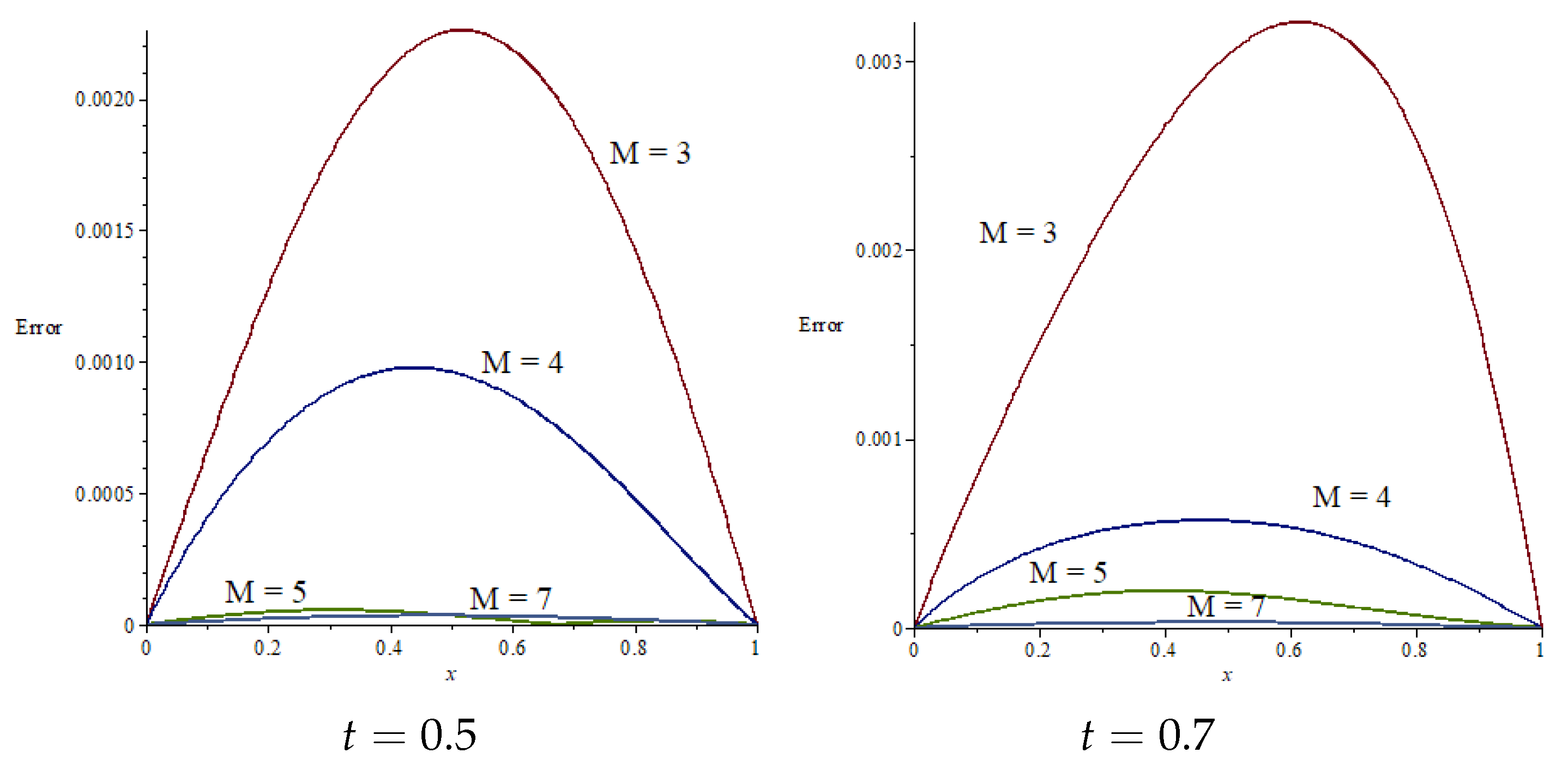
5. Convergence and Error Analysis of the Chebyshev Wavelet
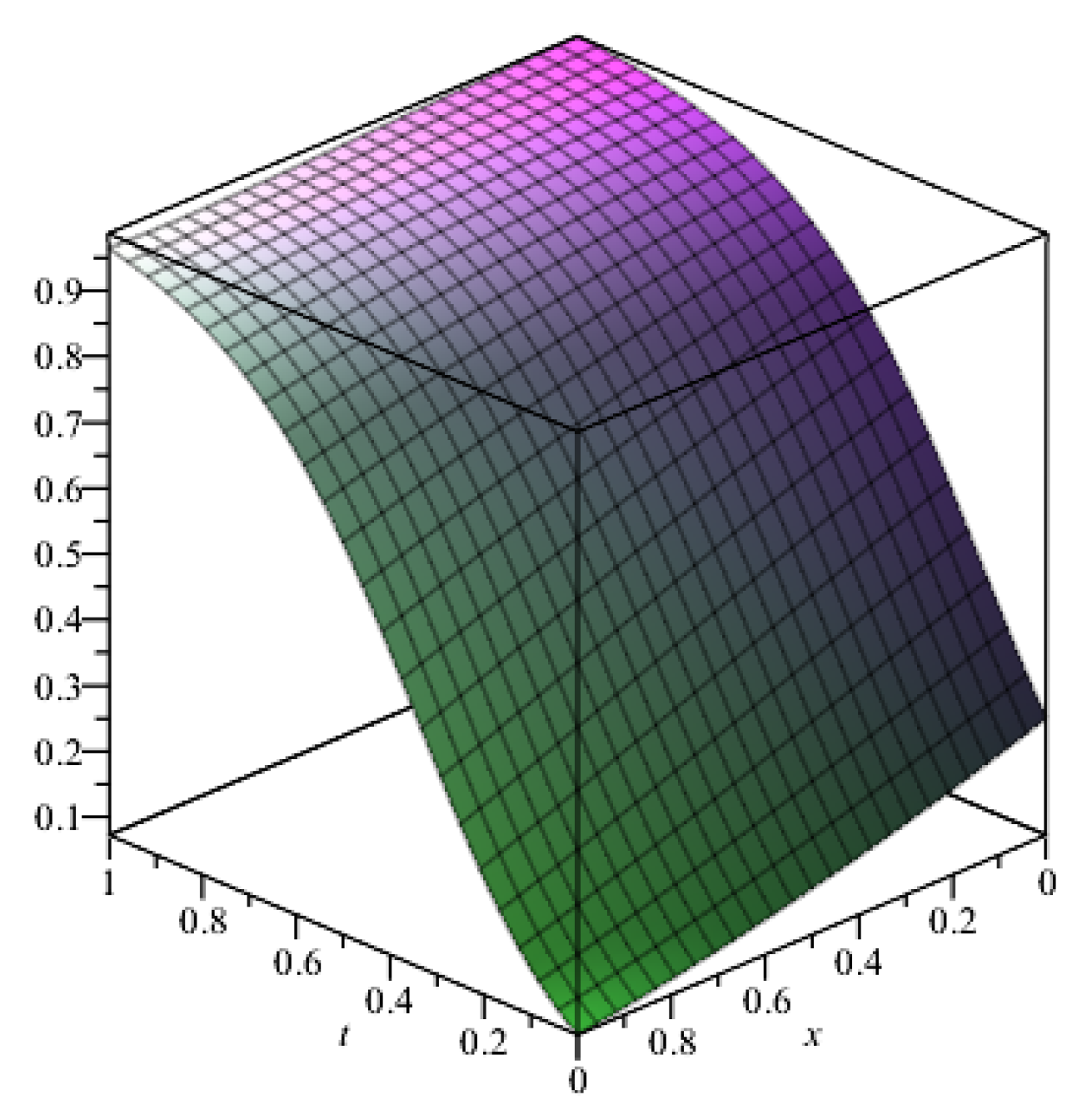
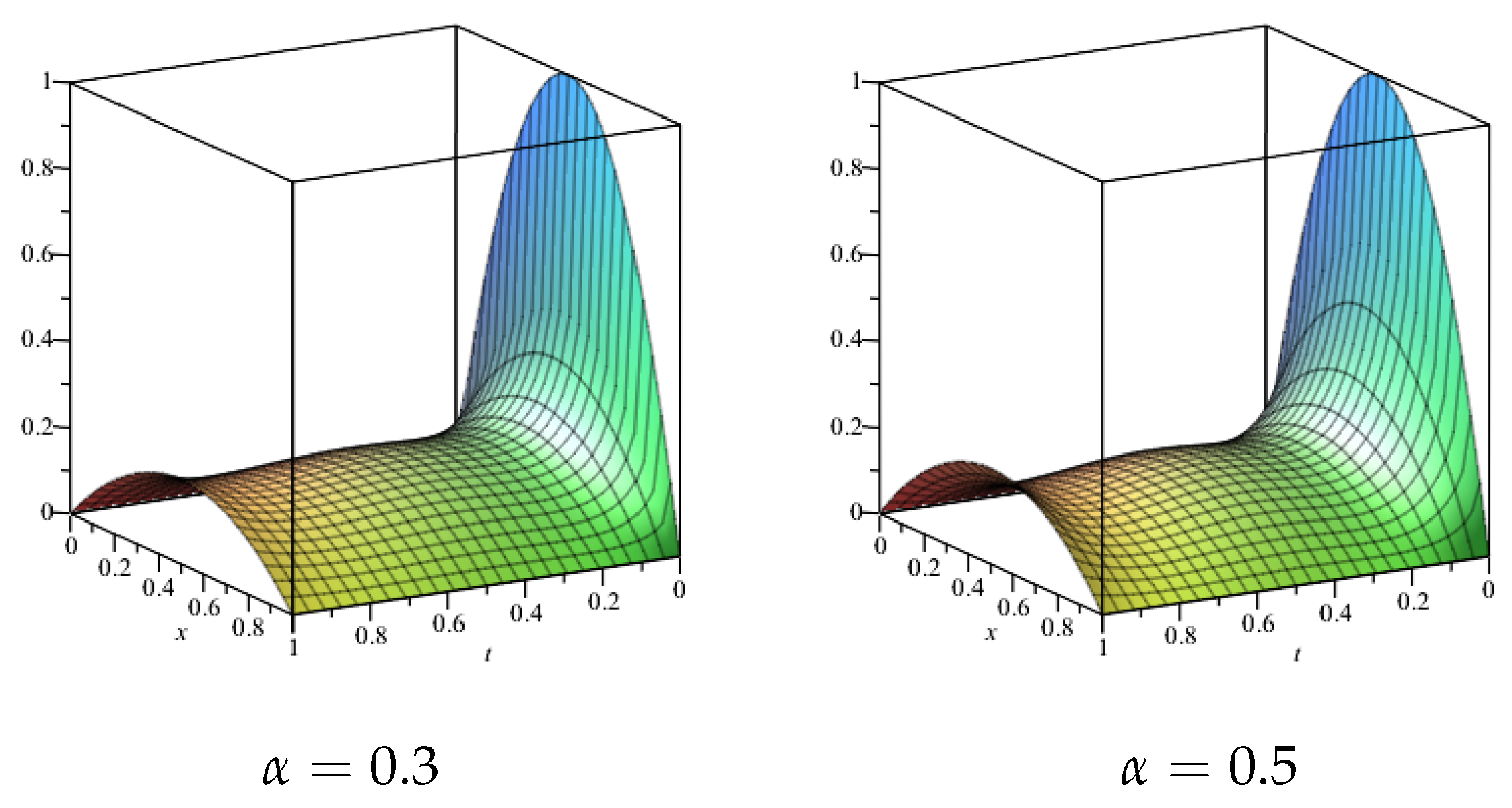
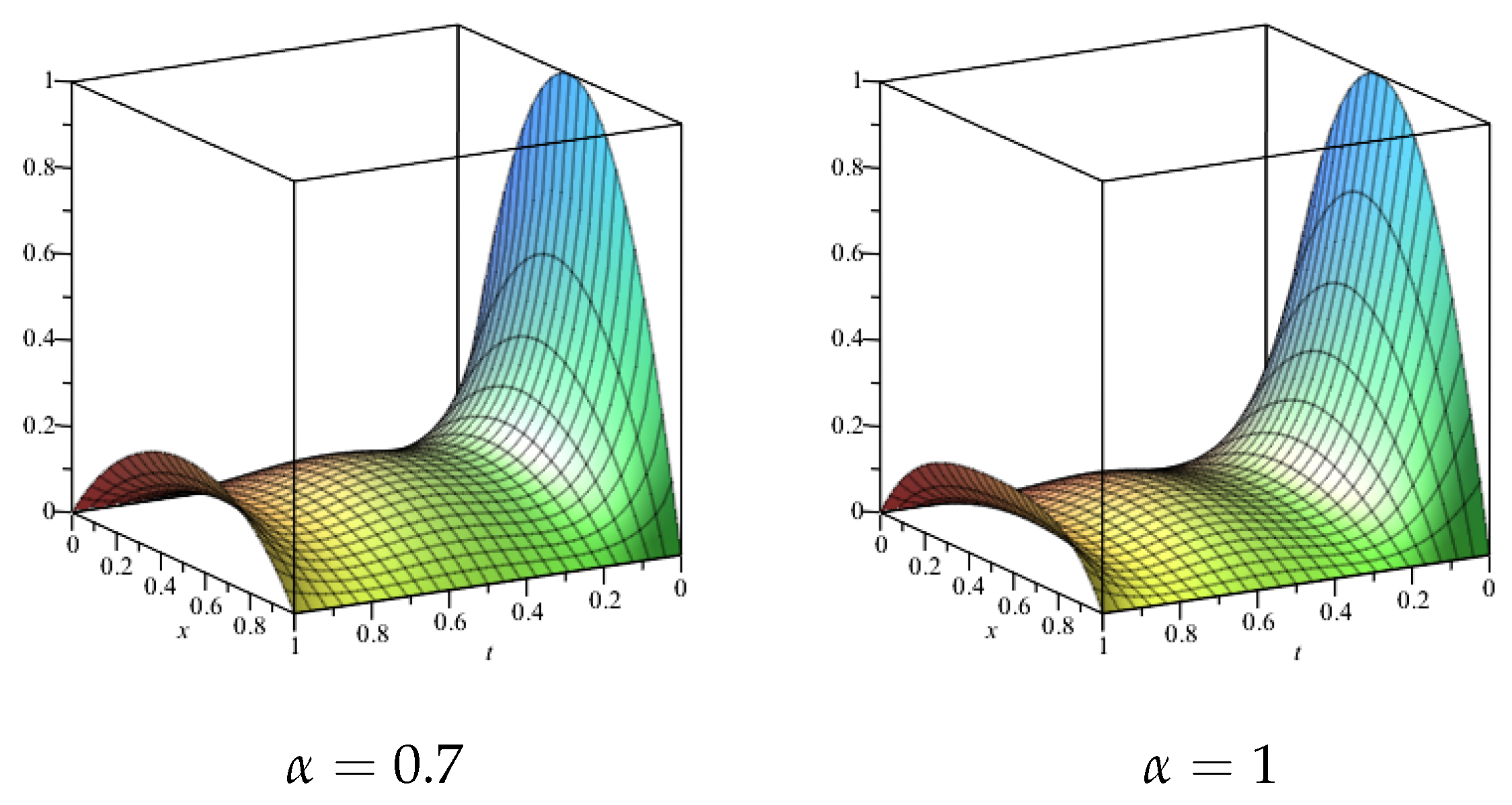
6. Chebyshev Wavelet Solutions for the Time Fractional Kpp Equations
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Jara, B.M.V. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K.; Sharma, K. Haar wavelet method for solving Fisher’s equation. Appl. Math. Comput. 2009, 211, 284–292. [Google Scholar] [CrossRef]
- Chandraker, V.; Awasthi, A.; Jayaraj, S. A numerical treatment of Fisher equation. Procedia Eng. 2015, 127, 1256–1262. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. An efficient numerical technique for the nonlinear fractional Kolmogorov-Petrovskii-Piskunov equation. Mathematics 2019, 7, 265. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by laplace transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Allahviranloo, T.; Gouyandeh, Z.; Armand, A. Numerical solutions for fractional differential equations by Tau-Collocation method. Appl. Math. Comput. 2015, 271, 979–990. [Google Scholar] [CrossRef]
- İbiş, B.; Bayram, M. Numerical comparison of methods for solving fractional differential-algebraic equations (FDAEs). Comput. Math. Appl. 2011, 62, 3270–3278. [Google Scholar] [CrossRef]
- Turut, V.; Guzel, N. On solving partial differential equations of fractional order by using the variational iteration method and multivariate Pade approximations. Eur. J. Pure Appl. Math. 2013, 6, 147–171. [Google Scholar]
- Al-Khaled, K. Numerical solution of time-fractional partial differential equations using Sumudu decomposition method. Rom. J. Phys. 2015, 60, 99–110. [Google Scholar]
- Mashayekhi, S.; Razzaghi, M. Numerical solution of nonlinear fractional integro-differential equations by hybrid functions. Eng. Anal. Bound. Elem. 2015, 56, 81–89. [Google Scholar] [CrossRef]
- Nemati, S.; Sedaghat, S.; Mohammadi, I. A fast numerical algorithm based on the second kind Chebyshev polynomials for fractional integro-differential equations with weakly singular kernels. J. Comput. Appl. Math. 2016, 308, 231–242. [Google Scholar] [CrossRef]
- Pakdaman, M.; Ahmadian, A.; Effati, S.; Salahshour, S.; Baleanu, D. Solving differential equations of fractional order using an optimization technique based on training artificial neural network. Appl. Math. Comput. 2017, 293, 81–95. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, L.; Liu, L.; Xie, J. The Chebyshev wavelet method for solving fractional integral and differential equations of Bratu-type. J. Comput. Inf. Syst. 2013, 9, 5601–5609. [Google Scholar]
- Gupta, A.; Ray, S.S. Numerical treatment for the solution of fractional fifth-order Sawada-Kotera equation using second kind Chebyshev wavelet method. Appl. Math. Model. 2015, 39, 5121–5130. [Google Scholar] [CrossRef]
- Yi, M.; Wang, L.; Huang, J. Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. Appl. Math. Model. 2016, 40, 3422–3437. [Google Scholar] [CrossRef]
- Heydari, M.; Hooshmandasl, M.; Ghaini, F.M. A new approach of the Chebyshev wavelets method for partial differential equations with boundary conditions of the telegraph type. Appl. Math. Model. 2014, 38, 1597–1606. [Google Scholar] [CrossRef]
- Ray, S.S.; Gupta, A.K. Wavelet Methods for Solving Partial Differential Equations and Fractional Differential Equations; Chapman and Hall/CRC: London, UK, 2018. [Google Scholar]
- Awashie, G.E.; Amoako-Yirenkyi, P.; Dontwi, I.K. Chebyshev wavelets collocation method for simulating a two-phase flow of immiscible fluids in a reservoir with different capillary effects. J. Pet. Explor. Prod. Technol. 2019, 9, 2039–2051. [Google Scholar] [CrossRef]
- Oruç, Ö.; Bulut, F.; Esen, A. Chebyshev Wavelet Method for Numerical Solutions of Coupled Burgers’ Equation. Hacet. J. Math. Stat. 2019, 48, 1–16. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations; CRC Press: London, UK, 2004. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Babolian, E.; Fattahzadeh, F. Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration. Appl. Math. Comput. 2007, 188, 417–426. [Google Scholar] [CrossRef]
- Schacke, K. On the Kronecker Product. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2004. [Google Scholar]
- Dayar, T.; Orhan, M.C. On vector-Kronecker product multiplication with rectangular factors. SIAM J. Sci. Comput. 2015, 37, S526–S543. [Google Scholar] [CrossRef]
- Horn, R.A. The hadamard product. Proc. Symp. Appl. Math. 1990, 40, 87–169. [Google Scholar]
- Adibi, H.; Assari, P. Chebyshev wavelet method for numerical solution of Fredholm integral equations of the first kind. Math. Probl. Eng. 2010, 2010, 138408. [Google Scholar] [CrossRef]
- Liu, N.; Lin, E.B. Legendre wavelet method for numerical solutions of partial differential equations. Numer. Methods Partial Differ. Equ. Int. J. 2010, 26, 81–94. [Google Scholar] [CrossRef]


| t | x | Abs. Error | Abs. Error | |||
|---|---|---|---|---|---|---|
| 0.35842 | 0.35797 | 0.35828 | ||||
| 0.30231 | 0.30112 | 0.30189 | ||||
| 0.25000 | 0.24850 | 0.24930 | ||||
| 0.20264 | 0.20142 | 0.20257 | ||||
| 0.16105 | 0.16057 | 0.16101 | ||||
| 0.64349 | 0.64348 | 0.64346 | ||||
| 0.59063 | 0.59059 | 0.59042 | ||||
| 0.53444 | 0.53439 | 0.53404 | ||||
| 0.47606 | 0.47601 | 0.47627 | ||||
| 0.41687 | 0.41685 | 0.41690 | ||||
| 0.84057 | 0.84057 | 0.84031 | ||||
| 0.81044 | 0.81047 | 0.80999 | ||||
| 0.77580 | 0.77584 | 0.77555 | ||||
| 0.73641 | 0.73647 | 0.73610 | ||||
| 0.69225 | 0.69228 | 0.69226 | ||||
| 0.93645 | 0.93643 | 0.93650 | ||||
| 0.92320 | 0.92313 | 0.92331 | ||||
| 0.90739 | 0.90727 | 0.90749 | ||||
| 0.88863 | 0.88849 | 0.88867 | ||||
| 0.86650 | 0.86642 | 0.86650 | ||||
| 0.97589 | 0.97594 | 0.97581 | ||||
| 0.97067 | 0.97086 | 0.97047 | ||||
| 0.96435 | 0.96471 | 0.96410 | ||||
| 0.95671 | 0.95714 | 0.95667 | ||||
| 0.94751 | 0.94774 | 0.94749 |
| t | x | CW () | FD sol. | Abs. Error |
|---|---|---|---|---|
| 0.15311 | 0.15375 | |||
| 0.37476 | 0.37435 | |||
| 0.45356 | 0.04532 | |||
| 0.37476 | 0.37435 | |||
| 0.15311 | 0.15375 | |||
| 0.03334 | 0.03385 | |||
| 0.08441 | 0.08409 | |||
| 0.10264 | 0.10275 | |||
| 0.08441 | 0.08409 | |||
| 0.03334 | 0.03385 | |||
| 0.04432 | 0.04405 | |||
| 0.09821 | 0.09820 | |||
| 0.11448 | 0.14424 | |||
| 0.09821 | 0.09820 | |||
| 0.04432 | 0.04405 | |||
| 0.03388 | 0.03336 | |||
| 0.08258 | 0.02868 | |||
| 0.09984 | 0.09978 | |||
| 0.08258 | 0.02868 | |||
| 0.03388 | 0.03336 | |||
| 0.03467 | 0.03477 | |||
| 0.07426 | 0.07454 | |||
| 0.08511 | 0.08536 | |||
| 0.07426 | 0.07454 | |||
| 0.03467 | 0.03477 |
| t | x | |||||
|---|---|---|---|---|---|---|
| 0.07964 | 0.09655 | 0.11655 | 0.13990 | 0.15307 | ||
| 0.19225 | 0.23413 | 0.28375 | 0.34183 | 0.37473 | ||
| 0.23141 | 0.28223 | 0.34248 | 0.41306 | 0.45307 | ||
| 0.19225 | 0.23413 | 0.28375 | 0.34183 | 0.37473 | ||
| 0.07964 | 0.09655 | 0.11655 | 0.13990 | 0.15307 | ||
| 0.05989 | 0.05687 | 0.05059 | 0.04035 | 0.03379 | ||
| 0.14423 | 0.13762 | 0.12318 | 0.09935 | 0.08414 | ||
| 0.17349 | 0.16578 | 0.14867 | 0.12034 | 0.10226 | ||
| 0.14423 | 0.13762 | 0.12318 | 0.09935 | 0.08414 | ||
| 0.05989 | 0.05687 | 0.05059 | 0.04035 | 0.03379 | ||
| 0.06147 | 0.06109 | 0.05848 | 0.05137 | 0.04484 | ||
| 0.14675 | 0.14496 | 0.13691 | 0.11652 | 0.09822 | ||
| 0.17602 | 0.17353 | 0.16317 | 0.13738 | 0.11439 | ||
| 0.14675 | 0.14496 | 0.13691 | 0.11652 | 0.09822 | ||
| 0.06147 | 0.06109 | 0.05848 | 0.05137 | 0.04484 | ||
| 0.05586 | 0.05096 | 0.04473 | 0.03777 | 0.03398 | ||
| 0.13349 | 0.12173 | 0.10709 | 0.09125 | 0.08278 | ||
| 0.16017 | 0.14604 | 0.12857 | 0.10987 | 0.09994 | ||
| 0.13349 | 0.12173 | 0.10709 | 0.09125 | 0.08278 | ||
| 0.05586 | 0.05096 | 0.04473 | 0.03777 | 0.03398 | ||
| 0.05763 | 0.05470 | 0.04928 | 0.04032 | 0.03497 | ||
| 0.13694 | 0.12854 | 0.11323 | 0.08846 | 0.07403 | ||
| 0.16400 | 0.15339 | 0.13410 | 0.10309 | 0.08513 | ||
| 0.13694 | 0.12854 | 0.11323 | 0.08846 | 0.07403 | ||
| 0.05763 | 0.05470 | 0.04928 | 0.04032 | 0.03497 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkiatsakul, T.; Koonprasert, S.; Neamprem, K. New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions. Mathematics 2019, 7, 813. https://doi.org/10.3390/math7090813
Korkiatsakul T, Koonprasert S, Neamprem K. New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions. Mathematics. 2019; 7(9):813. https://doi.org/10.3390/math7090813
Chicago/Turabian StyleKorkiatsakul, Thanon, Sanoe Koonprasert, and Khomsan Neamprem. 2019. "New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions" Mathematics 7, no. 9: 813. https://doi.org/10.3390/math7090813
APA StyleKorkiatsakul, T., Koonprasert, S., & Neamprem, K. (2019). New Analytical Solutions for Time-Fractional Kolmogorov-Petrovsky-Piskunov Equation with Variety of Initial Boundary Conditions. Mathematics, 7(9), 813. https://doi.org/10.3390/math7090813





