On Uniquely 3-Colorable Plane Graphs without Adjacent Faces of Prescribed Degrees

Abstract

A graph G is uniquely k-colorable if the chromatic number of G is k and G has only one k-coloring up to the permutation of the colors. For a plane graph G, two faces $f_1$ and $f_2$ of G are adjacent $(i,j)$-faces if $d(f_1)=i$, $d(f_2)=j$, and $f_1$ and $f_2$ have a common edge, where $d(f)$ is the degree of a face f. In this paper, we prove that every uniquely three-colorable plane graph has adjacent $(3,k)$-faces, where $k\le 5$. The bound of five for k is the best possible. Furthermore, we prove that there exists a class of uniquely three-colorable plane graphs having neither adjacent $(3,i)$-faces nor adjacent $(3,j)$-faces, where $i,j$ are fixed in $\{3,4,5\}$ and $i\ne j$. One of our constructions implies that there exists an infinite family of edge-critical uniquely three-colorable plane graphs with n vertices and $\frac{7}{3}n-\frac{14}{3}$ edges, where $n(\ge 11)$ is odd and $n\equiv 2(\mathrm{mod}3)$.

1. Introduction

Graph coloring is one of the most studied problems in graph theory, because it has many important applications [1,2,3]. The main aim of the problem is to assign colors to the elements of a graph, such as vertices, subject to certain constraints.

For a plane graph G, $V(G)$, $E(G)$, and $F(G)$ are the sets of vertices, edges, and faces of G, respectively. The degree of a vertex $v\in V(G)$, denoted by $d_G(v)$, is the number of neighbors of v in G. The degree of a face $f\in F(G)$, denoted by $d_G(f)$, is the number of edges in its boundary, cut edges being counted twice. When no confusion can arise, $d_G(v)$ and $d_G(f)$ are simplified as $d(v)$ and $d(f)$, respectively. A face f is a k-face if $d(f)=k$ and a $k^{+}$-face if $d(f)\ge k$. Two faces $f_1$ and $f_2$ of G are adjacent $(i,j)$-faces if $d(f_1)=i$, $d(f_2)=j$, and $f_1$ and $f_2$ have at least one common edge. Two distinct paths of G are internally disjoint if they have no internal vertices in common. For other terminologies and notations in graph theory, we refer to [4].

A k-coloring of a graph G is an assignment of k colors to the vertices of G such that no two adjacent vertices are assigned the same color. A graph G is k-colorable if G admits a k-coloring. The chromatic number of G, denoted by $\chi (G)$, is the minimum number k such that G is k-colorable. A graph G is uniquely k-colorable if $\chi (G)=k$ and G has only one k-coloring up to the permutation of the colors, where the coloring is called a unique k-coloring of G. In other words, all k-colorings of G induce the same partition of $V(G)$ into k independent sets, in which an independent set is called a color class of G. In addition, uniquely colorable graphs may be defined in terms of their chromatic polynomials, which was initiated by Birkhoff [5] for planar graphs in 1912 and for general graphs by Whitney [6] in 1932. A graph G is uniquely k-colorable if and only if its chromatic polynomial is $k!$. For a discussion of chromatic polynomials, see Read [7].

Uniquely colorable graphs were first studied by Harary and Cartwright [8] in 1968. They proved the following theorem.

Theorem 1

(Harary and Cartwright [8]). Let G be a uniquely k-colorable graph. Then, for any unique k-coloring of G, the subgraph induced by the union of any two color classes is connected.

As a corollary of Theorem 1, it can be seen that a uniquely k-colorable graph G has at least $(k-1)|V(G)|-(\genfrac{}{}{0pt}{}{k}{2})$ edges. There are many references on uniquely colorable graphs [9,10,11,12,13].

Dailey [14] proved that the problem of determining whether a graph G is uniquely colorable is NP-complete. However, it is still open for the case of planar graphs. Therefore, it is important to characterize the structure of uniquely colorable planar graphs.

Chartrand and Geller [10] in 1969 started to study uniquely colorable planar graphs. They proved that uniquely three-colorable planar graphs with at least four vertices contain at least two triangles, uniquely four-colorable planar graphs are maximal planar graphs, and uniquely five-colorable planar graphs do not exist. Aksionov [15] in 1977 improved the lower bound for the number of triangles in a uniquely three-colorable planar graph. He proved that a uniquely three-colorable planar graph with at least five vertices contains at least three triangles and gave a complete description of uniquely three-colorable planar graphs containing exactly three triangles. Li et al. [12] proved that if a uniquely three-colorable planar graph G has at most four triangles, then G has two adjacent triangles. Moreover, for any $k\ge 5$, they constructed a uniquely three-colorable planar graph with k triangles and without adjacent triangles.

Let G be a uniquely k-colorable graph. G is edge-critical if $G-e$ is not uniquely k-colorable for any edge $e\in E(G)$. Obviously, if a uniquely k-colorable graph G has exactly $(k-1)|V(G)|-(\genfrac{}{}{0pt}{}{k}{2})$ edges, then G is edge-critical. Mel’nikov and Steinberg [16] in 1977 asked to find an exact upper bound for the number of edges in an edge-critical uniquely three-colorable planar graph with n vertices. In 2013, Matsumoto [17] proved that an edge-critical uniquely three-colorable planar graph has at most $\frac{8}{3}n-\frac{17}{3}$ edges and constructed an infinite family of edge-critical uniquely three-colorable planar graphs with n vertices and $\frac{9}{4}n-6$ edges, where $n\equiv 0(\mathrm{mod}4)$. This upper bound was improved by Li et al. [13] to $\frac{5}{2}n-6$ when $n\ge 6$.

In this paper, we mainly prove Theorem 2.

Theorem 2.

If G is a uniquely three-colorable plane graph, then G has adjacent $(3,k)$-faces, where $k\le 5$. The bound five for k is the best possible.

Furthermore, by using constructions, we prove that there exist uniquely three-colorable plane graphs having neither adjacent $(3,i)$-faces nor adjacent $(3,j)$-faces, where $i,j$ are fixed in $\{3,4,5\}$ and $i\ne j$. One of our constructions implies that there exists an infinite family of edge-critical uniquely three-colorable plane graphs with n vertices and $\frac{7}{3}n-\frac{14}{3}$ edges, where $n(\ge 11)$ is odd and $n\equiv 2(\mathrm{mod}3)$. Our results further characterize the structure of the uniquely three-colorable plane graphs. The results can be used in optimal territorial distribution of mobile operators’ transmitters.

2. Proof of Theorem 2

Now, we prove Theorem 2. First we give a useful Lemma 1.

Lemma 1.

Let G be a plane graph with three faces. If G has no adjacent $(3,k)$-faces, where $k\le 5$, then $|E(G)|\ge 2|F(G)|$.

Proof. 

We prove this by using a simple charging scheme. Since G has no adjacent $(3,k)$-faces when $k\le 5$, for any edge e incident to a three-face f, e is incident to a face of degree at least six. Let $ch(f)=d(f)$ for any face $f\in F(G)$, and we call $ch(f)$ the initial charge of the face f. Let initial charges in G be redistributed according to the following rule.

Rule: For each three-face f of G and each edge e incident with f, the $6^{+}$-face incident with e sends $\frac{1}{3}$ charge to f through e.

Denote by $c{h}^{\prime }(f)$ the charge of a face $f\in F(G)$ after applying the redistributed rule. Then:

$$\sum _{f\in F(G)}c{h}^{\prime }(f)=\sum _{f\in F(G)}ch(f)=\sum _{f\in F(G)}d(f)=2|E(G)|$$

(1)

On the other hand, for any three-face f of G, since the degree of each face adjacent to f is at least six, then by the redistributed rule, $c{h}^{\prime }(f)=ch(f)+3·\frac{1}{3}=d(f)+1=4$. For any four-face or five-face f of G, $c{h}^{\prime }(f)=ch(f)=d(f)\ge 4$. For any $6^{+}$-face f of G, since f is incident to at most $d(f)$ edges, each of which is incident to a three-face, then $c{h}^{\prime }(f)\ge ch(f)-\frac{1}{3}d(f)=\frac{2}{3}d(f)\ge 4$. Therefore, we have:

$$\sum _{f\in F(G)}c{h}^{\prime }(f)\ge \sum _{f\in F(G)}4=4|F(G)|$$

(2)

By Formulae (1) and (2), we have $|E(G)|\ge 2|F(G)|$. □

Proof of Theorem 2.

Suppose that the theorem is not true, and let G be a counterexample to the theorem. Then, G has at least one three-face and no adjacent $(3,k)$-faces, where $k\le 5$. By Lemma 1, $|E(G)|\ge 2|F(G)|$. Using Euler’s Formula $|V(G)|-|E(G)|+|F(G)|=2$, we can obtain:

$$|E(G)|\le 2|V(G)|-4.$$

Since G is uniquely three-colorable, then by Theorem 1, we have $|E(G)|\ge 2|V(G)|-3.$ This is a contradiction.

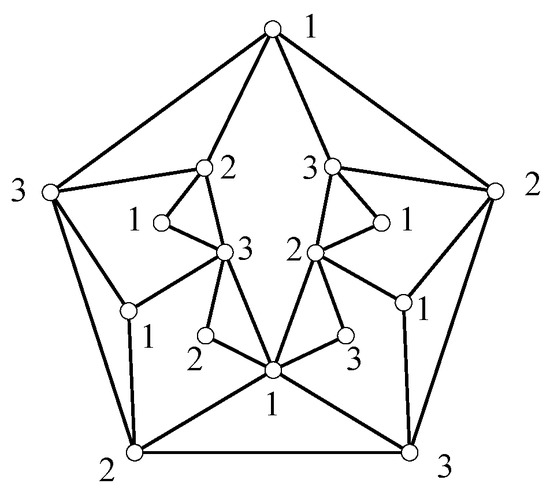
Note that the graph shown in Figure 1 is a uniquely three-colorable plane graph having neither adjacent $(3,3)$-faces nor adjacent $(3,4)$-faces. Therefore, the bound of five for k is the best possible. □

Figure 1. A uniquely three-colorable plane graph having neither adjacent $(3,3)$-faces nor adjacent $(3,4)$-faces.

Remark 1.

By piecing together more copies of the plane graph in Figure 1, one can construct an infinite class of uniquely three-colorable plane graphs having neither adjacent $(3,3)$-faces nor adjacent $(3,4)$-faces.

3. Construction of Uniquely Three-Colorable Plane Graphs without Adjacent (3,3)-Faces or Adjacent (3,5)-Faces

There are many classes of uniquely three-colorable plane graphs having neither adjacent $(3,4)$-faces nor adjacent $(3,5)$-faces, such as even maximal plane graphs (maximal plane graphs in which each vertex has even degree) and maximal outerplanar graphs with at least six vertices. Now, we construct a class of uniquely three-colorable plane graphs having neither adjacent $(3,3)$-faces nor adjacent $(3,5)$-faces and prove that these graphs are edge-critical.

We construct a graph $G_k$ as follows:

(1)

$V(G_k)=\{u,w,v_0,v_1,\dots ,v_{3k-1}\}$;

(2)

$E(G_k)=\{v_0{v}_1,v_1{v}_2,\dots ,v_{3k-2}{v}_{3k-1},v_{3k-1}{v}_0\}\cup \{u{v}_i:i\equiv 1$ or $2(\mathrm{mod}3)\}\cup \{w{v}_i:i\equiv 0$ or $1(\mathrm{mod}3)\}$, where k is odd and $k\ge 3$ (see an example $G_3$ shown in Figure 2).

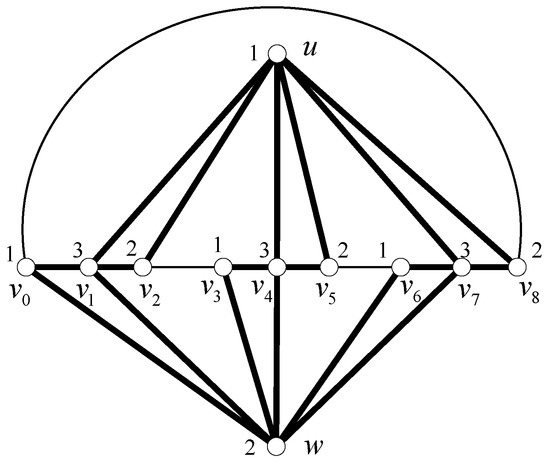Figure 2. An example $G_3$.

Theorem 3.

For any odd k with $k\ge 3$, $G_k$ is uniquely three-colorable.

Proof. 

Let f be any three-coloring of $G_k$. Since $v_0{v}_1\dots v_{3k-1}{v}_0$ is a cycle of odd length and each $v_i$ is adjacent to u or w, we have $f(u)\ne f(w)$. Without loss of generality, let $f(u)=1$ and $f(w)=2$. By the construction of $G_k$, we know that $v_{3j+1}$ is adjacent to both u and w, where $j=0,1,\dots ,k-1$. Therefore, $v_{3j+1}$ can only receive the color three, namely $f(v_{3j+1})=3$, $j=0,1,\dots ,k-1$. Since $v_{3j}$ is adjacent to both w and $v_{3j}$ in $G_k$, we have $f(v_{3j})=1$, $j=0,1,\dots ,k-1$. Similarly, we can obtain $f(v_{3j+2})=2$, $j=0,1,\dots ,k-1$. Therefore, the three-coloring f is uniquely decided as shown in Figure 2, and then, $G_k$ is uniquely three-colorable. □

Theorem 4.

For any odd k with $k\ge 3$, $G_k$ is edge-critical.

Proof. 

To complete the proof, it suffices to show that $G_k-e$ is not uniquely three-colorable for any edge $e\in E(G_k)$. Let f be a uniquely three-coloring of $G_k$ shown in Figure 2. Denote by $E_{ij}$ the set of edges in $G_k$ whose ends are colored by i and j, respectively, where $1\le i<j\le 3$. Namely:

$$E_{ij}=\{xy:xy\in E(G_k),f(x)=i,f(y)=j\},1\le i<j\le 3.$$

• Observation 1. Both the subgraphs $G_k\left[E_{13}\right]$ and $G_k\left[E_{23}\right]$ of $G_k$ induced by $E_{13}$ and $E_{23}$ are trees.
• Observation 2. The subgraph $G_k\left[E_{12}\right]$ of $G_k$ induced by $E_{12}$ consists of k internally disjoint paths $u{v}_{3i-1}{v}_{3i}w$, where $i=1,2,\dots ,k$.

If $e\in E_{13}\cup E_{23}$, then $G_k-e$ is not uniquely three-colorable by Observation 1. Suppose that $e\in E_{12}$. By Observation 2, there exists a number $t\in \{1,2,\dots ,k\}$ such that $e\in \{u{v}_{3t-1},v_{3t-1}{v}_{3t},v_{3t}w\}$. Moreover, $G_k-e$ contains at least one vertex of degree two. By repeatedly deleting vertices of degree two in $G_k-e$, we can obtain a subgraph $G_k-\{v_{3t-1},v_{3t}\}$ of $G_k$. Now, we prove that $G_k-\{v_{3t-1},v_{3t}\}$ is not uniquely three-colorable.

It can be seen that the restriction $f_0$ of f to the vertices of $G_k-\{v_{3t-1},v_{3t}\}$ is a three-coloring of $G_k-\{v_{3t-1},v_{3t}\}$. On the other hand, $G_k-\{v_{3t-1},v_{3t},u,w\}$ is a path, denoted by P. Let $f^{\prime }(u)=f^{\prime }(w)=1$, and alternately, color the vertices of P by the other two colors. We can obtain a three-coloring $f^{\prime }$ of $G_k-\{v_{3t-1},v_{3t}\}$, which is distinct from $f_0$. Since each three-coloring of $G_k-\{v_{3t-1},v_{3t}\}$ can be extended to a three-coloring of $G_k-e$, we know that $G_k-e$ is not uniquely three-colorable when $e\in E_{12}$.

Since $E(G_k)=E_{12}\cup E_{13}\cup E_{23}$, $G_k-e$ is not uniquely three-colorable for any edge $e\in E(G_k)$. □

Note that $G_k$ has $3k+2$ vertices and $7k$ edges by the construction. From Theorem 4, we can obtain the following result.

Corollary 1.

There exists an infinite family of edge-critical uniquely three-colorable plane graphs with n vertices and $\frac{7}{3}n-\frac{14}{3}$ edges, where $n(\ge 11)$ is odd and $n\equiv 2(\mathrm{mod}3)$.

Denote by $size(n)$ the upper bound of the number of edges of edge-critical uniquely three-colorable planar graphs with n vertices. Then, by Corollary 1 and the result due to Li et al. [13], we can obtain the following result.

Corollary 2.

For any odd integer n such that $n\equiv 2(\mathrm{mod}3)$ and $n\ge 11$, we have $\frac{7}{3}n-\frac{14}{3}\le size(n)\le \frac{5}{2}n-6$.

Proof. 

First, in [13], Li et al. proved that $size(n)\le \frac{5}{2}n-6$ for any edge-critical uniquely three-colorable planar graph G with $n(n\ge 6)$ vertices. Then, by Corollary 1, we can conclude that Corollary 2 is true. □

Corollary 2 improves the lower bound $\frac{9}{4}n-6$ of $size(n)$ given by Matsumoto [17] and gives a negative answer to a problem proposed by Mel’nikov and Steinberg [16], who asked that $size(n)=\frac{9}{4}n-6$ for any $n\ge 12$.

4. Conclusions and Conjectures

In this paper, we obtained a structural property of uniquely three-colorable plane graphs. We proved that every uniquely three-colorable plane graph has adjacent $(3,k)$-faces, where $k\le 5$, and the bound of five for k is the best possible. The graph in Figure 1 shows a uniquely three-colorable plane graph having neither adjacent $(3,3)$-faces nor adjacent $(3,4)$-faces. However this plane graph is two-connected. This prompts us to propose the following conjecture.

Conjecture 1.

Let G be a three-connected uniquely three-colorable plane graph. Then, G has adjacent $(3,k)$-faces, where $k\le 4$.

It can be seen that the uniquely three-colorable plane graph $G_k$ constructed in Section 3 is three-connected. So Therefore, Conjecture 1 is true, then the bound of four for k is the best possible. Moreover, because the family of graphs $G_k$ is the edge-critical uniquely three-colorable planar graphs with the largest number of edges found at present, we recall the follow conjecture proposed by Li et al [13].

Conjecture 2 

([13]). Let G be an edge-critical uniquely three-colorable planar graph with n vertices. Then, $size(n)\le \frac{7}{3}n-\frac{14}{3}$.