Iterative Algorithms for Split Common Fixed Point Problem Involved in Pseudo-Contractive Operators without Lipschitz Assumption

Abstract

Two iterative algorithms are suggested for approximating a solution of the split common fixed point problem involved in pseudo-contractive operators without Lipschitz assumption. We prove that the sequence generated by the first algorithm converges weakly to a solution of the split common fixed point problem and the second one converges strongly. Moreover, the sequence $\left\{x_n\right\}$ generated by Algorithm 3 strongly converges to $z={\mathrm{proj}}_{S}0,$ which is the minimum-norm solution of problem (1). Numerical examples are included.

1. Introduction

The split common fixed point problem was investigated in 2009 by Censor Y. and Segal A. [1]. Further research on this problem discussed in works by the authors of [2,3,4,5,6,7,8,9,10,11,12]. More specifically, given two Hilbert space ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, nonlinear operators $U:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $T:{\mathcal{H}}_2\to {\mathcal{H}}_2$ and a bounded linear operator A: ${\mathcal{H}}_1\to {\mathcal{H}}_2$. Let $x\in {\mathcal{H}}_1$ be a solution of split common fixed point problem satisfying

$$x\in F\left(U\right)\mathrm{and}Ax\in F\left(T\right)$$

(1)

where $F\left(U\right)$ and $F\left(T\right)$ mean the fixed point sets. If U and T are both metric projects, problem (1) is actually problem (2) [13,14], and further development of this topic made by [15,16,17,18,19]. To be more specific, given two nonempty closed convex sets $C\subset {\mathcal{H}}_1$ and $Q\subset {\mathcal{H}}_2$ and A is above mentioned. Let $x\in {\mathcal{H}}_1$ be a solution of split feasibility problem satisfying

$$x\in C\mathrm{and}Ax\in Q,$$

(2)

These two problems ((1) and (2)) have received much attention, and have been extensively investigated due to applications in signal processing, image reconstruction, [14], and intensity modulated radiation therapy [20]. Recently, Yen L. et al. [21] learn the problem (2) and applying it to a model in electricity production, they successfully established a Nash–Cournot equilibrium model with minimal environmental cost. Wang J. et al. [22] study the linear convergence of CQ algorithm for solving the problem (2) and investigate an application in gene regulatory network inference.

For solving the problem (1), Censor Y. and Segal A. [1] suggested the following scheme.

$$x_{n+1}=U(x_n-\tau A^{\ast }(I-T)A{x}_n),$$

(3)

where $\tau$ is a fixed stepsize and $A^{\ast }$ is the adjoint operator of A. Algorithm (3) was originally designed to solved problem (1) for directed operators. Noting that if the stepsize $\tau$ is chosen in $(0,2/\parallel A{\parallel }^2)$, then the iterative sequence $\left\{x_n\right\}$ generated by (3) weakly converges to a solution of the problem (1). Subsequently, iterative schemes and these variants [10,23] were explored to the demicontractive operators, quasi-nonexpansive operators and finite many directed operators.

Very recently, Wang F. [23] has been devoting himself to the study of problems (1). Accordingly, he proposed a new method for solving the problems (1) so that the variable stepsize does not need to compute the norm $\parallel A\parallel$:

$$x_{n+1}=x_n-{\rho }_n((I-U)x_n+A^{\ast }(I-T)A{x}_n),$$

(4)

where $\left\{{\rho }_n\right\}\subset (0,\infty )$ is chosen such that

$${\rho }_n=\frac{\parallel (I-U)x_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2}{\parallel (I-U)x_n+A^{\ast }(I-T)A{x}_n{\parallel }^2},$$

(5)

Wang obtained the weak convergence of algorithm (4).

In this paper, we extend a previous author’s results from the demicontractive operators [8,10,24], firmly-nonexpansive operators [25], quasi-nonexpansive operators [26], directed operators [1], nonexpansive operators [27], and strictly pseudo-contractive operators [28] to the more general pseudo-contractive operators. Subsequently, two algorithms are suggested based on (4) and (5) to solve the problem (1). Weak and strong convergence of the proposed algorithms are obtained.

2. Preliminaries

Let $\mathcal{H}$ be a real Hilbert space equipped up its inner product $⟨·,·⟩$ and norm $\parallel ·\parallel$ [8]. The notation $x_n\rightharpoonup x$ means weak convergence and $x_n\to x$ means strong one. The notation $Fix\left(T\right)$ stands for the set of fixed points of the operator T. The symbol ${\omega }_w\left(x_n\right)$ denotes the weak $\omega$-limit set of $\left\{x_n\right\}$, that is,

$$\begin{array}{c}{\omega }_w\left(x_n\right)=\{x:x_{n_i}\rightharpoonup x\mathrm{for}\mathrm{some}\mathrm{subsequence}\left\{x_{n_i}\right\}\mathrm{of}\left\{x_n\right\}\}.\hfill \end{array}$$

Let C be a nonempty closed convex subset of $\mathcal{H}$. Recall that the projection $P_C$ from $\mathcal{H}$ onto C defined by

$$\begin{array}{c}∥x-P_{C}x∥=min\{\parallel x-y\parallel :y\in C,x\in \mathcal{H}\}.\hfill \end{array}$$

Propsition 1

([10]). Given $x\in \mathcal{H}$ and $z\in C$.

(1) 

$z=P_{C}x\iff ⟨x-z,y-z⟩\le 0$, for all $y\in C$.

(2) 

$z=P_{C}x\iff {\parallel x-z\parallel }^2\le {\parallel x-y\parallel }^2-{\parallel y-z\parallel }^2,$ for all $y\in C$.

(3) 

$⟨x-y,P_{C}x-P_{C}y⟩\ge {∥P_{C}x-P_{C}y∥}^2,$ for all $y\in \mathcal{H}$, which hence implies that $P_C$ is nonexpansive.

Definition 1

([4]). Let $T:\mathcal{H}\to \mathcal{H}$ be a nonlinear operator.

• T is called nonexpansive if

  $$\begin{array}{c}∥Tx-Ty∥\le \parallel x-y\parallel ,\forall x,y\in \mathcal{H};\hfill \end{array}$$
• T is called firmly nonexpansive if

  $$\begin{array}{c}{∥Tx-Ty∥}^2\le {\parallel x-y\parallel }^2-{\parallel (I-T)x-(I-T)y\parallel }^2,\forall x,y\in \mathcal{H}\hfill \end{array}$$

  or equivalently

  $$\begin{array}{c}{∥Tx-Ty∥}^2\le ⟨Tx-Ty,x-y⟩,\forall x,y\in \mathcal{H}.\hfill \end{array}$$
  Also, the mapping I − T is firmly nonexpansive.
• T is called strictly pseudo-contractive if there exists $k<1$ such that

  $$\begin{array}{c}{∥Tx-Ty∥}^2\le {\parallel x-y\parallel }^2+k{\parallel (I-T)x-(I-T)y\parallel }^2,\forall x,y\in \mathcal{H}\hfill \end{array}$$
• L-Lipschitzian if there exists $L>0$ such that

  $$\begin{array}{c}∥Tx-Ty∥\le L\parallel x-y\parallel ,\forall x,y\in \mathcal{H};\hfill \end{array}$$

Definition 2

([24]). Let $T:\mathcal{H}\to \mathcal{H}$ be a nonlinear operator with $Fix\left(T\right)\ne \varnothing$.

• T is called demicontractive if there exists a constant $k\in [0,1)$ such that

  $$\begin{array}{c}{∥Tx-x^{\ast }∥}^2\le \parallel x-x^{\ast }{\parallel }^2+k{\parallel x-Tx\parallel }^2,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right)\hfill \end{array}$$

  or equivalently

  $$\begin{array}{c}⟨x-Tx,x-x^{\ast }⟩\ge \frac{1-k}{2}{\parallel x-Tx\parallel }^2,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right);\hfill \end{array}$$
• T is called directed if

  $$\begin{array}{c}{∥Tx-x^{\ast }∥}^2\le \parallel x-x^{\ast }{\parallel }^2-{\parallel x-Tx\parallel }^2,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right)\hfill \end{array}$$

  which is equivalent to

  $$\begin{array}{c}⟨x-Tx,x-x^{\ast }⟩\ge {\parallel x-Tx\parallel }^2,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right);\hfill \end{array}$$

Definition 3

([4]). Let $T:\mathcal{H}\to \mathcal{H}$ be a nonlinear operator.

T is called pseudo-contractive if

$$\begin{array}{c}⟨Tx-Ty,x-y⟩\le {\parallel x-y\parallel }^2,\forall x,y\in \mathcal{H}.\hfill \end{array}$$

It is well known that T is a pseudo-contractive operator if and only if

$$\begin{array}{c}{∥Tx-Ty∥}^2\le {\parallel x-y\parallel }^2+∥\left(I-T\right)x-\left(I-T\right)y∥,\forall x,y\in \mathcal{H}.\hfill \end{array}$$

Propsition 2

([29]). Let T be a pseudo-contractive operator with the nonempty fixed point set $Fix\left(T\right)$, then the following conclusion holds.

$$\begin{array}{c}⟨Tx-x,Tx-x^{\ast }⟩\le {∥Tx-x∥}^2,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right).\hfill \end{array}$$

Generally speaking, pseudo-contractive operators are also assumed to be L-Lipschitzian with $L>1$. Next, to overcome the L-Lipschitzian property, the authors of [29] assume that the pseudo-contractive operator T satisfies the following condition.

$$⟨Tx-x,Tx-x^{\ast }⟩\le 0,\forall (x,x^{\ast })\in \mathcal{H}\times Fix\left(T\right).$$

(6)

Definition 4

([23]). Let $T:\mathcal{H}\to \mathcal{H}$ be a nonlinear operator with $Fix\left(T\right)\ne \varnothing$. Then, $I-T$ is said to be demiclosed at zero, if, for any $\left\{x_n\right\}$ in $\mathcal{H}$, there holds the following implication:

$$\begin{array}{c}\hfill \left.\begin{array}{c}\hfill x_n\rightharpoonup x\\ \hfill (I-T)x_n\to 0\end{array}\right]\Rightarrow x\in Fix\left(T\right)\end{array}$$

The demiclosedness for pseudo-contractive operators in the following will often be used.

Lemma 1

([29]). Let $\mathcal{H}$ be a real Hilbert space, C a closed convex subset of $\mathcal{H}$. Let $T:C\to C$ be a continuous pseudo-contractive operator. Then

(1) 

$Fix\left(T\right)$ is a closed convex subset of C,

(2) 

$(I-T)$ is demiclosed at zero.

To attain weak convergence result, the following result is useful.

Lemma 2

([10]). Let $\mathcal{H}$ be a Hilbert space and $\left\{x_n\right\}$ be a bounded sequence in $\mathcal{H}$ such that there exists a nonempty closed convex set $C\in \mathcal{H}$ satisfying

(1) 

for every $w\in C$, ${lim}_{n\to \infty }\parallel x_n-w\parallel$ exists;

(2) 

each weak cluster point of the sequence $\left\{x_n\right\}$ is in C.

Then $\left\{x_n\right\}$ converges weakly to a point in C. More specifically, $x^{\ast }=li{m}_{n\to \infty P_S{x}_n}$.

To attain strong convergence result, we need to use the following lemmas.

Lemma 3

([8]). Let $\left\{a_n\right\}$ be a sequence of nonnegative real numbers satisfying the property

$$a_{n+1}\le (1-{\gamma }_n)a_n+{\sigma }_n,n\ge 0.$$

where $\left\{{\gamma }_n\right\}\subset$ (0,1) and $\left\{{\sigma }_n\right\}$ are such that

(1) 

${\sum }_{n=0}^{\infty }{\gamma }_n=\infty$;

(2) 

either ${lim\; sup}_{n\to \infty }\frac{{\sigma }_n}{{\gamma }_n}\le 0$ or ${\sum }_{n=0}^{\infty }\left|{\sigma }_n\right|<\infty$.

Then $\left\{a_n\right\}$ converges to zero.

Lemma 4

([4]). Let $\left\{u_n\right\}$ be a sequence of real numbers. Assume $\left\{u_n\right\}$ does not decrease at infinity, that is, there exists at least a subsequence $\left\{u_{n_k}\right\}$ of $\left\{u_n\right\}$ such that $u_{n_k}\le u_{n_k+1}$ for all $k\ge 0$. For every $n\ge N_0$, define an $\left\{\tau \right(n\left)\right\}$ as

$$\begin{array}{c}\tau \left(n\right)=max\left\{i\le n:u_{n_i}<u_{n_i+1}\right\}.\hfill \end{array}$$

Then $\tau \left(n\right)\to \infty$ as $n\to \infty$ and for all $n\ge N_0$,

$$\begin{array}{c}max\{u_{\tau \left(n\right)},u_n\}\le u_{\tau \left(n\right)+1}.\hfill \end{array}$$

In the following two sections, we consider the problem (1) for pseudo-contractive operators without Lipschitz assumption. For problem (1), the standard assumptions are usually the following.

• the problem (1) is consistent, notation S means the solution set;
• both T and U are continuous pseudo-contractive operators without Lipschitz assumption.

3. Weak Convergence Theorem

Next come the iterative scheme for approximating a solution of the problem (1) involved in pseudo-contractive operators without Lipschitz assumption.

Algorithm 1.

Initial guess $x_0$ is arbitrary chosen and assume that $x_n$ has been constructed. If

$$\parallel (I-U)x_n+A^{\ast }(I-T)A{x}_n\parallel =0,$$

(7)

then stop (i.e., $x_n$ solves the problem (1)); otherwise, calculate the next $x_{n+1}$ by the formula [23]:

$$\begin{array}{c}{x}_{n+1}=x_n-{\rho }_n((I-U)x_n+A^{\ast }(I-T)A{x}_n),\hfill \end{array}$$

where the stepsize sequence ${\tau }_n$ is chosen as

$$\begin{array}{c}{\rho }_n=\frac{\parallel (I-U)x_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2}{\parallel (I-U)x_n+A^{\ast }(I-T)A{x}_n{\parallel }^2},\hfill \end{array}$$

We need two lemmas to complete the convergence analysis of our proposed algorithm. The first lemma shows that the proposed algorithm is well defined.

Lemma 5.

Assume that (7) holds for $n\ge 0$, then $x_n$ solves the problem (1).

Proof. 

For any $w\in S$ and (6), we have

$$\begin{array}{ccc}0\hfill & =& ⟨(I-U)x_n+A^{\ast }(I-T)A{x}_n,x_n-w⟩\hfill \\ & =& ⟨x_n-U{x}_n,x_n-U{x}_n⟩+⟨(I-T)A{x}_n,A{x}_n-TA{x}_n⟩\hfill \\ & & +⟨x_n-U{x}_n,U{x}_n-w⟩+⟨(I-T)A{x}_n,TA{x}_n-Aw⟩\hfill \\ & \ge & \parallel x_n-U{x}_n{\parallel }^2+{\parallel A{x}_n-TA{x}_n\parallel }^2.\hfill \end{array}$$

Hence, $x_n=U{x}_n$ and $A{x}_n=TA{x}_n$, and the proof is thus complete. □

Lemma 6.

Assume that the sequence $x_n$ satisfies

$$\begin{array}{c}\underset{n\to \infty }{lim}\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}=0,\hfill \end{array}$$

then it follows that

$$\begin{array}{c}\underset{n\to \infty }{lim}\parallel x_n-U{x}_n\parallel =\underset{n\to \infty }{lim}\parallel (I-T)A{x}_n\parallel =0,\hfill \end{array}$$

Proof. 

By our hypothesis, we have

$$\begin{array}{cc}\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}\hfill & \ge \frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{2(\parallel x_n-U{x}_n{\parallel }^2+\parallel A^{\ast }(I-T)A{x}_n{\parallel }^2)}\hfill \\ & \ge \frac{\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2}{2\max (1,\parallel A{\parallel }^2)}\hfill \end{array}$$

Hence, the desired assertion follows. □

The second lemma analyzes the convergence of the proposed algorithm. Now the weakly convergence of Algorithm 1 presented below.

Theorem 1.

Let $\left\{x_n\right\}$ be the sequence generated by Algorithm 1. Then, $\left\{x_n\right\}$ converges weakly to a solution $x^{\ast }$ of problem (1), where $x^{\ast }=li{m}_{n\to \infty P_S{x}_n}$.

Proof. 

For any $w\in S$, by the expression of $y_n$, from (6), we obtain

$$\begin{array}{ccc}⟨y_n,x_n-w⟩\hfill & =& ⟨(I-U)x_n+A^{\ast }(I-T)A{x}_n,x_n-w⟩\hfill \\ & =& ⟨x_n-U{x}_n,x_n-U{x}_n⟩+⟨(I-T)A{x}_n,A{x}_n-TA{x}_n⟩\hfill \\ & & +⟨x_n-U{x}_n,U{x}_n-w⟩+⟨(I-T)A{x}_n,TA{x}_n-Aw⟩\hfill \\ & \ge & \parallel x_n-U{x}_n{\parallel }^2+{\parallel A{x}_n-TA{x}_n\parallel }^2.\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\parallel x_{n+1}{-w\parallel }^2\hfill & =\parallel x_n{-w\parallel }^2-2{\rho }_n⟨y_n,x_n-w⟩+{\rho }_n^2{\parallel y_n\parallel }^2\hfill \\ & \le \parallel x_n{-w\parallel }^2-\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}\hfill \end{array}$$

In particular, $\parallel x_{n+1}-w\parallel \le \parallel x_n-w\parallel$, so $\left\{x_n\right\}$ is Féjer-monotone w.r.s. S.

Since $\left\{x_n\right\}$ is Féjer-monotone, so $\{\parallel x_n-z\parallel \}$ is nonincreasing. Hence, $\left\{x_n\right\}$ is bounded, and so is the sequence $\left\{A{x}_n\right\}$. Moreover,

$$\sum _{n=0}^{\infty }\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}<\infty .$$

In particular, we have

$$\underset{n\to \infty }{lim}\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}=0.$$

By Lemma 6, this yields ${lim}_{n\to \infty }\parallel x_n-U{x}_n\parallel ={lim}_{n\to \infty }\parallel (I-T)A{x}_n\parallel =0.$ From Lemma 1 and Lemma 2, sequence $\left\{x_n\right\}$ weakly converges to $x^{\ast }$ of problem (1). □

Now, we use the result to solve the problem (2).

Algorithm 2.

An initial guess $x_0$ is arbitrarily chosen and we assume that $x_n$ has been constructed. If

$$\parallel (I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n\parallel =0,$$

then stop (i.e., $\left\{x_n\right\}$ solves the problem (2)); otherwise, calculate the next $x_{n+1}$ by the formula [23]

$$x_{n+1}=x_n-{\rho }_n((I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n),$$

(8)

where the stepsize sequence ${\tau }_n$ is chosen as

$$\begin{array}{c}{\rho }_n=\frac{\parallel (I-P_C)x_n{\parallel }^2+{\parallel (I-P_Q)A{x}_n\parallel }^2}{\parallel (I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n{\parallel }^2},\hfill \end{array}$$

Theorem 2.

Let $\left\{x_n\right\}$ be the sequence generated by (8). Then, $\left\{x_n\right\}$ converges weakly to a solution $x^{\ast }$ of problem (2).

4. Strong Convergence Theorem

We proposed a damped algorithm so that the strong convergence is obtained.

Algorithm 3.

Initial guess $x_0$ is arbitrarily chosen and we assume $x_n$ has been constructed. If

$$\parallel (I-U)x_n+A^{\ast }(I-T)A{x}_n\parallel =0,$$

then stop (i.e., $x_n$ solves the problem (1)); otherwise, calculate the next $x_{n+1}$ by the formula:

$$\begin{array}{c}{x}_{n+1}=(1-{\delta }_n)x_n+{\delta }_n(1-{\gamma }_n)(x_n-{\rho }_n((I-U)x_n+A^{\ast }(I-T)A{x}_n)),\hfill \end{array}$$

where the stepsize sequence ${\tau }_n$ is chosen as

$$\begin{array}{c}{\rho }_n=\frac{\parallel (I-U)x_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2}{\parallel (I-U)x_n+A^{\ast }(I-T)A{x}_n{\parallel }^2},\hfill \end{array}$$

Theorem 3.

Assume the parameters satisfy the following conditions.

(i) 

${lim}_{n\to \infty }{\gamma }_n=0$, ${\sum }_{n=0}^{\infty }{\gamma }_n=+\infty$;

(ii) 

$0<{lim\; inf}_{n\to \infty }{\delta }_n(1-{\gamma }_n)\le {lim\; sup}_{n\to \infty }{\delta }_n(1-{\gamma }_n)<1.$

Then the sequence $\left\{x_n\right\}$ generated by Algorithm 3 strongly converges to $z={\mathrm{proj}}_{S}0,$ which is the minimum-norm solution of problem (1).

Proof. 

Let $u_n=x_n-{\rho }_n((I-U)x_n+A^{\ast }(I-T)A{x}_n)$. Analogously,

$$\parallel u_n{-w\parallel }^2\le {\parallel x_n-w\parallel }^2-\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}$$

(9)

By (9), we obtain

$$\begin{array}{cc}\parallel x_{n+1}{-w\parallel }^2\hfill & \le (1-{\delta }_n){\parallel x_n-w\parallel }^2+{\delta }_n{∥(1-{\gamma }_n)u_n-w∥}^2\hfill \\ & \le (1-{\delta }_n)\parallel x_n{-w\parallel }^2+{\delta }_n(1-{\gamma }_n){∥x_n-w∥}^2+{\gamma }_n{\delta }_n{\parallel w\parallel }^2\hfill \\ & \le max\left\{\parallel x_n{-w\parallel }^2,{\parallel w\parallel }^2\right\},\hfill \end{array}$$

(10)

which shows the boundedness of $\left\{x_n\right\}$. Returning to (9) and (10), we have

$$\begin{array}{c}{\delta }_n(1-{\gamma }_n)\left(\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}\right)\le (1-{\gamma }_n{\delta }_n)\parallel x_n{-w\parallel }^2+{\gamma }_n{\delta }_n{\parallel w\parallel }^2-{\parallel x_{n+1}-w\parallel }^2.\hfill \end{array}$$

(11)

Two possible cases are considered.

Case one. Suppose $m>0$ and $n\ge m$ such that $\{\parallel x_n-w\parallel \}$ is nonincreasing. So, we have the existence of ${lim}_{n\to \infty }\parallel x_n-w\parallel$. This, together with (11) and conditions $\left(i\right)$ and $\left(ii\right)$, such that

$$\begin{array}{c}\underset{n\to \infty }{lim}\frac{{\left(\parallel x_n-U{x}_n{\parallel }^2+{\parallel (I-T)A{x}_n\parallel }^2\right)}^2}{\parallel x_n-U{x}_n+A^{\ast }(I-T)A{x}_n{\parallel }^2}=0.\hfill \end{array}$$

By Lemma 6, this yields ${lim}_{n\to \infty }\parallel x_n-U{x}_n\parallel ={lim}_{n\to \infty }\parallel (I-T)A{x}_n\parallel =0$. As shown in Theorem 1, we can get succession $\left\{x_{n_i}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_i}\rightharpoonup p$.

By the definition of $u_n$, we deduce that

$$\begin{array}{c}\underset{n\to \infty }{lim}\parallel u_n-x_n\parallel =0.\hfill \end{array}$$

Let $z_n=(1-{\gamma }_n)u_n=(1-{\gamma }_n)(x_n-{\rho }_n((I-U)x_n+A^{\ast }(I-T)A{x}_n))$, $n\ge 0$. Then

$$\begin{array}{c}\parallel z_n-x_n\parallel \le (1-{\gamma }_n)\parallel u_n-x_n\parallel +{\gamma }_n\parallel x_n\parallel .\hfill \end{array}$$

Furthermore, we obtain from $\left(i\right)$ and the properties of $\left\{x_n\right\}$ that

$$\begin{array}{c}\underset{n\to \infty }{lim}\parallel z_n-x_n\parallel =0.\hfill \end{array}$$

This together with $x_{n_i}\rightharpoonup p$ implies that $z_{n_i}\rightharpoonup p$. So,

$$\underset{n\to \infty }{lim\; sup}⟨w,z_n-w⟩=\underset{i\to \infty }{lim}⟨w,z_{n_i}-w⟩=⟨w,p-w⟩\ge 0.$$

(12)

From (9) and (10):

$$\begin{array}{cc}\parallel x_{n+1}{-w\parallel }^2\hfill & \le (1-{\delta }_n){\parallel x_n-w\parallel }^2+{\delta }_n\left((1-{\gamma }_n){\parallel u_n-w\parallel }^2+2⟨{\gamma }_n(-w),z_n-w⟩\right)\hfill \\ & \le (1-{\gamma }_n{\delta }_n){\parallel x_n-w\parallel }^2+2{\gamma }_n{\delta }_n⟨-w,z_n-w⟩.\hfill \end{array}$$

(13)

We deduce $x_n\to z$ from Lemma 3 and Equations (12) and (13).

Case two. Suppose $n_0\ge 0$, we have

$$\begin{array}{c}\parallel x_{n_0}-w\parallel \le \parallel x_{n_0+1}-w\parallel .\hfill \end{array}$$

Setting $v_n=\{\parallel x_n-w\parallel \}$, then we have

$$\begin{array}{c}{v}_{n_0}\le v_{n_0+1}.\hfill \end{array}$$

For all $n\ge n_0$, we now describe

$$\begin{array}{c}\tau \left(n\right)=max\{l\ge 1:n_0\le l\le n,v_l\le v_{l+1}\}.\hfill \end{array}$$

So $\left\{\tau \right(n\left)\right\}$ is non-decresing satisfying

$$\begin{array}{c}\underset{n\to \infty }{lim}\tau \left(n\right)=\infty \mathrm{and}{v}_{\tau \left(n\right)}\le v_{\tau \left(n\right)+1}.\hfill \end{array}$$

As shown in Case 1, we get

$$\begin{array}{c}\underset{n\to \infty }{lim}\parallel z_{\tau \left(n\right)}-x_{\tau \left(n\right)}\parallel =0.\hfill \end{array}$$

This implies that

$$\begin{array}{c}{\omega }_w\left(z_{\tau \left(n\right)}\right)\subset S.\hfill \end{array}$$

Thus, we obtain

$$\underset{n\to \infty }{lim\; sup}⟨w,z_{\tau \left(n\right)}-w⟩\ge 0.$$

(14)

By $v_{\tau \left(n\right)}\le v_{\tau \left(n\right)+1},$ we have from (13) that

$$\begin{array}{c}{v}_{\tau \left(n\right)}^2\le (1-{\gamma }_{\tau \left(n\right)}{\delta }_{\tau \left(n\right)})v_{\tau \left(n\right)}^2+2{\gamma }_{\tau \left(n\right)}{\delta }_{\tau \left(n\right)}⟨-w,z_{\tau \left(n\right)}-w⟩,\hfill \end{array}$$

(15)

then

$$\begin{array}{c}{v}_{\tau \left(n\right)}^2\le 2⟨-w,z_{\tau \left(n\right)}-w⟩.\hfill \end{array}$$

(16)

Combining (14) and (16), we get

$$\begin{array}{c}\underset{n\to \infty }{lim\; sup}{v}_{\tau \left(n\right)}\le 0\hfill \end{array}$$

and then

$$\begin{array}{c}\underset{n\to \infty }{lim}{v}_{\tau \left(n\right)}=0.\hfill \end{array}$$

(17)

By (15),

$$\begin{array}{c}\underset{n\to \infty }{lim\; sup}{v}_{\tau \left(n\right)+1}^2\le \underset{n\to \infty }{lim\; sup}{v}_{\tau \left(n\right)}^2.\hfill \end{array}$$

Using the above inequality and (17), we have

$$\begin{array}{c}\underset{n\to \infty }{lim}{v}_{\tau \left(n\right)+1}=0.\hfill \end{array}$$

By Lemma 4, this yields

$$\begin{array}{c}0\le v_n\le max\{v_{\tau \left(n\right)},v_{\tau \left(n\right)+1}\},\hfill \end{array}$$

therefore, $v_n\to 0$, i.e., $x_n\to z$. □

Algorithm 4.

Initial guess $x_0$ is arbitrarily chosen and we assume $x_n$ has been constructed. If

$$\parallel (I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n\parallel =0,$$

then stop (i.e., $x_n$ solves problem (2)); otherwise, calculate the next $x_{n+1}$ by the formula

$$x_{n+1}=(1-{\delta }_n)x_n+{\delta }_n(1-{\gamma }_n)(x_n-{\rho }_n((I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n),$$

(18)

where the stepsize sequence ${\tau }_n$ is chosen as

$$\begin{array}{c}{\rho }_n=\frac{\parallel (I-P_C)x_n{\parallel }^2+{\parallel (I-P_Q)A{x}_n\parallel }^2}{\parallel (I-P_C)x_n+A^{\ast }(I-P_Q)A{x}_n{\parallel }^2},\hfill \end{array}$$

Theorem 4.

Assume the parameters satisfy the following conditions.

• ${lim}_{n\to \infty }{\gamma }_n=0$, ${\sum }_{n=0}^{\infty }{\gamma }_n=+\infty$;
• $0<{lim\; inf}_{n\to \infty }{\delta }_n(1-{\gamma }_n)\le {lim\; sup}_{n\to \infty }{\delta }_n(1-{\gamma }_n)<1.$

Then the sequence $\left\{x_n\right\}$ generated by (18) strongly converges to $z={\mathrm{proj}}_{S}0,$ which is the minimum-norm solution of the sproblem (2).

5. Numerical Example

Now, we illustrate the theoretical result by numerical examples.

Let $\mathcal{H}=\mathbf{R}$, inner product $⟨x,y⟩=xy$, and norm $|·|.$ Let $x\in C$, $C=[0,+\infty )$ and $Ux=x+\frac{4}{x+1}-1$. Clearly, Fix(U) = 3. It now

$$\begin{array}{c}⟨x-y,Ux-Uy⟩=⟨x-y,x+\frac{4}{x+1}-y-\frac{4}{y+1}⟩\le {|x-y|}^2\hfill \end{array}$$

for all $x,y\in C$. Hence, U is a pseudo-contractive operator. So is $Tx=x+\frac{3}{x+2}-1$. Truly, both U and T are satisfy the condition (6). For more detail of condition (6), please see the work by the authors of [29].

Let $x\in \mathbf{R}$, $Ax=\frac{1}{3}x$, $n\ge 1$, ${\alpha }_n=\frac{1}{n}$, ${\beta }_n=\frac{1}{8}$, then 3 is the approximation point of the Algorithm 1. Obviously, $A^{\ast }=A$, $Fix\left(U\right)=3$, $Fix\left(T\right)=1$ and $S=\left\{3\right\}$. Next, we rewrite Algorithm 1:

$$\begin{array}{c}{x}_{n+1}=x_n-\frac{3(x_n+6)(x_n-3)}{(4x_n+19)(x_n+1)}-\frac{3(x_n+1)(x_n-3)}{(4x_n+19)(x_n+6)},n\ge 1.\hfill \end{array}$$

Choosing initial values $x_1=5$ and $x_1=1$, respectively, we can see from Figure 1 and the numerical results in Table 1 that the theoretical result of Theorem 1 was demonstrated.

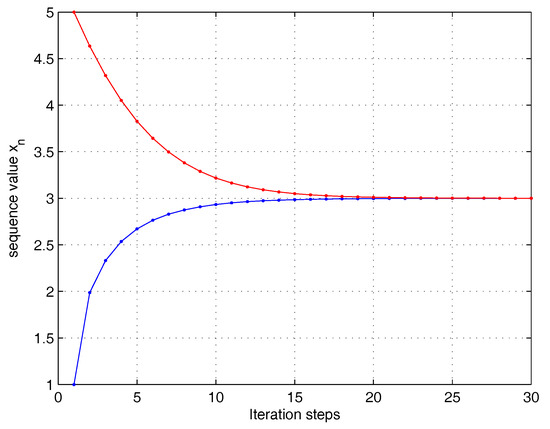
Figure 1. Weak convergence of $\left\{x_n\right\}$.

Table 1. The values of the sequence $x_n$.

n	${\mathit{x}}_{\mathit{n}}$	${\mathit{x}}_{\mathit{n}}$
1	5.000000000000000	1.000000000000000
2	4.634032634032634	1.987577639751553
3	4.318344257776301	2.331041217153439
4	4.050603724176485	2.536578840898608
5	3.827440529292961	2.671476773834111
...	...	...
27	3.001367761622588	2.999614025877529
28	3.001011222409336	2.999714678296111
29	3.000747602653792	2.999789081412396
30	3.000552695614674	2.999844081577622

Analogously, we now rewrite Algorithm 3 as follows.

$$\begin{array}{c}{x}_{n+1}=\frac{7}{8}{x}_n+\frac{n-1}{8n}\left(x_n-\frac{3(x_n+6)(x_n-3)}{(4x_n+19)(x_n+1)}-\frac{3(x_n+1)(x_n-3)}{(4x_n+19)(x_n+6)}\right),n\ge 1.\hfill \end{array}$$

Also, choosing initial values $x_1=5$ and $x_1=1$, respectively, we can see from Figure 2 and the numerical results in Table 2 that the theoretical result of Theorem 3 was demonstrated.

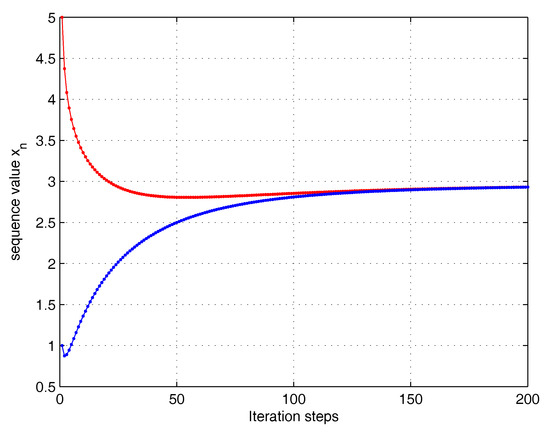
Figure 2. Strong convergence of $\left\{x_n\right\}$.

Table 2. The values of the sequence $x_n$.

n	${\mathit{x}}_{\mathit{n}}$	${\mathit{x}}_{\mathit{n}}$
1	5.000000000000000	1.000000000000000
2	4.375000000000000	0.875000000000000
3	4.084269250864560	0.890072601010101
4	3.895009196768486	0.944633146701975
5	3.754974188264774	1.012848796437149
...	...	...
197	2.930979205568247	2.929539367125689
198	2.931392607026035	2.930001859115338
199	2.931801371854751	2.930458028257748
200	2.932205567529454	2.930908000516816

We can see from Figure 1 and Figure 2 that the rate of weak convergence may be faster than the strong one by comparing the iteration steps.

6. Conclusions

In this paper, we investigated the problem (1) involved in pseudo-contractive operators without Lipschitz assumption. By extending someone’s results from [1,8,10,24,25,26,27,28] to the more general pseudo-contractive operators, we constructed two algorithm for solving the problem (1). Weak and strong convergence theorems are obtained under some mild hypotheses. Besides, we get the minimum-norm solution of problem (1); this is another interesting point. The results of this paper can be applied to engineering, network, and biotechnology.