Abstract
Over the last decade, high dimensional data have been popularly paid attention to in bioinformatics. These data increase the likelihood of detecting the most promising novel information. However, there are limitations of high-performance computing and overfitting issues. To overcome the issues, alternative strategies need to be explored for the detection of true important features. A two-stage approach, filtering and variable selection steps, has been receiving attention. Filtering methods are divided into two categories of individual ranking and feature subset selection methods. Both have issues with the lack of consideration for joint correlation among features and computing time of an NP-hard problem. Therefore, we proposed a new filter ranking method (PF) using the elastic net penalty with sure independence screening (SIS) based on resampling technique to overcome these issues. We demonstrated that SIS-LASSO, SIS-MCP, and SIS-SCAD with the proposed filtering method achieved superior performance of not only accuracy, AUROC, and geometric mean but also true positive detection compared to those with the marginal maximum likelihood ranking method (MMLR) through extensive simulation studies. In addition, we applied it in a real application of colon and lung cancer gene expression data to investigate the classification performance and power of detecting true genes associated with colon and lung cancer.
1. Introduction
In the last decade, high dimensional data has appeared with the development of high throughput techniques, especially in the research area of machine learning [1,2] and data mining [3,4] in biology. The possibility of finding novel true important variables has potentially become high with a huge amount of data. However, due to limitations of computing capabilities and overfitting issues, two-stage approaches of filtering and variable selection for prediction purpose has been popular. These include methods for microarray [5,6,7,8] and RNA-Seq [9,10] data, and genome-wide association studies (GWAS) [11,12]. Filtering methods, which reduce dimensionality and try to retain the most promising features as possible, have long been under development. A number of filtering methods has been proposed to rank features, such as Information gain [13], Markov blanket [14], Bayesian variable selection [15], Boruta [16], Fisher score [17], Relief [18], maximum relevance and minimum redundancy (MRMR) [19], marginal maximum likelihood score (MMLs) [20], among which MMLS is one of the simplest and computationally efficient methods of feature selection with some criteria.
Feature selection methods are divided into two categories of marginal feature ranking and feature subset selection considering relationship among features. Marginal feature ranking methods order individual features by their scores and then drop out irrelevant features with small scores using the desired criteria. [21] utilized the Relief statistical method to rank features. [20] gave a marginal maximum likelihood estimator as a feature ranking method and improved classification accuracy. [22] also developed a novel method to rank features and then chose the optimal subset of features. Individual ranking methods have been widely used in high throughput data analysis because of their simplicity and computational time efficiency but a predetermined threshold is required before variable selection stage. To overcome this issue, the sure independent screening (SIS) approach [23] was developed to ensure that all true important variables survive after the variable screening with probability tending to one. Feature subset selection methods [24,25,26] detect an optimal subset of features leading to the best performance of prediction. However, these methods have heavy computational time leading to be NP-hard [27] under a high dimensional setting.
In this paper, we proposed a filter ranking method (PF) utilizing selection probability with an elastic net based on resampling technique with SIS. The selected features are then applied to three popular variable selection algorithms such as least absolute shrinkage and selection operator (LASSO) [28], minimax concave penalty (MCP) [29], and smoothly clipped absolute deviation (SCAD) [30].
The rest of this article is organized as follows. In Section 2, we described three penalized logistic methods of LASSO, MCP, and SCAD, marginal maximum likelihood ranking method, sure independence screening method (SIS), the proposed statistical methods for filter ranking and its algorithm, and metrics of performance including accuracy, area under the receiver operating characteristic (AUROC), and geometric mean of sensitivity and specificity (G-mean). In Section 3, we describe the superior performance of our proposed method compared to an individual ranking method of marginal maximum likelihood logistic regression (MMLR) with SIS through the extensive simulation studies. We next applied the proposed method to the high dimensional colon gene expression data and investigate the biological meaning of selected genes. Finally, in Section 4, we discuss our findings.
2. Materials and Methods
We split this section into several subsections describing the methods used in the study. The section of sparse logistic regression, such as LASSO, adaptive LASSO, SCAD, and MCP, is discussed. A filtering method with SIS used as a reference is briefly described and then our proposed method is explained in detail. The final section considers metrics of the performance including accuracy, AUROC, and G-mean. All simulations and real applications were done with R software and the corresponding codes, results, and data are available at [31].
2.1. Penalized Logistic Regression Method
Binary logistic regression is widely used in the classification of clinical outcomes of cancer using gene expression data to identify the relationship between the outcome and a set of predictors to build prediction models. However, the logistic regression has limited use in high dimensional settings when N << P because the inverted matrix does not exist for the estimation of regression coefficients. Embedded methods such as LASSO, SCAD, and MCP are the most popular methods in gene selection under a high dimensional setting because they are allowed to select a sparse subset of genes by continuously shrinking unimportant covariates’ regression coefficients into zero. A number of penalty based embedded methods has been extensively studied and modified in the area of cancer genes selection under high throughput data [32,33,34,35,36,37,38,39,40,41,42,43].
Let the expression levels of genes in individual be denoted as and d is a total number of genes. Given a training data set where , = 0 indicates that individual is in normal group and = 1 in cancer group. Assuming that , the logistic regression is defined as follows:
The following formula is for the maximum log-likelihood estimator of logistic regression (MLR). is defined as follows:
The estimation of parameters can be calculated by maximizing the above log-likelihood function . The criterion for classification is that if , then the individual belongs to the cancer group, otherwise, normal group. The penalized logistic regression (PLR) is a combination of logistic regression with penalty function and parameters can be estimated by minimizing the log-likelihood function with penalty function as follows:
where is a penalty function.
One of the most popular penalty functions is LASSO [12,13,14,15,16,17,18]. It forces most of the unimportant genes’ regression coefficients into zero. Although it is widely used in high throughput biomedical data, it has the tendency to randomly choose one of the genes with high correlation and then throw out the rest of the genes. The estimation of regression coefficients can be done by minimizing the following likelihood:
Another popular sparse logistic regression is SCAD with a concave penalty that complements the limitation of lasso mentioned above. To estimate parameters of regression coefficients, the following log-likelihood can be minimized:
The is
The minimax concave penalty (MCP) is also popular as much as SCAD. The estimation of regression coefficients can be achieved by minimizing the following log-likelihood function:
is written as follows.
2.2. Variable Ranking with MMLR
In practice, gene expression data usually contain irrelevant genes that lead to low classification performance under high dimensional settings. Therefore, the analysis with respect to important variable detection has become a main part of the classification. Filter methods have been paid attention to such a goal. These methods essentially measure the strength of the relationship of each of genes with a binary outcome and then ranks them [44]. They have serval benefits for the analysis of huge amounts of gene expression data. First of all, they reduce high dimension into the appropriate dimension as well as the cost of computation time. Furthermore, they can also help improve the classification performance by increasing the likelihood to choose true important genes. There are a lot of filter methods applied to big data analysis of gene expression. One of the popular ranking methods is a logistic regression as a classifier. The value of maximum marginal likelihood estimator of logistic regression (MMLR) in each gene can be calculated using Equation (2) with a single gene. According to this method, a significant gene should have a large magnitude for its MMLR. Likewise, the list of ranking genes is made by the marginal strength of association with the response. That is, the top-ranked genes considered as most promising features have larger values of MMLR. To make a decision, the threshold of selecting top genes from the list, SIS would be used. It is a simple and effective algorithm which includes the true significant variables with probability tending toward one [43]. The cutoff value to select top-ranked genes is set up with . Those filtered genes would be plugged into the sparse logistic regression models such as LASSO, MCP, and SCAD to further evaluate the performance of classification as well as gene selection. The Algorithm 1 describes the procedure of the proposed two-stage approach.
| Algorithm 1 Proposed two-step procedure |
| Step 1: Sample 70% of samples randomly without replacement from the training set. |
| Step 2: Count frequency of each of genes from 100 models of λ values. |
| Step 3: Repeat Step 1 and Step 2 100 times. |
| Step 4: Calculate selection probability for each of variables based on Equation (10) and then rank them. |
| Step 5: Select top genes with the highest frequency. |
| Step 6: Apply them to sparse logistic regression methods to build prognostic models. |
2.3. The Proposed Variable Ranking Method
We utilize the following elastic net ( penalized regression method based on resampling technique to rank the features of importance using frequency. Elastic net is a combination of and it has the benefit of performing well with highly correlated variables.
The following is the equation of selection probability in each gene based on the elastic net.
where K is the number of resampling, L is the number of , is the regression coefficient corresponding gene l, and I( ) is the indicator variable. In each of K resampling, 100 values of are considered to build variable selection models. With SIS approach, top genes are selected and then applied those genes to LASSO, MCP, and SCAD penalized logistic regression method. The following is the algorithm of our proposed filter ranking method to rank the variable of importance. Figure 1 describes the schema of the proposed two-step approach.
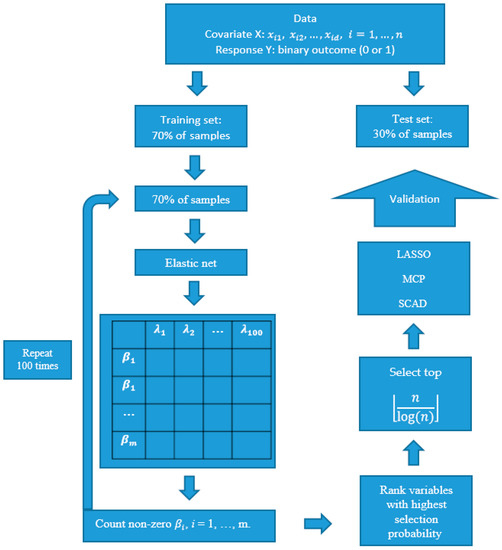
Figure 1.
Diagram showing the proposed two-step procedure.
2.4. Metrics of Performance
We calculated accuracy, the geometric mean of sensitivity and specificity (G-mean), and area under the receiver operating characteristic curve (AUROC). The accuracy is done with the following equation:
where TP is the number of true positives, TN the number of true negatives, FP the number of false positives, and FN the number of false negatives.
The geometric mean of sensitivity and specificity was used to check the joint performance. The equation is as follows:
AUROC was also considered to evaluate the overall classification performance of the proposed method. A perfect overall classification produces an AUROC = 1 whereas a random overall classification has an AUROC = 0.5.
3. Results
3.1. Simulation Results
The response variable is generated by a sequence of Bernoulli trial with the following probability:
Data in each iteration are generated by using a multivariate normal distribution with mean 0 and variance-covariance matrix with compound symmetry correlation structure whose diagonal elements are 1 and off-diagonal elements are , respectively. The following is the variance-covariance matrix:
is the row of design matrix X and is a binary outcome generated by a Bernoulli trial with the probability from Equation (13). 100 datasets, where n is 200 and d is 1000, are generated and six true regression coefficients are generated from a uniform distribution with min and max values which are 2 and 4, respectively. The simulation data are applied to PF as well as MMLR as a first stage to show the superiority of performance that true variables are highly ranked. The variable ranking procedure in PF was run 100 times with resampling technique. Then the calculated average selection probabilities of each of the 1000 variables were used to rank them. The result of filtering performance was summarized as boxplots described in Figure 2. As seen in boxplots with three different correlation structures, the ranking of six true important variables is higher than that of MMLR. Under the correlation coefficient of 0.2, the average ranking of the six true variables with the proposed ranking method was at 22nd among 1000 variables, whereas the MMLR method was at 44th. In case of high correlation coefficients of 0.5 and 0.7, the proposed one was 59th and 62nd while MMLR was 132nd and 139th.
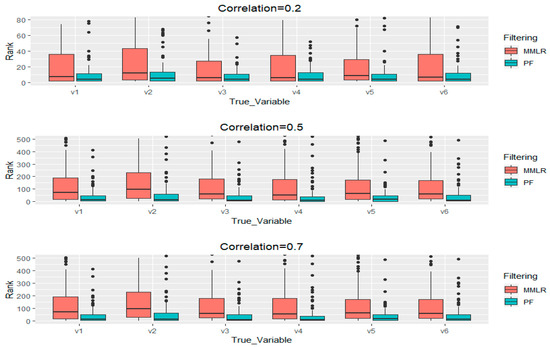
Figure 2.
The boxplots of ranking true variables with the proposed filter method (PF) and MMLR method under correlation coefficients 0.2, 0.5, and 0.7 with 100 iterations.
In addition, an average number of true variables included in filtered data with SIS is reported in Table 1. As seen in Table 1, the proposed method includes more true variables than MMLR in the various correlation settings. For each correlation setting, we used a paired two-sample t-test to check for significance level for the mean difference of the true number of variables between the two methods through 100 iterations, and all three were significant. That is, the proposed method is superior to MMLR for filtering true variables with SIS.

Table 1.
An average number of true positives from the proposed PF and MMLR with SIS and a significance level of paired two-sample t-test for the mean difference of the number of true positives between two methods using the number of true positives obtained over 100 iterations.
Table 2 shows that the performance of prediction as well as geometric mean with SIS-LASSO, SIS-MCP, and SIS-SCAD based on the proposed filter method are better than that of MMLR. As seen in TP (average number of true positives) of Table 2, all three variable selection methods capture mostly a true number of variable filtered from each of PF and MMLR. However, model size (MS) with the proposed filter ranking method is larger than that of MMLR because the methods with more true variables have a tendency to select unimportant variables highly correlated with the true variables. Figure 3 shows the boxplots of the area under the receiver operating characteristic (AUROC) for each of three methods with both proposed filter ranking and MMLR ranking methods based on SIS under three different correlation coefficients (). It also demonstrated that the AUROCs of SIS-methods based on the proposed filter ranking method is better performed compared to those of MMLR.

Table 2.
Classification performance of proposed filtering (PF) compared to marginal maximum likelihood logistic regression estimator (MMLR) with SIS-LASSO, SIS-MCP, and SIS-SCAD over 100 iterations.
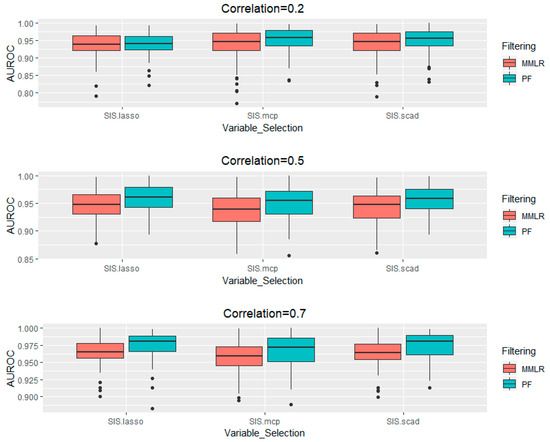
Figure 3.
Comparison of area under the receiver operating characteristic (AUROC) with SIS-LASSO, SIS-MCP, and SIS-SCAD after filtering with both proposed filter ranking method and MMLR method under three correlation settings.
The variable selection procedures of SIS-LASSO, SIS-MCP, and SIS-SCAD with both PF and MMRL filtered data were run 100 times using compound symmetry correlation structure with 0.2, 0.5, and 0.7. In each iteration, accuracy, area under the receiver operating characteristic (AUROC), geometric mean (G-mean) for sensitivity and specificity, true positives (TP), and false positives (FP). The results of performance for the variable selection methods with both filter ranking methods are summarized in Table 2.
3.2. Real Data Analysis
To test the performance of SIS-LASSO, SIS-MCP, and SIS-SCAD after filtering with the proposed method, we analyzed colon cancer gene expression data. The dataset contains 62 samples, which included 40 colon tumors and 22 normal colon tissue samples and 2000 genes whose gene expression information was extracted from DNA microarray data resulting from preprocessing; all 2,000 genes have unique expressed tags (ESTs) named. We also analyzed lung cancer gene expression data, GSE10072. The dataset includes 107 samples, which are made up of 49 normal lung and 58 lung tumor samples with 22,283 genes. Initially, we calculated the pairwise correlation for the normal and cancer samples combined to check the extent of overall correlation among genes in the colon cancer. The pairwise correlation is summarized in Figure 4 as a histogram with boxplot. The mean correlation between genes is 0.428 with a standard deviation of 0.203. It is clear that there is a high correlation between genes and this falls between the values tested in the simulation studies. In case of the lung cancer, the mean correlation between genes is 0.012 with a standard deviation of 0.246 because we used a full gene expression data unlike the colon gene expression data.
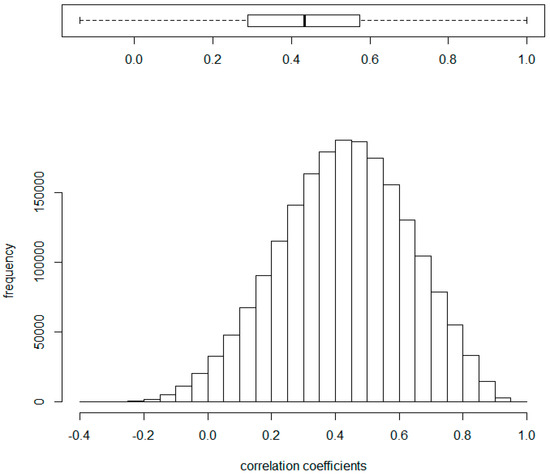
Figure 4.
The histogram and boxplot of pairwise correlation coefficients between 2000 expression levels of genes for the colon and normal group combined. The number of correlation coefficients is 1,999,000. Two plots show that average pairwise correlation is 0.428 (median = 0.433) with a standard deviation of 0.203.
To obtain reliable results of the performance of accuracy, AUROC, and G-mean with screened variables, we iterated 100 times of both the colon and lung cancer data with resampling technique. In each iteration, we firstly divided the data into a training set of 70% of samples and a testing set of 30% of samples. Secondly, we select top ranked number of genes with SIS to plug into LASSO, MCP, and SCAD. Finally, we select genes with non-zero coefficients in the model and estimate the performance. We also count genes appeared in the models across three variable selection methods to build lists of ranking genes.
As in the simulation studies, we estimated the average of accuracy, AUROC, G-mean, and model size as the results of using three methods with PF. The results are reported in Table 3. SIS-LASSO with the performance of accuracy and AUROC, each of which is 0.803 and 0.886 with the standard deviations of 0.098 and 0.077 for colon and 0.976 and 0.998 with standard of 0.017 and 0.007, respectively, is relatively better compared to those of other variable selection methods in both datasets. We also presented the top 10 genes selected from each of the three lists of ranking genes across the three variable selection methods based on 100 resampling for the colon cancer and lung cancer data in both Table 4 and Table 5. There are eight common genes of G50753, M76378, H08393 H55916, M63391, T62947, R80427, and T71025 among top 10 ranked genes from the results of three methods in the colon data.

Table 3.
Classification performance of the proposed selection method with SIS-LASSO, SIS-MCP, and SIS-SCAD in both colon and lung cancer. It is the average performance resulting from 100 iterations.

Table 4.
Top 10 ranked genes with highest selection frequency from the lists of ranking genes using 100 times resampling approach across three methods of SIS-LASSO, SIS-MCP, and SIS-SCAD on both the colon cancer and the lung cancer gene expression data.

Table 5.
Top 10 ranked genes with highest selection frequency from lists of gene ranking using 100 times resampling approach of three methods of SIS-LASSO, SIS-MCP, and SIS-SCAD on the lung cancer gene expression data.
The gene of R87126 is common between the results of SIS-LASSO and SIS-MCP, T47377 between SIS-LASSO and SIS-SCAD, and T64012 between SIS-SCAD and SIS-MCP. In particular, G50753, H08393, and H55916 were consistently ranked.
G50753, M63391, and M76378 were reported as significant genes related to colon cancer in [45]. M76378, H08393, H55916, M63391, R87126, and T47377 were also reported as genes associated with colon cancer in [46]. In addition, H08393 (collagen alpha 2(XI) chain) involved in cell adhesion is also known as a gene related to colon carcinoma whose cell has collagen-degrading activity as part of the metastatic process. T62947 has the potential to affect colon cancer by playing a role in controlling cell growth and proliferation through the selective translation of particular classes of mRNA. R80427 is also identified as genes distinguishing colon cancer in [47].
Likewise, the top 10 ranked genes in Table 4 from SIS-LASSO, SIS-MCP, and SIS-SCAD with PF were shown to play an important role in colon cancer. Figure 5 shows the boxplots of significantly differentially expressed genes between normal and colon samples on the eight genes found in all three methods. H08393 and H55916 are significantly expressed and downregulated while the other six are upregulated. In case of lung cancer data, there are five common genes of 21957_s_at, 209555_s_at, 209875_s_at, 209074_s_at, and 219213_at among top 10 ranked genes in lung cancer. The genes of 205357_s_at, 203980_at, 208982_at, and 220,170 are common between the results of SIS-LASSO and SIS-MCP. The gene of 32625_at is common gene between SIS-LASSO and SIS-SCAD. Specially, first top four genes between the results of SIS-LASSO and SIS-SCAD have the same ranking. In addition, there are four unique genes of 209614_at from SIS-SCAD, 206209_s_at, 204271_s_at, 204396_s_at, and 219719_at from SIS-MCP. 219597_s_at (DUOX1) usually is downregulated and associated with lung breast cancer [48,49]. 209555_s_at (CD36) is also related to breast cancer [50] and affects the progression of lung cancer [51]. 209875_s_at (SPP1) is reported as a prognostic biomarker for lung adenocarcinoma [52,53]. 209074_s_at (FAM107A) is also emphasized as a lung cancer biomarker downregulated [54]. Although 219213_at (JAM2) are not directly known as a variant of lung cancer, it is worthwhile to be further investigated as a potential biomarker related to lung adenocarcinoma. We also found that most of five common genes play significant roles in lung cancer. Figure 6 also represents the boxplots of significantly differentially expressed genes between normal and colon samples on the five genes found commonly in the top ten ranked genes in all three methods. Only the gene of 209875_s_at (SPP1) is upregulated while the rest of them are downregulated.
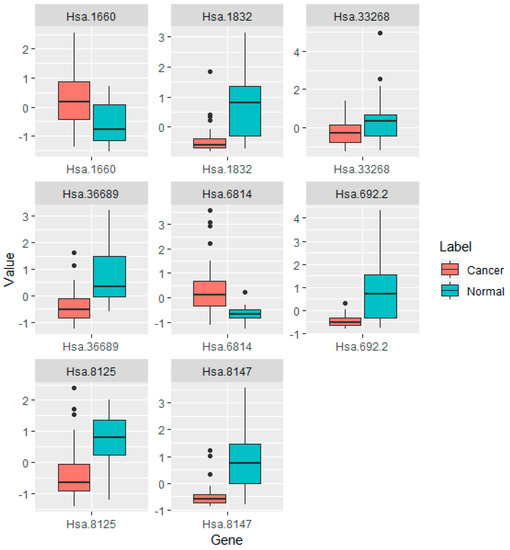
Figure 5.
Boxplots of differential expression level between normal and colon samples on eight genes from SIS-LASSO, SIS-MCP, and SIS-SCAD with the ranked data. Each boxplot contains the p-value of mean differential expression between two groups with a two-sample t-test.
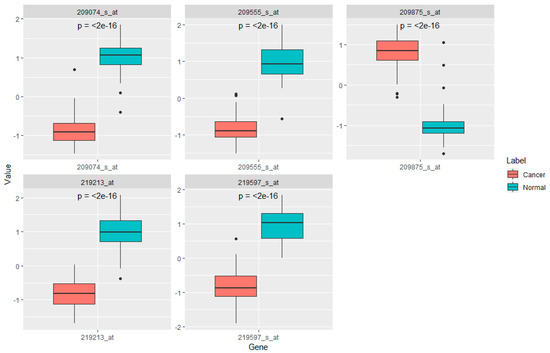
Figure 6.
Boxplots of differential expression level between normal and lung samples on five genes from SIS-LASSO, SIS-MCP, and SIS-SCAD with the ranked data. Each boxplot contains the p-value of mean differential expression between two groups with a two-sample t-test.
4. Discussion
We explored the feasibility of using the proposed feature ranking method as a filtering stage with Elastic net ( based on a resampling approach followed by SIS as screening in conjunction with LASSO, MCP, and SCAD penalized logistic variable selection methods in high dimensional settings to improve the performance of variable selection and classification prediction. One of the currently popular methods achieving such a goal is MMLR. It ranks variables in order from largest to smallest scores of maximum likelihood. It performs poorly with important variables that are marginally weak but jointly and strongly associated with the response since it screens out such variables. The simulation studies demonstrated that the PF method retained more true important variables when compared to MMLR in Table 1. PF method also showed a better performance of retaining a true number of variables as the correlation of the variables was increased than MMRL. It is clear that the elastic net-based PF takes into account correlation among true important variables, while MMLR only considers marginal strength with the outcome variable. However, as seen in the results of using three variable selection methods with SIS based on both filtered data, the proportion of unimportant variables in the models is still high.
For further confirmation of the PF in selecting the most promising genes for superior classification performance, we applied it to a real example of both colon and lung cancer gene expression data. The SIS-LASSO method produced the best performance scores compared to SIS-MCP and SIS-SCAD. We also selected the top 10 ranked genes with highest selection frequency from the lists of ranking genes generated by the resampling approach in each of three variable selection methods to check gene selection consistency as well as biological significance connecting to colon and lung cancer. There were eight and five overlapped genes among top 10 ranked genes from the results of three methods in Table 4 and Table 5, respectively. Most of the genes are reported as significant genes related to colon and lung carcinoma. In addition, some of the genes was consistently highly ranked across the three methods.
5. Conclusions
In this study, the proposed PF demonstrated the superiority of ranking true variables highly as a filtering stage compared to MMLR through extensive simulation studies. Furthermore, the combination of SIS-LASSO, SIS-MCP, and SIS-SCAD with the PF also had better performance of classification as well as detection of true important variables than those with MMLR. Even in real applications of colon and lung gene expression data, it was demonstrated that the proposed two-stage procedure with PF consistently captures the most promising features related to colon and lung cancer. As future research, we plan to develop the methodology of variable selection with PF to increase the power of detecting true important variables as well as prediction of classification.
Author Contributions
All authors drafted the manuscript, and read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank the referees for reading the manuscript very carefully and making a number of valuable and kind comments that improve the presentation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sangjin, K.; Susan, H. High Dimensional Variable Selection with Error Control. Biomed. Res. Int. Vol. 2016, 2016. [Google Scholar] [CrossRef]
- Shuangge, M.; Jian, H. Penalized feature selection and classification in bioinformatics. Brief. Bioinform. 2008, 9, 392–403. [Google Scholar]
- Abhishek, B.; Shailendra, S. Gene Selection Using High Dimensional Gene Expression Data: An Appraisal. Curr. Bioinform. 2018, 13, 225–233. [Google Scholar] [CrossRef]
- Hassan, T.; Elf, E.; lan, W. An efficient approach for feature construction of high-dimensional microarray data by random projections. PLoS ONE 2018, 13, e0196385. [Google Scholar] [CrossRef]
- Bourgon, R. Independent filtering increases detection power for high-throughput experiments. Proc. Natlacad. Sci. 2010, 107, 9546–9951. [Google Scholar] [CrossRef] [PubMed]
- Bourgon, R.; Gentleman, R.; Huber, W. Reply to Talloen et al.: Independent filtering is a generic approach that needs domain-specific adaptation. Proc. Natl Acad. Sci. USA 2010, 107, E175. [Google Scholar] [CrossRef]
- Lu, J.; Peddada, S.D.; Bushel, P.R. Principal component analysis-based filtering improves detection for Affymetrix gene expression arrays. Nucleic Acids Res. 2011, e86, 39. [Google Scholar] [CrossRef]
- Jiang, H.; Doerge, R.W. A two-step multiple comparison procedure for a large number of tests and multiple treatments. Stat. Appl. Genet. Mol. Biol. 2006, 5. [Google Scholar] [CrossRef]
- Ramskold, E.; Kerns, R.T. An abundance of ubiquitously expressed genes revealed by tissue transcriptome sequence data. PLoS Comput. Biol. 2009, 5, e1000598. [Google Scholar] [CrossRef]
- Sultan, M.; Schulz, M.H.; Richard, H.; Magen, A.; Klingenhoff, A.; Scherf, M.; Seifert, M.; Borodina, T.; Soldatov, A.; Parkhomchuk, D.; et al. A global view of gene activity and alternative splicing by deep sequencing of the human transcriptome. Science 2008, 321, 956–960. [Google Scholar] [CrossRef]
- Calle, M.L.; Urrea, V.; Malats, V.N.; Steen, K.V. Improving strategies for detecting genetic patterns of disease susceptibility in association studies. Stat. Med. 2008, 27, 6532–6546. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Kabesch, M.; Bouzigon, E.; Demenais, F.; Farrall, M.; Moffatt, M.F.; Lin, X.; Liang, L. Using eQTL weights to improve power for genome-wide association studies: A genetic study of childhood asthma. Fron. Genet. 2013, 4, 103. [Google Scholar] [CrossRef] [PubMed]
- Taqwa, A.A.; Siraj, M.M.; Zainal, A.; Elshoush, H.T.; Elhaj, F. Feature Selection Using Information Gain for Improved Structural-Based Alert Correlation. PLoS ONE 2016, 11, e0166017. [Google Scholar] [CrossRef]
- Tan, Y.; Liu, Z. Feature selection and prediction with a Markov blanket structure learning algorithm. BMC Bioinform. 2013, 14, A3. [Google Scholar] [CrossRef]
- Kakourou, A.; Mertens, B. Bayesian variable selection logistic regression with paired proteomic measurements. Biom. J. 2018. [Google Scholar] [CrossRef] [PubMed]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Okeh, U.M.; Oyeka, I.C.A. Estimating the fisher’s scoring matrix formula from the logistic model. Am. J. Theor. Appl. Stat. 2013, 2, 221–227. [Google Scholar]
- Urbanowicz, R.J.; Meekerb, M.; La Cavaa, W.; Olsona, R.S.; Moorea, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef]
- Milos, R.; Mohamed, G.; Nenad, F.; Zoran, O. Minimum redundancy maximum relevance feature selection approach for temporal gene expression data. BMC Bioinform. BMC Ser. 2017, 18, 9. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Lee, M.H. A two-stage sparse logistic regression for optimal gene selection in high-dimensional microarray data classification. Adv. Data Anal. Classif. 2018, 1–19. [Google Scholar] [CrossRef]
- Le, T.T.; Urbanowicz, R.J.; Moore, J.H.; McKinney, B.A. Statistical Inference Relief (STIR) feature selection. Bioinformatics 2018, 788. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aal, R.E. GMDH-based feature ranking and selection for improved classification of medical data. J. Biomed. Inf. 2005, 38, 456–468. [Google Scholar] [CrossRef] [PubMed]
- Fan, J. Sure Independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. B 2008, 70, 849–911. [Google Scholar] [CrossRef]
- Dizler, G.; Morrison, J.C.; Lan, Y.; Rosen, G.L. Fizzy: Feature subset selection for metagenomics. BMC Bioinform. 2015, 1, 358. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Wei, M.; Chow, T.W.S.; Chan, R.H.M. Heterogeneous feature subset selection using mutual information based feature transformation. Neurocomputing 2015, 168, 706–718. [Google Scholar] [CrossRef]
- Su, C.-T.; Yang, C.-H. Feature selection for the SVM: An application to hypertension diagnosis. Expert Syst. Appl. 2008, 34, 754–763. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Two-Stage-Resources-2019. Available online: https://sites.google.com/site/sangjinkim0716/data-repository/two-stage-resources-2019 (accessed on 29 May 2019).
- Pappua, V.; Panagopoulosb, O.P.; Xanthopoulosb, P.; Pardalosa, P.M. Sparse proximal support vector machines for features selection in high dimensional datasets. Expert Syst. Appl. 2015, 42, 9183–9191. [Google Scholar] [CrossRef]
- Liao, J.G.; Chin, K.-V. Logistic regression for disease classification using micro data: Model selection in a large p and small n case. Bioinformatics 2007, 23, 1945–1951. [Google Scholar] [CrossRef] [PubMed]
- Park, M.Y.; Hastie, T. Penalized logistic regression for detecting gene interactions. Biostatistics 2008, 9, 30–50. [Google Scholar] [CrossRef] [PubMed]
- Bielza, C.; Robles, V.; Larrañaga, P. Regularized logistic regression without a penalty term: An application to cancer classification with microarray data. Expert Syst. Appl. 2011, 38, 5110–5118. [Google Scholar] [CrossRef]
- Bootkrajang, J.; Kabán, A. Classification of mislabelled microarrays using robust sparse logistic regression. Bioinformatics 2013, 29, 870–877. [Google Scholar] [CrossRef] [PubMed]
- Cawley, G.C.; Talbot, N.L.C. Gene selection in cancer classification using sparse logistic regression with Bayesian regularization. Bioinformatics 2006, 22, 2348–2355. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jia, Y.; Zhao, Z. Partly adaptive elastic net and its application to microarray classification. Neural Comput. Appl. 2012, 22, 1193–1200. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S. Penalized logistic regression for high-dimensional DNA methylation data with case-control studies. Bioinformatics 2012, 28, 1368–1375. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Hastie, T. Classification of gene microarrays by penalized logistic regression. Biostatistics 2004, 5, 427–443. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, C.; Luan, X.-Z.; Leung, K.-S.; Chan, T.-M.; Xu, Z.-B.; Zhang, H. Sparse logistic regression with an L1/2 penalty for gene selection in cancer classification. BMC Bioinform. 2013, 14, 198–211. [Google Scholar] [CrossRef]
- Huang, H.H.; Liu, X.Y.; Liang, Y. Feature selection and cancer classification via sparse logistic regression with the hybrid L1/2 + 2 regularization. PLoS ONE 2016, 11, e0149675. [Google Scholar] [CrossRef] [PubMed]
- Algamal, Z.Y.; Lee, M.H. Penalized logistic regression with the adaptive LASSO for gene selection in high-dimensional cancer classification. Expert Syst. Appl. 2015, 42, 9326–9332. [Google Scholar] [CrossRef]
- Ben Brahim, A.; Limam, M. A hybrid feature selection method based on instance learning and cooperative subset search. Pattern Recogn. Lett. 2016, 69, 28–34. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.-G.; Lu, Y. Informative Gene Selection for Microarray Classification via Adaptive Elastic Net with Conditional Mutual Information. Appl. Math. Model. 2019, 71, 286–297. [Google Scholar] [CrossRef]
- Patrick, M.; John, S.; Rebecca, W. Methods for Bayesian Variable Selection with Binary Response Data using the EM algorithm. arXiv 2016, arXiv:1605.05429. [Google Scholar]
- Castellanos-Garzon, J.A.; Ramos-Gonzalez, J. A Gene Selection Approach based on Clustering for Classification Tasks in Colon Cancer. Adv. Distrib. Comput. Artif. Intell. J. 2015, 4. [Google Scholar] [CrossRef]
- Fortunato, R.S.; Gomes, L.R.; Munford, V.; Pessoa, C.F.; Quinet, A.; Hecht, F.; Kajitani, G.S.; Milito, C.B.; Carvalho, D.P.; Martins Menck, C.F. DUOX1 Silencing in Mammary Cell Alters the Response to Genotoxic Stress. Oxid. Med. Cell. Longev. 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
- Little, A.C.; Sham, D.; Hristova, M.; Danyal, K.; Heppner, D.E.; Bauer, R.A.; Sipsey, L.M.; Habibovic, A.; van der Vliet, A. DUOX1 silencing in lung cancer promotes EMT, cancer stem cell characteristics and invasive properties. Oncogenesis 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Han, H.; Liu, L.; Duan, Y.; Yang, X.; Ma, C.; Zhu, Y.; Han, J.; Li, X.; Chen, Y. CD36 plays a critical role in proliferation, migration and tamoxifen-inhibited growth of ER-positive breast cancer cells. Oncogenesis 2018, 7, 98. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhang, W.; Guo, F. Hypermethylated CD36 gene affected the progression of lung cancer. Genetics 2018, 678, 395–406. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Fan, J.; Chen, Q.; Lei, C.; Qiao, B.; Liu, Q. SPP1 and AGER as potential prognostic biomarkers for lung adenocarcinoma. Oncol. Lett. 2018, 15, 7028–7036. [Google Scholar] [CrossRef] [PubMed]
- Ioanna, G.; Vasilieios, P.; Ioannis, L.; Nikolaos, K.; Theodora, A.; Georgios, S. Tumor cell-derived osteopontin promotes lung metastasis via both cell-autonomous and paracrine pathways. Eur. Respir. J. 2016, 48. [Google Scholar] [CrossRef]
- Pastuszak-Lewandoska, D.; Czarnecka, K.H.; Nawrot, E.; Domanska, D.; Kiszalkiewicz, J. Decreased FAM107A Expression in Patients with Non-small Cell Lung Cancer. Adv. Exp. Med. Biol. 2015, 852, 39–48. [Google Scholar] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).