Abstract
This paper is concerned with the combinatorial facts of the lattice graphs of , , and . We show that the lattice graph of is realizable as a convex polytope. We also show that the diameter of the lattice graph of is and its girth is 4.
1. Introduction
The relation between the structure of a group and the structure of its subgroups constitutes an important domain of research in both group theory and graph theory. The topic has enjoyed a rapid development starting with the first half of the twentieth century.
The main object of this paper is to study the interplay of group-theoretic properties of a group G with graph-theoretic properties of its lattice graph L(G). Every group has a corresponding lattice graph, which can be finite or infinite depending upon the order of the group. This study helps illuminate the structure of the set of subgroups of G.
The lattice graph of a finite cyclic group G is obtained as follows: Each vertex of corresponds to an element of , and two vertices corresponding to two elements of are connected by an edge if and only if and that there is no element K of such that (see [1,2]), thus ≤ is used when is proper maximal subgroup of . The notation ≤ is used as subgroup. Degree of a vertex is the number of edges attached to that vertex. A vertex is defined to be even or odd if its degree is even or odd. The degree vector of a graph is the sequence of degrees of its vertices arranged in non-increasing order [3]. The diameter diam of a connected graph G is the maximum distance among vertices of G [4,5]. The girth of a graph G is the length of a smallest cycle in G, and is infinity if G is acyclic [6]. It is a fact that the lattice of subgroups of a given group can rarely be drawn without its edges crossing [1,2]. The crossing number cr of a graph G is the minimum number of crossings of its edges among the drawings of G in the plane. A graph is considered Eulerian if there exists a Eulerian path in which we can start at a vertex, traverse through every edge only once, and return to the same vertex where we started. A connected graph G is Eulerian if each vertex has even degree, and is semi-Eulerian if it has exactly two vertices with odd degrees [7].
A polytope is a finite region of enclosed by a finite number of hyper-planes. A polytope is called convex if its points form a convex subset of . Combinatorial aspects of the groups can be computed using its lattice graphs [8,9]. The authors discussed some finite simple groups of low rank in [8]. Tarnauceanu introduced new arithmetic method of counting the subgroups of a finite Abelian group in [10]. The author of [11] described the finite groups Ghaving cyclic subgroups. Saeedi and Farrokhi [12] computed factorization number of some finite groups. Tarnauceanu [13] characterized elementary Abelian two-groups. Tarnauceanu and Toth discussed cyclicity degree of finite groups in [14]. Tarnauceanu [15] discussed finite groups with dismantlable subgroup lattices.
In the present article, we are interested in the lattices of finite groups. We demonstrate that the lattice graph of can be viewed as a convex polytope, and that the diameter of the lattice graph of is and its girth is 4. We also compute many other properties of these lattices. We are interested developing some combinatorial invariants of the groups coming from their lattice graphs. The main motivation comes from the fact that finite graphs are relatively easier to handle than the finite groups. One is interested in capturing facts of the group while studying the graph associated to it. This study ultimately relates some parameters of the graphs with some parameters of the groups. Several authors computed some combinatorial aspects of finite graphs such as diameter, girth and radius but, for the lattice graph, similar questions are still open and need to be addressed. This article can be considered as a step forward in this direction. We, naturally, pose problems about the exact values of these parameters for more general classes of groups such as , , and sporadic groups.
2. The Results
In this section, we give the combinatorial results about the lattice graphs of , , and . In the end, we give the general results about .
2.1.
Theorem 1.
The lattice graph of is realizable as a convex polytope with vertices.
Proof.
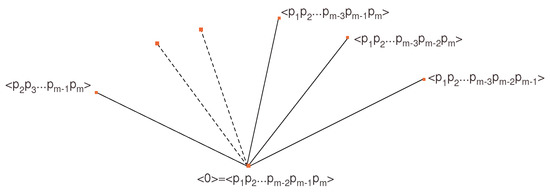
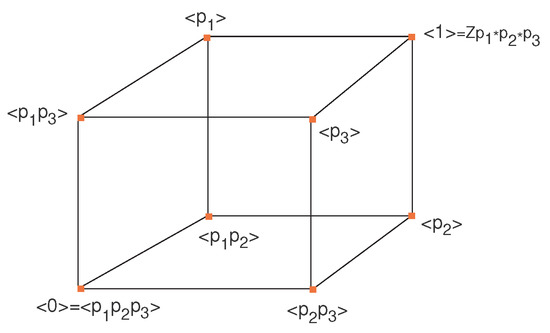
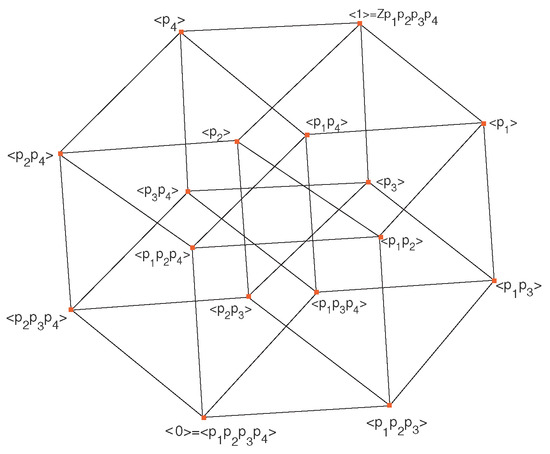
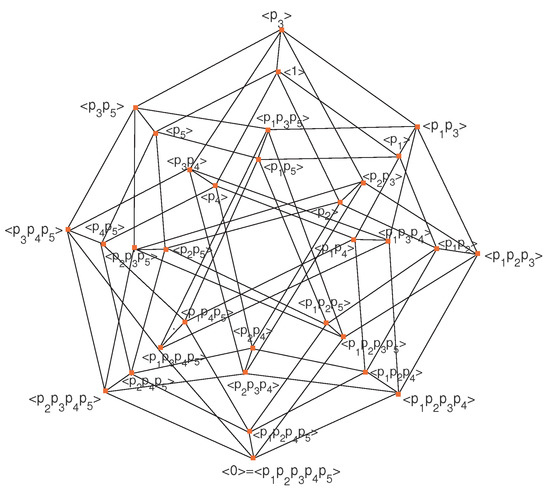
We prove it using all possible maximal chains of subgroups of . It is clear that is finite cyclic group, thus, for each possible divisor of n, there exist a unique subgroup of this group, up to isomorphism. This leads us to the set of all subgroups of ; . Now, the maximal chains: The subgroup = is contained immediately in m subgroups of : = = = , as shown in Figure 1.

Figure 1.
First step graph.
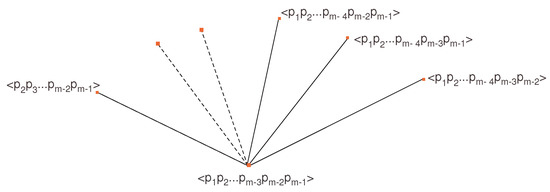
Each is contained in subgroups of : For instance, is contained in , (see Figure 2).

Figure 2.
Intermediate step Graph.
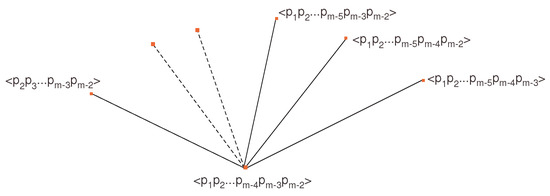
Similarly, every is contained in subgroups of : is contained in subgroups of (see Figure 3).

Figure 3.
Intermediate step Graph.
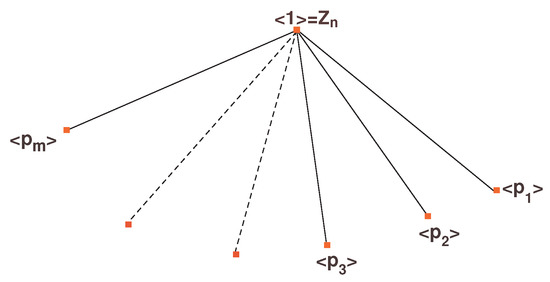
The process will continue until we receive , … at the second last stage. Now, each one of these is contained in = and the process is finished (see Figure 4).

Figure 4.
Last step Graph.
It is clear that there are m possibilities of subgroups of containing trivial group, possibilities of each of to be contained in other subgroups of , possibilities for each of to be contained in next subgroups and so on. Thus, by the product rule, the number of all possibilities of maximal chains is . Now, we put all these chains of subgroup in the plane such that each subgroup is identified to itself occurring in all these series. Thus, the same subgroups that appear in more than one series, appear only as a single vertex of the lattice graph in the plane. This lattice graph starts of at the identity and finishes at because these subgroups appear in all series. This may have crossings. If we imagine this gluing in avoiding all crossings in higher dimension, we get a convex polytope with vertices, one vertex corresponding to each element of . For instance, the cases for are shown in Figure 5, Figure 6 and Figure 7, respectively.

Figure 5.
.

Figure 6.
.

Figure 7.
.
Corollary 1.
- (a) The number of maximal subgroups of is m.
- (b) The length of each maximal series is .
- (c) The diameter of is m.
- (d) is m-regular.
Proof.
(a) It is clear that is cyclic, thus, for each divisor, we have a unique subgroup. Prime divisor of n yields maximum quotient, thus these numbers correspond to the maximal subgroups of , which are .
(b) This can be shown by simply counting the number of vertices of along a path from to ; see, for instance, a typical series: .
(c) diam is one less than the length of a maximal series, which is the length of each path from to .
(d) At the first stage, the degree of the vertex is m because it is adjacent to m vertices , in the second stage, as shown in the construction of .
The degree of each vertex at the second stage is m as each vertex is adjacent to vertices lying higher to it and to one vertex lying below it. For instance, is attached with , . Similarly, is m. Continuing this process, we receive that the vertices corresponding to are adjacent to the vertex corresponding to , giving the degree of the last vertex m too. Thus, each vertex of has degree m, and the proof is finished. ☐
Remark 1.
It should be remarked that the lattice graph of is a small-world network in which nearly all nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of steps. Thus, it is a connected graph [16].
2.2.
The construction of is given by using all maximal chains from the set . The subgroup is contained immediately in two subgroups and which are further contained in . The subgroup is contained in , which is contained in next two subgroups, and . is contained in other two subgroups of . The process will continue until we receive a subgroup that is contained in next two subgroups, and . Both are further contained in , which itself is contained in . This process is continued until we obtain a subgroup , which is continued in , and thus we receive a series of subgroups of ; for instance, . We obtain all other series of subgroups similarly. Now, gluing all maximal series, we obtain the lattice graph of , as shown in Figure 8.
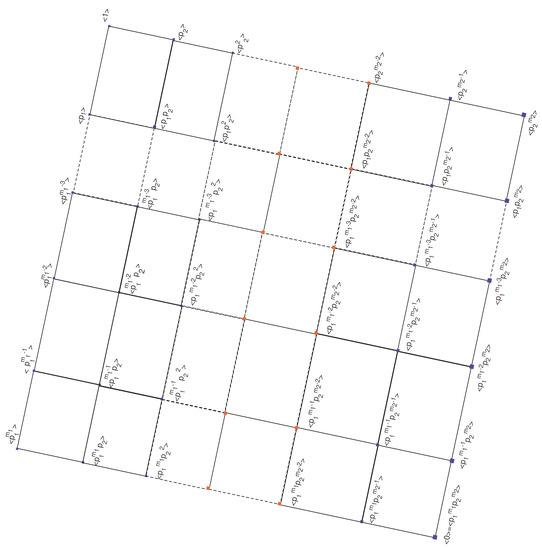
Figure 8.
.
From the construction, we reach at the results:
Proposition 1.
- (a) is planar.
- (b) Length of maximal series of is .
- (c) The diameter of lattice graph of is .
Proof.
(a) This is obvious from the construction of .
(b) Again, this is obvious; see a typical maximal series: .
(c) In this case, the diameter is exactly one less than the number of elements in a maximal series. ☐
2.3. On the Lattice Graph of
The set of subgroups of is . The subgroup is contained immediately in three subgroups , and . The first two of these are contained in . The subgroup is contained in which is further contained in two subgroups and . The subgroup is contained in other two subgroups of . The process will continue till we receive a subgroup . It is contained in three subgroups , and . The subgroup is contained in . It is contained in . Continuing this process till we obtain which is contained in , and we will receive series of subgroups of ; for instance, . Similarly, all the remaining subgroups will form other series of subgroups. At the end, gluing the vertices occurring in all maximal series, we obtain the required graph, as shown in Figure 9.
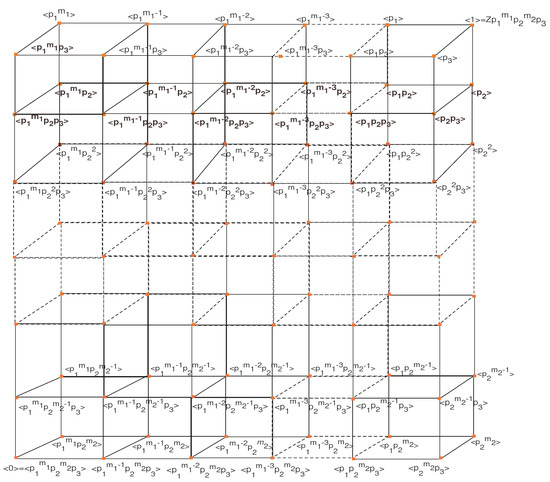
Figure 9.
.
Proposition 2.
The crossing number of is .
The following proposition relates the number of crossings and number of subgroups of .
Proposition 3.
cr.
Proof.
We proceed as follows: . However, as in Proposition 2.4, we have, , which leads to the given result. ☐
Similarly, the following corollary provides a link between number of crossings and number of subgroups of .
Corollary 2.
cr.
Proof.
The result follows immediately from the relation . ☐
Proposition 4.
The length of maximal series of is .
Proof.
A typical maximal series of subgroups of is , which consists of . Since each maximal series has the same number of elements, we are done. ☐
Proposition 5.
The diameter of is .
Proof.
The diameter is one less than the length of the maximal series of . ☐
Proposition 6.
Girth of the lattice graphs of , , , and is 4.
Proof.
If the degree of each vertex of a graph is at least2, then then there exists a cycle. It is clear that the degree of each vertex of L() is 2 except , thus there exists a cycle and the length of shortest cycle is 4. Thus, the girth of L() is 4 except . Similarly, the girth of and is 4. ☐
Finally, the information about the diameter and girth is enclosed in the most general result:
Theorem 2 (The Main Theorem).
If G is the group , then:
(a) The length of the maximal series of G is .
(b) The diameter of is .
(c)
Proof.
(a) The set of subgroups of G is = This set consists of elements; this number is actually the number of divisors of the order of G. Now, take elements of and form a (maximal) series from to . A typical series of such kind is:
This maximal series contains subgroups. Since each maximal series contains exactly the same number of subgroups, the length of maximal series is .
(b) It now follows that the diameter of is , which, in our case, is actually one less than the length of maximal series of G. This completes the proof.
(c)Case I. ()
Consider two typical maximal series of subgroups of G:
.
and
.
On gluing these maximal series in this a way, the subgroup is contained immediately in two subgroups: = and = . Both these are further contained in = , and we obtain a closed path . We can split this closed path in two closed paths, and . For if , we receive a contradiction that there does not exist a closed path of length 3.
Similarly, gluing the vertices occurring in all maximal series, we obtain a graph in which one vertex is joined at least with two vertices which are further joined with another vertex, but these two vertices are not joined with each other. This confirms that the length of shortest cycle is 4.
Case II. ()
In this case, since we receive just a finite path, . ☐
Theorem 3.
- (a) is Eulerian if m is even and is non-Eulerian if is odd.
- (b) is non-Eulerian if and .
- (c) is non-Eulerian.
3. Conclusions
In this article, we discuss some metrical aspects of the lattice graphs of some families of finite groups. We obtain the diameter and girth as well as many other aspects of these lattice graphs. Along with many other results, the following are the main contributions of this article.
Theorem 4 (The Main Theorem).
If G is the group , then:
- (a) The length of the maximal series of G is .
- (b) The diameter of is .
- (c)
and
Theorem 5.
- (a) is Eulerian if m is even and is non-Eulerian if is odd.
- (b) is non-Eulerian if and .
- (c) is non-Eulerian.
Author Contributions
The main ideas were conceived by M.M. and J.-B.L.; and the article was drafted by A.R.N. and Q.-u.-A.M.
Funding
This research was funded by the China Postdoctoral Science Foundation under Grant 2017M621579; the Postdoctoral Science Foundation of Jiangsu Province under Grant 1701081B; Project of Anhui Jianzhu University under Grant no. 2016QD116 and 2017dc03.
Acknowledgments
The authors are extremely grateful to the anonymous referees for constructive comments and suggestions, which have led to an improved version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Starr, C.L.; Turner, G.E. Planar Group. J. Algebr. Comb. 2004, 19, 283–295. [Google Scholar] [CrossRef]
- Bohanon, J.P.; Reid, L. Finite Groups with Planar Subgroup Lattices. J. Algebr. Comb. 2006, 23, 207–223. [Google Scholar] [CrossRef]
- Diestel, R. Graph Theory, 4th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ma, X.L.; Wei, H.Q.; Zhong, G. The Cyclic Graph of a Finite Group. Algebra 2013, 11, 7. [Google Scholar] [CrossRef]
- Akbari, S.; Mohammadian, A.; Radjavi, H.; Raja, P. On The Diameters of Commuting Graphs. J. Linear Algebra Appl. 2006, 418, 161–176. [Google Scholar] [CrossRef][Green Version]
- Anderson, D.F.; Lavingston, P.S. The Zero-Divisor Graph of a Commutative Ring. J. Algebra 1999, 217, 434–447. [Google Scholar] [CrossRef]
- Gary, C.; Zhang, P. Introduction to Graph Theory; Posts and Telecom Press: Beijing, China, 2006. [Google Scholar]
- Pellegrini, M.A.; Tamburini, M.C. Finite simple groups of low rank: Hurwitz generation and (2,3)-generation. Int. J. Group Theory 2015, 3, 13–19. [Google Scholar]
- Aschbacher, M. Overgroup lattices in finite groups of Lie type containing a parabolic. J. Algebra 2013, 382, 71–99. [Google Scholar] [CrossRef]
- Tarnauceanu, M. An Arithmetic Method of Counting the Subgroups of a Finite Abelian Group. Bull. Math. Soc. Sci. Math. Roum. 2010, 53, 373–386. [Google Scholar]
- Tarnauceanu, M. Finite Groups With a Certain Number of Cyclic Subgroups. Am. Math. Mon. 2015, 122, 275–276. [Google Scholar] [CrossRef]
- Saeedi, F.; Farrokhi, D.G. Factorization numbers of some finite groups. Glasgow Math. J. 2012, 54, 345–354. [Google Scholar] [CrossRef]
- Tarnauceanu, M. A characterization of elementary abelian 2-groups. Arch. Math. 2014, 102, 11–14. [Google Scholar] [CrossRef]
- Tarnauceanu, M.; Toth, L. Cyclicity degrees of finite groups. Acta Math. Hung. 2015, 145, 489–504. [Google Scholar] [CrossRef]
- Tarnauceanu, M. On finnite groups with dismantlable subgroup lattices. Can. Math. Bull. 2015, 52, 182–187. [Google Scholar] [CrossRef]
- Shang, Y. Lack of Gromov-hyperbolicity in small-world networks. Cent. Eur. J. Math. 2012, 10, 1152–1158. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
