The Odd Gamma Weibull-Geometric Model: Theory and Applications
Abstract
:1. Introduction
2. The OGWG Distribution
2.1. Main Probability Functions
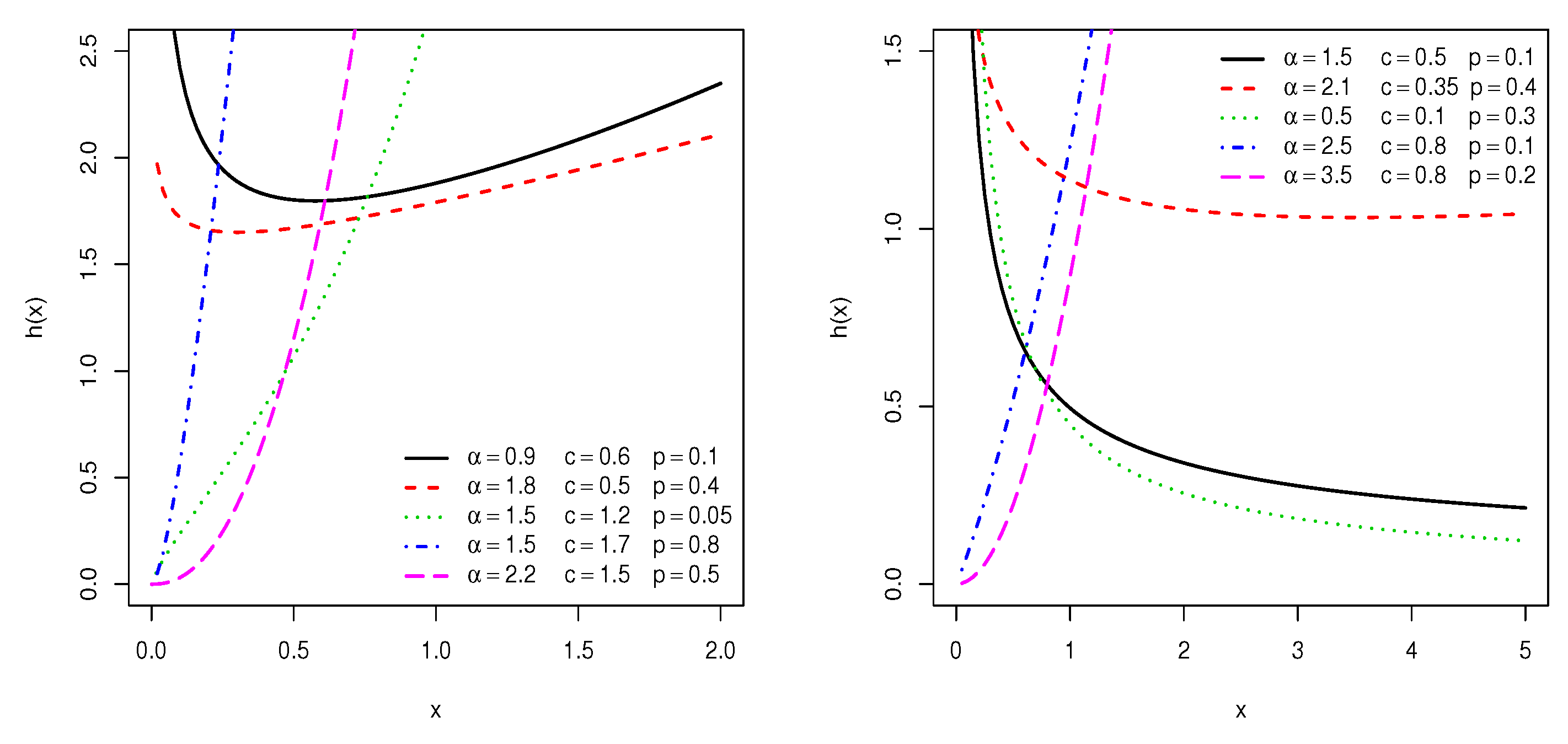
2.2. Analytical Properties of the Shapes
3. Some Mathematical Properties of the OGWG Distribution
3.1. Quantile Function
3.2. Some Characterizations
3.3. Series Expansion of the OGWG pdf
3.4. Moments
3.5. Moment Generating Function
3.6. Incomplete Moments
3.7. Stochastic Ordering
4. Estimation of Parameters
4.1. Maximum Likelihood Estimation
4.2. Monte Carlo Simulation Study
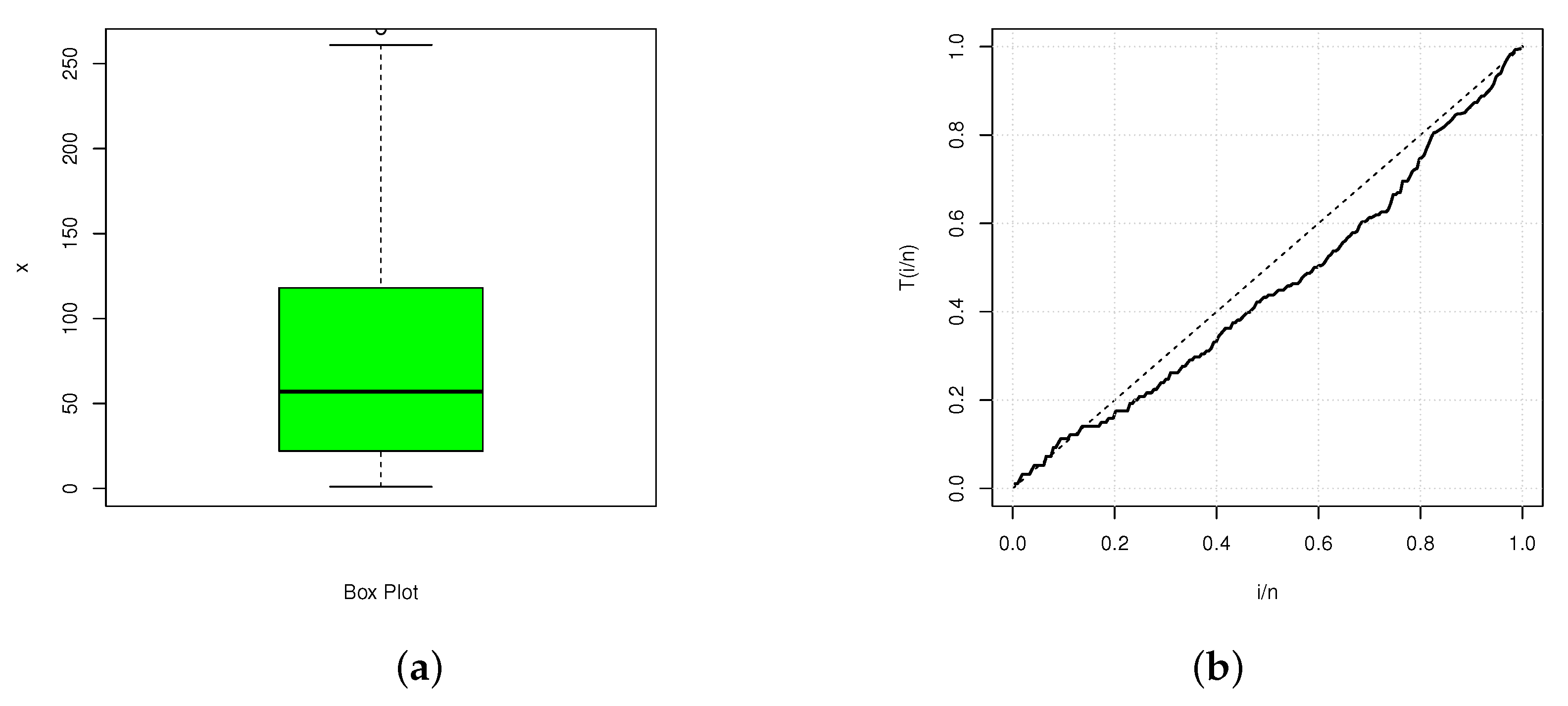
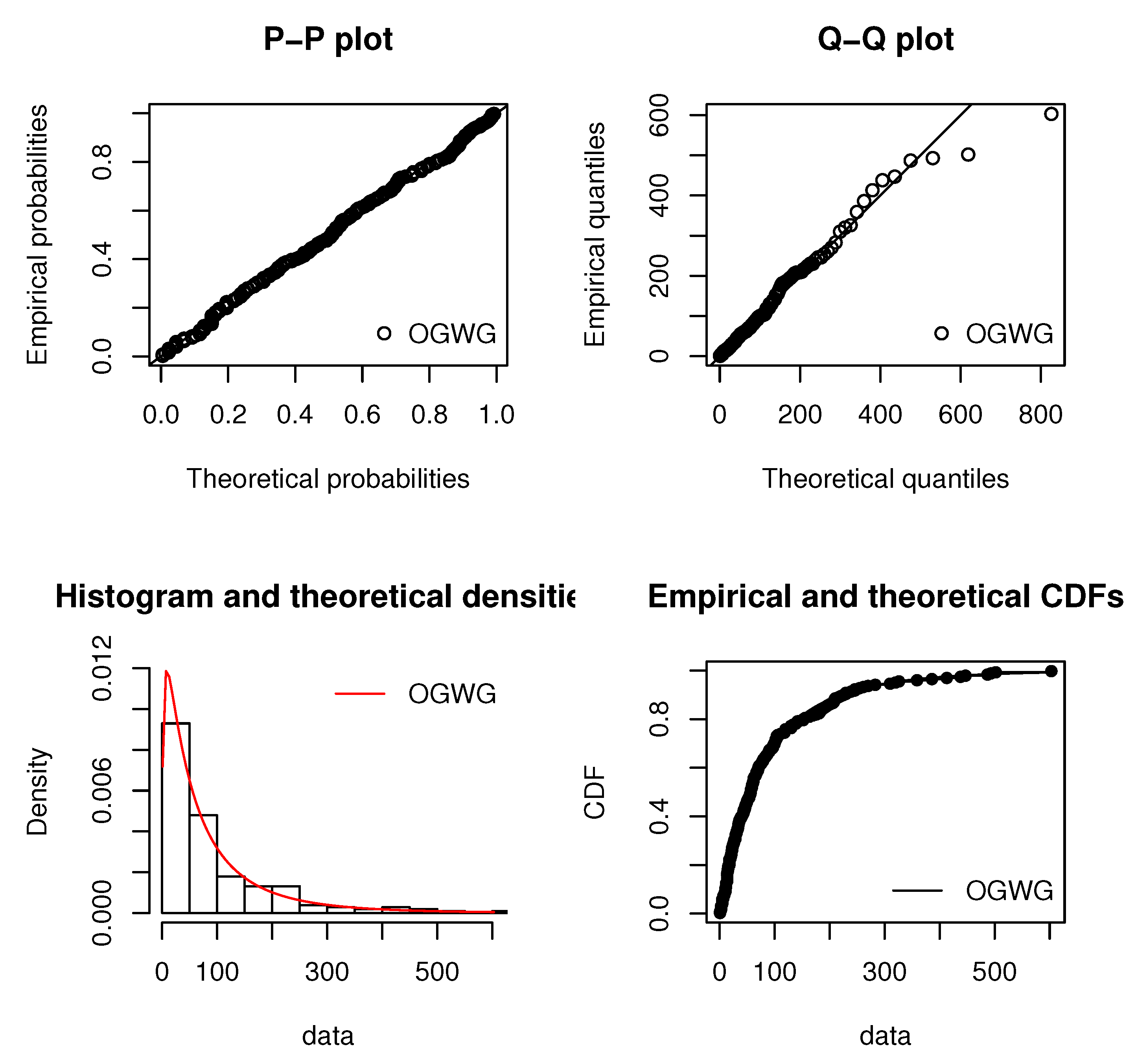
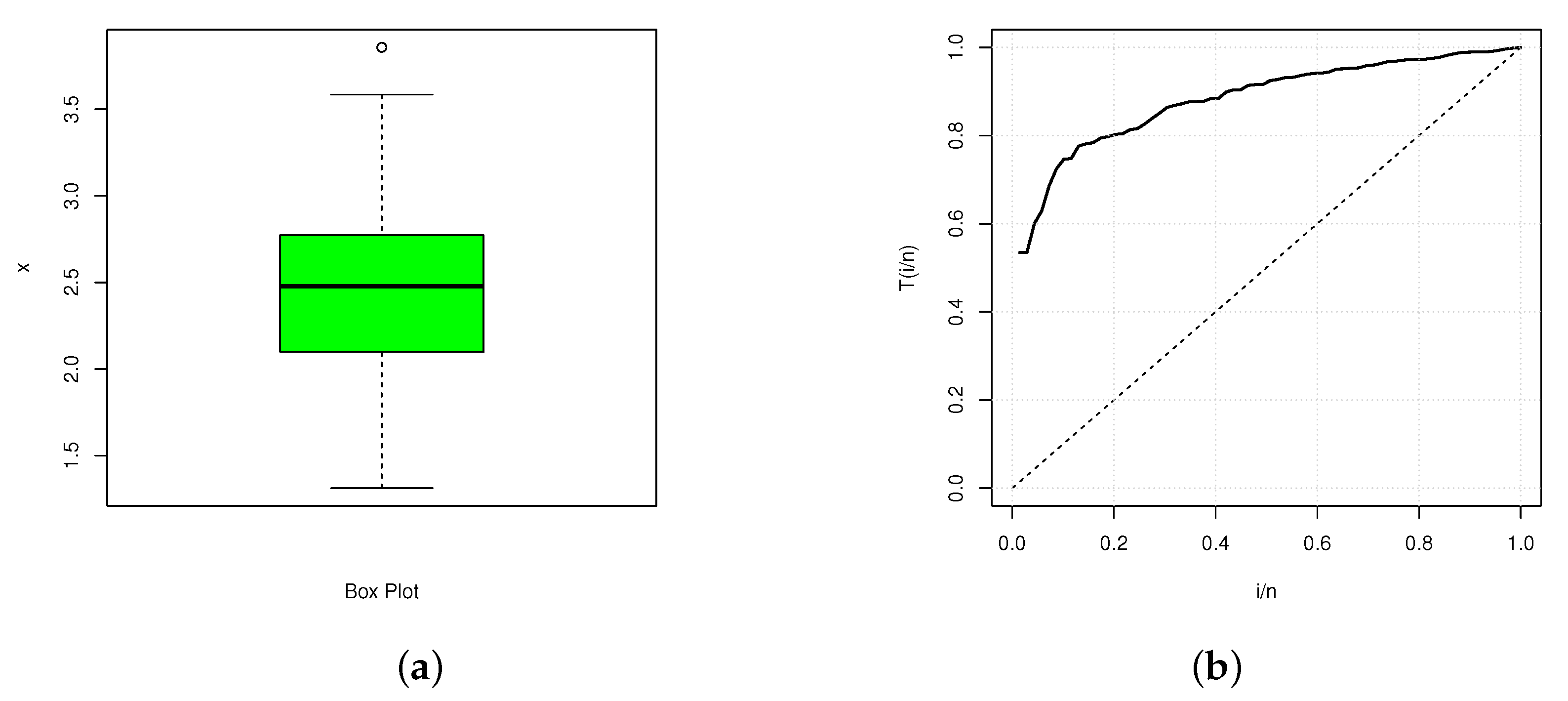
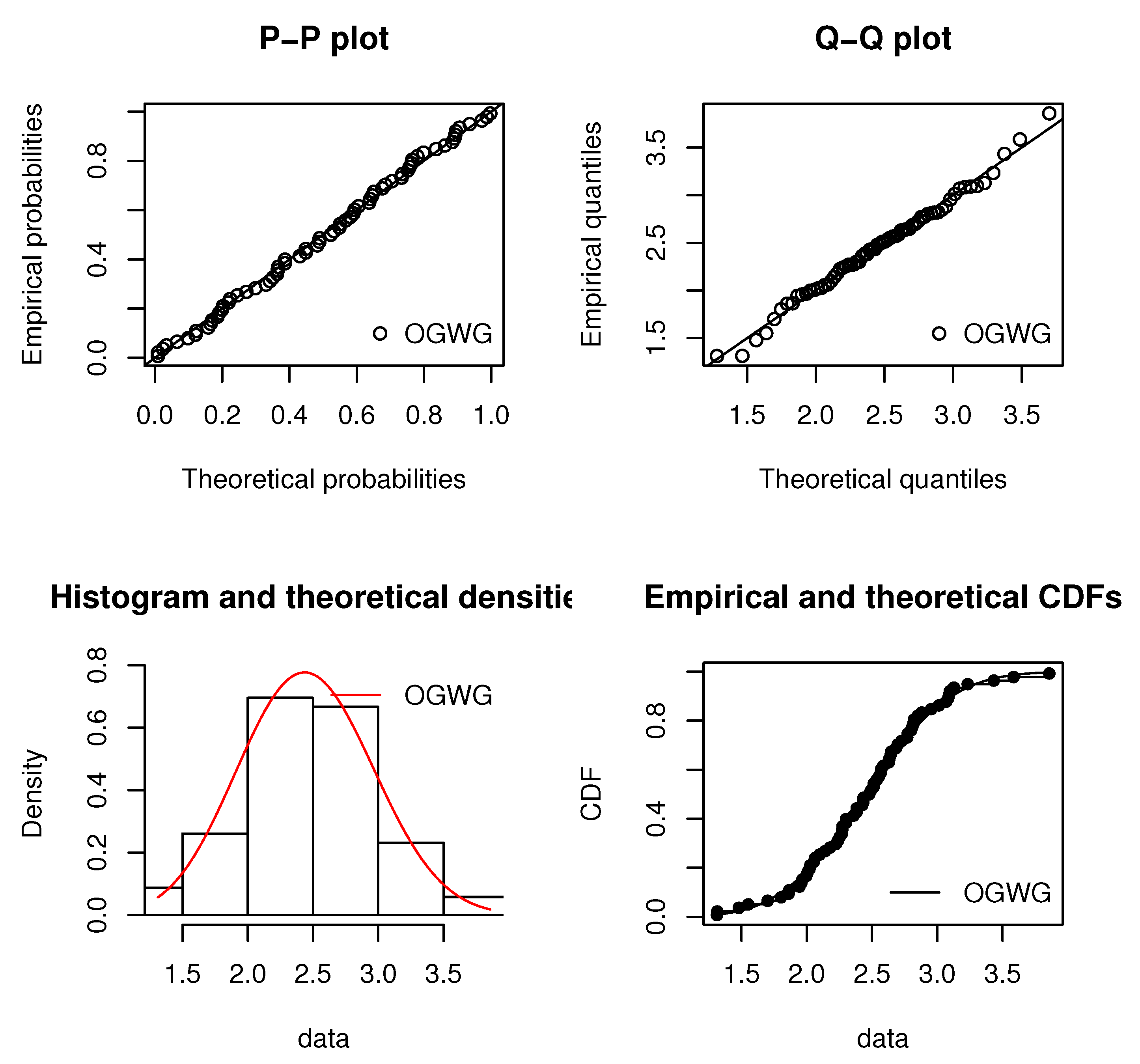
5. Data Analysis
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tahir, M.H.; Cordeiro, G.M. Compounding of distributions: A survey and new generalized classes. J. Stat. Dist. Appl. 2016, 3, 1–35. [Google Scholar] [CrossRef]
- Saghir, A.; Hamedani, G.G.; Tazeem, S.; Khadim, A. Weighted Distributions: A Brief Review, Perspective and Characterizations. Int. J. Stat. Probab. 2017, 6, 109–131. [Google Scholar] [CrossRef]
- Zografos, K.; Balakrishnan, N. On families of beta- and generalized gamma-generated distributions and associated inference. Stat. Method 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Ristíc, M.M.; Balakrishnan, N. The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 2002, 82, 1191–1206. [Google Scholar] [CrossRef]
- Torabi, H.; Montazeri, N.H. The gamma uniform distribution and its applications. Kybernetika 2012, 48, 16–30. [Google Scholar]
- Hosseini, B.; Afshari, M.; Alizadeh, M. The Generalized Odd Gamma-G Family of Distributions: Properties and Applications. Aust. J. Stat. 2018, 47, 69–89. [Google Scholar]
- Oluyede, B.O.; Pu, S.; Makubate, B.; Qiu, Y. The Gamma-Weibull-G Family of Distributions with Applications. Aust. J. Stat. 2018, 47, 45–76. [Google Scholar] [CrossRef]
- Barreto-Souza, W.; Morais, A.L.; Cordeiro, G.M. The Weibull-geometric distribution. J. Stat. Comput. Simul. 2011, 81, 645–657. [Google Scholar] [CrossRef]
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics, 3rd ed.; Chapman and Hall Ltd.: Rahway, NJ, USA, 1962. [Google Scholar]
- Moors, J.J. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. D 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Parzen, E. Nonparametric statistical modelling (with comments). J. Am. Stat. Assoc. 1979, 74, 105–131. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders and Their Applications; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Press, W.H.; Teukolsky, A.A.; Vetterling, W.T.; Flanner, Y.B.P. Numerical Recipes in C: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull Distribution: Some Properties and Applications to Censored Data. J. Modern Appl. Stat. Methods 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Chen, G.; Balakrishnan, N. A general purpose approximate goodness-of-fit test. J. Qual. Tech. 1995, 27, 154–161. [Google Scholar] [CrossRef]
- Proschan, F. Theoretical explanation of observed decreasing failure rate. Technometrics 1963, 5, 375–383. [Google Scholar] [CrossRef]
- Bader, M.G.; Priest, A.M. Statistical aspects of fiber and bundle strength in hybrid composites. In Progress in Science and Engineering Composites; Elsevier: Amsterdam, The Netherlands, 1982; pp. 1129–1136. [Google Scholar]
- Pešta, M. Total least squares and bootstrapping with application in calibration. Stat.: J. Theo. Appl. Stat. 2013, 5, 966–991. [Google Scholar] [CrossRef]

| (i) | (ii) | (iii) | (iv) | (v) | (vi) | |
|---|---|---|---|---|---|---|
| 0.0449 | 0.0472 | 3.0687 | 1.4307 | 12.8356 | 1.5471 | |
| 0.0674 | 1.5278 | 137.2844 | 44.8664 | 598.1401 | 2.9802 | |
| 0.2314 | 87.1821 | 8749.1190 | 12489.1710 | 38083.25 | 6.7361 | |
| 1.2680 | 6047.4790 | 640578.8 | 169843.6 | 2776370 | 17.2563 | |
| 0.0654 | 1.5256 | 127.8670 | 42.8193 | 433.3854 | 0.5865 | |
| 13.3020 | 46.1489 | 5.2168 | 8.2173 | 2.13697 | 0.6909 | |
| 286.7989 | 2591.0480 | 33.0687 | 7.086025 | 3.3211 | 3.4358 |
| I | II | III | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Bias | MSE | CP | Bias | MSE | CP | Bias | MSE | CP | |
| c | 50 | 0.028 | 0.098 | 0.99 | 0.146 | 0.535 | 0.94 | 0.511 | 1.433 | 0.96 |
| 100 | 0.011 | 0.043 | 0.97 | 0.164 | 0.309 | 0.95 | 0.374 | 0.871 | 0.95 | |
| 200 | −0.008 | 0.021 | 0.96 | 0.195 | 0.228 | 0.97 | 0.089 | 0.313 | 0.98 | |
| 50 | 0.250 | 0.410 | 0.94 | 0.172 | 0.241 | 1.00 | 0.118 | 0.913 | 0.95 | |
| 100 | 0.104 | 0.351 | 0.95 | 0.053 | 0.065 | 0.96 | 0.091 | 0.403 | 0.98 | |
| 200 | −0.091 | 0.182 | 0.96 | 0.001 | 0.031 | 0.97 | 0.016 | 0.048 | 0.97 | |
| p | 50 | 0.002 | 0.072 | 0.96 | 0.311 | 0.163 | 0.99 | 0.053 | 0.171 | 0.97 |
| 100 | −0.025 | 0.062 | 0.98 | 0.271 | 0.132 | 0.95 | 0.050 | 0.121 | 0.96 | |
| 200 | −0.082 | 0.049 | 0.97 | 0.222 | 0.100 | 0.96 | 0.020 | 0.065 | 0.95 | |
| 50 | 0.258 | 0.912 | 0.95 | −0.062 | 0.022 | 0.95 | 0.211 | 0.391 | 0.93 | |
| 100 | 0.150 | 0.627 | 0.96 | −0.059 | 0.017 | 0.96 | 0.100 | 0.253 | 0.95 | |
| 200 | 0.088 | 0.414 | 0.97 | −0.051 | 0.011 | 0.98 | 0.093 | 0.191 | 0.96 |
| Statistics | n | Mean | Median | Mode | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Data 1 | 213 | 93.1408 | 57 | 14 | 106.76 | 2.1118 | 4.9249 |
| Distribution | Estimates | K-S | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1527 | 11.5290 | 0.8340 | 0.0249 | 0.2506 | 0.0338 | 0.0379 | 2353.8560 | 2363.0490 | |
| (0.0520) | (2.4351) | (0.1133) | (0.0320) | ||||||
| 3.6631 | 0.1333 | 0.6803 | 0.3258 | 0.2964 | 0.0383 | 0.0391 | 2357.3430 | 2370.7880 | |
| (0.6564) | (0.0098) | (0.0025) | (0.0025) | ||||||
| 1.1719 | 0.7071 | 0.0056 | 0.2957 | 0.0425 | 0.0390 | 2354.6050 | 2364.6890 | ||
| (0.0956) | (0.1196) | (0.0011) | |||||||
| 0.2868 | 2.7657 | 0.0342 | 1.0608 | 0.1717 | 0.0573 | 2363.5300 | 2373.6140 | ||
| (0.0679) | (0.7995) | (0.0292) | |||||||
| CI | c | p | ||
|---|---|---|---|---|
| 95% | [0.0507 0.2546] | [6.7562 16.3017] | [0.6119 1.0560] | [0 0.0876] |
| 99% | [0.0185 0.2868] | [5.2464 17.8115] | [0.5416 1.1263] | [0 0.1074] |
| Statistics | n | Mean | Median | Mode | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Data 2 | 69 | 2.4551 | 2.4780 | 2.2500 | 0.5052 | 0.1020 | 0.2253 |
| Distribution | Estimates | K-S | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1.8247 | 5.6103 | 0.9449 | 0.1931 | 0.1705 | 0.0188 | 0.0328 | 104.6965 | 111.6329 | |
| (0.1062) | (1.1340) | (0.0898) | (0.1349) | ||||||
| 2.6824 | 1.0947 | 3.2891 | 0.4510 | 0.1736 | 0.0211 | 0.0433 | 108.5069 | 117.4433 | |
| (2.6516) | (3.4755) | (2.1102) | (0.2442) | ||||||
| 7.5850 | 0.8884 | 0.3046 | 0.1899 | 0.0252 | 0.0423 | 106.5669 | 113.2692 | ||
| (1.1497) | (0.1321) | (0.0327) | |||||||
| 0.5060 | 12.1478 | 2.5990 | 0.1810 | 0.0221 | 0.0443 | 106.5870 | 113.2894 | ||
| (0.4747) | (14.2268) | (6.7712) | |||||||
| CI | c | p | ||
|---|---|---|---|---|
| 95% | [1.6165 2.0328] | [3.3876 7.8329] | [0.7704 1.1193] | [0 0.4575] |
| 99% | [1.5507 2.0986] | [2.6845 8.5360] | [0.7158 1.1745] | [0 0.5411] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, R.M.I.; Chesneau, C.; Jamal, F. The Odd Gamma Weibull-Geometric Model: Theory and Applications. Mathematics 2019, 7, 399. https://doi.org/10.3390/math7050399
Arshad RMI, Chesneau C, Jamal F. The Odd Gamma Weibull-Geometric Model: Theory and Applications. Mathematics. 2019; 7(5):399. https://doi.org/10.3390/math7050399
Chicago/Turabian StyleArshad, Rana Muhammad Imran, Christophe Chesneau, and Farrukh Jamal. 2019. "The Odd Gamma Weibull-Geometric Model: Theory and Applications" Mathematics 7, no. 5: 399. https://doi.org/10.3390/math7050399
APA StyleArshad, R. M. I., Chesneau, C., & Jamal, F. (2019). The Odd Gamma Weibull-Geometric Model: Theory and Applications. Mathematics, 7(5), 399. https://doi.org/10.3390/math7050399







