Robust H_∞-Control for Uncertain Stochastic Systems with Impulsive Effects

Abstract

Robust stabilization and $H_{\infty }$ controller design for uncertain systems with impulsive and stochastic effects have been deeply discussed. Some sufficient conditions for the considered system to be robustly stable are derived in terms of linear matrix inequalities (LMIs). In addition, an example with simulations is given to better demonstrate the usefulness of the proposed $H_{\infty }$ controller design method.

1. Introduction

Analysis and synthesis of dynamical systems with impulsive effects have attracted recurring interest for the past few decades [1,2,3]. The sudden change of system states at a certain point is the characteristic of a pulse dynamic system. Take an example from economics. When higher prices cause inflation, the government may raise the interest rate in real time to quickly reduce the circulation of money in the market, which is a typical pulse phenomenon. For a deterministic case, a large number of conclusions about stability and control for systems with impulsive perturbations can be found; see [4,5,6,7,8] and the reference therein.

However, because science and engineering applications offer stochastic models a great role in many areas, stochastic system theory has received widespread attention. Many basic results of systems without stochastic disturbance have been expanded to stochastic systems [9,10,11,12,13,14,15,16]. At the same time, the theory and application of stochastic differential equations have made great progress because it has played a key role in many fields; for example, option investment, population growth forecast, system control and filtering [17,18,19,20,21]. Among them, Ref. [21] gave a survey of impulsive differential equation theory that has been developed in recent years. Parameter uncertainties appear in stochastic impulsive systems, and exponential stability was analyzed in [22], guaranteed cost control was discussed in [23] and $H_{\infty }$ filtering has been dealt with in [24,25]. It should be noted that for uncertain systems with impulsive and stochastic effects, little research has been carried out on robust $H_{\infty }$ control, which aroused our interest.

In this note, the studies of robust stabilization and $H_{\infty }$ controller design are conducted for an uncertain stochastic system with impulsive effects. Its time-varying uncertain parameters, which appear both in state, control and disturbance part, are supposed to be norm-bounded. An LMI-based sufficient condition is derived for an existing memoryless state feedback controller guaranteeing asymptotic stability and meeting $H_{\infty }$ performance.

The note has the following arrangement: Section 2 begins with the problem formulation and reviews some useful definitions and lemmas; Section 3 discusses the robust stability and robust stabilization; Section 4 develops LMI-based $H_{\infty }$ controller design method; Section 5 gives an example, which illustrates the applicability of the theoretical results; Section 6 summarizes the full text.

Notations.$X>0$$(X\ge 0)$ indicates that a symmetric positive (semi-positive) definite matrix; $X^{\mathrm{T}}$ and $X^{-1}$ represents the transpose and the inverse of X; ${\mathbb{R}}^n$ is the n-dimensional Euclidean space; ${\mathfrak{L}}_2[0,\infty )$ (respectively, ${\mathfrak{l}}_2[0,\infty )$) is the space of the square-integrable vector functions (respectively, the squares and vector sequences) on $[0,\infty )$; $|·|$ denotes the Euclidean vector norm; ${\parallel ·\parallel }_{{\mathfrak{L}}_2}$ (respectively, ${\parallel ·\parallel }_{{\mathfrak{l}}_2}$) represents the ${\mathfrak{L}}_2[0,\infty )$ (respectively, ${\mathfrak{l}}_2[0,\infty )$) norm on $[0,\infty )$; while ${\parallel ·\parallel }_{{\mathbf{E}}_2}$ indicates the norm in ${\mathfrak{L}}_2((\mathsf{\Omega },\mathbb{F},\mathbb{P}),[0,\infty ))$; $(\mathsf{\Omega },\mathbb{F},\mathbb{P}))$ is the complete probability space with $\mathsf{\Omega }$ the sample space and $\mathbb{F}$ the $\sigma$-algebra of subsets of the sample space; $\mathcal{E}(·)$ corresponds to the mathematical expectation; the maximum (minimum) eigenvalues of a matrix are represented by ${\lambda }_{max}(·)$ (${\lambda }_{min}(·)$).

2. Problem Description and Preliminaries

We consider the uncertain stochastic system with impulsive effects:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dx\left(t\right)=[(A+\Delta A\left(t\right))x\left(t\right)+(B+\Delta B\left(t\right))u\left(t\right)+(B_v+\Delta B_v\left(t\right))v\left(t\right)]dt\hfill \\ +[(H+\Delta H\left(t\right))x\left(t\right)+(G+\Delta G\left(t\right))u\left(t\right)+(G_v+\Delta G_v\left(t\right))v\left(t\right)]dw\left(t\right),t\ne {\iota }_{\kappa },\hfill \\ x\left({\iota }_{\kappa }\right)=C_{\kappa }x\left({\iota }_{\kappa }^{-}\right)+D_{\kappa }\delta \left({\iota }_{\kappa }\right),t={\iota }_{\kappa },\kappa =0,1,\cdots ,\hfill \\ z\left(t\right)=C_{z}x\left(t\right)+B_{z}u\left(t\right)+D_{z}v\left(t\right),\hfill \\ x\left(t_0\right)=x_0,t_0=0,\hfill \end{array}\right.\end{array}$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^{n_1}$ is the system state, $z\left(t\right)\in {\mathbb{R}}^{n_3}$ is the controlled output, and $u\left(t\right)\in {\mathbb{R}}^{n_2}$ is the control input, $v\left(t\right)\in {\mathbb{R}}^{m_1}$ is the continuous disturbance of ${\mathfrak{L}}_2[0,\infty )$. $\delta \left({\iota }_{\kappa }\right)\in {\mathcal{R}}^{m_2}$ is the discrete disturbance of ${\mathfrak{l}}_2[0,\infty )$. $w\left(t\right)$ is a one-dimensional Brownian motion defined on a complete probability space $(\mathsf{\Omega },\mathbb{F},\mathbb{P})$. $\{{\iota }_{\kappa },\kappa =0,1,\cdots \}$ are the impulsive time instants and satisfy $0={\iota }_0<{\iota }_1<\cdots <{\iota }_{\kappa }<{\iota }_{\kappa +1}<\cdots$. Assume that $A,B,B_v,H,G,G_v,C_{\kappa },D_{\kappa },C_z,B_z$ and $D_z$ are known matrices with appropriate dimensions, and $\Delta A\left(t\right),\Delta B\left(t\right),\Delta B_v\left(t\right),\Delta H\left(t\right),\Delta G\left(t\right)$ and $\Delta G_v\left(t\right)$ are unknown matrices denoting norm-bounded time-varying parameter uncertainties with the forms:

$$\begin{array}{c}[\Delta A\left(t\right)\Delta B\left(t\right)\Delta H\left(t\right)\Delta G\left(t\right)\Delta B_v\left(t\right)\Delta G_v\left(t\right)]\hfill \\ =MF\left(t\right)\left[N_A{N}_B{N}_H{N}_G{N}_{B_v}{N}_{G_v}\right],\hfill \end{array}$$

(2)

where $M,N_A,N_B,N_H,N_G,N_{B_v}$ and $N_{G_v}$ are known constant matrices, and $F\left(t\right)\in {\mathbb{R}}^{\kappa \times l}$ is an unknown time-varying matrix function satisfying

$$\begin{array}{c}\hfill F{\left(t\right)}^{\mathrm{T}}F\left(t\right)\le I,\forall t.\end{array}$$

(3)

For convenience, abbreviating $\Delta A\left(t\right)$, $\Delta B\left(t\right)$, $\Delta B_v\left(t\right)$, $\Delta H\left(t\right)$, $\Delta G\left(t\right)$, $\Delta G_v\left(t\right)$, $x\left(t\right)$, $v\left(t\right)$, $u\left(t\right)$ and $w\left(t\right)$ to $\Delta A$, $\Delta B$, $\Delta B_v$, $\Delta H$, $\Delta G$, $\Delta G_v$, x, v, u and w, where $\Delta A$, $\Delta B$, $\Delta B_v$, $\Delta H$, $\Delta G$ and $\Delta G_v$ are considered admissible if both (2) and (3) hold.

Now, we recall some basic concepts about robust stability and stabilization.

Definition 1 ([13]).

The impulsive stochastic system (1) is said to be mean-square stable with $u=0$, $\delta \left({\iota }_{\kappa }\right)=0$ and $v=0$, if there is a $\alpha \left(\epsilon \right)>0$ for ∀$\epsilon >0$, when $\mathcal{E}|x_0|<\alpha \left(\epsilon \right)$, $t>0$, such that ${\mathcal{E}\left|x\right|}^2<\epsilon$. If ${\displaystyle \underset{t\to \infty }{lim}\mathcal{E}{\left|x\right|}^2=0}$ satisfies any initial conditions, then (1) with $u=0$, $\delta \left({\iota }_{\kappa }\right)=0$ and $v=0$ is called mean-square asymptotically stable. And, the system $\left(1\right)$ is said to be robustly stochastic stability (RSS for short) if (1) with $v=0,\delta \left({\iota }_{\kappa }\right)=0$ and $u=0$ is mean-square asymptotically stable for all admissible uncertainties $\Delta A$ and $\Delta H$.

Definition 2 ([13]).

Given a real number $\gamma >0$, the system $\left(1\right)$ is said to be RSS and the $H_{\infty }$ performance γ exists, if it is RSS in the sense of Definition 1 and under zero initial conditions, for all $v\in {\mathfrak{L}}_2[0,\infty ),\delta \in {\mathfrak{l}}_2[0,\infty )$ and all admissible uncertainties $\Delta A,\Delta H$, the inequality ${\parallel z\parallel }_{{\mathbf{E}}_2}\le {\gamma (\parallel v\parallel }_{{\mathfrak{L}}_2}^2+{\parallel \delta \parallel }_{{\mathfrak{l}}_2}^2{)}^{1/2}$ holds.

Next, We list two lemmas, which are very important for the discussion in later chapters.

Lemma 1 ([26]).

Let matrices $\mathfrak{R},\mathfrak{Q},\mathfrak{H},\mathfrak{N}$ and F with appropriate dimensions satisfying $\mathfrak{N}>0$ and $F^{\mathrm{T}}F\le I$, then:

(1) 

For scalar $ϵ>0$ and vectors $a,b\in {\mathbb{R}}^n$,

$$\begin{array}{c}\hfill 2a^T\mathfrak{Q}F\mathfrak{H}b\le {ϵ}^{-1}{a}^T\mathfrak{Q}{\mathfrak{Q}}^{T}a+ϵb^T{\mathfrak{H}}^T\mathfrak{H}b;\end{array}$$

(2) 

For ∀$ϵ>0$ to make $\mathfrak{N}-ϵ\mathfrak{Q}{\mathfrak{Q}}^T>0$,

$$\begin{array}{c}\hfill {(\mathfrak{R}+\mathfrak{Q}F\mathfrak{H})}^T{\mathfrak{N}}^{-1}(\mathfrak{R}+\mathfrak{Q}F\mathfrak{H})\le {\mathfrak{R}}^T{(\mathfrak{N}-ϵ\mathfrak{Q}{\mathfrak{Q}}^T)}^{-1}\mathfrak{R}+{ϵ}^{-1}{\mathfrak{H}}^T\mathfrak{H}.\end{array}$$

Lemma 2 ([27]).

Let ${\Delta }_1,{\Delta }_2,{\Delta }_3$ be given matrices, where ${\Delta }_1={\Delta }_1^{\mathrm{T}}$, ${\Delta }_2>0$ and ${\Delta }_3={\Delta }_3^{\mathrm{T}}$, then the following inequalities are equivalent:

(1) 

${\Delta }_1+{\Delta }_2{\Delta }_3^{-1}{\Delta }_2^{\mathrm{T}}<0;$

(2) 

$\left[\begin{array}{cc}{\Delta }_1& {\Delta }_2\\ {\Delta }_2^{\mathrm{T}}& -{\Delta }_3\end{array}\right]<0.$

3. Robust Stabilization

In this chapter, we restrict our study to the uncontrolled system (i.e., $v\left(t\right)=0$ and $\delta \left({\iota }_{\kappa }\right)=0$ in (1)):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dx\left(t\right)=\left[\right(A+\Delta A\left)x\right(t)+(B+\Delta B\left)u\right(t\left)\right]dt\hfill \\ +[(H+\Delta H)x\left(t\right)+(G+\Delta G)u\left(t\right)]dw\left(t\right),t\ne {\iota }_{\kappa },\hfill \\ x\left({\iota }_{\kappa }\right)=C_{\kappa }x\left({\iota }_{\kappa }^{-}\right),t={\iota }_{\kappa },\kappa =0,1,\cdots ,\hfill \\ z\left(t\right)=C_{z}x\left(t\right)+B_{z}u\left(t\right),\hfill \\ x\left(t_0\right)=x_0,t_0=0.\hfill \end{array}\right.\end{array}$$

(4)

First of all, we present some sufficient conditions for RSS of (4) with $u\left(t\right)=0$.

Theorem 1.

Assume there exist two positive scalars ${\epsilon }_1>0$, ${\epsilon }_2>0$ and matrix $X>0$, such that:

$$\begin{array}{c}\left[\begin{array}{cccc}X{A}^{\mathrm{T}}+AX+{\epsilon }_{1}M{M}^{\mathrm{T}}& X{N}_A^{\mathrm{T}}& X{N}_H^{\mathrm{T}}& X{H}^{\mathrm{T}}\\ N_{A}X& -{\epsilon }_1& 0& 0\\ N_{H}X& 0& -{\epsilon }_2& 0\\ HX& 0& 0& -(X-{\epsilon }_{2}M{M}^{\mathrm{T}})\end{array}\right]<0,\hfill \end{array}$$

(5)

$$\begin{array}{c}\left[\begin{array}{cc}-X& X{C}_{\kappa }^{\mathrm{T}}\\ C_{\kappa }X& -X\end{array}\right]\le 0,\kappa =0,1,\cdots ,\hfill \end{array}$$

(6)

then (4) with $u\left(t\right)=0$ is mean-square asymptotically stable.

Proof. 

Consider (4) with $u\left(t\right)=0$, that is,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dx\left(t\right)=\left[(A+\Delta A)x\left(t\right)\right]dt+\left[(H+\Delta H)x\left(t\right)\right]dw\left(t\right),t\ne {\iota }_{\kappa },\hfill \\ x\left({\iota }_{\kappa }\right)=C_{\kappa }x\left({\iota }_{\kappa }^{-}\right),t={\iota }_{\kappa },\kappa =0,1,\cdots ,\hfill \\ x\left(t_0\right)=x_0,t_0=0.\hfill \end{array}\right.\end{array}$$

(7)

Let ∀${\epsilon }_1>0$, ${\epsilon }_2>0$, and matrix $X>0$ be a solution of (5) and (6). Let

$$\begin{array}{c}\hfill P=X^{-1}.\end{array}$$

(8)

For $t>0$ and $t\in [{\iota }_{\kappa },{\iota }_{\kappa +1})$, Define

$$\begin{array}{c}\hfill \mathrm{V}\left(x\right)=x^{\mathrm{T}}Px.\end{array}$$

(9)

Then, along the trajectory of (7) and apply the Itô’s formula [12], we can get

$$\begin{array}{c}\hfill d\mathrm{V}\left(x\right)=\mathbb{L}\mathrm{V}\left(x\right)dt+2x^{\mathrm{T}}P[H+\Delta H]xdw,\end{array}$$

(10)

where

$$\begin{array}{c}\hfill \mathbb{L}\mathrm{V}\left(x\right)=2x^{\mathrm{T}}P(A+\Delta A)x+x^{\mathrm{T}}{[H+\Delta H]}^{\mathrm{T}}P[H+\Delta H]x.\end{array}$$

(11)

Applying (2), (3) and Lemma 1, for ∀$\epsilon >0$,

$$\begin{array}{c}2x^{\mathrm{T}}P(A+\Delta A)x=2x^{\mathrm{T}}P(A+MF\left(t\right)N_A)x\hfill \\ \le x^{\mathrm{T}}(A^{\mathrm{T}}P+PA+{\epsilon }_{1}PM{M}^{\mathrm{T}}P+{\epsilon }_1^{-1}{N}_A^{\mathrm{T}}{N}_A)x,\hfill \end{array}$$

(12)

and

$$\begin{array}{c}{x}^{\mathrm{T}}\left[{(H+\Delta H)}^{\mathrm{T}}P(H+\Delta H)\right]x\hfill \\ =x^T\left[{(H+MF{N}_H)}^{T}P(H+MF{N}_H)\right]x\hfill \\ \le x^{\mathrm{T}}[H^{\mathrm{T}}{(P^{-1}-{\epsilon }_{2}M{M}^{\mathrm{T}})}^{-1}H+{\epsilon }_2^{-1}{N}_H^{\mathrm{T}}{N}_H]x.\hfill \end{array}$$

(13)

Hence, from (11)–(13), we have

$$\begin{array}{c}\mathbb{L}\mathrm{V}\left(x\right)\le x^{\mathrm{T}}[A^{\mathrm{T}}P+PA+{\epsilon }_{1}PM{M}^{\mathrm{T}}P+{\epsilon }_1^{-1}{N}_A^{\mathrm{T}}{N}_A\hfill \\ +H^{\mathrm{T}}{(P^{-1}-{\epsilon }_{2}M{M}^{\mathrm{T}})}^{-1}H+{\epsilon }_2^{-1}{N}_H^{\mathrm{T}}{N}_H]x\hfill \\ =x^{\mathrm{T}}\mathsf{\Xi }x,\hfill \end{array}$$

(14)

where $\mathsf{\Xi }=A^{\mathrm{T}}P+PA+{\epsilon }_{1}PM{M}^{\mathrm{T}}P+{\epsilon }_1^{-1}{N}_A^{\mathrm{T}}{N}_A+H^{\mathrm{T}}{(P^{-1}-{\epsilon }_{2}M{M}^{\mathrm{T}})}^{-1}H+{\epsilon }_2^{-1}{N}_H^{\mathrm{T}}{N}_H$.

Pre- and post-multiplying (5) by diag $\{P,I,I,I\}$, and by means of Lemma 2, we can get that

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}{A}^{\mathrm{T}}P+PA+{\epsilon }_{1}PM{M}^{\mathrm{T}}P& N_A^{\mathrm{T}}& N_H^{\mathrm{T}}& H^{\mathrm{T}}\\ N_A& -{\epsilon }_1& 0& 0\\ N_H& 0& -{\epsilon }_2& 0\\ H& 0& 0& -(P^{-1}-{\epsilon }_{2}M{M}^{\mathrm{T}})\end{array}\right]<0.\end{array}$$

(15)

By Lemma 2 again, $\mathsf{\Xi }$ is equivalent to (15), which shows $\mathsf{\Xi }$ is negative-definite. Considering (14), for $t\in [{\iota }_{\kappa },{\iota }_{\kappa +1})$ and ∀$x\ne 0$, we can obtain

$$\begin{array}{c}\hfill \mathbb{L}\mathrm{V}\left(x\right)\le -{\lambda \left|x\right|}^2,\end{array}$$

(16)

where $\lambda ={\lambda }_{min}(-\mathsf{\Xi })>0.$ Therefore

$$\begin{array}{c}\hfill d\mathrm{V}\left(x\right)\le -{\lambda \left|x\right|}^{2}dt+2x^{\mathrm{T}}P[H+\Delta H]xdw.\end{array}$$

(17)

Setting $\xi =\lambda /{\lambda }_{max}\left(P\right)>0$, by using the integration-by-parts Formula [28] for (17), one get

$$\begin{array}{c}\hfill d\left[e^{\xi t}\mathrm{V}\left(x\right)\right]\le 2e^{\xi t}{x}^{\mathrm{T}}P[H+\Delta H]xdw.\end{array}$$

The inequality integral from ${\iota }_{\kappa }$ to t, we yields

$$\begin{array}{c}\hfill \mathcal{E}\left[\mathrm{V}\left(x\left(t\right)\right)\right]\le e^{\xi ({\iota }_{\kappa }-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right].\end{array}$$

(18)

In view of (6), pre- and post-multiplying by P, it gives

$$\begin{array}{c}\hfill C_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P\le 0,\kappa =0,1,\cdots .\end{array}$$

(19)

Then we have

$$\begin{array}{c}\hfill \mathcal{E}\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)-\mathcal{E}\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)=\mathcal{E}\left[x^{\mathrm{T}}\left({\iota }_{\kappa }^{-}\right)(C_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P)x\left({\iota }_{\kappa }^{-}\right)\right]\le 0.\end{array}$$

That is,

$$\begin{array}{c}\hfill \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right],\kappa =0,1,\cdots .\end{array}$$

(20)

So, for $t\in [{\iota }_{\kappa },{\iota }_{\kappa +1})$, by (18) and (20), we prove that

$$\begin{array}{c}\hfill \mathcal{E}\left[\mathrm{V}\left(x\left(t\right)\right)\right]\le e^{\xi ({\iota }_{\kappa }-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]\le e^{\xi ({\iota }_{\kappa }^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right].\end{array}$$

(21)

Similarly, we have

$$\begin{array}{c}{e}^{\xi ({\iota }_{\kappa }^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right]\le e^{\xi ({\iota }_{\kappa -1}^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -1}^{-}\right)\right)\right],\hfill \\ e^{\xi ({\iota }_{\kappa -1}^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -1}^{-}\right)\right)\right]\le e^{\xi ({\iota }_{\kappa -2}^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -2}^{-}\right)\right)\right],\hfill \\ ⋮\hfill \\ e^{\xi ({\iota }_1^{-}-t)}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_1^{-}\right)\right)\right]\le e^{-\xi t}\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_0\right)\right)\right].\hfill \end{array}$$

These implies for ∀$t\ge 0$,

$$\begin{array}{c}\hfill \mathcal{E}\left[\mathrm{V}\left(x\right)\right]\le e^{-\xi t}\mathcal{E}\left[\mathrm{V}\left(x_0\right)\right],\end{array}$$

(22)

Thus, let $\eta =\mathcal{E}\left[\mathrm{V}\left(x_0\right)\right]/{\lambda }_{min}\left(P\right)$, we can deduce

$$\begin{array}{c}\hfill {\mathcal{E}\left|x\right|}^2\le e^{-\xi t}\eta \end{array}$$

which means that (7) is mean-square asymptotically stable. □

We will design a memoryless state feedback controller with the form:

$$\begin{array}{c}\hfill u\left(t\right)=Kx\left(t\right)\end{array}$$

(23)

Making the resulting closed-loop system is RSS, $K\in {\mathcal{R}}^{m\times n}$ is a constant gain.

Applying (23) to (4), generate the following closed-loop systems:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dx\left(t\right)=\left[(\tilde{A}+\Delta \tilde{A})x\left(t\right)\right]dt+(\tilde{H}+\Delta \tilde{H})x\left(t\right)]dw\left(t\right),t\ne {\iota }_{\kappa },\hfill \\ x\left({\iota }_{\kappa }\right)=C_{\kappa }x\left({\iota }_{\kappa }^{-}\right),t={\iota }_{\kappa },\kappa =0,1,\cdots ,\hfill \\ x\left(t_0\right)=x_0,t_0=0,\hfill \end{array}\right.\end{array}$$

(24)

where $\tilde{A}=A+BK$, $\Delta \tilde{A}=\Delta A+\Delta BK$, $\tilde{H}=H+GK$ and $\Delta \tilde{H}=\Delta H+\Delta GK$, in which $N_{\tilde{A}}=N_A+N_{B}K$ and $N_{\tilde{H}}=N_H+N_{G}K$.

Invoking by Theorem 1, it gives

Theorem 2.

For the uncertain impulsive stochastic system (24), assume there are ${\epsilon }_1>0,{\epsilon }_2>0$, and a matrices $X>0$, such that:

$$\begin{array}{c}\left[\begin{array}{cccc}X{\tilde{A}}^{\mathrm{T}}+\tilde{A}X+{\epsilon }_{1}M{M}^{\mathrm{T}}& X{N}_{\tilde{A}}^{\mathrm{T}}& X{N}_{\tilde{H}}^{\mathrm{T}}& X{\tilde{H}}^{\mathrm{T}}\\ N_{\tilde{A}}X& -{\epsilon }_1& 0& 0\\ N_{\tilde{H}}X& 0& -{\epsilon }_2& 0\\ \tilde{H}X& 0& 0& -(X-{\epsilon }_{2}M{M}^{\mathrm{T}})\end{array}\right]<0,\hfill \end{array}$$

(25)

$$\begin{array}{c}\left[\begin{array}{cc}-X& X{C}_{\kappa }^{\mathrm{T}}\\ C_{\kappa }X& -X\end{array}\right]\le 0,\kappa =0,1,\cdots ,\hfill \end{array}$$

(26)

then (4) is robustly stable with controller (23) and $K=Y{X}^{-1}$.

In order to synthesize the gain of the controller, we transform (25) into an easy to calculate form. Note

$$\begin{array}{c}\tilde{A}X=(A+BK)X,N_{\tilde{A}}X=(N_A+N_{B}K)X,\hfill \\ \tilde{H}X=(H+GK)X,N_{\tilde{H}}X=(N_H+N_{G}K)X.\hfill \end{array}$$

Letting $K=Y{X}^{-1}$, (25) is equivalent to the following LMI:

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}{\mathsf{\Psi }}_1& X{N}_A^{\mathrm{T}}+Y^{\mathrm{T}}{N}_B^{\mathrm{T}}& X{N}_H^{\mathrm{T}}+Y^{\mathrm{T}}{N}_G^{\mathrm{T}}& X{H}^{\mathrm{T}}+Y^{\mathrm{T}}{G}^{\mathrm{T}}\\ N_{A}X+N_{B}Y& -{\epsilon }_1& 0& 0\\ N_{H}X+N_{G}Y& 0& -{\epsilon }_2& 0\\ HX+GY& 0& 0& -(X-{\epsilon }_{2}M{M}^{\mathrm{T}})\end{array}\right]<0,\end{array}$$

(27)

where ${\mathsf{\Psi }}_1=X{A}^{\mathrm{T}}+AX+BY+Y^{\mathrm{T}}{B}^{\mathrm{T}}+{\epsilon }_{1}M{M}^{\mathrm{T}}.$

Remark 1.

Theorem 2 gives a sufficient condition for robust stability of (4), which can be validated effectively by LMIs method. We can also stabilize the feedback gain (4) by solving LMIs.

4. Robust $H_{\infty }$ Control

This part is mainly used to study the robust $H_{\infty }$-control problem for (1).

Theorem 3.

For the uncertain impulsive stochastic system (1). Given $\gamma >0$, if there are ${\widehat{\epsilon }}_1>0$, ${\widehat{\epsilon }}_2>0$, matrices $X>0$ and Y, such that:

$$\begin{array}{c}\hfill \left[\begin{array}{cccccc}{\mathsf{\Psi }}_2& B_v& X{N}_A^{\mathrm{T}}+Y^{\mathrm{T}}{N}_B^{\mathrm{T}}& X{N}_H^{\mathrm{T}}+Y^{\mathrm{T}}{N}_G^{\mathrm{T}}& X{C}_z^{\mathrm{T}}+Y^{\mathrm{T}}{B}_z^{\mathrm{T}}& X{H}^{\mathrm{T}}+Y^{\mathrm{T}}{G}^{\mathrm{T}}\\ B_v^{\mathrm{T}}& -{\gamma }^{2}I& N_{B_v}^{\mathrm{T}}& N_{G_v}^{\mathrm{T}}& D_z^{\mathrm{T}}& G_v^{\mathrm{T}}\\ N_{A}X+N_{B}Y& N_{B_v}& -{\widehat{\epsilon }}_{1}I& 0& 0& 0\\ N_{H}X+N_{G}Y& N_{G_v}& 0& -{\widehat{\epsilon }}_{2}I& 0& 0\\ C_{z}X+B_{z}Y& D_z& 0& 0& -I& 0\\ HX+GY& G_v& 0& 0& 0& {\widehat{\epsilon }}_{2}M{M}^{\mathrm{T}}-X\end{array}\right]<0,\end{array}$$

(28)

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}-X& 0& X{C}_{\kappa }^{\mathrm{T}}\\ 0& -{\gamma }^{2}I& D_{\kappa }^{\mathrm{T}}\\ C_{\kappa }X& D_{\kappa }& -X\end{array}\right]\le 0,\kappa =0,1,\cdots ,\end{array}$$

(29)

where ${\mathsf{\Psi }}_2=X{A}^{\mathrm{T}}+AX+BY+Y^{\mathrm{T}}{B}^{\mathrm{T}}+{\epsilon }_{1}M{M}^{\mathrm{T}}$, then (1) is called have $H_{\infty }$ performance level γ under zero initial condition. Under this circumstance, an $H_{\infty }$ state feedback controller can be selected by

$$\begin{array}{c}\hfill u\left(t\right)=Kx\left(t\right),\end{array}$$

(30)

in which $K=Y{X}^{-1}$.

Proof. 

By substituting (30), (1) becomes

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dx\left(t\right)=[(\tilde{A}+\Delta \tilde{A})x\left(t\right)+(B_v+\Delta B_v)v\left(t\right)]dt\hfill \\ +[(\tilde{H}+\Delta \tilde{H})x\left(t\right)+(G_v+\Delta G_v)v\left(t\right)]dw\left(t\right),t\ne {\iota }_{\kappa },\hfill \\ x\left({\iota }_{\kappa }\right)=C_{\kappa }x\left({\iota }_{\kappa }^{-}\right)+D_{\kappa }\delta \left({\iota }_{\kappa }\right),t={\iota }_{\kappa },\kappa =0,1,\cdots ,\hfill \\ z\left(t\right)=(C_z+B_{z}K)x\left(t\right)+D_{z}v\left(t\right)\hfill \\ x\left(t_0\right)=x_0,t_0=0.\hfill \end{array}\right.\end{array}$$

(31)

By (28), it is easy to infer that the LMI in (25) holds. Therefore, from the theorem 2, it can be concluded that the closed-loop system (31) is robustly stable. The next, we will prove (31) satisfies

$$\begin{array}{c}\hfill {\parallel z\parallel }_{{\mathbf{E}}_2}\le {\gamma (\parallel v\parallel }_{{\mathfrak{L}}_2}^2+{\parallel \delta \parallel }_{{\mathfrak{l}}_2}^2{)}^{1/2}\end{array}$$

(32)

for all nonzero $v\left(t\right)\in {\mathbb{R}}^{m_1}$, $\delta \left({\iota }_{\kappa }\right)\in {\mathbb{R}}^{m_2}$ under zero initial condition.

Let $X=P^{-1}$. Pre-and post-multiplying (28) by diag $[P,I,I,I,I,I]$, it gives

$$\begin{array}{c}\hfill \left[\begin{array}{cccccc}P\tilde{A}+{\tilde{A}}^{\mathrm{T}}P+{\widehat{\epsilon }}_{1}PM{M}^{\mathrm{T}}P& P{B}_v& N_{\tilde{A}}^{\mathrm{T}}& N_{\tilde{H}}^{\mathrm{T}}& C_z^{\mathrm{T}}+K^{\mathrm{T}}{B}_z^{\mathrm{T}}& {\tilde{H}}^{\mathrm{T}}\\ B_v^{\mathrm{T}}P& -{\gamma }^{2}I& N_{B_v}^{\mathrm{T}}& N_{G_v}^{\mathrm{T}}& D_z^{\mathrm{T}}& G_v^{\mathrm{T}}\\ N_{\tilde{A}}& N_{B_v}& -{\widehat{\epsilon }}_{1}I& 0& 0& 0\\ N_{\tilde{H}}& N_{G_v}& 0& -{\widehat{\epsilon }}_{2}I& 0& 0\\ C_z+B_{z}K& D_z& 0& 0& -I& 0\\ \tilde{H}& G_v& 0& 0& 0& {\widehat{\epsilon }}_{2}M{M}^{\mathrm{T}}-P^{-1}\end{array}\right]<0.\end{array}$$

(33)

For (31), applying the Itô’s formula to $\mathrm{V}\left(x\right)=x^{\mathrm{T}}Px$, for $t\in [{\iota }_{\kappa },{\iota }_{\kappa +1})$, we have that

$$\begin{array}{c}d\mathrm{V}\left(x\right)=\mathbb{L}\mathrm{V}\left(x\right)dt+[x^{\mathrm{T}}{(\tilde{H}+\Delta \tilde{H})}^{\mathrm{T}}Px+v^{\mathrm{T}}{(G_v+\Delta G_v)}^{\mathrm{T}}Px]dw\hfill \\ +[x^{\mathrm{T}}P(\tilde{H}+\Delta \tilde{H})x+x^{\mathrm{T}}P(G_v+\Delta G_v)v]dw,\hfill \end{array}$$

(34)

where

$$\begin{array}{c}\mathbb{L}\mathrm{V}\left(x\right)=2x^{\mathrm{T}}P[(\tilde{A}+\Delta \tilde{A})x+(B_v+\Delta B_v)v]\hfill \\ +{[(\tilde{H}+\Delta \tilde{H})x+(G_v+\Delta G_v)v]}^{\mathrm{T}}P\hfill \\ \times [(\tilde{H}+\Delta \tilde{H})x+(G_v+\Delta G_v)v].\hfill \end{array}$$

(35)

Noting $P^{-1}-{\widehat{\epsilon }}_{2}M{M}^{\mathrm{T}}>0$ and in view of Lemma 1, it can be shown that for ${\widehat{\epsilon }}_1>0$, ${\widehat{\epsilon }}_2>0$

$$\begin{array}{c}2x^{\mathrm{T}}P[(\tilde{A}+\Delta \tilde{A})x+(B_v+\Delta B_v)v]\hfill \\ \le 2x^{\mathrm{T}}P\tilde{A}x+2x^{\mathrm{T}}P{B}_{v}v+{\widehat{\epsilon }}_1{x}^{\mathrm{T}}PM{M}^{\mathrm{T}}Px\hfill \\ +{\widehat{\epsilon }}_1^{-1}{(N_{\tilde{A}}x+N_{B_v}v)}^{\mathrm{T}}(N_{\tilde{A}}x+N_{B_v}v),\hfill \end{array}$$

(36)

and

$$\begin{array}{c}{[(\tilde{H}+\Delta \tilde{H})x+(G_v+\Delta G_v)v]}^{\mathrm{T}}P[(\tilde{H}+\Delta \tilde{H})x+(G_v+\Delta G_v)v]\hfill \\ \le {(\tilde{H}x+G_{v}v)}^{\mathrm{T}}{(P^{-1}-{\widehat{\epsilon }}_{2}M{M}^{\mathrm{T}})}^{-1}(\tilde{H}x+G_{v}v)\hfill \\ +{\widehat{\epsilon }}_2^{-1}{(N_{\tilde{H}}x+N_{G_v}v)}^{\mathrm{T}}(N_{\tilde{H}}x+N_{G_v}v).\hfill \end{array}$$

(37)

From (35)–(37), we get

$$\begin{array}{c}\hfill \mathbb{L}\mathrm{V}\left(x\right)\le \left[\begin{array}{cc}{x}^{\mathrm{T}}& v^{\mathrm{T}}\end{array}\right]{\mathsf{{\rm Y}}}_1\left[\begin{array}{c}x\\ v\end{array}\right].\end{array}$$

(38)

where

$$\begin{array}{c}{\mathsf{{\rm Y}}}_1=\left[\begin{array}{cc}P\tilde{A}+{\tilde{A}}^{\mathrm{T}}P+{\widehat{\epsilon }}_{1}PM{M}^{\mathrm{T}}P& P{B}_v\\ B_v^{\mathrm{T}}P& 0\end{array}\right]+{\widehat{\epsilon }}_1^{-1}\left[\begin{array}{c}{N}_{\tilde{A}}^{\mathrm{T}}\\ N_{B_v}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}{N}_{\tilde{A}}& N_{B_v}\end{array}\right]\hfill \\ +\left[\begin{array}{c}{\tilde{H}}^{\mathrm{T}}\\ G_v^{\mathrm{T}}\end{array}\right]{(P^{-1}-{\widehat{\epsilon }}_{2}M{M}^{\mathrm{T}})}^{-1}\left[\begin{array}{cc}\tilde{H}& G_v\end{array}\right]+{\widehat{\epsilon }}_2^{-1}\left[\begin{array}{c}{N}_{\tilde{H}}^{\mathrm{T}}\\ N_{G_v}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}{N}_{\tilde{H}}& N_{G_v}\end{array}\right].\hfill \end{array}$$

It can be inferred that ${\mathsf{{\rm Y}}}_1<0$ from (33). Thus, combined with (34) and (38), we obtain

$$\begin{array}{c}d\mathrm{V}\left(x\right)\le \left[\begin{array}{cc}{x}^{\mathrm{T}}& v^{\mathrm{T}}\end{array}\right]{\mathsf{{\rm Y}}}_1\left[\begin{array}{c}x\\ v\end{array}\right]dt\hfill \\ +2x^{\mathrm{T}}P[(\tilde{H}+\Delta \tilde{H})x+(G_v+\Delta G_v)v]dw.\hfill \end{array}$$

(39)

Then, the sides of (34) are integrated from ${\iota }_{\kappa }$ to t, we have

$$\begin{array}{c}\mathcal{E}\left[\mathrm{V}\left(x\left(t\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]=\mathcal{E}[{\int }_{{\iota }_{\kappa }}^{t}d\mathrm{V}\left(x\left(\mu \right)\right)]=\mathcal{E}[{\int }_{{\iota }_{\kappa }}^t\mathbb{L}\mathrm{V}\left(x\left(\mu \right)\right)d\mu ],\hfill \end{array}$$

(40)

By means of (39) and (40), we get

$$\begin{array}{c}\mathcal{E}\left[\mathrm{V}\left(x\left(t\right)\right)\right]=\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]+\mathcal{E}[{\int }_{{\iota }_{\kappa }}^t\mathbb{L}\mathrm{V}\left(x\left(\mu \right)\right)d\mu ]\hfill \\ \le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]+\mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t\left[\begin{array}{cc}{x}^{\mathrm{T}}\left(\mu \right)& v^{\mathrm{T}}\left(\mu \right)\end{array}\right]{\mathsf{{\rm Y}}}_1\left[\begin{array}{c}x\left(\mu \right)\\ v\left(\mu \right)\end{array}\right]d\mu \}.\hfill \end{array}$$

(41)

Therefore, for ∀$t\in [{\iota }_{\kappa },{\iota }_{\kappa +1})$,

$$\begin{array}{c}\mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t[z^{\mathrm{T}}\left(\mu \right)z\left(\mu \right)-{\gamma }^2{v}^{\mathrm{T}}\left(\mu \right)v\left(\mu \right)+\mathbb{L}V\left(x\left(\mu \right)\right)]d\mu \}\hfill \\ =\mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t{[(C_z+B_{z}K)x\left(\mu \right)+D_{z}v\left(\mu \right)]}^{\mathrm{T}}[(C_z+B_{z}K)x\left(\mu \right)+D_{z}v\left(\mu \right)]-{\gamma }^2{v}^{\mathrm{T}}\left(\mu \right)v\left(\mu \right)+\mathbb{L}V\left(x\left(\mu \right)\right)d\mu \}\hfill \\ \le \mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t\left[\begin{array}{cc}{x}^{\mathrm{T}}\left(\mu \right)& v^{\mathrm{T}}\left(\mu \right)\end{array}\right]\mathsf{{\rm Y}}\left[\begin{array}{c}x\left(\mu \right)\\ v\left(\mu \right)\end{array}\right]d\mu \},\hfill \end{array}$$

(42)

where

$$\begin{array}{c}\mathsf{{\rm Y}}=\left[\begin{array}{cc}P\tilde{A}+{\tilde{A}}^{\mathrm{T}}P+{\widehat{\epsilon }}_{1}PM{M}^{\mathrm{T}}P& P{B}_v\\ B_v^{\mathrm{T}}P& -{\gamma }^2\end{array}\right]+{\widehat{\epsilon }}_1^{-1}\left[\begin{array}{c}{N}_{\tilde{A}}^{\mathrm{T}}\\ N_{B_v}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}{N}_{\tilde{A}}& N_{B_v}\end{array}\right]\hfill \\ +\left[\begin{array}{c}{\tilde{H}}^{\mathrm{T}}\\ G_v^{\mathrm{T}}\end{array}\right]{(P^{-1}-{\widehat{\epsilon }}_{2}M{M}^T)}^{-1}\left[\begin{array}{cc}\tilde{H}& G_v\end{array}\right]+{\widehat{\epsilon }}_2^{-1}\left[\begin{array}{c}{N}_{\tilde{H}}^{\mathrm{T}}\\ N_{G_v}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}{N}_{\tilde{H}}& N_{G_v}\end{array}\right]\hfill \\ +\left[\begin{array}{c}{(C_z+B_{z}K)}^{\mathrm{T}}\\ D_z^{\mathrm{T}}\end{array}\right]\left[\begin{array}{cc}{C}_z+B_{z}K& D_z\end{array}\right].\hfill \end{array}$$

Because of $\mathsf{{\rm Y}}<0$, it can be deduced from (38)–(42) that

$$\begin{array}{c}\mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t[z^{\mathrm{T}}\left(\mu \right)z\left(\mu \right)-{\gamma }^2{v}^{\mathrm{T}}\left(\mu \right)v\left(\mu \right)]d\mu \}<\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right].\hfill \end{array}$$

(43)

Let $X=P^{-1}$. Pre- and post-multiplying (29) by diag $\{P,I,I\}$, we have

$$\begin{array}{c}\hfill C_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P+C_{\kappa }^{\mathrm{T}}P{D}_{\kappa }{({\gamma }^{2}I-D_{\kappa }^{\mathrm{T}}P{D}_{\kappa })}^{-1}{D}_{\kappa }^{\mathrm{T}}P{C}_{\kappa }\le 0,\end{array}$$

(44)

where ${\gamma }^{2}I-D_{\kappa }^{\mathrm{T}}P{D}_{\kappa }>0.$ By (31), we can confirm

$$\begin{array}{c}-{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa }\right)\delta \left({\iota }_{\kappa }\right)+\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right]\hfill \\ =\mathcal{E}\{\left[\begin{array}{cc}{x}^{\mathrm{T}}\left({\iota }_{\kappa }^{-}\right)& {\delta }^{\mathrm{T}}\left({\iota }_{\kappa }\right)\end{array}\right]\left[\begin{array}{cc}{C}_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P& C_{\kappa }^{\mathrm{T}}P{D}_{\kappa }\\ D_{\kappa }^{\mathrm{T}}P{C}_{\kappa }& D_{\kappa }^{\mathrm{T}}P{D}_{\kappa }-{\gamma }^{2}I\end{array}\right]\left[\begin{array}{c}x\left({\iota }_{\kappa }^{-}\right)\\ \delta \left({\iota }_{\kappa }\right)\end{array}\right]\}\hfill \\ \le \mathcal{E}\{x^{\mathrm{T}}\left({\iota }_{\kappa }^{-}\right)[C_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P+C_{\kappa }^{\mathrm{T}}P{D}_{\kappa }{({\gamma }^{2}I-D_{\kappa }^{\mathrm{T}}P{D}_{\kappa })}^{-1}{D}_{\kappa }^{\mathrm{T}}P{C}_{\kappa }]x\left({\iota }_{\kappa }^{-}\right)\}\le 0.\hfill \end{array}$$

(45)

That is, relying on (19), we can know

$$\begin{array}{c}\hfill \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right]=\mathcal{E}\left[x^{\mathrm{T}}\left({\iota }_{\kappa }^{-}\right)(C_{\kappa }^{\mathrm{T}}P{C}_{\kappa }-P)x\left({\iota }_{\kappa }^{-}\right)\right]\le 0.\end{array}$$

Namely, $\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right]\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right].$ So, combined with (45), we infer that

$$\begin{array}{c}\hfill -{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa }\right)\delta \left({\iota }_{\kappa }\right)\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right],\end{array}$$

(46)

Also, we have

$$\begin{array}{c}-{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa }^{-}\right)\delta \left({\iota }_{\kappa }^{-}\right)\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -1}^{-}\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }^{-}\right)\right)\right],\hfill \\ -{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa -1}^{-}\right)\delta \left({\iota }_{\kappa -1}^{-}\right)\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -2}^{-}\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa -1}^{-}\right)\right)\right],\hfill \\ ⋮\hfill \\ -{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_1^{-}\right)\delta \left({\iota }_1^{-}\right)\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_0\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_1^{-}\right)\right)\right].\hfill \end{array}$$

(47)

From the above inequalities, we deduce

$$\begin{array}{c}\hfill -\sum _{{\iota }_{\kappa }\in (0,t)}{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa }\right)\delta \left({\iota }_{\kappa }\right)\le \mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_0\right)\right)\right]-\mathcal{E}\left[\mathrm{V}\left(x\left({\iota }_{\kappa }\right)\right)\right].\end{array}$$

(48)

Note the zero initial conditions and (43) over all possible ${\iota }_{\kappa }$ in $[0,t]$, it results in

$$\begin{array}{c}\hfill \mathcal{E}\{{\int }_{{\iota }_{\kappa }}^t[z^{\mathrm{T}}\left(\mu \right)z\left(\mu \right)-{\gamma }^2{v}^{\mathrm{T}}\left(\mu \right)v\left(\mu \right)]d\mu \}-\sum _{{\iota }_{\kappa }\in (0,t)}{\gamma }^2{\delta }^{\mathrm{T}}\left({\iota }_{\kappa }\right)\delta \left({\iota }_{\kappa }\right)<0,\end{array}$$

(49)

which means that (32) is satisfied. This proof is complete. □

5. An Example

In this chapter, we will provide an example to better illustrate the usefulness of the proposed method.

Example 1.

Consider a two-dimensional uncertain impulsive stochastic system (1) with the following parameters:

$$\begin{array}{c}A=\left[\begin{array}{cc}-2& 1.2\\ 0.8& -2\end{array}\right],B=\left[\begin{array}{cc}-1& 2\\ 0.4& 3\end{array}\right],B_v=\left[\begin{array}{cc}2& 0\\ 0.2& -1\end{array}\right],H=\left[\begin{array}{cc}1.2& 0\\ -2& 0.5\end{array}\right],\hfill \\ G=\left[\begin{array}{cc}0.5& 0\\ -1& 2\end{array}\right],G_v=\left[\begin{array}{cc}2& 0.4\\ -1& -4\end{array}\right],C_{\kappa }=\left[\begin{array}{cc}0.9& 0\\ 0& 0.9\end{array}\right],D_{\kappa }=\left[\begin{array}{cc}-0.2& 1\\ 0.3& -0.2\end{array}\right],\hfill \\ C_z=\left[\begin{array}{cc}1& 0\\ 1.2& 0.1\end{array}\right],B_z=\left[\begin{array}{cc}0.1& 1\\ 0.2& -0.1\end{array}\right],D_z=\left[\begin{array}{cc}0.5& 0\\ 0.2& -0.1\end{array}\right],M=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right],\hfill \\ N_A=\left[\begin{array}{cc}0.1& -0.2\end{array}\right],N_B=\left[\begin{array}{cc}0.2& 0.4\end{array}\right],N_H=\left[\begin{array}{cc}0.1& 0.3\end{array}\right],N_G=\left[\begin{array}{cc}0.2& -0.1\end{array}\right],\hfill \\ N_{B_v}=\left[\begin{array}{cc}0.1& -0.1\end{array}\right],N_{G_v}=\left[\begin{array}{cc}0.2& 0.3\end{array}\right].\hfill \end{array}$$

Set $\gamma =1.7$, using the Matlab LMI Control toolbox, we can get the solutions to LMIs (28) and (29) are as follows:

$$\begin{array}{c}\hfill X=\left[\begin{array}{cc}4.2597& -5.4180\\ -5.4180& 23.3299\end{array}\right],Y=\left[\begin{array}{cc}-7.5133& 9.2519\\ -3.8391& -0.3219\end{array}\right],{\widehat{\epsilon }}_1=2.9631,{\widehat{\epsilon }}_2=1.5302.\end{array}$$

Therefore, from Theorem 3, the $H_{\infty }$ control law can be chosen as:

$$\begin{array}{c}\hfill u\left(t\right)=\left[\begin{array}{cc}-1.7874& -0.0185\\ -1.3040& -0.3166\end{array}\right]x\left(t\right).\end{array}$$

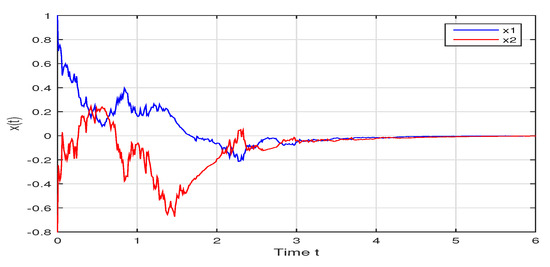
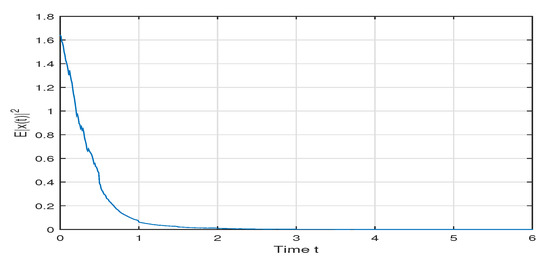
We select initial value $x_0={[1,-0.8]}^{\mathrm{T}}$ and the impulsive interval ${\iota }_{\kappa +1}={\iota }_{\kappa }+0.5$. Figure 1 depicts the state of the uncertain impulsive stochastic system. It is obvious from Figure 2 that the closed-loop system is mean-square asymptotically stable, where ${\displaystyle {\mathcal{E}\left|x\left(t\right)\right|}^2=\frac{1}{1000}\sum _{j=1}^{1000}[{\left(x_1^j\left(t\right)\right)}^2+{\left(x_2^j\left(t\right)\right)}^2]}$ which $x_s^j,s=1,2$ is the jth sample path.

Figure 1. State path of Example 1.

Figure 2. Trajectory of the average value of 1000 sample paths.

6. Conclusions

Robust stabilization and $H_{\infty }$ control are considered in this paper for stochastic systems with uncertainties and impulsive effects. As for robust stability and robust stabilization, LMIs-based sufficient conditions have been established. Moreover, we proposed a reasonable $H_{\infty }$ controller design method and its effectiveness has been demonstrated by a numerical example.