An Estimation of Sensitive Attribute Applying Geometric Distribution under Probability Proportional to Size Sampling

Abstract

In this paper, we extended Yennum et al.’s model, in which geometric distribution is used as a randomization device for a population that consists of different-sized clusters, and clusters are obtained by probability proportional to size (PPS) sampling. Estimators of a sensitive parameter, their variances, and their variance estimators are derived under PPS sampling and equal probability two-stage sampling, respectively. We also applied these sampling schemes to Yennum et al.’s generalized model. Numerical studies were carried out to compare the efficiencies of the proposed sampling methods for each case of Yennum et al.’s model and Yennum et al.’s generalized model.

1. Introduction

The randomized response model (RRM) was suggested by [1] to estimate the true population proportion of sensitive characteristics, such as illegal gambling, drug-abuse, tax evasion, the extent of illegal income, and the experience of abortion, among others [2,3,4].

Since Warner’s work, many scholars have developed the RRM in various ways. In [5,6], they arranged, summarized, and systemized various RRMs and emphasized their importance. In [7], sampling survey of sensitive attributes applied two-stage cluster sampling to RRM for a population consisting of equal-sized clusters, and [8] considered the cluster RRM for a population consisting of different-sized clusters, where the clusters are selected by probability proportional to size (PPS) sampling.

Recently, Yennum et al. [9] suggested a new randomization device to gather sensitive data in two-stages under the assumption of geometric distribution and made a generalization of their model encompassing generalized geometric distribution using [10] model.

Based on Yennum et al.’s work, it is assumed that the respondents are selected by simple random sampling with replacements, but a real survey selects respondents from various sampling schemes.

Now, we can consider a large sample of clusters. For example, to estimate the true population proportion of drug-abuse among high school students, it is possible to use a randomization device like Yennum et al.’s model via proportional sampling by considering the primary sampling unit as the school and the secondary sampling unit as the students.

From this point of view, we extend Yennum et al.’s model, in which geometric distribution is used as a randomization device based on a population that consists of different-sized clusters, and the clusters are selected by PPS sampling. Estimators of a sensitive parameter, their variances, and their variance estimators are derived by PPS sampling and equal probability two-stage sampling, respectively.

We also apply these methods to the case of Yennum et al.’s generalized model. Numerical studies are carried out to compare the efficiencies of the suggested methods in each case of Yennum et al.’s model and Yennum et al.’s generalized model.

2. An Estimation of Sensitive Attributes with Probability Proportional to Size Sampling under Yennum et al.’s Model

In Section 2, we consider a new sampling scheme to estimate sensitive attributes using Yennum et al.’s model, in which geometric distribution is used as a randomization device when $n$ clusters are selected with proportional to size (PPS) sampling or equal probability sampling from a population that consists of $N$ clusters of size, $M_i\left(i=1,2,\cdots ,N\right)$ and $m_i\left(i=1,2,\cdots ,n\right)$ units are selected by simple random sampling from each sampled cluster.

In Section 2.1, we consider the sampling method for the clusters via PPS sampling with replacements. Clusters by PPS sampling without replacement are considered in Section 2.2, and clusters by equal probability sampling are examined in Section 2.3.

2.1. PPS Sampling with Replacement

Let the population be composed of $\mathrm{N}$ clusters. In the first stage, the size of the $n$ sample of the first sampling units (FSU) is selected with replacement by the selection probability $p_i$ for the $i$th cluster. In the second stage, $m_i$ second sampling units (SSU) are drawn by simple random sampling with replacement (SRSWR) from each FSU and are guided to carry out Yennum et al.’s randomization device.

First of all, the randomization device consists of two elements. The first randomization device for the $i$th cluster consists of two kinds of urns with white and black balls, where the selection probability of a white ball is $W_i$, and the selection probability of a black ball is $1-W_i$.

On the other hand, the second randomization device is composed of two kinds of urns with balls. The first device with balls contains a slip of paper including two statements, such as “I have a sensitive attribute” with selection probability $P_i$, and the other balls includes a statement such as “I do not have a sensitive attribute” with selection probability $1-P_i$. The second device with balls contains a slip of paper with the statement “I do not have a sensitive attribute” with selection probability $T_i$ and balls with the statement “I have a sensitive attribute” with selection probability $1-T_i$.

In the first stage, for the $i$th cluster, each interviewee draws a ball from the first randomization device, such as the urn with the white and black balls. When he or she selects a white ball, he or she is guided to pick balls from the first urn of the second randomization device, one after another, with replacement, until the first ball containing a statement matching his or her own status appears.

We assume that $X_{i1}$ is the total number of balls drawn before he or she obtains the first ball including his or her own status in the $i$th cluster, and $X_{i2}$ is the total number of balls drawn before he or she obtains the first ball with his or her own status of not having a sensitive attribute in the $i$th cluster. Similarly, when he or she draws a black ball, he or she is guided to pick balls from the second urn of the second randomization device, one after another, with replacement, until the first ball containing a statement matching his or her own status appears.

For the $i$th cluster, using the randomization device in Figure 1, the total number of balls taken by interviewees $X_{i1},X_{i2},Y_{i1},Y_{i2}$ are distributed via generalized geometric distribution. Let ${\pi }_i$ and $1-{\pi }_i$ be the true population proportion of persons who have a sensitive attribute $A_i$ and $A_i^c$ for the $i$th cluster. Assume that each interviewee in the $i$th cluster is drawn by SRSWR.

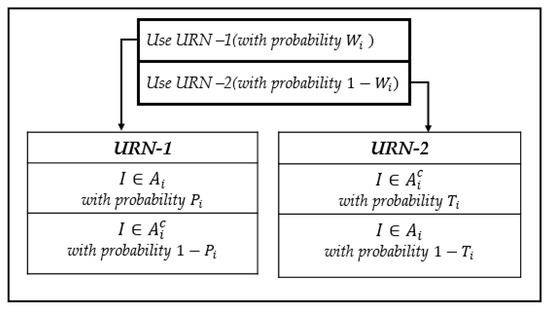
Figure 1. Randomization device for the $i$th cluster.

For the $i$th cluster, the total number for each ball selected by interviewees through the proposed two-stage device distributes one of the following random variables: $X_{i1}\sim Ge\left(P_i\right)$, $X_{i2}\sim Ge\left(1-P_i\right)$, $Y_{i1}\sim Ge\left(T_i\right)$ and $Y_{i2}\sim Ge\left(1-T_i\right)$, where $Ge(·)$ represents the geometric distribution with a success probability. Let ${\pi }_i$ and $1-{\pi }_i$ be the true population proportions of persons who have a sensitive attribute ($A_i$ and $A_i^c$, respectively) for the $i$th cluster. Assume that each interviewee in the $i$th cluster is drawn by SRSWR.

Let $Z_{ij}$ be the $j$th observed answer in the $i$th cluster; $Z_{ij}$ can be expressed as

$$Z_{ij}=\{\begin{array}{c}{X}_{i1},withprobability{W}_i{\pi }_i\hfill \\ Y_{i2},withprobability(1-W_i){\pi }_i\hfill \\ X_{i2},withprobability{W}_i(1-{\pi }_i)\hfill \\ Y_{i1},withprobability(1-W_i)(1-{\pi }_i)\hfill \end{array}$$

(1)

Then, we can find the expected value of $Z_{ij}$ as follows:

$$\begin{array}{cc}\hfill E(Z_{ij})& ={\pi }_i\left[\frac{W_i}{P_i}+\frac{(1-W_i)}{(1-T_i)}\right]+(1-{\pi }_i)\left[\frac{W_i}{(1-P_i)}+\frac{(1-W_i)}{T_i}\right]\hfill \\ & ={\pi }_i\left[\frac{W_i}{P_i}+\frac{(1-W_i)}{(1-T_i)}-\frac{W_i}{(1-P_i)}-\frac{(1-W_i)}{T_i}\right]+\frac{W_i}{(1-P_i)}+\frac{(1-W_i)}{T_i}.\hfill \end{array}$$

(2)

The expected value (2) can be expressed as follows:

$$\frac{(1-T_i)P_i\left\{E(Z_{ij})(1-P_i)T_i-W_i{T}_i-(1-W_i)(1-P_i)\right\}}{P_i{T}_i(1-P_i)(1-T_i)}=\frac{{\pi }_i{\psi }_i}{P_i{T}_i(1-P_i)(1-T_i)},$$

(3)

where ${\psi }_i=W_i\left(1-2P_i\right)T_i\left(1-T_i\right)+\left(1-W_i\right)\left(2T_i-1\right)P_i\left(1-P_i\right)$.

Now the estimator ${\widehat{\pi }}_i$ for the true population proportion ${\pi }_i$ in the $i$th cluster is given by:

$${\widehat{\pi }}_i=\frac{1}{{\psi }_i}\left[P_i{T}_i(1-P_i)(1-T_i)\frac{1}{m_i}{\displaystyle \sum _{i=1}^{m_i}{Z}_{ij}-W_i{T}_i{P}_i(1-T_i)-P_i(1-W_i)(1-P_i)(1-T_i)}\right].$$

(4)

When the interviewees are drawn by SRSWR from the $i$th cluster selected with a replacement by the sampling probability $p_i$, the estimator ${\widehat{\pi }}_{ppswr}$ of the true population proportion $\pi$ for a sensitive character is given by:

$$\begin{array}{cc}\hfill {\widehat{\pi }}_{ppswr}& =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_i}{p_i}}\hfill \\ & =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i}{p_i{\psi }_i}}\left[P_i{T}_i(1-P_i)(1-T_i)\frac{1}{m_i}{\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-W_i{T}_i{P}_i(1-T_i)-P_i(1-W_i)(1-P_i)(1-T_i)}\right],\hfill \end{array}$$

(5)

where $M_0={\displaystyle {\sum }_{i=1}^N{M}_i}$.

Theorem 1:

The estimator ${\widehat{\pi }}_{ppswr}$ of the true population proportion of a sensitive attribute $\pi$ under PPS with a replacement sampling scheme is an unbiased estimator.

Proof: 

$$\begin{array}{cc}\hfill E_1{E}_2\left({\widehat{\pi }}_{ppswr}\right)& =E_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_i}{p_i}}\right]\hfill \\ & =E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{E}_2({\widehat{\pi }}_i)}{p_i}}\right],\hfill \end{array}$$

and since:

$$\begin{array}{cc}\hfill E_2\left({\widehat{\pi }}_i\right)& =\frac{1}{{\psi }_i}\left[P_i{T}_i(1-P_i)(1-T_i)\frac{1}{m_i}{\displaystyle \sum _{i=1}^{m_i}{E}_2\left(Z_{ij}\right)-W_i{T}_i{P}_i(1-T_i)-P_i(1-W_i)(1-P_i)(1-T_i)}\right]\hfill \\ & ={\pi }_i.\hfill \end{array}$$

we can obtain:

$$\begin{array}{cc}\hfill E_1{E}_2\left({\widehat{\pi }}_{ppswr}\right)& =E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\pi }_i}{p_i}}\right]\hfill \\ & =\frac{1}{M_0}{\displaystyle \sum _{i=1}^N{p}_i\frac{M_i{\pi }_i}{p_i}}\hfill \\ & =\pi .\hfill \end{array}$$

 □

Theorem 2:

The variance of ${\widehat{\pi }}_{ppswr}$ is obtained from a two-stage procedure, such that a sample of size $n$ FSU is selected by replacement with sampling probability $p_i$ for the unit $i$ from the population of $N$ clusters with size $M_i$ elements in the $i$th cluster, and the SSUs with size $m_i$ are drawn by SRSWR from each FSU, as given by:

$$\begin{array}{cc}\hfill V({\widehat{\pi }}_{ppswr})& =\frac{1}{n{M}_0^2}{{\displaystyle \sum _{i=1}^N{p}_i\left[\frac{M_i{\pi }_i}{p_i}-M_0\pi \right]}}^2\hfill \\ & +\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i{p}_i}\left[{\pi }_i(1-{\pi }_i)-\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right]},\hfill \end{array}$$

(6)

where:

$$\begin{array}{cc}\hfill A_i& =W_i(1-2P_i)(2-P_i+P_i^2)T_i^2{(1-T_i)}^2+(1-W_i)(2T_i-1)(2-T_i+T_i^2)P_i^2{(1-P_i)}^2\hfill \\ & +W_i^2{T}_i^2{(1-T_i)}^2(2P_i-1)+{(1-W_i)}^2{P}_i^2{(1-P_i)}^2(1-2T_i)\hfill \\ & +2W_i(1-W_i)P_i{T}_i(1-P_i)(1-T_i)(P_i-T_i),\hfill \end{array}$$

$$B_i={(1-T_i)}^2{P}_i^2\{W_i(1-W_i){(P_i+T_i-1)}^2+W_i{P}_i{T}_i^2+(1-W_i)(1-T_i){(1-P_i)}^2\}.$$

Proof: 

Given $X_{i1}\sim G(P_i)$, $X_{i2}\sim G(1-P_i)$, $Y_{i1}\sim G(T_i)$, $Y_{i2}\sim G(1-T_i)$, where $G$ represents the geometric distribution with a success probability. Since the expected values of $Z_{ij}$ and $Z_{ij}^2$ are

$$E(Z_{ij})={\pi }_i\left[\frac{W_i}{P_i}+\frac{(1-W_i)}{(1-T_i)}\right]+(1-{\pi }_i)\left[\frac{W_i}{(1-P_i)}+\frac{(1-W_i)}{T_i}\right],$$

(7)

then:

$$E(Z_{ij}^2)={\pi }_i\left[\frac{W_i(2-P_i)}{P_i^2}\right]+(1-{\pi }_i)\left[\frac{W_i(1+P_i)}{{(1-P_i)}^2}\right]+(1-{\pi }_i)(1-V_i)\left[\frac{(2-T_i)}{T_i^2}\right]+{\pi }_i(1-W_i)\left[\frac{(1+T_i)}{{(1-T_i)}^2}\right].$$

(8)

Based on (7) and (8), the variance of $Z_{ij}$ is:

$${\sigma }_{iZ}^2=E(Z_{ij}^2)-{\left[E(Z_{ij})\right]}^2,$$

(9)

and, since $Z_{ij}$ is independent, the variance of ${\widehat{\pi }}_i$ can be expressed by:

$$\begin{array}{cc}\hfill V({\widehat{\pi }}_i)& =V\left[\frac{1}{{\psi }_i}\left(\frac{P_i{T}_i(1-P_i)(1-T_i)}{m_i}{\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-W_i{T}_i{P}_i(1-T_i)-P_i(1-W_i)(1-P_i)(1-T_i)}\right)\right]\hfill \\ & =\frac{P_i^2{T}_i^2{(1-P_i)}^2{(1-T_i)}^2}{n_h^2{\psi }_h^2}{\displaystyle \sum _{j=1}^{m_i}{\sigma }_{iZ}^2}\hfill \\ & =\frac{{\pi }_i(1-{\pi }_i)}{m_i}+\frac{{\pi }_i}{m_i{\psi }_i^2}{A}_i+\frac{1}{m_i{\psi }_i^2}{B}_i.\hfill \end{array}$$

(10)

Since $V({\widehat{\pi }}_{ppswr})=V_1{E}_2({\widehat{\pi }}_{ppswr})+E_1{V}_2({\widehat{\pi }}_{ppswr})$, then the first and second terms are given, respectively, as:

$$\begin{array}{cc}\hfill V_1{E}_2({\widehat{\pi }}_{ppswr})& =V_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_i}{p_i}}\right]\hfill \\ & =V_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\pi }_i}{p_i}}\right]\hfill \\ & =\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N{p}_i}{\left[\frac{M_i{\pi }_i}{p_i}-M_0\pi \right]}^2,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill E_1{V}_2({\widehat{\pi }}_{ppswr})& =E_1{V}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_i}{p_i}}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i^2}{V}_2({\widehat{\pi }}_i)}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i^2}{V}_2\left\{\frac{1}{{\psi }_i}{P}_i{T}_i(1-P_i)(1-T_i)\frac{1}{m_i}{\displaystyle \sum _{i=1}^{m_i}{Z}_{ij}-W_i{T}_i{P}_i(1-T_i)-P_i(1-W_i)(1-P_i)(1-T_i)}\right\}}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{}^{}\frac{M_i^2}{m_i{p}_i^2}\left\{{\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right\}}\right].\hfill \end{array}$$

Then, we can obtain the variance (10).

Moreover, an unbiased estimator of $V({\widehat{\pi }}_{ppswr})$ is given by

$$\begin{array}{cc}\hfill \widehat{V}({\widehat{\pi }}_{ppswr})& =\frac{1}{n{M}_0^2}{{\displaystyle \sum _{i=1}^n{p}_i\left[\frac{M_i{\widehat{\pi }}_i}{p_i}-M_0{\widehat{\pi }}_{ppswr}\right]}}^2\hfill \\ & +\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i(m_i-1)}\left[{\widehat{\pi }}_i(1-{\widehat{\pi }}_i)-\frac{{\widehat{\pi }}_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right]}.\hfill \end{array}$$

(11)

 □

If the FSUs are selected proportional to size with $M_i$, then $p_i=M_i/M_0$. For this reason, we call this method “probability proportional to size” (PPS) sampling. When a sample of the FSU is selected by PPS sampling with replacement via sampling probability, $p_i=M_i/M_0$ for the $i$th cluster, and $m_i$ SSU are selected by SRSWR from each FSU. The estimator ${\widehat{\pi }}_{ppswr}$ of $\pi$ is given by:

$$\begin{array}{cc}\hfill {\widehat{\pi }}_{ppswr}& =\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{\pi }}_i}\hfill \\ & =\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{1}{m_i}\left[{\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right]},\hfill \end{array}$$

(12)

and the variance of ${\widehat{\pi }}_{ppswr}$ and its estimator are as follows:

$$\begin{array}{cc}\hfill V\left({\widehat{\pi }}_{ppswr}\right)& =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^N{M}_i{({\pi }_i-\pi )}^2}\hfill \\ & +\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^N\frac{M_i}{m_i}}\left[{\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \widehat{V}\left({\widehat{\pi }}_{ppswr}\right)& =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n{M}_i{({\widehat{\pi }}_i-{\widehat{\pi }}_{ppswr})}^2}\hfill \\ & +\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i}{m_i-1}}\left[{\widehat{\pi }}_i(1-{\widehat{\pi }}_i)+\frac{{\widehat{\pi }}_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right].\hfill \end{array}$$

(14)

2.2. The PPS without Replacement

In this subsection, we consider PPS sampling without replacement to estimate the true population proportion of a sensitive character by applying Yennum et al.’s model, in which $n$ FSUs are drawn by PPS sampling without replacement from the population of $N$ clusters with $M_i$ elementary units for the $i$th cluster, and $m_i$ SSUs are drawn by SRSWR from each FSU.

From this two-stage sampling, the estimator ${\widehat{\pi }}_{ppswor}$ of $\pi$ is:

$${\widehat{\pi }}_{ppswor}=\frac{1}{M_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_i}{{\theta }_i}},$$

(15)

where ${\theta }_i$ is the first inclusion probability for the $i$th cluster.

The variance of ${\widehat{\pi }}_{ppswor}$ is given by:

$$\begin{array}{cc}\hfill V\left({\widehat{\pi }}_{ppswor}\right)& =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j>i}^N({\theta }_i{\theta }_j-{\theta }_{ij})}{\left[\frac{M_i{\pi }_i}{{\theta }_i}-\frac{M_j{\pi }_j}{{\theta }_j}\right]}^2}\hfill \\ & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i{\theta }_i}}\left[{\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right],\hfill \end{array}$$

(16)

where ${\theta }_{ij}$ is the second inclusion probability of the $i$th and $j$th clusters.

Furthermore, the variance estimator of ${\widehat{\pi }}_{ppswor}$ is as follows:

$$\begin{array}{cc}\hfill \widehat{V}\left({\widehat{\pi }}_{ppswor}\right)& =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j>i}^n\frac{({\theta }_i{\theta }_j-{\theta }_{ij})}{{\theta }_{ij}}}{\left[\frac{M_i{\widehat{\pi }}_i}{{\theta }_i}-\frac{M_j{\widehat{\pi }}_j}{{\theta }_j}\right]}^2}\hfill \\ & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{{\theta }_i(m_i-1)}}\left[{\widehat{\pi }}_i(1-{\widehat{\pi }}_i)+\frac{{\widehat{\pi }}_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right].\hfill \end{array}$$

(17)

2.3. Two-Stage Equal Probability Sampling

In this subsection, we consider a two-stage equal probability sampling design to estimate the true population proportion of a sensitive characteristic by applying Yennum et al.’s model, in which $n$ FSUs are drawn by simple random sampling without replacement (SRSWOR) from a population of $N$ clusters with $M_i$ elementary units for the $i$th cluster, and $m_i$ SSUs are drawn by SRSWR from each FSU.

From this two-stage sampling, the estimator ${\widehat{\pi }}_{wr}$ of $\pi$ is given by:

$${\widehat{\pi }}_{wr}=\frac{N}{n{M}_0}{\displaystyle \sum _{i=1}^n{M}_i{\widehat{\pi }}_i},$$

(18)

where ${\widehat{\pi }}_i$ is an estimator of the true population proportion for a sensitive characteristic for the $i$th cluster, which is the same as (4).

The variance of ${\widehat{\pi }}_{wr}$ and its estimator are given as:

$$\begin{array}{cc}\hfill V\left({\widehat{\pi }}_{wr}\right)& =\frac{N^2}{n{M}_0^2}\frac{1}{(N-1)}{\displaystyle \sum _{i=1}^N{(M_i{\pi }_i-\overline{M}\pi )}^2}\hfill \\ & +\frac{N}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i}}\left[{\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right],\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \widehat{V}\left({\widehat{\pi }}_{wr}\right)& =\frac{N^2}{n{M}_0^2}\frac{1}{(n-1)}{\displaystyle \sum _{i=1}^n{(M_i{\widehat{\pi }}_i-\overline{M}{\widehat{\pi }}_{wr})}^2}\hfill \\ & +\frac{N}{n{M}_0^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{m_i-1}}\left[{\widehat{\pi }}_i(1-{\widehat{\pi }}_i)+\frac{{\widehat{\pi }}_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}{B}_i\right],\hfill \end{array}$$

(20)

where $\overline{M}=M_0/N$.

3. An Estimation of Sensitive Attributes with Probability Proportional to Size Sampling Under Yennum et al.’s Generalized Model

We consider Yennum et al.’s generalized model, in which generalized geometric distribution is used as a randomization device when $n$ clusters are sampled by PPS sampling or equal probability sampling from the population, which consists of $N$ clusters with size $M_i(i=1,2,\cdots ,N)$, and $m_i(i=1,2,\cdots ,n)$ units are drawn by simple random sampling from each sampled cluster.

We develop the sampling schemes for PPS sampling with replacement in Section 3.1 and those for PPS sampling without replacement in Section 3.2. Finally, equal probability sampling is presented in Section 3.3.

3.1. PPS Sampling with Replacement

Let the population be composed of $N$ clusters. In the first stage, a sample of $n$ FSUs is drawn by replacement with the sampling probability $p_i$ for the $i$th cluster. In the second stage, $m_i$ SSUs are selected by SRSWR from each FSU and guided to apply Yennum et al.’s generalized randomization device.

If the interviewees in the $i$th cluster choose a white ball during the first stage, and if they have a sensitive attribute $A$ (or $A^c$), then they are guided to pick replacement balls from the first urn of the second stage device until they take $k_{i2}$ (or $k_{i1}$) successive balls with their actual status for the first time and are then asked to determine the total number of balls as $X_{i1}$ (or $X_{i2}$).

If the interviewee in the $i$th cluster draws a black ball in the first stage, and if they have a sensitive attribute $A^c$ (or $A$), then they are guided to take replacement balls from the second urn of the second stage device until they take $k_{i2}$ (or $k_{i1}$) successive balls with their actual status for the first time and are then asked to determine the total number of balls as $Y_{i1}$ (or $Y_{i2}$).

For the $i$th cluster, using the randomization device in Figure 1, the total number of balls taken by interviewees $X_{i1}$, $X_{i2}$, $Y_{i1}$, and $Y_{i2}$ are distributed via generalized geometric distribution. Let ${\pi }_i$ and $1-{\pi }_i$ be the true population proportion of persons who have a sensitive attribute $A$ and $A^c$ for the $i$th cluster. Assume that each interviewee in the $i$th cluster is drawn by SRSWR.

For the $j$th surveyed answer in the $i$th cluster, $Z_{ij}$ can be expressed as:

$$Z_{ij}=\{\begin{array}{cc}{X}_{i1}\mathrm{with}\mathrm{probability}\hfill & W_i{\pi }_i,\\ Y_{i2}\mathrm{with}\mathrm{probability}\hfill & (1-W_i){\pi }_i,\\ X_{i2}\mathrm{with}\mathrm{probability}\hfill & W_i(1-{\pi }_i),\\ Y_{i1}\mathrm{with}\mathrm{probability}\hfill & (1-W_i)(1-{\pi }_i),\end{array}.$$

(21)

The expected value of $Z_{ij}$ is given by:

$$\begin{array}{cc}\hfill E(Z_{ij})& =W_i{\pi }_{i}E(X_{i1})+{\pi }_i(1-W_i)E(Y_{i2})+(1-{\pi }_i)W_{i}E(X_{i2})+(1-W_i)(1-{\pi }_i)E(Y_{i1})\hfill \\ & ={\pi }_i\left[W_i\left\{\frac{1-P_i^{k_{i1}}}{(1-P_i)P_i^{k_{i1}}}-\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right\}+(1-W_i)\left\{\frac{1-{(1-T_i)}^{k_{i1}}}{T_i{(1-T_i)}^{k_{i1}}}-\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right\}\right]\hfill \\ & +W_i\left\{\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right\}+(1-W_i)\left\{\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right\}.\hfill \end{array}$$

(22)

Then, the formula (22) can be expressed as:

$$\begin{array}{l}E(Z_{ij})-W_i\left\{\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right\}-(1-W_i)\left\{\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right\}\hfill \\ \begin{array}{cc}\hfill & \hfill \end{array}={\pi }_i\left[W_i\left\{\frac{1-P_i^{k_{i1}}}{(1-P_i)P_i^{k_{i1}}}-\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right\}+(1-W_i)\left\{\frac{1-{(1-T_i)}^{k_{i2}}}{T_i{(1-T_i)}^{k_{i2}}}-\frac{1-T_i^{k_{i1}}}{(1-T_i)T_i^{k_{i1}}}\right\}\right].\hfill \end{array}$$

(23)

The estimator ${\widehat{\pi }}_{iG}$ of the population proportion ${\pi }_i$ for the $i$th cluster is given by:

$${\widehat{\pi }}_{iG}=\frac{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}}{m_i{\phi }_{i2}}\left({\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-{\phi }_{i1}}\right),$$

(24)

where:

$$\begin{array}{ll}{\phi }_{i1}\hfill & =W_i\{1-{(1-P_i)}^{k_{i2}}\}{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}(1-P_i)P_i^{k_{i1}}\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)(1-T_i^{{}^{k_{i2}}})P_i^{{}^{k_{i1}+1}}{(1-P_i)}^{k_{i2}+1}{T}_i{(1-T_i)}^{k_{i1}+1},\hfill \end{array}$$

(25)

and:

$$\begin{array}{ll}{\phi }_{i2}\hfill & =W_i\left[{(1-P_i)}^{k_{i1}}{P}_i{T}_i^{k_{i2}+1}{(1-T_i)}^{k_{i1}+1}{(1-P_i)}^{k_{i2}}-\{1-{(1-P_i)}^{k_{i2}}\}{P}_i^{{}^{k_{i1}}}(1-P_i)T_i^{k_{i2}+1}{(1-T_i)}^{k_{i1}+1}\right]\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)\left[\{1-{(1-T_i)}^{k_{i1}}\}{P}_i^{{}^{k_{i1}+1}}(1-T_i){(1-P_i)}^{k_{i2}+1}{T}_i^{k_{i2}}-(1-T_i^{k_{i2}})P_i^{{}^{k_{i1}+1}}{T}_i{(1-P_i)}^{k_{i2}+1}{(1-T_i)}^{k_{i1}}\right].\hfill \end{array}$$

(26)

When the interviewees are sampled by SRSWR for the $i$th cluster selected with a replacement by sampling probability $p_i$, the estimator ${\widehat{\pi }}_{Gppswr}$ of the true population proportion $\pi$ of a sensitive attribute is:

$$\begin{array}{cc}\hfill {\widehat{\pi }}_{Gppswr}& =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_{iG}}{p_i}}\hfill \\ & =\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i}{p_i}}\left[\frac{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}}{m_i{\phi }_{i2}}\left({\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-{\phi }_{i1}}\right)\right],\hfill \end{array}$$

(27)

where $M_0={\displaystyle {\sum }_{i=1}^N{M}_i}$.

Theorem 3:

The estimator ${\widehat{\pi }}_{Gppswr}$ of the true population proportion $\pi$ of a sensitive character is an unbiased estimator.

Proof: 

$$E_1{E}_2\left({\widehat{\pi }}_{Gppswr}\right)=E_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_{iG}}{p_i}}\right]=E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{E}_2({\widehat{\pi }}_{iG})}{p_i}}\right],$$

and, since:

$$\begin{array}{cc}\hfill E_2\left({\widehat{\pi }}_{iG}\right)& =E_2\left[\frac{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}}{m_i{\phi }_{i2}}\left({\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-{\phi }_{i1}}\right)\right]\hfill \\ & =\frac{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}}{m_i{\phi }_{i2}}\left({\displaystyle \sum _{j=1}^{m_i}{E}_2(Z_{ij})-{\phi }_{i1}}\right)\hfill \\ & ={\pi }_i,\hfill \end{array}$$

we can obtain:

$$E_1{E}_2\left({\widehat{\pi }}_{Gppswr}\right)=E_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\pi }_i}{p_i}}\right]=\frac{1}{M_0}{\displaystyle \sum _{i=1}^N{p}_i\frac{M_i{\pi }_i}{p_i}}=\pi .$$

 □

Theorem 4:

The variance of ${\widehat{\pi }}_{Gppswr}$ is obtained by a two-stage sampling scheme, such that a sample of $n$ FSU is selected with replacement by sampling probability $p_i$ for the $i$th cluster from the population of $N$ clusters consisting of $M_i$ elements for the $i$th cluster, and $m_i$ SSUs are drawn by SRSWR from each FSU, as given by:

$$\begin{array}{cc}\hfill V\left({\widehat{\pi }}_{Gppswr}\right)& =\frac{1}{n{M}_0^2}{{\displaystyle \sum _{i=1}^N{p}_i\left[\frac{M_i{\pi }_i}{p_i}-M_0\pi \right]}}^2\hfill \\ & +\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i{p}_i}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right],}\hfill \end{array}$$

(28)

where:

$$\begin{array}{cc}\hfill {\sigma }_{iZ}^2& =E(Z_{ij}^2)-{(E(Z_{ij}))}^2\hfill \\ & ={\pi }_i[W_i\left(\frac{1-(2k_{i1}+1)(1-P_i)P_i^{k_{i1}}-P_i^{2k_{i1}+1}+{(1-P_i^{k_{i1}})}^2}{{(1-P_i)}^2{P}_i^{2k_{i1}}}\right)\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)\left(\frac{1-(2k_{i1}+1)T_i{(1-T_i)}^{k_{i1}}-{(1-T_i)}^{2k_{i1}+1}+{(1-{(1-T_i)}^{k_{i1}})}^2}{T_i^2{(1-T_i)}^{2k_{i1}}}\right)]\hfill \\ & \begin{array}{cc}+(1-{\pi }_i)[W_i\left(\frac{1-(2k_{i2}+1)P_i{(1-P_i)}^{k_{i2}}-{(1-P_i)}^{2k_{i2}+1}+(1-{(1-P_i^{k_{i1}})}^2)}{P_i^2{(1-P_i)}^{2k_{i2}}}\right)\hfill & \hfill \end{array}\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)\left(\frac{1-(2k_{i2}+1)(1-T_i)T_i{}^{k_{i2}}-T_i{}^{2k_{i2}+1}+{(1-T_i{}^{k_{i2}})}^2}{{(1-T_i)}^2{T}_i{}^{2k_{i2}}}\right)]\hfill \\ & -\begin{array}{cc}[{\pi }_i\{\begin{array}{c}\hfill \\ \hfill \end{array}{W}_i\left(\frac{1-P_i^{k_{i1}}}{(1-P_i)P_i^{2k_{i1}}}-\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right)+(1-W_i)\left(\frac{1-{(1-T_i)}^{k_{i1}}}{T_i{(1-T_i)}^{k_{i1}}}-\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right)\}\hfill & \hfill \end{array}\hfill \\ & \begin{array}{cc}{+(1-{\pi }_i)\{\begin{array}{c}\hfill \\ \hfill \end{array}{W}_i\left(\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right)+(1-W_i)\left(\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right)\}]}^2.\hfill & \hfill \end{array}\hfill \end{array}$$

(29)

Proof: 

The total number of balls taken by interviewees for the $i$th cluster, $X_{i1},X_{i2},Y_{i1}$ and $Y_{i2}$, are random variables with variances:

$$V(X_{i1})=\frac{1-(2k_{i1}+1)(1-P_i)P_i^{k_{i1}}-P_i^{2k_{i1}+1}}{{(1-P_i)}^2{P}_i^{2k_{i1}}},$$

(30)

$$V(X_{i2})=\frac{1-(2k_{i2}+1)P_i{(1-P_i)}^{2k_{i2}}-{(1-P_i)}^{2k_{i2}+1}}{P_i^2{(1-P_i)}^{2k_{i2}}},$$

(31)

$$V(Y_{i1})=\frac{1-(2k_{i2}+1)(1-T_i)T_i^{k_{i2}}-T_i^{2k_{i2}+1}}{{(1-T_i)}^2{T}_i^{2k_{i2}}},$$

(32)

$$V(Y_{i2})=\frac{1-(2k_{i1}+1)T_i{(1-T_i)}^{k_{i1}}-{(1-T_i)}^{2k_{i1}+1}}{T_i^2{(1-T_i)}^{2k_{i1}}}.$$

(33)

From (21), to drive the variance of ${\widehat{\pi }}_{Gppswr}$ we can obtain the expected values of $Z_{ij}$ and $Z_{ij}^2$ as follows:

$$\begin{array}{ll}E(Z_{ij})\hfill & ={\pi }_i\left[W_i\left(\frac{1-P_i^{k_{i1}}}{(1-P_i)P_i^{k_{i1}}}\right)+(1-W_i)\left(\frac{1-{(1-T_i)}^{k_{i1}}}{T_i{(1-T_i)}^{k_{i1}}}\right)\right]\hfill \\ & \begin{array}{ccc}\hfill & \hfill & \hfill \end{array}+(1-{\pi }_i)\left[W_i\left(\frac{1-{(1-P_i)}^{k_{i2}}}{P_i{(1-P_i)}^{k_{i2}}}\right)+(1-W_i)\left(\frac{1-T_i^{k_{i2}}}{(1-T_i)T_i^{k_{i2}}}\right)\right],\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill E(Z_{ij}^2)& ={\pi }_i\left[W_{i}E(X_{i1}^2)+(1-W_i)E(Y_{i2}^2)\right]+(1-{\pi }_i)\left[W_{i}E(X_{i2}^2)+(1-W_i)E(Y_{i2}^2)\right]\hfill \\ & ={\pi }_i[\begin{array}{c}\hfill \\ \hfill \end{array}{W}_i\left(\frac{1-(2k_{i1}+1)(1-P_i)P_i^{k_{i1}}-P_i^{2k_{i1}+1}+{(1-P_i^{k_{i1}})}^2}{{(1-P_i)}^2{P}_i^{2k_{i1}}}\right)\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)\left(\frac{1-(2k_{i1}+1)T_i{(1-T_i)}^{k_{i1}}-{(1-T_i)}^{2k_{i1}+1}+{\{1-{(1-T_i)}^{k_{i1}}\}}^2}{T_i^2{(1-T_i)}^{2k_{i1}}}\right)\begin{array}{c}\hfill \\ \hfill \end{array}]\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-{\pi }_i)[\begin{array}{c}\hfill \\ \hfill \end{array}{W}_i\left(\frac{1-(2k_{i2}+1)P_i{(1-P_i)}^{k_{i2}}-{(1-P_i)}^{2k_{i2}+1}+\{1-{(1-P_i^{k_{i2}})}^2\}}{P_i^2{(1-P_i)}^{2k_{i2}}}\right)\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+(1-W_i)\left(\frac{1-(2k_{i2}+1)(1-T_i)T_i^{k_{i2}}-T_i^{2k_{i2}+1}+{(1-T_i^{k_{i2}})}^2}{{(1-T_i)}^2{T}_i^{2k_{i2}}}\right)\begin{array}{c}\hfill \\ \hfill \end{array}].\hfill \end{array}$$

(35)

Since $V({\widehat{\pi }}_{Gppswr})=V_1{E}_2({\widehat{\pi }}_{Gppswr})+E_1{V}_2({\widehat{\pi }}_{Gppswr})$,

$$\begin{array}{cc}\hfill V_1{E}_2({\widehat{\pi }}_{Gppswr})& =V_1{E}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_{iG}}{p_i}}\right]\hfill \\ & =V_1\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\pi }_i}{p_i}}\right]\hfill \\ & =\frac{1}{n{M}_0^2}{{\displaystyle \sum _{i=1}^N{p}_i\left[\frac{M_i{\pi }_{iG}}{p_i}-M_0\pi \right]}}^2,\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill E_1{V}_2({\widehat{\pi }}_{Gppswr})& =E_1{V}_2\left[\frac{1}{n{M}_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_{iG}}{p_i}}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i^2}{V}_2({\widehat{\pi }}_{iG})}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i^2}{V}_2\left\{\frac{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}}{m_i{\phi }_{i2}}\left({\displaystyle \sum _{j=1}^{m_i}{Z}_{ij}-{\phi }_{i1}}\right)\right\}}\right]\hfill \\ & =E_1\left[\frac{1}{{(n{M}_0)}^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i^2}\frac{1}{m_i}\left\{\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right\}}\right]\hfill \\ & =\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i{p}_i}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P_i)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right]}.\hfill \end{array}$$

We can then obtain the variance (28). Also, an unbiased estimator of $V({\widehat{\pi }}_{Gppswr})$ is given by:

$$\begin{array}{l}\widehat{V}\left({\widehat{\pi }}_{Gppswr}\right)=\frac{1}{n{M}_0^2}{{\displaystyle \sum _{i=1}^n{p}_i\left[\frac{M_i{\widehat{\pi }}_{iG}}{p_i}-M_0{\widehat{\pi }}_{Gppswr}\right]}}^2\hfill \\ \begin{array}{cccc}\hfill & \hfill & \hfill & \hfill \end{array}+\frac{1}{n{M}_0^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{p_i(m_i-1)}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\widehat{\sigma }}_{iZ}^2\right].}\hfill \end{array}$$

(36)

 □

3.2. PPS Sampling Without Replacement

In this subsection, we consider PPS sampling without replacement to estimate the true population proportion of a sensitive characteristic by applying Yennum et al.’s generalized model, in which $n$ FSUs are drawn by PPS sampling without replacement from a population of $N$ clusters with $M_i$ elementary units for the $i$th cluster, and $m_i$ SSUs are drawn by SRSWR from each FSU.

From this procedure, the estimator ${\widehat{\pi }}_{Gppswor}$ of $\pi$ is given by:

$${\widehat{\pi }}_{Gppswor}=\frac{1}{M_0}{\displaystyle \sum _{i=1}^n\frac{M_i{\widehat{\pi }}_{iG}}{{\theta }_i}},$$

(37)

where ${\theta }_i$ is the first inclusion probability for the $i$th cluster.

The variance of ${\widehat{\pi }}_{Gppswor}$ is given by:

$$\begin{array}{cc}\hfill V\left({\widehat{\pi }}_{Gppswor}\right)& =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j>i}^N({\theta }_i{\theta }_j-{\theta }_{ij})}{\left[\frac{M_i{\pi }_i}{{\theta }_i}-\frac{M_j{\pi }_j}{{\theta }_j}\right]}^2}\hfill \\ & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i{\theta }_i}}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right],\hfill \end{array}$$

(38)

where ${\theta }_{ij}$ is the second inclusion probability for $i$th and $j$th clusters.

Also, the variance estimator of ${\widehat{\pi }}_{Gppswor}$ is:

$$\begin{array}{cc}\hfill \widehat{V}\left({\widehat{\pi }}_{Gppswor}\right)& =\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j>i}^n\frac{({\theta }_i{\theta }_j-{\theta }_{ij})}{{\theta }_{ij}}}{\left[\frac{M_i{\widehat{\pi }}_{iG}}{{\theta }_i}-\frac{M_j{\widehat{\pi }}_{jG}}{{\theta }_j}\right]}^2}\hfill \\ & +\frac{1}{M_0^2}{\displaystyle \sum _{i=1}^n\frac{M_i^2}{{\theta }_i(m_i-1)}}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\widehat{\sigma }}_{iZ}^2\right].\hfill \end{array}$$

(39)

3.3. Two-Stage Equal Probability Sampling

In this subsection, we consider a two-stage equal probability sampling scheme to estimate the true population proportion of a sensitive attribute by applying Yennum et al.’s generalized model, in which $n$ FSUs are drawn by SRSWOR from a population of $N$ clusters consisting of $M_i$ elementary units for the $i$th cluster, and $m_i$ SSUs are drawn by SRSWR from each FSU.

From this procedure, the estimator ${\widehat{\pi }}_{Gwr}$ of the true population proportion $\pi$ for a sensitive attribute is given by:

$${\widehat{\pi }}_{Gwr}=\frac{N}{n{M}_0}{\displaystyle \sum _{i=1}^n{M}_i{\widehat{\pi }}_{iG}},$$

(40)

where the estimator ${\widehat{\pi }}_{iG}$ is the estimator of a sensitive characteristic of the $i$th cluster, which is the same as (24).

The variance and variance estimator of ${\widehat{\pi }}_{Gwr}$ are:

$$\begin{array}{l}V\left({\widehat{\pi }}_{Gwr}\right)=\frac{N^2}{n{M}_0^2}{{\displaystyle \sum _{i=1}^N\frac{1}{N-1}\left[M_i{\pi }_i-\overline{M}\pi \right]}}^2\hfill \\ \begin{array}{cccc}\hfill & \hfill & \hfill & \hfill \end{array}+\frac{N}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right],}\hfill \end{array}$$

(41)

and:

$$\begin{array}{l}\widehat{V}\left({\widehat{\pi }}_{Gwr}\right)=\frac{N^2}{n{M}_0^2}{{\displaystyle \sum _{i=1}^n\frac{1}{n-1}(M_i{\widehat{\pi }}_{iG}-\overline{M}{\widehat{\pi }}_{Gwr})}}^2\hfill \\ \begin{array}{cccc}\hfill & \hfill & \hfill & \hfill \end{array}+\frac{N}{n{M}_0^2}{\displaystyle \sum _{i=1}^N\frac{M_i^2}{m_i-1}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\widehat{\sigma }}_{iZ}^2\right],}\hfill \end{array}$$

(42)

respectively, where $\overline{M}=M_0/N$.

4. Efficiency Comparisons

4.1. PPSWR Sampling versus Equal Probability Two-Stage Sampling in Yennum et al.’s Model

If we assume $N-1\doteq N$, then the difference between the variance of equal probability two-stage sampling, (19), and the variance of PPS with replacement sampling, (6), is given by:

$$\begin{array}{cc}\hfill V({\widehat{\pi }}_{wr})-V({\widehat{\pi }}_{ppswr})& =\frac{1}{n{M}_0\overline{M}}[{\displaystyle \sum _{i=1}^N{(M_i-\overline{M})}^2{\pi }_i^2+\overline{M}\left\{{\displaystyle \sum _{i=1}^N(M_i-\overline{M})({\pi }_i^2-{\pi }^2)}\right\}}\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+{\displaystyle \sum _{i=1}^N{(M_i-\overline{M})}^2}\frac{1}{m_i}\left({\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}B\right)\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+\overline{M}\left\{{\displaystyle \sum _{i=1}^N(M_i-\overline{M})\frac{1}{m_i}\left({\pi }_i(1-{\pi }_i)+\frac{{\pi }_i}{{\psi }_i^2}{A}_i+\frac{1}{{\psi }_i^2}B\right)}\right\}].\hfill \end{array}$$

(43)

In (43), we can see that $V({\widehat{\pi }}_{wr})=V({\widehat{\pi }}_{ppswr})$ under the condition $M_i=\overline{M}=M_0/N$; i.e., if the cluster sizes are equal, the selection probabilities of the PPS with replacement sampling are all $N^{-1}$ and equal to those of equal probability two-stage replacement sampling.

If the size of a cluster, $M_i$ is significantly different, then ${{\displaystyle {\sum }_{i=1}^N(M_i-\overline{M})}}^2{\pi }_i^2$, the first term on the right side of (43), has large values, and the second term, ${{\displaystyle {\sum }_{i=1}^N(M_i-\overline{M})}}^2({\pi }_i^2-{\pi }^2)$, has relatively small values. Hence, the estimation by PPS with replacement sampling is more efficient than that by equal probability two-stage replacement sampling.

We used the relative efficiency (RE) to compare the efficiency of the two sampling methods—PPS with replacement sampling and equal probability two-stage replacement sampling:

$$R{E}_1=\frac{V({\widehat{\pi }}_{wr})}{V({\widehat{\pi }}_{ppswr})}\times 100(\%).$$

Values of $R{E}_1$ over 100% indicate that the estimator obtained by the PPS with the replacement sampling method was more efficient than the estimator obtained by the equal probability two-stage replacement sampling.

In calculating REs, we set the parameters as follows:

$$\begin{array}{l}{M}_0=10,000,M_1=1,000,M_2=2,000,M_3=3,000,M_4=4,000\hfill \\ m_0=1,000,m_1=100,m_2=200,m_3=300,m_4=400,\hfill \\ p_1=0.235,p_2=0.441,p_3=0.609,p_4=0.715.\hfill \end{array}$$

From Table 1, when the selection probability $W$ for the first-stage randomization device increased from 0.1 to 0.9 by 0.2 and the second stage randomization devices $T$ increased from 0.6 to 0.8 by 0.1 and $P$ from 0.65 to 0.90 by 0.05, REs increase under the fixed proportion of a sensitive attribute (particularly when the selection probability of the second randomization device $T$ increased), and the RE increased according to the conditions of $P$ and ${\pi }_i$.

Table 1. The relative efficiencies (REs) of a sensitive estimator between the probability proportional to size (PPS) sampling with replacement and the equal probability two-stage sampling with replacement in Yennum et al.’s model to change ${\pi }_i$ and $W$.

${\mathit{\pi }}_{\mathit{i}}$		W
	T	0.1			0.3			0.5			0.7			0.9
	P	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8
0.1	0.65	56.59	95.07	123.5	48.08	61.06	91.71	52.73	46.18	55.97	63.18	52.59	39.63	75.51	71.08	61.88
	0.7	54.42	89.17	120	50	54.61	81.69	58.65	48.28	48.17	71.01	60.85	45.08	83.88	80.2	72.61
	0.75	52.93	81.67	114.8	53.61	51.26	70.48	64.76	53.56	45.34	77.67	69.08	54.13	90.33	87.46	81.68
	0.8	52.61	72.72	106.4	58.15	51.63	59.9	70.32	60.37	48.28	83.01	76.38	64.29	95.2	93.08	88.97
	0.85	53.84	63.67	93.17	62.84	55.3	53.48	75.02	67.37	55.79	87.17	82.48	73.91	98.87	97.41	94.69
	0.9	56.57	57.65	74.27	67.15	61.05	54.47	78.79	73.8	65.52	90.32	87.41	82.23	101.6	100.7	99.15
0.2	0.65	82.74	134.4	153.1	50.22	92.87	130.8	60.29	48.44	86.05	90.64	61.69	34.18	117.4	108.9	89.02
	0.7	75.82	129.7	151.4	51.78	76.68	121.8	77.73	48.28	65.5	108.7	84.97	43.35	130.7	125.1	111.8
	0.75	68.56	122.7	148.7	60.97	61.93	108.4	94.15	62.33	48.62	121.2	104.6	67.95	139	135.4	127
	0.8	62.59	111.6	144.1	74.34	56.05	88.85	107.2	82.13	48.28	129.7	118.9	94	144.4	142.1	137
	0.85	61.04	94.57	135	87.93	64.32	66.55	116.7	100.4	68.61	135.4	128.9	114.4	148	146.5	143.6
	0.9	66.6	74.23	114.3	99.4	82.02	61.52	123.5	114.4	95.72	139.3	135.8	128.5	150.4	149.6	148.1
0.3	0.65	106.8	152.4	164.9	54.34	117.7	149.2	70.41	53.88	109.9	119	74.13	31.19	148.1	139.5	115.9
	0.7	98.24	149.4	163.9	53.64	99.37	142.7	100.6	48.28	85.26	139.9	111.1	42.92	159	154.4	141.5
	0.75	87.63	144.7	162.4	70.27	76.57	132.3	124	73.92	55.9	151.7	135.4	85.58	164.8	162.2	155.2
	0.8	76.17	136.6	159.9	94.79	61.53	114	139.2	107.4	48.28	158.6	149.6	122.7	168.2	166.6	162.8
	0.85	69.9	121.6	154.7	116.5	75.47	83.46	148.7	131.9	85.14	162.8	158	145.2	170.2	169.4	167.4
	0.9	78.83	94.88	140.8	131.9	107.7	69.61	154.7	146.9	126.4	165.4	163.1	157.6	171.6	171.1	170.2
0.4	0.65	124.6	162.1	171.2	59.97	134.4	159.3	82.29	61.29	126.3	141.7	88.14	30.06	166.3	159.3	136.7
	0.7	116.5	160	170.5	55.58	117.6	154.6	122.6	48.28	102.2	160.3	133.3	43.6	173.7	170.4	159.7
	0.75	105.4	156.9	169.6	81.25	91.92	146.7	147.4	87.35	65.18	169.2	156.3	103.3	177.3	175.5	170.3
	0.8	91.07	151.5	168	116.6	67.99	131.8	160.8	130.8	48.28	173.8	167.6	144.2	179.1	178.2	175.5
	0.85	80.35	140.6	164.9	142.3	88.79	100.6	168.2	155.2	103.2	176.4	173.5	164	180.2	179.7	178.4
	0.9	93.87	116	156.4	157	133.7	78.99	172.3	167.2	150.6	178	176.6	173.2	180.9	180.6	180.1

On the other hand, RE increased when the first-stage selection probability $W$ was less than 0.5, and the values of $T$, $P$, and ${\pi }_i$ (from 0.1 to 0.4) decreased, but the RE decreased when the value of $W$ was greater than 0.5 under a fixed value for $T$, $P$, and ${\pi }_i$.

Furthermore, the greater the true population proportion of a sensitive attribute ${\pi }_i$, the higher the overall efficiency of Yennum et al.’s model, as shown by the values of the bottom cells in Table 1. This result agrees with the typical sampling survey methodology as the true population proportion of a sensitive attribute ${\pi }_i$ increases.

4.2. PPSWR Sampling versus Equal Probability Two-Stage Sampling in Yennum et al.’s Generalized Model

If we assume $N-1\doteq N$, then the difference between the variance of equal probability two-stage sampling scheme (41) and the variance of the PPS with replacement sampling scheme (28) is given by:

$$\begin{array}{cc}\hfill V({\widehat{\pi }}_{Gwr})-V({\widehat{\pi }}_{Gppswr})& =\frac{1}{n{M}_0\overline{M}}[{\displaystyle \sum _{i=1}^N{(M_i-\overline{M})}^2{\pi }_i^2+\overline{M}\left\{{\displaystyle \sum _{i=1}^N(M_i-\overline{M})({\pi }_i^2-{\pi }^2)}\right\}}\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+{\displaystyle \sum _{i=1}^N{(M_i-\overline{M})}^2}\frac{1}{m_i}\left[\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right]\hfill \\ & \begin{array}{cc}\hfill & \hfill \end{array}+\overline{M}\left\{{\displaystyle \sum _{i=1}^N(M_i-\overline{M})\frac{1}{m_i}\left(\frac{{\left\{{(1-T_i)}^{k_{i1}+1}{T}_i^{k_{i2}+1}{(1-P)}^{k_{i2}+1}{P}_i^{k_{i1}+1}\right\}}^2}{{\phi }_{i2}^2}{\sigma }_{iZ}^2\right)}\right\}].\hfill \end{array}$$

(44)

In (44), we can see that $V({\widehat{\pi }}_{Gwr})=V({\widehat{\pi }}_{Gppswr})$ under the condition $M_i=\overline{M}=M_0/N$, i.e., if the cluster sizes are equal, the selection probabilities of the PPS with replacement sampling are all $N^{-1}$ and equal to those of the equal probability two-stage replacement sampling.

If cluster sizes, $M_i$, were significantly different, then ${{\displaystyle {\sum }_{i=1}^N(M_i-\overline{M})}}^2{\pi }_i^2$, the first term of the right-hand side in (44), had large values, and the second term, ${{\displaystyle {\sum }_{i=1}^N(M_i-\overline{M})}}^2({\pi }_i^2-{\pi }^2)$, had relatively small values. Hence, the estimation by PPS with replacement sampling is more efficient than that by equal probability two-stage replacement sampling.

We used the relative efficiency (RE) to compare the efficiency of the two sampling designs (PPS with replacement sampling and equal probability two-stage replacement sampling):

$$R{E}_2=\frac{V({\widehat{\pi }}_{Gwr})}{V({\widehat{\pi }}_{Gppswr})}\times 100(\%)$$

Values of $R{E}_2$ over 100% indicate that the estimator obtained by PPS with the replacement sampling method was more efficient than the estimator obtained by equal probability two-stage replacement sampling.

Table 2 shows the results of the REs obtained by increasing the true population proportion ${\pi }_i$ from 0.1 to 0.4 by 0.1. The selection probabilities of the randomized response model ($W$, $T$ and $P$) are shown in Section 4.1.

Table 2. The REs for a sensitive estimator between the PPS with replacement sampling and equal probability two-stage sampling with replacement in Yennum et al.’s generalized model for changing ${\pi }_i$ and $W$.

${\mathit{\pi }}_{\mathit{i}}$		W
	T	0.1			0.3			0.5			0.7			0.9
	P	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8	0.6	0.7	0.8
0.1	0.65	171.5	172.8	172.8	163	166.9	167.9	145.4	155.4	159.1	104.1	126.5	138.8	48.17	52.15	68.27
	0.7	167.5	169.7	170.1	152.7	160.2	163.1	119.1	139.1	148.9	57.85	83.09	111	78.98	76.63	58.68
	0.75	162.2	165.9	167	135.6	150.2	156.7	79	111	133.1	54.18	48.22	69.55	116.3	124.4	117.6
	0.8	154.2	160.9	163.3	106.2	133.1	147.2	48.74	68.09	105.6	88.1	76.9	50.14	136.5	148.1	152.8
	0.85	139.8	153.1	158.5	64.63	99.62	130.1	64.15	50.65	60.85	116.4	120.1	102.3	147	159.4	168.3
	0.9	108.4	136	150.3	49.94	51.5	89.01	96.84	95.38	69.51	133	144.7	150.1	152.7	165.1	175.3
0.2	0.65	180.9	181.1	181	177	178.1	178.3	168.4	172	173.1	140.7	154.2	160	48.39	59.25	87.17
	0.7	178.9	179.5	179.5	172.1	174.6	175.5	152.4	162.4	166.8	75.03	112.8	137.8	120.5	111	71.17
	0.75	176.4	177.5	177.8	163.1	169.2	171.8	113.3	142.1	156.1	67.28	48.47	88.43	159.6	161.5	149
	0.8	172.6	174.9	175.8	143.4	159.1	166.1	50.3	91.74	133.4	132.9	110.7	52.83	171.6	175.4	173.9
	0.85	165.8	171	173.1	91.83	133.9	154.7	94.45	55.74	74.87	160	159	135.4	176.4	180.4	182.1
	0.9	147.3	162.3	168.5	55.09	58.5	118.4	145.2	139.7	94.09	170.3	174.6	173.7	178.6	182.6	185.2
0.3	0.65	184	184	183.9	181.6	182	182	176.2	178	178.5	157.3	165.5	168.9	48.68	66.76	101.4
	0.7	182.8	183	182.9	178.5	179.7	180.2	165.6	171.4	174	91.45	130.8	151.3	145.6	132.9	81.96
	0.75	181.2	181.7	181.8	172.9	176.1	177.6	134.5	156.5	166.1	81.89	48.76	102.6	174.4	173.9	161.9
	0.8	178.9	180	180.4	159.7	169.3	173.6	52.38	109.5	147.9	155.9	132.1	55.54	181.2	182.4	180.1
	0.85	174.8	177.5	178.6	114.3	150.9	165.5	120.4	61.6	86.84	174.9	172.4	151.2	183.6	185.3	185.4
	0.9	163.6	172.1	175.6	62.66	66.66	135.6	166.4	160.1	112.1	180.7	182.3	180.3	184.7	186.4	187.3
0.4	0.65	185.5	185.5	185.4	183.9	184.1	184	180	181	181.3	166.1	171.6	173.8	49.04	74.03	112.4
	0.7	184.7	184.8	184.7	181.7	182.4	182.6	172.3	176.1	177.9	105.3	142.5	159.4	159.6	146.4	91.15
	0.75	183.5	183.8	183.9	177.7	179.7	180.7	147.7	164.5	171.7	95.48	49.07	113.7	180.5	179.2	168.8
	0.8	181.9	182.6	182.9	168.2	174.7	177.7	54.79	122.6	156.8	167.6	145.4	58.24	184.8	185.2	182.8
	0.85	179.2	180.8	181.6	130.6	160.5	171.4	138.7	67.61	97.01	181	178.3	160.1	186.3	187	186.7
	0.9	171.7	177.1	179.3	71.76	75	146.8	176	170.1	125	184.7	185.3	183.2	186.9	187.8	188.1

In calculating the REs, we set the parameters as follows:

$$\begin{array}{l}{M}_0=10,000,M_1=1,000,M_2=2,000,M_3=3,000,M_4=4,000\hfill \\ m_0=1,000,m_1=100,m_2=200,m_3=300,m_4=400,\hfill \\ p_1=0.235,p_2=0.441,p_3=0.609,p_4=0.715,\hfill \\ k_1=2,k_2=1.\hfill \end{array}$$

From the results of Table 2, the efficiencies vary according to changes in the probabilities of selection during the first stage $W$ and the second stage $T$ and $P$ in the randomization device, but when the first-stage selection probability $W$ is fixed, and the second-stage selection probabilities $T$ and $P$ increase, then the relative efficiency of the PPS sampling is better than that of the equal probability two-stage sampling in Yennum et al.’s model.

5. Conclusions

We extended Yennum et al.’s model, in which geometric distribution is used as a randomization device for a population consisting of different-sized clusters, and clusters are selected by PPS sampling. Estimators for the true population proportion of a sensitive attribute, their variances, and their variance estimators are derived under PPS sampling and equal probability two-stage sampling.

We also applied these sampling designs to the case of Yennum et al.’s generalized model. Numerical studies were carried out to compare the efficiencies of the proposed methods in each case of Yennum et al.’s model and Yennum et al.’s generalized model in cases with a replacement.

Although the experiments were assumed to use a replacement, we expected similar results for a case without replacement, as per typical sampling theory.

From the numerical study, we found that the efficiency of the two-stage sampling for probability proportional to size depends on the given parameter values, but the efficiency of Yennum et al.’s generalized model is preferred for most combinations of parameters over around 80%.