Significance of Double Stratification in Stagnation Point Flow of Third-Grade Fluid towards a Radiative Stretching Cylinder

Abstract

The present article is devoted to examine the significance of double stratification in third grade stagnation point flow towards a radiative stretching cylinder. The stagnation point is discussed categorically. Analysis is scrutinized in the presence of Thermophoresis, Brownian diffusion, double stratification and heat source/sink. Suitable typical transformations are used to drive the system of ordinary differential equation. The governing system is subjected to optimal homotopy analysis method (OHAM) for convergent series solutions. The impact of pertinent fluid parameters on the velocity field, temperature distribution and concentration of the nanoparticles is shown graphically. Numerical data is compiled in tabulare form for skin friction, Nusselt and Sherwood numbers to analyze the variation caused by the present model and to see the impact for industrial and engineering point of view.

1. Introduction

The study of stratification analyzes the variations and effects in thermal stratified object (medium) for the so-called common fluids. In industrial as well as natural processes, stratification plays an important role. Reason behind the existence of this phenomena is variation in temperature, variation of densities in different fluids and the concentration differences. Transfer of heat and mass simultaneously, doubles the stratification that belongs to the context of thermal stratification. Thermal stratification can be seen very often in the reservoirs and oceans. Another type of stratification is salinity stratification that is witnessed in rivers, estuaries, reservoirs storing the ground water, atmospheric heterogeneous mixtures, food industries and various manufacturing processes etc. A very few researchers in the past have made a significant contribution in investigating the effect of mass and thermal stratification over heat as well as mass transfer by a naturally convective flow. Keeping in view the above mentioned facts, double stratification gained a significant importance in the eyes of some researchers like Srinivasacharya and RamReddy [1,2] who investigated the double stratification’s effect numerically. The medium was first considered non-porous and afterwards Darcian (porous) as well. Mixing process of oxygen with water in the bottom of reservoirs through biological processes can be controlled by using the tool of thermal stratification (see [3]). Stratification has also major contribution in environmental sciences. It can be very helpful in balancing the temperature differences and concentrations of oxygen and hydrogen to control the growth rates of various species in naturally unbalanced and less productive environments, Ibrahim and Makinde [4]. Various engineering processes occurring at a very high temperature direly depend upon a deep understanding and knowledge of thermal radiation. Combustion energy processes happening in fossil fuel, flows in astrophysics, harnessing the energy of sun in solar technology, turbines, devices for converting mechanical energy into propulsive force in aircraft, missiles and space-ships etc. are best examples of the importance and usage of the study of thermal radiations (see [5]). In some objects, fluid flow encounters a certain point where fluid motion becomes zero. In Geop physical setups, physical models and fluid mechanics, the point is called stagnation point. This stagnation point can be anywhere on the surface of object. However, the fluid continues flowing in neighborhood of this point, called stagnation point flow. Such an object is termed as impermeable object (see [6]). Stagnation point is sub-divided into two main categories (i) orthogonal and (ii) slanted stagnation point. In first case, the fluid particles act orthogonal to a rigid/solid surface and consequently, the resulting velocity is zero. The orthogonality of fluid particles at certain point makes it a perpendicular or orthogonal stagnation point. In second case, the fluid particles act on the rigid body through some random arbitrary angle of incidence. One can say that this point is a dual of orthogonal and shear stagnation point flow flowing parallel to the object. Numerous researches has been carried out on stagnation point flow. Describing the fluid motion near stagnation regions of a solid surface, the stagnation point flow was first studied by Hiemenz [7] using a similarity transformation for reducing the Navier-Stokes equations to Non-linear ODEs. Accordingly, stagnation flow can be categorized in various types depending upon the behavior of flow. Analyzing the density one can characterize it as inviscid or viscous flow, steady or unsteady flow, geometrically it can be two or three dimensional flow. The stagnation point flow can also be characterized according to the symmetry. Therefore, it can be symmetric or asymmetric, normal or slanted. Analyzing the flow behavior, it can be treated as homogeneous or immiscible fluid and forward or reverse fluid (see [8,9]). Importance of stagnation point flow can be witnessed in natural and industrial phenomena. Fluid striking the tips of submarines, oil-ships and air-crafts are best examples of stagnation point flow. The blood flowing through a junction in an artery is another biological example of stagnation point flow. Mabood et al. [10] investigated the radiation effects on stagnation point flow with melting heat transfer. Meanwhile, stagnation point flow of Tangent-hyperbolic liquid visualized by Shafiq et al. [11] witnesses its importance and significance in different aspects.

Process of natural convection can be witnessed in various physical phenomenon especially fire and heat engineering, nuclear science, reservoirs used for petroleum etc. The presence of heat (source/sink) and thermal radiation is a key factor in natural convection process. Such processes has been studied extensively because of naturally frequent existence. Ghoshdastidar [12] has explained various areas witnessing the applications of free convection. For example, the transfer of heat from heater to the neighborhood or heat dissipation through coil of refrigerator unit to the neighborhood etc. The encounter of such phenomena is common in wide range of thermal applications. Cheng [13,14] studied the boundary layer flow as natural convection. The medium was a vertical surface with Newtonian heating. The chemical reaction and thermal radiation are important aspects in engineering setups involving Riga patterns (see [15]). Boundary layer flow and the study of heat transfer in fluid mechanics and engineering is a contemporary research area (see [16]). Furthermore, Rasool et al. [17] reported MHD nanofluid flow over stretching surface with simple temperature attributes whereas, Rasool et al. [18] reported a study in the same representation using Cattaneo Christov heat and mass flux model over a stretching surface. Many researchers in the past have remained focused on this area and their work have been published. For example Kuznetsov and Nield [19] studied this phenomena of boundary layer flow analytically using the Brownian motion model. The effects of thermophoresis were taken into account. The results proved that Nusselt number is a decreasing function of the parameters of Brownian motion. Presence of gravity is a key element for density differences which plays a vital role in the mixing of heterogeneous fluids and their dynamics. A similar kind of boundary layer flow through a porous medium was investigated by Lesnic et al. [20]. Recently, Shafiq et al. [21] investigated a boundary-Layer flow of Walters’ B fluid in Newtonian heating depicted the heat transfer phenomena. The study highlights usefulness of boundary layer flow. The Newtonian heating, its effects and applications has been discussed in this research in detail. The study of two-dimensional boundary layer flow using an unsteady and permeable stretching surface is yet another recent improvement linking the effects of thermal radiations in boundary layer flows (see [22]). In this study Shafiq et al. investigated the effects of electric and magnetic fields. In present study the analysis is carried out by finding the optimal convergence. For details one can read the optimal control convergence procedure adopted in solving linearized Navier-Stokes equations in netlike domain [23] and pipeline flow [24].

In the literature mentioned above, the studies have been mainly reported on stretching surfaces with various assumptions including the porosity factor, Brownian diffusion and thermophoresis using HAM [25,26,27,28,29,30,31]. However, no research is found emphasizing the role of stagnation point in third grade fluid towards stretching surface (cylinder) which affirms the novelty of the present problem. Here the objective is to discuss the stagnation point and boundary layer flow, to analyze the corresponding results in the presence of sink/source and to graphically interpret various physical parameters involved in model using Optimal Homotopy approach.

2. Formulation

We consider a third grade stagnation point flow towards a radiative stretching cylinder in the context of double stratification. The stagnation point is discussed categorically. Analysis is scrutinized in the presence of Thermophoresis, Brownian diffusion, double stratification and heat source/sink. Suitable typical transformations are used to drive the system of ordinary differential equation. The governing system is subjected to optimal homotopy analysis method (OHAM) for convergent series solutions.. The effect of double stratification and thermal radiation is accounted. We assume that z-axis is directed along the given stretching cylinder whereas the radial r-axis goes perpendicular to it. Thus,

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(1)

$$\begin{array}{ccc}\hfill \rho \left(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)& =& W_e\frac{d{w}_e}{d_z}+\mu \left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)+{\alpha }_1\left[\frac{w}{r}\frac{{\partial }^{2}w}{\partial r\partial z}+\frac{u}{r}\frac{{\partial }^{2}w}{\partial r^2}+\frac{3}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial z}\right.\hfill \\ & & +\frac{1}{r}\frac{\partial u}{\partial r}\frac{\partial w}{\partial r}+4\frac{\partial w}{\partial r}\frac{{\partial }^{2}w}{\partial r\partial z}+w\frac{{\partial }^{3}w}{\partial r^2\partial z}+2\frac{\partial u}{\partial r}\frac{{\partial }^{2}w}{\partial r^2}\hfill \\ & & \left.+u\frac{{\partial }^{3}w}{\partial r^3}+3\frac{{\partial }^{2}w}{\partial r^2}\frac{\partial w}{\partial z}+\frac{{\partial }^{2}u}{\partial r^2}\frac{\partial w}{\partial r}\right]+{\alpha }_2\left[\frac{2}{r}\frac{\partial u}{\partial r}\frac{\partial w}{\partial r}+\frac{2}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial z}\right.\hfill \\ & & +2\frac{{\partial }^{2}u}{\partial r^2}\frac{\partial w}{\partial r}+2\frac{\partial u}{\partial r}\frac{{\partial }^{2}w}{\partial r^2}+2\frac{{\partial }^{2}w}{\partial r^2}\frac{\partial w}{\partial z}\hfill \\ & & \left.+4\frac{\partial w}{\partial r}\frac{{\partial }^{2}w}{\partial r\partial z}\right]+{\beta }_3\left[\frac{2}{r}{\left(\frac{\partial w}{\partial r}\right)}^3+6{\left(\frac{\partial w}{\partial r}\right)}^2\frac{{\partial }^{2}w}{\partial r^2}\right],\hfill \end{array}$$

(2)

$$u\frac{\partial T}{\partial r}+\frac{w\partial T}{\partial z}=\frac{k}{\rho c_p}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1\partial T}{r\partial r}\right)+\frac{16\sigma T_{\infty }^3}{3k^{*}\rho c_p}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1\partial T}{r\partial r}\right)+\frac{Q_0}{\rho c_p}\left(T-T_{\infty }\right),$$

(3)

$$u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}=D\left(\frac{{\partial }^{2}C}{\partial r^2}+\frac{1\partial C}{r\partial r}\right),$$

(4)

with

$$\begin{array}{ccc}w\left(r,z\right)& =\hfill & W_w\left(z\right)=\frac{W_{0}z}{l},u\left(r,z\right)=0,T\left(r,z\right)=T_0+b\left(\frac{z}{l}\right),C\left(r,z\right)=C_0+d\left(\frac{z}{l}\right)\mathrm{at}r=R,\hfill \\ w\left(r,z\right)& ⟶\hfill & W_e\left(z\right)=\frac{w_{\infty }z}{l},T\left(r,z\right)\to T_0+c\left(\frac{z}{l}\right),C\left(r,z\right)\to C_0+e\left(\frac{z}{l}\right)\mathrm{at}r⟶\infty .\hfill \end{array}$$

(5)

where r represents radial distance while z is assigned to axial distance. $u,$ $v,$ correspond to r and z component of fluid velocity, $T,$ $T_{\infty }$ represent surface & ambient temperature while C and $C_{\infty }$ represent surface & ambient concentration, respectively. Here $\rho ,$ $\nu$ correspond to fluid density and kinematic viscosity while $c_p$ and k are the specific heat at constant pressure and thermal conductivity, respectively. The constants $b,d,$ e and c are dimensionless. $k^{*}$ is designated as coefficient of mean absorption, $\sigma$ is Stephen Boltzman constant, reference length is represented by l , $W_w$ is stretching velocity while $W_e$ is the free stream velocity. $Q_0$ is used to represent the coefficient of heat generation as well as absorption. It is pertinent to mention that $Q_0^{+}$ (the positive values) behaves as source (heat generation) while $Q_0^{-}$ (the negative values) behaves as sink (heat absorption). Using suitable transformations

$$\begin{array}{ccc}w\left(r,z\right)& =\hfill & \frac{W_{0}z}{l}{f}^{\prime }\left(\eta \right),u\left(r,z\right)=-\sqrt{\frac{\nu W_0}{l}}\frac{R}{r}f\left(\eta \right),\eta =\sqrt{\frac{W_0}{\nu l}}\left(\frac{r^2-R^2}{2R}\right),\hfill \\ \theta \left(\eta \right)& =\hfill & \frac{T-T_{\infty }}{T_W-T_0},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_0}.\hfill \end{array}$$

(6)

It can easily be verified that the balance of mass given by Equation (1) is identically satisfied. On substituting Equation (6) into Equations (2)–(5) and then rearranging we have:

$$\begin{array}{ccc}& \hfill & \left(1+2\gamma \eta \right)f^{‴}+A^2+2\gamma f^{″}-f^{\prime }{}^2+f{f}^{″}\hfill \\ & \hfill & +{\alpha }_1\left[\left(1+2\gamma \eta \right)\left\{2f^{\prime }{f}^{‴}-f{f}^{\left(iv\right)}+3f^{″}{}^2\right\}+\gamma \left(6f^{\prime }{f}^{″}-2f{f}^{‴}\right)\right]\hfill \\ & \hfill & +{\alpha }_2\left[2\left(1+2\gamma \eta \right)f^{″}{}^2+\gamma \left(2f^{\prime }{f}^{″}+2f{f}^{‴}\right)\right]\hfill \\ & \hfill & +\beta Re\left[6{\left(1+2\gamma \eta \right)}^2{f}^{″}{}^2{f}^{‴}+8\gamma \left(1+2\gamma \eta \right)f^{″}{}^3\right],\hfill \end{array}$$

(7)

$$f^{\prime }\left(0\right)=1,f\left(0\right)=0,f^{\prime }\left(\infty \right)=A,$$

(8)

$$\left(1+\frac{4}{3}{R}_d\right)(1+2\gamma \eta ){\theta }^{″}+2\gamma \left(1+\frac{4}{3}{R}_d\right){\theta }^{\prime }-Pr\left(f^{\prime }\theta +f^{\prime }\theta \right)-SPr{f}^{\prime }+Qg=0,$$

(9)

$$\theta \left(0\right)=1-S,\theta (\infty )⟶0,$$

(10)

$$(1+2\gamma \eta ){\varphi }^{″}+2\gamma {\varphi }^{\prime }+Sc(f{\varphi }^{\prime }-f^{\prime }\varphi )-ScSt\left(f^{\prime }\right)=0,$$

(11)

$$\varphi \left(0\right)=1-S{t}_{,}\varphi (\infty )⟶0,$$

(12)

where

$$\begin{array}{ccc}{\alpha }_1& =\hfill & \frac{{\alpha }_1^{*}{W}_0}{l\mu },{\alpha }_2=\frac{{\alpha }_2^{*}{W}_0}{l\mu },\beta =\frac{{\beta }_3{W}_0^2}{l^2\mu },Re=\frac{Wz}{\nu },\hfill \\ R_d& =\hfill & \frac{4{\sigma }^{*}{T}_{\infty }^3}{k^{*}k},Pr=\frac{\mu c_p}{\rho },\gamma ={\left(\frac{\nu l}{W_0{R}^2}\right)}^{1/2},\hfill \\ Q& =\hfill & \frac{Q_0}{\rho c_p{W}_w},S=\frac{c}{b},St=\frac{e}{d},\hfill \end{array}$$

(13)

which respectively indicate the dimensionless third-grade parameters $\left({\alpha }_1,{\alpha }_2,\beta \right)$, the Reynolds number $\left(R_e\right)$, thermal radiation parameter $\left(R_d\right)$, the Prandtl number $\left(Pr\right),$ the curvature parameter $\left(\gamma \right),$ heat generation/absorption parameter $\left(Q\right)$, thermal stratification parameter $\left(St\right)$ and solute stratification parameter $\left(Sc\right)$. Expression of physical quantities are,

$$N{u}_z=\frac{z{q}_w}{k(T_w-T_0)},\mathrm{where}{q}_w=-k{\left(\frac{\partial T}{\partial r}\right)}_{r=R},$$

(14)

$$C_f=\frac{T_{rz}}{\rho W_e^2},$$

(15)

$$S{h}_z=\frac{z{h}_w}{D_w(C_w-C_0)},\mathrm{where}{h}_w=-D{\left(\frac{\partial C}{\partial r}\right)}_{r=R},$$

(16)

Such that

$$N{u}_z{Re}_z^{-1/2}=-(1+\frac{4}{3}Rd)(1-S){\theta }^{\prime }\left(0\right),$$

(17)

$${Re}_z^{-1/2}{C}_f=[1+3{\alpha }_1+3\beta Re{\left(f^{″}\left(0\right)\right)}^2]f^{″}\left(0\right),$$

(18)

$$S{h}_z{Re}_z^{-1/2}=-(1-St){\varphi }^{\prime }\left(0\right),$$

(19)

where ${Re}_z=W_{w}l/\nu$ is the local Reynolds number.

3. Optimal Homotopic Solutions

The initial guesses and linear operators for the construction of series solutions are

$$f\left(\eta \right)=A\eta +(1-A)(1-Exp(-\eta ),{\theta }_0\left(\eta \right)=(1-S)Exp(-\eta ),{\varphi }_0\left(\eta \right)=(1-St)Exp(-\eta ),$$

(20)

$${\mathcal{L}}_f\left(f\right)=\frac{d^{3}f}{d{\eta }^3}-\frac{df}{d\eta },{\mathcal{L}}_{\theta }\left(\theta \right)=\frac{d^2\theta }{d{\eta }^2}-\theta ,{\mathcal{L}}_{\varphi }\left(\theta \right)=\frac{d^2\theta }{d{\eta }^2}-\theta ,$$

(21)

with

$${\mathcal{L}}_f\left[A_1+A_{2}exp\left(\eta \right)+A_{3}exp(-\eta )\right]=0,$$

(22)

$${\mathcal{L}}_{\theta }\left[A_{4}exp\left(\eta \right)+A_{5}exp(-\eta )\right]=0,$$

(23)

$${\mathcal{L}}_{\varphi }\left[A_{6}exp\left(\eta \right)+A_{7}exp(-\eta )\right]=0,$$

(24)

where $A_i$ $\left(i=1,2,\dots ,7\right)$ are the arbitrary constants.

4. Optimal Convergence Control Parameters

The parameters $h_f$ and $h_{\theta }$ are called convergence control parameters that are computed using the numerical BVPh2.0 package. Resulting optimal numerical values of these parameters are usually determined by the min of the average error. To significantly reduce the processing time of CPU, the tactic of average residual error is used at the m^th-order of approximation, such that,

$${\epsilon }_m^f\left({\hslash }_f\right)=\frac{1}{N+1}\sum _{j=0}^N{\left[\sum _{i=0}^k{\left(f_i\right)}_{\eta =j\pi }\right]}^2,$$

(25)

$${\epsilon }_m^{\theta }\left({\hslash }_f,{\hslash }_{\theta }\right)=\frac{1}{N+1}\sum _{j=0}^N{\left[\sum _{i=0}^k{\left(f_i\right)}_{\eta =j\pi },\sum _{i=0}^k{\left({\theta }_i\right)}_{\eta =j\pi }\right]}^2,$$

(26)

and

$${\epsilon }_m^{\theta }\left({\hslash }_f,{\hslash }_{\varphi }\right)=\frac{1}{N+1}\sum _{j=0}^N{\left[\sum _{i=0}^k{\left(f_i\right)}_{\eta =j\pi },\sum _{i=0}^k{\left({\theta }_i\right)}_{\eta =j\pi }\right]}^2.$$

(27)

The optimal values of the convergence control parameters are $h_f=-0.32677,$ $h_{\theta }=-0.56129$ and $h_{\varphi }=-0.46129,$ when ${\alpha }_1={\alpha }_2=\beta =0.1,$ $Re=\gamma =S=0.2,$ $A=1.5,$ $R_d=0.4,$ $Q=0.2,$ $Sc=1.2,$ $St=0.3,$ $Pr=1$. The values of convergence control parameters are choosen very carefully. The admissible ranges of parameters are taken. The results are convergent within the ranges of these values. The values assigned to the fluid parameters are chosen carefully to satisfy the convergence criteria of OHAM. Beyond these values, the solution might not converge. One can see the total residual error in Figure 1.

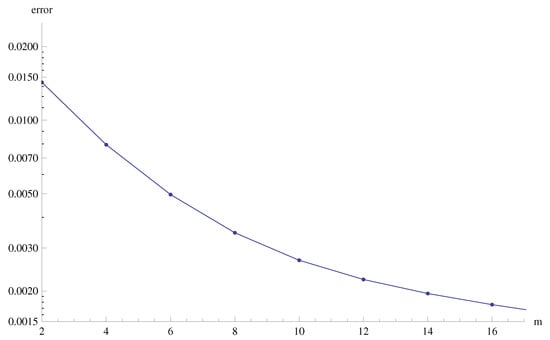
Figure 1. Total error vs order of approximations.

5. Discussions

The physical insights of parameters, used in this research, on velocity, concentration distribution and temperature are key aspects to be discussed in this section. Significance and impact of $\gamma$ (curvature parameter) over the velocity field is shown in Figure 2. It is witnessed from Figure 2 that initially an inverse proportion between $\gamma$ and velocity field as well as boundary layer thickness converts into a direct proportion at far away from the cylinder. The thickness of boundary layer and the velocity distribution with a certain decrease near the cylinder gradually starts increasing in fluid far away from cylinder. More the fluid is near to the cylinder, more is the affect of resistance. Figure 3 shows the behavior of ratio parameter on velocity distribution. Therefore, it can be noticed that velocity field goes higher and higher in both cases for $A>1$ and $A<1$ while the boundary layer shows a different behavior. Even At $A=1$, there are no visuals of boundary layer. The significance of $\beta$, a third grade parameter, in the fluid velocity is depicted in Figure 4. The more the value of $\beta$, the low is the viscosity that causes enhancement in velocity distribution. Consequently, the velocity profile is enhanced. Figure 5, depicts the the impact of Reynolds $Re$ on the velocity field. Certain decrease in the velocity field is noticed in moving from near the cylinder to away and finally, it vanishes at far away from surface. The reason behind this vanishing is the high value of Reynolds number that reduces the friction in between the surface and fluid. Figure 6 shows the variation of A, the ratio parameter, on temperature distribution. Higher is the value of A, the lesser is thickness of thermal and temperature boundary layer. Curvature parameter $\gamma$ on $\theta \left(\eta \right)$ is analyzed in Figure 7. Both, the thermal field and connected/associated boundary layer are found as increasing functions of the $\gamma$. The Impact of well known Prandtl number on $\theta \left(\eta \right)$ is plotted in Figure 8. There is an inverse relation seen in thermal distributions for Prandtl. The smaller is the Prandtl factor, the higher is the temperature and thermal boundary layer thickness. The decremented thermal diffusion due to increment in Prandtl number forces the temperature distribution to decrease. One can conclude that fluids having low Prandtl numbers normally have high thermal diffusivity. The influence of heat generation and absorption on $\theta \left(\eta \right)$ is shown in Figure 9. An increase in heat generation parameter $Q>0$ and decrease in heat absorption parameter $Q<0$ ensures the increase in temperature field. Further, the increase in heat generation increases the thickness of thermal boundary layer because the heat generation produces more heat that certainly allows a temperature hike. $R_d$ on $\theta \left(\eta \right)$ in Figure 10 shows the variation in temperature distribution due to thermal radiation. More is the thermal radiation $R_d$, lesser is the temperature distribution. The stratification parameter S over $\theta \left(\eta \right)$ is analyzed in Figure 11. An increase in S certainly decreases the $\theta \left(\eta \right)$ significantly whereas the thickness of thermal boundary layer goes higher and higher over a decrease in S. This is justified with the reason that a hike in S reduces the difference between surface of cylinder and corresponding temperature. The effect of curvature parameter $\gamma$ over $\varphi \left(\eta \right)$ is analyzed in Figure 12. Nearby the cylinder, the concentration profile attains a decrement and goes on increasing away from the cylinder. Figure 13 shows the behavior and variation of Schmidt number $Sc$, ratio of momentum and mass diffusivity, over $\varphi \left(\eta \right)$. The more is $Sc$, $\varphi \left(\eta \right)$ goes on increasing while thickness of solute boundary layer decreases. Higher is the value of $Sc$, smaller is the mass diffusivity and therefore, $\varphi \left(\eta \right)$ achieves an increment. Finally, the variation and behavior of solute stratified parameter $St$ over the concentration profile is displayed in Figure 14. Decrements in concentration profile are noted for high values of $St$. Hence, an increase in $St$ is responsible for decreasing concentration distribution existent between surface and ambient fluid. Consequently, the concentration field decreases. Optimal convergence control parameters are enlisted in Table 1. It shows the individually calculated average squared r-errors in momentum and energy equations at different order of approximation. A decrease in squared residual errors is noted as compared to the order of approximation. Behavior of the coefficient of skin-friction is enlisted in Table 2. It is evident that for large values of ${\alpha }_1,$ $\beta ,$ $\gamma$ and $Re$, skin friction increases. The skin friction decreases for augmented values of ${\alpha }_2$ and A. Table 3 enlists the variation in Nusselt number due to different parameters. Higher the values of ${\alpha }_1,$ ${\alpha }_2,$ $\beta ,$ $A,$ $\gamma ,$ $Q,$ $St$ and $R_d$, higher is the Nusselt number. However, it decreases with Pr. Table 4 shows the influence of numerous parameters on Sherwood number. Higher the values of $S,$ ${\alpha }_1,$ ${\alpha }_2,$ and $\beta$, higher is the Sherwood number. However, it experiences a decrease in values with $\gamma ,$ $St$ and $Sc$.

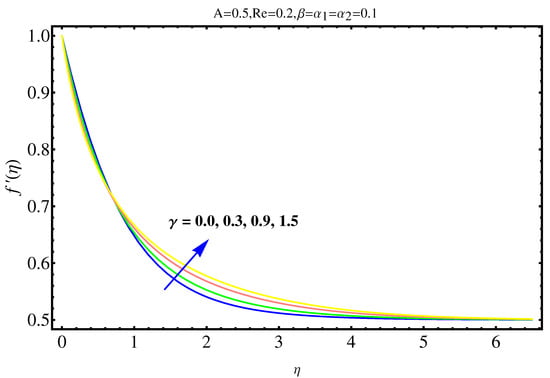
Figure 2. Impact of $\gamma$ on $f^{\prime }\left(\eta \right)$.

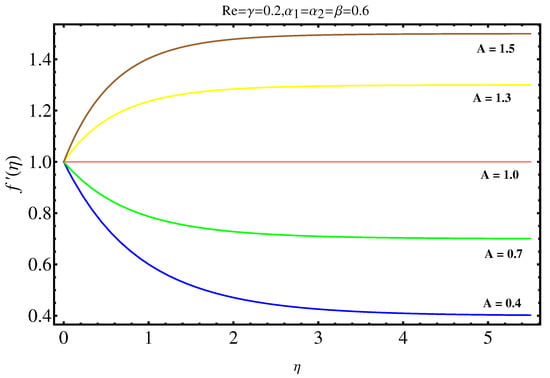
Figure 3. Impact of A on $f^{\prime }\left(\eta \right)$.

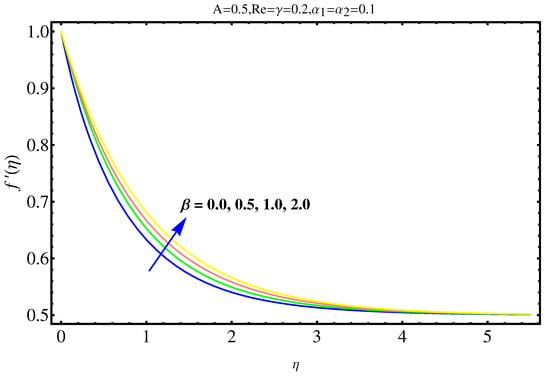
Figure 4. Impact of $\beta$ on $f^{\prime }\left(\eta \right)$.

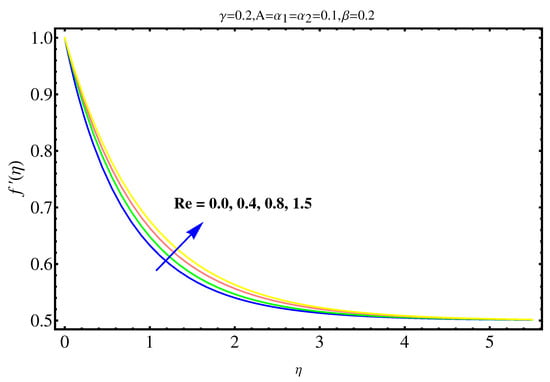
Figure 5. Impact of Re on $f^{\prime }\left(\eta \right)$.

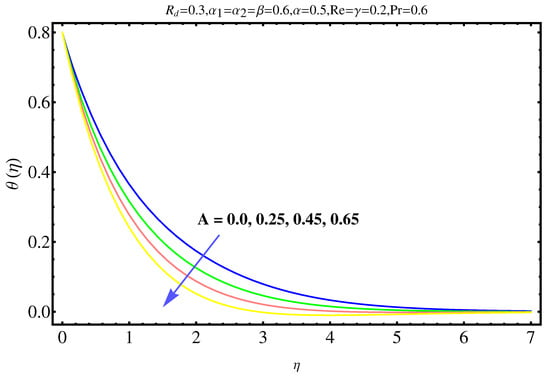
Figure 6. Impact of A on $\theta \left(\eta \right)$.

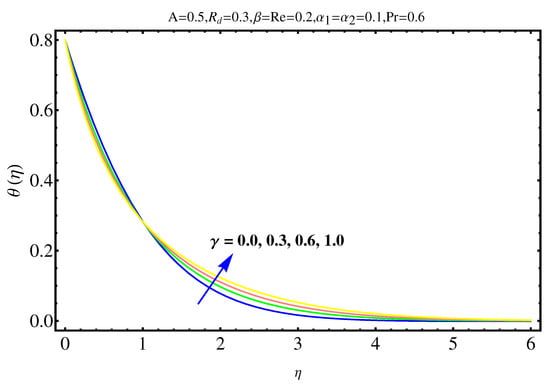
Figure 7. Impact of $\gamma$ on $\theta \left(\eta \right)$.

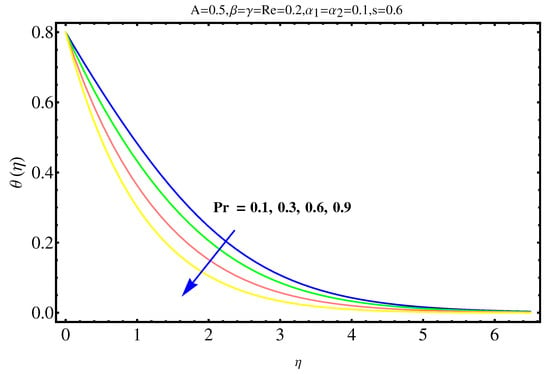
Figure 8. Impact of $Pr$ on $\theta \left(\eta \right)$.

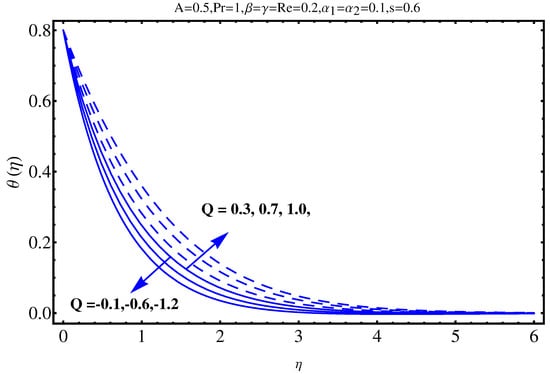
Figure 9. Impact of Q on $\theta \left(\eta \right)$.

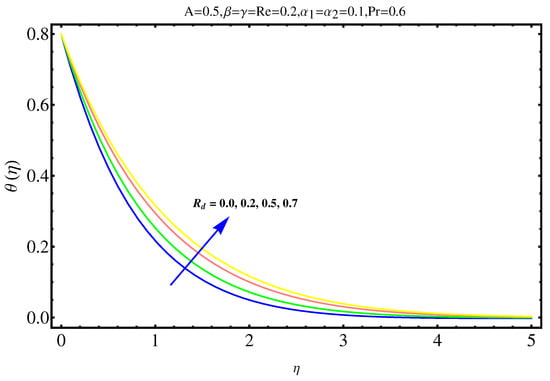
Figure 10. Impact of $R_d$ on $\theta \left(\eta \right)$.

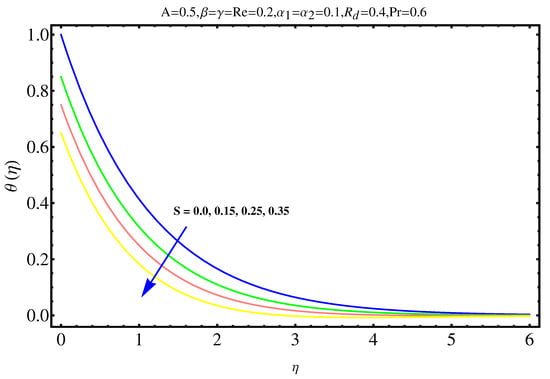
Figure 11. Impact of S on $\theta \left(\eta \right)$.

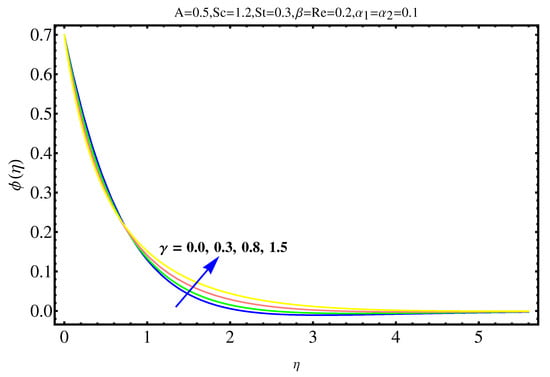
Figure 12. Impact of $\gamma$ on $\varphi \left(\eta \right)$.

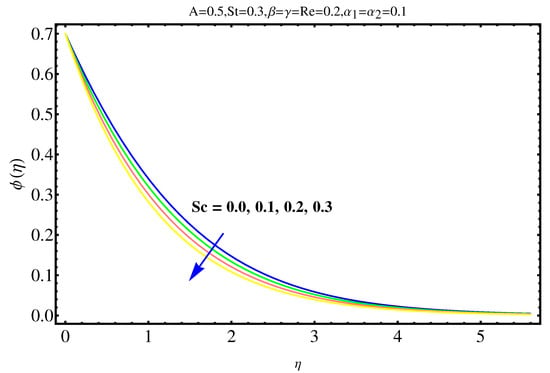
Figure 13. Impact of $Sc$ on $\varphi \left(\eta \right)$.

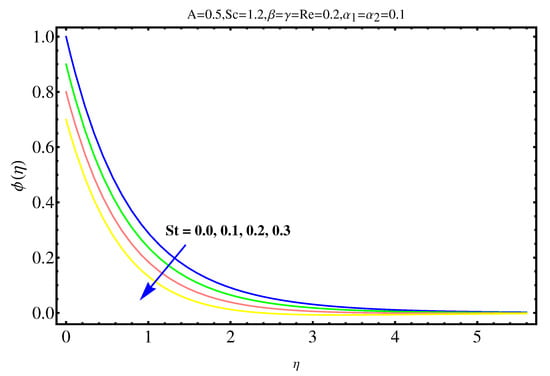
Figure 14. Impact of $St$ on $\varphi \left(\eta \right)$.

Table 1. Residual errors at ${\alpha }_1={\alpha }_2=\beta =0.1,$Re$=\gamma =S=0.2,$ $A=1.5,$ $R_d=0.4,$ $Q=0.2,$ $Sc=1.2,$ $St=0.3,$ $Pr=1$ by means of optimal control parameters ${\hslash }_f=-0.32677,$ ${\hslash }_{\theta }=-0.56129$ and ${\hslash }_{\varphi }=-0.46129.$

m	${\mathit{ϵ}}_{\mathit{m}}^{\mathit{f}}$	${\mathit{ϵ}}_{\mathit{m}}^{\mathit{\theta }}$	${\mathit{ϵ}}_{\mathit{m}}^{\mathit{\varphi }}$	$\mathit{CPU}$Time [s]
$2.0$	$0.00108904$	$0.0161511$	$0.136643$	$3.84396$
$4.0$	$7.87184\times {10}^{-6}$	$0.0145533$	$0.117591$	$20.2511$
$6.0$	$1.15481\times {10}^{-6}$	$0.0135712$	$0.105814$	$48.3618$
$8.0$	$2.90966\times {10}^{-7}$	$0.012861$	$0.0975497$	$111.334$
10	$1.64734\times {10}^{-7}$	$0.0123001$	$0.0915131$	$229.121$
14	$7.54581\times {10}^{-8}$	$0.0114404$	$0.0838574$	$822.825$
18	$4.06748\times {10}^{-8}$	$0.0107921$	$0.081305$	$2398.66$
20	$3.10657\times {10}^{-8}$	$0.0105197$	$0.0803804$	$3958.69$

Table 2. Numerical values of Skin friction for various physical parameters.

${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	$\mathit{\beta }$	$\mathit{\gamma }$	A	Re	$-{\mathit{Re}}_{\mathit{r}}^{1/2}{\mathit{C}}_{\mathit{f}}$
0.0	0.1	0.1	0.2	0.6	0.4	1.04320
0.1						1.16269
0.2						1.19544
0.1	0.0	0.1	0.2	0.6	0.4	0.58384
	0.1					0.57578
	0.2					0.56811
0.1	0.1	0.0	0.2	0.6	0.4	0.57440
		0.1				0.57718
		0.2				0.57985
0.1	0.1	0.1	0.0	0.6	0.4	0.57310
			0.1			0.57440
			0.2			0.57578
0.1	0.1	0.1	0.2	0.0	0.4	1.21411
				0.1		1.16269
				0.2		1.09544
0.0	0.1	0.1	0.2	0.6	0.0	0.58381
					0.1	0.64578
					0.2	0.76811

Table 3. Numerical values of local Nusselt number for various physical parameters.

${\mathit{R}}_{\mathit{d}}$	Pr	$\mathit{St}$	Q	$\mathit{\gamma }$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	A	$\mathit{\beta }$	${\mathit{Re}}_{\mathit{r}}^{-1/2}{\mathit{Nu}}_{\mathit{r}}$
0.4	1.0	0.3	0.3	0.2	0.1	0.1	0.6	0.1	1.01341
0.7									1.36421
1.0									1.65732
0.3	0.1	0.3	0.3	0.2	0.1	0.1	0.6	0.1	1.41321
	0.5								1.36969
	1.0								1.12294
0.3	1.0	0.0	0.3	0.2	0.1	0.1	0.6	0.1	1.11411
		0.5							1.26969
		1.0							1.39294
0.3	1.0	0.3	0.0	0.2	0.1	0.1	0.6	0.1	1.38941
			0.5						1.62315
			1.0						1.89561
0.3	1.0	0.3	0.3	0.0	0.1	0.1	0.6	0.1	1.12303
				0.1					1.35344
				0.5					1.67423
0.0	1.0	0.3	0.3	0.2	0.0	0.1	0.6	0.1	1.12141
					0.5				1.24922
					1.0				1.41034
0.3	1.0	0.3	0.3	0.2	0.1	0.0	0.6	0.1	1.30312
						0.5			1.32601
						1.0			1.38923
0.3	1.0	0.3	0.3	0.2	0.1	1.0	0.0	0.1	1.12423
							0.5		1.24921
							1.0		1.41235
0.3	1.0	0.3	0.3	0.2	0.1	1.0	0.6	0.0	1.25309
								0.5	1.31985
								1.0	1.51225

Table 4. Numerical values of local Sherwood number for various physical parameters when $A=0.6$ and Re = 0.2.

$\mathit{\gamma }$	$\mathit{St}$	S	$\mathit{Sc}$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	$\mathit{\beta }$	${\mathit{Re}}_{\mathit{r}}^{-1/2}{\mathit{Sh}}_{\mathit{r}}$
0.0	0.3	0.2	1.2	0.1	0.1	0.1	0.98740
0.1							0.92745
0.2							0.90462
0.3	0.0	0.2	1.2	0.1	0.1	0.1	1.98741
	0.1						1.74501
	0.2						1.25019
0.3	0.3	0.0	1.2	0.1	0.1	0.1	1.11523
		0.1					1.32751
		0.2					1.89154
0.3	0.3	0.2	0.0	0.1	0.1	0.1	0.54315
			0.1				0.38612
			0.2				0.18612
0.3	0.3	0.2	1.2	0.0	0.1	0.1	0.81913
				0.1			0.83997
				0.2			0.91251
0.3	0.3	0.2	1.2	0.1	0.0	0.1	1.28712
					0.1		1.59874
					0.2		1.98717
0.3	0.3	0.2	1.2	0.1	0.1	0.0	1.71231
						0.1	1.82127
						0.2	1.92351

6. Concluding Remarks

Here we have considered an axisymmetric stagnation point third grade fluid flow over a radiative stretching surface/cylinder. The stagnation point is discussed in detail. Analysis is scrutinized in the presence of double stratification, heat generation/absorption and Brownian motion. Optimal homotopy method (OHAM) is used for final solutions. Salient features are listed below:

• Due to the effect of temperature, smaller values of stratified parameters results in higher values of velocity and temperature distributions.
• Velocity profile enhances with $\beta$ and $Re.$
• Radiation parameter enhances while ratio parameter reduces the temperature distribution.
• The coefficient of skin friction is higher for higher values of ${\alpha }_1,$ $\beta ,$ $\gamma$ and $Re$.
• An increase in Q and $\gamma$ results in more convenient heat transfer.