Some Identities Involving Hermite Kampé de Fériet Polynomials Arising from Differential Equations and Location of Their Zeros

Abstract

In this paper, we study differential equations arising from the generating functions of Hermit Kamp$\acute{e}$ de F$\acute{e}$riet polynomials. Use this differential equation to give explicit identities for Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials. Finally, use the computer to view the location of the zeros of Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials.

1. Introduction

Numerous studies have been conducted on Bernoulli polynomials, Euler polynomials, tangent polynomials, Hermite polynomials and Laguerre polynomials (see [1,2,3,4,5,6,7,8,9,10,11,12,13]). The special polynomials of the two variables provided a new way to analyze solutions of various kinds of partial differential equations that are often encountered in physical problems. Most of the special function of mathematical physics and their generalization have been proposed as physical problems. For example, we recall that the two variables Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ defined by the generating function (see [2])

$$\sum _{n=0}^{\infty }{H}_n(x,y){\displaystyle \frac{t^n}{n!}}=e^{xt+y{t}^2}=F(t,x,y)$$

(1)

are the solution of heat equation

$${\displaystyle \frac{\partial }{\partial y}}{H}_n(x,y)={\displaystyle \frac{{\partial }^2}{\partial x^2}}{H}_n(x,y),H_n(x,0)=x^n.$$

We note that $H_n(2x,-1)=H_n(x),$ where $H_n(x)$ are the classical Hermite polynomials (see [1]). The differential equation and relation are given by

$$\left(2y{\displaystyle \frac{{\partial }^2}{\partial x^2}}+x{\displaystyle \frac{\partial }{\partial x}}-n\right)H_n(x,y)=0\mathrm{and}{\displaystyle \frac{\partial }{\partial y}}{H}_n(x,y)={\displaystyle \frac{{\partial }^2}{\partial x^2}}{H}_n(x,y),$$

respectively.

By (1) and Cauchy product, we get

$$\begin{array}{ll}{\displaystyle \sum _{n=0}^{\infty }}{H}_n(x_1+x_2,y){\displaystyle \frac{t^n}{n!}}& =e^{(x_1+x_2)t+y{t}^2}\\ & ={\displaystyle \sum _{n=0}^{\infty }}{H}_n(x_1,y){\displaystyle \frac{t^n}{n!}}{\displaystyle \sum _{n=0}^{\infty }}{x}_2^n{\displaystyle \frac{t^n}{n!}}\\ & ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right)H_l(x_1,y)x_2^{n-l}\right){\displaystyle \frac{t^n}{n!}}.\end{array}$$

(2)

By comparing the coefficients on both sides of (2), we have the following theorem:

Theorem 1.

For any positive integer n, we have

$$H_n(x_1+x_2,y)=\sum _{l=0}^n\left(\genfrac{}{}{0pt}{}{n}{l}\right)H_l(x_1,y)x_2^{n-l}.$$

The following elementary properties of the two variables Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ are readily derived from (1).

Theorem 2.

For any positive integer n, we have

$$\begin{array}{l}(1)H_n(x,y_1+y_2)=n!{\displaystyle \sum _{l=0}^{\left[\frac{n}{2}\right]}}{\displaystyle \frac{H_{n-2l}(x,y_1)y_2^l}{l!(n-2l)!}},\\ (2)H_n(x,y)={\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right)H_l(x)H_{n-l}(-x,y+1),\\ (3)H_n(x_1+x_2,y_1+y_2)={\displaystyle \sum _{l=0}^n}\left(\genfrac{}{}{0pt}{}{n}{l}\right)H_l(x_1,y_1)H_{n-l}(x_2,y_2).\end{array}$$

Recently, many mathematicians have studied differential equations that occur in the generating functions of special polynomials (see [8,9,14,15,16]). The paper is organized as follows. We derive the differential equations generated from the generating function of Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials:

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)-a_0(N,x,y)F(t,x,y)-\cdots -a_N(N,x,y)t^{N}F(t,x,y)=0.$$

By obtaining the coefficients of this differential equation, we obtain explicit identities for the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials in Section 2. In Section 3, we investigate the zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials using numerical methods. Finally, we observe the scattering phenomenon of the zeros of Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials.

2. Differential Equations Associated with Hermite Kamp$\acute{\mathit{e}}$ de F$\acute{\mathit{e}}$riet Polynomials

In order to obtain explicit identities for special polynomials, differential equations arising from the generating functions of special polynomials are studied by many authors (see [8,9,14,15,16]). In this section, we introduce differential equations arising from the generating functions of Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials and use these differential equations to obtain the explicit identities for the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials.

Let

$$F=F(t,x,y)=e^{xt+y{t}^2}=\sum _{n=0}^{\infty }{H}_n(x,y){\displaystyle \frac{t^n}{n!}},x,y,t\in \mathbb{C}.$$

(3)

Then, by (3), we have

$$\begin{array}{ll}{F}^{(1)}& ={\displaystyle \frac{\partial }{\partial t}}F(t,x,y)={\displaystyle \frac{\partial }{\partial t}}\left(e^{xt+y{t}^2}\right)=e^{xt+y{t}^2}(x+2yt)\\ & =(x+2yt)F(t,x,y),\end{array}$$

$$\begin{array}{ll}{F}^{(2)}& ={\displaystyle \frac{\partial }{\partial t}}{F}^{(1)}(t,x,y)=2yF(t,x,y)+(x+2yt)F^{(1)}(t,x,y)\\ & =(2y+x^2+(4xy)t+4y^2{t}^2)F(t,x,y),\end{array}$$

and

$$\begin{array}{ll}{F}^{(3)}& ={\displaystyle \frac{\partial }{\partial t}}{F}^{(2)}(t,x,y)\\ & =(4xy+8y^{2}t)F(t,x,y)+(2y+x^2+(4xy)t+4y^2{t}^2)F^{(1)}(t,x,y)\\ & =(6xy+x^3)F^{(2)}(t,x,y)\\ & +(8y^2+4x^{2}y+4y^2+2x^{2}y)tF(t,x,y)\\ & +(4x{y}^2+8x{y}^2)t^{2}F(t,x,y).\end{array}$$

If we continue this process, we can guess as follows:

$$F^{(N)}={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)=\sum _{i=0}^N{a}_i(N,x,y)t^{i}F(t,x,y),(N=0,1,2,\dots ).$$

(4)

Differentiating (4) with respect to t, we have

$$\begin{gathered} \begin{array}{ll}{F}^{(N+1)}& ={\displaystyle \frac{\partial F^{(N)}}{\partial t}}\\ & ={\displaystyle \sum _{i=0}^N}{a}_i(N,x,y)i{t}^{i-1}F(t,x,y)+{\displaystyle \sum _{i=0}^N}{a}_i(N,x,y)t^i{F}^{(1)}(t,x,y)\\ & ={\displaystyle \sum _{i=0}^N}{a}_i(N,x,y)i{t}^{i-1}F(t,x,y)+{\displaystyle \sum _{i=0}^N}{a}_i(N,x,y)t^i(x+2yt)F(t,x,y)\\ & ={\displaystyle \sum _{i=0}^N}i{a}_i(N,x,y)t^{i-1}F(t,x,y)+{\displaystyle \sum _{i=0}^N}x{a}_i(N,x,y)t^{i}F(t,x,y) \\ +{\displaystyle \sum _{i=0}^N}2y{a}_i(N,x,y)t^{i+1}F(t,x,y)\\ & ={\displaystyle \sum _{i=0}^{N-1}}(i+1)a_{i+1}(N,x,y)t^{i}F(t,x,y)+{\displaystyle \sum _{i=0}^N}x{a}_i(N,x,y)t^{i}F(t,x,y) \\ +{\displaystyle \sum _{i=1}^{N+1}}2y{a}_{i-1}(N,x,y)t^{i}F(t,x,y).\end{array} \end{gathered}$$

(5)

Now, replacing N by $N+1$ in (4), we find

$$F^{(N+1)}=\sum _{i=0}^{N+1}{a}_i(N+1,x,y)t^{i}F(t,x,y).$$

(6)

Comparing the coefficients on both sides of (5) and (6), we obtain

$$\begin{array}{l}{a}_0(N+1,x,y)=a_1(N,x,y)+x{a}_0(N,x,y),\\ a_N(N+1,x,y)=x{a}_N(N,x,y)+2y{a}_{N-1}(N,x,y),\\ a_{N+1}(N+1,x,y)=2y{a}_N(N,x,y),\end{array}$$

(7)

and

$$a_i(N+1,x,y)=(i+1)a_{i+1}(N,x,y)+x{a}_i(N,x,y)+2y{a}_{i-1}(N,x,y),(1\le i\le N-1).$$

(8)

In addition, by (4), we have

$$F(t,x,y)=F^{(0)}(t,x,y)=a_0(0,x,y)F(t,x,y),$$

(9)

which gives

$$a_0(0,x,y)=1.$$

(10)

It is not difficult to show that

$$\begin{array}{l}xF(t,x,y)+2ytF(t,x,y)\\ =F^{(1)}(t,x,y)\\ ={\displaystyle \sum _{i=0}^1}{a}_i(1,x,y)F(t,x,y)\\ =a_0(1,x,y)F(t,x,y)+a_1(1,x,y)tF(t,x,y).\end{array}$$

(11)

Thus, by (11), we also find

$$a_0(1,x,y)=x,a_1(1,x,y)=2y.$$

(12)

From (7), we note that

$$\begin{array}{l}{a}_0(N+1,x,y)=a_1(N,x,y)+x{a}_0(N,x,y),\\ a_0(N,x,y)=a_1(N-1,x,y)+x{a}_0(N-1,x,y),\dots \\ a_0(N+1,x,y)={\displaystyle \sum _{i=0}^N}{x}^i{a}_1(N-i,x,y)+x^{N+1},\end{array}$$

(13)

$$\begin{array}{l}{a}_N(N+1,x,y)=x{a}_N(N,x,y)+2y{a}_{N-1}(N,x,y),\\ a_{N-1}(N,x,y)=x{a}_{N-1}(N-1,x,y)+2y{a}_{N-2}(N-1,x,y),\dots \\ a_N(N+1,x,y)=(N+1)x{(2y)}^N,\end{array}$$

(14)

and

$$\begin{array}{l}{a}_{N+1}(N+1,x,y)=2y{a}_N(N,x,y),\\ a_N(N,x,y)=2y{a}_{N-1}(N-1,x,y),\dots \\ a_{N+1}(N+1,x,y)={(2y)}^{N+1}.\end{array}$$

(15)

For $i=1$ in (8), we have

$$a_1(N+1,x,y)=2\sum _{k=0}^N{x}^k{a}_2(N-k,x,y)+(2y)\sum _{k=0}^N{x}^k{a}_0(N-k,x,y).$$

(16)

Continuing this process, we can deduce that, for $1\le i\le N-1,$

$$a_i(N+1,x,y)=(i+1)\sum _{k=0}^N{x}^k{a}_{i+1}(N-k,x,y)+(2y)\sum _{k=0}^N{x}^k{a}_{i-1}(N-k,x,y).$$

(17)

Note that here the matrix $a_i{(j,x,y)}_{0\le i,j\le N+1}$ is given by

$$\left(\begin{array}{cccccc}1& x& 2y+x^2& 6xy+x^3& \cdots & ·\\ 0& 2y& 2x(2y)& ·& \cdots & ·\\ 0& 0& {(2y)}^2& 3x{(2y)}^2& \cdots & ·\\ 0& 0& 0& {(2y)}^3& \ddots & ·\\ ⋮& ⋮& ⋮& ⋮& \ddots & (N+1)x{(2y)}^N\\ 0& 0& 0& 0& \cdots & {(2y)}^{N+1}\end{array}\right).$$

Therefore, we obtain the following theorem.

Theorem 3.

For$N=0,1,2,\dots ,$the differential equation

$$F^{(N)}={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)=\left(\sum _{i=0}^N{a}_i(N,x,y)t^i\right)F(t,x,y)$$

has a solution

$$F=F(t,x,y)=e^{xt+y{t}^2},$$

where

$$\begin{array}{l}{a}_0(N,x,y)={\displaystyle \sum _{k=0}^{N-1}}{x}^i{a}_1(N-1-k,x,y)+x^N,\\ a_{N-1}(N,x,y)=Nx{(2y)}^{N-1},\\ a_N(N,x,y)={(2y)}^N,\\ a_i(N+1,x,y)=(i+1){\displaystyle \sum _{k=0}^N}{x}^k{a}_{i+1}(N-k,x,y)+(2y){\displaystyle \sum _{k=0}^N}{x}^k{a}_{i-1}(N-k,x,y),\\ (1\le i\le N-2).\end{array}$$

Making N-times derivative for (3) with respect to t, we have

$${\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^N{e}^{xt+y{t}^2}=\sum _{m=0}^{\infty }{H}_{m+N}(x,y){\displaystyle \frac{t^m}{m!}}.$$

(18)

By Cauchy product and multiplying the exponential series $e^{xt}=\sum _{m=0}^{\infty }{x}^m{\displaystyle \frac{t^m}{m!}}$ in both sides of (18), we get

$$\begin{array}{ll}{e}^{-nt}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)& =\left({\displaystyle \sum _{m=0}^{\infty }}{(-n)}^m{\displaystyle \frac{t^m}{m!}}\right)\left({\displaystyle \sum _{m=0}^{\infty }}{H}_{m+N}(x,y){\displaystyle \frac{t^m}{m!}}\right)\\ & ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{k=0}^m}\left(\genfrac{}{}{0pt}{}{m}{k}\right){(-n)}^{m-k}{H}_{N+k}(x,y)\right){\displaystyle \frac{t^m}{m!}}.\end{array}$$

(19)

For non-negative integer m, assume that $\left\{a(m)\right\},\left\{b(m)\right\},\left\{c(m)\right\},\left\{\overline{c}(m)\right\}$ are four sequences given by

$$\sum _{m=0}^{\infty }a(m){\displaystyle \frac{t^n}{m!}},\sum _{m=0}^{\infty }b(m){\displaystyle \frac{t^m}{m!}},\sum _{m=0}^{\infty }c(m){\displaystyle \frac{t^m}{m!}},\sum _{m=0}^{\infty }\overline{c}(m){\displaystyle \frac{t^m}{m!}}.$$

If $\sum _{m=0}^{\infty }c(m){\displaystyle \frac{t^m}{m!}}\times \sum _{m=0}^{\infty }\overline{c}(m){\displaystyle \frac{t^m}{m!}}=1,$ we have the following inverse relation:

$$a(m)=\sum _{k=0}^m\left(\genfrac{}{}{0pt}{}{m}{k}\right)c(k)b(m-k)⟺b(m)=\sum _{k=0}^m\left(\genfrac{}{}{0pt}{}{m}{k}\right)\overline{c}(k)a(m-k).$$

(20)

By (20) and the Leibniz rule, we have

$$\begin{array}{l}{e}^{-nt}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)\\ ={\displaystyle \sum _{k=0}^N}\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^k\left(e^{-nt}F(t,x,y)\right)\\ ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{k=0}^N}\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{H}_{m+k}(x-n,y)\right){\displaystyle \frac{t^m}{m!}}.\end{array}$$

(21)

Hence, by (19) and (21), and comparing the coefficients of ${\displaystyle \frac{t^m}{m!}}$ gives the following theorem.

Theorem 4.

Let $m,n,N$ be nonnegative integers. Then,

$$\sum _{k=0}^m\left(\genfrac{}{}{0pt}{}{m}{k}\right){(-n)}^{m-k}{H}_{N+k}(x,y)=\sum _{k=0}^N\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{H}_{m+k}(x-n,y).$$

(22)

If we take $m=0$ in (22), then we have the following:

Corollary 1.

For $N=0,1,2,\dots ,$ we have

$$H_N(x,y)=\sum _{k=0}^N\left(\genfrac{}{}{0pt}{}{N}{k}\right)n^{N-k}{H}_k(x-n,y).$$

For $N=0,1,2,\dots ,$ the differential equation

$$F^{(N)}={\left({\displaystyle \frac{\partial }{\partial t}}\right)}^{N}F(t,x,y)=\left(\sum _{i=0}^N{a}_i(N,x,y)t^i\right)F(t,x,y)$$

has a solution

$$F=F(t,x,y)=e^{xt+y{t}^2}.$$

Here is a plot of the surface for this solution.

In Figure 1 (left), we choose $-3\le x\le 3,-1\le t\le 1,$ and $y=3$. In Figure 1 (right), we choose $-3\le x\le 3,-1\le t\le 1,$ and $y=-3$.

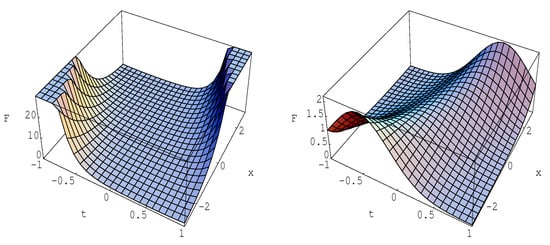
Figure 1. The surface for the solution $F(t,x,y)$.

3. Zeros of the Hermite Kamp$\acute{\mathit{e}}$ de F$\acute{\mathit{e}}$riet Polynomials

By using software programs, many mathematicians can explore concepts more easily than in the past. These experiments allow mathematicians to quickly create and visualize new ideas, review properties of figures, create many problems, and find and guess patterns. This numerical survey is particularly interesting because it helps many mathematicians understand basic concepts and solve problems. In this section, we examine the distribution and pattern of zeros of Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ according to the change of degree n. Based on these results, we present a problem that needs to be approached theoretically.

By using a computer, the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ can be determined explicitly. First, a few examples of them are as follows:

$$\begin{array}{l}{H}_0(x,y)=1,\\ H_1(x,y)=x,\\ H_2(x,y)=x^2+2y,\\ H_3(x,y)=x^3+6xy,\\ H_4(x,y)=x^4+12x^{2}y+12y^2,\\ H_5(x,y)=x^5+20x^{3}y+60x{y}^2,\\ H_6(x,y)=x^6+30x^{4}y+180x^2{y}^2+120y^3,\\ H_7(x,y)=x^7+42x^{5}y+420x^3{y}^2+840x{y}^3,\\ H_8(x,y)=x^8+56x^{6}y+840x^4{y}^2+3360x^2{y}^3+1680y^4,\\ H_9(x,y)=x^9+72x^{7}y+1512x^5{y}^2+10,080x^3{y}^3+15,120x{y}^4,\\ H_{10}(x,y)=x^{10}+90x^{8}y+2520x^6{y}^2+25,200x^4{y}^3+75,600x^2{y}^4+30,240y^5.\end{array}$$

Using a computer, we investigate the distribution of zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$.

Plots the zeros of the polynomial $H_n(x,y)$ for $n=20,y=2,-2,2+i,-2+i$ and $x\in \mathbb{C}$ are as follows (Figure 1). In Figure 2 (top-left), we choose $n=20$ and $y=2$. In Figure 2 (top-right), we choose $n=20$ and $y=-2$. In Figure 2 (bottom-left), we choose $n=20$ and $y=2+i$. In Figure 2 (bottom-right), we choose $n=20$ and $y=-2-i$.

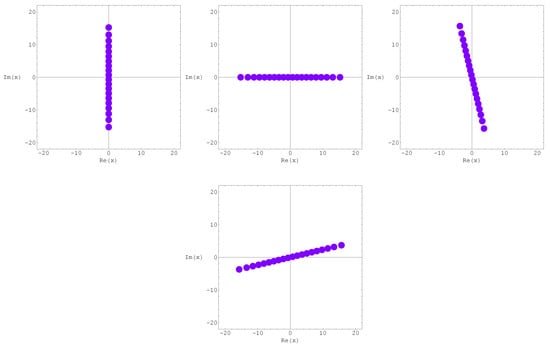
Figure 2. Zeros of $H_n(x,y)$.

Stacks of zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ for $1\le n\le 20$ from a 3D structure are presented (Figure 3). In Figure 3 (top-left), we choose $y=2$. In Figure 3 (top-right), we choose $y=-2$. In Figure 3 (bottom-left), we choose $y=2+i$. In Figure 3 (bottom-right), we choose $y=-2-i$. Our numerical results for approximate solutions of real zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ are displayed (Table 1,Table 2,Table 3).

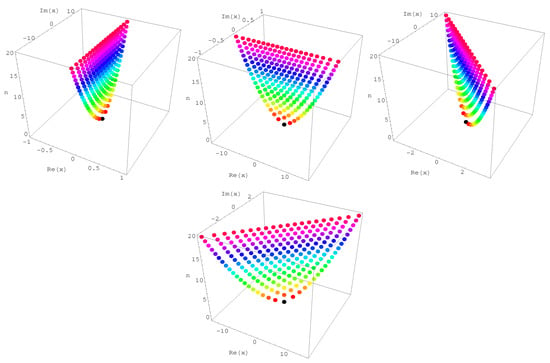
Figure 3. Stacks of zeros of $H_n(x,y),1\le n\le 20$.

Table 1. Numbers of real and complex zeros of $H_n(x,-2)$.

Degree n	Real Zeros	Complex Zeros
1	1	0
2	2	0
3	3	0
4	4	0
5	5	0
6	6	0
7	7	0
8	8	0
9	9	0
10	10	0
11	11	0
12	12	0
13	13	0
14	14	0
⋮	⋮	⋮
29	29	0
30	30	0

Table 2. Numbers of real and complex zeros of $H_n(x,2)$.

Degree n	Real Zeros	Complex Zeros
1	0	1
2	0	2
3	0	3
4	0	4
5	0	5
6	0	6
7	0	7
8	0	8
9	0	9
10	0	10
11	0	11
12	0	12
13	0	13
14	0	14
⋮	⋮	⋮
29	0	29
30	0	30

Table 3. Approximate solutions of $H_n(x,-2)=0,x\in \mathbb{R}$.

Degree n	x
1	0
2	−2.0000, 2.0000
3	−3.4641, 0, 3.4641
4	−4.669, −1.4839, 1.4839, 4.669
5	−5.714, −2.711, 0, 2.711, 5.714
6	−6.65, −3.778, −1.233, 1.233, 3.778, 6.65
7	−7.50, −4.73, −2.309, 0, 2.309, 4.73, 7.50
8	−8.3, −5.6, −3.27, −1.078, 1.078, 3.27, 5.6, 8.3

The plot of real zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ for $1\le n\le 20$ structure are presented (Figure 4). It is expected that $H_n(x,y),x\in \mathbb{C},y>0$, has $Im(x)=0$ reflection symmetry analytic complex functions (see Figure 2 and Figure 3). We also expect that $H_n(x,y),x\in \mathbb{C},y<0$, has $Re(x)=0$ reflection symmetry analytic complex functions (see Figure 2, Figure 3 and Figure 4). We observe a remarkable regular structure of the complex roots of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ for $y<0$. We also hope to verify a remarkable regular structure of the complex roots of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$ for $y<0$ (Table 1). Next, we calculated an approximate solution that satisfies $H_n(x,y)=0,x\in \mathbb{C}$. The results are shown in Table 3.

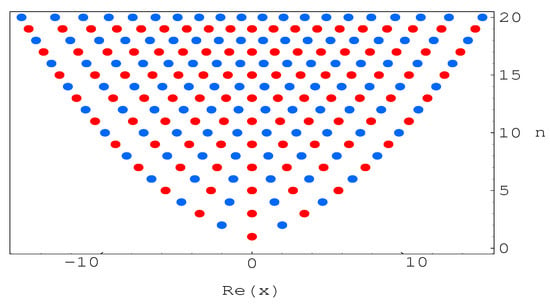
Figure 4. Real zeros of $H_n(x,-2)for1\le n\le 20$.

4. Conclusions and Future Developments

This study obtained the explicit identities for Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials $H_n(x,y)$. The location and symmetry of the roots of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials were investigated. We examined the symmetry of the zeros of the Hermite Kamp$\acute{e}$ de F$\acute{e}$riet polynomials for various variables x and y, but, unfortunately, we could not find a regular pattern. However, the following special cases showed regularity. Through numerical experiments, we will make the following series of conjectures.

If $y>0$, we can see that $H_n(x,y)$ has $Re(x)=0$ reflection symmetry. Therefore, the following conjecture is possible.

Conjecture 1.

Prove or disprove that$H(x,y),x\in \mathbb{C}$and$y>0,$has$Im(x)=0$reflection symmetry analytic complex functions. Furthermore,$H_n(x,y)$has$Re(x)=0$reflection symmetry for$y<0$.

As a result of investigating more n variables, it is still unknown whether the conjecture is true or false for all variables n (see Figure 1).

Conjecture 2.

Prove or disprove that $H_n(x,y)=0$ has n distinct solutions.

Let’s use the following notations. $R_{H_n(x,y)}$ denotes the number of real zeros of $H_n(x,y)$ lying on the real plane $Im(x)=0$ and $C_{H_n(x,y)}$ denotes the number of complex zeros of $H_n(x,y)$. Since n is the degree of the polynomial $H_n(x,y)$, we have $R_{H_n(x,y)}=n-C_{H_n(x,y)}$ (see Table 1 and Table 2).

Conjecture 3.

Prove or disprove that

$$R_{H_n(x,y)}=\left\{\begin{array}{ll}n,\hfill & ify<0,\hfill \\ 0,\hfill & ify>0,\hfill \end{array}\right.$$

$$C_{H_n(x,y)}=\left\{\begin{array}{ll}0,\hfill & ify<0,\hfill \\ n,\hfill & ify>0.\hfill \end{array}\right.$$