A Time-Non-Homogeneous Double-Ended Queue with Failures and Repairs and Its Continuous Approximation

Abstract

We consider a time-non-homogeneous double-ended queue subject to catastrophes and repairs. The catastrophes occur according to a non-homogeneous Poisson process and lead the system into a state of failure. Instantaneously, the system is put under repair, such that repair time is governed by a time-varying intensity function. We analyze the transient and the asymptotic behavior of the queueing system. Moreover, we derive a heavy-traffic approximation that allows approximating the state of the systems by a time-non-homogeneous Wiener process subject to jumps to a spurious state (due to catastrophes) and random returns to the zero state (due to repairs). Special attention is devoted to the case of periodic catastrophe and repair intensity functions. The first-passage-time problem through constant levels is also treated both for the queueing model and the approximating diffusion process. Finally, the goodness of the diffusive approximating procedure is discussed.

1. Introduction

Double-ended queues are often adopted as stochastic models for queueing systems characterized by two flows of agents, i.e., customers and servers/resources. When there are a customer and a server in the system, the match between the request and service occurs immediately, and then, both agents leave the system. As a consequence, there cannot be simultaneously customers and servers in the system. Namely, denoting by $N(t)$ the state of the system at time t, it is assumed that $N(t)=n$, $n\in \mathbb{N}$, if there are n customers waiting for available servers, whereas $N(t)=-n$, $n\in \mathbb{N}$, if there are n servers waiting for new customers, and $N(t)=0$, if the system is empty. Hence, typical models for $N(t)$ are bilateral continuous-time Markov chains or similar stochastic processes.

Double-ended queueing systems can be applied to model numerous situations in real-world scenarios. A classical example is provided by taxi-passenger systems, where the role of customers and servers is played by passengers and taxis, respectively. We recall the first papers on this topic by Kashyap [1,2] and the subsequent contributions by Sharma and Nair [3], Tarabia [4] and Conolly et al. [5]. Other examples are provided by the dynamical allocation of live organs (servers) to candidates (customers) needing transplantation (cf. Elalouf et al. [6] and the references therein). Double-ended queues are suitable also to describe different streams arriving at a system (see Takahashi et al. [7]).

In this area, the interest is typically in the determination of the transient distribution and the asymptotic distribution of the system state, the busy period density, the waiting time density and related indices such as means and variances. The difficulties related to the resolution of the birth-death processes describing the length of the queue, in some cases, can be overcome by means of suitable transformations as those presented in Di Crescenzo et al. [8]. Such a transformation-based approach has been successfully exploited also for diffusion processes (see Di Crescenzo et al. [9]), this being of interest for the analysis of customary diffusion approximations of queue-length processes.

Attention is given often also to variants of the relevant stochastic processes that are adopted to describe more complex situations, such as bulk arrivals, truncated queues, the occurrence of disasters and repairs, and so on. In this respect, we recall the recent paper by Di Crescenzo et al. [10], which is centered on the analysis (i) of a continuous-time stochastic process describing the state of a double-ended queue subject to disasters and repairs and (ii) of the Wiener process with jumps arising as a heavy-traffic approximation to the previous model.

In many queueing models of manufacturing systems, it is assumed that the times to failure and the times to repair of each machine are exponentially distributed. However, exponential distributions do not always accurately represent distributions encountered in real manufacturing systems. Some of these models adopt the phase-type distributions for failure and repair times (see, for instance, Altiok [11,12,13] and Dallery [14]).

In this paper, we propose and analyze an extension of the queueing model treated in [10] to a time-non-homogeneous setting in which the intensities of arrivals, services, disasters and repairs are suitably time dependent. Similarly, we investigate the related heavy-traffic jump-diffusion approximation, as well. The key features of our analysis and the motivations of the proposed study are based mainly on the following issues:

• Queueing systems subject to disasters are appropriate to model more realistic situations in which the number of customers is subject to an abrupt decrease by the effect of catastrophes occurring randomly in time and due to external causes. The literature on the area of stochastic systems evolving in the presence of catastrophes is very broad. We restrict ourselves to mentioning the papers by Economou and Fakinos [15,16], Kyriakidis and Dimitrakos [17], Krishna Kumar et al. [18], Di Crescenzo et al. [19], Zeifman and Korotysheva [20], Zeifman et al. [21] and Giorno et al. [22]. The analysis of some time-dependent queueing models with catastrophes has been performed in Di Crescenzo et al. [23] and, more recently, in Giorno et al. [24], with special attention to the $M(t)/M(t)/1$ and $M(t)/M(t)/\infty$ queues.
• We include a repair mechanism in the queueing system under investigation, since it is essential to model instances when the (random) repair times are not negligible. We remark that the interest in this feature is increasing in the recent literature on queueing theory (see, for instance, Dimou and Economou [25]).
• Heavy-traffic approximations are very often proposed in order to describe the queueing systems under proper limit conditions of the parameters involved. This allows one to come to more manageable formulas for the description of the queue content. Typically, a customary rescaling procedure allows one to approximate the queue length process by a diffusion process, as indicated in Giorno et al. [26]. Examples of diffusion models arising from heavy-traffic approximations of double-ended queues and of similar matching systems can be found in Liu et al. [27] and Büke and Chen [28], respectively. In the case of queueing systems subject to catastrophes, a customary approach leads to jump-diffusion approximating processes (see, for instance, Di Crescenzo et al. [29] and Dharmaraja et al. [30]).

Plan of the Paper

In Section 2, we consider a non-homogeneous double-ended queue, whose arrivals and departures occur with time-varying intensity functions $\lambda (t)>0$ and $\mu (t)>0$, respectively. We discuss various features of such a model, including the first-passage time through a constant level.

In Section 3, we consider the non-homogeneous double-ended queue subject to disasters and repairs, both occurring with time-varying rates. Specifically, we assume that catastrophes occur according to a non-homogeneous Poisson process with intensity function $\nu (t)>0$. The effect of catastrophes moves the system into a spurious failure state, say F. The completion of a system’s repair occurs with time-varying intensity function $\eta (t)>0$. After any repair, the system starts afresh from the zero state. Our first aim is to determine the probability $q(t|t_0)$ that the system at time t is in the failure state and the probability $p_{0,n}(t|t_0)$ that the system at time t is in the state $n\in \mathbb{Z}$ (working state).

In Section 4, we study the asymptotic behavior of the state probabilities in two different cases: (i) when the rates $\lambda (t)$, $\mu (t)$, $\nu (t)$, $\eta (t)$ admit finite positive limits as t tends to infinity and (ii) when the double-ended queue is time-homogeneous, the catastrophe intensity function $\nu (t)$ and the repair intensity function $\eta (t)$ being periodic functions with common period Q.

In Section 5, we consider a diffusion approximation, under a heavy-traffic regime, of the non-homogeneous double-ended queue discussed in Section 2. In this case, the approximating process is a time-non-homogeneous Wiener process. We discuss various results on this model, including a first-passage-time problem through a constant level.

In Section 6, we deal with the heavy-traffic jump-diffusion approximation for the discrete model with catastrophes and repairs. Various results shown for the basic diffusion process treated in the previous section are thus extended to the present case characterized by jumps. In both Section 5 and Section 6, the goodness of the approximating procedure is discussed, as well.

In Section 7, we finally consider the asymptotic behavior of the densities in the same cases considered in Section 4. In conclusion, we perform some comparisons between the relevant quantities of the queueing system and of the approximating diffusion process under the heavy-traffic regime.

2. The Underlying Non-Homogeneous Double-Ended Queue

This section is devoted to the analysis of the basic time-non-homogeneous double-ended queue.

Let $\{\tilde{N}(t),t\ge t_0\}$, with $t_0\ge 0$, be a continuous-time Markov chain describing the number of customers in a time-non-homogeneous double-ended queueing system, with state-space $\mathbb{Z}=\{\dots ,-1,0,1,\dots \}$. We assume that arrivals (upward jumps) and departures (downward jumps) at time t occur with intensity functions $\lambda (t)>0$ and $\mu (t)>0$, respectively, where $\lambda (t)$ and $\mu (t)$ are bounded and continuous functions for $t\ge t_0$, such that ${\int }_{t_0}^{+\infty }\lambda (t)dt=+\infty$ and ${\int }_{t_0}^{+\infty }\mu (t)dt=+\infty$. The given assumptions ensure that the eventual transitions from any state occur w.p. 1. The state diagram of $\tilde{N}(t)$ is shown in Figure 1.

Figure 1. State diagram of the non-homogeneous double-ended queueing system.

For all $j,n\in \mathbb{Z}$ and $t>t_0\ge 0$, the transition probabilities ${\tilde{p}}_{j,n}(t|t_0)=P\{\tilde{N}(t)=n|\tilde{N}(t_0)=j\}$ are solutions of the system of Kolmogorov forward equations:

$$\frac{d{\tilde{p}}_{j,n}(t|t_0)}{dt}=\lambda (t){\tilde{p}}_{j,n-1}(t|t_0)-[\lambda (t)+\mu (t)]{\tilde{p}}_{j,n}(t|t_0)+\mu (t){\tilde{p}}_{j,n+1}(t|t_0),j,n\in \mathbb{Z},$$

(1)

with the initial condition ${lim}_{t\downarrow t_0}{\tilde{p}}_{j,n}(t|t_0)={\delta }_{j,n}$, where ${\delta }_{j,n}$ is the Kronecker delta function. For $t\ge t_0$ and $0\le z\le 1$, let:

$${\tilde{G}}_j(z,t|t_0)=\mathrm{E}\left[z^{\tilde{N}(t)}|\tilde{N}(t_0)=j\right]=\sum _{n=-\infty }^{+\infty }{z}^n{\tilde{p}}_{j,n}(t|t_0),j\in \mathbb{Z}$$

(2)

be the probability generating function of $\tilde{N}(t)$. For any $t\ge t_0$, we denote the cumulative arrival and service intensity functions by:

$$\Lambda (t|t_0)={\int }_{t_0}^t\lambda (\tau )d\tau ,M(t|t_0)={\int }_{t_0}^t\mu (\tau )d\tau .$$

(3)

Due to (1), for $t\ge t_0$, the probability generating Function (2) is the solution of the partial differential equation:

$$\frac{\partial }{\partial t}{\tilde{G}}_j(z,t|t_0)=\left\{-[\lambda (t)+\mu (t)]+\lambda (t)z+\frac{\mu (t)}{z}\right\}{\tilde{G}}_j(z,t|t_0),j\in \mathbb{Z}$$

to be solved with the initial condition ${lim}_{t\downarrow t_0}{\tilde{G}}_j(z,t|t_0)=z^j$. Hence, (2) can be expressed in terms of (3) as follows:

$${\tilde{G}}_j(z,t|t_0)=z^{j}exp\left\{-\left[\Lambda (t|t_0)+M(t|t_0)\right]+\Lambda (t|t_0)z+\frac{M(t|t_0)}{z}\right\},j\in \mathbb{Z}.$$

(4)

Recalling that (cf. Abramowitz [31], p. 376, n. 9.6.33):

$$exp\left\{\frac{s}{2}\left(r+\frac{1}{r}\right)\right\}=\sum _{n=-\infty }^{+\infty }{r}^n{I}_n(s)(r\ne 0),$$

(5)

where:

$$I_{\nu }(z)=\sum _{m=0}^{\infty }\frac{{(z/2)}^{\nu +2m}}{m!\Gamma (\nu +m+1)}(\nu \in \mathbb{R})$$

denotes the modified Bessel function of first kind and by setting:

$$s=2\sqrt{\Lambda (t|t_0)M(t|t_0)},r=z\sqrt{\frac{\Lambda (t|t_0)}{M(t|t_0)}}$$

in (5), from (4), one has:

$${\tilde{G}}_j(z,t|t_0)=e^{-\left[\Lambda (t|t_0)+M(t|t_0)\right]}\sum _{k=-\infty }^{+\infty }{z}^{j+k}{\left[\frac{\Lambda (t|t_0)}{M(t|t_0)}\right]}^{k/2}{I}_k\left[2\sqrt{\Lambda (t|t_0)M(t|t_0)}\right],j\in \mathbb{Z}.$$

Hence, recalling (2), one obtains the transition probabilities:

$${\tilde{p}}_{j,n}(t|t_0)=e^{-\left[\Lambda (t|t_0)+M(t|t_0)\right]}{\left[\frac{\Lambda (t|t_0)}{M(t|t_0)}\right]}^{(n-j)/2}{I}_{n-j}\left[2\sqrt{\Lambda (t|t_0)M(t|t_0)}\right],j,n\in \mathbb{Z}.$$

(6)

We remark that, since $I_n(z)=I_{-n}(z)$ for $n\in \mathbb{N}$, the following symmetry relation holds:

$${\tilde{p}}_{j,n}(t|t_0)={\left[\frac{\Lambda (t|t_0)}{M(t|t_0)}\right]}^{n-j}{\tilde{p}}_{j,2j-n}(t|t_0)j,n\in \mathbb{Z}.$$

Moreover, from (6), we recover the conditional mean and variance of $\tilde{N}(t)$, for $t\ge t_0$ and $j\in \mathbb{Z}$:

$$\mathrm{E}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j]=j+\Lambda (t|t_0)-M(t|t_0),\mathrm{Var}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j]=\Lambda (t|t_0)+M(t|t_0).$$

(7)

We point out that the transition probabilities given in (6) constitute the probability distribution of the difference of two independent non-homogeneous Poisson processes with intensities $\lambda (t)$ and $\mu (t)$, respectively, originated at zero (cf. Irwin [32] or Skellam [33] for the homogeneous case).

Let us now consider the first-passage-time (FPT) of $\tilde{N}(t)$ through the state $n\in \mathbb{Z}$, starting from the initial state $j\in \mathbb{Z}$. Such a random variable will be denoted as:

$${\tilde{\mathcal{T}}}_{j,n}(t_0)=inf\{t\ge t_0:\tilde{N}(t)=n\},\tilde{N}(t_0)=j,j\ne n,$$

where ${\tilde{g}}_{j,n}(t|t_0)$ is its probability density function (pdf). Special interest is given to ${\tilde{\mathcal{T}}}_{j,0}(t_0)$, which represents the busy period of the double-ended queue, with initial state $\tilde{N}(t_0)=j$. As is well-known, due to the Markov property, ${\tilde{g}}_{j,n}(t|t_0)$ satisfies the integral equation:

$${\tilde{p}}_{j,n}(t|t_0)={\int }_{t_0}^t{\tilde{g}}_{j,n}(\tau |t_0){\tilde{p}}_{n,n}(t|\tau )d\tau ,j,n\in \mathbb{Z},j\ne n.$$

(8)

Hereafter, we consider the special case in which the arrival and departure intensity functions are proportional.

Remark 1.

Let $\lambda (t)=\lambda \phi (t)$ and $\mu (t)=\mu \phi (t)$, with $\lambda ,\mu$ positive constants, where $\phi (t)$ is a positive, bounded and continuous function of $t\ge t_0$, such that ${\int }_{t_0}^{\infty }\phi (t)dt=+\infty$. By setting $\varrho =\lambda /\mu$ and:

$$\Phi (t|t_0)={\int }_{t_0}^t\phi (\tau )d\tau ,t\ge t_0,$$

(9)

then the transition probabilities (6) of the non-homogeneous double-ended queueing system $\tilde{N}(t)$ can be expressed as:

$${\tilde{p}}_{j,n}(t|t_0)=e^{-(\lambda +\mu )\Phi (t|t_0)}{\varrho }^{(n-j)/2}{I}_{n-j}\left[2\lambda \mu \Phi (t|t_0)\right],j,n\in \mathbb{Z}.$$

(10)

Hence, from the results given in Section 5 of Giorno et al. [24], we have:

$${\tilde{g}}_{j,n}(t|t_0)=\frac{|n-j|\phi (t)}{\Phi (t|t_0)}{\tilde{p}}_{j,n}(t|t_0),j,n\in \mathbb{Z},j\ne n.$$

(11)

Furthermore, the FPT ultimate probability is given by:

$$P\{{\tilde{\mathcal{T}}}_{j,n}(t_0)<+\infty \}={\int }_{t_0}^{+\infty }{\tilde{g}}_{j,n}(t|t_0)dt=\left\{\begin{array}{cc}1,\hfill & (\lambda -\mu )(n-j)\ge 0,\hfill \\ {\displaystyle {\varrho }^{n-j},}\hfill & (\lambda -\mu )(n-j)<0.\hfill \end{array}\right.$$

3. The Queueing System with Catastrophes and Repairs

This section deals with the analysis of the queueing system with catastrophes and repairs.

Let $\{N(t),t\ge t_0\}$, with $t_0\ge 0$, be a continuous-time Markov chain that describes the number of customers of a time-non-homogeneous double-ended queueing system subject to disasters and repairs. The state-space of $\{N(t),t\ge t_0\}$ is denoted by $S=\{F\}\cup \mathbb{Z}=\{F,0,\pm 1,\pm 2,\dots \}$, where F denotes the failure state. We assume that the catastrophes occur according to a non-homogeneous Poisson process with intensity function $\nu (t)$. If a catastrophe occurs, then the system goes instantaneously into the failure state F, and further, the completion of a repair occurs according to the intensity function $\eta (t)$ (cf. the diagram shown in Figure 2). We assume that the rates $\nu (t)$ and $\eta (t)$ are positive, bounded and continuous functions for $t\ge t_0$, such that ${\int }_{t_0}^{\infty }\nu (t)dt=+\infty$ and ${\int }_{t_0}^{\infty }\eta (t)dt=+\infty$. After every repair, the system starts again from the zero state.

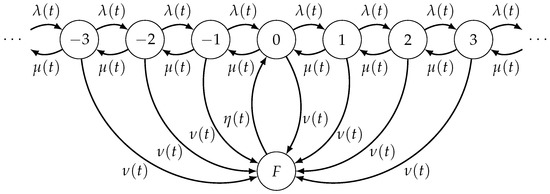
Figure 2. State diagram of the time-non-homogeneous double-ended queueing system with catastrophes and repairs.

For any $n\in \mathbb{Z}$ and $t>t_0\ge 0$, we set:

$$p_{0,n}(t|t_0)=P\{N(t)=n|N(t_0)=0\},q(t|t_0)=P\{N(t)=F|N(t_0)=0\}.$$

(12)

Hence, $p_{0,n}(t|t_0)$ is the transition probability from zero, at time $t_0$, to state n, at time t, when the system is active (in this case, we say that the system is in the “on” state), whereas $q(t|t_0)$ is the probability that the queueing system is in the state F (called the “failure” state) at time t starting from zero at time $t_0$. The probabilities given in (12) are the solution of the forward Kolmogorov system of differential equations:

$$\begin{array}{c}\frac{dq(t|t_0)}{dt}=-\eta (t)q(t|t_0)+\nu (t)[1-q(t|t_0)],\hfill \end{array}$$

(13)

$$\begin{array}{c}\frac{d{p}_{0,0}(t|t_0)}{dt}=-[\lambda (t)+\mu (t)+\nu (t)]p_{0,0}(t|t_0)+\lambda (t)p_{0,-1}(t|t_0)+\mu (t)p_{0,1}(t|t_0)+\eta (t)q(t|t_0),\hfill \end{array}$$

(14)

$$\begin{array}{c}\frac{d{p}_{0,n}(t|t_0)}{dt}=-[\lambda (t)+\mu (t)+\nu (t)]p_{0,n}(t|t_0)+\lambda (t)p_{0,n-1}(t|t_0)+\mu (t)p_{0,n+1}(t|t_0),n\in \mathbb{Z}\setminus \{0\},\hfill \end{array}$$

(15)

to be solved with the following initial conditions, based on the Kronecker delta function:

$$\underset{t\downarrow t_0}{lim}{p}_{n,0}(t|t_0)={\delta }_{n,0},\underset{t\downarrow t_0}{lim}q(t|t_0)=0.$$

(16)

Conditions (16) imply that at initial time $t_0$, the system is active and it starts from the zero state. In order to determine the transient probabilities of $N(t)$, similarly as in (3), in the following, we denote the cumulative catastrophe and repair intensity functions by:

$$V(t|t_0)={\int }_{t_0}^t\nu (\tau )d\tau ,H(t|t_0)={\int }_{t_0}^t\eta (\tau )d\tau ,t\ge t_0,$$

(17)

respectively.

Transient Probabilities

We first determine the probability that the system is under repair at time t. By solving Equation (13) with the second of the initial conditions (16), recalling (17), one obtains the probability that the process $N(t)$ is in the state F (“failure” state) at time t, starting from zero at time $t_0$:

$$q(t|t_0)={\int }_{t_0}^t\nu (\tau )e^{-[V(t|\tau )+H(t|\tau )]}d\tau ,t\ge t_0.$$

(18)

The transient analysis of the process $N(t)$ can be performed by relating the transient probabilities to those of the same process in the absence of catastrophes. Indeed, by conditioning on the time of the last catastrophe of $N(t)$ before t, the probabilities $p_{0,n}(t|t_0)$ can be expressed in terms of ${\tilde{p}}_{0,n}(t|t_0)$ as follows, for $n\in \mathbb{Z}$ and $t\ge t_0$ (cf. [10,15,16]):

$$p_{0,n}(t|t_0)=e^{-V(t|t_0)}{\tilde{p}}_{0,n}(t|t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}{\tilde{p}}_{0,n}(t|\tau )d\tau .$$

(19)

We note that the first term on the right-hand side of (19) expresses the probability that process $N(t)$ occupies state n at time t and that no catastrophes occurred in $[0,t]$. Similarly, the second term gives the probability that process $N(t)$ occupies state n at time t and that at least one catastrophe (with successive repair) occurred in $[0,t]$, i.e.,

-

starting from zero at time $t_0$, at least a catastrophe and the subsequent repair occur before t; let $\tau \in (0,t)$ be the instant at which the last repair occurs, so that a transition entering in the zero state occurs at time $\tau$ with intensity $\eta (\tau )$;

-

no catastrophe occurs in the interval $(\tau ,t)$; then the system, starting from the zero state at time $\tau$, reaches the state n at time t.

Note that Equation (19) is the suitable extension of (2.7) of [10], which refers to the case of constant rates. Furthermore, we remark that from (18) and (19), one obtains:

$$\sum _{n=-\infty }^{+\infty }{p}_{0,n}(t|t_0)+q(t|t_0)=1,t\ge t_0.$$

(20)

Making use of (6) and (18) in (19), for $t\ge t_0$ and $n\in \mathbb{Z}$, one has the following expression for the transition probabilities of $N(t)$:

$$\begin{array}{c}{p}_{0,n}(t|t_0)=e^{-[\Lambda (t|t_0)+M(t|t_0)+V(t|t_0)]}{\left[\frac{\Lambda (t|t_0)}{M(t|t_0)}\right]}^{n/2}{I}_n\left[2\sqrt{\Lambda (t|t_0)M(t|t_0)}\right]\hfill \\ +{\int }_{t_0}^{t}d\tau \eta (\tau )e^{-[\Lambda (t|\tau )+M(t|\tau )+V(t|\tau )]}{\left[\frac{\Lambda (t|\tau )}{M(t|\tau )}\right]}^{n/2}{I}_n\left[2\sqrt{\Lambda (t|\tau )M(t|\tau )}\right]{\int }_{t_0}^{\tau }\nu (\vartheta )e^{-[V(\tau |\vartheta )+H(\tau |\vartheta )]}d\vartheta .\hfill \end{array}$$

Let us now introduce the r-th conditional moment of $N(t)$, for $r\in \mathbb{N}$:

$${\mathcal{M}}_r(t|t_0):=\mathrm{E}\left[N^r(t)\right|N(t)\in \mathbb{Z},N(t_0)=0]=\frac{1}{1-q(t|t_0)}\sum _{n=-\infty }^{+\infty }{n}^r{p}_{0,n}(t|t_0).$$

(21)

From (19), it is not hard to see that the moments (21) can be expressed in terms of the conditional moments ${\tilde{\mathcal{M}}}_r(t|t_0):=\mathrm{E}\left[{\tilde{N}}^r(t)\right|\tilde{N}(t_0)=0]$ as follows, for $r\in \mathbb{N}$ and $t\ge t_0$:

$${\mathcal{M}}_r(t|t_0)=\frac{1}{1-q(t|t_0)}\left\{e^{-V(t|t_0)}{\tilde{\mathcal{M}}}_r(t|t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}{\tilde{\mathcal{M}}}_r(t|\tau )d\tau \right\}.$$

(22)

Hence, by virtue of (7), from (22), the conditional mean and second order moment of $N(t)$ can be evaluated based on the knowledge of the relevant intensity functions.

Hereafter, we see that if the arrival and departure rates are constant, then some simplifications hold for the transition probabilities and conditional moments.

Theorem 1.

For the queueing system with catastrophes and repairs, having constant arrival rates $\lambda (t)=\lambda$ and departure rates $\mu (t)=\mu$, for $t\ge t_0$ and $n\in \mathbb{Z}$, one has:

$$p_{0,n}(t|t_0)=e^{-V(t|t_0)}{\tilde{p}}_{0,n}(t-t_0|0)+{\int }_0^{t-t_0}dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}{\tilde{p}}_{0,n}(u|0)du$$

(23)

and, for $r\in \mathbb{N}$,

$${\mathcal{M}}_r(t|t_0)=\frac{1}{1-q(t|t_0)}\left\{e^{-V(t|t_0)}{\tilde{\mathcal{M}}}_r(t-t_0|0)+{\int }_0^{t-t_0}q(t-x|t_0)\eta (t-x)e^{-V(t|t-x)}{\tilde{\mathcal{M}}}_r(x|0)dx\right\}.$$

(24)

Furthermore, it results:

$$\begin{array}{c}{p}_{0,n}(t|t_0)={\int }_{t_0}^t{p}_{0,0}(\tau |t_0)e^{-V(t|\tau )}{\tilde{g}}_{0,n}(t|\tau )d\tau ,n\in \mathbb{Z}\setminus \{0\},t\ge t_0.\hfill \end{array}$$

(25)

Proof. 

Since $\lambda (t)=\lambda$ and $\mu (t)=\mu$, by virtue of (18), Relation (23) follows from (19), whereas Equation (24) derives from (22). Moreover, making use of (19) in the right-hand side of (25), one has:

$$\begin{array}{c}{\int }_{t_0}^t{p}_{0,0}(u|t_0)e^{-V(t|u)}{\tilde{g}}_{0,n}(t|u)du=e^{-V(t|t_0)}{\int }_{t_0}^t{\tilde{p}}_{0,0}(u|t_0){\tilde{g}}_{0,n}(t|u)du\hfill \\ +{\int }_{t_0}^{t}d\tau e^{-V(t|\tau )}\eta (\tau )q(\tau |t_0){\int }_{\tau }^t{\tilde{p}}_{0,0}(u|\tau ){\tilde{g}}_{0,n}(t|u)du.\hfill \end{array}$$

(26)

By virtue of (6), we note that ${\tilde{p}}_{0,0}(t|t_0)={\tilde{p}}_{n,n}(t|t_0)$ for $n\in \mathbb{Z}$ and $t\ge t_0$. Moreover, since $\lambda (t)=\lambda$ and $\mu (t)=\mu$, we obtain:

$$\begin{array}{c}{\int }_{t_0}^t{\tilde{p}}_{0,0}(u|t_0){\tilde{g}}_{0,n}(t|u)du={\int }_{t_0}^t{\tilde{p}}_{n,n}(u|t_0){\tilde{g}}_{0,n}(t|u)du\hfill \\ ={\int }_0^{t-t_0}{\tilde{p}}_{n,n}(t-t_0|\tau ){\tilde{g}}_{0,n}(\tau |0)d\tau ={\tilde{p}}_{0,n}(t-t_0|0)={\tilde{p}}_{0,n}(t|t_0).\hfill \end{array}$$

(27)

Substituting (27) in (26), by virtue of (19), Relation (25) immediately follows. ☐

The integrand on the right-hand side of Equation (25) refers to the sample-paths of $N(t)$ that start from zero at time $t_0$, then reach the state zero at time $\tau \in (t_0,t)$ and, finally, go from zero at time $\tau$ to n at time t for the first time, without the occurrence of catastrophes in $(\tau ,t)$.

4. Asymptotic Probabilities

In this section, we analyze the asymptotic behavior of the probabilities $q(t|t_0)$ and $p_{j,n}(t|t_0)$ of the process $N(t)$ in two different cases:

(i)

the intensity functions $\lambda (t),\mu (t),\nu (t)$ and $\eta (t)$ admit finite positive limits as $t\to +\infty$,

(ii)

the intensity functions $\lambda (t)$ and $\mu (t)$ are constant, whereas the rates $\nu (t)$ and $\eta (t)$ are periodic functions with common period Q.

4.1. Asymptotically-Constant Intensity Functions

In the following theorem, we determine the steady-state probabilities and the asymptotic failure probability of the process $N(t)$ when the intensity functions $\lambda (t),\mu (t),\nu (t)$ and $\eta (t)$ admit finite positive limits as t tends to $+\infty$.

Theorem 2.

If:

$$\underset{t\to +\infty }{lim}\lambda (t)=\lambda ,\underset{t\to +\infty }{lim}\mu (t)=\mu ,\underset{t\to +\infty }{lim}\nu (t)=\nu ,\underset{t\to +\infty }{lim}\eta (t)=\eta ,$$

(28)

with $\lambda ,\mu ,\nu ,\eta$ positive constants, then the steady-state probabilities and the asymptotic failure probability of the process $N(t)$ are:

$$\begin{array}{c}{q}^{*}:=\underset{t\to +\infty }{lim}q(t|t_0)=\frac{\nu }{\nu +\eta },\hfill \\ p_0^{*}:=\underset{t\to +\infty }{lim}{p}_{0,0}(t|t_0)=\frac{\nu (1-q)}{\sqrt{{(\lambda +\mu +\nu )}^2-4\lambda \mu }},\hfill \end{array}$$

(29)

$$\begin{array}{c}{p}_n^{*}:=\underset{t\to +\infty }{lim}{p}_{0,n}(t|t_0)={\left[\frac{\lambda +\mu +\nu -\sqrt{{(\lambda +\mu +\nu )}^2-4\lambda \mu }}{2\mu }\right]}^n{p}_0^{*},n\in \mathbb{N},\hfill \\ p_{-n}^{*}:=\underset{t\to +\infty }{lim}{p}_{0,-n}(t|t_0)={\left[\frac{\lambda +\mu +\nu -\sqrt{{(\lambda +\mu +\nu )}^2-4\lambda \mu }}{2\lambda }\right]}^n{p}_0^{*},n\in \mathbb{N}.\hfill \end{array}$$

(30)

Furthermore, the asymptotic conditional mean, second order moment and variance are:

$$\begin{array}{c}{\mathcal{M}}_1^{*}=\underset{t\to +\infty }{lim}{\mathcal{M}}_1(t|t_0)=\frac{\lambda -\mu }{\nu },{\mathcal{M}}_2^{*}=\underset{t\to +\infty }{lim}{\mathcal{M}}_2(t|t_0)=\frac{2{(\lambda -\mu )}^2}{{\nu }^2}+\frac{(\lambda +\mu )}{\nu },\hfill \\ {\mathcal{V}}^{*}=\underset{t\to +\infty }{lim}\mathrm{Var}(t|t_0)=\underset{t\to +\infty }{lim}\{{\mathcal{M}}_2(t|t_0)-{\left[{\mathcal{M}}_1(t|t_0)\right]}^2\}=\frac{{(\lambda -\mu )}^2}{{\nu }^2}+\frac{\lambda +\mu }{\nu }.\hfill \end{array}$$

(31)

Proof. 

The steady-state probabilities and the asymptotic failure probability of $N(t)$ can be obtained by taking the limit as $t\to +\infty$ in Equations (13)–(15), and then solving the corresponding balance equations. From (21), making use of (29) and (30), the asymptotic conditional mean and variance (31) immediately follow. ☐

4.2. Periodic Catastrophe and Repair Intensity Functions

Let us assume that the arrival and departure intensity functions are constant, whereas the catastrophe intensity function $\nu (t)$ and the repair intensity function $\eta (t)$ are periodic, such that $\nu (t+kQ)=\nu (t)$ and $\eta (t+kQ)=\eta (t)$ for all $k\in \mathbb{N}$, $t\ge t_0$, for a given constant period $Q>0$. We denote by:

$${\nu }^{*}=\frac{1}{Q}{\int }_0^Q\nu (u)du,{\eta }^{*}=\frac{1}{Q}{\int }_0^Q\eta (u)du,$$

(32)

the average catastrophe and repair rates over the period Q. Since $\nu (t)$ and $\eta (t)$ are periodic functions, from (17), we have, for $t\ge t_0$:

$$V(t+kQ)={\int }_t^{t+kQ}\nu (u)du=kQ{\nu }^{*},H(t+kQ)={\int }_t^{t+kQ}\eta (u)du=kQ{\eta }^{*},k\in \mathbb{N}.$$

(33)

Let us now investigate the asymptotic distribution for the process $N(t)$, which can be defined as follows, for $t\ge t_0$:

$$q^{*}(t)=\underset{k\to +\infty }{lim}q(t+kQ|t_0),p_{0,n}^{*}(t)=\underset{k\to +\infty }{lim}{p}_{0,n}(t+kQ|t_0),n\in \mathbb{Z}.$$

(34)

Theorem 3.

For the queueing system with catastrophes and repairs, having constant arrival rates $\lambda (t)=\lambda >0$ and departure rates $\mu (t)=\mu >0$, with $\nu (t)$ and $\eta (t)$ continuous, positive and periodic functions, with period Q, for $t\ge t_0$, one has:

$$\begin{array}{c}{p}_{0,n}^{*}(t)={\int }_0^{+\infty }dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}{\tilde{p}}_{0,n}(u|0)du,n\in \mathbb{Z}.\hfill \end{array}$$

(35)

$$\begin{array}{c}{q}^{*}(t)={\int }_0^{+\infty }\nu (t-x)e^{-[V(t|t-x)+H(t|t-x)]}dx.\hfill \end{array}$$

(36)

Furthermore, an alternative expression for the failure asymptotic probability is:

$$q^{*}(t)=\frac{1}{e^{Q({\nu }^{*}+{\eta }^{*})}-1}{\int }_0^Q\nu (t+u)e^{[V(t+u|t)+H(t+u|t)]}du,$$

(37)

with ${\nu }^{*}$ and ${\eta }^{*}$ given in (32).

Proof. 

Since $\lambda (t)=\lambda$ and $\mu (t)=\mu$, from (23), for $k\in {\mathbb{N}}_0$ and $t\ge t_0$, one has:

$$\begin{array}{c}{p}_{0,n}(t+kQ|t_0)=e^{-V(t+kQ|t_0)}{\tilde{p}}_{0,n}(t-t_0+kQ|0)+{\int }_0^{t-t_0+kQ}dx\nu (t-x)e^{-V(t+kQ|t-x+kQ)}\hfill \\ \times {\int }_0^x\eta (t-u)e^{-H(t-u+kQ|t-x+kQ)}{\tilde{p}}_{0,n}(u|0)du.\hfill \end{array}$$

(38)

Due to the periodicity of $\nu (t)$ and $\eta (t)$, the following equalities hold:

$$V(t+kQ|t-x+kQ)=V(t|t-x),H(t-u+kQ|t-x+kQ)=H(t-u|t-x).$$

Hence, from (38), it follows:

$$\begin{array}{c}{p}_{0,n}(t+kQ|t_0)=e^{-V(t+kQ|t_0)}{\tilde{p}}_{0,n}(t-t_0+kQ|0)+{\int }_0^{t-t_0+kQ}dx\nu (t-x)e^{-V(t+|t-x)}\hfill \\ \times {\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}{\tilde{p}}_{0,n}(u|0)du.\hfill \end{array}$$

(39)

Then, taking the limit as $k\to +\infty$ in (39) and recalling the second of (34), one obtains (35). Hence, we note that:

$$\begin{array}{c}\sum _{n=-\infty }^{+\infty }{p}_{0,n}^{*}(t)={\int }_0^{+\infty }dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}du\hfill \\ =1-{\int }_0^{+\infty }\nu (t-x)e^{-[V(t|t-x)+H(t|t-x)]}dx.\hfill \end{array}$$

(40)

Consequently, by virtue of (20), Equation (36) immediately follows. To prove Equation (37), we first consider (18), which implies:

$$q(t+kQ|t_0)=e^{-kQ({\nu }^{*}+{\eta }^{*})}\left[{\int }_{t_0}^t\nu (\tau )e^{-[V(t|\tau )+H(t|\tau )]}d\tau +{\int }_t^{t+kQ}\nu (\tau )e^{[V(t|\tau )+H(t|\tau )]}d\tau \right].$$

(41)

Since $\nu (t)$ and $\eta (t)$ are periodic functions, one has:

$$\begin{array}{c}{\int }_t^{t+kQ}\nu (\tau )e^{[V(t|\tau )+H(t|\tau )]}d\tau ]=\sum _{r=0}^{k-1}{\int }_0^Q\nu (t+x)e^{[V(t+rQ+x|t)+H(t+rQ+x|t)]}dx\hfill \\ =\left[{\int }_0^Q\nu (t+x)e^{[V(t+x|t)+H(t+x|t)]}dx\right]\sum _{r=0}^{k-1}{e}^{rQ({\nu }^{*}+{\eta }^{*})}\hfill \\ =\frac{e^{kQ({\nu }^{*}+{\eta }^{*})}-1}{e^{Q({\nu }^{*}+{\eta }^{*})}-1}\left[{\int }_0^Q\nu (t+x)e^{[V(t+x|t)+H(t+x|t)]}dx\right].\hfill \end{array}$$

(42)

Substituting (42) in (41) and taking the limit as $k\to +\infty$, one finally is led to (37). ☐

Under the assumptions of Theorem 3, by virtue of the periodicity of $\nu (t)$ and $\eta (t)$, from (35)–(37), one has that $p_{0,n}^{*}(t)$ and $q^{*}(t)$ are periodic functions with period Q. From (21), making use of (35), the asymptotic conditional moments are expressed as:

$$\begin{array}{c}{\mathcal{M}}_r^{*}(t):=\underset{k\to +\infty }{lim}{\mathcal{M}}_r(t+kQ|t_0)\hfill \\ =\frac{1}{1-q^{*}(t)}{\int }_0^{+\infty }dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}{\tilde{\mathcal{M}}}_r(u|0)du,\hfill \end{array}$$

(43)

with ${\tilde{\mathcal{M}}}_r(t|0):=\mathrm{E}\left[{\tilde{N}}^r(t)\right|\tilde{N}(0)=0]$ and $q^{*}(t)$ given in (36) or (37).

Example 1.

Assume that $N(t)$ has constant arrival rates $\lambda (t)=\lambda >0$ and departure rates $\mu (t)=\mu >0$. Furthermore, let the periodic catastrophe and repair intensity functions be given by:

$$\nu (t)=\nu +\frac{\pi a}{Q}sin\left(\frac{2\pi t}{Q}\right),\eta (t)=\eta +\frac{\pi b}{Q}cos\left(\frac{2\pi t}{Q}\right),t\ge 0,$$

(44)

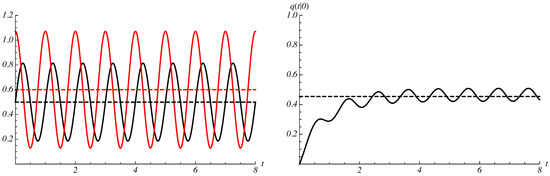
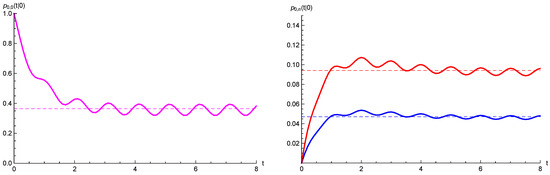
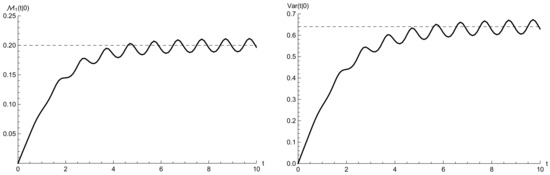
with $a>0$, $b>0$, $\nu >\pi a/Q$ and $\eta >\pi b/Q$. Clearly, from (32) and (44), we have that the averages of $\nu (t)$ and $\eta (t)$ in the period Q are equal to ν and η, respectively. In Figure 3, Figure 4 and Figure 5, the relevant parameters are taken as:

$$\lambda =0.2,\mu =0.1,Q=1,\nu =0.5,a=0.1,\eta =0.6,b=0.15.$$

Figure 3. On the left: the periodic catastrophe intensity function (black curve) and repair intensity function (red curve), with their averages (dashed lines). On the right: the failure probability $q(t|t_0)$, given in (18), and the limit $q^{*}$ (dashed line), given in (29). The parameters are specified in Example 1.

Figure 4. On the left: $p_0(t|0)$ and steady-state probability $p_0^{*}$ (dashed line). On the right: $p_{-1}(t|0)$ (blue curve) and $p_1(t|0)$ (red curve), with steady-state probabilities $p_{-1}^{*}$ and $p_1^{*}$ (dashed lines), given in (30). The parameters are specified in Example 1.

Figure 5. Plots of the mean ${\mathcal{M}}_1(t|0)$ (left) and the variance of $\mathrm{Var}(t|0)$ (right) of the process $N(t)$, obtained by means of (24). The dashed lines indicate the asymptotic values ${\mathcal{M}}_1^{*}$ and ${\mathcal{V}}^{*}$. The parameters are specified in Example 1.

On the left of Figure 3, the catastrophe intensity function $\nu (t)$ (black curve) is plotted with its average $\nu =0.5$ (black dashed line). The repair intensity function $\eta (t)$ (red curve) is plotted, as well, with its average $\eta =0.6$ (red dashed line). On the right of Figure 3, the failure probability $q(t|0)$, given in (18), is plotted and is compared with the asymptotic failure probability $q^{*}=\nu /(\nu +\eta )=0.454545$. The latter is obtained by considering constant intensity functions $\nu (t)=\nu$ and $\eta (t)=\eta$. As proved in Theorem 3, $q(t|0)$ admits an asymptotic periodic behavior, which is highlighted on the right of Figure 3. Instead, in Figure 4, we plot the probability $p_0(t|0)$ (magenta curve), on the left. Moreover, on the right of Figure 4, we show the probabilities $p_{-1}(t|0)$ (blue curve) and $p_1(t|0)$ (red curve), given in (23). The dashed lines indicate the steady-state probabilities $p_0^{*}=0.364447$ (magenta dashed line), $p_{-1}^{*}=0.0470761$ (blue dashed line) and $p_1^{*}=0.0941522$ (red dashed line), obtained by considering constant intensity functions $\nu (t)=\nu$ and $\eta (t)=\eta$. As shown in Figure 4, the probabilities admit an asymptotic periodic behavior, with period $Q=1$. Finally, in Figure 5, the mean ${\mathcal{M}}_1(t|0)$ and the variance $\mathrm{Var}(t|0)$ of the process $N(t)$, obtained via (24), are plotted and compared with the asymptotic values (dashed lines) ${\mathcal{M}}_1^{*}=0.2$ and ${\mathcal{V}}^{*}=0.64$, given in (31). Figure 3, Figure 4 and Figure 5 show that the relevant quantities reflect the periodic nature of the rates and illustrate the limiting behavior as t grows.

5. Diffusion Approximation of the Double-Ended Queueing System

With reference to the time-non-homogeneous double-ended queueing system discussed in Section 2, hereafter, we consider a heavy-traffic diffusion approximation of the queue-length process. This is finalized to obtain a more manageable description of the queueing system under a heavy-traffic regime. To this purpose, we shall adopt a suitable scaling procedure based on a scaling parameter $\epsilon$. We first rename the intensity functions related to the double-ended process $\tilde{N}(t)$, by setting:

$$\lambda (t)=\frac{\widehat{\lambda }(t)}{\epsilon }+\frac{{\omega }^2(t)}{2{\epsilon }^2},\mu (t)=\frac{\widehat{\mu }(t)}{\epsilon }+\frac{{\omega }^2(t)}{2{\epsilon }^2},n\in \mathbb{Z}.$$

(45)

Here, functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$ and ${\omega }^2(t)$ are positive, bounded and continuous for $t\ge t_0$ and satisfy the conditions ${\int }_{t_0}^{+\infty }\widehat{\lambda }(t)dt=+\infty$, ${\int }_{t_0}^{+\infty }\widehat{\mu }(t)dt=+\infty$ and ${\int }_{t_0}^{+\infty }{\omega }^2(t)dt=+\infty$. Furthermore, the constant $\epsilon$ in the right-hand sides of (45) is positive and plays a relevant role in the following approximating procedure.

Let us consider the Markov process $\{{\tilde{N}}_{\epsilon }(t),t\ge t_0\}$, having state-space $\{0,\pm \epsilon ,\pm 2\epsilon ,\dots \}$. Namely, it is defined as ${\tilde{N}}_{\epsilon }(t)=ϵ\tilde{N}(t)$, provided that the intensity functions are modified as in (45). By a customary scaling procedure similar to that adopted in [10,30], under suitable limit conditions and for $\epsilon \downarrow 0$, the scaled process ${\tilde{N}}_{\epsilon }(t)$ converges weakly to a diffusion process $\{\tilde{X}(t),t\ge t_0\}$ having state-space $\mathbb{R}$ and transition probability density function (pdf):

$$\tilde{f}(x,t|x_0,t_0)=\frac{\partial }{\partial x}P\{\tilde{X}(t)\le x|\tilde{X}(t_0)=x_0\},x,x_0\in \mathbb{R},t\ge t_0.$$

Indeed, with reference to System (1), substituting ${\tilde{p}}_{j,n}(t|t_0)$ with $\tilde{f}(n\epsilon ,t|j\epsilon ,t_0)\epsilon$ in the Chapman–Kolmogorov forward differential-difference equation for ${\tilde{N}}_{\epsilon }(t)$, we have:

$$\begin{array}{c}\frac{\partial \tilde{f}(n\epsilon ,t|j\epsilon ,t_0)}{\partial t}=\left[\frac{\widehat{\lambda }(t)}{\epsilon }+\frac{{\omega }^2(t)}{2{\epsilon }^2}\right]\tilde{f}[(n-1)\epsilon ,t|j\epsilon ,t_0]-\left[\frac{\widehat{\lambda }(t)}{\epsilon }+\frac{\widehat{\mu }(t)}{\epsilon }+\frac{{\omega }^2(t)}{{\epsilon }^2}\right]\tilde{f}(n\epsilon ,t|j\epsilon ,t_0)\hfill \\ +\left[\frac{\widehat{\mu }(t)}{\epsilon }+\frac{{\omega }^2(t)}{2{\epsilon }^2}\right]\tilde{f}[(n+1)\epsilon ,t|j\epsilon ,t_0],j,n\in \mathbb{Z}.\hfill \end{array}$$

After setting $x=n\epsilon$ and $x_0=j\epsilon$, expanding $\tilde{f}$ as Taylor series and taking the limit as $\epsilon \downarrow 0$, we obtain the following partial differential equation:

$$\frac{\partial }{\partial t}\tilde{f}(x,t|x_0,t_0)=-[\widehat{\lambda }(t)-\widehat{\mu }(t)]\frac{\partial }{\partial x}\tilde{f}(x,t|x_0,t_0)+\frac{{\omega }^2(t)}{2}\frac{{\partial }^2}{\partial x^2}\tilde{f}(x,t|x_0,t_0),x,x_0\in \mathbb{R}.$$

(46)

The associated initial condition is ${lim}_{t\downarrow t_0}\tilde{f}(x,t|x_0,t_0)=\delta (x-x_0)$, where $\delta (x)$ is the Dirac delta-function. We remark that, due to (45), the limit $\epsilon \downarrow 0$ leads to a heavy-traffic condition about the rates $\lambda (t)$ and $\mu (t)$ of process $\tilde{N}(t)$. Hence, $\tilde{X}(t)$ is a time-non-homogeneous Wiener process with drift $\widehat{\lambda }(t)-\widehat{\mu }(t)$ and infinitesimal variance ${\omega }^2(t)$, with initial state $x_0$ at time $t_0$. For $t\ge t_0$ and $s\in \mathbb{R}$, let:

$$H(s,t|x_0,t_0)=E\left[e^{is\tilde{X}(t)}\right|\tilde{X}(t_0)=x_0]={\int }_{-\infty }^{+\infty }{e}^{isx}\tilde{f}(x,t|x_0,t_0)dx,x_0\in \mathbb{R}$$

(47)

be the characteristic function of $\tilde{X}(t)$. Due to (46), the characteristic function (47) is the solution of the partial differential equation:

$$\frac{\partial }{\partial t}H(s,t|x_0,t_0)=\left\{is[\lambda (t)-\mu (t)]-\frac{s^2}{2}{\omega }^2(t)\right\}H(s,t|x_0,t_0),x_0\in \mathbb{R},$$

to be solved with the initial condition ${lim}_{t\downarrow t_0}H(s,t|x_0,t_0)=e^{is{x}_0}$. Hence, for $t\ge t_0$, one has:

$$H(s,t|x_0,t_0)=exp\left\{is\left[x_0+\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0)\right]-\frac{s^2}{2}\Omega (t|t_0)\right\},x_0\in \mathbb{R},$$

(48)

where we have set:

$$\widehat{\Lambda }(t|t_0)={\int }_{t_0}^t\widehat{\lambda }(\tau )d\tau ,\widehat{M}(t|t_0)={\int }_{t_0}^t\widehat{\mu }(\tau )d\tau ,\Omega (t|t_0)={\int }_{t_0}^t{\omega }^2(\tau )d\tau ,t\ge t_0.$$

(49)

Clearly, (48) is a normal characteristic function, so that the solution of (46) is the Gaussian pdf:

$$\tilde{f}(x,t|x_0,t_0)=\frac{1}{\sqrt{2\pi \Omega (t|t_0)}}exp\left\{-\frac{{\left[x-x_0-\widehat{\Lambda }(t|t_0)+\widehat{M}(t|t_0)\right]}^2}{2\Omega (t|t_0)}\right\},x,x_0\in \mathbb{R},t\ge t_0.$$

(50)

Then, the conditional mean and variance are:

$$\mathrm{E}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=x_0]=x_0+\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0),\mathrm{Var}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=x_0]=\Omega (t|t_0),t\ge t_0.$$

(51)

Let us now consider a first-passage-time problem for $\tilde{X}(t)$. We denote by ${\tilde{T}}_{x_0,x}(t_0)$ the random variable describing the FPT of $\tilde{X}(t)$ trough state $x\in \mathbb{R}$, starting from $x_0$ at time $t_0$, with $x_0\ne x$. In analogy to (8), the Markov property yields:

$$\tilde{f}(x,t|x_0,t_0)={\int }_{t_0}^t\tilde{g}(x,\tau |x_0,t_0)\tilde{f}(x,t|x,\tau )d\tau ,x_0,x\in \mathbb{R},x\ne x_0,$$

(52)

where $\tilde{g}(x,t|x_0,t_0)$ is the pdf of ${\tilde{T}}_{x_0,x}(t_0)$.

Hereafter, we deal with a special case, in which the functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$ and ${\omega }^2(t)$ are proportional.

Remark 2.

Let $\widehat{\lambda }(t)=\widehat{\lambda }\phi (t)$, $\widehat{\mu }(t)=\widehat{\mu }\phi (t)$ and ${\omega }^2(t)={\omega }^2\phi (t)$, where $\widehat{\lambda },\widehat{\mu }$, ω are positive constants and $\phi (t)$ is a positive, bounded and continuous function for $t\ge t_0$, such that ${\int }_{t_0}^{\infty }\phi (t)dt=+\infty$. Then, the transition pdf of $\tilde{X}(t)$ becomes:

$$\tilde{f}(x,t|x_0,t_0)=\frac{1}{\sqrt{2\pi {\omega }^2\Phi (t|t_0)}}exp\left\{-\frac{{\left[x-x_0-(\widehat{\lambda }-\widehat{\mu })\Phi (t|t_0)\right]}^2}{2{\omega }^2\Phi (t|t_0)}\right\},x,x_0\in \mathbb{R},t\ge t_0,$$

where $\Phi (t|t_0)$ is defined in (9). Moreover, the FPT pdf of ${\tilde{T}}_{x_0,x}(t_0)$ can be expressed as (see, for instance, [26]):

$$\tilde{g}(x,t|x_0,t_0)=\frac{|x-x_0|\phi (t)}{\Phi (t|t_0)}\tilde{f}(x,t|x_0,t_0),x_0,x\in \mathbb{R},x\ne x_0.$$

The corresponding FPT ultimate probability is given by:

$$P\{{\tilde{T}}_{x_0,x}(t_0)<+\infty \}={\int }_{t_0}^{+\infty }\tilde{g}(x,t|x_0,t_0)dt=\left\{\begin{array}{cc}1,\hfill & (\widehat{\lambda }-\widehat{\mu })(x-x_0)\ge 0,\hfill \\ {\displaystyle e^{2(\widehat{\lambda }-\widehat{\mu })(x-x_0)/{\omega }^2},}\hfill & (\widehat{\lambda }-\widehat{\mu })(x-x_0)<0.\hfill \end{array}\right.$$

Clearly, ${\tilde{T}}_{x_0,0}(t_0)$ is a suitable approximation of the busy period ${\tilde{\mathcal{T}}}_{j,0}(t_0)$ considered in Section 2.

Goodness of the Approximating Procedure

Thanks to the above heavy-traffic approximation, the state of the time-non-homogeneous double-ended queue $\tilde{N}(t)$ has been approximated by the non-homogeneous Wiener process $\tilde{X}(t)$, with the transition pdf given in (50).

A first confirmation of the goodness of the approximating procedure can be obtained by the comparing mean and variance of $\tilde{N}(t)$ with those of $\tilde{X}(t)/\epsilon$, for $\lambda (t)$ and $\mu (t)$ chosen as in (45). Recalling (7) and (51), the means satisfy the following identity, for all $\epsilon >0$:

$$\mathrm{E}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=j\epsilon ]=\epsilon \mathrm{E}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j].$$

(53)

Moreover, for the variances, we have:

$$\underset{\epsilon \downarrow 0}{lim}\frac{\mathrm{Var}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j]}{\mathrm{Var}[\frac{\tilde{X}(t)}{\epsilon }\left|\frac{\tilde{X}(t_0)}{\epsilon }=j\right]}=\underset{\epsilon \downarrow 0}{lim}\frac{{\epsilon }^2\mathrm{Var}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j]}{\mathrm{Var}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=j\epsilon ]}=\underset{\epsilon \downarrow 0}{lim}\frac{{\epsilon }^2[\Lambda (t|t_0)+M(t|t_0)]}{\Omega (t|t_0)}=1,$$

so that for $\epsilon$ close to zero, one has:

$$\mathrm{Var}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=j\epsilon ]\simeq {\epsilon }^2\mathrm{Var}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=j].$$

(54)

The discussion of the goodness of the heavy-traffic approximation involves also the probability distributions. Let us denote by ${\tilde{p}}_{j,n}^{(\epsilon )}(t)$ the transition probabilities of the process $\tilde{N}(t)$, for $\lambda (t)$ and $\mu (t)$ given in (45), and for $n=x/\epsilon$, $j=x_0/\epsilon$. The following theorem holds.

Theorem 4.

For $t\ge t_0$, one has:

$$\underset{\genfrac{}{}{0pt}{}{\epsilon \downarrow 0,}{n\epsilon =x,j\epsilon =x_0}}{lim}\frac{{\tilde{p}}_{j,n}^{(\epsilon )}(t|t_0)}{\epsilon }=\tilde{f}(x,t|x_0,t_0),$$

(55)

with $\tilde{f}(x,t|x_0,t_0)$ given in (50).

Proof. 

To prove (55), we consider separately the following cases: (i) $n=j$ and (ii) $n\ne j$, with $j,n\in \mathbb{Z}$.

(i) For $n=j$, from (6), one has:

$${\tilde{p}}_{n,n}^{(\epsilon )}(t|t_0)=exp\left\{-\frac{\widehat{\Lambda }(t|t_0)+\widehat{M}(t|t_0)}{\epsilon }-\frac{\Omega (t|t_0)}{{\epsilon }^2}\right\}{I}_0\left[2\sqrt{\left[\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]\left[\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}\right].$$

(56)

We recall that $I_{\nu }(z)\simeq e^z/\sqrt{2\pi z}$ (cf. [31], p. 377, n. 9.71) when $\left|z\right|$ is large, for $\nu$ fixed. Hence, from (56) as $\epsilon$ is close to zero, one has:

$$\begin{array}{c}\frac{{\tilde{p}}_{n,n}^{(\epsilon )}(t|t_0)}{\epsilon }\simeq \frac{1}{2\epsilon \sqrt{\pi }}{\left[\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}^{-1/4}{\left[\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}^{-1/4}\hfill \\ \times exp\left\{-{\left[\sqrt{\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}}-\sqrt{\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}}\right]}^2\right\},n\in \mathbb{Z}.\hfill \end{array}$$

(57)

We note that:

$$\begin{array}{c}\underset{\epsilon \downarrow 0}{lim}\frac{1}{2\epsilon \sqrt{\pi }}{\left[\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}^{-1/4}{\left[\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}^{-1/4}\hfill \\ =\frac{1}{2\sqrt{\pi }}\underset{\epsilon \downarrow 0}{lim}{\left[\epsilon \widehat{\Lambda }(t|t_0)+\frac{\Omega (t|t_0)}{2}\right]}^{-1/4}{\left[\epsilon \widehat{M}(t|t_0)+\frac{\Omega (t|t_0)}{2}\right]}^{-1/4}=\frac{1}{\sqrt{2\pi \Omega (t|t_0)}}\hfill \end{array}$$

and:

$$\begin{array}{c}\underset{\epsilon \downarrow 0}{lim}exp\left\{-{\left[\sqrt{\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}}-\sqrt{\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}}\right]}^2\right\}\hfill \\ =\underset{\epsilon \downarrow 0}{lim}exp\left\{-{\left[\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0)\right]}^2{\left[\sqrt{\epsilon \widehat{\Lambda }(t|t_0)+\frac{\Omega (t|t_0)}{2}}+\sqrt{\epsilon \widehat{M}(t|t_0)+\frac{\Omega (t|t_0)}{2}}\right]}^{-2}\right\}\hfill \\ =exp\left\{-\frac{{\left[\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0)\right]}^2}{2\Omega (t|t_0)}\right\},\hfill \end{array}$$

so that, taking the limit as $\epsilon \downarrow 0$ in (57), Equation (55) follows for $n=j$ and $x=x_0$.

(ii) For $n\ne j$, recalling that $I_n(z)=I_{-n}(z)$, from (6), one has:

$$\begin{array}{c}{\tilde{p}}_{j,n}^{(\epsilon )}(t|t_0)=exp\left\{-\frac{\widehat{\Lambda }(t|t_0)+\widehat{M}(t|t_0)}{\epsilon }-\frac{\Omega (t|t_0)}{{\epsilon }^2}\right\}{\left[\frac{2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)}{2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)}\right]}^{(x-x_0)/(2\epsilon )}\hfill \\ \times I_{|x-x_0|/\epsilon }\left[2\sqrt{\left[\frac{\widehat{\Lambda }(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]\left[\frac{\widehat{M}(t|t_0)}{\epsilon }+\frac{\Omega (t|t_0)}{2{\epsilon }^2}\right]}\right].\hfill \end{array}$$

(58)

Making use of the asymptotic result (cf. [31], p. 378, n. 9.7.7):

$$I_{\nu }(\nu z)\simeq \frac{1}{\sqrt{2\pi \nu }{(1+z^2)}^{1/4}}exp\left\{\nu \left[\sqrt{1+z^2}+ln\frac{z}{1+\sqrt{1+z^2}}\right]\right\},\nu \to +\infty ,0<z<+\infty ,$$

from (58), we obtain:

$$\begin{array}{c}\hfill \frac{{\tilde{p}}_{j,n}^{(\epsilon )}(t|t_0)}{\epsilon }\simeq \prod _{j=1}^4{A}_j^{(\epsilon )}(x,t|x_0,t_0),\end{array}$$

(59)

where:

$$\begin{array}{c}{A}_1^{(\epsilon )}(x,t|x_0,t_0)={\left[\frac{2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)}{2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)}\right]}^{(x-x_0)/(2\epsilon )}\hfill \\ A_2^{(\epsilon )}(x,t|x_0,t_0)=\frac{1}{\sqrt{2\pi }}{\left\{{\epsilon }^2{(x-x_0)}^2+\left[2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)\right]\left[2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)\right]\right\}}^{-1/4}\hfill \\ A_3^{(\epsilon )}(x,t|x_0,t_0)={\left\{\frac{\sqrt{\left[2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)\right][2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)}]}{\epsilon |x-x_0|+\sqrt{{\epsilon }^2{(x-x_0)}^2+\left[2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)\right][2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)}]}\right\}}^{\frac{|x-x_0|}{\epsilon }}\hfill \\ A_4^{(\epsilon )}(x,t|x_0,t_0)=exp\left\{-\frac{\widehat{\Lambda }(t|t_0)+\widehat{M}(t|t_0)}{\epsilon }-\frac{\Omega (t|t_0)}{{\epsilon }^2}\right\}\hfill \\ \times exp\left\{\frac{1}{{\epsilon }^2}\sqrt{{\epsilon }^2{(x-x_0)}^2+\left[2\epsilon \widehat{\Lambda }(t|t_0)+\Omega (t|t_0)\right]\left[2\epsilon \widehat{M}(t|t_0)+\Omega (t|t_0)\right]}\right\}.\hfill \end{array}$$

Since:

$$\begin{array}{c}\underset{\epsilon \downarrow 0}{lim}{A}_1^{(\epsilon )}(x,t|x_0,t_0)=exp\left\{(x-x_0)\frac{\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0)}{\Omega (t|t_0)}\right\},\hfill \\ \underset{\epsilon \downarrow 0}{lim}{A}_2^{(\epsilon )}(x,t|x_0,t_0)=\frac{1}{\sqrt{2\pi \Omega (t|t_0)}},\hfill \\ \underset{\epsilon \downarrow 0}{lim}{A}_3^{(\epsilon )}(x,t|x_0,t_0)=exp\left\{-\frac{{(x-x_0)}^2}{\Omega (t|t_0)}\right\},\hfill \\ \underset{\epsilon \downarrow 0}{lim}{A}_4^{(\epsilon )}(x,t|x_0,t_0)=exp\left\{\frac{{(x-x_0)}^2}{2\Omega (t|t_0)}\right\}exp\left\{-\frac{{[\widehat{\Lambda }(t|t_0)-\widehat{M}(t|t_0)]}^2}{2\Omega (t|t_0)}\right\},\hfill \end{array}$$

by taking the limit as $\epsilon \downarrow 0$ in (59), Equation (55) follows for $n\ne j$ and $x\ne x_0$. ☐

Finally, the goodness of the heavy-traffic approximation is confirmed by the approximation:

$${\tilde{p}}_{j,n}^{(\epsilon )}(t|t_0)\simeq \epsilon \tilde{f}(x,t|x_0,t_0),$$

which is a consequence of Equation (55) and is valid for $\epsilon$ close to zero.

6. Diffusion Approximation of the Double-Ended Queueing System with Catastrophes and Repairs

In this section, we consider a heavy-traffic approximation of the time-non-homogeneous double-ended queueing system subject to disasters and repairs, discussed in Section 3. The continuous approximation of the discrete model leads to a jump-diffusion process and is similar to the scaling procedure employed in Section 5. The relevant difference is that the state-space of the process $N(t)$ presents also a spurious state F.

Let us now consider the continuous-time Markov process $\{N_{\epsilon }(t),t\ge t_0\}$, having state-space $\{F,0,\pm \epsilon ,\pm 2\epsilon ,\dots \}$. Under suitable limit conditions, as $\epsilon \downarrow 0$, the scaled process $N_{\epsilon }(t)$ converges weakly to a jump-diffusion process $\{X(t),t\ge t_0\}$ having state-space $\{F\}\cup \mathbb{R}$. The limiting procedure is analogous to that used in Buonocore et al. [34], which involves spurious states, as well. As in the previous section, for the approximating procedure, we first assume that the rates $\lambda (t)$ and $\mu (t)$ are modified as in (45). Hence, the limit $\epsilon \downarrow 0$ leads to a heavy-traffic condition about such intensity functions. Instead, the catastrophe rate $\nu (t)$ and the repair rate $\eta (t)$ are not affected by the scaling procedure.

We note that $X(t)$ describes the motion of a particle, which starts at the origin at time $t_0$ and then behaves as a non-homogeneous Wiener process, with drift $\widehat{\lambda }(t)-\widehat{\mu }(t)$ and infinitesimal variance ${\omega }^2(t)$, until a catastrophe occurs. We remark that the catastrophes arrive according to a time-non-homogeneous Poisson process with intensity function $\nu (t)$. As soon as a catastrophe occurs, the process enters into the failure state F and remains therein for a random time (corresponding to the repair time) that ends according to the time-dependent intensity function $\eta (t)$. Clearly, catastrophes are not allowed during a repair period. The effect of a repair is the instantaneous transition of the process $X(t)$ to the state zero. After that, the motion is subject again to diffusion and proceeds as before. We recall that $\nu (t)$ and $\eta (t)$ are positive, bounded and continuous functions for $t\ge t_0$, such that ${\int }_{t_0}^{+\infty }\nu (t)dt=+\infty$ and ${\int }_{t_0}^{+\infty }\eta (t)dt=+\infty$. We denote by:

$$f(x,t|0,t_0)=\frac{\partial }{\partial x}P\{X(t)\le x|X(t_0)=0\},x\in \mathbb{R},t\ge 0$$

(60)

the transition density of $X(t)$ and by $q(t|t_0)=P\{X(t)=F|X(t_0)=0\}$ the probability that the process is in the failure-state at time t starting from zero at time $t_0$. We point out that the adopted scaling procedure does not affect the spurious state, so that $q(t|t_0)$ is identical to the analogous probability of the process $N(t)$ and is given in (18). From (), proceeding similarly as for (46), one obtains that (60) is the solution of the following partial differential equation, for $t>t_0$:

$$\frac{\partial }{\partial t}f(x,t|0,t_0)=-\nu (t)f(x,t|0,t_0)-[\widehat{\lambda }(t)-\widehat{\mu }(t)]\frac{\partial }{\partial x}f(x,t|0,t_0)+\frac{{\omega }^2(t)}{2}\frac{{\partial }^2}{\partial x^2}f(x,t|0,t_0),x\in \mathbb{R}\setminus \{0\},$$

(61)

to be solved with the initial condition ${lim}_{t\downarrow t_0}f(x,t|0,t_0)=\delta (x)$ and, in analogy to (20), with the compatibility condition:

$${\int }_{-\infty }^{+\infty }f(x,t|0,t_0)dx+q(t|t_0)=1,t\ge t_0.$$

(62)

6.1. Transient Distribution

Similarly to the discrete model discussed in Section 3, the pdf (60) can be expressed as follows, in terms of the transition pdf of the time-non-homogeneous Wiener process $\tilde{X}(t)$ treated in Section 5:

$$f(x,t|0,t_0)=e^{-V(t|t_0)}\tilde{f}(x,t|0,t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}\tilde{f}(x,t|0,\tau )d\tau ,x\in \mathbb{R},t\ge 0,$$

(63)

with $q(t|t_0)$ and $\tilde{f}(x,t|x_0,t_0)$ given in (18) and (50), respectively. Making use of (18) and (50) in (63), for $t\ge t_0$ and $x\in \mathbb{R}$, one has:

$$\begin{array}{c}f(x,t|0,t_0)=\frac{e^{-V(t|t_0)}}{\sqrt{2\pi \Omega (t|t_0)}}exp\left\{-\frac{{\left[x-\widehat{\Lambda }(t|t_0)+\widehat{M}(t|t_0)\right]}^2}{2\Omega (t|t_0)}\right\}\hfill \\ +{\int }_{t_0}^{t}d\tau \eta (\tau )\frac{e^{-V(t|\tau )}}{\sqrt{2\pi \Omega (t|\tau )}}exp\left\{-\frac{{\left[x-\widehat{\Lambda }(t|\tau )+\widehat{M}(t|\tau )\right]}^2}{2\Omega (t|\tau )}\right\}{\int }_{t_0}^{\tau }\nu (\vartheta )e^{-[V(\tau |\vartheta )+H(\tau |\vartheta )]}d\vartheta .\hfill \end{array}$$

(64)

For $r\in \mathbb{N}$, let us now consider the r-th conditional moment of $X(t)$:

$${\mathfrak{M}}_r(t|t_0):=\mathrm{E}\left[X^r(t)\right|X(t)\in \mathbb{R},X(t_0)=0]=\frac{1}{1-q(t|t_0)}{\int }_{-\infty }^{+\infty }{x}^{r}f(x,t|0,t_0)dx.$$

(65)

From (63), for $r\in \mathbb{N}$, it results:

$${\mathfrak{M}}_r(t|t_0)=\frac{1}{1-q(t|t_0)}\left\{e^{-V(t|t_0)}{\tilde{\mathfrak{M}}}_r(t|t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}{\tilde{\mathfrak{M}}}_r(t|\tau )d\tau \right\},$$

(66)

where ${\tilde{\mathfrak{M}}}_r(t|t_0):=\mathrm{E}\left[{\tilde{X}}^r(t)\right|\tilde{X}(t_0)=0]$ is the r-th conditional moment of $\tilde{X}(t)$. Hence, by virtue of (51), from (66), we obtain the conditional moments ${\mathfrak{M}}_r(t|t_0)$.

In the following theorem, we discuss the special case when the functions $\widehat{\lambda }(t)-\widehat{\mu }(t)$ and ${\omega }^2(t)$ are constant.

Theorem 5.

Consider the process $X(t)$ such that $\widehat{\lambda }(t)-\widehat{\mu }(t)=\widehat{\lambda }-\widehat{\mu }$ and ${\omega }^2(t)={\omega }^2$ for all $t\ge t_0$. Then, for $t\ge t_0$ and $x\in \mathbb{R}$, one has:

$$f(x,t|0,t_0)=e^{-V(t|t_0)}\tilde{f}(x,t-t_0|0,0)+{\int }_0^{t-t_0}dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}\tilde{f}(x,u|0,0)du$$

(67)

and, for $r\in \mathbb{N}$,

$${\mathfrak{M}}_r(t|t_0)=\frac{1}{1-q(t|t_0)}\left\{e^{-V(t|t_0)}{\tilde{\mathfrak{M}}}_r(t-t_0|0)+{\int }_0^{t-t_0}q(t-x|t_0)\eta (t-x)e^{-V(t|t-x)}{\tilde{\mathfrak{M}}}_r(x|0)dx\right\}.$$

(68)

Furthermore, it results:

$$\begin{array}{c}f(x,t|0,t_0)={\int }_{t_0}^{t}f(0,\tau |0,t_0)e^{-V(t|\tau )}\tilde{g}(x,t|0,\tau )d\tau ,x\in \mathbb{R}\setminus \{0\},t\ge t_0,\hfill \end{array}$$

(69)

where $\tilde{g}(x,t|0,\tau )$ is the FPT pdf of ${\tilde{T}}_{0,x}(\tau )$, introduced in Section 5.

Proof. 

It proceeds similarly to the proof of Theorem 1. ☐

6.2. Goodness of the Approximating Procedure

Let us now analyze the goodness of the heavy-traffic approximation considered above. The time-non-homogeneous process describing the state of the double-ended queueing system with catastrophes and repairs has been approximated by the diffusion process $X(t)$, whose transition pdf is given in (63).

First of all, we compare the mean, second order moment and variance of $N(t)$ with those of $X(t)/\epsilon$, when $\lambda (t)$ and $\mu (t)$ are chosen as in (45). By virtue of (53) and (54), one has:

$$\begin{array}{c}{\tilde{\mathfrak{M}}}_1(t|t_0)=\mathrm{E}\left[\tilde{X}(t)\right|\tilde{X}(t_0)=0]=\epsilon \mathrm{E}\left[\tilde{N}(t)\right|\tilde{N}(t_0)=0]=\epsilon {\mathcal{M}}_1(t|t_0),\hfill \\ {\tilde{\mathfrak{M}}}_2(t|t_0)=\mathrm{E}\left[{\tilde{X}}^2(t)\right|\tilde{X}(t_0)=0]\simeq {\epsilon }^2\mathrm{E}\left[{\tilde{N}}^2(t)\right|\tilde{N}(t_0)=0]={\mathcal{M}}_2(t|t_0)\mathrm{as}\epsilon \downarrow 0.\hfill \end{array}$$

Hence, recalling (22) and (66), one has:

$${\mathfrak{M}}_1(t|t_0)\equiv \mathrm{E}\left[X(t)\right|X(t_0)=0]=\epsilon \mathrm{E}\left[N(t)\right|N(t_0)=0]\equiv \epsilon {\mathcal{M}}_1(t|t_0).$$

Moreover,

$$\underset{\epsilon \downarrow 0}{lim}\frac{\mathrm{E}\left[N^2(t)\right|N(t_0)=0]}{E[\frac{X^2(t)}{{\epsilon }^2}\left|\frac{X(t_0)}{\epsilon }=0\right]}=\underset{\epsilon \downarrow 0}{lim}\frac{{\epsilon }^2\left[e^{-V(t|t_0)}{\tilde{\mathcal{M}}}_2(t|t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}{\tilde{\mathcal{M}}}_2(t|\tau )d\tau \right]}{e^{-V(t|t_0)}{\tilde{\mathfrak{M}}}_2(t|t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}{\tilde{\mathfrak{M}}}_2(t|\tau )d\tau }=1,$$

so that the variances satisfy the following relation, for $\epsilon$ close to zero:

$$\mathrm{Var}\left[X(t)\right|X(t_0)=0]\simeq {\epsilon }^2\mathrm{Var}\left[N(t)\right|N(t_0)=0].$$

Furthermore, we denote by $p_{j,n}^{(\epsilon )}(t)$ the transition probabilities of the process $N(t)$, when $n=x/\epsilon$ and the intensity functions $\lambda (t)$ and $\mu (t)$ are given in (45). The following theorem holds.

Theorem 6.

For $t\ge t_0$, one has:

$$\underset{\epsilon \downarrow 0,n\epsilon =x}{lim}\frac{p_{0,n}^{(\epsilon )}(t|t_0)}{\epsilon }=f(x,t|0,t_0),$$

(70)

with $f(x,t|,0,t_0)$ given in (63).

Proof. 

From (19), one obtains:

$$\frac{p_{0,n}^{(\epsilon )}(t|t_0)}{\epsilon }=e^{-V(t|t_0)}\frac{{\tilde{p}}_{0,n}^{(\epsilon )}(t|t_0)}{\epsilon }+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}\frac{{\tilde{p}}_{0,n}^{(\epsilon )}(t|\tau )}{\epsilon }d\tau .$$

(71)

Taking the limit as $\epsilon \downarrow 0$ on both sides of (71) and recalling (55), for $t\ge t_0$, one has:

$$\underset{\epsilon \downarrow 0,n\epsilon =x}{lim}\frac{p_{0,n}^{(\epsilon )}(t|t_0)}{\epsilon }=e^{-V(t|t_0)}\tilde{f}(x,t|0,t_0)+{\int }_{t_0}^{t}q(\tau |t_0)\eta (\tau )e^{-V(t|\tau )}\tilde{f}(x,t|0,\tau )d\tau ,$$

so that (70) immediately follows by using (63). ☐

As a consequence of Theorem 6, for $\lambda (t)$ and $\mu (t)$ chosen as in (45) and under heavy-traffic conditions, the probability $p_{0,n}^{(\epsilon )}(t|t_0)$ of the discrete process $N(t)$ is close to $\epsilon f(n\epsilon ,t|0,t_0)$ for $\epsilon$ near to zero.

7. Asymptotic Distributions

Similar to the analysis performed in Section 4, in this section, we consider the asymptotic behavior of the density $f(x,t|0,t_0)$ of the process $X(t)$ in two different cases:

(i)

the functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$, ${\omega }^2(t)$, $\nu (t)$ and $\eta (t)$ admit finite positive limits as $t\to +\infty$,

(ii)

the functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$ and ${\omega }^2(t)$ are constant, and the rates $\nu (t)$ and $\eta (t)$ are periodic functions with common period Q.

7.1. Asymptotically-Constant Intensity Functions

We assume that the functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$, ${\omega }^2(t)$, $\nu (t)$ and $\eta (t)$ admit finite positive limits as t tends to $+\infty$. In this case, the failure asymptotic probability $q^{*}={lim}_{t\to +\infty }q(t|t_0)$ of the process $X(t)$ is provided in (29). Moreover, the steady-state density of the process $X(t)$ is an asymmetric bilateral exponential density, as given in the following theorem.

Theorem 7.

Assuming that:

$$\underset{t\to +\infty }{lim}\lambda (t)=\lambda ,\underset{t\to +\infty }{lim}\mu (t)=\mu ,\underset{t\to +\infty }{lim}{\omega }^2(t)={\omega }^2,\underset{t\to +\infty }{lim}\nu (t)=\nu ,\underset{t\to +\infty }{lim}\eta (t)=\eta ,$$

(72)

with $\widehat{\lambda }$, $\widehat{\mu }$, ${\omega }^2$, ν, η positive constants, then the steady-state pdf of the process $X(t)$ is, for $x\in \mathbb{R}$,

$$f^{*}(x):=\underset{t\to +\infty }{lim}f(x,t|0,t_0)=\frac{\eta \nu }{\eta +\nu }\frac{1}{\sqrt{{(\widehat{\lambda }-\widehat{\mu })}^2+2{\omega }^2\nu }}exp\left\{\frac{(\widehat{\lambda }-\widehat{\mu })}{{\omega }^2}x-\frac{\sqrt{{(\widehat{\lambda }-\widehat{\mu })}^2+2{\omega }^2\nu }}{{\omega }^2}\left|x\right|\right\}.$$

(73)

Furthermore, the asymptotic conditional mean, second order moment and variance are:

$$\begin{array}{c}\underset{t\to +\infty }{lim}{\mathfrak{M}}_1(t|t_0)=\frac{\widehat{\lambda }-\widehat{\mu }}{\nu },\underset{t\to +\infty }{lim}{\mathfrak{M}}_2(t|t_0)=\frac{2{(\widehat{\lambda }-\widehat{\mu })}^2}{{\nu }^2}+\frac{{\omega }^2}{\nu },\hfill \\ \underset{t\to +\infty }{lim}\mathrm{Var}(t|t_0)=\underset{t\to +\infty }{lim}\{{\mathfrak{M}}_2(t|t_0)-{\left[{\mathfrak{M}}_1(t|t_0)\right]}^2\}=\frac{{(\widehat{\lambda }-\widehat{\mu })}^2}{{\nu }^2}+\frac{{\omega }^2}{\nu }.\hfill \end{array}$$

(74)

Proof. 

The steady-state density can be obtained by taking the limit as $t\to +\infty$ in Equations (61) and (62) and recalling (29). Moreover, the asymptotic conditional mean and variance (74) follow from (65), making use of (29) and (73). ☐

7.2. Periodic Intensity Functions

Let us assume that the functions $\widehat{\lambda }(t)$, $\widehat{\mu }(t)$ and ${\omega }^2(t)$ are constant and that the catastrophe intensity function $\nu (t)$ and the repair intensity function $\eta (t)$ are periodic, so that $\nu (t+kQ)=\nu (t)$ and $\eta (t+kQ)=\eta (t)$ for $k\in \mathbb{N}$ and $t\ge t_0$. The average catastrophe and repair rates in the period Q are defined in (32). The asymptotic distribution of the process $X(t)$ is described by the following functions, for $t\ge t_0$,

$$q^{*}(t):=\underset{k\to +\infty }{lim}q(t+kQ|t_0),f^{*}(x,t):=\underset{k\to +\infty }{lim}f(x,t+kQ|0,t_0),x\in \mathbb{R}.$$

(75)

Note that the asymptotic failure probability $q^{*}(t)$ is given in (36) or, alternatively, in (37). Moreover, the asymptotic density $f^{*}(x,t)$ is determined in the following theorem.

Theorem 8.

Consider the stochastic process $X(t)$ and assume $\widehat{\lambda }(t)-\widehat{\mu }(t)=\widehat{\lambda }-\widehat{\mu }$ and ${\omega }^2(t)={\omega }^2$, and that the intensities $\nu (t)$ and $\eta (t)$ are continuous, positive and periodic functions with period Q. Then, one has:

$$f^{*}(x,t)={\int }_0^{+\infty }dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}\tilde{f}(x,u|0,0)du,x\in \mathbb{R}.$$

(76)

Proof. 

It proceeds similarly to the proof of Theorem 3, by starting from Equation (67). ☐

By virtue of the periodicity of $\nu (t)$ and $\eta (t)$, from (76), one has that $f^{*}(x,t)$ is a periodic function with period Q. From (65), making use of (76), the asymptotic conditional moments are:

$$\begin{array}{c}{\mathfrak{M}}_r^{*}(t):=\underset{k\to +\infty }{lim}{\mathfrak{M}}_r(t+kQ|t_0)\hfill \\ =\frac{1}{1-q^{*}(t)}{\int }_0^{+\infty }dx\nu (t-x)e^{-V(t|t-x)}{\int }_0^x\eta (t-u)e^{-H(t-u|t-x)}{\tilde{\mathfrak{M}}}_r(u|0)du,\hfill \end{array}$$

(77)

where ${\tilde{\mathfrak{M}}}_r(t|0)=\mathrm{E}\left[\tilde{X}{(t)}^r\right|\tilde{X}(0)=0]$ and where $q^{*}(t)$ is given in (36) or in (37).

The following illustrative example concludes the section.

Example 2.

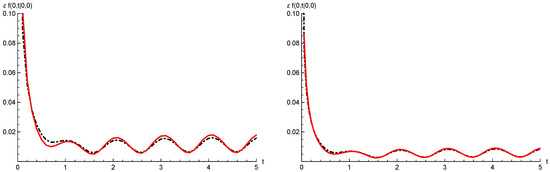
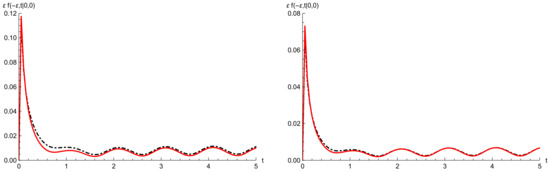
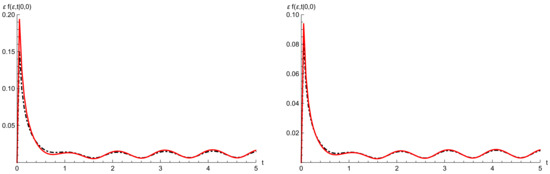
Let $X(t)$ be the approximating jump-diffusion process, subject to disasters and repairs, with drift $\widehat{\lambda }-\widehat{\mu }$ and infinitesimal variance ${\omega }^2$, where $\widehat{\lambda }=2.0$, $\widehat{\mu }=1.0$ and ${\omega }^2=0.2$ and with periodic catastrophe intensity function $\nu (t)$ and repair intensity function $\eta (t)$ given by (44). The parameters ν, a, η, b, Q are taken as in Example 1. For these choices, probability $q(t|0)$ is identical as for the discrete model. It is plotted in Figure 3, on the right.

We now consider the two choices $\epsilon =0.05$ and $\epsilon =0.025$. Then, the parameters λ and μ are determined according to (45), so that for $\epsilon =0.05$, we have $\lambda =80$ and $\mu =60$, whereas for $\epsilon =0.025$, we have $\lambda =240$ and $\mu =200$. To show the validity of the approximating procedure, we compare the quantity $\epsilon f(\epsilon n,t|0,0)$ with the probability $p_{0,n}(t|0)$, for $n=0,-1,1$, in Figure 6, Figure 7 and Figure 8, respectively. The case $\epsilon =0.05$ is shown on the left, and $\epsilon =0.025$ is on the right. Recall that $f(x,t|0,0)$ is given in (67), whereas $p_{0,n}(t|0)$ is given in (23). We note that the goodness of the continuous approximation for $p_{0,n}(t|0)$ improves as ε decreases, this corresponding to an increase of traffic in the double-ended queue with catastrophes and repairs, due to (45).

Figure 6. For $\widehat{\lambda }=2.0$, $\widehat{\mu }=1.0$, ${\omega }^2=0.2$, the function $\epsilon f(0,t|0,0)$ (red curve) is shown with the probability $p_{0,0}(t|0)$ (black dashed curve) for $\epsilon =0.05$ (left) and $\epsilon =0.025$ (right). The parameters $\lambda$ and $\mu$ are shown in Example 2, according to (45).

Figure 7. For the same choices of parameters of Figure 6, the function $\epsilon f(-\epsilon ,t|0,0)$ (red curve) is compared with the probability $p_{0,-1}(t|0)$ (black dashed curve) for $\epsilon =0.05$ (left) and $\epsilon =0.025$ (right).

Figure 8. For the same choices of parameters of Figure 6, the function $\epsilon f(\epsilon ,t|0,0)$ (red curve) is compared with the probability $p_{0,1}(t|0)$ (black dashed curve) for $\epsilon =0.05$ (left) and $\epsilon =0.025$ (right).

8. Conclusions

We analyzed a continuous-time stochastic process that describes the state of a double-ended queue subject to disasters and repairs. The system is time-non-homogeneous, since arrivals, services, disasters and repairs are governed by time-varying intensity functions. This model is a suitable generalization of the queueing system investigated in [10]. Indeed, the previous model is characterized by constant rates of arrivals, services, catastrophes and repairs. However, motivated by the need to describe more realistic situations in which the system evolution reflects daily or seasonal fluctuations, in this paper, we investigated the case where all such rates are time-dependent. Whereas in the previous model, the approach involved the Laplace transforms, in the present case, the analysis cannot be based on such a method, but rather on a direct analysis of the relevant equations. Our analysis involved also the heavy-traffic approximation of the system, which leads to a time-non-homogeneous diffusion process useful to describe the queue-length dynamics via more manageable formulas. Future developments of the present investigation will be centered on the inclusion of multiple types of customers and more general forms of catastrophe/repair mechanisms.