Family of Enneper Minimal Surfaces

Abstract

We consider a family of higher degree Enneper minimal surface $E_m$ for positive integers m in the three-dimensional Euclidean space ${\mathbb{E}}^3$. We compute algebraic equation, degree and integral free representation of Enneper minimal surface for $m=1,2,3$. Finally, we give some results and relations for the family $E_m$.

1. Introduction

Minimal surfaces have an important role in the mathematics, physics, biology, architecture, etc. These kinds of surfaces have been studied over the centuries by many mathematicians and also geometers. A minimal surface in ${\mathbb{E}}^3$ is a regular surface for which the mean curvature vanishes identically.

There are many important classical works on minimal surfaces in the literature such as [1,2,3,4,5,6,7,8,9,10]. However, we only see a few notable works about algebraic minimal surfaces, including general results and the properties. They were given by Enneper [11,12], Henneberg [13,14] and Weierstrass [9,15].

One of them is the classical Enneper minimal surface that was given by Enneper. See [11,12] for details. About Enneper minimal surface, many nice papers were done such as [16,17,18,19,20,21,22,23,24] in the last few decades.

In this paper, we introduce a family of higher degree Enneper minimal surface $E_m$ for positive integers m in the three-dimensional Euclidean space ${\mathbb{E}}^3$. In Section 2, we give the family of Enneper minimal surfaces $E_m.$ We obtain the algebraic equation and degree of surface $E_1$ (resp., $E_2,$ $E_3$). Using the integral free form of Weierstrass, we find some algebraic functions for $E_m$ $(m\ge 1,$ $m\in \mathbb{Z})$ in Section 3. Finally, we give some general findings for a family of higher degree Enneper minimal surface $E_m$ with a table in the last section.

2. The Family of Enneper Minimal Surfaces $E_m$

We will often identify $\overrightarrow{x}$ and $\overrightarrow{x^t}$ without further comment. Let ${\mathbb{E}}^3$ be a three-dimensional Euclidean space with natural metric $⟨.,.⟩=d{x}^2+d{y}^2+d{z}^2.$

Let $\mathcal{U}$ be an open subset of $\mathbb{C}$. A minimal (or isotropic) curve is an analytic function $\mathsf{\Psi }:\mathcal{U}\to {\mathbb{C}}^n$ such that ${\mathsf{\Psi }}^{\prime }\left(\zeta \right)·{\mathsf{\Psi }}^{\prime }\left(\zeta \right)=0,$ where $\zeta \in \mathcal{U}$, and ${\mathsf{\Psi }}^{\prime }:=\frac{\partial \mathsf{\Psi }}{\partial \zeta }.$ In addition, if ${\mathsf{\Psi }}^{\prime }·\overline{{\mathsf{\Psi }}^{\prime }}={\left|{\mathsf{\Psi }}^{\prime }\right|}^2\ne 0,$ then $\mathsf{\Psi }$ is a regular minimal curve.

Thus, let see the following lemma for complex minimal curves.

Lemma 1.

Let $\mathsf{\Psi }:\mathcal{U}\to {\mathbb{C}}^3$ be a minimal curve and write ${\mathsf{\Psi }}^{\prime }=\left({\phi }_1,{\phi }_2,{\phi }_3\right).$ Then,

$$\mathcal{F}=\frac{{\phi }_1-i{\phi }_2}{2}and\mathcal{G}=\frac{{\phi }_3}{{\phi }_1-i{\phi }_2}$$

lead to the Weierstrass representation of $\mathsf{\Psi }.$ That is,

$${\mathsf{\Psi }}^{\prime }=\left(\mathcal{F}\left(1-{\mathcal{G}}^2\right),i\mathcal{F}\left(1+{\mathcal{G}}^2\right),2\mathcal{F}\mathcal{G}\right).$$

Therefore, we have minimal surfaces in the associated family of a minimal curve, as given by the following Weierstrass representation theorem [9] for minimal surfaces:

Theorem 1.

Let $\mathcal{F}$ and $\mathcal{G}$ be two holomorphic functions defined on a simply connected open subset $\mathcal{U}$ of $\mathbb{C}$ such that F does not vanish on $\mathcal{U}$. Then, the map

$$\mathbf{x}\left(\zeta \right)=\mathrm{Re}{\int }^{\zeta }\left(\begin{array}{c}\mathcal{F}\left(1-{\mathcal{G}}^2\right)\\ i\mathcal{F}\left(1+{\mathcal{G}}^2\right)\\ 2\mathcal{F}\mathcal{G}\end{array}\right)d\zeta$$

is a minimal, conformal immersion of $\mathcal{U}$ into ${\mathbb{C}}^3,$ and $\mathbf{x}$ is called the Weierstrass patch.

We now consider the Enneper’s curve of value m:

Lemma 2.

The Enneper’s curve of value m

$$E_m\left(\zeta \right)=\left(\zeta -\frac{{\zeta }^{2m+1}}{2m+1},i\left(\zeta +\frac{{\zeta }^{2m+1}}{2m+1}\right),2\frac{{\zeta }^{m+1}}{m+1}\right)$$

(1)

is a minimal curve in ${\mathbb{C}}^3$, where $m\in \mathbb{R}-\left\{-1,-1/2\right\},$ $\zeta \in \mathbb{C}$, $i=\sqrt{-1}$.

Then, we have $E_m^{\prime }·E_m^{\prime }=0$. Hence, Enneper’s surface of value m in ${\mathbb{E}}^3$ is

$$E_m\left(\zeta \right)=\mathrm{Re}\int E_m^{\prime }\left(\zeta \right)d\zeta .$$

(2)

Lemma 3.

The Weierstrass patch determined by the functions

$$F\left(\zeta \right)=1and\mathcal{G}\left(\zeta \right)={\zeta }^m$$

is a representation of Enneper’s higher degree surfaces $E_m$, where $m\ge 2.$

For $m=1$, we get the classical Enneper’s surface $E_1$ (see also [4,11,25] for details).

Remark 1.

Note that the catenoid and classical Enneper’s surface are the only complete regular minimal surfaces in ${\mathbb{E}}^3$ with finite total curvature $-4\pi$.

See [5] for details.

Gray, Abbena and Salamon [26] gave the complex forms of the Enneper’s curve and surface of value m. Therefore, the associated family of minimal surfaces is described by

$$\begin{array}{ccc}\hfill E\left(r,\theta ;\alpha \right)& =& \mathrm{Re}\int e^{-i\alpha }{E}_m^{\prime }\hfill \\ & =& cos\left(\alpha \right)\mathrm{Re}\int E_m^{\prime }+sin\left(\alpha \right)\mathrm{Im}\int E_m^{\prime }\hfill \\ & =& cos\left(\alpha \right)E_m\left(r,\theta \right)+sin\left(\alpha \right)E_m^{\ast }\left(r,\theta \right).\hfill \end{array}$$

When $\alpha =0$ (resp. $\alpha =\pi /2),$ we have the Enneper’s surface of value m (resp. the conjugate surface $E_m^{\ast }$).

The parametric equation of $E_m$, in polar coordinates, is

$$E_m\left(r,\theta \right)=\left(\begin{array}{c}r\cos \left(\theta \right)-\frac{r^{2m+1}}{2m+1}\cos \left[\left(2m+1\right)\theta \right]\\ -r\sin \left(\theta \right)-\frac{r^{2m+1}}{2m+1}\sin \left[\left(2m+1\right)\theta \right]\\ 2\frac{r^{m+1}}{m+1}\cos \left[\left(m+1\right)\theta \right]\end{array}\right).$$

(3)

Using the binomial formula, we obtain the following parametric equations of $E_m\left(u,v\right):$

$$\begin{array}{c}x(u,v)=\mathrm{Re}\left\{u+iv-\frac{1}{2m+1}\left[{\sum }_{k=0}^{2m+1}\left(\genfrac{}{}{0pt}{}{2m+1}{k}\right)u^{2m+1-k}{\left(iv\right)}^k\right]\right\},\hfill \\ y(u,v)=\mathrm{Re}\left\{-v+iu+\frac{i}{2m+1}\left[{\sum }_{k=0}^{2m+1}\left(\genfrac{}{}{0pt}{}{2m+1}{k}\right)u^{2m+1-k}{\left(iv\right)}^k\right]\right\},\hfill \\ z(u,v)=\mathrm{Re}\left\{\frac{2}{m+1}\left[{\sum }_{k=0}^{m+1}\left(\genfrac{}{}{0pt}{}{m+1}{k}\right)u^{m+1-k}{\left(iv\right)}^k\right]\right\}.\hfill \end{array}$$

(4)

Next, we will focus on the algebraic equation and degree of surface $E_m.$

With ${\mathbb{R}}^3=\{(x,y,z)\mid x,y,z\in \mathbb{R}\},$ the set of roots of a polynomial $f(x,y,z)=0$ gives an algebraic surface. An algebraic surface is said to be of $degree$ n, when $n=\mathrm{deg}\left(f\right).$

It is seen that $\mathrm{deg}\left(x\right)=2m+1,$ $\mathrm{deg}\left(y\right)=2m+1,$ $\mathrm{deg}\left(z\right)=m+1$ for $E_m\left(u,v\right)$ (see also Table 1 for details). Using polynomial eliminate methods, we calculate the algebraic equations and degrees of the surfaces $E_1,$ $E_2,$ $E_3$. For the surface $E_1$ (i.e., classical Enneper surface), it is known that the surface has degree 9. Thus, it is also an algebraic minimal surface. For expanded results of $E_1$, see [4].

2.1. Algebraic Equation of Enneper Minimal Surface $E_1$

The simplest Weierstrass representation $\left(\mathcal{F},\mathcal{G}\right)=\left(1,\zeta \right)$ gives classical Enneper minimal surfaceof value 1. In polar coordinates, the parametric equation of $E_1$ is

$$E_1\left(r,\theta \right)=\left(\begin{array}{c}r\cos \left(\theta \right)-\frac{r^3}{3}\cos \left(3\theta \right)\\ -r\sin \left(\theta \right)-\frac{r^3}{3}\sin \left(3\theta \right)\\ r^2\cos \left(2\theta \right)\end{array}\right),$$

(5)

where $r\in [-1,1]$, $\theta \in [0,\pi ]$. The parametric form of the surface $E_1,$ in $\left(u,v\right)$ coordinates, is

$$E_1\left(u,v\right)=\left(\begin{array}{c}-\frac{1}{3}{u}^3+u{v}^2+u\\ -u^{2}v+\frac{1}{3}{v}^3-v\\ u^2-v^2\end{array}\right),$$

(6)

where $u,v\in \mathbb{R}$.

Lemma 4.

A plane intersects an algebraic minimal surface in an algebraic curve [13].

See also [4] for details. Considering the above lemma, we find the algebraic equation of the curve

$$E_1\left(u,0\right)={\gamma }_1\left(u\right)=\left(u-\frac{u^3}{3},0,u^2\right)$$

on the $xz$-plane is as follows (see Figure 1, left):

$$z^3-6z^2-9x^2+9z=0,$$

and its degree is $deg\left({\gamma }_1\right)=3.$ Thus, $xz$-plane intersects the algebraic minimal surface $E_1$ in an algebraic curve ${\gamma }_1\left(u\right)$.

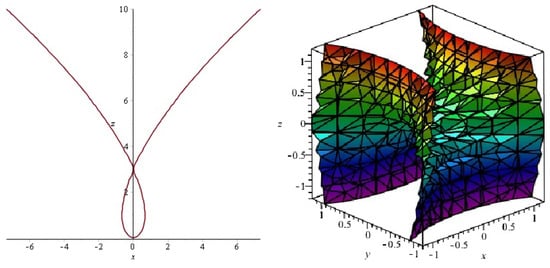
Figure 1. left: algebraic curve ${\gamma }_1\left(u\right)$; right: algebraic surface $E_1(x,y,z)=0$.

Using the polynomial eliminate method, we calculate the irreducible algebraic equation $E_1(x,y,z)=0$ of surface $E_1(u,v)$ by hand as follows (see Figure 1, right):

$$\begin{array}{c}-64z^9+432x^2{z}^6-432y^2{z}^6+1215x^4{z}^3+6318x^2{y}^2{z}^3+3888x^2{z}^5\hfill \\ +1215y^4{z}^3+3888y^2{z}^5+1152z^7+729x^6-2187x^4{y}^2+4374x^4{z}^2\hfill \\ +2187x^2{y}^4+6480x^2{z}^4-729y^6-4374y^4{z}^2-6480y^2{z}^4-729x^{4}z\hfill \\ +1458x^2{y}^{2}z-3888x^2{z}^3-729y^{4}z-3888y^2{z}^3-5184z^5=0.\hfill \end{array}$$

Its degree is $deg\left(E_1\right)=9$. Therefore, $E_1$ is an algebraic minimal surface. All of these results for classical Enneper surface $E_1$ were obtained first in [11] by Enneper.

Next, we study algebraic equations and degrees of the higher degree Enneper minimal surfaces for values m = 2 and m = 3.

2.2. Algebraic Equation of Enneper Minimal Surface $E_2$

In polar coordinates, the parametric equation of $E_2$ is

$$E_2\left(r,\theta \right)=\left(\begin{array}{c}r\cos \left(\theta \right)-\frac{r^5}{5}\cos \left(5\theta \right)\\ -r\sin \left(\theta \right)-\frac{r^5}{5}\sin \left(5\theta \right)\\ \frac{2}{3}{r}^3\cos \left(3\theta \right)\end{array}\right),$$

(7)

where $r\in [-1,1]$, $\theta \in [0,\pi ]$. The parametric form of the surface $E_2,$ in $\left(u,v\right)$ coordinates, is

$$E_2\left(u,v\right)=\left(\begin{array}{c}u-\frac{1}{5}{u}^5+2u^3{v}^2-u{v}^4\\ -v-u^{4}v+2u^2{v}^3-\frac{1}{5}{v}^5\\ \frac{2}{3}{u}^3-2u{v}^2\end{array}\right),$$

(8)

where $u,v\in \mathbb{R}$.

Using the polynomial eliminate method, we find the algebraic equation of the curve

$$E_2\left(u,0\right)={\gamma }_2\left(u\right)=\left(u-\frac{u^5}{5},0,\frac{2}{3}{u}^3\right)$$

on the $xz$-plane as follows (see Figure 2, left)

$$-243z^5-4000x^3-5400x{z}^2+6000z=0,$$

and its degree is $deg\left({\gamma }_2\right)=5.$ Hence, $xz$-plane intersects the algebraic minimal surface $E_2$ in an algebraic curve ${\gamma }_2\left(u\right)$.

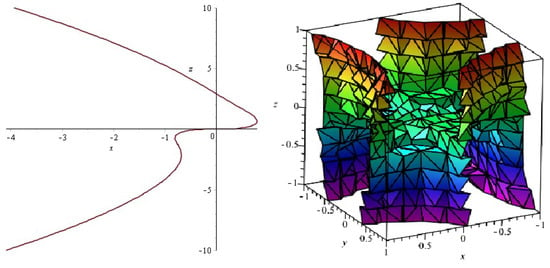
Figure 2. left: algebraic curve ${\gamma }_2\left(u\right)$; right: algebraic surface $E_2(x,y,z)=0$.

We calculate the irreducible algebraic equation $E_2(x,y,z)=0$ of surface $E_2(u,v)$ by using Maple software (version 17, Waterloo Maple Inc., Waterloo, ON, Canada) as follows (see Figure 2, right)

$$\begin{array}{c}847288609443z^{25}+4358480501250x^3{z}^{20}-13075441503750x{y}^2{z}^{20}\hfill \\ -131157978046875x^6{z}^{15}-474186536015625x^4{y}^2{z}^{15}\hfill \\ +107\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}=0,\hfill \end{array}$$

and its degree is $deg\left(E_2\right)=25$. Hence, $E_2$ is an algebraic minimal surface.

2.3. Algebraic Equation of Enneper Minimal Surface $E_3$

The parametric equation of Enneper’s minimal surface of value 3, in polar coordinates, is

$$E_3\left(r,\theta \right)=\left(\begin{array}{c}r\cos \left(\theta \right)-\frac{r^7}{7}\cos \left(7\theta \right)\\ -r\sin \left(\theta \right)-\frac{r^7}{7}\sin \left(7\theta \right)\\ \frac{1}{2}{r}^4\cos \left(4\theta \right)\end{array}\right),$$

(9)

where $r\in [-1,1]$, $\theta \in [0,\pi ]$. In $\left(u,v\right)$ coordinates, $E_3$ has the following form:

$$E_3\left(u,v\right)=\left(\begin{array}{c}u-\frac{1}{7}{u}^7+3u^5{v}^2-5u^3{v}^4+u{v}^6\\ -v-u^{6}v+5u^4{v}^3-3u^2{v}^5+\frac{1}{7}{v}^7\\ \frac{1}{2}{u}^4-3u^2{v}^2+\frac{1}{2}{v}^4\end{array}\right),$$

(10)

where $u,v\in \mathbb{R}$.

We get the algebraic equation of the curve

$$E_3\left(u,0\right)={\gamma }_3\left(u\right)=\left(u-\frac{u^7}{7},0,\frac{u^4}{2}\right)$$

on the $xz$-plane as follows:

$$128z^7-1568z^4-2401x^4-5488x^2{z}^2+4802z=0.$$

Its degree is $deg\left({\gamma }_3\right)=7.$ Then, we see that the $xz$-plane intersects the algebraic minimal surface $E_3$ in an algebraic curve ${\gamma }_3\left(u\right)$.

In Cartesian coordinates $x,y,z,$ the algebraic equation $E_3(x,y,z)=0$ of surface $E_3(u,v)$ by using Maple software is as follows:

$$\begin{array}{c}-2475880078570760549798248448z^{49}+5079604062565768134821675008x^4{z}^{42}\hfill \\ -30477624375394608808930050048x^2{y}^2{z}^{42}+5079604062565768134821675008y^4{z}^{42}\hfill \\ +633850350654216217766624493568x^8{z}^{35}+406\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}=0.\hfill \end{array}$$

Its degree is $deg\left(E_3\right)=49$. Thus, $E_3$ is an algebraic minimal surface.

Corollary 1.

The family of higher degree (also classical) Enneper minimal surfaces $E_m\left(u,v\right)$ are algebraic minimal surfaces, where $m\in \mathbb{Z},$ $m\ge 1$ (see Table 1).

Next, we obtain the general algebraic equation for the curve ${\gamma }_m$:

Corollary 2.

We consider the curve

$$E_m\left(u,0\right)={\gamma }_m\left(u\right)=\left(u-\frac{u^{2m+1}}{2m+1},0,\frac{2u^{m+1}}{m+1}\right)$$

on the $xz$-plane. By using Mathematica (version 8, Wolfram Research Inc., Champaign, IL, USA; Oxfordshire, UK; Tokyo, Japan; Boston, MA, USA), we get the following algebraic equation:

$$(2m+1){(x-2^{-\frac{1}{m+1}}{\left[(m+1)z\right]}^{\frac{1}{m+1}})}^{m+1}+(2^{-1}(m+1)z]{)}^{2m+1}=0,$$

(11)

where $m+1\ne 0,$ $2m+1\ne 0,$ and its degree is $deg\left({\gamma }_m\right)=2m+1.$

3. Integral Free Form

Integral free form of the Weierstrass representation (see [15]) is

$$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\mathrm{Re}\left(\begin{array}{c}\left(1-w^2\right){\varphi }^{″}\left(w\right)+2w{\varphi }^{\prime }\left(w\right)-2\varphi \left(w\right)\\ i\left[\left(1+w^2\right){\varphi }^{″}\left(w\right)-2w{\varphi }^{\prime }\left(w\right)+2\varphi \left(w\right)\right]\\ 2\left[w{\varphi }^{″}\left(w\right)-{\varphi }^{\prime }\left(w\right)\right]\end{array}\right)\equiv \mathrm{Re}\left(\begin{array}{c}{f}_1\left(w\right)\\ f_2\left(w\right)\\ f_3\left(w\right)\end{array}\right),$$

(12)

where algebraic function $\varphi \left(w\right)$ and the functions $f_i\left(w\right)$ are connected by the relation

$$\varphi \left(w\right)=\frac{1}{4}\left(w^2-1\right)f_1\left(w\right)-\frac{i}{4}\left(w^2+1\right)f_2\left(w\right)-\frac{1}{2}w{f}_3\left(w\right)$$

(13)

for $w\in \mathbb{C}.$ Integral free form is suitable for algebraic minimal surfaces. For instance, $\varphi \left(w\right)=\frac{1}{6}{w}^3$ gives rise to classical Enneper minimal surface $E_1$ (see [4] for details).

After some calculations by using the last two equations above, we get following corollary:

Corollary 3.

We obtain algebraic functions $\varphi \left(w\right)$, and then get the function $\varphi \left(w\right)=\frac{w^3}{2}-\frac{w^4}{3}+\frac{w^5}{10},$ which leads to Enneper minimal surface $E_2$. We also find $\varphi \left(w\right)=\frac{w^3}{2}-\frac{w^5}{4}+\frac{w^7}{14}$ for $E_3,$ $\varphi \left(w\right)=\frac{w^3}{2}-\frac{w^6}{5}+\frac{w^9}{18}$ for $E_4,$ and so on.

Hence, we have following lemma:

Lemma 5.

The algebraic function in the integral free form for a higher degree (also classical) Enneper minimal surfaces $E_m$ is as follows:

$${\varphi }_{E_m}\left(w\right)=\frac{w^3}{2}-\frac{w^{m+2}}{m+1}+\frac{w^{2m+1}}{2(2m+1)},$$

(14)

where $m\ge 1,m\in \mathbb{Z}.$

4. Conclusions

Briefly, we give all findings, calculated in Section 2 and Section 3 for the Enneper surface family, in Table 1 as follows.

Table 1. Algebraic Enneper minimal surfaces $E_m,$ $m\ge 1,m\in \mathbb{Z}$.

Surface	$\mathrm{deg}(\mathit{x},\mathit{y},\mathit{z})$	$\mathrm{deg}\left({\mathit{E}}_{\mathit{m}}\right)$	$\mathrm{deg}\left({\mathit{\gamma }}_{\mathit{m}}\right)$	Algebraic Function
$E_1$$\left(classical\right)$	$(3,3,2)$	9	3	$\frac{1}{6}{w}^3$
$E_2$	$(5,5,3)$	25	5	$\frac{1}{2}{w}^3-\frac{1}{3}{w}^4+\frac{1}{10}{w}^5$
$E_3$	$(7,7,4)$	49	7	$\frac{1}{2}{w}^3-\frac{1}{4}{w}^5+\frac{1}{14}{w}^7$
⋮	⋮	⋮	⋮	⋮
$E_m$	$(2m+1,2m+1,m+1)$	${(2m+1)}^2$	$2m+1$	$\frac{1}{2}{w}^3-\frac{1}{m+1}{w}^{m+2}+\frac{1}{2(2m+1)}{w}^{2m+1}$

Looking at the table above, we also have the following results:

Corollary 4.

We find the following relation between degree of algebraic function ${\varphi }_{E_m}\left(w\right)$ in the integral free form and curve ${\gamma }_m$ of surface $E_m$:

$$\mathrm{deg}\left({\gamma }_m\right)=2m+1=\mathrm{deg}\left({\varphi }_{E_m}\right)$$

and

$$\mathrm{deg}\left(E_m\right)={(2m+1)}^2={\left(\mathrm{deg}\left({\gamma }_m\right)\right)}^2={\left(\mathrm{deg}\left({\varphi }_{E_m}\right)\right)}^2,$$

where integers $m\ge 1$.

Remark 2.

For integers $m\ge 4$, algebraic equations and also degrees of Enneper minimal surfaces $E_m$ can be calculated. However, calculation is a time problem for software programmes.