Certain Notions of Neutrosophic Topological K-Algebras

Abstract

The concept of neutrosophic set from philosophical point of view was first considered by Smarandache. A single-valued neutrosophic set is a subclass of the neutrosophic set from a scientific and engineering point of view and an extension of intuitionistic fuzzy sets. In this research article, we apply the notion of single-valued neutrosophic sets to K-algebras. We introduce the notion of single-valued neutrosophic topological K-algebras and investigate some of their properties. Further, we study certain properties, including $C{}_5$-connected, super connected, compact and Hausdorff, of single-valued neutrosophic topological K-algebras. We also investigate the image and pre-image of single-valued neutrosophic topological K-algebras under homomorphism.

1. Introduction

A new kind of logical algebra, known as K-algebra, was introduced by Dar and Akram in [1]. A K-algebra is built on a group G by adjoining the induced binary operation on G. The group G is particularly of the type in which each non-identity element is not of order 2. This algebraic structure is, in general, non-commutative and non-associative with right identity element [1,2,3]. Akram et al. [4] introduced fuzzy K-algebras. They then developed fuzzy K-algebras with other researchers worldwide. The concepts and results of K-algebras have been broadened to the fuzzy setting frames by applying Zadeh’s fuzzy set theory and its generalizations, namely, interval-valued fuzzy sets, intuitionistic fuzzy sets, interval-valued intuitionistic fuzzy sets, bipolar fuzzy sets and vague sets [5]. In handling information regarding various aspects of uncertainty, non-classical logic is considered to be a more powerful tool than the classical logic. It has become a strong mathematical tool in computer science, medical, engineering, information technology, etc. In 1998, Smarandache [6] introduced neutrosophic set as a generalization of intuitionistic fuzzy set [7]. A neutrosophic set is identified by three functions called truth-membership $(T)$, indeterminacy-membership $(I)$ and falsity-membership $(F)$ functions. To apply neutrosophic set in real-life problems more conveniently, Smarandache [6] and Wang et al. [8] defined single-valued neutrosophic sets which takes the value from the subset of [0, 1]. Thus, a single-valued neutrosophic set is an instance of neutrosophic set.

Algebraic structures have a vital place with vast applications in various areas of life. Algebraic structures provide a mathematical modeling of related study. Neutrosophic set theory has also been applied to many algebraic structures. Agboola and Davazz introduced the concept of neutrosophic $BCI/BCK$-algebras and discuss elementary properties in [9]. Jun et al. introduced the notion of $(\varphi ,\psi )$ neutrosophic subalgebra of a $BCK/BCI$-algebra [10]. Jun et al. [11] defined interval neutrosophic sets on $BCK/BCI$-algebra [11]. Jun et al. [12] proposed neutrosophic positive implicative N-ideals and study their extension property [12] Several set theories and their topological structures have been introduced by many researchers to deal with uncertainties. Chang [13] was the first to introduce the notion of fuzzy topology. Later, Lowan [14], Pu and Liu [15], and Chattopadhyay and Samanta [16] introduced other concepts related to fuzzy topology. Coker [17] introduced the notion of intuitionistic fuzzy topology as a generalization of fuzzy topology. Salama and Alblowi [18] defined the topological structure of neutrosophic set theory. Akram and Dar [19] introduced the concept of fuzzy topological K-algebras. They extended their work on intuitionistic fuzzy topological K-algebras [20]. In this paper, we introduce the notion of single-valued neutrosophic topological K-algebras and investigate some of their properties. Further, we study certain properties, including $C{}_5$-connected, super connected, compact and Hausdorff, of single-valued neutrosophic topological K-algebras. We also investigate the image and pre-image of single-valued neutrosophic topological K-algebras under homomorphism.

2. Preliminaries

The notion of K-algebra was introduced by Dar and Akram in [1].

Definition 1.

[1] Let $(G,·,e)$ be a group in which each non-identity element is not of order 2. A K-algebra is a structure $\mathcal{K}=(G,·,\odot ,e)$ over a particular group G, where ⊙ is an induced binary operation $\odot :G\times G\to G$ is defined by $\odot (s,t)=s\odot t=s.t^{-1},$ and satisfy the following conditions:

(i) 

$(s\odot t)\odot (s\odot u)=(s\odot ((e\odot u)\odot (e\odot t)))\odot s;$

(ii) 

$s\odot (s\odot t)=(s\odot (e\odot t)\odot s;$

(iii) 

$s\odot s=e;$

(iv) 

$s\odot e=s;$ and

(v) 

$e\odot s=s^{-1}$

for all s, t, $u\in G$. The homomorphism between two K-algebras ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$ is a mapping $f:{\mathcal{K}}_1\to {\mathcal{K}}_2$ such that, for all u, v $\in {\mathcal{K}}_1$, $f(u\odot v)=f(u)\odot f(v)$.

In [6], Smarandache initiated the idea of neutrosophic set theory which is a generalization of intuitionistic fuzzy set theory. Later, Smarandache and Wang et al. introduced a single-valued neutrosophic set (SNS) as an instance of neutrosophic set in [8].

Definition 2.

[8] Let Z be a space of points with a general element $s\in Z$. A SNS $\mathcal{A}$ in Z is equipped with three membership functions: truth membership function (${\mathcal{T}}_{\mathcal{A}}$), indeterminacy membership function (${\mathcal{I}}_{\mathcal{A}}$) and falsity membership function(${\mathcal{F}}_{\mathcal{A}}$), where ∀$s\in Z$, ${\mathcal{T}}_{\mathcal{A}}(s),{\mathcal{I}}_{\mathcal{A}}(s),{\mathcal{F}}_{\mathcal{A}}(s)\in [0,1]$. There is no restriction on the sum of these three components. Therefore, $0\le {\mathcal{T}}_{\mathcal{A}}(s)+{\mathcal{I}}_{\mathcal{A}}(s)+{\mathcal{F}}_{\mathcal{A}}(s)\le 3$.

Definition 3.

[8] A single-valued neutrosophic empty set $({\varnothing }_{SN})$ and single-valued neutrosophic whole set $(1_{SN})$ on Z is defined as:

• ${\varnothing }_{SN}(u)=\{u\in Z:(u,0,0,1)\}.$
• $1_{SN}(u)=\{u\in Z:(u,1,1,0)\}.$

Definition 4.

[8] If f is a mapping from a set $Z_1$ into a set $Z_2,$ then the following statements hold:

(i) 

Let $\mathcal{A}$ be a SNS in $Z_1$ and $\mathcal{B}$ be a SNS in $Z_2$, then the pre-image of $\mathcal{B}$ is a SNS in $Z_1$, denoted by $f^{-1}(\mathcal{B}),$ defined as:

$f^{-1}(\mathcal{B})=\{z_1\in Z_1:f^{-1}({\mathcal{T}}_{\mathcal{B}})(z_1)={\mathcal{T}}_{\mathcal{B}}(f(z_1)),f^{-1}({\mathcal{I}}_{\mathcal{B}})(z_1)={\mathcal{I}}_{\mathcal{B}}(f(z_1)),f^{-1}({\mathcal{F}}_{\mathcal{B}})(z_1)={\mathcal{F}}_{\mathcal{B}}(f(z_1))\}$.

(ii) 

Let $\mathcal{A}=\{z_1\in Z_1:{\mathcal{T}}_{\mathcal{A}}(z_1),{\mathcal{I}}_{\mathcal{A}}(z_1),{\mathcal{F}}_{\mathcal{A}}(z_1)\}$ be a SNS in $Z_1$ and $\mathcal{B}=\{z_2\in Z_2:{\mathcal{T}}_{\mathcal{B}}(z_2),{\mathcal{I}}_{\mathcal{B}}(z_2),{\mathcal{F}}_{\mathcal{B}}(z_2)\}$ be a SNS in $Z_2$. Under the mapping f, the image of $\mathcal{A}$ is a SNS in $Z_2$, denoted by $f(\mathcal{A}),$ defined as: $f(\mathcal{A})=\{z_2\in Z_2:f_{sup}({\mathcal{T}}_{\mathcal{A}})(z_2),f_{sup}({\mathcal{I}}_{\mathcal{A}})(z_2),f_{inf}({\mathcal{F}}_{\mathcal{A}})(z_2)\},$ where for all $z_2\in Z_2.$

$$f_{sup}({\mathcal{T}}_{\mathcal{A}})(z_2)=\left\{\begin{array}{ll}\underset{z_1\in f^{-1}{}_{(z_2)}{\mathcal{T}}_{\mathcal{A}}(Z_1)}{sup},& \mathit{if}{f}_{(z_2)}^{-1}\ne \varnothing ,\\ 0,& \mathit{otherwise},\end{array}\right.$$

$$f_{sup}({\mathcal{I}}_{\mathcal{A}})(z_2)=\left\{\begin{array}{ll}\underset{z_1\in f^{-1}{}_{(z_2)}{\mathcal{I}}_{\mathcal{A}}(Z_1)}{sup},& \mathit{if}{f}_{(z_2)}^{-1}\ne \varnothing ,\\ 0,& \mathit{otherwise},\end{array}\right.$$

$$f_{inf}({\mathcal{F}}_{\mathcal{A}})(z_2)=\left\{\begin{array}{ll}\underset{z_1\in f^{-1}{}_{(z_2)}{\mathcal{F}}_{\mathcal{A}}(Z_1)}{inf},& \mathit{if}{f}_{(z_2)}^{-1}\ne \varnothing ,\\ 0,& \mathit{otherwise}.\end{array}\right.$$

We formulate the following proposition.

Proposition 1.

Let $f:Z_1\to Z_2$ and $\mathcal{A},({\mathcal{A}}_j,j\in J)$ be a SNS in $Z_1$ and $\mathcal{B}$ be a SNS in $Z_2$. Then, f possesses the following properties:

(i) 

If f is onto, then $f(1_{SN})=1_{SN}.$

(ii) 

$f({\varnothing }_{SN})={\varnothing }_{SN}.$

(iii) 

$f^{-1}(1_{SN})=1_{SN}.$

(iv) 

$f^{-1}({\varnothing }_{SN})={\varnothing }_{SN}.$

(v) 

If f is onto, then $f(f^{-1}(\mathcal{B})=\mathcal{B}.$

(vi) 

$f^{-1}({\displaystyle \bigcup _{i=1}^n}{\mathcal{A}}_i)={\displaystyle \bigcup _{i=1}^n}{f}^{-1}({\mathcal{A}}_i).$

3. Neutrosophic Topological K-algebras

Definition 5.

Let Z be a nonempty set. A collection χ of single-valued neutrosophic sets (SNSs) in Z is called a single-valued neutrosophic topology (SNT) on Z if the following conditions hold:

(a) 

${\varnothing }_{SN},1_{SN}\in \chi$

(b) 

If $\mathcal{A},\mathcal{B}\in \chi$, then $\mathcal{A}\bigcap \mathcal{B}\in \chi$

(c) 

If ${\mathcal{A}}_i\in \chi$, $\forall i\in I$, then ${\bigcup }_{i\in I}{\mathcal{A}}_i\in \chi$

The pair $(Z,\chi )$ is called a single-valued neutrosophic topological space (SNTS). Each member of χ is said to be χ-open or single-valued neutrosophic open set (SNOS) and compliment of each open single-valued neutrosophic set is a single-valued neutrosophic closed set (SNCS). A discrete topology is a topology which contains all single-valued neutrosophic subsets of Z and indiscrete if its elements are only ${\varnothing }_{SN}$, $1_{SN}$.

Definition 6.

Let $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ be a single-valued neutrosophic set in $\mathcal{K}$. Then, $\mathcal{A}$ is called a single-valued neutrosophic K-subalgebra of $\mathcal{K}$ if following conditions hold for $\mathcal{A}$:

(i) 

${\mathcal{T}}_{\mathcal{A}}(e)\ge {\mathcal{T}}_{\mathcal{A}}(s),$${\mathcal{I}}_{\mathcal{A}}(e)\ge {\mathcal{I}}_{\mathcal{A}}(s),$${\mathcal{F}}_{\mathcal{A}}(e)\le {\mathcal{F}}_{\mathcal{A}}(s).$

(ii) 

${\mathcal{T}}_{\mathcal{A}}(s\odot t)\ge min\{{\mathcal{T}}_{\mathcal{A}}(s),{\mathcal{T}}_{\mathcal{A}}(t)\},$

${\mathcal{I}}_{\mathcal{A}}(s\odot t)\ge min\{{\mathcal{I}}_{\mathcal{A}}(s),{\mathcal{I}}_{\mathcal{A}}(t)\},$

${\mathcal{F}}_{\mathcal{A}}(s\odot t)\le max\{{\mathcal{F}}_{\mathcal{A}}(s),{\mathcal{F}}_{\mathcal{A}}(t)\}$∀$s,t\in \mathcal{K}.$

Example 1.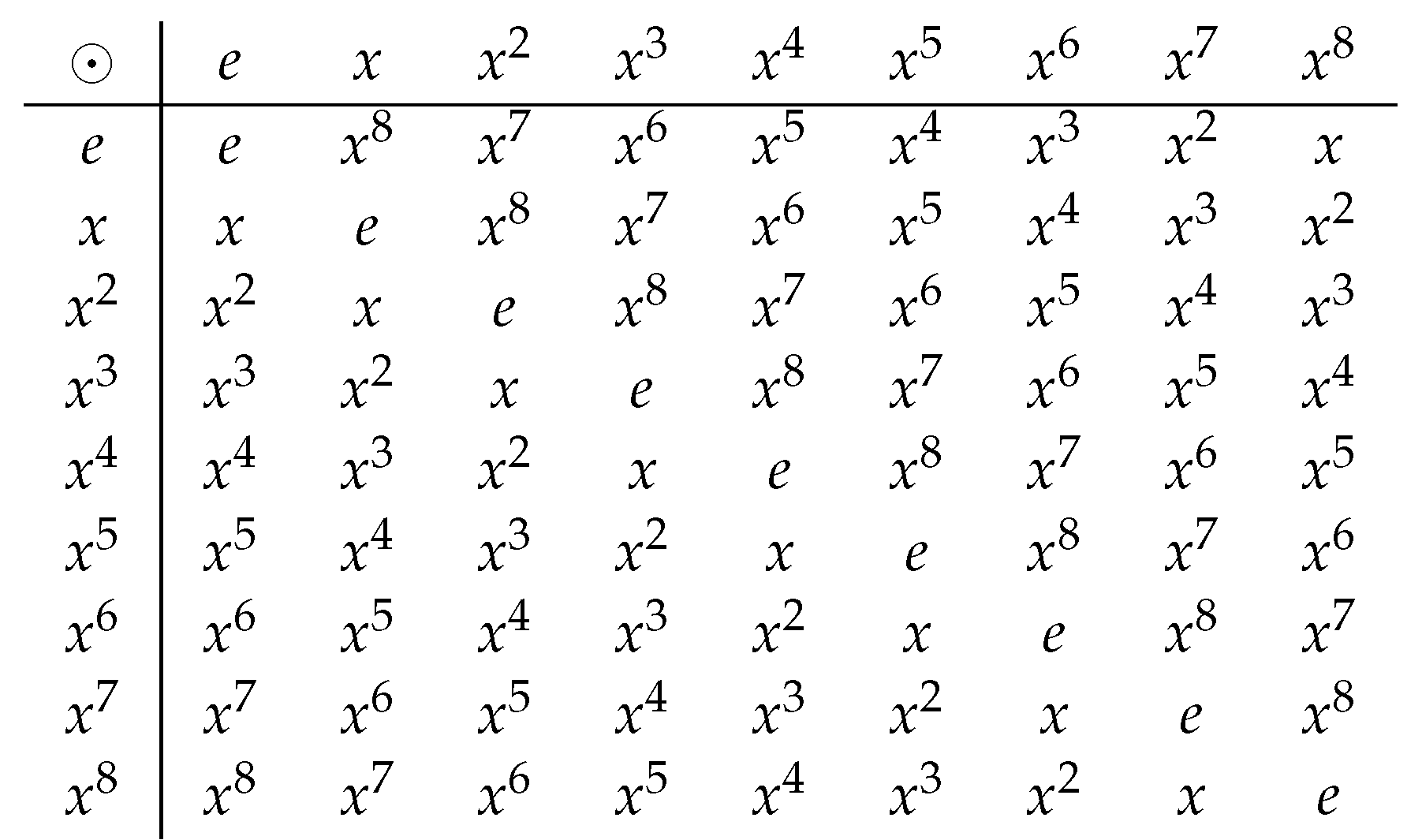

Consider a K-algebra $\mathcal{K}=(G,·,\odot ,e)$, where $G=\{e,x,x^2,x^3,x^4,x^5,x^6,x^7,x^8\}$ is the cyclic group of order 9 and Caley’s table for ⊙ is given as:

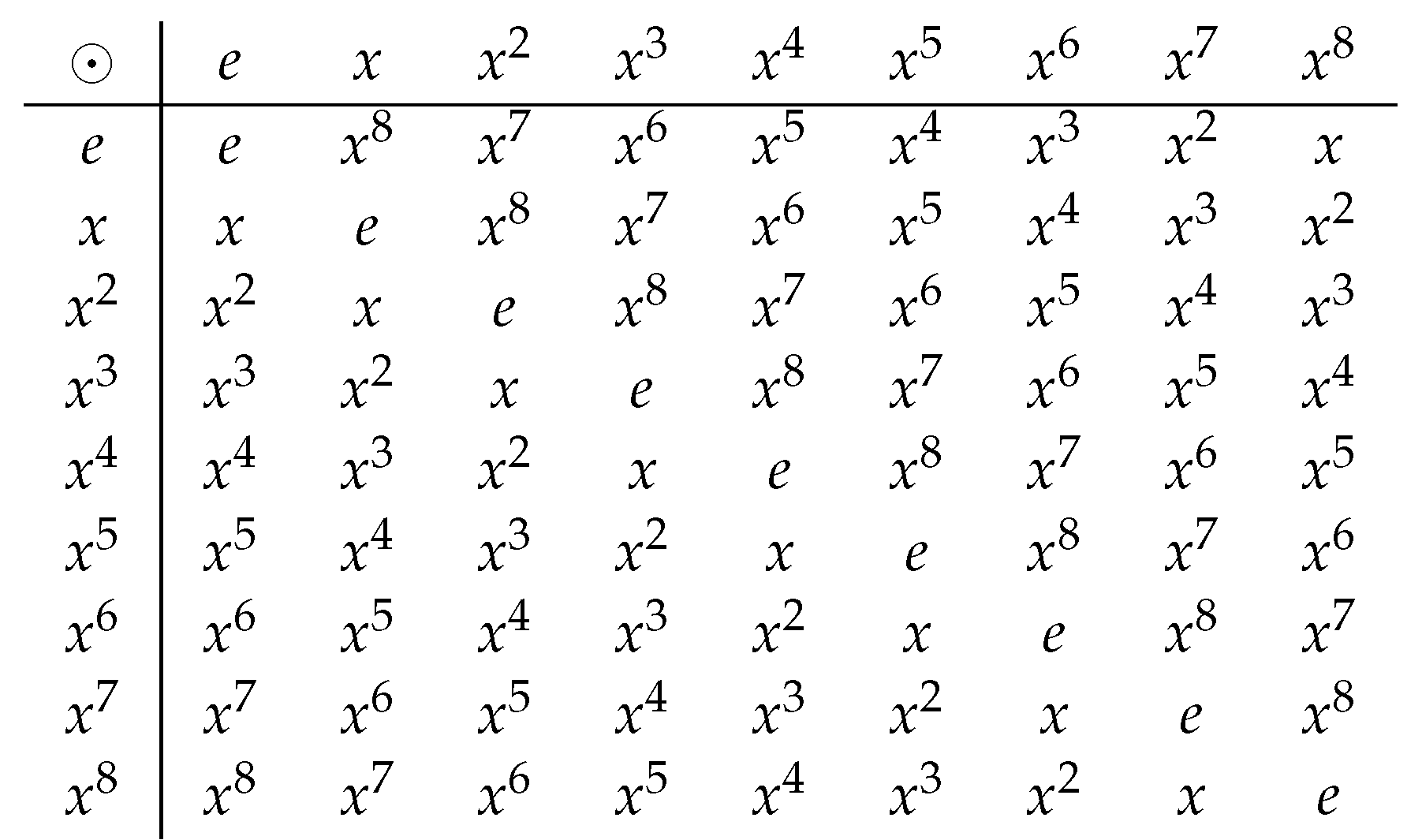
If we define a single-valued neutrosophic set $\mathcal{A},\mathcal{B}$ in $\mathcal{K}$ such that:

$$\begin{array}{c}\hfill \mathcal{A}=\{(e,0.4,0.5,0.8),(s,0.3,0.4,0.7)\},\\ \hfill \mathcal{B}=\{(e,0.3,0.4,0.8),(s,0.2,0.3,0.6)\}\end{array}$$

∀$\mathit{s}\ne \mathit{e}\in \mathit{G}.$

According to Definition 5, the family $\{{\varnothing }_{SN},1_{SN},\mathcal{A},\mathcal{B}\}$ of SNSs of K-algebra is a SNT on $\mathcal{K}$. We define a SNS $\mathcal{A}=\{{\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}}\}$ in $\mathcal{K}$ such that ${\mathcal{T}}_{\mathcal{A}}(e)=0.7,{\mathcal{I}}_{\mathcal{A}}(e)=0.5,{\mathcal{F}}_{\mathcal{A}}(e)=0.2,{\mathcal{T}}_{\mathcal{A}}(s)=0.2,{\mathcal{I}}_{\mathcal{A}}(s)=0.4,{\mathcal{F}}_{\mathcal{A}}(s)=0.6$. Clearly, $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ is a SN K-subalgebra of $\mathcal{K}$.

Definition 7.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra and let ${\chi }_{\mathcal{K}}$ be a topology on $\mathcal{K}$. Let $\mathcal{A}$ be a SNS in $\mathcal{K}$ and let ${\chi }_{\mathcal{K}}$ be a topology on $\mathcal{K}$. Then, an induced single-valued neutrosophic topology on $\mathcal{A}$ is a collection or family of single-valued neutrosophic subsets of $\mathcal{A}$ which are the intersection with $\mathcal{A}$ and single-valued neutrosophic open sets in $\mathcal{K}$ defined as ${\chi }_{\mathcal{A}}=\{\mathcal{A}\cap F:F\in {\chi }_{\mathcal{K}}\}$. Then, ${\chi }_{\mathcal{A}}$ is called single-valued neutrosophic induced topology on $\mathcal{A}$ or relative topology and the pair $(\mathcal{A},{\chi }_{\mathcal{A}})$ is called an induced topological space or single-valued neutrosophic subspace of $(\mathcal{K},{\chi }_{\mathcal{K}})$.

Definition 8.

Let $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be two SNTSs and let $f:({\mathcal{K}}_1,{\chi }_{{}_1})\to ({\mathcal{K}}_2,{\chi }_{{}_2})$. Then, f is called single-valued neutrosophic continuous if following conditions hold:

(i) 

For each SNS $\mathcal{A}\in {\chi }_{{}_2}$, $f^{-1}(\mathcal{A})\in {\chi }_{{}_1}$.

(ii) 

For each SN K-subalgebra $\mathcal{A}\in {\chi }_{{}_2}$, $f^{-1}(\mathcal{A})$ is a SN K-subalgebra $\in {\chi }_{{}_1}$.

Definition 9.

Let $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be two SNTSs and let $(\mathcal{A},{\chi }_{\mathcal{A}})$ and $(\mathcal{B},{\chi }_{\mathcal{B}})$ be two single-valued neutrosophic subspaces over $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$. Let f be a mapping from $({\mathcal{K}}_1,{\chi }_{{}_1})$ into $({\mathcal{K}}_2,{\chi }_{{}_2})$, then f is a mapping from $(\mathcal{A},{\chi }_{\mathcal{A}})$ to $(\mathcal{B},{\chi }_{\mathcal{B}})$ if $f(\mathcal{A})\subset \mathcal{B}$.

Definition 10.

Let f be a mapping from $(\mathcal{A},{\chi }_{\mathcal{A}})$ to $(\mathcal{B},{\chi }_{\mathcal{B}})$. Then, f is relatively single-valued neutrosophic continuous if for every SNOS $Y_{\mathcal{B}}$ in ${\chi }_{\mathcal{B}}$, $f^{-1}(Y_{\mathcal{B}})\cap \mathcal{A}\in {\chi }_{\mathcal{A}}$.

Definition 11.

Let f be a mapping from $(\mathcal{A},{\chi }_{\mathcal{A}})$ to $(\mathcal{B},{\chi }_{\mathcal{B}})$. Then, f is relatively single-valued neutrosophic open if for every SNOS $X_{\mathcal{A}}$ in ${\chi }_{\mathcal{A}}$, the image $f(X_{\mathcal{A}})\in {\chi }_{\mathcal{B}}$.

Proposition 2.

Let $(\mathcal{A},{\chi }_{\mathcal{A}})$ and $(\mathcal{B},{\chi }_{\mathcal{B}})$ be single-valued neutrosophic subspaces of $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$, where ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$ are K-algebras. If f is a single-valued neutrosophic continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2$ and $f(\mathcal{A})\subset \mathcal{B}$. Then, f is relatively single-valued neutrosophic continuous function from $\mathcal{A}$ into $\mathcal{B}$.

Definition 12.

Let $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be two SNTSs. A mapping $f:({\mathcal{K}}_1,{\chi }_{{}_1})\to ({\mathcal{K}}_2,{\chi }_{{}_2})$ is called a single-valued neutrosophic homomorphism if following conditions hold:

(i) 

f is a one-one and onto function.

(ii) 

f is a single-valued neutrosophic continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2.$

(iii) 

$f^{-1}$ is a single-valued neutrosophic continuous function from ${\mathcal{K}}_2$ to ${\mathcal{K}}_1.$

Theorem 1.

Let $({\mathcal{K}}_1,{\chi }_{{}_1})$ be a SNTS and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be an indiscrete SNTS on K-algebras ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$, respectively. Then, each function f defined as $f:({\mathcal{K}}_1,{\chi }_{{}_1})\to ({\mathcal{K}}_2,{\chi }_{{}_2})$ is a single-valued neutrosophic continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2$. If $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be two discrete SNTSs ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$, respectively, then each homomorphism $f:({\mathcal{K}}_1,{\chi }_{{}_1})\to ({\mathcal{K}}_2,{\chi }_{{}_2})$ is a single values neutrosophic continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2$.

Proof. 

Let f be a mapping defined as $f:{\mathcal{K}}_1\to {\mathcal{K}}_2$. Let ${\chi }_{{}_1}$ be SNT on ${\mathcal{K}}_1$ and ${\chi }_{{}_2}$ be SNT on ${\mathcal{K}}_2$, where ${\chi }_{{}_2}=\{{\varnothing }_{SN},1_{SN}\}$. We show that $f^{-1}(\mathcal{A})$ is a single-valued neutrosophic K-subalgebra of ${\mathcal{K}}_1$, i.e., for each $\mathcal{A}\in {\chi }_{{}_2},f^{-1}(\mathcal{A})\in {\chi }_{{}_1}$. Since ${\chi }_{{}_2}=\{{\varnothing }_{SN},1_{SN}\}$, then for any $u\in {\chi }_{{}_1},$ consider ${\varnothing }_{SN}\in {\chi }_{{}_2}$ such that $f^{-1}({\varnothing }_{SN})(u)={\varnothing }_{SN}(f(u))={\varnothing }_{SN}(u)$.

Therefore, $(f^{-1}({\varnothing }_{SN}))={\varnothing }_{SN}\in {\chi }_{{}_1}.$ Likewise, $(f^{-1}(1_{SN}))=1_{SN}\in {\chi }_{{}_1}.$ Hence, f is a SN continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2.$

Now, for the second part of the theorem, where both ${\chi }_{{}_1}$ and ${\chi }_{{}_2}$ are SNTSs on ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$, respectively, and $f:({\mathcal{K}}_1,{\chi }_{{}_1})\to ({\mathcal{K}}_2,{\chi }_{{}_2})$ is a homomorphism. Therefore, for all $\mathcal{A}\in {\chi }_{{}_2}$ and $f^{-1}\mathcal{A}\in {\chi }_{{}_1}$, where f is not a usual inverse homomorphism. To prove that $f^{-1}(\mathcal{A})$ is a single-valued neutrosophic K-subalgebra in of ${\mathcal{K}}_1.$ Let for $u,v\in {\mathcal{K}}_1,$

$$\begin{array}{ll}{f}^{-1}({\mathcal{T}}_{\mathcal{A}})(u\odot v)& ={\mathcal{T}}_{\mathcal{A}}(f(u\odot v))\\ & ={\mathcal{T}}_{\mathcal{A}}(f(u)\odot f(v))\\ & \ge min\{{\mathcal{T}}_{\mathcal{A}}(f(u))\odot {\mathcal{T}}_{(}f(v))\}\\ & =min\{f^{-1}({\mathcal{T}}_{\mathcal{A}})(u),f^{-1}({\mathcal{T}}_{\mathcal{A}})(v)\},\\ f^{-1}({\mathcal{I}}_{\mathcal{A}})(u\odot v)& ={\mathcal{I}}_{\mathcal{A}}(f(u\odot v))\\ & ={\mathcal{I}}_{\mathcal{A}}(f(u)\odot f(v))\\ & \ge min\{{\mathcal{I}}_{\mathcal{A}}(f(u))\odot {\mathcal{I}}_{(}f(v))\}\\ & =min\{f^{-1}({\mathcal{I}}_{\mathcal{A}})(u),f^{-1}({\mathcal{I}}_{\mathcal{A}})(v)\},\\ f^{-1}({\mathcal{F}}_{\mathcal{A}})(u\odot v)& ={\mathcal{F}}_{\mathcal{A}}(f(u\odot v))\\ & ={\mathcal{F}}_{\mathcal{A}}(f(u)\odot f(v))\\ & \le max\{{\mathcal{F}}_{\mathcal{A}}(f(u))\odot {\mathcal{F}}_{(}f(v))\}\\ & =max\{f^{-1}({\mathcal{F}}_{\mathcal{A}})(u),f^{-1}({\mathcal{F}}_{\mathcal{A}})(v)\}.\end{array}$$

Hence, f is a single-valued neutrosophic continuous function from ${\mathcal{K}}_1$ to ${\mathcal{K}}_2.$ □

Proposition 3.

Let ${\chi }_{{}_1}$ and ${\chi }_{{}_2}$ be two SNTSs on $\mathcal{K}$. Then, each homomorphism $f:(\mathcal{K},{\chi }_{{}_1})\to (\mathcal{K},{\chi }_{{}_2})$ is a single-valued neutrosophic continuous function.

Proof. 

Let $(\mathcal{K},{\chi }_1)$ and $(\mathcal{K},{\chi }_{{}_2})$ be two SNTSs, where $\mathcal{K}$ is a K-algebra. To prove the above result, it is enough to show that result is false for a particular topology. Let $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}},)$ and $\mathcal{B}=({\mathcal{T}}_{\mathcal{B}},{\mathcal{I}}_{\mathcal{B}},{\mathcal{F}}_{\mathcal{B}})$ be two SNSs in $\mathcal{K}$. Take ${\chi }_1=\{\varnothing {}_{SN},1{}_{SN},\mathcal{A}\}$ and ${\chi }_2=\{\varnothing {}_{SN},1{}_{SN},\mathcal{B}\}$. If $f:(\mathcal{K},{\chi }_1)\to (\mathcal{K},{\chi }_{{}_2})$, defined by $f(u)=e\odot u$, for all $u\in \mathcal{K}$, then f is a homomorphism. Now, for $u\in \mathcal{A}$, $v\in {\chi }_{{}_2}$, $(f^{-1}(\mathcal{B}))(u)=\mathcal{B}(f(u))=\mathcal{B}(e\odot u)=\mathcal{B}(u)$,

∀$u\in \mathcal{K}$, i.e., $f^{-1}(\mathcal{B})=\mathcal{B}$. Therefore, $(f^{-1}(\mathcal{B}))\notin {\chi }_{{}_1}.$ Hence, f is not a single-valued neutrosophic continuous mapping. □

Definition 13.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra and χ be a SNT on $\mathcal{K}$. Let $\mathcal{A}$ be a single-valued neutrosophic K-algebra (K-subalgebra) of $\mathcal{K}$ and ${\chi }_{\mathcal{A}}$ be a SNT on $\mathcal{A}$. Then, $\mathcal{A}$ is said to be a single-valued neutrosophic topological K-algebra (K-subalgebra) on $K$ if the self mapping ${\rho }_a:(\mathcal{A},{\chi }_{\mathcal{A}})\to (\mathcal{A},{\chi }_{\mathcal{A}})$ defined as ${\rho }_a(u)=u\odot a$, $\forall a\in \mathcal{K}$, is a relatively single-valued neutrosophic continuous mapping.

Theorem 2.

Let ${\chi }_{{}_1}$ and ${\chi }_{{}_2}$ be two SNTSs on ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$, respectively, and $f:{\mathcal{K}}_1\to {\mathcal{K}}_2$ be a homomorphism such that $f^{-1}({\chi }_2)={\chi }_1$. If $\mathcal{A}=\{{\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}}\}$ is a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_2,$ then $f^{-1}(\mathcal{A})$ is a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_1$.

Proof. 

Let $\mathcal{A}=\{{\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}}\}$ be a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_2$. To prove that $f^{-1}(\mathcal{A})$ be a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_1$. Let for any $u,v\in {\mathcal{K}}_1,$

$$\begin{array}{ll}{\mathcal{T}}_{f^{-1}(\mathcal{A})}(u\odot v)& ={\mathcal{T}}_{\mathcal{A}}(f(u\odot v))\\ & \ge min\{{\mathcal{T}}_{\mathcal{A}}(f(u)),{\mathcal{T}}_{\mathcal{A}}(f(v))\}\\ & =min\{{\mathcal{T}}_{f^{-1}(\mathcal{A})}(u),{\mathcal{T}}_{f^{-1}(\mathcal{A})}(v)\},\end{array}$$

$$\begin{array}{ll}{\mathcal{I}}_{f^{-1}(\mathcal{A})}(u\odot v)& ={\mathcal{I}}_{\mathcal{A}}(f(u\odot v))\\ & \ge min\{{\mathcal{I}}_{\mathcal{A}}(f(u)),{\mathcal{I}}_{\mathcal{A}}(f(v))\}\\ & =min\{{\mathcal{I}}_{f^{-1}(\mathcal{A})}(u),{\mathcal{I}}_{f^{-1}(\mathcal{A})}(v)\},\end{array}$$

$$\begin{array}{ll}{\mathcal{F}}_{f^{-1}(\mathcal{A})}(u\odot v)& ={\mathcal{F}}_{\mathcal{A}}(f(u\odot v))\\ & \le max\{{\mathcal{F}}_{\mathcal{A}}(f(u)),{\mathcal{F}}_{\mathcal{A}}(f(v))\}\\ & =max\{{\mathcal{F}}_{f^{-1}(\mathcal{A})}(u),{\mathcal{F}}_{f^{-1}(\mathcal{A})}(v)\}.\end{array}$$

Hence, $f^{-1}(\mathcal{A})$ is a single-valued neutrosophic K-algebra of ${\mathcal{K}}_1$.

Now, we prove that $f^{-1}(\mathcal{A})$ is single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_1$. Since f is a single-valued neutrosophic continuous function, then by proposition $3.1$, f is also a relatively single-valued neutrosophic continuous function which maps $(f^{-1}(\mathcal{A}),{\chi }_{f^{-1}(\mathcal{A})})$ to $(\mathcal{A},{\chi }_{\mathcal{A}})$.

Let $a\in {\mathcal{K}}_1$ and Y be a SNS in ${\chi }_{\mathcal{A}},$ and let X be a SNS in ${\chi }_{f^{-1}(\mathcal{A})}$ such that

$$f^{-1}(Y)=X.$$

(1)

We are to prove that ${\rho }_a:(f^{-1}(\mathcal{A}),{\chi }_{f^{-1}(\mathcal{A})})\to (f^{-1}(\mathcal{A}),{\chi }_{f^{-1}(\mathcal{A})})$ is relatively single-valued neutrosophic continuous mapping, then for any $a\in {\mathcal{K}}_1,$ we have

$$\begin{array}{ll}{\mathcal{T}}_{{\rho }_a^{-1}(X)}(u)& ={\mathcal{T}}_{(X)}({\rho }_a(u))={\mathcal{T}}_{(X)}(u\odot a)\\ & ={\mathcal{T}}_{f^{-1}(Y)}(u\odot a)={\mathcal{T}}_{(Y)}(f(u\odot a))\\ & ={\mathcal{T}}_{(Y)}(f(u)\odot f(a))={\mathcal{T}}_{(Y)}(\rho {}_{f(a)}(f(u)))\\ & =\mathcal{T}{}_{{\rho }^{-1}f(a)Y}(f(u))=\mathcal{T}{}_{f^{-1}}({\rho }_{f(a)}^{-1}(Y)(u)),\end{array}$$

$$\begin{array}{ll}{\mathcal{I}}_{{\rho }_a^{-1}(X)}(u)& ={\mathcal{I}}_{(X)}({\rho }_a(u))={\mathcal{I}}_{(X)}(u\odot a)\\ & ={\mathcal{I}}_{f^{-1}(Y)}(u\odot a)={\mathcal{I}}_{(Y)}(f(u\odot a))\\ & ={\mathcal{I}}_{(Y)}(f(u)\odot f(a))={\mathcal{I}}_{(Y)}(\rho {}_{f(a)}(f(u)))\\ & =\mathcal{I}{}_{{\rho }^{-1}f(a)Y}(f(u))=\mathcal{I}{}_{f^{-1}}({\rho }_{f(a)}^{-1}(Y)(u)),\end{array}$$

$$\begin{array}{ll}{\mathcal{F}}_{{\rho }_a^{-1}(X)}(u)& ={\mathcal{F}}_{(X)}({\rho }_a(u))={\mathcal{F}}_{(X)}(u\odot a)\\ & ={\mathcal{F}}_{f^{-1}(Y)}(u\odot a)={\mathcal{F}}_{(Y)}(f(u\odot a))\\ & ={\mathcal{F}}_{(Y)}(f(u)\odot f(a))={\mathcal{F}}_{(Y)}(\rho {}_{f(a)}(f(u)))\\ & =\mathcal{F}{}_{{\rho }^{-1}f(a)Y}(f(u))=\mathcal{F}{}_{f^{-1}}({\rho }_{f(a)}^{-1}(Y)(u)).\end{array}$$

It concludes that ${\rho }_a^{-1}(X)=f^{-1}({\rho }_{f(a)}^{-1}(Y))$. Thus, ${\rho }_a^{-1}(X)\cap f^{-1}(\mathcal{A})=f^{-1}({\rho }_{f(a)}^{-1}(Y))\cap f^{-1}(\mathcal{A})$ is a SNS in $f^{-1}(\mathcal{A})$ and a SNS in ${\chi }_{f^{-1}(\mathcal{A})}$. Hence, $f^{-1}(\mathcal{A})$ and a single-valued neutrosophic topological K-algebra of $\mathcal{K}$. Hence, the proof. □

Theorem 3.

Let $({\mathcal{K}}_1,{\chi }_{{}_1})$ and $({\mathcal{K}}_2,{\chi }_{{}_2})$ be two SNTSs on ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$, respectively, and let f be a bijective homomorphism of ${\mathcal{K}}_1$ into ${\mathcal{K}}_2$ such that $f({\chi }_1)={\chi }_2$. If $\mathcal{A}$ is a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_1$, then $f(\mathcal{A})$ is a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_2$.

Proof. 

Suppose that $\mathcal{A}=\{{\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}}\}$ is a SN topological K-algebra of ${\mathcal{K}}_1$. To prove that $f(\mathcal{A})$ is a single-valued neutrosophic topological K-algebra of ${\mathcal{K}}_2$, let, for $u,v\in {\mathcal{K}}_2$,

$$f(\mathcal{A})=(f_{sup}({\mathcal{T}}_{\mathcal{A}})(v),f_{sup}({\mathcal{I}}_{\mathcal{A}})(v),f_{inf}({\mathcal{F}}_{\mathcal{A}})(v)).$$

Let $a_o\in f^{-1}(u)$, $b_o\in f^{-1}(v)$ such that

$$\begin{array}{c}{sup}_{x\in f^{-1}(u)}{\mathcal{T}}_{\mathcal{A}}(x)={\mathcal{T}}_{\mathcal{A}}(a_o),{sup}_{x\in f^{-1}(v)}{\mathcal{T}}_{\mathcal{A}}(x)={\mathcal{T}}_{\mathcal{A}}(b_o),\\ {sup}_{x\in f^{-1}(u)}{\mathcal{I}}_{\mathcal{A}}(x)={\mathcal{I}}_{\mathcal{A}}(a_o),{sup}_{x\in f^{-1}(v)}{\mathcal{I}}_{\mathcal{A}}(x)={\mathcal{I}}_{\mathcal{A}}(b_o),\\ {inf}_{x\in f^{-1}(u)}{\mathcal{F}}_{\mathcal{A}}(x)={\mathcal{F}}_{\mathcal{A}}(a_o),{inf}_{x\in f^{-1}(v)}{\mathcal{F}}_{\mathcal{A}}(x)={\mathcal{F}}_{\mathcal{A}}(b_o).\end{array}$$

Now,

$$\begin{array}{cc}\hfill {\mathcal{T}}_{f(\mathcal{A})}(u\odot v)& ={\displaystyle \underset{x\in f^{-1}(u\odot v)}{sup}}{\mathcal{T}}_{\mathcal{A}}(x)\hfill \\ & \ge {\mathcal{T}}_{\mathcal{A}}(a_o,b_o)\hfill \\ & \ge min\{{\mathcal{T}}_{\mathcal{A}}(a_o),{\mathcal{T}}_{\mathcal{A}}(b_o)\}\hfill \\ & =min\{{\displaystyle \underset{x\in f^{-1}(u)}{sup}}{\mathcal{T}}_{\mathcal{A}}(x),{\displaystyle \underset{x\in f^{-1}(v)}{sup}}{\mathcal{T}}_{\mathcal{A}}(x)\}\hfill \\ & =min\{{\mathcal{T}}_{f(\mathcal{A})}(u),{\mathcal{T}}_{f(\mathcal{A})}(v)\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{I}}_{f(\mathcal{A})}(u\odot v)& ={\displaystyle \underset{x\in f^{-1}(u\odot v)}{sup}}{\mathcal{I}}_{\mathcal{A}}(x)\hfill \\ & \ge {\mathcal{I}}_{\mathcal{A}}(a_o,b_o)\hfill \\ & \ge min\{{\mathcal{I}}_{\mathcal{A}}(a_o),{\mathcal{I}}_{\mathcal{A}}(b_o)\}\hfill \\ & =min\{{\displaystyle \underset{x\in f^{-1}(u)}{sup}}{\mathcal{I}}_{\mathcal{A}}(x),{\displaystyle \underset{x\in f^{-1}(v)}{sup}}{\mathcal{I}}_{\mathcal{A}}(x)\}\hfill \\ & =min\{{\mathcal{I}}_{f(\mathcal{A})}(u),{\mathcal{I}}_{f(\mathcal{A})}(v)\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{F}}_{f(\mathcal{A})}(u\odot v)& ={\displaystyle \underset{x\in f^{-1}(u\odot v)}{inf}}{\mathcal{F}}_{\mathcal{A}}(x)\hfill \\ & \le {\mathcal{F}}_{\mathcal{A}}(a_o,b_o)\hfill \\ & \le max\{{\mathcal{F}}_{\mathcal{A}}(a_o),{\mathcal{F}}_{\mathcal{A}}(b_o)\}\hfill \\ & =max\{{\displaystyle \underset{x\in f^{-1}(u)}{inf}}{\mathcal{F}}_{\mathcal{A}}(x),{\displaystyle \underset{x\in f^{-1}(v)}{inf}}{\mathcal{F}}_{\mathcal{A}}(x)\}\hfill \\ & =max\{{\mathcal{F}}_{f(\mathcal{A})}(u),{\mathcal{F}}_{f(\mathcal{A})}(v)\}.\hfill \end{array}$$

Hence, $f(\mathcal{A})$ is a single-valued neutrosophic K-subalgebra of ${\mathcal{K}}_2.$ Now, we prove that the self mapping ${\rho }_b:(f(\mathcal{A}),{\chi }_f(\mathcal{A}))\to (f(\mathcal{A}),{\chi }_f(\mathcal{A})),$ defined by ${\rho }_b(v)=v\odot b$, for all $b\in {\mathcal{K}}_2$, is a relatively single-valued neutrosophic continuous mapping. Let $Y_{\mathcal{A}}$ be a SNS in ${\chi }_{\mathcal{A}}$, there exists a SNS $‘‘Y"$ in ${\chi }_1$ such that $Y_{\mathcal{A}}=Y\cap \mathcal{A}$. We show that for a SNS in ${\chi }_{f(\mathcal{A})}$,

$${\rho }^{-1}{}_b(Y_{f(\mathcal{A})})\cap f(\mathcal{A})\in {\chi }_{f(\mathcal{A})}$$

Since f is an injective mapping, then $f(Y_{\mathcal{A}})=f(Y\cap \mathcal{A})=f(Y)\cap f(\mathcal{A})$ is a SNS in ${\chi }_{f(\mathcal{A})}$ which shows that f is relatively single-valued neutrosophic open. In addition, f is surjective, then for all $b\in {\mathcal{K}}_2,a=f(b)$, where $a\in {\mathcal{K}}_1$.

Now,

$$\begin{array}{ll}{\mathcal{T}}_{f^{-1}({\rho }^{-1}{}_b(Y_{f(\mathcal{A})}))}(u)\hfill & ={\mathcal{T}}_{f^{-1}({\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})}))}(u)\hfill \\ & ={\mathcal{T}}_{{\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})})}(f(u))\hfill \\ & ={\mathcal{T}}_{(Y_{f(\mathcal{A})})}({\rho }_{f(a)}(f(u)))\hfill \\ & ={\mathcal{T}}_{(Y_{f(\mathcal{A})})}(f(u)\odot f(a))\hfill \\ & ={\mathcal{T}}_{f^{-1}(Y_{f(\mathcal{A})})}(u\odot a)\hfill \\ & ={\mathcal{T}}_{f^{-1}(Y_{f(\mathcal{A})})}({\rho }_a(u))\hfill \\ & ={\mathcal{T}}_{{\rho }^{-1}{}_{(}a)}(f^{-1}(Y_{f(\mathcal{A})}))(u),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{I}}_{f^{-1}({\rho }^{-1}{}_b(Y_{f(\mathcal{A})}))}(u)& ={\mathcal{I}}_{f^{-1}({\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})}))}(u)\hfill \\ & ={\mathcal{I}}_{{\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})})}(f(u))\hfill \\ & ={\mathcal{I}}_{(Y_{f(\mathcal{A})})}({\rho }_{f(a)}(f(u)))\hfill \\ & ={\mathcal{I}}_{(Y_{f(\mathcal{A})})}(f(u)\odot f(a))\hfill \\ & ={\mathcal{I}}_{f^{-1}(Y_{f(\mathcal{A})})}(u\odot a)\hfill \\ & ={\mathcal{I}}_{f^{-1}(Y_{f(\mathcal{A})})}({\rho }_a(u))\hfill \\ & ={\mathcal{I}}_{{\rho }^{-1}{}_{(}a)}(f^{-1}(Y_{f(\mathcal{A})}))(u),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{F}}_{f^{-1}({\rho }^{-1}{}_b(Y_{f(\mathcal{A})}))}(u)& ={\mathcal{F}}_{f^{-1}({\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})}))}(u)\hfill \\ & ={\mathcal{F}}_{{\rho }^{-1}{}_f(a)(Y_{f(\mathcal{A})})}(f(u))\hfill \\ & ={\mathcal{F}}_{(Y_{f(\mathcal{A})})}({\rho }_{f(a)}(f(u)))\hfill \\ & ={\mathcal{F}}_{(Y_{f(\mathcal{A})})}(f(u)\odot f(a))\hfill \\ & ={\mathcal{F}}_{f^{-1}(Y_{f(\mathcal{A})})}(u\odot a)\hfill \\ & ={\mathcal{F}}_{f^{-1}(Y_{f(\mathcal{A})})}({\rho }_a(u))\hfill \\ & ={\mathcal{F}}_{{\rho }^{-1}{}_{(}a)}(f^{-1}(Y_{f(\mathcal{A})}))(u).\hfill \end{array}$$

This implies that $f^{-1}({\rho }_{(b)}^{-1}((Y_{f(\mathcal{A})})))={\rho }_{(a)}^{-1}(f^{-1}(Y_{(\mathcal{A})}))$. Since ${\rho }_a:(\mathcal{A},{\chi }_{\mathcal{A}})\to (\mathcal{A},{\chi }_{\mathcal{A}})$ is relatively single-valued neutrosophic continuous mapping and f is relatively single-valued neutrosophic continues mapping from $(\mathcal{A},{\chi }_{\mathcal{A}})$ into $(f(\mathcal{A}),{\chi }_{f(\mathcal{A})})$, $f^{-1}({\rho }_{(b)}^{-1}((Y_{f(\mathcal{A})})))\cap \mathcal{A}={\rho }_{(a)}^{-1}(f^{-1}(Y_{(\mathcal{A})}))\cap \mathcal{A}$ is a SNS in ${\chi }_{\mathcal{A}}$. Hence, $f(f^{-1}({\rho }_{(b)}((Y_{f(\mathcal{A})})))\cap \mathcal{A})={\rho }_{(b)}^{-1}(Y_{f(\mathcal{A})})\cap f(\mathcal{A})$ is a SNS in ${\chi }_{\mathcal{A}}$, which completes the proof. □

Example 2.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra, where $G=\{e,x,x^2,x^3,x^4,x^5,x^6,x^7,x^8\}$ is the cyclic group of order 9 and Caley’s table for ⊙ is given in Example 1. We define a SNS as:

$$\begin{array}{c}\hfill \mathcal{A}=\{(e,0.4,0.5,0.8),(s,0.3,0.4,0.6)\},\\ \hfill \mathcal{B}=\{(e,0.3,0.4,0.8),(s,0.2,0.3,0.6)\},\end{array}$$

for all $\mathit{s}\ne \mathit{e}\in \mathit{G},$ where $\mathcal{A},\mathcal{B}\in [0,1]$. The collection ${\chi }_{\mathcal{K}}=\{{\varnothing }_{SN},1_{SN},\mathcal{A},\mathcal{B}\}$ of SNSs of $\mathcal{K}$ is a SNT on $\mathcal{K}$ and $(\mathcal{K},{\chi }_{\mathcal{K}})$ is a SNTS. Let $\mathcal{C}$ be a SNS in $\mathcal{K}$, defined as:

$$\mathcal{C}=\{(e,0.7,0.5,0.2),(s,0.5,0.4,0.6)\}\forall s\ne e\in G.$$

Clearly, $\mathcal{C}$ is a single-valued neutrosophic K-subalgebra of $\mathcal{K}$. By direct calculations relative topology ${\chi }_{\mathcal{C}}$ is obtained as ${\chi }_{\mathcal{C}}=\{{\varnothing }_{\mathcal{A}},1_{\mathcal{A}},\mathcal{A}\}$. Then, the pair $(\mathcal{C},{\chi }_{\mathcal{C}})$ is a single-valued neutrosophic subspace of $(\mathcal{K},{\chi }_{\mathcal{K}})$. We show that $\mathcal{C}$ is a single-valued neutrosophic topological K-subalgebra of $\mathcal{K}$, i.e., the self mapping ${\rho }_a:(\mathcal{C},{\chi }_{\mathcal{C}})\to (\mathcal{C},{\chi }_{\mathcal{C}})$ defined by ${\rho }_a(u)=u\odot a,\forall a\in \mathcal{K}$ is relatively single-valued neutrosophic continuous mapping, i.e., for a SNOS $\mathcal{A}$ in $(\mathcal{C},{\chi }_{\mathcal{C}})$, ${\rho }_a^{-1}(\mathcal{A})\cap \mathcal{C}\in {\chi }_{\mathcal{C}}$. Since ${\rho }_a$ is homomorphism, then ${\rho }_a^{-1}(\mathcal{A})\cap \mathcal{C}=\mathcal{A}\in {\chi }_{\mathcal{C}}$. Therefore, ${\rho }_a:(\mathcal{C},{\chi }_{\mathcal{C}})\to (\mathcal{C},{\chi }_{\mathcal{C}})$ is relatively single-valued neutrosophic continuous mapping. Hence, $\mathcal{C}$ is a single-valued neutrosophic topological K-algebra of $\mathcal{K}$.

Example 3.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra, where $G=\{e,x,x^2,x^3,x^4,x^5,x^6,x^7,x^8\}$ is the cyclic group of order 9 and Caley’s table for ⊙ is given in Example 3.1. We define a SNS as:

$$\begin{array}{c}\hfill \mathcal{A}=\{(e,0.4,0.5,0.8),(s,0.3,0.4,0.6)\},\\ \hfill \mathcal{B}=\{(e,0.3,0.4,0.8),(s,0.2,0.3,0.6)\},\\ \hfill \mathcal{D}=\{(e,0.2,0.1,0.3),(s,0.1,0.1,0.5)\},\end{array}$$

for all $\mathit{s}\ne \mathit{e}\in \mathit{G},$ where $\mathcal{A},\mathcal{B}\in [0,1]$. The collection ${\chi }_1=\{{\varnothing }_{SN},1_{SN},\mathcal{D}\}$ and ${\chi }_2=\{{\varnothing }_{SN},1_{SN},\mathcal{A},\mathcal{B}\}$ of SNSs of $\mathcal{K}$ are SNTs on $\mathcal{K}$ and $(\mathcal{K},{\chi }_1)$, $(\mathcal{K},{\chi }_2)$ be two SNTSs. Let $\mathcal{C}$ be a SNS in $(\mathcal{K},{\chi }_2)$, defined as:

$$\mathcal{C}=\{(e,0.7,0.5,0.2),(s,0.5,0.4,0.6)\},\forall s\ne e\in G.$$

Now, Let $f:(\mathcal{K},{\chi }_1)\to (\mathcal{K},{\chi }_2)$ be a homomorphism such that $f^{-1}({\chi }_2)={\chi }_1$ (we have not consider $\mathcal{K}$ to be distinct), then, by Proposition 3, f is a single-valued neutrosophic continuous function and f is also relatively single-valued neutrosophic continues mapping from $(\mathcal{K},{\chi }_1)$ into $(\mathcal{K},{\chi }_2)$. Since $\mathcal{C}$ is a SNS in $(\mathcal{K},{\chi }_2)$ and with relative topology ${\chi }_{\mathcal{C}}=\{{\varnothing }_{\mathcal{A}},1_{\mathcal{A}},\mathcal{A}\}$ is also a single-valued neutrosophic topological K-algebra of $(\mathcal{K},{\chi }_2)$. We prove that $f^{-1}(\mathcal{C})$ is a single-valued neutrosophic topological K-algebra in $(\mathcal{K},{\chi }_1)$. Since f is a continuous function, then, by Definition 8, $f^{-1}(\mathcal{C})$ is a single-valued neutrosophic K-subalgebra in $(K,{\chi }_1)$. To prove that $f^{-1}(c)$ is a single-valued neutrosophic topological K-algebra, then for $b\in {\mathcal{K}}_1$ take

$${\rho }_b:(f^{-1}(\mathcal{C}),{\chi }_{f^{-1}(\mathcal{C})})\to (f^{-1}(\mathcal{C}),{\chi }_{f^{-1}(\mathcal{C})}),$$

for $\mathcal{A}\in {\chi }_{f^{-1}(C)},{\rho }_b^{-1}(\mathcal{A})\cap f^{-1}(\mathcal{C})\in {\chi }_{f^{-1}(C)}$ which shows that $f^{-1}(C)$ is a single-valued neutrosophic topological K-algebra in $(\mathcal{K},{\chi }_1)$. Similarly, we can show that $f(\mathcal{C})$ is a a single-valued neutrosophic topological K-algebra in $(\mathcal{K},{\chi }_2)$ by considering a bijective homomorphism.

Definition 14.

Let χ be a SNT on $\mathcal{K}$ and $(\mathcal{K},\chi )$ be a SNTS. Then, $(\mathcal{K},\chi )$ is called single-valued neutrosophic $C_5$-disconnected topological space if there exist a SNOS and SNCS $\mathcal{H}$ such that $\mathcal{H}=({\mathcal{T}}_{\mathcal{H}},{\mathcal{I}}_{\mathcal{H}},{\mathcal{F}}_{\mathcal{H}},)\ne 1_{SN}$ and $\mathcal{H}=({\mathcal{T}}_{\mathcal{H}},{\mathcal{I}}_{\mathcal{H}},{\mathcal{F}}_{\mathcal{H}},)\ne {\varnothing }_{SN}$, otherwise $(\mathcal{K},\chi )$ is called single-valued neutrosophic $C_5$-connected.

Example 4.

Every indiscrete SNT space on $\mathcal{K}$ is $C_5$-connected.

Proposition 4.

Let $({\mathcal{K}}_1,{\chi }_1)$ and $({\mathcal{K}}_2,{\chi }_2)$ be two SNTSs and $f:({\mathcal{K}}_1,{\chi }_1)\to ({\mathcal{K}}_2,{\chi }_2)$ be a surjective single-valued neutrosophic continuous mapping. If $({\mathcal{K}}_1,{\chi }_1)$ is a single-valued neutrosophic $C_5$-connected space, then $({\mathcal{K}}_2,{\chi }_2)$ is also a single-valued neutrosophic $C_5$-connected space.

Proof. 

Suppose on contrary that $({\mathcal{K}}_2,{\chi }_2)$ is a single-valued neutrosophic $C_5$-disconnected space. Then, by Definition 14, there exist both SNOS and SNCS $\mathcal{H}$ be such that $\mathcal{H}\ne 1_{SN}$ and $\mathcal{H}\ne {\varnothing }_{SN}$. Since f is a single-valued neutrosophic continuous and onto function, so $f^{-1}(\mathcal{H})=1_{SN}$ or $f^{-1}(\mathcal{H})={\varnothing }_{SN}$, where $f^{-1}(\mathcal{H})$ is both SNOS and SNCS. Therefore,

$$\mathcal{H}=f(f^{-1}(\mathcal{H}))=f(1_{SN})=1_{SN}$$

(2)

and

$$\mathcal{H}=f(f^{-1}(\mathcal{H}))=f({\varnothing }_{SN})={\varnothing }_{SN},$$

(3)

a contradiction. Hence, $({\mathcal{K}}_2,{\chi }_2)$ is a single-valued neutrosophic $C_5$-connected space. □

Corollary 1.

Let χ be a SNT on $\mathcal{K}$. Then, $(\mathcal{K},\chi )$ is called a single-valued neutrosophic $C_5$-connected space if and only if there does not exist a single-valued neutrosophic continuous map $f:(\mathcal{K},\chi )\to ({\mathcal{F}}_T,{\chi }_T)$ such that $f\ne 1_{SN}$ and $f\ne {\varnothing }_{SN}$

Definition 15.

Let $\mathcal{A}=\{{\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}}\}$ be a SNS in $\mathcal{K}$. Let χ be a SNT on $\mathcal{K}$. The interior and closure of $\mathcal{A}$ in $\mathcal{K}$ is defined as:

${\mathcal{A}}^{Int}$: The union of SNOSs which contained in $\mathcal{A}.$

${\mathcal{A}}^{Clo}$: The intersection of SNCSs for which $\mathcal{A}$ is a subset of these SNCSs.

Remark 1.

Being union of SNOS ${\mathcal{A}}^{Int}$ is a SNO and ${\mathcal{A}}^{Clo}$ being intersection of SNCS is SNC.

Theorem 4.

Let $\mathcal{A}$ be a SNS in a SNTS $(\mathcal{K},\chi )$. Then, ${\mathcal{A}}^{Int}$ is such an open set which is the largest open set of $\mathcal{K}$ contained in $\mathcal{A}$.

Corollary 2.

$\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ is a SNOS in $\mathcal{K}$ if and only if ${\mathcal{A}}^{Int}=\mathcal{A}$ and $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ is a SNCS in $\mathcal{K}$ if and only if ${\mathcal{A}}^{Clo}=\mathcal{A}$.

Proposition 5.

Let $\mathcal{A}$ be a SNS in $\mathcal{K}$. Then, following results hold for $\mathcal{A}$:

(i) 

${(1_{SN})}^{Int}=1_{SN}.$

(ii) 

${({\varnothing }_{SN})}^{Clo}={\varnothing }_{SN}.$

(iii) 

${\overline{(\mathcal{A})}}^{Int}=\overline{{(\mathcal{A})}^{Clo}}.$

(iv) 

${\overline{(\mathcal{A})}}^{Clo}=\overline{{(\mathcal{A})}^{Int}}.$

Definition 16.

Let $\mathcal{K}$ be a K-algebra and χ be a SNT on $\mathcal{K}$. A SNOS $\mathcal{A}$ in $\mathcal{K}$ is said to be single-valued neutrosophic regular open if

$$\mathcal{A}={({\mathcal{A}}^{Clo})}^{Int}.$$

(4)

Remark 2.

Every SNOS which is regular is single-valued neutrosophic open and every single-valued neutrosophic closed and open set is a single-valued neutrosophic regular open.

Definition 17.

A single-valued neutrosophic super connected K-algebra is such a K-algebra in which there does not exist a single-valued neutrosophic regular open set $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ such that $\mathcal{A}\ne {\varnothing }_{SN}$ and $\mathcal{A}\ne 1_{SN}$. If there exists such a single-valued neutrosophic regular open set $\mathcal{A}=({\mathcal{T}}_{\mathcal{A}},{\mathcal{I}}_{\mathcal{A}},{\mathcal{F}}_{\mathcal{A}})$ such that $\mathcal{A}\ne {\varnothing }_{SN}$ and $\mathcal{A}\ne 1_{SN}$, then K-algebra is said to be a single-valued neutrosophic super disconnected.

Example 5.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra, where $G=\{e,x,x^2,x^3,x^4,x^5,x^6,x^7,x^8\}$ is the cyclic group of order 9 and Caley’s table for ⊙ is given in Example 1 We define a SNS as:

$$\mathcal{A}=\{(e,0.2,0.3,0.8),(s,0.1,0.2,0.6)\}.$$

Let ${\chi }_{\mathcal{K}}=\{{\varnothing }_{SN},1_{SN},\mathcal{A}\}$ be a SNT on $\mathcal{K}$ and let $\mathcal{B}=\{(e,0.3,0.3,0.8),(s,0.2,0.2,0.6)\}$ be a SNS in $\mathcal{K}$. here

$$\begin{array}{c}SNOSs:{\varnothing }_{SN}=\{0,0,1\},1_{SN}=\{1,1,0\},\mathcal{A}=\{(e,0.2,0.3,0.8),(s,0.1,0.2,0.6)\}.\hfill \\ SNCSs:{({\varnothing }_{SN})}^c={(\{0,0,1\})}^c=(\{1,1,0\})=1_{SN},{(1_{SN})}^c={(\{1,1,0\})}^c=(\{0,0,1\})={\varnothing }_{SN},\hfill \\ {(\mathcal{A})}^c={(\{(e,0.2,0.3,0.8),(s,0.1,0.2,0.6)\})}^c=(\{(e,0.8,0.3,0.2),(s,0.6,0.2,0.1)\})={\mathcal{A}}^{{}^{\prime }}(say).\hfill \end{array}$$

Then, closure of $\mathcal{B}$ is the intersection of closed sets which contain $\mathcal{B}$. Therefore,

$${\mathcal{A}}^{\prime }={\mathcal{B}}^{Clo}.$$

(5)

Now, interior of $\mathcal{B}$ is the union of open sets which contain in $\mathcal{B}$. Therefore,

$${\varnothing }_{SN}\bigcup \mathcal{A}=\mathcal{A}$$

$$\mathcal{A}={\mathcal{B}}^{Int}.$$

(6)

Note that ${({\mathcal{B}}^{Clo})}^{Clo}={\mathcal{B}}^{Clo}$. Now, if we consider a SNS $\mathcal{A}=\{(e,0.2,0.3,0.8),(s,0.1,0.2,0.6)\}$ in a K-algebra $\mathcal{K}$ and if ${\chi }_{\mathcal{K}}=\{{\varnothing }_{SN},1_{SN},\mathcal{A}\}$ is a SNT on $\mathcal{K}$. Then, ${(\mathcal{A})}^{Clo}=\mathcal{A}$ and ${(\mathcal{A})}^{Int}=\mathcal{A}$. Consequently,

$$\mathcal{A}={({\mathcal{A}}^{Clo})}^{Int},$$

(7)

which shows that $\mathcal{A}$ is a SN regular open set in K-algebra $\mathcal{K}$. Since $\mathcal{A}$ is a SN regular open set in $\mathcal{K}$ and $\mathcal{A}\ne {\varnothing }_{SN},\mathcal{A}\ne 1_{SN},$ then, by Definition 17, K-algebra $\mathcal{K}$ is a single-valued neutrosophic supper disconnected K-algebra.

Proposition 6.

Let $\mathcal{K}$ be a K-algebra and let $\mathcal{A}$ be a SNOS. Then, the following statements are equivalent:

(i) 

A K-algebra is single-valued neutrosophic super connected.

(ii) 

${(\mathcal{A})}^{Clo}=1{}_{SN}$, for each SNOS $\mathcal{A}\ne \varnothing {}_{SN}$.

(iii) 

${(\mathcal{A})}^{Int}=\varnothing {}_{SN}$, for each SNCS $\mathcal{A}\ne 1{}_{SN}$.

(iv) 

There do not exist SNOSs $\mathcal{A},\mathcal{F}$ such that $\mathcal{A}\subseteq \overline{\mathcal{F}}$ and $\mathcal{A}\ne \varnothing {}_{SN}\ne \mathcal{F}$ in K-algebra $\mathcal{K}$.

Definition 18.

Let $(\mathcal{K},\chi )$ be a SNTS, where $\mathcal{K}$ is a K-algebra. Let S be a collection of SNOSs in $\mathcal{K}$ denoted by $S=\{({\mathcal{T}}_{{\mathcal{A}}_j},{\mathcal{I}}_{{\mathcal{A}}_j},{\mathcal{F}}_{{\mathcal{A}}_j}):j\in J\}$. Let $\mathcal{A}$ be a SNOS in $\mathcal{K}$. Then, S is called a single-valued neutrosophic open covering of $\mathcal{A}$ if $\mathcal{A}\subseteq \bigcup S$.

Definition 19.

Let $\mathcal{K}$ be a K-algebra and $(\mathcal{K},\chi )$ be a SNTS. Let L be a finite sub-collection of S. If L is also a single-valued neutrosophic open covering of $\mathcal{A}$, then it is called a finite sub-covering of S and $\mathcal{A}$ is called single-valued neutrosophic compact if each single-valued neutrosophic open covering S of $\mathcal{A}$ has a finite sub-cover. Then, $(\mathcal{K},\chi )$ is called compact K-algebra.

Remark 3.

If either $\mathcal{K}$ is a finite K-algebra or χ is a finite topology on $\mathcal{K}$, i.e., consists of finite number of single-valued neutrosophic subsets of $\mathcal{K}$, then the SNT $(\mathcal{K},\chi )$ is a single-valued neutrosophic compact topological space.

Proposition 7.

Let $({\mathcal{K}}_1,{\chi }_1)$ and $({\mathcal{K}}_2,{\chi }_2)$ be two SNTSs and f be a single-valued neutrosophic continuous mapping from ${\mathcal{K}}_1$ into ${\mathcal{K}}_2$. Let $\mathcal{A}$ be a SNS in $({\mathcal{K}}_1,{\chi }_1)$. If $\mathcal{A}$ is single-valued neutrosophic compact in $({\mathcal{K}}_1,{\chi }_1)$, then $f(\mathcal{A})$ is single-valued neutrosophic compact in $({\mathcal{K}}_2,{\chi }_2).$

Proof. 

Let $f:({\mathcal{K}}_1,{\chi }_1)\to ({\mathcal{K}}_2,{\chi }_2)$ be a single-valued neutrosophic continuous function. Let $\acute{S}=(f^{-1}({\mathcal{A}}_j:j\in J))$ be a single-valued neutrosophic open covering of $\mathcal{A}$ since $\mathcal{A}$ be a SNS in $({\mathcal{K}}_1,{\chi }_1)$. Let $\acute{L}=({\mathcal{A}}_j:j\in J)$ be a single-valued neutrosophic open covering of $f(\mathcal{A})$. Since $\mathcal{A}$ is compact, then there exists a single-valued neutrosophic finite sub-cover ${\displaystyle \bigcup _{j=1}^n}{f}^{-1}({\mathcal{A}}_j)$ such that

$$\mathcal{A}\subseteq \underset{j=1}{\bigcup ^n}{f}^{-1}({\mathcal{A}}_j)$$

We have to prove that there also exists a finite sub-cover of $\acute{L}$ for $f(\mathcal{A})$ such that

$$f(\mathcal{A})\subseteq \underset{j=1}{\bigcup ^n}({\mathcal{A}}_j)$$

Now,

$$\begin{array}{c}\mathcal{A}\subseteq {\displaystyle \bigcup _{j=1}^n}{f}^{-1}({\mathcal{A}}_j)\hfill \\ f(\mathcal{A})\subseteq f({\displaystyle \bigcup _{j=1}^n}{f}^{-1}({\mathcal{A}}_j))\hfill \\ f(\mathcal{A})\subseteq {\displaystyle \bigcup _{j=1}^n}(f(f^{-1}({\mathcal{A}}_j)))\hfill \\ f(\mathcal{A})\subseteq {\displaystyle \bigcup _{j=1}^n}({\mathcal{A}}_j).\hfill \end{array}$$

Hence, $f(\mathcal{A})$ is single-valued neutrosophic compact in $({\mathcal{K}}_2,{\chi }_2).$ □

Definition 20.

A single-valued neutrosophic set $\mathcal{A}$ in a K-algebra $\mathcal{K}$ is called a single-valued neutrosophic point if

$${\mathcal{T}}_{\mathcal{A}}(v)=\left\{\begin{array}{cc}\alpha \in (0,1],\hfill & \mathit{if}v=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{I}}_{\mathcal{A}}(v)=\left\{\begin{array}{cc}\beta \in (0,1],\hfill & \mathit{if}v=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{F}}_{\mathcal{A}}(v)=\left\{\begin{array}{cc}\gamma \in [0,1),\hfill & \mathit{if}v=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

with support u and value $(\alpha ,\beta ,\gamma )$, denoted by $u(\alpha ,\beta ,\gamma )$. This single-valued neutrosophic point is said to “belong to" a SNS $\mathcal{A},$ written as $u(\alpha ,\beta ,\gamma )\in \mathcal{A}$ if ${\mathcal{T}}_{\mathcal{A}}(u)\ge \alpha ,{\mathcal{I}}_{\mathcal{A}}(u)\ge \beta ,{\mathcal{F}}_{\mathcal{A}}(u)\le \gamma$ and said to be “quasi-coincident with" a SNS $\mathcal{A}$, written as $u(\alpha ,\beta ,\gamma )q\mathcal{A}$ if ${\mathcal{T}}_{\mathcal{A}}(u)+\alpha >1,{\mathcal{I}}_{\mathcal{A}}(u)+\beta >1,{\mathcal{F}}_{\mathcal{A}}(u)+\gamma <1.$

Definition 21.

Let $\mathcal{K}$ be a K-algebra and let $(\mathcal{K},\chi )$ be a SNTS. Then, $(\mathcal{K},\chi )$ is called a single-valued neutrosophic Hausdorff space if and only if, for any two distinct single-valued neutrosophic points $u_1,u_2\in \mathcal{K}$, there exist SNOSs ${\mathcal{B}}_1=({\mathcal{T}}_{{\mathcal{B}}_1},{\mathcal{I}}_{{\mathcal{B}}_1},{\mathcal{F}}_{{\mathcal{B}}_1}),{\mathcal{B}}_2=({\mathcal{T}}_{{\mathcal{B}}_2},{\mathcal{I}}_{{\mathcal{B}}_2},{\mathcal{F}}_{{\mathcal{B}}_2})$ such that $u_1\in {\mathcal{B}}_1,u_2\in {\mathcal{B}}_2$, i.e.,

$${\mathcal{T}}_{{\mathcal{B}}_1}(u_1)=1,{\mathcal{I}}_{{\mathcal{B}}_1}(u_1)=1,{\mathcal{F}}_{{\mathcal{B}}_1}(u_1)=0,$$

$${\mathcal{T}}_{{\mathcal{B}}_2}(u_2)=1,{\mathcal{I}}_{{\mathcal{B}}_2}(u_2)=1,{\mathcal{F}}_{{\mathcal{B}}_2}(u_2)=0$$

and satisfy the condition that ${\mathcal{B}}_1\cap {\mathcal{B}}_2=\varnothing {}_{SN}.$ Then, $(\mathcal{K},\chi )$ is called single-valued neutrosophic Hausdorff space and K-algebra is said to ba a Hausdorff K-algebra. In fact, $(\mathcal{K},\chi )$ is a Hausdorff K-algebra.

Example 6.

Let $\mathcal{K}=(G,·,\odot ,e)$ be a K-algebra and let $(\mathcal{K},{\chi }_{\mathcal{K}})$ be a SNTS on $\mathcal{K}$, where $G=\{e,x,x^2,x^3,x^4,x^5,x^6,x^7,x^8\}$ is the cyclic group of order 9 and Caley’s table for ⊙ is given in Example 1. We define two SNSs as $\mathcal{A}=\{(e,1,1,0),(s,0,0,1)\}.$ $\mathcal{B}=\{(e,0,0,1),(s,1,1,0)\}.$ Consider a single-valued neutrosophic point for $e\in \mathcal{K}$ such that

$${\mathcal{T}}_{\mathcal{A}}(e)=\left\{\begin{array}{cc}0.3,\hfill & \mathit{if}e=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{I}}_{\mathcal{A}}(e)=\left\{\begin{array}{cc}0.2,\hfill & \mathit{if}e=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{F}}_{\mathcal{A}}(e)=\left\{\begin{array}{cc}0.4,\hfill & \mathit{if}e=u\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Then, $e(0.3,0.2,0.4)$ is a single-valued neutrosophic point with support e and value $(0.3,0.2,0.4)$. This single-valued neutrosophic point belongs to SNS $‘‘A"$ but not SNS $‘‘B"$.

Now, for all $s\ne e\in \mathcal{K}$

$${\mathcal{T}}_{\mathcal{B}}(s)=\left\{\begin{array}{cc}0.5,\hfill & \mathit{if}s=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{I}}_{\mathcal{B}}(s)=\left\{\begin{array}{cc}0.4,\hfill & \mathit{if}s=u\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}\right.$$

$${\mathcal{F}}_{\mathcal{B}}(s)=\left\{\begin{array}{cc}0.3,\hfill & \mathit{if}s=u\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Then, $s(0.5,0.4,0.3)$ is a single-valued neutrosophic point with support s and value $(0.5,0.4,0.3)$. This single-valued neutrosophic point belongs to SNS $‘‘B"$ but not SNS $‘‘A"$. Thus, $e(0.3,0.2,0.4)\in \mathcal{A}$ and $e(0.3,0.2,0.4)\notin \mathcal{B}$, $s(0.5,0.4,0.3)\in \mathcal{B}$ and $s(0.5,0.4,0.3)\notin \mathcal{A}$ and $\mathcal{A}\bigcap \mathcal{B}={\varnothing }_{SN}$. Thus, K-algebra is a Hausdorff K-algebra and $(\mathcal{K},{\chi }_{\mathcal{K}})$ is a Hausdorff topological space.

Theorem 5.

Let $({\mathcal{K}}_1,{\chi }_1)$, $({\mathcal{K}}_2,{\chi }_2)$ be two SNTSs. Let f be a single-valued neutrosophic homomorphism from $({\mathcal{K}}_1,{\chi }_1)$ into $({\mathcal{K}}_2,{\chi }_2)$. Then, $({\mathcal{K}}_1,{\chi }_1)$ is a single-valued neutrosophic Hausdorff space if and only if $({\mathcal{K}}_2,{\chi }_2)$ is a single-valued neutrosophic Hausdorff K-algebra.

Proof. 

Let $({\mathcal{K}}_1,{\chi }_1)$, $({\mathcal{K}}_2,{\chi }_2)$ be two SNTSs. Let ${\mathcal{K}}_1$ be a single-valued neutrosophic Hausdorff space, then, according to the Definition 21, there exist two SNOSs X and Y for two distinct single-valued neutrosophic points $u_1,u_2\in {\chi }_2$ also $a,b\in {\mathcal{K}}_1(a\ne b)$ such that $X\bigcap Y={\varnothing }_{SN}$.

Now, for $w\in {\mathcal{K}}_1$, consider $(f^{-1}(u_1))(w)=u_1(f^{-1}(w))$, where $u_1(f^{-1}(w))=s\in (0,1]$ if $w=f^{-1}(a)$, otherwise 0. That is, $(f^{-1}(u_1))(w)={((f^{-1}(u))}_1(w))$. Therefore, we have $f^{-1}(u_1)={(f^{-1}(u))}_1$. Similarly, $f^{-1}(u_2)={(f^{-1}(u))}_2$. Now, since $f^{-1}$ is a single-valued neutrosophic continuous mapping from ${\mathcal{K}}_2$ into ${\mathcal{K}}_1$, there exist two SNOSs $f(X)$ and $f(Y)$ of $u_1$ and $u_2$, respectively, such that $f(X)\bigcap f(Y)=f({\varnothing }_{SN})={\varnothing }_{SN}.$ This implies that ${\mathcal{K}}_2$ is a single-valued neutrosophic Hausdorff K-algebra. The converse part can be proved similarly. □

Theorem 6.

Let f be a single-valued neutrosophic continuous function which is both one-one and onto, where f is a mapping from a single-valued neutrosophic compact K-algebra ${\mathcal{K}}_1$ into a single-valued neutrosophic Hausdorff K-algebra ${\mathcal{K}}_2$. Then, f is a homomorphism.

Proof. 

Let $f:{\mathcal{K}}_1\to {\mathcal{K}}_2$ be a single-valued neutrosophic continuous bijective function from single-valued neutrosophic compact K-algebra ${\mathcal{K}}_1$ into a single-valued neutrosophic Hausdorff K-algebra ${\mathcal{K}}_2$. Since f is a single-valued neutrosophic continuous mapping from ${\mathcal{K}}_1$ into ${\mathcal{K}}_2$, f is a homomorphism. Since f is bijective, we only prove that f is single-valued neutrosophic closed. Let $\mathcal{D}=({\mathcal{T}}_{\mathcal{D}},{\mathcal{I}}_{\mathcal{D}},{\mathcal{F}}_{\mathcal{D}})$ be a single-valued neutrosophic closed in ${\mathcal{K}}_1$. If $\mathcal{D}={\varnothing }_{SN}$ is single-valued neutrosophic closed in ${\mathcal{K}}_1$, then $f(\mathcal{D})={\varnothing }_{SN}$ is single-valued neutrosophic closed in ${\mathcal{K}}_2$. However, if $\mathcal{D}\ne {\varnothing }_{SN}$, then $\mathcal{D}$ will be a single-valued neutrosophic compact, being subset of a single-valued neutrosophic compact K-algebra. Then, $f(\mathcal{D})$, being single-valued neutrosophic continuous image of a single-valued neutrosophic compact K-algebra, is also single-valued neutrosophic compact. Therefore, ${\mathcal{K}}_2$ is closed, which implies that mapping f is closed. Thus, f is a homomorphism. □

4. Conclusions

Non-classical logic is considered as a powerful tool for inspecting uncertainty and indeterminacy found in real world problems. Being a great extension of classical logic, neutrosophic set theory is considered as a useful mathematical tool to cope up with uncertainties in science, technology, and computer science. We have used this mathematical model with a topological structure to investigate the uncertainty in K-algebras. We have introduced the notion of single-valued neutrosophic topological K-algebras and presented certain concepts, including continuous function between two topological on K-algebras, relatively continuous function and homomorphism. We have investigated the image and pre-image of single-valued neutrosophic topological K-algebras under this homomorphism. We have proposed some conclusive concepts, including single-valued neutrosophic compact K-algebras and single-valued neutrosophic Hausdorff K-algebras. We plan to extend our study to: (i) single-valued neutrosophic soft topological K-algebras; and (ii) bipolar neutrosophic soft topological K-algebras.

For other notations and terminologies, readers are referred to [21,22,23,24,25,26].