Isometric Deformation of (m,n)-Type Helicoidal Surface in the Three Dimensional Euclidean Space

Abstract

We consider a new kind of helicoidal surface for natural numbers $(m,n)$ in the three-dimensional Euclidean space. We study a helicoidal surface of value $(m,n)$, which is locally isometric to a rotational surface of value $(m,n)$. In addition, we calculate the Laplace–Beltrami operator of the rotational surface of value $(0,1)$.

1. Introduction

The notion of the finite-type immersion of submanifolds of a Euclidean space has been used in classifying and characterizing well-known Riemannian submanifolds [1]. Chen posed the problem of classifying the finite-type surfaces in the three-dimensional Euclidean space ${\mathbb{E}}^3$. Then, the theory of submanifolds of a finite type was studied by many geometers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21].

Lawson [22] gave the general definition of the Laplace–Beltrami operator in his lecture notes. Takahashi [23] stated that minimal surfaces and spheres are the only surfaces in ${\mathbb{E}}^3$ satisfying the condition $\Delta r=\lambda r,$ $\lambda \in \mathbb{R}.$ Ferrandez, Garay and Lucas [10] proved that the surfaces of ${\mathbb{E}}^3$ satisfying $\Delta H=AH$, $A\in Mat(3,3)$ are either minimal, or an open piece of a sphere, or of a right circular cylinder. Choi and Kim [5] characterized the minimal helicoid in terms of a pointwise one-type Gauss map of the first kind.

Dillen, Pas and Verstraelen [7] proved that the only surfaces in ${\mathbb{E}}^3$ satisfying $\Delta r=Ar+B,$ $A\in Mat(3,3),$ $B\in Mat(3,1)$ are the minimal surfaces, the spheres and the circular cylinders. Senoussi and Bekkar [24] studied helicoidal surfaces $M^2$ in ${\mathbb{E}}^3$, which are of the finite type in the sense of Chen with respect to the fundamental forms $I,II$ and $III$.

The right helicoid (resp. catenoid) is the only ruled (resp. rotational) surface that is minimal in classical surface geometry in Euclidean space. If we focus on the ruled (helicoid) and rotational characters, we see Bour’s theorem in [25]. The French mathematician Edmond Bour used the semi-geodesic coordinates and found a number of new cases of the deformation of surfaces in 1862. He also gave in [25] a well-known theorem about the helicoidal and rotational surfaces.

Kenmotsu [26] focused on the surfaces of revolution with the prescribed mean curvature. Regarding helicoidal surfaces, do Carmo and Dajczer [3] proved that, by using a result of Bour [25], there exists a two-parameter family of helicoidal surfaces isometric to a given helicoidal surface. Hitt and Roussos [27] also studied the helicoidal surfaces with constant mean curvature. Ikawa [14,15] determined pairs of surfaces by Bour’s theorem. Güler [28] also studied the isometric helicoidal and rotational surfaces of value m. Güler and Yaylı [12] focused on the generalized Bour’s theorem in three-space.

We consider a new kind of helicoidal surface of value $(m,n)$ in Euclidean three-space ${\mathbb{E}}^3$ in this paper. We give some basic notions of the three-dimensional Euclidean geometry in Section 2. In Section 3, we give the definition of a helicoidal surface of value $(m,n)$ and obtain isometric helicoidal and rotational surfaces of value $(m,n)$ (resp. of value $(0,1)$ in Section 4) via Bour’s theorem. We also calculate the mean curvature and the Gaussian curvature of the rotational surface of value $(0,1)$ in Section 4. Moreover, in Section 5, we calculate the Laplace–Beltrami operator of the rotational surface of value $(0,1)$. Finally, we give the rotational surface satisfying $\Delta {\mathbf{R}}_{0,1}=A{\mathbf{R}}_{0,1}$ in ${\mathbb{E}}^3$ in the last section.

2. Preliminaries

We shall identify a vector (a,b,c) with its transpose. In this section, we will obtain the rotational and helicoidal surfaces in ${\mathbb{E}}^3$. The reader can find basic elements of differential geometry in [29,30].

We define the rotational surface and helicoidal surface in ${\mathbb{E}}^3$. For an open interval $I\subset$ $\mathbb{R}$, let $\gamma :I⟶\Pi$ be a curve in a plane $\Pi$, and let ℓ be a straight line in $\Pi$. A rotational surface in ${\mathbb{E}}^3$ is defined as a surface rotating the curve $\gamma$ around the line ℓ (these are called the profile curve and the axis, respectively). Suppose that when a profile curve $\gamma$ rotates around the axis ℓ, it simultaneously displaces parallel lines orthogonal to the axis ℓ, so that the speed of displacement is proportional to the speed of rotation. Then, the resulting surface is called the helicoidal surface with axis ℓ and pitch $a\in {\mathbb{R}}^{+}$.

Let ℓ be the line spanned by the vector $(0,0,1)$. The orthogonal matrix that fixes the above vector is given by

$$M\left(\theta \right)=\left(\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right),\theta \in \mathbb{R}.$$

The matrix M is found by solving the following equations: $M\ell =\ell ,$ $M^{t}M=M{M}^t=I_3,$ $detM=1,$ simultaneously. When the axis of rotation is ℓ, there is a Euclidean transformation by which the axis is ℓ transformed to the z-axis of ${\mathbb{E}}^3$. The profile curve is given by $\gamma \left(r\right)=(r,0,\phi \left(r\right)),$ where $\phi \left(r\right):I\subset \mathbb{R}⟶\mathbb{R}$ is a differentiable function for all $r\in I$. A helicoidal surface in three-dimensional Euclidean space which is spanned by the vector $(0,0,1)$ with pitch a is as follows

$$\mathbf{H}(r,\theta )=M\left(\theta \right)\gamma \left(r\right)+a\theta \ell .$$

When $a=0$, the helicoidal surface is just a rotational surface.

3. Helicoidal Surfaces of Value (m,n)

We define a new type of helicoidal surface. Using Bour’s theorem on the helicoidal surface, we obtain an isometric rotational surface in this section.

Definition 1.

A helicoidal surface of value $(m,n)$ is given by

$${\mathbf{H}}_{m,n}\left(r,\theta \right)={\mathbf{H}}_m^1\left(r,\theta \right)+{\mathbf{H}}_{m,n}^2\left(r,\theta \right),$$

(1)

where $m,n\in \mathbb{N},$ ${\mathbf{H}}_m^1\left(r,\theta \right)={\Re }_m^1.{\gamma }_m^1+\frac{1}{2}a\theta \ell ,$ ${\mathbf{H}}_{m,n}^2\left(r,\theta \right)={\Re }_{m,n}^2.{\gamma }_{m,n}^2+\frac{1}{2}a\theta \ell ,$ the rotating matrices ${\Re }_m^1$ and ${\Re }_{m,n}^2$ are

$${\Re }_m^1\left(\theta \right)=\left(\begin{array}{ccc}cos\left[\left(m+1\right)\theta \right]& sin\left[\left(m+1\right)\theta \right]& 0\\ -sin\left[\left(m+1\right)\theta \right]& cos\left[\left(m+1\right)\theta \right]& 0\\ 0& 0& 1\end{array}\right)$$

and

$${\Re }_{m,n}^2\left(\theta \right)=\left(\begin{array}{ccc}cos\left[\left(m+2n+1\right)\theta \right]& -sin\left[\left(m+2n+1\right)\theta \right]& 0\\ sin\left[\left(m+2n+1\right)\theta \right]& cos\left[\left(m+2n+1\right)\theta \right]& 0\\ 0& 0& 1\end{array}\right).$$

$\ell =\left(0,0,1\right)$ is the rotating axis, and the profile curves are

$${\gamma }_m^1\left(r\right)=\left(\frac{r^{m+1}}{m+1},0,\frac{1}{2}\phi \left(r\right)\right),{\gamma }_{m,n}^2\left(r\right)=\left(-\frac{r^{m+2n+1}}{m+2n+1},0,\frac{1}{2}\phi \left(r\right)\right),$$

$m\in \mathbb{R}-\left\{-1\right\}$ in ${\gamma }_m^1,$ $m\in \mathbb{R}-\left\{-1-2n\right\}$ in ${\gamma }_{m,n}^2,$ $r\in {\mathbb{R}}^{+},$ $0\le \theta \le 2\pi$ and the pitch $a\in {\mathbb{R}}^{+}.$ Since the helicoidal surface is given by rotating the profile curves γ around the axis ℓ and simultaneously displacing parallel lines orthogonal to the axis ℓ, the speed of displacement is proportional to the speed of rotation.

Next, we give a theorem about locally isometric helicoidal-rotational surfaces of value $(m,n).$

Theorem 1.

A helicoidal surface of value $(m,n)$

$${\mathbf{H}}_{m,n}\left(r,\theta \right)=\left(\begin{array}{c}\frac{r^{m+1}}{m+1}cos\left[\left(m+1\right)\theta \right]-\frac{r^{m+2n+1}}{m+2n+1}cos\left[\left(m+2n+1\right)\theta \right]\\ -\frac{r^{m+1}}{m+1}sin\left[\left(m+1\right)\theta \right]-\frac{r^{m+2n+1}}{m+2n+1}sin\left[\left(m+2n+1\right)\theta \right]\\ \phi \left(r\right)+a\theta \end{array}\right)$$

(2)

is isometric to the rotational surface of value $(m,n)$

$${\mathbf{R}}_{m,n}(r_{\mathbf{R}},{\theta }_{\mathbf{R}})=\left(\begin{array}{c}\frac{r_{\mathbf{R}}^{m+1}}{m+1}cos\left[\left(m+1\right){\theta }_{\mathbf{R}}\right]-\frac{r_{\mathbf{R}}^{m+2n+1}}{m+2n+1}cos\left[\left(m+2n+1\right){\theta }_{\mathbf{R}}\right]\\ -\frac{r_{\mathbf{R}}^{m+1}}{m+1}sin\left[\left(m+1\right){\theta }_{\mathbf{R}}\right]-\frac{r_{\mathbf{R}}^{m+2n+1}}{m+2n+1}sin\left[\left(m+2n+1\right){\theta }_{\mathbf{R}}\right]\\ {\phi }_{\mathbf{R}}\left(r_{\mathbf{R}}\right)\end{array}\right)$$

(3)

by Bour’s theorem, where

$$\begin{array}{ccc}\hfill {\phi }_{\mathbf{R}}^{\prime 2}& =& \frac{{\left[\begin{array}{c}{G}^{m+n-1}\{\left(m+3n\right)G^{2n}+2\left(m+2n\right)G^{n}cos\left[2(m+n+1)\theta \right]\\ -2G^{n}sin\left[2(m+n+1)\theta \right]+m+n\}\end{array}\right]}^{2}detI}{{\left[\begin{array}{c}{r}^{2m+2n}\{\left(2m+6n\right)r^{4n-1}+\left(4m+8n\right)r^{2n}cos\left[2(m+n+1)\theta \right]\\ +\left(2m+2\right)r^{-1}\}\end{array}\right]}^{2}G}\hfill \\ & & +\frac{4r_{\mathbf{R}}^{4m+4n+2}{sin}^2\left[2(m+n+1){\theta }_{\mathbf{R}}\right]}{r_{\mathbf{R}}^{2m+2}\left(r_{\mathbf{R}}^{4n}+2r_{\mathbf{R}}^{2n}cos\left[2(m+n+1){\theta }_{\mathbf{R}}\right]+1\right)}\hfill \\ & & -r_{\mathbf{R}}^{2m}\left[r_{\mathbf{R}}^{4n}-2r_{\mathbf{R}}^{2n}cos\left(2\left(m+n+1\right){\theta }_{\mathbf{R}}\right)+1\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill r_{\mathbf{R}}& =& \sqrt{G},\hfill \\ \hfill {\theta }_{\mathbf{R}}& =& \theta +\int \frac{F}{G}dr,\hfill \\ \hfill E& =& r^{2m}\left(r^{4n}-2r^{2n}cos\left[2(m+n+1)\theta \right]+1\right)+{\phi }^{\prime 2},\hfill \\ \hfill F& =& 2r^{2m+2n+1}sin\left[2(m+n+1)\theta \right]+a{\phi }^{\prime },\hfill \\ \hfill G& =& r^{2m+2}\left(r^{4n}+2r^{2n}cos\left[2(m+n+1)\theta \right]+1\right)+a^2,\hfill \\ \hfill detI& =& EG-F^2,\hfill \end{array}$$

$m\in \mathbb{R}-\left\{-1,-1-2n\right\},$$n\in \mathbb{R},$$r\in {\mathbb{R}}^{+},$$\theta \in I\subset \mathbb{R}$ and the pitch $a\in {\mathbb{R}}^{+}.$

Proof. 

The line element of the the helicoidal surface ${\mathbf{H}}_{m,n}(r,\theta )$ is

$$\begin{array}{c}d{s}^2=\{r^{2m}(r^{4n}-2r^{2n}cos\left[2(m+n+1)\theta \right]+1)+{\phi }^{\prime 2}\}d{r}^2\\ +2\{2r^{2m+2n+1}sin\left[2(m+n+1)\theta \right]+a{\phi }^{\prime }\}drd\theta \\ +\{r^{2m+2}\left(r^{4n}+2r^{2n}cos\left[2(m+n+1)\theta \right]+1\right)+a^2\}d{\theta }^2.\end{array}$$

(4)

Helices in ${\mathbf{H}}_{m,n}$ are curves defined by $r=const.$ Therefore curves in ${\mathbf{H}}_{m,n}$ that are orthogonal to helices supply the orthogonality condition F $dr+G$ $d\theta =0.$ Thus, we obtain $\theta =-\int \frac{F}{G}$ $dr+c,$ where c is constant. Hence, if we put $\overline{\theta }=\theta +\int \frac{F}{G}$ $dr,$ then curves orthogonal to helices are given by $\overline{\theta }=const.$ Substituting the equation $d\theta =d\overline{\theta }-\frac{F}{G}dr$ into the line element (4), we have

$$d{s}^2=\frac{Q}{G}d{r}^2+Gd{\overline{\theta }}^2,$$

(5)

where $Q:=detI.$ Setting $\overline{r}:=\sqrt{\frac{Q}{G}}$ $dr,$ $\Omega \left(\overline{r}\right):=\sqrt{G},$ (5) becomes

$$d{s}^2=d{\overline{r}}^2+{\Omega }^2\left(\overline{r}\right)d{\overline{\theta }}^2.$$

(6)

The rotational surface (3) has the line element

$$d{s}_{\mathbf{R}}^2=\frac{Q_{\mathbf{R}}}{G_{\mathbf{R}}}d{r}_{\mathbf{R}}^2+G_{\mathbf{R}}d{\overline{\theta }}_{\mathbf{R}}^2,$$

(7)

where

$$\begin{array}{ccc}\hfill E_{\mathbf{R}}& =& r_{\mathbf{R}}^{2m}(r_{\mathbf{R}}^{4n}+1-2r_{\mathbf{R}}^{2n}cos\left[2(m+n+1){\theta }_{\mathbf{R}}\right])+{\phi }_{\mathbf{R}}^{\prime 2},\hfill \\ \hfill F_{\mathbf{R}}& =& 2r_{\mathbf{R}}^{2m+2n+1}sin\left[2(m+n+1){\theta }_{\mathbf{R}}\right],\hfill \\ \hfill G_{\mathbf{R}}& =& r_{\mathbf{R}}^{2m+2}\left(r_{\mathbf{R}}^{4n}+1+2r_{\mathbf{R}}^{2n}cos\left[2(m+n+1){\theta }_{\mathbf{R}}\right]\right).\hfill \end{array}$$

Again, setting ${\overline{r}}_{\mathbf{R}}:=\sqrt{\frac{Q_{\mathbf{R}}}{G_{\mathbf{R}}}}d{r}_{\mathbf{R}},$ ${\Omega }_{\mathbf{R}}\left({\overline{r}}_{\mathbf{R}}\right):=\sqrt{G_{\mathbf{R}}},$ then (7) becomes

$$d{s}_{\mathbf{R}}^2=d{\overline{r}}_{\mathbf{R}}^2+{\Omega }_{\mathbf{R}}^2\left({\overline{r}}_{\mathbf{R}}\right)d{\overline{\theta }}_{\mathbf{R}}^2.$$

(8)

Comparing (6) with (8), if we take $\overline{r}={\overline{r}}_{\mathbf{R}},$ $\overline{\theta }={\overline{\theta }}_{\mathbf{R}},$ $\Omega \left(\overline{r}\right)={\Omega }_{\mathbf{R}}\left({\overline{r}}_{\mathbf{R}}\right),$ then we have an isometry between ${\mathbf{H}}_{m,n}(r,\theta )$ and ${\mathbf{R}}_{m,n}(r_{\mathbf{R}},{\theta }_{\mathbf{R}})$. Therefore, it follows that

$$\sqrt{\frac{Q}{G}}dr=\sqrt{\frac{Q_{\mathbf{R}}}{G_{\mathbf{R}}}}d{r}_{\mathbf{R}}.$$

(9)

Substituting the equation

$$d{r}_{\mathbf{R}}=\sqrt{\frac{G_{\mathbf{R}}{\left[{\left(G\right)}_r\right]}^2}{{\left[{\left(G_{\mathbf{R}}\right)}_r\right]}^{2}G}}dr$$

into (9), we get the function ${\phi }_{\mathbf{R}}.$ ☐

4. Helicoidal Surface of Value (0,1)

We give the helicoidal surface of value $(0,1)$ using Bour’s theorem in this section.

Proposition 1.

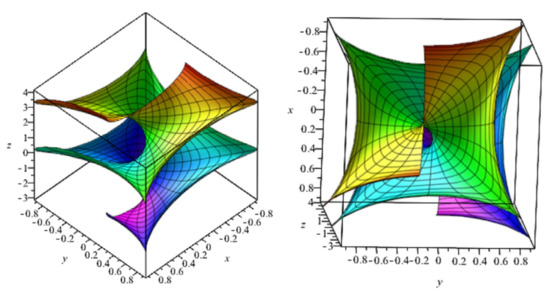
A helicoidal surface of value $(0,1)$: (see Figure 1)

$${\mathbf{H}}_{0,1}\left(r,\theta \right)=\left(\begin{array}{c}rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\\ -rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\\ \phi \left(r\right)+a\theta \end{array}\right),$$

(10)

is isometric to the rotational surface of value $(0,1)$

$${\mathbf{R}}_{0,1}(r_{\mathbf{R}},{\theta }_{\mathbf{R}})=\left(\begin{array}{c}\sqrt{G}cos\left[\left(\theta +\int \frac{F}{G}dr\right)\right]-\frac{1}{3}\sqrt{G^3}cos\left[3\left(\theta +\int \frac{F}{G}dr\right)\right]\\ -\sqrt{G}sin\left[\left(\theta +\int \frac{F}{G}dr\right)\right]-\frac{1}{3}\sqrt{G^3}sin\left[3\left(\theta +\int \frac{F}{G}dr\right)\right]\\ {\phi }_{\mathbf{R}}\left(r_{\mathbf{R}}\right)\end{array}\right),$$

(11)

where

$$\begin{array}{ccc}\hfill {\phi }_{\mathbf{R}}^{\prime 2}& =& \frac{{\left[\{3G^2+4Gcos\left(4\theta \right)-2Gsin\left(4\theta \right)+1\}\right]}^{2}detI}{{\left[r^2\{6r^3+8r^{2}cos\left(4\theta \right)+2r^{-1}\}\right]}^{2}G}\hfill \\ & & +\frac{4G^3{sin}^2\left[4\left(\theta +\int \frac{F}{G}dr\right)\right]}{G\left[G^2+2Gcos\left[4\left(\theta +\int \frac{F}{G}dr\right)\right]+1\right]}\hfill \\ & & -\left[G^2-2Gcos\left[4\left(\theta +\int \frac{F}{G}dr\right)\right]+1\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill E& =& r^4-2r^{2}cos\left(4\theta \right)+1+{\phi }^{\prime 2},\hfill \\ \hfill F& =& 2r^{3}sin\left(4\theta \right)+a{\phi }^{\prime },\hfill \\ \hfill G& =& r^2\left[r^4+2r^{2}cos\left(4\theta \right)+1\right]+a^2,\hfill \end{array}$$

$detI=EG-F^2,$$r,a\in {\mathbb{R}}^{+},$$0\le \theta \le 2\pi .$

Figure 1. Two views of the helicoidal surface of value $(0,1),$ $\phi \left(r\right)=r^2$.

Proof. 

Taking $m=0,$ $n=1$ in the previous theorem, we easily get the results. ☐

Corollary 1.

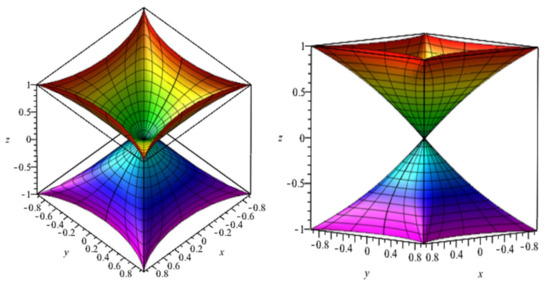
When $a=0,$ $\phi \left(r\right)=r$ in (10), we obtain a rotational surface of value $(0,1)$ (see Figure 2).

Figure 2. Two views of the rotational surface of value $(0,1),$ $\phi \left(r\right)=r$.

Corollary 2.

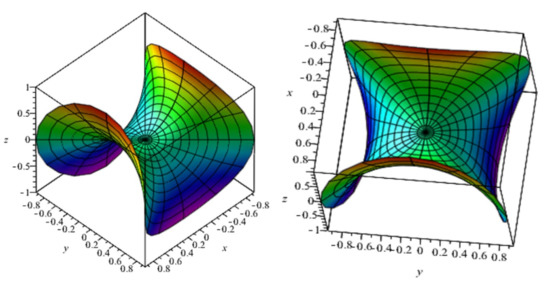
When $a=0$ and $\phi \left(r\right)=r^{2}cos\left(2\theta \right)$ in (10), we have Enneper’s minimal surface (see Figure 3).

Figure 3. Two views of the Enneper minimal surface of value $(0,1),a=0,\phi \left(r\right)=r^{2}cos\left(2\theta \right)$.

Proposition 2.

The mean curvature and the Gaussian curvature of (10) are as follows

$$\begin{array}{ccc}\hfill H& =& \frac{1}{2{\left(detI\right)}^{3/2}}\{r(r^4-1)(r^6+2r^{4}cos\left(4\theta \right)+r^2+a^2){\phi }^{\prime \prime }\hfill \\ & & +r^2(3r^4+2r^{2}cos\left(4\theta \right)-1){\phi }^{\prime 3}-6a{r}^{3}sin\left(4\theta \right){\phi }^{\prime 2}\hfill \\ & & +[2r^2(-5r^6+r^2-3a^2)cos\left(4\theta \right)+r^{10}-8r^6+4a^2{r}^4\hfill \\ & & -r^2-2a^2]{\phi }^{\prime }+2ar\left(6r^6-2r^2+a^2\right)sin\left(4\theta \right)\}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill K& =& \frac{1}{{\left(detI\right)}^2}\left(\right\{[3r^{11}+2r^5(r^4-1)cos\left(4\theta \right)-4r^7+r^3]{\phi }^{\prime }\hfill \\ & & -2a{r}^5(r^4-1)sin\left(4\theta \right)\}{\phi }^{\prime \prime }+[-2r^6(3r^4+1)\hfill \\ & & -2r^4(r^6-1)cos\left(4\theta \right)]{\phi }^{\prime 2}-2a{r}^3(3-11r^4)sin\left(4\theta \right)]{\phi }^{\prime }\hfill \\ & & +4a^2{r}^2(3r^4-1)cos\left(4\theta \right)-a^2\left(9r^8-2r^4+1\right).\hfill \end{array}$$

respectively, where $detI=EG-F^2,$ ${\phi }^{\prime }=\frac{d\phi }{dr},$ $r,a\in {\mathbb{R}}^{+},$ $0\le \theta \le 2\pi$.

Proof. 

Taking the differential with respect to $r,$ $\theta$ to ${\mathbf{H}}_{0,1},$ we have

$${\left({\mathbf{H}}_{0,1}\right)}_r=\left(\begin{array}{c}cos\left(\theta \right)-r^{2}cos\left(3\theta \right)\\ -sin\left(\theta \right)-r^{2}sin\left(3\theta \right)\\ {\phi }^{\prime }\end{array}\right).$$

and

$${\left({\mathbf{H}}_{0,1}\right)}_{\theta }=\left(\begin{array}{c}-rsin\left(\theta \right)+r^{3}sin\left(3\theta \right)\\ -rcos\left(\theta \right)-r^{3}cos\left(3\theta \right)\\ a\end{array}\right),$$

The coefficients of the first fundamental form of the surface are

$$\begin{array}{ccc}\hfill E& =& \left[r^4-2r^{2}cos\left(4\theta \right)+1\right]+{\phi }^{\prime 2},\hfill \\ \hfill F& =& 2r^{3}sin\left(4\theta \right)+a{\phi }^{\prime },\hfill \\ \hfill G& =& r^2\left[r^4+2r^{2}cos\left(4\theta \right)+1\right]+a^2,\hfill \end{array}$$

Then, we get

$$\begin{array}{ccc}\hfill detI& =& [r^6+2r^{4}cos\left(4\theta \right)+r^2]{\phi }^{\prime 2}-4a{r}^{3}sin\left(4\theta \right){\phi }^{\prime }\hfill \\ & & +r^{10}-2r^6+a^2{r}^4-2a^2{r}^{2}cos\left(4\theta \right)+r^2+a^2.\hfill \end{array}$$

Using the second differentials

$${\left({\mathbf{H}}_{0,1}\right)}_{rr}=\left(\begin{array}{c}-2rcos\left(3\theta \right)\\ -2rsin\left(3\theta \right)\\ {\phi }^{\prime \prime }\end{array}\right),{\left({\mathbf{H}}_{0,1}\right)}_{r\theta }=\left(\begin{array}{c}-sin\left(\theta \right)+3r^{2}sin\left(3\theta \right)\\ -cos\left(\theta \right)-3r^{2}cos\left(3\theta \right)\\ 0\end{array}\right),$$

$${\left({\mathbf{H}}_{0,1}\right)}_{\theta \theta }=\left(\begin{array}{c}-rcos\left(\theta \right)+3r^{3}cos\left(3\theta \right)\\ rsin\left(\theta \right)+3r^{3}sin\left(3\theta \right)\\ 0\end{array}\right),$$

and the Gauss map (the unit normal)

$$e=\frac{1}{\sqrt{detI}}\left(\begin{array}{c}(r^{3}cos\left(3\theta \right)+rcos\left(\theta \right)){\phi }^{\prime }-a(r^{2}sin\left(3\theta \right)+sin\left(\theta \right))\\ (r^{3}sin\left(3\theta \right)-rsin\left(\theta \right)){\phi }^{\prime }+a(r^{2}cos\left(3\theta \right)-cos\left(\theta \right))\\ r^5-r\end{array}\right)$$

of the surface ${\mathbf{H}}_{0,1}$, we have the coefficients of the second fundamental form of the surface as follows

$$\begin{array}{ccc}\hfill L& =& \frac{1}{\sqrt{detI}}[(r^5-r){\phi }^{\prime \prime }-r^2(r^2+cos\left(4\theta \right)){\phi }^{\prime }-2arsin\left(4\theta \right)],\hfill \\ \hfill M& =& \frac{1}{\sqrt{detI}}[2r^{3}sin\left(3\theta \right){\phi }^{\prime }-3a{r}^4+2a{r}^{2}cos\left(4\theta \right)+a],\hfill \\ \hfill N& =& \frac{1}{\sqrt{detI}}[(3r^6-r^2+2r^{4}cos\left(4\theta \right)){\phi }^{\prime }-2a{r}^{3}sin\left(4\theta \right)].\hfill \end{array}$$

Therefore, we can see the results easily. ☐

Corollary 3.

If the helicoidal surface of value $(0,1)$ is minimal, then we get the differential equation as follows

$$\begin{array}{c}r(r^4-1)(r^6+2r^{4}cos\left(4\theta \right)+r^2+a^2){\phi }^{\prime \prime }\hfill \\ +r^2(3r^4+2r^{2}cos\left(4\theta \right)-1){\phi }^{\prime 3}-6a{r}^{3}sin\left(4\theta \right){\phi }^{\prime 2}\hfill \\ +[2r^2(-5r^6+r^2-3a^2)cos\left(4\theta \right)+r^{10}-8r^6+4a^2{r}^4\hfill \\ -r^2-2a^2]{\phi }^{\prime }+2ar\left(6r^6-2r^2+a^2\right)sin\left(4\theta \right)=0.\hfill \end{array}$$

The helicoidal surface of value $(1,1)$ is the same surface for value three in [28].

5. Laplace–Beltrami Operator

The Laplace–Beltrami operator of a smooth function $\varphi =\varphi (r,\theta ){\mid }_{\mathbf{D}}$ $(\mathbf{D}\subset {\mathbb{R}}^3)$ of class $C^2$ with respect to the first fundamental form of surface $\mathbf{M}$ is the operator $\Delta$, which is defined as follows

$$\Delta \varphi =\frac{1}{\sqrt{g}}\sum _{i,j=1}^2\frac{\partial }{\partial x^i}\left(\sqrt{g}{g}^{ij}\frac{\partial \varphi }{\partial x^j}\right),$$

(12)

where $\left(g^{ij}\right)={\left(g_{kl}\right)}^{-1}$ and $g=det\left(g_{ij}\right).$ Clearly, we write $\Delta \varphi$ as follows

$$\Delta \varphi =\frac{1}{\sqrt{g}}\left[\begin{array}{c}\frac{\partial }{\partial x^1}\left(\sqrt{g}{g}^{11}\frac{\partial \varphi }{\partial x^1}\right)-\frac{\partial }{\partial x^1}\left(\sqrt{g}{g}^{12}\frac{\partial \varphi }{\partial x^2}\right)\\ -\frac{\partial }{\partial x^2}\left(\sqrt{g}{g}^{21}\frac{\partial \varphi }{\partial x^1}\right)+\frac{\partial }{\partial x^2}\left(\sqrt{g}{g}^{22}\frac{\partial \varphi }{\partial x^2}\right)\end{array}\right].$$

(13)

Using a more transparent notation, we get

$$\Delta \varphi =\frac{1}{\sqrt{detI}}\left[\frac{\partial }{\partial u}\left(\frac{G{\varphi }_u-F{\varphi }_v}{\sqrt{detI}}\right)-\frac{\partial }{\partial v}\left(\frac{F{\varphi }_u-E{\varphi }_v}{\sqrt{detI}}\right)\right],$$

(14)

where $g=det\left(g_{ij}\right)=detI.$

Now, we consider the rotational surface

$${\mathbf{R}}_{0,1}\left(r,\theta \right)=\left(\begin{array}{c}rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\\ -rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\\ \phi \left(r\right)\end{array}\right).$$

(15)

The first fundamental matrix of the surface is as follows

$$I=\left(\begin{array}{cc}{r}^4-2r^{2}cos\left(4\theta \right)+1+{\phi }^{\prime 2}& 2r^{3}sin\left(4\theta \right)\\ 2r^{3}sin\left(4\theta \right)& r^2(r^4+2r^{2}cos\left(4\theta \right)+1)\end{array}\right).$$

The inverse matrix of I is as follows

$$\left(I^{-1}\right)=\frac{1}{detI}\left(\begin{array}{cc}{r}^2\left(r^4+2r^{2}cos4\theta +1\right)& -2r^{3}sin4\theta \\ -2r^{3}sin4\theta & r^4-2r^{2}cos4\theta +1+{\phi }^{\prime 2}\end{array}\right),$$

where

$$detI=r^2(\left(r^4-2\right)r^4+\left(r^4+2r^{2}cos4\theta +1\right){\phi }^{\prime 2}+1).$$

The Laplace–Beltrami operator $\Delta {\mathbf{R}}_{0,1}$ of a rotational surface ${\mathbf{R}}_{0,1}$ is given by

$$\Delta \mathbf{R}=\frac{1}{\sqrt{detI}}\left(\frac{\partial }{\partial r}\mathbf{U}-\frac{\partial }{\partial \theta }\mathbf{V}\right),$$

where

$$\mathbf{U}=\frac{G{\mathbf{R}}_r-F{\mathbf{R}}_{\theta }}{\sqrt{detI}},\mathbf{V}=\frac{F{\mathbf{R}}_r-E{\mathbf{R}}_{\theta }}{\sqrt{detI}}.$$

Then, we obtain the following results

$$\begin{array}{ccc}\hfill \mathbf{U}& =& \frac{1}{\sqrt{detI}}\left(\begin{array}{c}-r^2\left(r^4-1\right)\left(cos\theta +r^{2}cos3\theta \right)\\ r^2\left(r^4-1\right)\left(sin\theta -r^{2}sin3\theta \right)\\ r^2{\phi }^{\prime }(r^4+2r^{2}cos\left(4\theta \right)+1)\end{array}\right),\hfill \\ \hfill \mathbf{V}& =& \frac{1}{\sqrt{detI}}\left(\begin{array}{c}r\left(\left(1+{\phi }^{\prime 2}-r^4\right)sin\theta +r^2\left(1-r^4-{\phi }^{2\prime }\right)sin3\theta \right)\\ r\left(\left(1+{\phi }^{2\prime }-r^4\right)cos\theta -r^2\left(1-r^4-{\phi }^{\prime 2}\right)cos3\theta \right)\\ 2r^3{\phi }^{\prime }sin\left(4\theta \right)\end{array}\right).\hfill \end{array}$$

Using differentials of $r,\theta$ on $\mathbf{U},\mathbf{V},$ respectively, we get

$$\begin{array}{ccc}\hfill {\Delta }^I\mathbf{R}& =& \frac{1}{\sqrt{detI}}\left(\frac{\partial }{\partial r}\left(\mathbf{U}\right)-\frac{\partial }{\partial \theta }\left(\mathbf{V}\right)\right)\hfill \\ & =& \frac{r^3}{{\left(detI\right)}^2}\left(\begin{array}{c}{J}_1{\phi }^{\prime }{\phi }^{\prime \prime }+J_2{\phi }^{\prime 4}+J_3{\phi }^{\prime 2}+J_4\\ T_1{\phi }^{\prime }{\phi }^{\prime \prime }+T_2{\phi }^{\prime 4}+T_3{\phi }^{\prime 2}+T_4\\ Q_1{\phi }^{\prime 3}{\phi }^{\prime \prime }+Q_2{\phi }^{\prime 2}{\phi }^{\prime \prime }+Q_3{\phi }^{\prime }{\phi }^{\prime \prime }+Q_4{\phi }^{\prime 3}+Q_5\end{array}\right),\hfill \end{array}$$

where

• $J_1=r\left(1+r^4-2r^8\right)cos\theta +r^3\left(2-r^4-r^8\right)cos3\theta +r^3\left(1-r^4\right)cos5\theta +r^5\left(1-r^4\right)cos7\theta ,$
• $J_2=-cos\theta +4r^{4}cos\theta +3r^{6}cos3\theta +r^{2}cos5\theta +r^{4}cos7\theta ,$
• $J_3=\left(-3+r^4+14r^8\right)cos\theta +r^2\left(-6+7r^4+11r^8\right)cos3\theta +r^2\left(1+3r^4\right)cos5\theta +r^4\left(-3+7r^4\right)cos7\theta ,$
• $J_4=2\left(-1+3r^4-3r^8+r^{12}\right)cos\theta +6r^2\left(-1+3r^4-3r^8+r^{12}\right)cos3\theta ,$
• $T_1=r\left(1-r^8\right)sin\theta +r^3\left(-1+r^8\right)sin3\theta +2r^3\left(1-r^4\right)cos4\theta sin\theta +2r^5\left(-1+r^4\right)sin3\theta cos4\theta ,$
• $T_2=\left(-1+4r^4\right)cos\theta +3r^{6}cos3\theta +r^{2}cos5\theta +r^{4}cos7\theta ,$
• $T_3=\left(-2-3r^4+5r^8\right)cos\theta +\left(-1+6r^4+3r^8\right)sin\theta +r^2\left(3-6r^4-5r^8\right)sin3\theta +3r^2\left(-1-r^4+2r^8\right)cos3\theta +r^2\left(1-r^4\right)cos5\theta +8r^{6}sin\theta cos4\theta +4r^4\left(1-3r^4\right)sin3\theta cos4\theta +r^4\left(-1+r^4\right)cos7\theta ,$
• $T_4=\left(-1+3r^4-3r^8+r^{12}\right)\left(cos\theta +sin\theta +cos3\theta -sin3\theta \right),$
• $Q_1=r+4r^3+2r^5+r^9+4r^5\left(r^2+{cos}^{2}4\theta \right)cos4\theta ,$
• $Q_2=-r-2r^5-r^9-4r^3\left(1+r^4+r^{2}cos4\theta \right)cos4\theta ,$
• $Q_3=r-r^5-r^9+r^{13}+2r^3\left(1-2r^4+r^8\right)cos4\theta ,$
• $Q_4=1-4r^4+3r^8-2r^2\left(1-r^4\right)cos4\theta ,$
• $Q_5=1+7r^4-9r^8+r^{12}+r^2\left(-2+12r^4-10r^8\right)cos4\theta .$

Remark 1.

When the rotational surface ${\mathbf{R}}_{0,1}$ has the equation $\Delta {\mathbf{R}}_{0,1}=\mathbf{0},$ we have to solve the system of equations as follows

$$\begin{array}{cc}{J}_1{\phi }^{\prime }{\phi }^{\prime \prime }+J_2{\phi }^{\prime 4}+J_3{\phi }^{\prime 2}+J_4& =0,\\ T_1{\phi }^{\prime }{\phi }^{\prime \prime }+T_2{\phi }^{\prime 4}+T_3{\phi }^{\prime 2}+T_4& =0,\\ Q_1{\phi }^{\prime 3}{\phi }^{\prime \prime }+Q_2{\phi }^{\prime 2}{\phi }^{\prime \prime }+Q_3{\phi }^{\prime }{\phi }^{\prime \prime }+Q_4{\phi }^{\prime 3}+Q_5& =0.\end{array}$$

here, finding the function φ is a problem.

Corollary 4.

When $\phi =c=const.,$ then we get

$$\Delta {\mathbf{R}}_{\mathbf{0},\mathbf{1}}=\frac{-1+3r^4-3r^8+r^{12}}{r^2\left[\left(r^4-2\right)r^4+1\right]}\left(\begin{array}{c}2cos\theta +6r^{2}cos3\theta \\ cos\theta +sin\theta +3r^2\left(cos3\theta -sin3\theta \right)\\ 0\end{array}\right).$$

6. Rotational Surface Satisfying $\mathbf{\Delta }{\mathbf{R}}_{\mathbf{0}\mathbf{,}\mathbf{1}}\mathbf{=}\mathit{A}{\mathbf{R}}_{\mathbf{0}\mathbf{,}\mathbf{1}}$ in 𝔼³

Theorem 2.

Let ${\mathbf{R}}_{0,1}$: $M^2$⟶${\mathbb{E}}^3$ be an isometric immersion given by (15). Then, $\Delta {\mathbf{R}}_{0,1}=A{\mathbf{R}}_{0,1}$ if and only if $M^2$ has zero mean curvature.

Proof. 

The Gauss map of the rotational surface ${\mathbf{R}}_{0,1}$ is

$$e=\frac{1}{W}\left(\begin{array}{c}(cos\theta +r^{2}cos3\theta ){\phi }^{\prime }\\ (-sin\theta +r^{2}sin3\theta ){\phi }^{\prime }\\ -1+r^4\end{array}\right),$$

where

$$W=\sqrt{\left(r^4-2\right)r^4+\left(r^4+2r^{2}cos4\theta +1\right){\phi }^{\prime 2}+1}.$$

We use

$$-2He=A{\mathbf{R}}_{\mathbf{0},\mathbf{1}},$$

(16)

where $A=\left(a_{ij}\right)$ is a $3\times 3$ matrix. The equation $\Delta {\mathbf{R}}_{\mathbf{0},\mathbf{1}}=A{\mathbf{R}}_{\mathbf{0},\mathbf{1}}$ by means of

$$I=\left(\begin{array}{cc}{r}^4-2r^{2}cos\left(4\theta \right)+1+{\phi }^{\prime 2}& 2r^{3}sin\left(4\theta \right)\\ 2r^{3}sin\left(4\theta \right)& r^2(r^4+2r^{2}cos\left(4\theta \right)+1)\end{array}\right).$$

and $\Delta {\mathbf{R}}_{\mathbf{0},\mathbf{1}}=-2He$ give rise to the following system of ODEs

$$\begin{array}{c}\hfill \Omega (cos\theta +r^{2}cos3\theta ){\phi }^{\prime }-a_{11}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)-a_{12}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)=\phi a_{13},\end{array}$$

$$\begin{array}{c}\hfill \Omega (-sin\theta +r^{2}sin3\theta ){\phi }^{\prime }-a_{21}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)-a_{22}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)=\phi a_{23},\end{array}$$

$$\Omega \left(-1+r^4\right)=a_{31}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)+a_{32}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)+\phi a_{33},$$

where $\Omega \left(r\right)=\frac{2H}{W}.$ Differentiating the ODEs with respect to $\theta ,$ we have

$$a_{13}=a_{23}=a_{33}=0,\Omega \left(r\right)=0.$$

(17)

From (17), we get

$$\begin{array}{ccc}\hfill -a_{11}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)-a_{12}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)& =& 0,\hfill \\ \hfill -a_{21}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)-a_{22}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)& =& 0,\hfill \\ \hfill a_{31}\left(rcos\left(\theta \right)-\frac{r^3}{3}cos\left(3\theta \right)\right)+a_{32}\left(-rsin\left(\theta \right)-\frac{r^3}{3}sin\left(3\theta \right)\right)& =& 0.\hfill \end{array}$$

here, cos and sin are linearly independent functions of $\theta$, then we have that $a_{ij}=0$. From $\Omega \left(r\right)=\frac{2H}{W}$, we obtain $H=0$. Finally, ${\mathbf{R}}_{\mathbf{0},\mathbf{1}}$ is a minimal rotational hypersurface. ☐