On Edge Irregular Reflexive Labellings for the Generalized Friendship Graphs

Abstract

We study an edge irregular reflexive k-labelling for the generalized friendship graphs, also known as flowers (a symmetric collection of cycles meeting at a common vertex), and determine the exact value of the reflexive edge strength for several subfamilies of the generalized friendship graphs.

1. Introduction

All graphs considered in this paper are simple, finite and undirected. Chartrand et al. in [1] proposed the following problem. Assign positive integer labels from the set $\{1,2,\dots ,k\}$ to the edges of a simple connected graph of order at least three in such a way that the graph becomes irregular, i.e., the weights (label sums) at each vertex are distinct. What is the minimum value of the largest label k over all such irregular assignments? This parameter of a graph G is well known as the irregularity strength of the graph G. An excellent survey on the irregularity strength is given by Lehel in [2]. For recent results, see the papers by Amar and Togni [3], Dimitz et al. [4], Gyárfás [5] and Nierhoff [6].

Motivated by these papers in [7], an edge irregular k-labelling as a vertex labelling $\rho :V(G)\to \{1,2,\dots ,k\}$ was defined, such that for every two different edges $xy$ and $x^{\prime }{y}^{\prime }$, there is $w_{\rho }(xy)\ne w_{\rho }(x^{\prime }{y}^{\prime })$, where the weight of an edge $xy\in E(G)$ is $w_{\rho }(xy)=\rho (x)+\rho (y)$. The minimum k for which the graph G has an edge irregular k-labelling is called the edge irregularity strength of the graph G, denoted by $es(G)$. In [7] are estimated the bounds of the parameter $es(G)$, and the exact values of the edge irregularity strength for several families of graphs are determined, namely paths, stars, double stars and the Cartesian product of two paths.

In [8], the authors defined the total labelling $\phi :V(G)\cup E(G)\to \{1,2,\dots ,k\}$ to be an edge irregular total k-labelling of the graph G if for every two different edges $xy$ and $x^{\prime }{y}^{\prime }$ of G one has $w{t}_{\phi }(xy)=\phi (x)+\phi (xy)+\phi (y)\ne w{t}_{\phi }(x^{\prime }{y}^{\prime })=\phi (x^{\prime })+\phi (x^{\prime }{y}^{\prime })+\phi (y^{\prime })$. The total edge irregularity strength, $\mathrm{tes}(G)$, is defined as the minimum k for which G has an edge irregular total k-labelling. Estimations of this parameter are obtained in [8], which provides the precise values of the total edge irregularity strength for paths, cycles, stars, wheels and friendship graphs. Further results on the total edge irregularity strength can be found in [9,10,11,12,13,14,15].

The seminal problem for irregular labellings from [1] arose from a consideration of graphs with distinct degrees. In a simple graph, it is not possible to construct a graph in which every vertex has a unique degree; however, this is possible in multigraphs (graphs in which we allow multiple edges between the adjacent vertices). The question then became: “What is the smallest number of parallel edges between two vertices required to ensure that the graph displays vertex irregularity?” This problem is equivalent to the labelling problem as described at the beginning of this section.

Using both [1,8] as the motivation, in [16], the authors decreed that the vertex labels should represent loops at the vertex. The consequence was two-fold; first, each vertex label was required to be an even integer, since each loop added two to the vertex degree; and second, unlike in total irregular labelling, the label 0 was permitted as representing a loopless vertex. Edges continued to be labelled by integers from one to k.

Thus, for a graph G, in [16] are defined labellings $f_e:E(G)\to \{1,2,\dots ,k_e\}$ and $f_v:V(G)\to \{0,2,\dots ,2k_v\}$, and then, labelling f is a total k-labelling of G defined such that $f(x)=f_v(x)$ if $x\in V(G)$ and $f(x)=f_e(x)$ if $x\in E(G)$, where $k=max\{k_e,2k_v\}$.

The total k-labelling f is called an edge irregular reflexive k-labelling of the graph G if for every two different edges $xy$ and $x^{\prime }{y}^{\prime }$ of G, one has $wt(xy)=f_v(x)+f_e(xy)+f_v(y)\ne wt(x^{\prime }{y}^{\prime })=f_v(x^{\prime })+f_e(x^{\prime }{y}^{\prime })+f_v(y^{\prime })$. The smallest value of k for which such labelling exists is called the reflexive edge strength of the graph G and is denoted by $\mathrm{res}(G)$.

The result of this variation was not widely manifest in the labelling strengths, but did produce some important outcomes:

$$\mathrm{tes}(K_5)=5\mathrm{whereas}\mathrm{res}(K_5)=4$$

The effect of this change was immediate in the following conjecture where we were able to remove the pesky exception.

Conjecture 1.

From [12]. Any graph G with maximum degree $\Delta (G)$ other than $K_5$ satisfies:

$$\mathrm{tes}(G)=max\left\{⌈\frac{\Delta +1}{2}⌉,⌈\frac{|E(G)+2}{3}⌉\right\}$$

In terms of reflexive edge irregularity strength, we now propose:

Conjecture 2.

Any graph G with maximum degree $\Delta (G)$ satisfies:

$$\mathrm{res}(G)=max\left\{⌊\frac{\Delta +2}{2}⌋,⌈\frac{|E(G)|}{3}⌉+r\right\}$$

where $r=1$ for $|E(G)|\equiv 2,3(mod6)$, and zero otherwise.

In this paper, we investigate the reflexive edge strength for generalized friendship graphs. The friendship graph $f_m$ is a collection of m triangles with a common vertex. It may be also pictured as a wheel with every alternate rim edge removed. Let us mention that the reflexive edge strength for wheels can be found in [17]. The generalized friendship graph $f_{n,m}$ is a collection of m cycles (all of order n), meeting at a common vertex. We will refer to the friendship graph $f_m$ as an instance of the generalized friendship graph and write it as $f_{3,m}$. The generalized friendship graph may also be referred to as a flower; see [18]. In this nomenclature, the cycles are referred to as petals. For our purposes, we refer to vertices in the following way: the central vertex is named x, and all other vertices are addressed in the form $x_i^j$, where j, $1\le j\le m$ indicates which cycle contains the vertex and i, $1\le i\le n$ points to the position of the vertex within the cycle. Therefore, $x=x_n^j$ for all j. Then, we denote the edge set of the generalized friendship graph such that $E(f_{n,m})=\{x_i^j{x}_{i+1}^j:1\le i\le n-2,1\le j\le m\}\cup \{x{x}_1^j,x{x}_{n-1}^j:1\le j\le m\}$.

2. Constructing an Edge Irregular Reflexive Labelling for ${\mathit{f}}_{\mathit{n},\mathit{m}}$, $\mathit{n}=\mathbf{3},\mathbf{4},\mathbf{5}$

Let us recall the following lemma proven in [16] and the theorem proven in [19].

Lemma 1.

From [16]. For every graph G,

$$\begin{array}{cc}\hfill \mathrm{res}(G)& \ge \left\{\begin{array}{cc}⌈\frac{|E(G)|}{3}⌉\hfill & if|E(G)|\not\equiv 2,3(mod6),\hfill \\ ⌈\frac{|E(G)|}{3}⌉+1\hfill & if|E(G)|\equiv 2,3(mod6).\hfill \end{array}\right.\hfill \end{array}$$

The lower bound for $\mathrm{res}(G)$ follows from the fact that the minimal edge weight under an edge irregular reflexive labelling is one, and the minimum of the maximal edge weights, that is $|E(G)|$, can be achieved only as the sum of three numbers, at least two of which are even.

Theorem 1.

From [19]. For every positive integer $n\ge 3$:

$$\begin{array}{c}\hfill \mathrm{res}(C_n)=\left\{\begin{array}{cc}\lceil \frac{n}{3}\rceil \hfill & ifn\not\equiv 2,3(mod6),\hfill \\ \lceil \frac{n}{3}\rceil +1\hfill & ifn\equiv 2,3(mod6).\hfill \end{array}\right.\end{array}$$

In this section, we determine the exact value of the reflexive edge strength for the generalized friendship graphs $f_{n,m}$, $n=3,4,5$, $m\ge 1$.

Theorem 2.

For every positive integer $m\ge 1$:

$$\begin{array}{c}\hfill \mathrm{res}(f_{3,m})=\left\{\begin{array}{cc}3\hfill & ifm=2,\hfill \\ m\hfill & ifmiseven,m\ge 4,\hfill \\ m+1\hfill & ifmisodd.\hfill \end{array}\right.\end{array}$$

Proof. 

The graph $f_{3,m}$ has $3m$ edges; thus by Lemma 1, we have:

$$\begin{array}{c}\hfill \mathrm{res}(f_{3,m})\ge \left\{\begin{array}{cc}m\hfill & \mathrm{if}m\mathrm{is}\mathrm{even},\hfill \\ m+1\hfill & \mathrm{if}m\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.\end{array}$$

As $f_{3,1}$ is isomorphic to $C_3$, thus according to Theorem 1, we get $\mathrm{res}(C_3)=2$.

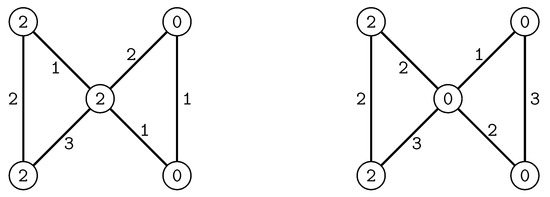
It is easy to see that $\mathrm{res}(f_{3,2})\ge 3$. Two non-isomorphic edge irregular reflexive three-labellings for $f_{3,2}$ are illustrated in Figure 1.

Figure 1. Two non-isomorphic edge irregular reflexive three-labellings of $f_{3,2}$.

For $m\ge 3$, we distinguish two cases.

Case 1. When m is even, we define an m-labelling f of $f_{3,m}$ such that:

$$\begin{array}{cc}\hfill f(x)& =m-2,\hfill \\ \hfill f(x_1^j)& =0\hfill & j=1,2,\dots ,m-2,\hfill \\ \hfill f(x_1^j)& =m\hfill & j=m-1,m,\hfill \\ \hfill f(x_2^j)& =2\lceil \frac{j}{2}\rceil -2\hfill & j=1,2,\dots ,m-2,\hfill \\ \hfill f(x_2^j)& =m\hfill & j=m-1,m,\hfill \\ \hfill f(x{x}_1^j)& =j\hfill & j=1,2,\dots ,m-2,\hfill \\ \hfill f(x{x}_1^{m-1})& =m-3,\hfill \\ \hfill f(x{x}_1^m)& =m-1,\hfill \\ \hfill f(x{x}_2^j)& =m-1\hfill & j=1,3,\dots ,m-3,\hfill \\ \hfill f(x{x}_2^j)& =m\hfill & j=2,4,\dots ,m,\hfill \\ \hfill f(x{x}_2^{m-1})& =m-2,\hfill \\ \hfill f(x_1^j{x}_2^j)& =1\hfill & j=1,3,\dots ,m-3,\hfill \\ \hfill f(x_1^j{x}_2^j)& =2\hfill & j=2,4,\dots ,m-2,\hfill \\ \hfill f(x_1^{m-1}{x}_2^{m-1})& =m-1,\hfill \\ \hfill f(x_1^m{x}_2^m)& =m.\hfill \end{array}$$

Then, we get:

$$\begin{array}{cc}\hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=(m-2)+j+0=m+j-2\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2,\hfill \\ \hfill w{t}_f(x{x}_1^{m-1})=& f(x)+f(x{x}_1^{m-1})+f(x_1^{m-1})=(m-2)+(m-3)+m=3m-5,\hfill \\ \hfill w{t}_f(x{x}_1^m)=& f(x)+f(x{x}_1^m)+f(x_1^m)=(m-2)+(m-1)+m=3m-3,\hfill \\ \hfill w{t}_f(x{x}_2^j)=& f(x)+f(x{x}_2^j)+f(x_2^j)=(m-2)+(m-1)+(2\lceil \frac{j}{2}\rceil -2)=2m-4+j\hfill \\ & \mathrm{for}j=1,3,\dots ,m-3,\hfill \\ \hfill w{t}_f(x{x}_2^j)=& f(x)+f(x{x}_2^j)+f(x_2^j)=(m-2)+m+(2\lceil \frac{j}{2}\rceil -2)=2m-4+j\hfill \\ & \mathrm{for}j=2,4,\dots ,m-2,\hfill \\ \hfill w{t}_f(x{x}_2^{m-1})=& f(x)+f(x{x}_2^{m-1})+f(x_2^{m-1})=(m-2)+(m-2)+m=3m-4,\hfill \\ \hfill w{t}_f(x{x}_2^m)=& f(x)+f(x{x}_2^m)+f(x_2^m)=(m-2)+m+m=3m-2,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+1+(2\lceil \frac{j}{2}\rceil -2)=j\hfill \\ & \mathrm{for}j=1,3,\dots ,m-3,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+2+(2\lceil \frac{j}{2}\rceil -2)=j\hfill \\ & \mathrm{for}j=2,4,\dots ,m-2,\hfill \\ \hfill w{t}_f(x_1^{m-1}{x}_2^{m-1})=& f(x_1^{m-1})+f(x_1^{m-1}{x}_2^{m-1})+f(x_2^{m-1})=m+(m-1)+m=3m-1,\hfill \\ \hfill w{t}_f(x_1^m{x}_2^m)=& f(x_1^m)+f(x_1^m{x}_2^m)+f(x_2^m)=m+m+m=3m.\hfill \end{array}$$

It is not difficult to see that the edge weights are from the set $\{1,2,\dots ,3m\}$. This shows that f is an edge irregular reflexive labelling of $f_{3,m}$ for $m\ge 4$ even.

Case 2. When m is odd, we define an $(m+1)$-labelling f of $f_{3,m}$ such that:

$$\begin{array}{cc}\hfill f(x)& =m-1,\hfill \\ \hfill f(x_1^j)& =0\hfill & j=1,2,\dots ,m-1,\hfill \\ \hfill f(x_1^m)& =m-1,\hfill \\ \hfill f(x_2^j)& =2\lceil \frac{j}{2}\rceil -2\hfill & j=1,2,\dots ,m-1,\hfill \\ \hfill f(x_2^m)& =m+1,\hfill \\ \hfill f(x{x}_1^j)& =j\hfill & j=1,2,\dots ,m,\hfill \\ \hfill f(x{x}_2^j)& =m\hfill & j=1,3,\dots ,m-2,\hfill \\ \hfill f(x{x}_2^j)& =m+1\hfill & j=2,4,\dots ,m-1,\hfill \\ \hfill f(x{x}_2^m)& =m-1,\hfill \\ \hfill f(x_1^j{x}_2^j)& =1\hfill & j=1,3,\dots ,m-2,\hfill \\ \hfill f(x_1^j{x}_2^j)& =2\hfill & j=2,4,\dots ,m-1,\hfill \\ \hfill f(x_1^m{x}_2^m)& =m.\hfill \end{array}$$

Thus, the vertices are labelled with even numbers, and the edge weights are:

$$\begin{array}{cc}\hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=(m-1)+j+0=m+j-1\hfill \\ & \mathrm{for}j=1,2,\dots ,m-1,\hfill \\ \hfill w{t}_f(x{x}_1^m)=& f(x)+f(x{x}_1^m)+f(x_1^m)=(m-1)+m+(m-1)=3m-2,\hfill \\ \hfill w{t}_f(x{x}_2^j)=& f(x)+f(x{x}_2^j)+f(x_2^j)=(m-1)+m+(2\lceil \frac{j}{2}\rceil -2)=2m-2+j\hfill \\ & \mathrm{for}j=1,3,\dots ,m-2,\hfill \\ \hfill w{t}_f(x{x}_2^j)=& f(x)+f(x{x}_2^j)+f(x_2^j)=(m-1)+(m+1)+(2\lceil \frac{j}{2}\rceil -2)=2m-2+j\hfill \\ & \mathrm{for}j=2,4,\dots ,m-1,\hfill \\ \hfill w{t}_f(x{x}_2^m)=& f(x)+f(x{x}_2^m)+f(x_2^m)=(m-1)+(m-1)+(m+1)=3m-1,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+1+(2\lceil \frac{j}{2}\rceil -2)=j\hfill \\ & \mathrm{for}j=1,3,\dots ,m-2,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+2+(2\lceil \frac{j}{2}\rceil -2)=j\hfill \\ & \mathrm{for}j=2,4,\dots ,m-1,\hfill \\ \hfill w{t}_f(x_1^m{x}_2^m)=& f(x_1^m)+f(x_1^m{x}_2^m)+f(x_2^m)=(m-1)+m+(m+1)=3m.\hfill \end{array}$$

Thus also for n odd, $m\ge 3$, the edge weights are distinct numbers from the set $\{1,2,\dots ,3m\}$.

This concludes the proof. ☐

Theorem 3.

For every positive integer $m\ge 1$:

$$\begin{array}{c}\hfill \mathrm{res}(f_{4,m})=\left\{\begin{array}{cc}\lceil \frac{4m}{3}\rceil \hfill & ifm\equiv 0,1(mod3),\hfill \\ \lceil \frac{4m}{3}\rceil +1\hfill & ifm\equiv 2(mod3).\hfill \end{array}\right.\end{array}$$

Proof. 

Let us denote $m=3r+t$, where $r\ge 0$ and $t\in \{0,1,2\}$.

As $|E(f_{4,3r+t})|=4(3r+t)=12r+4t$, then according to Lemma 1, we get:

$$\begin{array}{c}\hfill \mathrm{res}(f_{4,3r+t})\ge \left\{\begin{array}{cc}\lceil \frac{12r+4t}{3}\rceil \hfill & \mathrm{if}t\ne 2,\hfill \\ \lceil \frac{12r+4t}{3}\rceil +1\hfill & \mathrm{if}t=2.\hfill \end{array}\right.\end{array}$$

that is:

$$\mathrm{res}(f_{4,3r+t})\ge 4r+2t$$

for every $r\ge 0$ and $t\in \{0,1,2\}$.

We define a $(4r+2t)$-labelling f of $f_{4,3r+t}$ such that:

$$\begin{array}{cc}\hfill f(x)& =0,\hfill \\ \hfill f(x_i^j)& =0\hfill & j=1,2,\dots ,r+t,i=1,3,\hfill \\ \hfill f(x_i^j)& =2j-2\hfill & j=r+t+1,r+t+2,\dots ,2r+t,i=1,3,\hfill \\ \hfill f(x_i^j)& =4r+2t\hfill & j=2r+t+1,2r+t+2,\dots ,3r+t,i=1,3,\hfill \\ \hfill f(x_2^j)& =4r+2t\hfill & j=1,2,\dots ,3r+t,\hfill \\ \hfill f(x{x}_1^j)& =2j-1\hfill & j=1,2,\dots ,r+t,\hfill \\ \hfill f(x{x}_1^j)& =1\hfill & j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill f(x{x}_1^j)& =6r+2t+2-2j\hfill & j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill f(x{x}_3^j)& =2j\hfill & j=1,2,\dots ,r+t,\hfill \\ \hfill f(x{x}_3^j)& =2\hfill & j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill f(x{x}_3^j)& =6r+2t+1-2j\hfill & j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill f(x_1^j{x}_2^j)& =2r-1+2j\hfill & j=1,2,\dots ,r+t,\hfill \\ \hfill f(x_1^j{x}_2^j)& =2r+1\hfill & j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill f(x_1^j{x}_2^j)& =8r+2t+2-2j\hfill & j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill f(x_3^j{x}_2^j)& =2r+2j\hfill & j=1,2,\dots ,r+t,\hfill \\ \hfill f(x_3^j{x}_2^j)& =2r+2\hfill & j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill f(x_3^j{x}_2^j)& =8r+2t+1-2j\hfill & j=2r+t+1,2r+t+2,\dots ,3r+t.\hfill \end{array}$$

Evidently, the vertices are labelled by even numbers, and none of the labels are greater than $4r+2t$. Moreover, for the edge weights, we get the following:

$$\begin{array}{cc}\hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(2j-1)+0=2j-1\hfill \\ & \mathrm{for}j=1,2,\dots ,r+t,\hfill \\ \hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+1+(2j-2)=2j-1\hfill \\ & \mathrm{for}j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(6r+2t+2-2j)+(4r+2t)=10r+4t+2-2j\hfill \\ & \mathrm{for}j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill w{t}_f(x{x}_3^j)=& f(x)+f(x{x}_3^j)+f(x_3^j)=0+2j+0=2j\hfill \\ & \mathrm{for}j=1,2,\dots ,r+t,\hfill \\ \hfill w{t}_f(x{x}_3^j)=& f(x)+f(x{x}_3^j)+f(x_3^j)=0+2+(2j-2)=2j\hfill \\ & \mathrm{for}j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill w{t}_f(x{x}_3^j)=& f(x)+f(x{x}_3^j)+f(x_3^j)=0+(6r+2t+1-2j)+(4r+2t)=10r+4t+1-2j\hfill \\ & \mathrm{for}j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+(2r-1+2j)+(4r+2t)=6r+2t-1+2j\hfill \\ & \mathrm{for}j=1,2,\dots ,r+t,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=(2j-2)+(2r+1)+(4r+2t)=6r+2t-1+2j\hfill \\ & \mathrm{for}j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=(4r+2t)+(8r+2t+2-2j)+(4r+2t)\hfill \\ \hfill =& 16r+6t+2-2j\hfill \\ & \mathrm{for}j=2r+t+1,2r+t+2,\dots ,3r+t,\hfill \\ \hfill w{t}_f(x_3^j{x}_2^j)=& f(x_3^j)+f(x_3^j{x}_2^j)+f(x_2^j)=0+(2r+2j)+(4r+2t)=6r+2t+2j\hfill \\ & \mathrm{for}j=1,2,\dots ,r+t,\hfill \\ \hfill w{t}_f(x_3^j{x}_2^j)=& f(x_3^j)+f(x_3^j{x}_2^j)+f(x_2^j)=(2j-2)+(2r+2)+(4r+2t)=6r+2t+2j\hfill \\ & \mathrm{for}j=r+t+1,r+t+2,\dots ,2r+t,\hfill \\ \hfill w{t}_f(x_3^j{x}_2^j)=& f(x_3^j)+f(x_3^j{x}_2^j)+f(x_2^j)=(4r+2t)+(8r+2t+1-2j)+(4r+2t)\hfill \\ \hfill =& 16r+6t+1-2j\hfill \\ & \mathrm{for}j=2r+t+1,2r+t+2,\dots ,3r+t.\hfill \end{array}$$

It is not difficult to see that the edge weights are from the set $\{1,2,\dots ,12r+4t\}$. This shows that f is an edge irregular reflexive labelling of $f_{4,m}$ for $m\ge 1$. ☐

Theorem 4.

For every positive integer $m\ge 1$:

$$\begin{array}{c}\hfill \mathrm{res}(f_{5,m})=\left\{\begin{array}{cc}\lceil \frac{5m}{3}\rceil \hfill & ifm\not\equiv 3,4(mod6),\hfill \\ \lceil \frac{5m}{3}\rceil +1\hfill & ifm\equiv 3,4(mod6).\hfill \end{array}\right.\end{array}$$

Proof. 

As the number of edges of $f_{5,m}$ is $5m$, then using Lemma 1, we obtain:

$$\begin{array}{c}\hfill \mathrm{res}(f_{5,m})\ge k=\left\{\begin{array}{cc}\lceil \frac{5m}{3}\rceil \hfill & \mathrm{if}m\not\equiv 3,4(mod6),\hfill \\ \lceil \frac{5m}{3}\rceil +1\hfill & \mathrm{if}m\equiv 3,4(mod6).\hfill \end{array}\right.\end{array}$$

It is easy to see that for $m\equiv 5(mod6)$, the number k is odd, and otherwise, k is even.

As $f_{5,1}$ is isomorphic to $C_5$, thus according to Theorem 1, we get $\mathrm{res}(C_5)=2$.

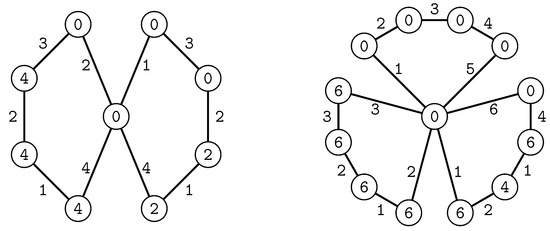
From the lower bound for $\mathrm{res}(f_{5,m})$, we get that $\mathrm{res}(f_{5,2})\ge 4$ and $\mathrm{res}(f_{5,3})\ge 6$. A corresponding edge irregular reflexive four-labelling for $f_{5,2}$ and an edge irregular reflexive six-labelling for $f_{5,3}$ are illustrated in Figure 2.

Figure 2. An edge irregular reflexive four-labelling for $f_{5,2}$ and an edge irregular reflexive six-labelling for $f_{5,3}$.

Let $m\ge 4$. We distinguish two cases according to the parity of k.

Case 1. When $m\not\equiv 5(mod6)$, that is when k is an even number, we define a k-labelling f of $f_{5,m}$ in the following way:

$$\begin{array}{cc}\hfill f(x)& =0,\hfill \\ \hfill f(x_i^j)& =0\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,i=1,4,\hfill \\ \hfill f(x_i^j)& =k-2\lceil \frac{m-4}{6}\rceil \hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,i=1,4,\hfill \\ \hfill f(x_i^j)& =k\hfill & j=1,2,\dots ,m,i=2,3,\hfill \\ \hfill f(x{x}_1^j)& =2j-1\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x{x}_1^j)& =2m+2-2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x{x}_4^j)& =2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x{x}_4^j)& =2m+1-2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x_1^j{x}_2^j)& =k+2-2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x_1^j{x}_2^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -1+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 0(mod6),\hfill \\ \hfill f(x_1^j{x}_2^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -3+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 1,2(mod6),\hfill \\ \hfill f(x_1^j{x}_2^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -7+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 3(mod6),\hfill \\ \hfill f(x_1^j{x}_2^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -9+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 4(mod6),\hfill \\ \hfill f(x_3^j{x}_4^j)& =k+1-2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil +2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 0(mod6),\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -2+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 1,2(mod6),\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -6+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 3(mod6),\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil -8+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ & & m\equiv 4(mod6),\hfill \\ \hfill f(x_2^j{x}_3^j)& =k+1-j\hfill & j=1,2,\dots ,m,m\equiv 0(mod6),\hfill \\ \hfill f(x_2^j{x}_3^j)& =k-j\hfill & j=1,2,\dots ,m,m\equiv 1(mod6),\hfill \\ \hfill f(x_2^j{x}_3^j)& =k-1-j\hfill & j=1,2,\dots ,m,m\equiv 2(mod6),\hfill \\ \hfill f(x_2^j{x}_3^j)& =k-2-j\hfill & j=1,2,\dots ,m,m\equiv 3(mod6),\hfill \\ \hfill f(x_2^j{x}_3^j)& =k-3-j\hfill & j=1,2,\dots ,m,m\equiv 4(mod6).\hfill \end{array}$$

For the edge weights, we get:

$$\begin{array}{cc}\hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(2j-1)+0=2j-1\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(2m+2-2j)+(k-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& 2m+k-2\lceil \frac{m-4}{6}\rceil +2-2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x{x}_4^j)=& f(x)+f(x{x}_4^j)+f(x_4^j)=0+2j+0=2j\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x{x}_4^j)=& f(x)+f(x{x}_4^j)+f(x_4^j)=0+(2m+1-2j)+(k-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& 2m+k-2\lceil \frac{m-4}{6}\rceil +1-2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+(k+2-2j)+k=2k+2-2j\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil .\hfill \end{array}$$

For $j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m$, we have:

$$\begin{array}{cc}\hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=(k-2\lceil \frac{m-4}{6}\rceil )+f(x_1^j{x}_2^j)+k\hfill \\ \hfill =& \left\{\begin{array}{cc}3k-2m-6\lceil \frac{m-4}{6}\rceil -1+2j,\hfill & m\equiv 0(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -3+2j,\hfill & m\equiv 1,2(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -7+2j,\hfill & m\equiv 3(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -9+2j,\hfill & m\equiv 4(mod6).\hfill \end{array}\right.\hfill \end{array}$$

Furthermore, the weights of edges $x_3^j{x}_4^j$ for $j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil$ are:

$$\begin{array}{cc}\hfill w{t}_f(x_3^j{x}_4^j)=& f(x_3^j)+f(x_3^j{x}_4^j)+f(x_4^j)=k+(k+1-2j)+0=2k+1-2j,\hfill \end{array}$$

and for $j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m$, the weights are:

$$\begin{array}{cc}\hfill w{t}_f(x_3^j{x}_4^j)=& f(x_3^j)+f(x_3^j{x}_4^j)+f(x_4^j)=k+f(x_3^j{x}_4^j)+(k-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& \left\{\begin{array}{cc}3k-2m-6\lceil \frac{m-4}{6}\rceil +2j,\hfill & m\equiv 0(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -2+2j,\hfill & m\equiv 1,2(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -6+2j,\hfill & m\equiv 3(mod6),\hfill \\ 3k-2m-6\lceil \frac{m-4}{6}\rceil -8+2j,\hfill & m\equiv 4(mod6).\hfill \end{array}\right.\hfill \end{array}$$

Additionally, for $j=1,2,\dots ,m$, we get:

$$\begin{array}{cc}\hfill w{t}_f(x_2^j{x}_3^j)=& f(x_2^j)+f(x_2^j{x}_3^j)+f(x_3^j)=k+f(x_2^j{x}_3^j)+k\hfill \\ \hfill =& \left\{\begin{array}{cc}3k+1-j,\hfill & m\equiv 0(mod6),\hfill \\ 3k-j,\hfill & m\equiv 1(mod6),\hfill \\ 3k-1-j,\hfill & m\equiv 2(mod6),\hfill \\ 3k-2-j,\hfill & m\equiv 3(mod6),\hfill \\ 3k-3-j,\hfill & m\equiv 4(mod6).\hfill \end{array}\right.\hfill \end{array}$$

Its is not difficult to see that the edge weights are distinct numbers from the set $\{1,2,\dots ,5m\}$.

Case 2. When $m\equiv 5(mod6)$, that is when $k=\lceil \frac{5m}{3}\rceil$ is odd, then we define a k-labelling f of $f_{5,m}$ such that:

$$\begin{array}{cc}\hfill f(x)& =0\hfill \\ \hfill f(x_i^j)& =0\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,i=1,4,\hfill \\ \hfill f(x_i^j)& =k-1-2\lceil \frac{m-4}{6}\rceil \hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,i=1,4,\hfill \\ \hfill f(x_i^j)& =k-1\hfill & j=1,2,\dots ,m,i=2,3,\hfill \\ \hfill f(x{x}_1^j)& =2j-1\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x{x}_1^j)& =2m+2-2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x{x}_4^j)& =2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x{x}_4^j)& =2m+1-2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x_1^j{x}_2^j)& =k+1-2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x_1^j{x}_2^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil +2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2j\hfill & j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill f(x_3^j{x}_4^j)& =k-2m-4\lceil \frac{m-4}{6}\rceil +1+2j\hfill & j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill f(x_2^j{x}_3^j)& =k+1-j\hfill & j=1,2,\dots ,m.\hfill \end{array}$$

The edge weights are:

$$\begin{array}{cc}\hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(2j-1)+0=2j-1\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x{x}_1^j)=& f(x)+f(x{x}_1^j)+f(x_1^j)=0+(2m+2-2j)+(k-1-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& 2m+k-2\lceil \frac{m-4}{6}\rceil +1-2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x{x}_4^j)=& f(x)+f(x{x}_4^j)+f(x_4^j)=0+2j+0=2j\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x{x}_4^j)=& f(x)+f(x{x}_4^j)+f(x_4^j)=0+(2m+1-2j)+(k-1-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& 2m+k-2\lceil \frac{m-4}{6}\rceil -2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=0+(k+1-2j)+(k-1)=2k-2j\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x_1^j{x}_2^j)=& f(x_1^j)+f(x_1^j{x}_2^j)+f(x_2^j)=(k-1-2\lceil \frac{m-4}{6}\rceil )+(k-2m-4\lceil \frac{m-4}{6}\rceil +2j)+(k-1)\hfill \\ \hfill =& 3k-2m-6\lceil \frac{m-4}{6}\rceil -2+2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x_3^j{x}_4^j)=& f(x_3^j)+f(x_3^j{x}_4^j)+f(x_4^j)=(k-1)+(k-2j)+0=2k-1-2j\hfill \\ & \mathrm{for}j=1,2,\dots ,m-2\lceil \frac{m-4}{6}\rceil ,\hfill \\ \hfill w{t}_f(x_3^j{x}_4^j)=& f(x_3^j)+f(x_3^j{x}_4^j)+f(x_4^j)=k+(k-2m-4\lceil \frac{m-4}{6}\rceil +1+2j)+(k-2\lceil \frac{m-4}{6}\rceil )\hfill \\ \hfill =& 3k-2m-6\lceil \frac{m-4}{6}\rceil -1+2j\hfill \\ & \mathrm{for}j=m-2\lceil \frac{m-4}{6}\rceil +1,m-2\lceil \frac{m-4}{6}\rceil +2,\dots ,m,\hfill \\ \hfill w{t}_f(x_2^j{x}_3^j)=& f(x_2^j)+f(x_2^j{x}_3^j)+f(x_3^j)=(k-1)+(k+1-j)+(k-1)=3k-1-j\hfill \\ & \mathrm{for}j=1,2,\dots ,m.\hfill \end{array}$$

Also in this case, the edge weights are from the set $\{1,2,\dots ,5m\}$.

Thus, we constructed an edge irregular reflexive labelling of $f_{5,m}$ for $m\ge 1$. ☐

3. Conclusions

In this paper, we proved the precise values of the reflexive edge strength for the generalized friendship graphs $f_{n,m}$ for $n=3,4,5$, $m\ge 1$. According to Theorems 2–4, we conclude the paper with the following conjecture:

Conjecture 3.

For every positive integers $m\ge 1$ and $n\ge 6$:

$$\begin{array}{c}\hfill \mathrm{res}(f_{n,m})=\left\{\begin{array}{cc}\lceil \frac{mn}{3}\rceil \hfill & ifmn\not\equiv 2,3(mod6),\hfill \\ \lceil \frac{mn}{3}\rceil +1\hfill & ifmn\equiv 2,3(mod6).\hfill \end{array}\right.\end{array}$$