1. Introduction
Fractional differential equations (FDEs) are seeing a rapid rise in utility including applications in engineering, physics, economics, and chemistry [
1,
2,
3,
4,
5,
6,
7]. From a modeling point of view, FDEs or dynamic systems have been better compared with its counterpart of integer derivatives [
3,
6,
7]. However, analytic or numerical computation of the solution of fractional dynamic equations has been challenging. This is mainly because some of the basic properties enjoyed by integer derivatives such as the product rule and separation of variables are not available. Because of this, standard methods to numerically approximate solutions to FDEs are in high demand. In [
8], Euler’s method for numerically solving FDEs has been developed. In [
9], Picard’s method has been developed to solve fractional initial value problems (IVPs) when the forcing term satisfies a Lipschitz condition where the Lipschitz’s constant is time dependent and thus, these conditions are not global. In this work, we develop Picard’s method for Caputo FDEs with initial conditions, when the nonlinear term satisfies a time independent (global) Lipschitz’s condition. Another advantage of time independent Lipschitz condition is in proving global uniqueness and in computing global solutions when they exist. This is obviously true for population models and ecological models, which can be established using coupled lower upper solutions which act as bounds. As an application of the Picard’s method, we develop a numerical scheme and provide several numerical examples. Each iteration of this scheme is a solution of a particular integral equation which has been extensively studied numerically as in [
10]. Our method removes the complexity of computing fractional derivatives using the matrix method developed in [
11]. Our numerical method also provides a formula to compute the inverse Laplace transform of product functions. Unlike most methods, our method can be extended to a generalized monotone method using coupled lower and upper solutions where the solution’s interval of existence is guaranteed. The numerical examples provide some insight on the behavior of Picard Iterates.
2. Preliminary Results
Before we begin, we must define a few terms starting with the commonly used Gamma and Beta Functions. We use the following definitions for these functions.
Definition 1. The Gamma Function, , is defined byand the Beta Function, is defined by It should also be known that the Beta and Gamma Functions have the following relationship:
See [
12] for more information on this relationship.
In this work, we develop the Picard’s iterative method for Caputo FDEs. Thus, we only consider Caputo’s definition of a fractional derivative:
Definition 2. Let , and . Then the Caputo derivative of order α is given bywhere such that . In particular, if , an integer, then . To compare, we define the Riemann-Liouville integral of order for
Definition 3. The Riemann-Liouville fractional integral of arbitrary order α defined bywhere . Note that the definition of Riemann-Lioville integral of order for is the same as the Caputo integral of order
Consider the Caputo fractional IVP:
where
and
The integral representation of (1) is given by
In order to prove that the solution of the IVP (1) exists and is unique on some interval, it is enough to prove that the solution of the integral Equation (2) exists and is unique. This is precisely what is done in this work.
In [
13], they have proved the Peano’s theorem for the IVP (1) which guarantees the existence of a solution on some interval. For completeness, we state the result below.
Theorem 1. Assume that , where and , and let . Then, the IVP (1) posses at least one solution, on where .
Theorem 1 guarantees the existence of a solution to the IVP (1). Although Peano’s theorem proves the existence of a solution locally, it is not a constructive method to compute the solution analytically or numerically. In this work, our goal is to develop an iterative method which converges to the unique solution of the IVP (1). In order to develop the iterative method, namely Picard’s iterative method, we need the Lipschitz’s condition definition for the function in the IVP (1).
Definition 4. A function, is said to be a Lipschitz function in u if for any there exists an such that The condition above is called the global Lipschitz condition. However, if and are in a known closed interval containing then we say that is locally Lipshitzian.
The next definition is related to the Mittag-Leffler function which is useful in computing linear ordinary FDEs with initial conditions.
Definition 5. The two parameter Mittag-Leffler function is defined aswhere α, , and λ is a constant. Furthermore, for , (3) reduces to In particular, if
in (3), then we have:
and if
, then
where
is the usual exponential function.
For more information and details on Mittag-Leffler functions see [
3,
7,
14,
15].
3. Main Result
In this section, we develop Picard’s iterative method for the Caputo FDE. Our results yield the integer result as a special case. Although the result developed in this work is for scalar Caputo FDEs, it can be easily extended to systems of Caputo FDEs with initial conditions. Next, we state our main result.
Theorem 2. Consider the IVP (1), where f is a continuous Lipschitzian function on the closed rectangle . Let be such that . Then, the IVP (1) has a unique solution on where and Furthermore, the iterationswith the initial approximation being , converge uniformly to the solution to the IVP (1). We first prove the following lemmas which will be useful in the proof of Theorem 2.
Lemma 1. Under the hypothesis of Theorem 2, , , defined as in (7), is a continuous function for all .
Proof. This proof follows by method of induction. Clearly,
is continuous on
I, as it is constant. Since
f is continuous,
is also continuous. Now, if we assume for some
,
is continuous on
I, then it follows
is also continuous on
I. Thus by induction, the result holds for all
. ☐
Lemma 2. Under the hypothesis of Theorem 2, , the sequence , where , defined in (7), converges uniformly on I.
Proof. It is easy to observe that
Our goal is to show that the absolute value of the series defined by converges uniformly. This will imply, via the Weierstrass M-test, the sequence is uniformly convergent. As a byproduct, we obtain that the sequence is uniformly bounded.
First, since
f is a continuous function over a compact set, there exist an
such that
. Since
is Lipschitzian in
u, we aim to prove by method of induction that
Starting with
we have
Thus, our claim (9) is true for
Now assume (9) holds for some
, that is,
Since
is Lipschitzian in
u and using assumption (10), we see
Using the substitution
, we have
Hence,
and the induction is complete. Thus, the inequality (9) holds for all
.
Now considering the absolute value of the series (8), we can show that the sequence is uniformly convergent if the absolute value of the series (8) converges uniformly.
Thus, from the Weierstrass M-test, we get that the series (8) converges uniformly on I. Therefore, the sequence is uniformly convergent on I to some continuous function say . ☐
With these lemmas, what is left to prove of Theorem 2 is the sequence converges to the solution of the IVP (1).
Proof of Theorem 2. It is enough to show that the sequence
converge to the solution of the integral Equation (2). Now taking the limit on both sides of the equation (7) and using Lebesgue Dominated Convergence Theorem, we get (2). This proves there exists a solution on
Thus,
converges uniformly to
, the solution of the IVP (1). We claim that this solution is unique. If not, let
be another solution to the IVP (1). Consider the function
. Since both
u and
are solutions to the IVP (1), we see that
. Furthermore, we see that
Since
and
, the above inequality satisfies all the conditions of the Gronwall type inequality given as in [
16]. Thus, we have
Therefore, we can conclude that and hence, the solution of the IVP (1) exists on I and is unique. Therefore, the proof of Theorem 2 is complete. (It is easy to see that if , the proof is similar to Picard’s original proof for natural ordinary differential equations.) ☐
Note that our result can be easily extended to systems of Caputo FDEs with initial conditions. The proof follows on the same lines as Theorem 2 except that is to be used in place of absolute value.
4. Numerical Results and Applications
In this section, we present several numerical examples to demonstrate our method. It is to be noted that in a simple example in ordinary differential equation such as
one can compute the solution explicitly as
It is easy to see that this solution blows up at
This result is used as a tool (in fact as a lower solution) so that the corresponding reaction diffusion equation with the nonhomogeneous term as
blows up at
where
In order to study blow up results for fractional reaction diffusion equation, one easy approach is to show that the corresponding ordinary Caputo FDE blows up at some time
Unfortunately, we cannot compute the solution of the ordinary Caputo FDE explicitly. In
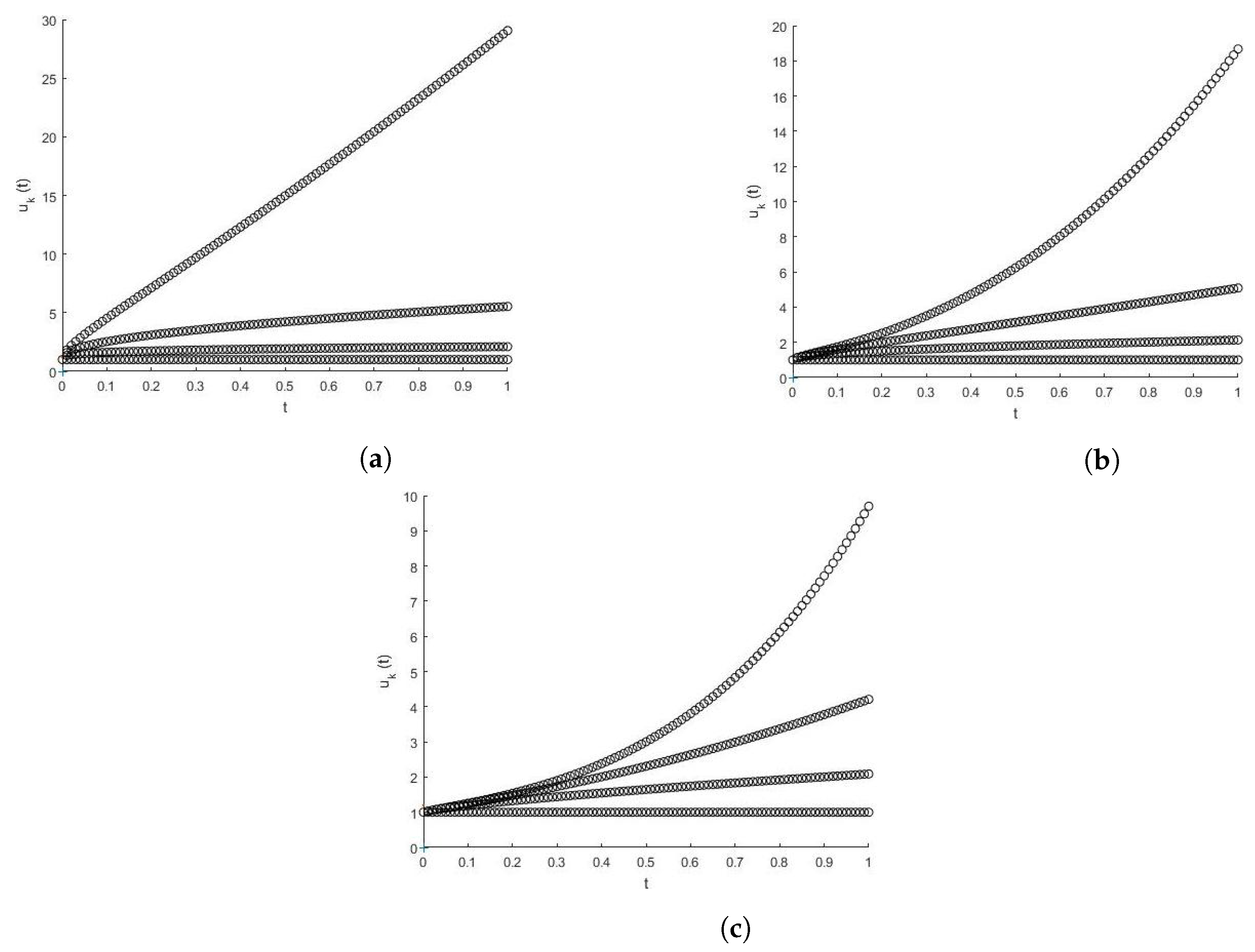
Figure 1, we provide an example and compute the Picard iterates. We see from our examples the iterates form an increasing sequence of functions.
Here, one can easily show, using the method of mathematical induction, that the nth Picard iterate of the ordinary Caputo FDE is greater or equal to the corresponding nth Picard iterate of the ordinary natural differential equation when the initial condition In order to establish this, we need which is true for It is to be noted that the solution of (11) blows up at some where when Also note that we cannot establish a similar result when is replaced by as in (11), since the solution blows up only as
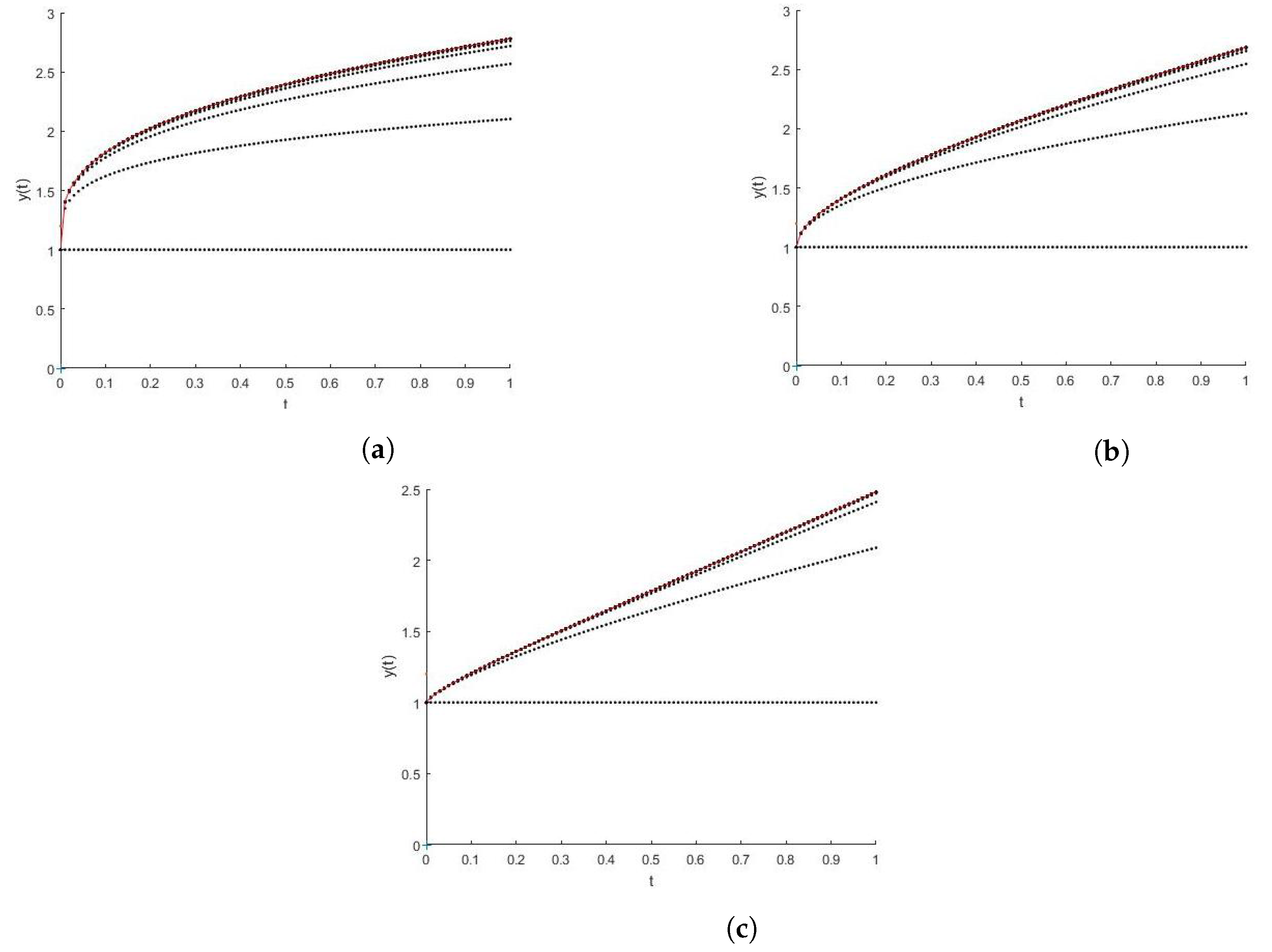
One can use Picard iterates to numerically approximate solutions to FDEs. The method is similar to the numerical scheme given in solving the Volterra integral equation of the second kind in [
10]. For comparison, we plot the solution given by FLMM2.m in red. More information on this code can be found in [
17].
In
Figure 2, we graph 50 iterations of our developed Picard’s Method with a step size of
of the IVP problems
for
,
, and
.
In
Figure 3, we graph 50 iterations of our developed Picard’s Method with a step size of
of the IVP problems
for
and
.
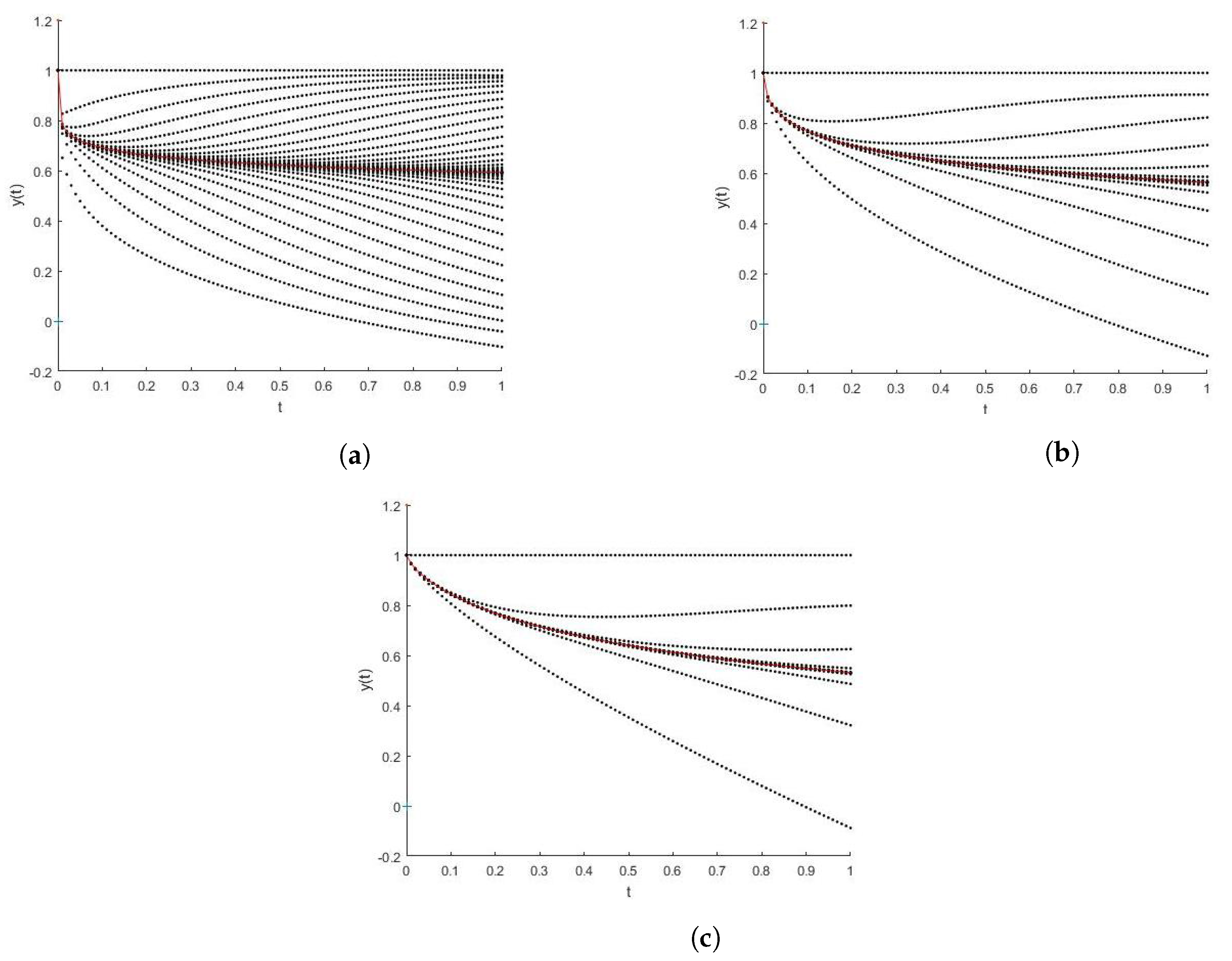
Notice the peculiar behavior in the last examples (
), where the iterates oscillate from above the solution to below the solution. The alternate behavior is a natural consequence of the comparison result for nonhomogeneous decreasing functions. This is a special case of the result in [
18] for Caputo FDE. For similar results for ordinary differential equations, see [
19,
20]. It has been called an alternating sequence or intertwined sequence [
18,
20].
5. Conclusions
Analytical solutions are rarely possible for even simple nonlinear FDEs. One can use numerical methods directly on the differential equation without using its integral form. However, the approximation for the derivative has to be done using the definition of derivatives of Grünwald-Letinikow type. It is easy to observe that this approximation is global in nature unlike in the case of ordinary derivatives. The Picard’s method we develop in this paper provides a relatively easier way to compute the approximation to the solution, mainly because we are approximating a Volterra type of integral. In addition, these integrals are of the convolution type. Numerical methods to compute such integrals are available in literature, as in [
10]. Of course, the methods need modification depending on the forcing function involved. In addition to the theoretical existence and uniqueness result, we provide numerical examples which are useful to develop blow up results. The numerical results we provide, also strongly support the theoretical results of the special case of the generalized monotone method where the forcing function is written as the sum of increasing and decreasing functions. The Picard’s method we develop can also easily be extended to systems. Numerical applications of systems are useful in studying a variety of modeling problems.