Solvable Analogue of V(x)=ix³

Abstract

Motivated by the recent doubts concerning the compatibility of the purely imaginary one-dimensional cubic-oscillator model with the standard postulates of quantum mechanics, we propose to replace its potential $V\left(x\right)=i{x}^3$ by an elementary piece-wise constant function. We prove that such a simplified non-Hermitian model with a purely imaginary interaction potential still possesses infinitely many bound states with real energies. These states are shown to coincide, incidentally, with their Hermitian square-well analogues in the strong-coupling limit.

1. Introduction

In the context of the recently popular quasi-Hermitian [1,2], also known as $\mathcal{PT}$-symmetric [3] or pseudo-Hermitian [4] reformulations of quantum mechanics, a key role of a benchmark toy-model example has been represented by the Hamiltonian

$$H_{BZ}=-{\displaystyle \frac{d^2}{d{x}^2}}+i{x}^3,x\in (-\infty ,\infty ).$$

(1)

Besides the marginal phenomenological relevance of such a model in field theory [5,6] and in the related methodical studies of the properties of perturbation expansions [7,8], extensive studies were only initiated when Bender, with Boettcher, pointed out that the models of dynamics of such a type “may be viewed as analytic continuations of conventional theories from real to complex phase space” [9].

The idea became fairly influential [10,11]. The related and not quite expectable strict reality of eigenvalues $E_{BZ}$ of the toy model of Equation (1) proved quite puzzling. In the context of physics, it inspired a conjecture of the existence of the whole “modified quantum mechanics”, paying attention to many other Hamiltonians containing the anomalous complex potentials [12,13,14]. Within this upgraded theoretical framework, many new and interesting questions were raised by an underlying replacement of the current Hermiticity of Hamiltonians through an alternative condition. For example, Mezincescu [15] pointed out that one of the new challenges emerges in connection with the less usual forms of the asymptotic behavior of the wave functions [16,17,18].

During the early developments in the field, multiple innovative proofs of the reality of the energies emerged. They were based on the WKB and perturbation-expansion techniques [19,20] as well as on the algebraic and analytic constructions [21,22,23,24,25,26,27,28,29]. New insight into these proofs was also obtained via the studies of the most elementary polynomial interactions [30,31,32].

From the point of view of experimental physics, the latter theoretical developments seem to have opened a broad new domain in the study of phenomena connected with such a change in paradigm, redirecting attention, e.g., to the well known but, until recently, rather formal concept of the so-called exceptional point (EP, [33]). In particular, especially the latter concept found, indeed, a broad new area of the real-world applicability ranging from classical optics [34] and non-linear optics [35,36] up to multiple new forms of various open systems [37,38,39].

The discovery and intensive experimental studies of the latter new classes of phenomena re-attracted, naturally, the attention of theoretical physicists (strongly inspired by the brand new ideas of an “analytically continued quantum mechanics” [9,16]) as well as of the much less enthusiastic mathematicians (who were always well aware of the deep subtlety of many related formal questions—see, e.g., [1,40,41]).

A climax in the latter skepticism can be dated back to the year 2012 when, in paper [42], Siegl, with Krejčiřík, published a rigorous mathematical proof that “the eigenvectors of the imaginary cubic oscillator do not form a Riesz basis” so that, as a consequence, “there is no quantum-mechanical Hamiltonian associated with it” [42].

Naturally, such a discovery (reconfirmed, in a not yet published preprint [43], by Günther and Stefani who, incidentally, used a rather different mathematical approach) was truly revolutionary. Indeed, in the abstract theoretical framework of the so-called quasi-Hermitian reformulation of quantum mechanics (QHQM; see, e.g., comprehensive reviews [1,2,4]) the problem of a correct physical interpretation of model (1) remains, at present, unresolved (cf., e.g., the recent review [44]).

2. Model

In such a context, we intend to propose here an extremely elementary $\mathcal{PT}$ symmetric model which would replace the BZ interaction $i{x}^3$ (which admits just a numerical treatment) with its exactly solvable imaginary-square-well alternative

$$V^{\left(ISQW\right)}\left(x\right)=\left\{\begin{array}{ccc}-i{T}^2,\hfill & x\in (-\infty ,-\pi ),\hfill & \\ 0,\hfill & x\in (-\pi ,\pi ),\hfill & \\ +i{T}^2,\hfill & x\in (\pi ,\infty ),\hfill & 0<T<\infty .\hfill \end{array}\right.$$

(2)

This means that we will consider and solve the ordinary differential Schrödinger equation

$$\left[-{\displaystyle \frac{\hslash }{2m}}{\displaystyle \frac{d}{d{x}^2}}+V^{\left(ISQW\right)}\left(x\right)\right]\psi \left(x\right)=E\psi \left(x\right)$$

(3)

under the conventional Dirichlet boundary conditions

$$\underset{x\to \pm \infty }{lim}\psi \left(x\right)=0.$$

(4)

Putting $\hslash =2m=1$, we will assume the unbroken $\mathcal{PT}$ symmetry. This means that at any energy $E=k^2$ (in the case of the unbroken $\mathcal{PT}$ symmetry, this energy will be real and positive [9]), we may abbreviate $\mathrm{i}{T}^2-E={\sigma }^2$ and obtain the asymptotically decreasing (i.e., normalizable though not yet normalized) wave function solutions such that

$$\psi \left(x\right)\sim \left\{\begin{array}{cc}exp(-\sigma x),\hfill & x>\pi \hfill \\ exp(+\sigma x),\hfill & x<-\pi \hfill \end{array}\right.$$

provided only that we set $\sigma =p+iq$ with $p\ge 0$ and $q\ge 0$. We also recall that $p^2+k^2=q^2$, and that $2pq=T^2$ as a consequence.

Due to the unbroken $\mathcal{PT}$ symmetry (cf., e.g., Ref. [45] for the details of this terminology) we will have wave functions such as $\psi \left(x\right)=\mathcal{PT}\psi \left(x\right)$ so that we may analyze just their half-line part with $x>0$ and, in the $x\to 0$ limit, with a variable G in the conditions

$$\psi \left(0\right)=1,{\partial }_x\psi \left(0\right)=iG.$$

(5)

Under the unbroken $\mathcal{PT}$-symmetry, we may, therefore, work with the ansatz

$$\psi \left(x\right)=\left\{\begin{array}{cc}coskx+Bsinkx,\hfill & x\in (0,\pi ),\hfill \\ (L+iN)exp(-\sigma x),\hfill & x\in (\pi ,\infty )\hfill \end{array}\right.$$

(6)

with a purely imaginary constant $B=iG/k$. Now, our goal and intention is to guarantee the full compatibility of ansatz (6) with the boundary-value convention of Equation (5).

3. Matching Conditions at $\mathit{x}=\mathit{\pi }$

The triplet of our most relevant parameters can be perceived as varying with an auxiliary variable $\alpha \in (0,\pi /2)$,

$$k=qsin\alpha ,p=qcos\alpha ,q=T/\sqrt{2cos\alpha }.$$

(7)

Moreover, using another complex upper-case parameter $\Omega$, we denote $\sigma /k=-tan\Omega \pi$, and we deduce that

$$cosk\pi +Bsink\pi =(L+iN)exp(-\sigma \pi ),$$

$$-sink\pi +Bcosk\pi =-{\displaystyle \frac{\sigma }{k}}(L+iN)exp(-\sigma \pi ).$$

The conventional condition of the matching of the logarithmic derivatives at $x=\pi$ then implies that

$$G=-iktan(k+\Omega )\pi .$$

(8)

As long as $\mathrm{Re}[tan(k+\Omega \left)\pi \right]=0$ we may abbreviate $tank\pi =X$ and find the two solutions $X=X_{1,2}$ of such a quadratic algebraic equation. Their form is compact,

$$X_1={\displaystyle \frac{p+q}{k}},X_2={\displaystyle \frac{p-q}{k}},$$

(9)

and it implies that in their fully expanded form we have two relations

$$tan\left[{\displaystyle \frac{\pi Tsin{\alpha }^{(+)}}{\sqrt{2cos{\alpha }^{(+)}}}}\right]=\tan \left[{\displaystyle \frac{\pi -{\alpha }^{(+)}}{2}}\right],$$

(10)

$$tan\left[{\displaystyle \frac{\pi Tsin{\alpha }^{(-)}}{\sqrt{2cos{\alpha }^{(-)}}}}\right]=tan\left[-{\displaystyle \frac{{\alpha }^{(-)}}{2}}\right].$$

(11)

Thus, what remains for us is to localize their real roots $\alpha ={\alpha }_n^{(\pm )}\in (0,\pi /2)$ which have to be intrepreted as characterizing the two respective infinite series of bound states.

4. Energies

A more detailed analysis of our two final Equations (10) and (11) reveals that the simpler expressions $\tan [(\pi -{\alpha }^{(+)})/2]\in (1,\infty )$ and $\tan [{\alpha }^{(-)}/2]\in (0,1)$ are just the slowly varying functions of their argument. This enables us to abbreviate $k=k\left({\alpha }_n^{(\pm )}\right)=k_n^{(\pm )}$, and to predict that

$$k_n^{(+)}\in \left(n+{\displaystyle \frac{1}{4}},n+{\displaystyle \frac{1}{2}}\right),n=0,1,\dots ,$$

$$k_m^{(-)}\in \left(m+{\displaystyle \frac{3}{4}},m+1\right)m=0,1,\dots .$$

Next, due to Equation (7), both of our fundamental Equations (10) and (11) become simplified, significantly, by the change in notation,

$$k_n^{(+)}=n+{\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\omega }_n^{(+)}}{4}},k_m^{(-)}=m+1-{\displaystyle \frac{{\omega }_m^{(-)}}{4}},{\omega }_n^{(\pm )}={\displaystyle \frac{2{\alpha }_n^{(\pm )}}{\pi }}\in (0,1).$$

(12)

It is now worth adding that there exists a possibility of a truly elegant further compactification of the two rules (10) and (11). For reasons which will be visible immediately (cf., in particular, Equation (13) below), it will make sense to abbreviate ${\omega }_n^{(+)}={\omega }_{2n}$ and ${\omega }_n^{(-)}={\omega }_{2n+1}$. On these grounds, we may finally combine the two relations of Equation (12) and obtain the ultimate single secular equation

$$sin\left({\displaystyle \frac{\pi }{2}}{\omega }_N\right)={\displaystyle \frac{2N+2-{\omega }_N}{4T}}·\sqrt{2cos\left({\displaystyle \frac{\pi }{2}}{\omega }_N\right)}N=0,1,\dots ,$$

(13)

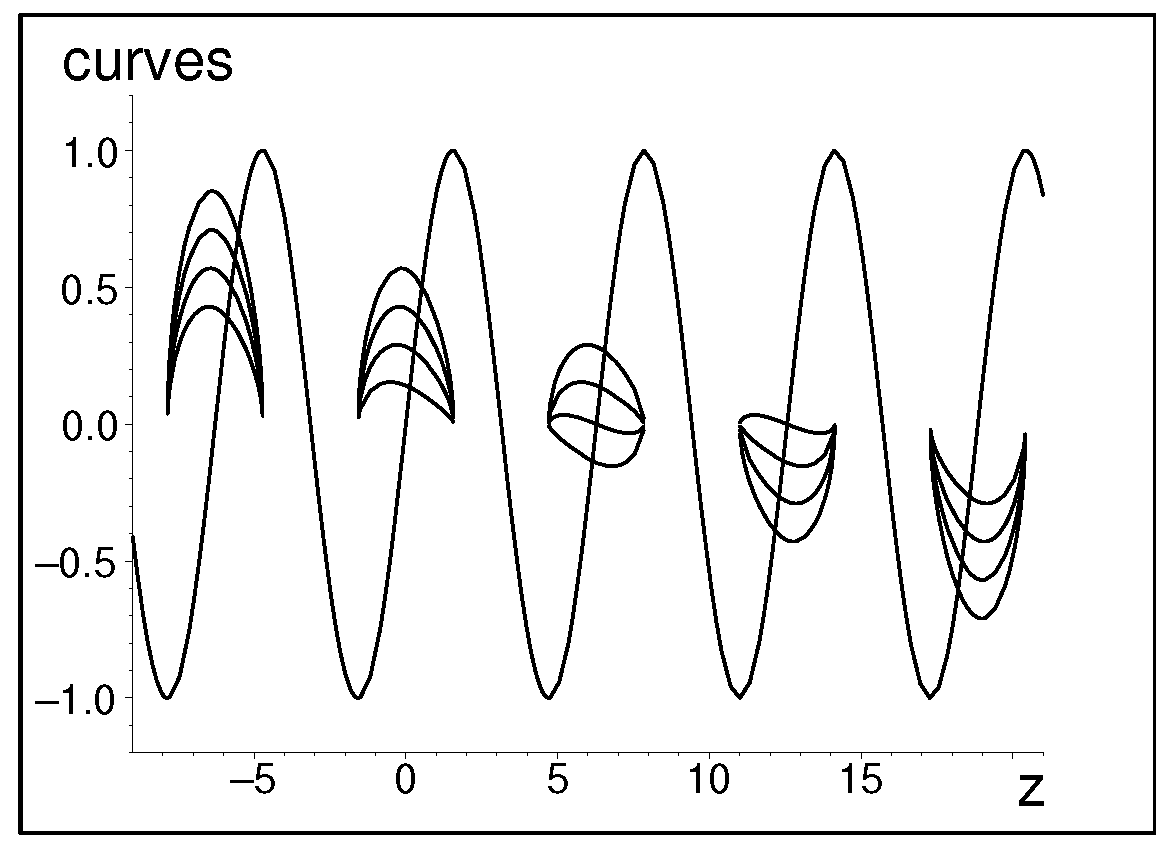
In a graphical interpretation (cf., e.g., Figure 1, which samples the graphical solution of the latter equation), this equation represents, at every level-counting integer N, an intersection of two sinus-like curves. One finds, therefore, infinitely many bound-state-energy roots ${\omega }_N\in (0,1)$ which are numbered by the integer N.

Figure 1. Graphical solution of Equation (13) at $T=5$ with $z=\pi {\omega }_N/2$ for $N=0,1,2$ and 3).

5. The Case of the Small Square-Well Height $\mathit{T}$

Once we have

$$G=G^{(\pm )}=-{\displaystyle \frac{k^2}{q\pm p}}$$

(14)

(cf. Equation (8) together with (10) and (11)), we have a full control of the shape of our bound-state wave functions near the origin [one just has to insert $B=iG/k$ in Equation (6)]. In this setting, another auxiliary abbreviation

$$\sqrt{R({\omega }_N,N)}={\displaystyle \frac{2N+2-{\omega }_N}{4T}}\in \left({\displaystyle \frac{N+1/2}{2T}},{\displaystyle \frac{N+1}{2T}}\right)$$

enables us to rewrite our secular Equation (13) with unknown $z=\pi {\omega }_N/2$ (cf. also Figure 1) in the following equivalent form

$$1-{cos}^{2}z=2R({\omega }_N,N)cosz.$$

This is the common quadratic equation with two solutions, with the positive one having the elementary form

$$cos\left({\displaystyle \frac{\pi }{2}}{\omega }_N\right)={(R({\omega }_N,N)+\sqrt{R^2({\omega }_N,N)+1})}^{-1}.$$

(15)

Obviously, this is just another, fully equivalent form of our secular equation.

In the domain of the large and almost constant $R\gg 1$ (i.e., in the weak-coupling dynamical regime with small T, or at the higher excitations), our new secular Equation (15) gives a better picture of our bound-state parameters ${\omega }_N=1-{\eta }_N$ which all lie very close to 1. The estimate

$${\displaystyle \frac{\pi }{2}}{\eta }_N=arcsin{\displaystyle \frac{1}{R+\sqrt{R^2+1}}}\approx {\displaystyle \frac{1}{2R}}-{\displaystyle \frac{5}{48R^3}}+\dots$$

represents also a quickly convergent iterative algorithm for the efficient numerical evaluation of the roots ${\omega }_N$. One can conclude that in a way compatible with our a priori expectations, the value of $p=p_N=\mathrm{Re}\sigma \approx q/2R$ is very close to zero and, as a consequence, the asymptotic decrease of our wave functions remains slow. We have $q=q_N=\mathrm{Im}\sigma \approx k$ so that, asymptotically, our wave functions very much resemble free waves $exp(-ikx)$. In the light of Equation (14), we also have $\psi \left(x\right)\approx exp(-ikx)$ near the origin.

6. The Case of the Large Square-Well Height $\mathit{T}$

Let us now turn our attention to the opposite dynamical regime in which the constant T is small and the confinement is strong. In such a case (involving, typically, the low-lying excitations in a deep square well with $T\gg 1$), of course, the values of R are small. This leads to the asymptotic expansion

$${\displaystyle \frac{\pi }{4}}{\omega }_N=arcsin\sqrt{{\displaystyle \frac{1}{2}}\left[R-\left(\sqrt{1+R^2}-1\right)\right]}\approx {\displaystyle \frac{1}{2}}R-{\displaystyle \frac{1}{4}}{R}^2+\dots \ll {\displaystyle \frac{\pi }{4}}.$$

Such a formula enables us to formulate several conclusions. Firstly, one can notice that there emerges an unexpected correspondence between our present model (based on a purely imaginary potential) and its conventional self-adjoint square-well analogue. Indeed, keeping their respective widths the same, $I=(-\pi ,\pi )$, and moving the respective couplings to infinity, the respective spectra happen to coincide.

The wave functions exhibit the similar tendency towards the unexpected parallels. In the outer region, they are proportional to $exp(-px)$ and decay very quickly since $p=\mathcal{O}\left(R^{-1/2}\right)$. The parameter $G^{(\pm )}$ becomes strongly superscript-dependent,

$$G^{(+)}=-{\displaystyle \frac{k^2}{q+p}}=\mathcal{O}\left(R^{3/2}\right),G^{(-)}=-(q+p)=\mathcal{O}\left(R^{-1/2}\right).$$

This means that in the interior domain of $x\in (-\pi ,\pi )$, the wave functions with the superscript ⁽⁺⁾ and ⁽⁻⁾ become dominated by their spatially even and odd components $coskx$ and $sinkx$, respectively. In this sense, the superscript mimics (or at least keeps the trace of) the quantum number of the slightly broken spatial parity $\mathcal{P}$.

Marginally, let us add that even at the finite Ts, the bound-state-energy values of our present imaginary square-well model grow quadratically with the quantum number N. Moreover, we may use the estimate

$${\displaystyle \frac{{(N+1/2)}^2}{4}}\le E_N\le {\displaystyle \frac{{(N+1)}^2}{4}}$$

(16)

which implies that the individual energy levels $E_N$ remain, at any excitation quantum number N, well separated. This means that the spectrum does not exhibit a tendency towards the Kato’s exceptional-point degeneracy [33].

7. Outlook

Our present constructive demonstration of the exact solvability of a quasi-Hermitian quantum system with Schrödinger Equation (3) throws new light on the possible mathematical structures behind the $\mathcal{PT}$ symmetric quantum systems which may be hardly accessible by approximative techniques. In the current literature, many new puzzles emerging in the field are being revealed.

Pars pro toto, let us mention the Siegl’s and Krejčiřík’s [42] critical comments on the emergence of certain mathematical “intrinsic-exceptional-point” pathologies characterizing the full-fledged imaginary cubic oscillator model (1) (cf. also an outline of their various possible phenomenological consequences in [46]). Indeed, for the reasons explained in [44], one of the remedies of these physics-influencing pathologies could be sought in a suitable discretization of the Hamiltonian as sampled, here, by our present toy model of Equation (2).

Another more mathematically oriented open question which emerged in connection with a deeper study of the imaginary cubic oscillator problem was mentioned in ref. [47], in which the authors revealed the existence of an irregular behavior of the nodal zeros in the complex plane. Our present example indicates that a surprising alternative to the conventional and standard Sturm–Liouville oscillation theorem could, perhaps, emerge in connection with a deeper study of some other exactly solvable models.