Multivalued Extensions of Krasnosel’skii-Type Fixed-Point Theorems in p-Normed Spaces

Abstract

This paper establishes new fixed-point theorems in the framework of complete p-normed spaces, where $p\in (0,1]$. By extending the classical Banach, Schauder, and Krasnosel’skii fixed-point theorems, we derive several results for the sum of contraction and compact operators acting on s-convex subsets. The analysis is further generalized to multivalued upper semi-continuous operators by employing Kuratowski and Hausdorff measures of noncompactness. These results lead to new Darbo–Sadovskii-type fixed-point theorems and global versions of Krasnosel’skii’s theorem for multifunctions in p-normed spaces. The theoretical findings are then applied to demonstrate the existence of solutions for nonlinear integral equations formulated in p-normed settings. A section on numerical applications is also provided to illustrate the effectiveness and applicability of the proposed results.

1. Introduction

The theory of fixed points ($\mathbb{FP}$s) forms a central and rich component of modern mathematics, drawing on ideas from analysis, topology, and geometry. Over the past five decades, $\mathbb{FP}$ methods have become indispensable in the study of nonlinear phenomena and now play a key role across numerous branches of mathematical sciences. They provide effective tools for establishing the solvability of integral equations, systems of linear equations, the existence of periodic trajectories in dynamical systems, economic equilibrium models, and solutions of ordinary and partial differential equations.

$\mathbb{FP}$ theory for multivalued operators represents an essential direction within set-valued analysis. Many classical $\mathbb{FP}$ results for single-valued mappings such as those due to Banach and Schauder have been successfully extended to multivalued operators in Banach spaces; see the monographs by Gorniewicz and co-authors [1,2]. More recently, Boriceanu [3] and Petrusel [4] established multivalued variants of Krasnosel’skii’s $\mathbb{FP}$ theorem. In 2011, Xiao and Zhu [5] have studied the existence of $\mathbb{FP}$s for different types of operators defined on s-convex sets in p-normed spaces with $p\in (0,1]$, $s\in (0,p]$ and extended some well known $\mathbb{FP}$ results to s-convex sets. In 2012, Alghamdi et al. [6] have shown Krasnosel’skii’s type of $\mathbb{FP}$ theorems and Sadovskii-type theorem for s-convex sets in p-normed spaces with $p\in (0,1]$, $s\in (0,p]$. In 2018, Xiao and Lu [7], by using a concept of measure of noncompactness, have obtained some $\mathbb{FP}$ theorems for single-valued and multivalued operators defined on s-convex sets in p-norm spaces with $p\in (0,1]$, $s\in (0,p]$. The class of p-normed spaces is considered an important generalization of the class of usual normed spaces as cited in many results on the study of these topics [8]. Several authors have further generalized the classical Krasnosel’skii theorem in various directions [9,10,11,12,13]. The purpose of this work is to develop new multivalued extensions of the Krasnosel’skii $\mathbb{FP}$ theorem in p-normed spaces.

A wide range of problems in applied sciences reduce, after mathematical formulation, to investigating the solvability of nonlinear differential equations or inclusions of the form

$$\xi =\mathcal{A}\left(\xi \right)+\mathcal{B}\left(\xi \right),\xi \in \mathcal{L},$$

(1)

and

$$\xi \in F\left(\xi \right)+\mathcal{B}\left(\xi \right),\xi \in \mathcal{L},$$

(2)

where F is a multivalued operator and $\mathcal{L}$ is a closed, convex subset of a Banach space $\mathcal{X}$. Many integral equations and inclusions can be recast in the form of (1) or (2); see, for instance, [14]. In 1958, Krasnosel’skii [15] proved that (1) admits a solution in $\mathcal{L}$, provided that $\mathcal{A}$ and $\mathcal{B}$ satisfy the following:

(C₁)

$\mathcal{A}\left(\xi \right)+\mathcal{B}\left(\eta \right)\in \mathcal{L}$ for all $\xi ,\eta \in \mathcal{L}$;

(C₂)

$\mathcal{A}$ is continuous on $\mathcal{L}$ and $\overline{\mathcal{A}\left(\mathcal{L}\right)}$ is compact in $\mathcal{X}$;

(C₃)

$\mathcal{B}$ is a $\sigma$-contraction.

This theorem links the Banach contraction principle with Schauder’s $\mathbb{FP}$ theorem. The problem of locating $\mathbb{FP}$ s for the sum of two operators has drawn considerable attention because of its extensive applications in nonlinear analysis. Numerous refinements and extensions of the Krasnosel’skii theorem have been proposed by relaxing or modifying the above assumptions; see, for example [9,10,11,12,13,16,17,18,19,20,21,22].

In this work, we establish what seems to be the first systematic framework for fixed-point theorems of the Krasnosel’skii type for multivalued operators in full p-normed spaces, where $p\in (0,1]$. Our goal is to apply the traditional “compact + contraction” approach to the operator sum $G+F$, where G might be contraction, nonexpansive, expansive, or condensing, and F is an upper semi-continuous multivalued mapping with s-convex values. Many of the traditional methods from Banach space theory are no longer applicable because the analysis is conducted in a non-locally convex environment. In order to overcome these challenges, we establish selection results appropriate for this context, modify measurements of noncompactness to the structure of p-normed spaces, and present new approximation techniques. These elements enable us to build a unified theory for operator equations in spaces like $H^p$ for $p<1$. Additionally, we provide explicit applications to nonlinear integral equations, which are complemented by numerical findings that show how applicable the theoretical framework is in real-world situations.

2. Preliminaries

In this section, we introduce the notation and recall of several basic concepts used throughout the paper. Let $\mathcal{X}$ be a vector space over $\mathbb{K}$, endowed with the zero element $\theta$, where $\mathbb{K}$ denotes either $\mathbb{R}$ or $\mathbb{C}$.

A non-negative functional ${\parallel ·\parallel }_p$, with $p\in (0,1]$, is called a p-norm if it satisfies the following:

(P₁)

${\parallel \xi \parallel }_p=0$ if and only if $\xi =\theta$;

(P₂)

${\parallel \mu \xi \parallel }_p={\left|\mu \right|}^p{\parallel \xi \parallel }_p$ for all $\xi \in \mathcal{X}$ and $\mu \in \mathbb{K}$;

(P₃)

${\parallel \xi +\eta \parallel }_p\le {\parallel \xi \parallel }_p+{\parallel \eta \parallel }_p$ for all $\xi ,\eta \in \mathcal{X}$.

When $p=1$, the pair $(\mathcal{X},\parallel ·\parallel )$ reduces to a classical normed space. For any subset $\mathcal{L}\subset \mathcal{X}$, we denote its interior, closure, and boundary by ${\mathcal{L}}^o$, $\overline{\mathcal{L}}$, and $\partial \mathcal{L}$, respectively. The sphere of radius $\xi$ centered at $\theta$ is written as

$$S(\theta ,\xi )=\{\zeta \in \mathcal{X}:\parallel \zeta {\parallel }_p=\xi \}.$$

The set $\mathbb{N}$ represents the natural numbers, and for any $\xi \in \mathcal{X}$ and $\zeta >0$, the open ball centered at $\xi$ with radius $\zeta$ is denoted by $B(\xi ,\zeta )$.

Let $s\in (0,1]$. A set $\mathcal{L}\subset \mathcal{X}$ is said to be s-convex if

$${(1-\eta )}^{{\displaystyle \frac{1}{s}}}\xi +{\eta }^{{\displaystyle \frac{1}{s}}}\upsilon \in \mathcal{L},\mathrm{for}\mathrm{all}\xi ,\upsilon \in \mathcal{L},\eta \in [0,1].$$

A point $\xi \in \mathcal{X}$ satisfying $\xi ={\sum }_{j=1}^n{\alpha }_j{\xi }_j$, where ${\xi }_j\in \mathcal{X}$, ${\alpha }_j\ge 0$, and ${\sum }_{j=1}^n{\alpha }_j^s=1$, is called an s-convex combination of ${\xi }_1,\dots ,{\xi }_n$. A set $\mathcal{L}$ is s-convex precisely when it contains every such s-convex combination of its elements. In particular, each ball $B(\theta ,\zeta )$ is s-convex for $\zeta >0$.

Proposition 1

([23]). Let $0<s<1$. Let $\mathcal{C}\subseteq {\mathbb{R}}^n$ be s-convex. Then, $c{v}_s\left(f\left(\mathcal{C}\right)\right)=f\left(c{v}_s\left(\mathcal{C}\right)\right)$ for any linear operator $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$.

The difference between the shapes of convex and s-convex hulls is given in the following example.

Example 1

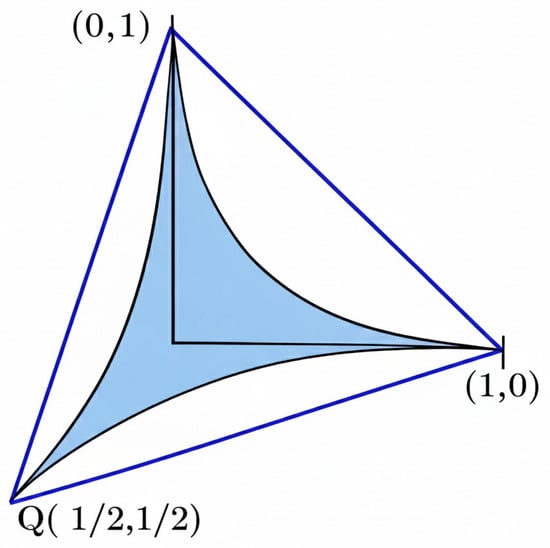
([23,24]). Let $\mathcal{C}=\{z_1,z_2,\dots ,z_n,q\}\subset {\mathbb{R}}^n$, with ${\left\{z_i\right\}}_{i=1}^n$ being linearly independent in ${\mathbb{R}}^n$ and $q=(a_1,a_2,\dots ,a_n)\ne 0$. By Proposition 1, suppose that $z_i=e_i$ (the canonical basis). This set, $c{v}_p\left(\mathcal{C}\right)={(z_1,z_2,\dots ,z_n,q)}_p$, can be viewed as the image of

$$\mathsf{\Lambda }=\left\{\lambda =({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n):{\lambda }_i\ge 0,1\le i\le n,\sum _{i=1}^n{\lambda }_i^p\le 1\right\}$$

under the operator $\mathsf{\Gamma }:\mathsf{\Lambda }\to {\mathbb{R}}^n$ given by $\mathsf{\Gamma }\left(\lambda \right)={\sum }_{i=1}^n{\lambda }_i{e}_i+rq$, where $r^p=1-{\sum }_{i=1}^n{\lambda }_i^p$.

Figure 1 illustrates two different shapes of $\mathsf{\Gamma }\left(\mathsf{\Lambda }\right)$ when it is equal to $c{v}_p\left(\mathcal{C}\right)$ (blue shaded area) and when it is equal to $cv\left(\mathcal{C}\right)$ (white area).

Figure 1. Illustration of the difference between the convex and s-convex sets.

Lemma 1

([25]). Suppose that x is a point of a p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, then the s-convex hull and the closure of the s-convex hull of $\left\{x\right\}$, where $p\in (0,1]$, $s\in (0,p]$, are given by

$$c{v}_s\left\{x\right\}=\left\{\begin{array}{cc}\{tx:0<t\le 1\},\hfill & ifx\ne \theta ,\hfill \\ \theta \hfill & x=\theta .\hfill \end{array}\right.$$

and

$$\overline{c{v}_s}\left\{x\right\}=\left\{\begin{array}{cc}\{tx:0\le t\le 1\},\hfill & ifx\ne \theta ,\hfill \\ \theta \hfill & x=\theta .\hfill \end{array}\right.$$

Remark 1

([5]).

1.

If $s=1$, one obtains the usual definition of convex sets.

2.

In a p-normed space, there is a significant difference between a convex set and a s-convex set. A s-convex set is not translation-invariant in the case $0<s<1$. If $\mathcal{C}$ is s-convex $(0<s<1)$ and $x_0\ne \theta$, then $\mathcal{C}-x_0$ is not s-convex in general.

3.

If $\mathcal{C}$ is a closed s-convex set $(0<s<1)$, then $\theta \in \mathcal{C}$.

Lemma 2

([25,26]). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a p-normed space with $p\in (0,1]$ and let $s\in (0,p]$. Then,

(a)​

$B(\theta ,\zeta )$ is s-convex for any $\zeta >0$.

(b)​

If $\mathcal{L}\subset \mathcal{X}$ is s-convex and $\lambda \in \mathbb{R}$, then $\lambda \mathcal{L}$ is s-convex.

(c)​

If ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$ are s-convex subsets of $\mathcal{X}$, then ${\mathcal{L}}_1+{\mathcal{L}}_2$ is s-convex.

(d)​

If $\{{\mathcal{L}}_i:i\in I\}$ is a family of s-convex sets, then ${\bigcap }_{i\in I}{\mathcal{L}}_i$ is s-convex.

(e)​

If $\mathcal{L}\subset \mathcal{X}$ and $\theta \in \mathcal{L}$, then $c{v}_s\left(\mathcal{L}\right)\subset cv\left(\mathcal{L}\right)$, where $cv\left(\mathcal{L}\right)$ denotes the convex hull of $\mathcal{L}$.

(f)​

If $\mathcal{L}$ is a closed s-convex set and $0<r<s$, then $\mathcal{L}$ is also a closed r-convex set.

Let $\mathcal{L}$ be an s-convex subset of $\mathcal{X}$ containing the origin. The mapping $q_{\mathcal{L}}:\mathcal{X}\to [0,+\infty ]$ defined by

$$q_{\mathcal{L}}\left(\xi \right)=inf\{r>0:\xi \in r^{1/s}\mathcal{L}\},$$

is called the Minkowski s-functional associated with $\mathcal{L}$. For any $\mathcal{L}\subset \mathcal{X}$, we write

$$q_{\mathcal{L}}\left(\mathcal{L}\right)=\{q_{\mathcal{L}}\left(\xi \right):\xi \in \mathcal{L}\}.$$

If $\mathcal{L}$ is a closed s-convex set with $s\in (0,1]$, then it necessarily contains the origin $\theta$; see [5,7].

We recall the following notions:

-

Distance from a point $\xi \in \mathcal{X}$ to a set $Y\in P\left(\mathcal{X}\right)$:

$$dist(\xi ,Y):=inf\{\parallel \xi -\eta {\parallel }_p:\eta \in Y\}.$$

-

The excess functional $E:\mathcal{P}\left(\mathcal{X}\right)\times \mathcal{P}\left(\mathcal{X}\right)\to [0,+\infty )$, defined by

$$E(Y,Z)=sup\{dist(\eta ,Z):\eta \in Y\}.$$

In general, $E(Y,Z)\ne E(Z,Y)$.

-

Pompeiu–Hausdorff metric: $H:\mathcal{P}\left(\mathcal{X}\right)\times \mathcal{P}\left(\mathcal{X}\right)\to {\mathbb{R}}^{+}\cup \{+\infty \}$, given by

$$H(Y,Z)=max\left\{E\right(Y,Z),E(Z,Y\left)\right\}\mathrm{whenever}Y\ne ⌀\ne Z.$$

An equivalent expression is

$$H(Y_1,Y_2)=inf\left\{\zeta >0:Y_2\subset Y_1+\zeta \overline{B(\theta ,1)},Y_1\subset Y_2+\zeta \overline{B(\theta ,1)}\right\}.$$

The pair $(P_{b,cl}\left(\mathcal{X}\right),H)$ forms a metric space.

We frequently identify a point $\xi \in \mathcal{X}$ with the singleton $\left\{\xi \right\}\in P\left(\mathcal{X}\right)$. Thus, we may write $E(\xi ,A)$, $E(A,\xi )$, $H(\xi ,A)$, and $B(\xi ,r)$.

It is known that

$$\underset{\xi \in \mathcal{X}}{sup}|E(\xi ,A)-E(\xi ,B)|=H(A,B),$$

and

$$|E(\xi ,A)-E(\eta ,A)|\le {\parallel \xi -\eta \parallel }_p.$$

We now recall some additional definitions used throughout the paper.

Let $(\mathcal{X},d)$ and $(Y,d)$ be metric spaces, and let $F:\mathcal{X}\to P_{cl}\left(Y\right)$ be a multivalued operator. For any $A\subset \mathcal{X}$, we write

$$F\left(A\right)=\bigcup _{\xi \in A}F\left(\xi \right).$$

A single-valued mapping $f:\mathcal{X}\to Y$ is called a selection of F, denoted $f\subset F$, if $f\left(\xi \right)\in F\left(\xi \right)$ for all $\xi \in \mathcal{X}$.

The operator $F:\mathcal{X}\to P\left(Y\right)$ is called compact (or quasicompact) if, for every bounded (respectively, relatively compact) subset $\mathcal{L}\subset \mathcal{X}$, the set $F\left(\mathcal{L}\right)$ is relatively compact. When Y is a p-normed space, the operator F is said to be s-convex-valued if $F\left(\xi \right)$ is an s-convex set for every $\xi \in \mathcal{X}$.

The operator F is upper semi-continuous on $\mathcal{X}$ if, for each ${\xi }_0\in \mathcal{X}$, the set $F\left({\xi }_0\right)$ is nonempty, and for every nonempty open set $W\subset Y$ containing $F\left({\xi }_0\right)$, ∃, an open neighborhood $\mathcal{O}$ of ${\xi }_0$ such that $F\left(\mathcal{O}\right)\subset W$. Equivalently, the set

$$F^{-}\left(W\right)=\{\xi \in \mathcal{X}:F\left(\xi \right)\subset W\}$$

is open for every open $W\subset Y$. A dual characterization is that, for each nonempty closed set $Z\subset Y$, the set

$$F^{+}\left(Z\right)=\{\xi \in \mathcal{X}:F\left(\xi \right)\cap Z\ne ⌀\}$$

is closed in $\mathcal{X}$.

Definition 1

([27]). A multivalued operator F is sequentially upper semi-continuous at ${\xi }_0\in \mathcal{X}$ if, for every sequence $\left\{{\xi }_n\right\}\subset \mathcal{X}$ converging to ${\xi }_0$ and every sequence $\left\{{\eta }_n\right\}$ with ${\eta }_n\in F\left({\xi }_n\right)$ for all n, we have

$$dist({\eta }_n,F\left({\xi }_0\right))⟶0asn\to +\infty .$$

When both $\mathcal{X}$ and Y are metric spaces, upper semi-continuity is equivalent to sequential upper semi-continuity.

If $\mathcal{X}$ is a nonempty set and $F:\mathcal{X}\to P\left(\mathcal{X}\right)$ is a multivalued operator, a point $\xi \in \mathcal{X}$ is called a $\mathbb{FP}$ of F if $\xi \in F\left(\xi \right)$. The corresponding $\mathbb{FP}$ set is

$$Fix\left(F\right):=\{\xi \in \mathcal{X}:\xi \in F(\xi \left)\right\}.$$

The graph of F is defined by

$$Graph\left(F\right):=\left\{\right(\xi ,\eta )\in \mathcal{X}\times \mathcal{X}:\eta \in F(\xi \left)\right\}.$$

A multivalued operator F is said to be closed if its graph $gphF$ is a closed subset of $\mathcal{X}\times \mathcal{X}$.

Lemma 3

([27]). If a multivalued operator F is sequentially upper semi-continuous, then it is closed.

Under an additional compactness assumption on the space Y, closedness implies sequential upper semi-continuity.

Theorem 1.

([27]). If the space Y is compact, then a multivalued operator F is sequentially upper semi-continuous if and only if it is closed.

A classical fact concerning multivalued mappings with closed graphs is the following.

Lemma 4.

Let $(\mathcal{X},d)$ be a space and $F:\mathcal{X}\to P\left(\mathcal{X}\right)$ be a multivalued operator for which $Graph\left(F\right)$ is closed in $\mathcal{X}\times \mathcal{X}$. Then, $F\left(\xi \right)\in P_{cl}\left(\mathcal{X}\right)$ for every $\xi \in \mathcal{X}$.

Proof. 

Fix $\xi \in \mathcal{X}$ and let ${\left\{{\eta }_n\right\}}_{n\in \mathbb{N}}\subset F\left(\xi \right)$ be a sequence such that ${\eta }_n\to \eta$ in $\mathcal{X}$. Then,

$$(\xi ,{\eta }_n)\in Graph\left(F\right)\mathrm{for}\mathrm{all}n\in \mathbb{N},$$

and ${(\xi ,\eta )}_n)\to (\xi ,\eta ))$ in $\mathcal{X}\times \mathcal{X}$. Since $Graph\left(F\right)$ is closed, it follows that $(\xi ,\eta )\in Graph\left(F\right)$, hence $\eta \in F\left(\xi \right)$. Thus, $F\left(\xi \right)$ is closed in $\mathcal{X}$, so $F\left(\xi \right)\in P_{cl}\left(\mathcal{X}\right)$.   ☐

Definition 2

([28,29]). A multivalued operator $F:\mathcal{X}\to P\left(\mathcal{X}\right)$ is called

(1)​

σ-Lipschitz if ∃$\sigma >0$ such that

$$H\left(F\right(\xi ),F(\eta \left)\right)\le \sigma d(\xi ,\eta )forall\xi ,\eta \in \mathcal{X};$$

(2)​

a contraction if it is σ-Lipschitz with $0\le \sigma <1$.

The next $\mathbb{FP}$ results will be used frequently.

Lemma 5

([5]). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$ and let $\mathcal{L}$ be a totally bounded subset of $\mathcal{X}$. Then, $\overline{c{v}_s}\mathcal{L}$ is compact for some $s\in (0,p]$.

Proposition 2

([30], Proposition 3, p. 42). Let $\mathcal{X}$ be compact and let $F:\mathcal{X}\to P_{cp}\left(Y\right)$ be upper semi-continuous. Then, $F\left(\mathcal{X}\right)$ is compact.

Theorem 2.

([31,32]). Let $\mathcal{X}$ and Y be metric spaces and let $F:\mathcal{X}\to P_{cl}\left(Y\right)$ be a multivalued operator. If F is upper semi-continuous, then F has a closed graph. Conversely, if F is quasicompact and has a closed graph, then F is upper semi-continuous.

Theorem 3.

([5], Kakutani-type). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space and let $\mathcal{L}$ be a compact s-convex subset of $\mathcal{X}$ with $0<p\le 1$ and $0<s\le p$. If $F:\mathcal{L}\to P_{cl,c{v}_s}\left(\mathcal{L}\right)$ is upper semi-continuous, then ∃$\zeta \in \mathcal{L}$ such that $\zeta \in F\left(\zeta \right)$.

Theorem 4.

([33], Nadler’s theorem). If $(\mathcal{X},d)$ is a complete metric space, then every contraction multivalued operator $T:\mathcal{X}\to P_{cl,b}\left(\mathcal{X}\right)$ has a $\mathbb{FP}$.

Theorem 5.

([5], Schauder-type). Let $\mathcal{J}$ be a compact s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$ with $p\in (0,1]$ and $s\in (0,p]$. If $\mathfrak{F}:\mathcal{J}\to \mathcal{J}$ is continuous, then $\mathfrak{F}$ has a $\mathbb{FP}$.

Theorem 6.

([6], $2\mathrm{nd}$ Schauder-type). Let $\mathcal{C}$ be a closed s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$ with $p\in (0,1]$ and $s\in (0,p]$. If $f:\mathcal{C}\to \mathcal{C}$ is completely continuous, then f admits a $\mathbb{FP}$.

3. Main Results

In this section, we present and establish our main fixed-point theorems.

3.1. Krasnosel’skii-Type Fixed-Point Theorem for Upper Semi-Continuous Multivalued Operators in p-Normed Spaces

Theorem 7.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$, and let $\mathcal{L}$ be a nonempty compact s-convex subset of $\mathcal{X}$. Assume that $F:\mathcal{L}\to P_{cp,cl,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator and that  $G\in \mathcal{L}\left(\mathcal{X}\right)$ satisfies the following:

(${\mathcal{H}}_1$)

$\parallel G^q{\parallel }_p<1$ for some $q\in \mathbb{N}$;

(${\mathcal{H}}_2$)

If $\xi \in G\left(\xi \right)+F\left(\eta \right)$ with $\eta \in \mathcal{L}$, then $\xi \in \mathcal{L}$.

Then, ∃$z\in \mathcal{L}$ such that $z\in G\left(z\right)+F\left(z\right)$.

Proof. 

From (${\mathcal{H}}_1$), the inequality $\parallel G^q{\parallel }_p<1$ guarantees that the Neumann series

$${(I-G^q)}^{-1}=\sum _{n=0}^{+\infty }{\left(G^q\right)}^n$$

converges in the operator p-norm. Hence, $I-G^q$ is invertible in $\mathcal{L}\left(\mathcal{X}\right)$. Using the factorization

$$I-G^q=(I-G)(I+G+\cdots +G^{q-1})=(I-G)S,$$

where S is a continuous linear operator, we obtain

$${(I-G)}^{-1}=S{(I-G^q)}^{-1}={(I-G^q)}^{-1}\sum _{k=0}^{q-1}{G}^k.$$

Thus, ${(I-G)}^{-1}\in \mathcal{L}\left(\mathcal{X}\right)$ is well defined and continuous.

Define

$$\mathrm{\Phi }\left(\xi \right)={(I-G)}^{-1}F\left(\xi \right)(\xi \in \mathcal{L}).$$

Since ${(I-G)}^{-1}$ is continuous and $F\left(\xi \right)\in P_{cl,c{v}_s}\left(\mathcal{X}\right)$, it follows that $\mathrm{\Phi }\left(\xi \right)\in P_{cl,c{v}_s}\left(\mathcal{X}\right)$.

To verify upper semi-continuity, let $Z\subset \mathcal{X}$ be closed. Then,

$${\mathrm{\Phi }}^{+}\left(Z\right)=\{\xi \in \mathcal{L}:\mathrm{\Phi }\left(\xi \right)\cap Z\ne ⌀\}=\{\xi \in \mathcal{L}:F\left(\xi \right)\cap (I-G)\left(Z\right)\ne ⌀\}.$$

Since $(I-G)$ is continuous, $(I-G)\left(Z\right)$ is closed. Because F is upper semi-continuous, $F^{+}\left((I-G)\left(Z\right)\right)$ is closed, so ${\mathrm{\Phi }}^{+}\left(Z\right)$ is closed. Hence, $\mathrm{\Phi }$ is upper semi-continuous.

Next, for any $\xi \in \mathcal{L}$ and $\hslash \in {(I-G)}^{-1}F\left(\xi \right)$, choose $\omega \in F\left(\xi \right)$ such that

$$\hslash ={(I-G)}^{-1}\left(\omega \right)\Rightarrow \hslash =G(\hslash )+\omega .$$

Thus, $\hslash \in G(\hslash )+F\left(\xi \right)$, and by (${\mathcal{H}}_2$), we obtain $\hslash \in \mathcal{L}$. Hence, $\mathrm{\Phi }\left(\mathcal{L}\right)\subset \mathcal{L}$.

Let $\left({\xi }_n\right)\subset \mathcal{L}$ with ${\xi }_n\to {\xi }^{*}$ and ${\xi }_n\in \mathrm{\Phi }\left({\xi }_n\right)$. Choose ${\omega }_n\in F\left({\xi }_n\right)$ such that

$${\xi }_n={(I-G)}^{-1}\left({\omega }_n\right)\Rightarrow {\omega }_n=(I-G){\xi }_n.$$

Since F is upper semi-continuous, there is a subsequence $\left({\omega }_{n_k}\right)$ converging to some $\omega \in F\left({\xi }^{*}\right)$. Then,

$${(I-G)}^{-1}\left({\omega }_{n_k}\right)\to {(I-G)}^{-1}\left(\omega \right)\in \mathrm{\Phi }\left({\xi }^{*}\right),$$

so ${\xi }^{*}\in \mathrm{\Phi }\left({\xi }^{*}\right)$. Thus, $\mathrm{\Phi }$ has a closed graph.

By Theorem 1, an upper semi-continuous operator with closed values has a closed graph; hence, $\mathrm{\Phi }$ is upper semi-continuous. Applying Theorem 3, $\mathrm{\Phi }$ admits a $\mathbb{FP}$$z\in \mathcal{L}$, and therefore,

$$z\in {(I-G)}^{-1}F\left(z\right)\iff z-G\left(z\right)\in F\left(z\right)\iff z\in G\left(z\right)+F\left(z\right).$$

☐

Theorem 8.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$, and let $\mathcal{L}$ be a nonempty closed bounded s-convex subset of $\mathcal{X}$. Assume that $F:\mathcal{L}\to P_{cl,c{v}_s}\left(\mathcal{X}\right)$ is upper semi-continuous and $G\in \mathcal{L}\left(\mathcal{X}\right)$ satisfies (${\mathcal{H}}_1$)–(${\mathcal{H}}_2$),

(${\mathcal{H}}_3$)

$F\left(\mathcal{L}\right)$ is relatively compact, and for every $\eta \in c{v}_{s}F\left(\mathcal{L}\right)$,

$$\xi \in G\left(\xi \right)+F\left(\eta \right)\Rightarrow \xi \in c{v}_{s}F\left(\mathcal{L}\right).$$

Then, ∃$z\in \mathcal{L}$ such that $z\in G\left(z\right)+F\left(z\right)$.

Proof. 

Let $\tilde{\mathcal{L}}=\overline{c{v}_s}F\left(\mathcal{L}\right)$, which is compact and s-convex. As in Theorem 7, define $\mathrm{\Phi }\left(\xi \right)={(I-G)}^{-1}F\left(\xi \right)$. If $x\in \mathrm{\Phi }\left(\tilde{\mathcal{L}}\right)$, then $x={(I-G)}^{-1}\left(\omega \right)$ for some $\eta \in \tilde{\mathcal{L}}$ and $\omega \in F\left(\eta \right)$, which implies

$$x-G\left(x\right)=\omega \in F\left(\eta \right).$$

Hence, $x\in G\left(x\right)+F\left(\eta \right)$, and by (${\mathcal{H}}_3$), we obtain $x\in \tilde{\mathcal{L}}$. Thus, $\mathrm{\Phi }\left(\tilde{\mathcal{L}}\right)\subset \tilde{\mathcal{L}}$, and Theorem 7 gives a $\mathbb{FP}$ of $\mathrm{\Phi }$ and, in turn, of $G+F$.   ☐

Theorem 9.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$, and let $\mathcal{L}$ be a nonempty compact s-convex subset of $\mathcal{X}$. Assume

$\left({\mathcal{H}}_{\phi }\right)$

If $\phi \in (0,1)$ and $\xi \in \phi G\left(\xi \right)+F\left(\eta \right)$ with $\eta \in \mathcal{L}$, then $\xi \in \mathcal{L}$.

Let$G\in \mathcal{L}\left(\mathcal{X}\right)$satisfy (${\mathcal{H}}_1$), and suppose$F:\mathcal{L}\to P_{cl,c{v}_s}\left(\mathcal{X}\right)$is upper semi-continuous. Then, ∃$z\in \mathcal{L}$ such that $z\in G\left(z\right)+F\left(z\right)$.

Proof. 

Choose a sequence $\left({\phi }_n\right)\subset (0,1)$ with ${\phi }_n\to 1$ and $\parallel {\phi }_n^{1/s}{G}^q{\parallel }_p<1$. By Theorem 7, for each n ∃${\xi }_n\in \mathcal{L}$ such that

$${\xi }_n\in {\phi }_n^{1/s}G\left({\xi }_n\right)+F\left({\xi }_n\right).$$

Since $\mathcal{L}$ is compact, a subsequence converges to some $z\in \mathcal{L}$. Define

$$\mathsf{\Gamma }(\phi ,\xi )={\phi }^{1/s}G\left(\xi \right)+F\left(\xi \right),\phi \in [0,1],\xi \in \mathcal{L}.$$

Because G is continuous, F is upper semi-continuous, and $\mathcal{L}$ is compact, $\mathsf{\Gamma }$ has a closed graph. Therefore,

$${\xi }_n\in \mathsf{\Gamma }({\phi }_n,{\xi }_n)\to z\in \mathsf{\Gamma }(1,z)=G\left(z\right)+F\left(z\right).$$

☐

Theorem 10.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$. Let $\mathcal{L}\subset \mathcal{X}$ be a nonempty closed s-convex subset, $s\in (0,p]$, and let $\mathcal{U}\subset \mathcal{L}$ be open with $\theta \in \mathcal{U}$. Assume that $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is upper semi-continuous and $G\in \mathcal{L}\left(\mathcal{X}\right)$ satisfies (${\mathcal{H}}_1$) and the condition

(${\mathcal{H}}_4$)

If $\xi \in G\left(\xi \right)+F\left(\eta \right)$ with $\eta \in \overline{\mathcal{U}}$, then $\xi \in \mathcal{L}$.

Then, at least one of the following holds:

(1)​

The equation $\xi \in G\left(\xi \right)+\omega F\left(\xi \right)$ has a solution for $\omega =1$;

(2)​

∃$\xi \in {\partial }_{\mathcal{L}}\mathcal{U}$ and some $\omega \in (0,1)$ such that

$$\xi \in G\left(\xi \right)+\omega F\left(\xi \right).$$

Proof. 

Assume that (2) fails and that $G+F$ has no $\mathbb{FP}$ on ${\partial }_{\mathcal{L}}\mathcal{U}$. Define

$$B=\{\xi \in \overline{\mathcal{U}}:\xi \in \omega {(I-G)}^{-1}F\left(\xi \right)\mathrm{for}\mathrm{some}\omega \in [0,1]\}.$$

Then, $0\in B$ (take $\omega =0$). Using compactness and the closed-graph property of F, one shows that B is compact. Since $B\cap {\partial }_{\mathcal{L}}\mathcal{U}=⌀$, Urysohn’s lemma gives a continuous function $\eta :\overline{\mathcal{U}}\to [0,1]$ such that

$$\eta \left(\xi \right)=\left\{\begin{array}{cc}1,\hfill & \xi \in B,\hfill \\ 0,\hfill & \xi \in {\partial }_{\mathcal{L}}\mathcal{U}.\hfill \end{array}\right.$$

Define

$$\mathrm{\Phi }\left(\xi \right)=\left\{\begin{array}{cc}\eta \left(\xi \right){(I-G)}^{-1}F\left(\xi \right),\hfill & \xi \in \overline{\mathcal{U}},\hfill \\ 0,\hfill & \xi \in \mathcal{L}\setminus \overline{\mathcal{U}}.\hfill \end{array}\right.$$

By compactness of $F\left(\mathcal{U}\right)$ and continuity of ${(I-G)}^{-1}$, the set

$$\mathcal{L}=\overline{c{v}_s}\left({(I-G)}^{-1}\left(F\left(\mathcal{U}\right)\right)\cup \left\{\theta \right\}\right)$$

is compact (Lemma 5). Hence, $\mathrm{\Phi }:\mathcal{L}\to P_{cl,c{v}_s}\left(\mathcal{L}\right)$ is upper semi-continuous. Applying Theorem 3 yields $\xi \in \mathcal{L}$ with $\xi \in \mathrm{\Phi }\left(\xi \right)$, which produces the desired alternative.   ☐

3.2. Approximation Techniques in Krasnosel’skii $\mathbb{FP}$ Theory

For a wide class of multifunctions with compact (and not necessarily convex) values, various authors have developed constructive schemes for obtaining approximate continuous selections. Notable contributions include the work of Cellina [34], Górniewicz, Granas, Kryszewski [35], as well as Górniewicz and Lassonde [36]. These approximation results form a foundation for the modern development of multivalued index theory.

Unlike the techniques employed in these classical approaches, the present section relies on a different type of approximation, tailored to Krasnosel’skii-type $\mathbb{FP}$ results in p-normed spaces. The following continuous approximation theorem serves as a key tool in our analysis.

Theorem 11

(Approximate Lipschitz Selection [37]). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a p-normed space and $(Y,\parallel ·{\parallel }_p)$ a complete p-normed space, where $p\in (0,1]$. Suppose $F:\mathcal{X}\to P_{c{v}_s}\left(Y\right)$ is an upper semi-continuous multivalued operator. Then, for every $\epsilon >0$∃, a locally Lipschitz function $f_{\epsilon }:\mathcal{X}\to Y$ satisfies the following:

1.​

$f_{\epsilon }\left(\xi \right)\in c{v}_{s}F\left(\mathcal{X}\right)$ for all $\xi \in \mathcal{X}$.

2.​

The graph of $f_{\epsilon }$ is ε-close to the graph of F in the product space, i.e.,

$$Graph\left(f_{\epsilon }\right)\subseteq Graph\left(F\right)+\epsilon B_0,$$

where $B_0$ denotes the open unit ball of $\mathcal{X}\times Y$ and the sum is understood in the Minkowski sense.

Proof. 

Since F is upper semi-continuous, for each fixed $\epsilon >0$ and every $\xi \in \mathcal{X}$∃$\delta \left(\xi \right)>0$ such that

$$F\left({\xi }^{*}\right)\subset F\left(\xi \right)+{\displaystyle \frac{\epsilon }{2}}{B}^0\mathrm{whenever}{\xi }^{*}\in B^0(\xi ,\delta \left(\xi \right)),$$

where $B^0(\xi ,\delta \left(\xi \right))$ denotes the open $\delta \left(\xi \right)$–ball centered at $\xi$, and $B^0$ is the open unit ball in Y. We may assume without loss of generality that $\delta \left(\xi \right)<{\displaystyle \frac{\epsilon }{2}}$.

The collection ${\left\{B^0(\xi ,\delta \left(\xi \right)/4)\right\}}_{\xi \in \mathcal{X}}$ is an open covering of $\mathcal{X}$. Since $\mathcal{X}$ is paracompact, ∃ a locally finite refinement ${\left\{V_i\right\}}_{i\in I}$ together with a locally Lipschitz partition of unity ${\left\{q_i\right\}}_{i\in I}$ subordinate to it.

For each i, choose ${\overline{\xi }}_i$ so that $V_i\subset B^0({\overline{\xi }}_i,\delta \left({\overline{\xi }}_i\right)/4)$ and select $m_i\in F\left({\overline{\xi }}_i\right)$. Define

$$f_{\epsilon }\left(\xi \right)=\sum _{i\in I}{q}_i\left(\xi \right)m_i.$$

The sum is well defined by local finiteness, and $f_{\epsilon }$ is locally Lipschitz as a finite combination of locally Lipschitz functions.

Since $f_{\epsilon }\left(\xi \right)$ is an s-convex combination of points $m_i\in F\left({\overline{\xi }}_i\right)\subset F\left(\mathcal{X}\right)$, we have

$$f_{\epsilon }\left(\xi \right)\in c{v}_{s}F\left(\mathcal{X}\right).$$

Fix $\xi \in \mathcal{X}$ and set $I\left(\xi \right)=\{i\mid q_i\left(\xi \right)>0\}$, which is finite. For each $i\in I\left(\xi \right)$, let ${\delta }_i=\delta \left({\xi }_i\right)$ and choose an index $j\in I\left(\xi \right)$ with ${\delta }_j={max}_i{\delta }_i$. Then, ${\xi }_i\in B^0({\xi }_j,{\delta }_j/2)$, so

$$m_i\in F\left(V_i\right)\subset F\left(B^0({\xi }_j,{\delta }_j)\right)\subset F\left({\xi }_j\right)+{\displaystyle \frac{\epsilon }{2}}{B}^0.$$

Thus, $f_{\epsilon }\left(\xi \right)$ lies within ${\displaystyle \frac{\epsilon }{2}}$ of $F\left({\xi }_j\right)$, and consequently,

$$(\xi ,f_{\epsilon }\left(\xi \right))\in Graph\left(F\right)+\epsilon B_0.$$

This yields

$$Graph\left(f_{\epsilon }\right)\subset Graph\left(F\right)+\epsilon B_0.$$

☐

Theorem 12.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$, and let $\mathcal{L}$ be a compact s-convex subset of $\mathcal{X}$. Suppose $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator, and $G:\mathcal{L}\to \mathcal{L}$ is single-valued. Assume

(${\mathcal{H}}_5$)

G is a contraction;

(${\mathcal{H}}_6$)

$G\left(\mathcal{L}\right)+F\left(\mathcal{L}\right)\subset \mathcal{L}$.

Then, the inclusion

$$\xi \in G\left(\xi \right)+F\left(\xi \right)$$

admits at least one solution.

Proof. 

By Theorem 11, for every $\epsilon >0$∃, a continuous map

$$f_{\epsilon }:\mathcal{L}\to \mathcal{X}$$

such that

$$f_{\epsilon }\left(\mathcal{L}\right)\subset c{v}_{s}F\left(\mathcal{L}\right)\mathrm{and}Graph\left(f_{\epsilon }\right)\subset Graph\left(F\right)+\epsilon B_0.$$

(3)

Using (${\mathcal{H}}_6$) and the s-convexity of $\mathcal{L}$,

$$G\left(\mathcal{L}\right)+f_{\epsilon }\left(\mathcal{L}\right)\subset G\left(\mathcal{L}\right)+c{v}_{s}F\left(\mathcal{L}\right)\subset \mathcal{L}.$$

For any fixed $\eta \in \mathcal{L}$, define

$$F_{\eta ,\epsilon }\left(\xi \right)=G\left(\xi \right)+f_{\epsilon }\left(\eta \right),\xi \in \mathcal{L}.$$

Since G is a contraction, the Banach $\mathbb{FP}$ theorem ensures the existence of a unique ${\overline{\xi }}_{\epsilon }\left(\eta \right)\in \mathcal{L}$ satisfying

$${\overline{\xi }}_{\epsilon }\left(\eta \right)=G\left({\overline{\xi }}_{\epsilon }\left(\eta \right)\right)+f_{\epsilon }\left(\eta \right),$$

equivalently,

$$(I-G)\left({\overline{\xi }}_{\epsilon }\left(\eta \right)\right)=f_{\epsilon }\left(\eta \right).$$

Because $I-G$ is a homeomorphism onto its image, ${(I-G)}^{-1}$ is continuous.

Define

$${\mathrm{\Phi }}_{\epsilon }\left(\xi \right)={(I-G)}^{-1}{f}_{\epsilon }\left(\xi \right),\xi \in \mathcal{L}.$$

It follows that ${\mathrm{\Phi }}_{\epsilon }$ satisfies the hypotheses of Theorem 5, so ∃${\overline{\xi }}_{\epsilon }\in \mathcal{L}$ with

$${\overline{\xi }}_{\epsilon }=G\left({\overline{\xi }}_{\epsilon }\right)+f_{\epsilon }\left({\overline{\xi }}_{\epsilon }\right).$$

Choose a sequence ${\epsilon }_n\to 0$ and pick ${\xi }_{{\epsilon }_n}\in \mathcal{L}$ such that

$${\xi }_{{\epsilon }_n}=G\left({\xi }_{{\epsilon }_n}\right)+f_{{\epsilon }_n}\left({\xi }_{{\epsilon }_n}\right).$$

Since $\mathcal{L}$ is compact, a subsequence $\left\{{\xi }_{{\epsilon }_{n_k}}\right\}$ converges to some $\xi \in \mathcal{L}$. From

$$f_{{\epsilon }_{n_k}}\left({\xi }_{{\epsilon }_{n_k}}\right)=(I-G)\left({\xi }_{{\epsilon }_{n_k}}\right),$$

and using (3),

$$dist\left(({\xi }_{{\epsilon }_{n_k}},f_{{\epsilon }_{n_k}}\left({\xi }_{{\epsilon }_{n_k}}\right)),Graph\left(F\right)\right)\le {\epsilon }_{n_k}.$$

Passing to the limit and using the closedness of the graph of F yields

$$(I-G)\left(\xi \right)\in F\left(\xi \right).$$

Thus,

$$\xi \in G\left(\xi \right)+F\left(\xi \right).$$

☐

Following a comparable line of reasoning, we now prove the next result.

Theorem 13.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space, and let $\mathcal{L}\subseteq \mathcal{X}$ be a closed, bounded, s-convex subset. Suppose $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator and $G:\mathcal{L}\to \mathcal{L}$ is a single-valued operator satisfying condition $\left({\mathcal{H}}_4\right)$. Additionally, assume that

(${\mathcal{H}}_7$)

$F\left(\mathcal{L}\right)$ is compact and $G\left(\mathcal{L}\right)+F\left(\mathcal{L}\right)\subseteq c{v}_{s}F\left(\mathcal{L}\right)$.

Then, the operator $G+F$ possesses at least one $\mathbb{FP}$.

Proof. 

Set $\tilde{\mathcal{L}}=\overline{c{v}_s}F\left(\mathcal{L}\right)$, which is compact and s-convex. As in the proof of Theorem 12, define ${\mathrm{\Phi }}_{ϵ}(·)={(I-G)}^{-1}{f}_{ϵ}(·)$. For any $\xi \in \tilde{\mathcal{L}}$, by the definition of ${\mathrm{\Phi }}_{ϵ}$, ∃$\eta \in {\mathrm{\Phi }}_{ϵ}\left(\tilde{\mathcal{L}}\right)$ such that

$$\eta ={(I-G)}^{-1}\left(f_{ϵ}\left(\xi \right)\right),$$

or equivalently,

$$(I-G)\left(\eta \right)=f_{ϵ}\left(\xi \right)⟹\eta =G\left(\eta \right)+f_{ϵ}\left(\xi \right)\subseteq G\left(\mathcal{L}\right)+F\left(\mathcal{L}\right)\subseteq c{v}_{s}F\left(\mathcal{L}\right)=\tilde{\mathcal{L}}.$$

Condition $\left({\mathcal{H}}_7\right)$ ensures that $\eta \in \tilde{\mathcal{L}}$, so ${\mathrm{\Phi }}_{ϵ}\left(\tilde{\mathcal{L}}\right)\subseteq \tilde{\mathcal{L}}$. Consequently, by Theorem 12, the operator $G+F$ has a $\mathbb{FP}$.   ☐

Theorem 14.

Assume that $(\mathcal{X},\parallel ·{\parallel }_p)$ is a complete p-normed space with $p\in (0,1]$, and let $\mathcal{L}$ be a nonempty, compact, s-convex subset of $\mathcal{X}$, where $s\in (0,p]$. Suppose that condition $\left({\mathcal{H}}_{\phi }\right)$ holds, G is a nonexpansive operator, and $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator. Then, the operator $G+F$ admits at least one $\mathbb{FP}$.

Proof. 

Let ${\left\{{\phi }_n\right\}}_{n\in \mathbb{N}}\subset (0,1)$ satisfy ${\phi }_n^{{\displaystyle \frac{1}{s}}}\to 1$, and define $T_n={\phi }_n^{{\displaystyle \frac{1}{s}}}{G}^q$. Then, $T_n$ is a contraction because

$$\parallel T_n\xi -T_n{\eta \parallel }_p\le {\phi }_n^{{\displaystyle \frac{p}{s}}}{\parallel \xi -\eta \parallel }_p,\mathrm{with}{\phi }_n^{{\displaystyle \frac{p}{s}}}<1.$$

By Theorem 12, ∃${\xi }_n\in \mathcal{L}$ such that

$${\xi }_n\in {\phi }_n^{{\displaystyle \frac{1}{s}}}G\left({\xi }_n\right)+F\left({\xi }_n\right).$$

Since $\mathcal{L}$ is compact, the sequence ${\left\{{\xi }_n\right\}}_{n\in \mathbb{N}}$ admits a subsequence converging to some $z\in \mathcal{L}$. Define $\mathsf{\Gamma }:[0,1]\times \mathcal{L}\to P_{cl}\left(\mathcal{X}\right)$ by

$$\mathsf{\Gamma }(\phi ,\xi )={\phi }^{{\displaystyle \frac{1}{s}}}G\left(\xi \right)+F\left(\xi \right).$$

Given that G is continuous, F is upper semi-continuous, and $\mathcal{L}$ is compact, the map $\mathsf{\Gamma }$ has a closed graph. Therefore,

$${\xi }_n\in \mathsf{\Gamma }({\phi }_n,{\xi }_n)⟹z\in \mathsf{\Gamma }(1,z)=G\left(z\right)+F\left(z\right),$$

which shows that z is a $\mathbb{FP}$ of $G+F$.   ☐

Theorem 15.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$. Suppose $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator and $G:\mathcal{X}\to \mathcal{X}$ satisfies condition $\left({\mathcal{H}}_5\right)$. Then, either of the following is unbounded:

(1)​

The inclusion $\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right)$ has a solution for $\omega =1$.

(2)​

The set $\{\xi \in \mathcal{X}:\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right),\omega \in (0,1)\}$.

Proof. 

Assume that alternative (2) does not hold, that is,

$$\mathrm{\Omega }=\left\{\xi \in \mathcal{X}:\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right),\omega \in [0,1]\right\}$$

is bounded. Then, ∃$\mathcal{M}>0$ such that

$${\parallel \xi \parallel }_p\le \mathcal{M}\mathrm{for}\mathrm{all}\xi \in \mathrm{\Omega }.$$

Define the open ball

$$\mathcal{U}=\{\xi \in \mathcal{X}:\parallel \xi {\parallel }_p<\mathcal{M}+1\}=B(\theta ,\mathcal{M}+1).$$

Thus, $\mathcal{U}$ is an open, bounded, p-convex set containing the origin $\theta$.

Since F is compact, $F\left(\mathcal{U}\right)={\bigcup }_{\xi \in \mathcal{U}}F\left(\xi \right)$ is relatively compact in $\mathcal{X}$, and hence $\overline{F\left(\mathcal{U}\right)}$ is compact.

Let $f_{ϵ}:\mathcal{X}\to \mathcal{X}$ be an $ϵ$-approximate selection of F such that

$$f_{ϵ}\left(\mathcal{X}\right)\subseteq c{v}_{p}F\left(\mathcal{X}\right).$$

Now, consider the set

$$B_{ϵ}=\left\{\xi \in \overline{\mathcal{U}}:\xi =\omega {(I-G)}^{-1}{f}_{ϵ}\left(\xi \right),\omega \in [0,1]\right\}.$$

Because ${\partial }_{\mathcal{L}}\mathcal{U}\cap B_{ϵ}=⌀$, Urysohn’s lemma provides a continuous function $\eta :\overline{\mathcal{U}}\to [0,1]$ satisfying

$$\eta \left(\xi \right)=\left\{\begin{array}{cc}1,\hfill & \xi \in B_{ϵ},\hfill \\ 0,\hfill & \xi \in {\partial }_{\mathcal{L}}\mathcal{U}.\hfill \end{array}\right.$$

For each $ϵ>0$, define the operator ${\mathrm{\Phi }}_{ϵ}$ by

$${\mathrm{\Phi }}_{ϵ}\left(\xi \right)=\left\{\begin{array}{cc}\eta \left(\xi \right){(I-G)}^{-1}{f}_{ϵ}\left(\xi \right),\hfill & \xi \in \overline{\mathcal{U}},\hfill \\ \theta ,\hfill & \xi \in \mathcal{X}\setminus \overline{\mathcal{U}}.\hfill \end{array}\right.$$

Owing to the compactness of F and the continuity of ${(I-G)}^{-1}$, the set

$$\mathcal{L}=\overline{c{v}_s}\left({(I-G)}^{-1}\left(F\left(\mathcal{U}\right)\right)\cup \left\{\theta \right\}\right)$$

is compact by Lemma 5. Hence, ${\mathrm{\Phi }}_{ϵ}:\mathcal{L}\to \mathcal{L}$ is a continuous, compact operator. Applying Schauder’s $\mathbb{FP}$ theorem (Theorem 5), we obtain a point $z\in \mathcal{X}$ such that $z={\mathrm{\Phi }}_{ϵ}\left(z\right)$. Finally, repeating the argument used in the proof of Theorem 12, we conclude that $G+F$ has at least one $\mathbb{FP}$.  ☐

3.3. A Krasnosel’skii-Type $\mathbb{FP}$ Theorem in the Expansive Setting

In this section, we establish a multivalued version of a Krasnosel’skii-type $\mathbb{FP}$ theorem in the context of expansive operators within p-normed spaces. The results extend those in [38], which were confined to Banach spaces $\mathcal{X}$.

Definition 3.

Let $(\mathcal{X},d)$ be a metric space and $\mathcal{L}\subseteq \mathcal{X}$. An operator  $G:\mathcal{L}\to \mathcal{X}$ is said to be expansive if ∃ a constant $\sigma >1$ such that

$$d\left(G\right(\xi ),G(\eta \left)\right)\ge \sigma d(\xi ,\eta )forall\xi ,\eta \in \mathcal{L}.$$

We now recall several auxiliary results that will be instrumental in the sequel.

Theorem 16

([39]). Let $(\mathcal{X},d)$ be a complete metric space, and let $\mathcal{L}\subseteq \mathcal{X}$ be closed. If $G:\mathcal{L}\to \mathcal{X}$ is expansive and satisfies $\mathcal{L}\subseteq G\left(\mathcal{L}\right)$, then ∃ is a unique $\xi \in \mathcal{L}$ such that $\xi =G\left(\xi \right)$.

Lemma 6

([38]). Assume $(\mathcal{X},d)$ is a complete metric space and that $G^n:\mathcal{X}\to \mathcal{X}$ is expansive for some $n\in \mathbb{N}$. If $\mathcal{L}\subseteq \mathcal{X}$ is closed and $\mathcal{L}\subseteq G\left(\mathcal{L}\right)$, then G has a unique $\mathbb{FP}$ in $\mathcal{L}$.

Lemma 7

([39]). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a p-normed linear space, $\mathcal{L}\subseteq \mathcal{X}$, and suppose $G:\mathcal{L}\to \mathcal{X}$ is expansive with constant $\sigma >1$. Then, the operator $T=I-G:\mathcal{L}\to (I-G)\left(\mathcal{L}\right)$ is invertible, and its inverse satisfies

$$\begin{array}{c}\hfill \parallel T^{-1}\left(\xi \right)-T^{-1}{\left(\eta \right)\parallel }_p\le {\displaystyle \frac{1}{\sigma -1}}{\parallel \xi -\eta \parallel }_p\mathrm{for}\mathrm{all}\xi ,\eta \in (I-G)\left(\mathcal{L}\right).\end{array}$$

We are now prepared to present the main results of this section.

Theorem 17.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space, and let $\mathcal{L}\subseteq \mathcal{X}$ be a compact, s-convex subset. Suppose $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is an upper semi-continuous multivalued operator, and $G:\mathcal{L}\to \mathcal{X}$ is a single-valued operator satisfying the following:

$\left({\mathcal{H}}_1^{*}\right)$

G is continuous and expansive;

$\left({\mathcal{H}}_2^{*}\right)$

For every $r\in c{v}_{s}F\left(\mathcal{L}\right)$, it holds that

$$\mathcal{L}\subseteq r+G\left(\mathcal{L}\right).$$

Then, the inclusion $\xi \in G\left(\xi \right)+F\left(\xi \right)$ admits at least one solution in $\mathcal{L}$.

Proof. 

By Theorem 11, for each $ϵ>0$ ∃ a continuous selection $f_{ϵ}:\mathcal{L}\to \mathcal{X}$ such that

$$Graph\left(f_{ϵ}\right)\subset Graph\left(F\right)+ϵB_0.$$

Fix $\eta \in \mathcal{L}$ and define the operator $F_{\eta ,\epsilon }:\mathcal{L}\to \mathcal{X}$ by

$$F_{\eta ,\epsilon }\left(\xi \right)=G\left(\xi \right)+f_{ϵ}\left(\eta \right),\xi \in \mathcal{L}.$$

Since G is expansive, so is $F_{\eta ,\epsilon }$. Hence, by Theorem 16, ∃ a unique ${\xi }_{ϵ}\left(\eta \right)\in \mathcal{L}$ such that

$${\xi }_{ϵ}\left(\eta \right)=G\left({\xi }_{ϵ}\left(\eta \right)\right)+f_{ϵ}\left(\eta \right).$$

Because G is expansive with constant $\sigma >1$, we have for any ${\eta }_1,{\eta }_2\in \mathcal{L}$,

$$\parallel G\left({\xi }_{ϵ}\left({\eta }_1\right)\right)-G\left({\xi }_{ϵ}\left({\eta }_2\right)\right){\parallel }_p\ge \sigma {\parallel {\xi }_{ϵ}\left({\eta }_1\right)-{\xi }_{ϵ}\left({\eta }_2\right)\parallel }_p.$$

It follows that

$$\parallel {\xi }_{ϵ}\left({\eta }_1\right)-{\xi }_{ϵ}\left({\eta }_2\right){\parallel }_p\le {\displaystyle \frac{1}{\sigma -1}}{\parallel f_{ϵ}\left({\eta }_1\right)-f_{ϵ}\left({\eta }_2\right)\parallel }_p.$$

Since $f_{ϵ}$ is continuous, the mapping $\eta \mapsto {\xi }_{ϵ}\left(\eta \right)$ is also continuous. Define

$${\mathrm{\Phi }}_{\epsilon }:\mathcal{L}\to \mathcal{L},{\mathrm{\Phi }}_{\epsilon }\left(\eta \right)={\xi }_{\epsilon }\left(f_{\epsilon }\left(\eta \right)\right).$$

Then, ${\mathrm{\Phi }}_{\epsilon }$ is continuous. By Schauder’s $\mathbb{FP}$ theorem (Theorem 5), ∃${\overline{\xi }}_{\epsilon }\in \mathcal{L}$ such that

$${\mathrm{\Phi }}_{\epsilon }\left({\overline{\xi }}_{\epsilon }\right)={\overline{\xi }}_{\epsilon },\mathrm{i}.\mathrm{e}.,{\overline{\xi }}_{\epsilon }=G\left({\overline{\xi }}_{\epsilon }\right)+f_{\epsilon }\left({\overline{\xi }}_{\epsilon }\right).$$

Finally, by the same limiting argument used in the proof of Theorem 12, one concludes that the operator $G+F$ possesses at least one $\mathbb{FP}$ in $\mathcal{L}$.   ☐

Using a similar approach, we obtain the following result.

Theorem 18.

Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space and $\mathcal{L}\subseteq \mathcal{X}$ be a compact, s-convex subset. Assume $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is upper semi-continuous and $G:\mathcal{L}\to \mathcal{X}$ is single-valued, satisfying conditions $\left({\mathcal{H}}_1^{*}\right)$ and $\left({\mathcal{H}}_2^{*}\right)$. Then, the inclusion

$$\xi \in G^{-1}(I-F)\left(\xi \right)$$

admits at least one solution in$\mathcal{L}$.

Proof. 

Since G is expansive, the inverse $G^{-1}:G\left(\mathcal{L}\right)\to \mathcal{L}$ exists and is a contraction. Moreover, the continuity of G implies that $G\left(\mathcal{L}\right)$ is closed.

For a given $\epsilon >0$, let $f_{\epsilon }:\mathcal{L}\to \mathcal{X}$ be an $\epsilon$-approximate continuous selection of F, so that

$$Graph\left(f_{\epsilon }\right)\subset Graph\left(F\right)+\epsilon B_0.$$

Fix $\eta \in \mathcal{L}$ and define $F_{\epsilon ,\eta }:\mathcal{L}\to \mathcal{L}$ by

$$F_{\epsilon ,\eta }\left(\xi \right)=G^{-1}\left(\xi \right)+f_{\epsilon }\left(\eta \right),\xi \in \mathcal{L}.$$

Since $G^{-1}$ is a contraction, $F_{\epsilon ,\eta }$ is a contraction as well. By the Banach contraction principle, ∃ a unique ${\xi }_{\epsilon }\left(\eta \right)\in G\left(\mathcal{L}\right)$ such that

$${\xi }_{\epsilon }\left(\eta \right)=G^{-1}\left({\xi }_{\epsilon }\left(\eta \right)\right)+f_{\epsilon }\left(\eta \right).$$

Let ${\eta }_1,{\eta }_2\in \mathcal{L}$. Then,

$$\begin{array}{cc}\hfill \parallel {\xi }_{\epsilon }\left({\eta }_1\right)-{\xi }_{\epsilon }\left({\eta }_2\right){\parallel }_p& =\parallel \left[G^{-1}\left({\xi }_{\epsilon }\left({\eta }_1\right)\right)-G^{-1}\left({\xi }_{\epsilon }\left({\eta }_2\right)\right)\right]+\left[f_{\epsilon }\left({\eta }_1\right)-f_{\epsilon }\left({\eta }_2\right)\right]{\parallel }_p\hfill \\ & \le \parallel G^{-1}\left({\xi }_{\epsilon }\left({\eta }_1\right)\right)-G^{-1}\left({\xi }_{\epsilon }\left({\eta }_2\right)\right){\parallel }_p+{\parallel f_{\epsilon }\left({\eta }_1\right)-f_{\epsilon }\left({\eta }_2\right)\parallel }_p\hfill \\ & \le {\displaystyle \frac{1}{k}}\parallel {\xi }_{\epsilon }\left({\eta }_1\right)-{\xi }_{\epsilon }\left({\eta }_2\right){\parallel }_p+{\parallel f_{\epsilon }\left({\eta }_1\right)-f_{\epsilon }\left({\eta }_2\right)\parallel }_p,\hfill \end{array}$$

where $k>1$ is the expansivity constant of G, so that $G^{-1}$ has Lipschitz constant $1/k<1$. Rearranging yields

$$\parallel {\xi }_{\epsilon }\left({\eta }_1\right)-{\xi }_{\epsilon }\left({\eta }_2\right){\parallel }_p\le {\displaystyle \frac{k}{k-1}}{\parallel f_{\epsilon }\left({\eta }_1\right)-f_{\epsilon }\left({\eta }_2\right)\parallel }_p.$$

Thus, the mapping ${\mathrm{\Phi }}_{\epsilon }\left(\eta \right)={\xi }_{\epsilon }\left(f_{\epsilon }\left(\eta \right)\right)$ is continuous from $\mathcal{L}$ into itself. By Theorem 5, ∃$z_{\epsilon }\in \mathcal{L}$ such that

$$z_{\epsilon }=G^{-1}\left(z_{\epsilon }\right)+f_{\epsilon }\left(z_{\epsilon }\right).$$

Passing to the limit as $\epsilon \to 0$ and using the argument from Theorem 12, we obtain a point $\xi \in \mathcal{L}$ satisfying

$$\xi \in G^{-1}\left(\xi \right)+F\left(\xi \right)⟺\xi \in G^{-1}(I-F)\left(\xi \right),$$

which completes the proof.   ☐

3.4. A Study of Krasnosel’skii’s Theorem Using Measures of Noncompactness

Definition 4

([40], p. 20). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space with $p\in (0,1]$, and let $P_b\left(\mathcal{X}\right)$ denote the family of bounded subsets of $\mathcal{X}$. For any $\mathcal{L}\in P_b\left(\mathcal{X}\right)$, the Kuratowski and Pompeiu–Hausdorff measures of noncompactness are defined, respectively, by

$$\begin{array}{cc}\hfill & {\beta }_K\left(\mathcal{L}\right)=inf\left\{\zeta >0:\mathcal{L}\subset \bigcup _{i=1}^n{\mathcal{L}}_i,diam\left({\mathcal{L}}_i\right)\le \zeta \right\},\hfill \\ \hfill & {\beta }_H\left(\mathcal{L}\right)=inf\left\{\zeta >0:\mathcal{L}\mathit{can}\mathit{be}\mathit{covered}\mathit{by}\mathit{finitely}\mathit{many}\mathit{balls}\mathit{of}\mathit{radius}\le \zeta \right\}.\hfill \end{array}$$

In a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, a set $\mathcal{A}\subset \mathcal{X}$ is called a $\zeta$-net of $\mathcal{L}$ if

$$\mathcal{L}\subset \mathcal{A}+\zeta \overline{B}(0,1)=\{a+\zeta b:a\in \mathcal{A},b\in \overline{B}(0,1)\}.$$

Consequently, an equivalent formulation of the Pompeiu–Hausdorff measure in this setting is

$${\beta }_H\left(\mathcal{L}\right)=inf\{\zeta >0:\mathcal{L}\mathrm{admits}\mathrm{a}\mathrm{finite}\zeta -\mathrm{net}\}.$$

For notational convenience, we let $\psi :P_b\left(\mathcal{X}\right)\to [0,+\infty )$ denote a generic measure of noncompactness (either ${\beta }_K$ or ${\beta }_H$).

Proposition 3

([7]). Let $(\mathcal{X},\parallel ·{\parallel }_p)$ be a complete p-normed space. Then, any measure of noncompactness $\psi :P_b\left(\mathcal{X}\right)\to [0,+\infty )$ satisfies the following properties:

(1)​

Regularity: $\psi \left(\mathcal{L}\right)=0$ if and only if $\mathcal{L}$ is relatively compact.

(2)​

Invariance under closure: $\psi \left(\mathcal{L}\right)=\psi \left(\overline{\mathcal{L}}\right)$.

(3)​

Semi-additivity: $\psi ({\mathcal{L}}_1\cup {\mathcal{L}}_2)=max\{\psi \left({\mathcal{L}}_1\right),\psi \left({\mathcal{L}}_2\right)\}$.

(4)​

Monotonicity: If ${\mathcal{L}}_1\subset {\mathcal{L}}_2$, then $\psi \left({\mathcal{L}}_1\right)\le \psi \left({\mathcal{L}}_2\right)$.

(5)​

Semi-homogeneity: $\psi \left(\lambda \mathcal{L}\right)={\left|\lambda \right|}^p\psi \left(\mathcal{L}\right)$ for all $\lambda \in \mathbb{R}$.

(6)​

Algebraic semi-additivity: $\psi (\mathcal{L}+\mathcal{M})\le \psi \left(\mathcal{L}\right)+\psi \left(\mathcal{M}\right)$.

(7)​

Invariance under translations: $\psi ({\xi }_0+\mathcal{L})=\psi \left(\mathcal{L}\right)$ for any ${\xi }_0\in \mathcal{X}$.

(8)​

Lipschitzianity: $|\psi \left(\mathcal{L}\right)-\psi \left(\mathcal{M}\right)|\le {\sigma }_{\delta }{D}_{\mathcal{P}}(\mathcal{L},\mathcal{M})$, where ${\sigma }_{\delta }=2$ if $\delta ={\beta }_K$ and ${\sigma }_{\delta }=1$ if $\delta ={\beta }_H$.

(9)​

Invariance under p-convex hull: $\psi \left(\mathcal{L}\right)=\psi \left(C_p\left(\mathcal{L}\right)\right)$.

Definition 5

([7]). Let ${\beta }_K$ (Kuratowski) and ${\beta }_H$ (Pompeiu–Hausdorff) be measures of noncompactness in $\mathcal{X}$.

(i)​

A multivalued operator $F:\mathcal{D}\left(F\right)\subset \mathcal{X}\to P\left(\mathcal{X}\right)$ is a σ–set-contraction (with respect to ${\beta }_K$ or ${\beta }_H$) if it is bounded and continuous, and ∃$\sigma \ge 0$ such that

$$\psi \left(F\right(\mathcal{L}\left)\right)\le \sigma \psi \left(\mathcal{L}\right)$$

for every bounded subset $\mathcal{L}\subset \mathcal{D}\left(F\right).$ In particular, if σ = 1$,then$ F is called 1-set-contractive.

(ii)​

A bounded continuous operator $F:\mathcal{D}\left(F\right)\subset \mathcal{X}\to P\left(\mathcal{X}\right)$ is ψ-condensing if

$$\psi \left(F\right(\mathcal{L}\left)\right)<\psi \left(\mathcal{L}\right)$$

 for every bounded $\mathcal{L}\subset \mathcal{D}\left(F\right)$ with  $\psi \left(\mathcal{L}\right)>0.$

Remark 2

([40,41]).

1.​

Every compact operator is a 0-set-contraction. Moreover, any Lipschitz operator with constant $\sigma \ge 0$ is a σ-set-contraction.

2.​

Every σ-set-contraction with $\sigma <1$ is ψ-condensing.

3.​

Every ψ-condensing operator is 1-set-contractive, though the converse does not hold in general (see [42]).

Definition 6

([13,20,43]). An operator $f:D\left(f\right)\subset \mathcal{X}\to \mathcal{X}$ is called ϕ-expansive if ∃ a function $\varphi :[0,+\infty )\to [0,+\infty )$ such that

$${\parallel f\left(\xi \right)-f\left(\eta \right)\parallel }_p\ge {\varphi (\parallel \xi -\eta \parallel }_p)forall\xi ,\eta \in D\left(f\right),$$

where ϕ satisfies the following:

(i)​

$\varphi \left(0\right)=0$;

(ii)​

$\varphi \left(r\right)>0$ for all $r>0$;

(iii)​

ϕ is either continuous or non-decreasing.

Lemma 8.

([13,43]). Let $\mathcal{L}$ be a nonempty, bounded, closed subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, $p\in (0,1]$. If $f:\mathcal{L}\to \mathcal{X}$ is ϕ-expansive, then f is injective and its inverse $f^{-1}:\mathcal{R}\left(f\right)\to \mathcal{L}$ is uniformly continuous.

Theorem 19

(Sadovski-type, [7]). Let $\mathcal{L}$ be a bounded, closed, s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$, where $p\in (0,1]$ and $s\in (0,p]$. If $f:\mathcal{L}\to \mathcal{L}$ is continuous and ψ-condensing (with respect to ${\beta }_K$ or ${\beta }_H$), then f has at least one $\mathbb{FP}$ in $\mathcal{L}$, and the set of all such $\mathbb{FP}$ s is compact.

Theorem 20.

Assume that $\mathcal{L}$ is a closed, bounded, s-convex subset of a complete p-normed space $(\mathcal{X},\parallel ·{\parallel }_p)$. Let $F:\mathcal{L}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ be an upper semi-continuous multivalued operator, and $G:\mathcal{L}\to \mathcal{X}$ be a continuous single-valued operator satisfying the following:

(${\mathcal{H}}_8$)

F is compact;

(${\mathcal{H}}_9$)

G is a σ-set-contraction with $\sigma <1$ (with respect to ${\beta }_K$ or ${\beta }_H$);

(${\mathcal{H}}_{10}$)

I − G is ϕ-expansive;

(${\mathcal{H}}_{11}$)

$F\left(\mathcal{L}\right)+G\left(\mathcal{L}\right)\subseteq \mathcal{L}$.

Then, the inclusion $\xi \in G\left(\xi \right)+F\left(\xi \right)$ admits at least one solution in $\mathcal{L}$.

Proof .

Fix $ϵ>0$. By Theorem 11, ∃ a continuous selection $f_{ϵ}:\mathcal{L}\to \mathcal{X}$ such that

$$Graph\left(f_{\epsilon }\right)\subseteq Graph\left(F\right)+\epsilon B_0,\mathrm{and}{f}_{ϵ}\left(\mathcal{L}\right)\subset c{v}_{s}F\left(\mathcal{L}\right).$$

Using $\left({\mathcal{H}}_{11}\right)$ and the s-convexity of $\mathcal{L}$, we obtain

$$\begin{array}{cc}\hfill G\left(\mathcal{L}\right)+f_{ϵ}\left(\mathcal{L}\right)& \subseteq G\left(\mathcal{L}\right)+c{v}_s\left(F\left(\mathcal{L}\right)\right)\hfill \\ \hfill & \subseteq c{v}_s\left(G\left(\mathcal{L}\right)+F\left(\mathcal{L}\right)\right)\hfill \\ \hfill & \subseteq c{v}_s\left(\mathcal{L}\right)=\mathcal{L}.\hfill \end{array}$$

Fix $\eta \in \mathcal{L}$ and define the operator

$$F_{\epsilon ,\eta }\left(\xi \right)=G\left(\xi \right)+f_{\epsilon }\left(\eta \right),\xi \in \mathcal{L}.$$

For any bounded $\mathcal{M}\subset \mathcal{L}$, we have

$$\psi \left(F_{\epsilon ,\eta }\left(\mathcal{M}\right)\right)=\psi \left(G\left(\mathcal{M}\right)\right)<\psi \left(\mathcal{M}\right),$$

since G is ψ-condensing by Remark 2 and $\left({\mathcal{H}}_9\right)$. As G is continuous and ψ-condensing, Theorem 19 yields a point ${\xi }_{ϵ}\left(\eta \right)\in \mathcal{L}$ such that

$${\xi }_{ϵ}\left(\eta \right)=G\left({\xi }_{ϵ}\left(\eta \right)\right)+f_{ϵ}\left({\xi }_{ϵ}\left(\eta \right)\right).$$

By Lemma 8 and $\left({\mathcal{H}}_{10}\right)$, the operator $I-G$ is injective and ${(I-G)}^{-1}:\mathcal{R}(I-G)\to \mathcal{L}$ is uniformly continuous. Hence,

$$f_{ϵ}\left({\xi }_{ϵ}\left(\eta \right)\right)\in (I-G)\left(\mathcal{L}\right)⟹{\xi }_{ϵ}\left(\eta \right)={(I-G)}^{-1}\left(f_{ϵ}\left({\xi }_{ϵ}\left(\eta \right)\right)\right).$$

Define ${\mathrm{\Phi }}_{ϵ}:\mathcal{L}\to \mathcal{L}$ by

$${\mathrm{\Phi }}_{ϵ}\left(\eta \right)={(I-G)}^{-1}\left(f_{ϵ}\left(\eta \right)\right).$$

The continuity of $f_{ϵ}$ and uniform continuity of ${(I-G)}^{-1}$ imply that ${\mathrm{\Phi }}_{ϵ}$ is continuous. Moreover, since $f_{ϵ}\left(\mathcal{L}\right)\subset c{v}_{s}F\left(\mathcal{L}\right)$ and F is compact, the image ${\mathrm{\Phi }}_{ϵ}\left(\mathcal{L}\right)$ is relatively compact. Thus, by Schauder’s $\mathbb{FP}$ theorem (Theorem 5), ∃${\overline{\xi }}_{\epsilon }\in \mathcal{L}$ such that

$${\overline{\xi }}_{\epsilon }=G\left({\overline{\xi }}_{\epsilon }\right)+f_{ϵ}\left({\overline{\xi }}_{\epsilon }\right).$$

Finally, by the standard limiting argument used in Theorem 12, the operator $G+F$ admits at least one $\mathbb{FP}$ in $\mathcal{L}$.   ☐

Theorem 21.

Let $\mathcal{L}$ be a closed, s-convex subset of a complete p-normed space with $\theta \in \mathcal{L}$. Suppose $F:\mathcal{X}\to P_{cp,c{v}_s}\left(\mathcal{X}\right)$ is upper semi-continuous, and $G:\mathcal{L}\to \mathcal{X}$ is continuous. In addition to $\left({\mathcal{H}}_8\right)$–$\left({\mathcal{H}}_{10}\right)$, assume

(${\mathcal{H}}_{12}$)

$G\left(\mathcal{L}\right)$ is bounded.

Then, either of the following is unbounded:

(1)​

The inclusion $\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right)$ has a solution for $\omega =1$.

(2)​

The set $\{\xi \in \mathcal{X}:\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right),\omega \in (0,1)\}$.

Consequently, the operator $G+F$ admits at least one solution.

Proof .

Assume that (2) fails, that is, the set

$$\mathrm{\Omega }=\left\{\xi \in \mathcal{X}:\xi \in \omega G\left(\frac{\xi }{\omega }\right)+\omega F\left(\xi \right),\omega \in [0,1]\right\}$$

is bounded. Then, ∃$\mathcal{M}>0$ such that

$$max\{\parallel \xi {\parallel }_p,\parallel G\left(\xi \right){\parallel }_p\}\le \mathcal{M}\mathrm{for}\mathrm{all}\xi \in \mathrm{\Omega }.$$

Define the open ball

$$\mathcal{U}=\{\xi \in \mathcal{X}:\parallel \xi {\parallel }_p<\mathcal{M}+1\}=B(\theta ,\mathcal{M}+1).$$

Then, $\mathcal{U}$ is open, bounded, p-convex, and contains θ.

Since F is compact, $F\left(\mathcal{U}\right)={\bigcup }_{\xi \in \mathcal{U}}F\left(\xi \right)$ is relatively compact, so $\overline{F\left(\mathcal{U}\right)}$ is compact. By Theorem 11, ∃ an ϵ-approximate selection $f_{ϵ}:\mathcal{X}\to \mathcal{X}$ of F satisfying

$$f_{ϵ}\left(\mathcal{X}\right)\subseteq c{v}_{p}F\left(\mathcal{X}\right).$$

Set

$$B_{ϵ}=\left\{\xi \in \overline{\mathcal{U}}:\xi =\omega {(I-G)}^{-1}{f}_{ϵ}\left(\xi \right),\omega \in [0,1]\right\}.$$

Since ${\partial }_{\mathcal{L}}\mathcal{U}\cap B_{ϵ}=⌀$, Urysohn’s lemma provides a continuous function $\eta :\overline{\mathcal{U}}\to [0,1]$ such that

$$\eta \left(\xi \right)=\left\{\begin{array}{cc}1,\hfill & \xi \in B_{ϵ},\hfill \\ 0,\hfill & \xi \in {\partial }_{\mathcal{L}}\mathcal{U}.\hfill \end{array}\right.$$

For each $ϵ>0$, define the operator ${\mathrm{\Phi }}_{ϵ}:\mathcal{X}\to \mathcal{X}$ by

$${\mathrm{\Phi }}_{ϵ}\left(\xi \right)=\left\{\begin{array}{cc}\eta \left(\xi \right){(I-G)}^{-1}{f}_{ϵ}\left(\xi \right),\hfill & \xi \in \overline{\mathcal{U}},\hfill \\ \theta ,\hfill & \xi \in \mathcal{X}\setminus \overline{\mathcal{U}}.\hfill \end{array}\right.$$

By the compactness of F and the uniform continuity of ${(I-G)}^{-1}$ (from $\left({\mathcal{H}}_{10}\right)$ and Lemma 8), the set

$$\mathcal{L}=\overline{c{v}_s}\left({(I-G)}^{-1}\left(F\left(\mathcal{U}\right)\right)\cup \left\{\theta \right\}\right)$$

is compact (by Lemma 5). Thus, ${\mathrm{\Phi }}_{ϵ}:\mathcal{L}\to \mathcal{L}$ is continuous. Moreover, since $f_{ϵ}\left(\mathcal{L}\right)$ is relatively compact, $\psi \left({\mathrm{\Phi }}_{ϵ}\left(\mathcal{M}\right)\right)=0<\psi \left(\mathcal{M}\right)$ for any bounded $\mathcal{M}\subset \mathcal{L}$ with $\psi \left(\mathcal{M}\right)>0$. Hence, ${\mathrm{\Phi }}_{ϵ}$ is ψ-condensing by Remark 2.

Applying Theorem 19, ∃$z\in \mathcal{L}$ such that $z={\mathrm{\Phi }}_{ϵ}\left(z\right)$. Finally, using the same limiting procedure as in Theorem 12, we conclude that $G+F$ possesses at least one $\mathbb{FP}$.   ☐

4. Application of Nonlinear Integral Equation of Hammerstein Type

For the applicability of the obtained Krasnosel’skii-type results in p-normed spaces, we consider a nonlinear integral equation of Hammerstein type

$$x\left(t\right)={\mathit{\int }}_0^{1}K(t,s)f(s,x\left(s\right))ds,t\in [0,1],$$

(4)

where $K(t,s)$ is a continuous kernel and $f(t,x)$ is a nonlinear function satisfying a Lipschitz condition. Equation (4) can be reformulated as a $\mathbb{FP}$ problem $x=G\left(x\right)+F\left(x\right)$, where

$$\left(Gx\right)\left(t\right)={\int }_0^{1}K(t,s)x\left(s\right)ds,\left(Fx\right)\left(t\right)={\int }_0^{1}K(t,s)[f(s,x\left(s\right))-x\left(s\right)]ds.$$

Under the assumptions of Theorem 7, one can guarantee the existence of at least one $\mathbb{FP}$ of $G+F$.

5. Numerical Application

To illustrate the applicability of the obtained Krasnosel’skii-type results in p-normed spaces, we present a numerical example based on a Chebyshev collocation discretization. Chebyshev-based spectral techniques have been proven effective for high-accuracy solutions of nonlinear and nanoscale boundary value problems [44], and they provide a convenient framework to verify the existence of $\mathbb{FP}$ s established in the theoretical sections of this work. The approach also complements recent extensions of $\mathbb{FP}$ theory in generalized metric structures [45].

The integral equation under consideration is of classical Hammerstein type:

$$x\left(t\right)={\int }_0^{1}K(t,s)f(s,x\left(s\right))ds,$$

which can be equivalently expressed in the abstract fixed-point form $x=G\left(x\right)+F\left(x\right)$ by setting $G\equiv 0$ and $F\left(x\right)\left(t\right)={\int }_0^{1}K(t,s)f(s,x\left(s\right))ds$. This decomposition aligns with the Krasnosel’skii fixed-point framework where one operator is compact (here, F) and the other is a contraction or identity-type map (here, trivially $G=0$). Thus, our numerical example directly realizes a canonical Hammerstein equation within the theoretical setting of the paper.

5.1. Chebyshev Collocation Approximation

For a numerical solution of (4), we expand $x\left(t\right)$ in terms of shifted Chebyshev polynomials of the first kind:

$$x_N\left(t\right)=\sum _{k=0}^N{a}_k{T}_k^{*}\left(t\right),T_k^{*}\left(t\right)=T_k(2t-1),$$

where $T_k\left(t\right)$ are the classical Chebyshev polynomials on $[-1,1]$ and $a_k$ are unknown coefficients.

By collocating (4) at the shifted Chebyshev–Gauss nodes

$$t_j={\displaystyle \frac{1}{2}}\left(1+cos{\displaystyle \frac{(2j-1)\pi }{2(N+1)}}\right),j=1,2,\dots ,N,$$

we obtain a nonlinear algebraic system

$$a_i=\sum _{j=1}^N{w}_{j}K(t_i,t_j)f(t_j,x_N\left(t_j\right)),i=1,2,\dots ,N,$$

(5)

where $w_j$ are the corresponding quadrature weights associated with the shifted Chebyshev nodes.

5.2. Illustrative Example

Consider the kernel and nonlinearity

$$K(t,s)=e^{-|t-s|},f(s,x)={\displaystyle \frac{x}{1+x^2}},$$

which appear in nonlinear diffusion-type models. We take $N=8$ collocation points and solve (5) using a Newton–Kantorovich iterative scheme. The resulting approximation $x_N\left(t\right)$ is compared with a reference solution obtained by fine discretization.

The residual error is defined as

$$E_N=\underset{t_i\in [0,1]}{max}\left|x_N\left(t_i\right)-{\int }_0^{1}K(t_i,s)f(s,x_N\left(s\right))ds\right|.$$

Table 1 shows the decay of $E_N$ with increasing N, confirming the spectral accuracy of the Chebyshev collocation method.

Table 1. Maximum residual error for different values of N.

N	Approximation Order	${\mathit{E}}_{\mathit{N}}$
4	5	$1.62\times {10}^{-4}$
6	7	$2.15\times {10}^{-6}$
8	9	$3.41\times {10}^{-8}$
10	11	$5.02\times {10}^{-10}$

5.3. Real-World Application: Spatial Population Dynamics with Density-Dependent Feedback

Hammerstein integral equations are widely used in mathematical ecology to model steady-state distributions of biological populations where growth is limited by local resource availability and individuals disperse across space. A prototypical model for a single species in a one-dimensional habitat $[0,1]$ is given by

$$x\left(t\right)={\int }_0^{1}K(t,s)r\left(s\right){\displaystyle \frac{x\left(s\right)}{1+\beta x\left(s\right)}}ds,$$

(6)

where

1.

$x\left(t\right)\ge 0$ denotes the equilibrium population density at location t;

2.

$r\left(s\right)>0$ is the spatially heterogeneous intrinsic growth rate (e.g., due to variation in sunlight, soil quality, or water);

3.

$\beta >0$ is a competition coefficient that models how per-capita reproduction declines with local density (Holling type II or Michaelis–Menten saturation);

4.

$K(t,s)\ge 0$ is a dispersal kernel describing the probability that an individual born at location s settles at location t.

We adopt the ecologically realistic Hammerstein model (6) with kernel $K(t,s)=e^{-\alpha |t-s|}$ ($\alpha =1.5$) modeling limited dispersal, sinusoidal growth rate $r\left(s\right)=2.5+sin\left(4\pi s\right)$ representing two favorable habitat zones, and competition parameter $\beta =1.2$. This yields a continuous, bounded nonlinearity $f(s,x)=r\left(s\right)x/(1+\beta x)$ and a compact integral operator F, satisfying the conditions of Krasnosel’skii-type fixed-point theorems in p-normed spaces and guaranteeing a non-negative steady-state solution. Using the Chebyshev collocation method from Section 5.1 with $N=12$ and a damped Newton–Kantorovich solver (tolerance ${10}^{-12}$), we obtain a highly accurate numerical solution ($E_N\approx 7.3\times {10}^{-9}$) that exhibits density peaks aligned with favorable habitats (see Figure 2). This demonstrates the relevance of our theoretical framework to real-world problems in spatial ecology, conservation, and habitat modeling [46].

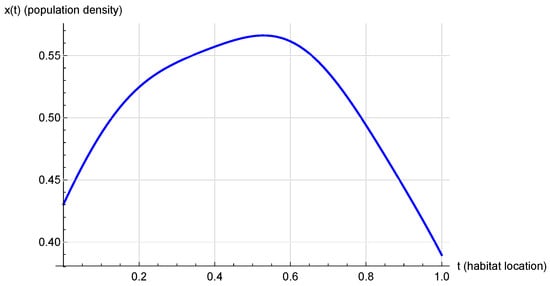
Figure 2. Equilibrium population density $x\left(t\right)$ for the ecological Hammerstein model (6) with $\alpha =1.5$, $\beta =1.2$, and $r\left(s\right)=2.5+sin\left(4\pi s\right)$. The solution was computed via fixed-point iteration on a fine grid and illustrates habitat-driven clustering.

The resulting steady-state population density is shown in Figure 2, which clearly reflects the influence of the spatially varying growth rate $r\left(s\right)$: higher densities emerge near $s\approx 0.125$ and $s\approx 0.625$, where $r\left(s\right)$ attains its maxima. The smoothness of the solution is a direct consequence of the diffusive-like dispersal encoded in the kernel $K(t,s)=e^{-\alpha |t-s|}$.

5.4. Discussion

The rapid convergence of $E_N$ demonstrates the efficiency of Chebyshev collocation in approximating the $\mathbb{FP}$ solution of nonlinear integral equations consistent with the Krasnosel’skii framework. This experiment validates the theoretical results obtained in Section 3 and highlights the feasibility of using spectral methods for computational verification in p-normed settings.

6. Abbreviations

For clarity of presentation, the abbreviations and notation are compiled in Table 2.

Table 2. Abbreviations with definitions and descriptions for families of subsets of $\mathcal{X}$.

Abbreviation	Definition	Description
$P\left(\mathcal{X}\right)$	$\{A\subset \mathcal{X}\mid A\ne ⌀\}$	Nonempty subsets of $\mathcal{X}$
$P_b\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid diam(A)<+\infty \}$	Nonempty bounded subsets of $\mathcal{X}$
$P_{cl}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{closed}\}$	Nonempty closed subsets of $\mathcal{X}$
$P_{cp}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{compact}\}$	Nonempty compact subsets of $\mathcal{X}$
$P_{b,cl}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{bounded},\mathrm{closed}\}$	Nonempty bounded, closed subsets of $\mathcal{X}$
$P_{c{v}_s}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{is}s-\mathrm{convex}\}$	Nonempty s-convex subsets of $\mathcal{X}$
$P_{cl,c{v}_s}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{closed},s-\mathrm{convex}\}$	Nonempty closed, s-convex subsets of $\mathcal{X}$
$P_{cp,c{v}_s}\left(\mathcal{X}\right)$	$\{A\in P(\mathcal{X})\mid A\mathrm{compact},s-\mathrm{convex}\}$	Nonempty compact, s-convex subsets of $\mathcal{X}$

7. Conclusions

This work develops fixed-point theory by developing a unified framework for Krasnosel’skii-type theorems in complete p-normed spaces with $p\in (0,1]$. We generalize classical results to the setting of multivalued operators and introduce several new tools, including an approximation theorem for upper semi-continuous mappings and measures of noncompactness adapted to the geometry of p-normed spaces. These ingredients allow us to address the difficulties that arise in non-locally convex environments, where standard Banach space techniques are no longer effective. The resulting theory suits a broad range of operator behaviors, from contractions to expansive mappings, and is supported by applications to Hammerstein integral equations with numerical verification based on the spectral collocation method. Taken together, these contributions fill gaps in the existing literature and provide a solid analytical framework for studying nonlinear problems in function spaces where classical convex methods fail, thereby opening further points for research in non-convex analysis and its applications.

8. Comparative Analysis of Fixed-Point Theory Developments

For convenience, the principal advancements relevant to fixed-point theory are organized and compared in Table 3, which outlines the core features and distinctions among existing approaches.

Table 3. Comparative Analysis of Fixed-Point Theory Developments.

Analytical Aspect	Classical Framework	Prior Work in p-Normed Spaces	Novel Contributions (This Paper)
Functional Setting	Normed/Banach spaces ($p=1$) with local convexity.	Extensions for $p\in (0,1]$; predominantly single-valued operator theory.	Complete p-normed spaces ($p\in (0,1]$) with systematic development of multivalued operator theory on s-convex subsets.
Fixed-Point Theorems	Krasnosel’skii (1958) [15]: $x=\mathcal{A}\left(x\right)+\mathcal{B}\left(x\right)$ with $\mathcal{A}$ compact, $\mathcal{B}$ contraction.	Limited extensions of Banach/ Schauder; no comprehensive theory for sums of multivalued operators.	Multivalued Krasnosel’skii-type theorems (Theorems 8–10, 12–15, 17 and 18) for $G+F$ where F is USC multivalued and G is single-valued (contraction/expansive/ nonexpansive).
Operator Classes	Single-valued: contractions, compact, nonexpansive. Multivalued: mostly convex-valued.	Single-valued focus.	Upper semi-continuous multivalued operators with s-convex values; expansive operators (Theorems 17 and 18); $\psi$-condensing operators (Theorems 19–21).
Noncompactness Measures	Well-developed: Kuratowski (${\beta }_K$) and Pompeiu–Hausdorff (${\beta }_H$) measures in Banach spaces.	Limited adaptation; mainly theoretical definitions without operative theorems.	Full theory of ${\beta }_K$ and ${\beta }_H$ in p-normed spaces; Darbo–Sadovskii theorems (Theorems 20 and 21) for $\psi$-condensing operators.
Approximation Methods	Cellina’s theorem: continuous selections for USC maps with convex values.	No known analog for p-normed spaces with s-convex values.	Theorem 11: Constructive $\epsilon$-approximate Lipschitz selections for USC multivalued operators in p-normed spaces.
Boundary Alternatives	Leray–Schauder principle: existence or alternative on boundary.	Rarely formulated for p-normed spaces, especially for multivalued operators.	Multivalued Leray–Schauder alternatives (Theorems 15 and 21) for inclusions $\xi \in G\left(\xi \right)+F\left(\xi \right)$.
Expansive Operators	Existence theory in Banach spaces (Xiang & Yuan, 2009 [39]).	Virtually unexplored in p-normed spaces.	First multivalued Krasnosel’skii theorems for expansive G (Theorems 17 and 18) in p-normed spaces.
Numerical Implementation	Often separate computational papers; not integrated with theory.	No numerical verification in theoretical p-normed space papers.	Integrated spectral method: Chebyshev collocation with error analysis (Section 5, Table 1); theory–computation bridge. Spatial Population Dynamics with Density-Dependent Feedback.
Unification Level	Fragmented: separate theories for single/ multivalued, convex/ non-convex.	Isolated results lacking synthesis.	Comprehensive framework unifying: single/multivalued, contraction/expansive/condensing, theoretical/numerical aspects.