Optical Mirage–Based Metaheuristic Optimization for Robust PEM Fuel Cell Parameter Estimation

Abstract

The parameter extraction of proton exchange membrane fuel cells (PEMFCs) has been an active area of study over the past few years, relying on metaheuristic optimizers and experimental datasets to achieve accurate current/voltage (I/V) curves. This work develops a mirage search optimizer (MSO) to precisely estimate the PEMFC model parameters. The MSO employs two search techniques based on the physical phenomena of light bending caused by atmospheric refractive index gradients: a superior mirage for global exploration and an inferior mirage for local exploitation. The MSO employs optical physics to direct search behavior, in contrast to conventional optimization approaches, allowing for a dynamic balance between exploration and exploitation. Convergence efficiency is increased by its iteration-dependent control and fitness-based influence. Using two common PEMFC modules, a comparison study with previously published methodologies and new, recently developed optimizers—the Educational Competition Optimizer (ECO), basketball team optimization (BTO), the fungal growth optimizer (FGO), and the naked mole rat optimizer (NMRO)—was conducted to evaluate the proposed MSO for parameter identification. Furthermore, the two models were tested under various temperatures and pressures. For the three examples studied, the MSO achieved the best sum of squared errors (SSE) values with an intriguing overall standard deviation (STD). It is undeniable that the STD and cropped SSE values, among other difficult techniques, are quite competitive and display the fastest convergence. According to the MSO, the BCS 500W, Ballard Mark V, and Modular SR-12 each have MSO values of 0.011697781, 0.852056, and 1.42098181379214 × 10⁻⁴, respectively. Additionally, the comparison results demonstrate that the proposed MSO can be successfully used to quickly and accurately define the PEMFC model.

1. Introduction

Precise PEMFC models support optimal stack design, component sizing, and thermal–water management. This is essential for scaling PEMFC technology from laboratory prototypes to large-scale industrial applications, transportation systems, and stationary power plants [1]. Furthermore, accurate parameters form the foundation for advanced control algorithms, real-time monitoring, and fault diagnosis. This capability is crucial for safe operation in electric vehicles, marine systems, aerospace, and backup power applications, where performance consistency is critical. It also enhances grid stability and enables low-carbon energy solutions for distributed and off-grid applications worldwide. Improved modeling accuracy reduces reliance on extensive experimental testing and trial-and-error design. This lowers development costs, accelerates commercialization, and minimizes maintenance expenses, supporting cost-effective global adoption of PEMFC technology [2].

PEMFC models typically involve nonlinear equations that relate current, voltage, temperature, pressure, and other physical phenomena. These models are often derived from semi-empirical formulations combining electrochemical kinetics, mass transport, and thermodynamic relationships. Because of this complexity, analytical solutions are impractical, and conventional linear techniques fail to yield accurate parameter values. The models exhibit strong parameter coupling, making the paramaters hard to isolate and estimate independently. This intrinsic nonlinearity makes the optimization landscape complex with multiple local minima, creating challenges in finding the true global optimum. To address these challenges, considerable research has focused on advanced estimation and optimization methodologies. A major trend in PEMFC parameter estimation is the use of modern metaheuristic algorithms, which do not require gradient information and can handle highly nonlinear and multimodal problems [3]. It is worth noting that the parameters of the semi-empirical PEMFC voltage model exhibit strong coupling, as the output voltage is determined by the combined effects of activation, ohmic, and concentration loss terms rather than by individual parameters in isolation. As a result, strict structural identifiability of all parameters cannot always be guaranteed. In this study, practical identifiability is emphasized by constraining all parameters within physically meaningful bounds reported in the literature and by fitting the model over a wide operating current range. This approach reduces ambiguity among correlated parameters and improves the robustness of the estimated values. Furthermore, repeated independent optimization runs yield consistent parameter sets with low variance, indicating stable convergence and reliable parameter estimation for engineering, modeling, control, and diagnostic applications.

Recently, a significant number of researchers have employed metaheuristic techniques for extracting the PEMFC model’s unidentified parameters, owing to major improvements in artificial intelligence–based methodologies. Metaheuristic techniques are the most effective and reliable methods for estimating PEMFC parameters, as this task is treated as an optimization problem [3,4]. The Flower Pollination Optimizer (FPO) [5] benefited from Lévy flight-based global search, which enhanced its ability to escape local optima during PEMFC parameter extraction. Despite this advantage, FPO may show high variability across runs, requiring multiple executions to ensure consistent parameter identification. Moreover, the whale optimization algorithm (WOA) [6] is easy to implement and performs well in capturing the nonlinear voltage–current characteristics of PEMFC models. Nevertheless, the WOA tends to suffer from premature convergence, particularly when estimating multiple highly correlated PEMFC parameters, which can lead to suboptimal solutions. The Grey Wolf Optimizer (GWO) [7] has been widely adopted for PEMFC parameter estimation because of its simple structure and fast convergence in early iterations. Nonetheless, the GWO may experience loss of population diversity during later stages, increasing the risk of stagnation near local optima. In [8], novel deep reinforcement learning was developed to reduce the operating costs of fuel cell hybrid electric buses (FCHEB), taking into consideration a predictive energy management strategy (PEMS) to enhance its optimization capability and driving condition adaptability.

The Bonobo Optimizer (BO) [9] exhibits strong global exploration capability, enabling it to identify feasible PEMFC parameter sets with acceptable accuracy. However, the BO often requires a relatively large population and many iterations to converge, resulting in increased computational cost and slower convergence for complex PEMFC stacks. The Slime Mould Optimizer (SMO) [10] has adaptively balanced exploration and exploitation, allowing it to handle the nonlinear and multimodal nature of PEMFC parameter estimation effectively. On the other hand, the SMO often requires a large number of fitness evaluations, increasing computational complexity. The grasshopper optimization algorithm (GOA) [11] has demonstrated strong global search ability and competitive estimation accuracy for PEMFC models. However, its performance is sensitive to control parameters, and improper tuning may degrade convergence speed and estimation reliability. The Shark Smell Optimizer (SSO) [12] has achieved high precision in PEMFC parameter extraction due to its gradient-inspired search mechanism. However, the SSO may struggle in highly multimodal search spaces and is sensitive to step-size parameters, which can affect stability and robustness.

The Jellyfish Search Optimizer (JSO) [13] incorporates adaptive movement strategies that enhance convergence stability in PEMFC parameter extraction problems. However, the JSO has exhibited oscillatory behavior near the optimal solution, which can limit fine local refinement of PEMFC parameters. The Manta Ray Foraging Optimizer (MRFO) [14] effectively balances exploration and exploitation, producing accurate PEMFC parameter estimates. Its limitation lies in relatively slow convergence during the final optimization stages, affecting overall efficiency. The chaotic Harris hawks optimizer (CHHO) [15] enhanced global exploration through chaotic dynamics, improving the accuracy of PEMFC parameter estimation. Nonetheless, the inclusion of chaos increases sensitivity to initial conditions and may reduce repeatability across independent runs. The Improved Artificial Ecosystem Optimizer (IAEO) [16] has enhanced solution accuracy and robustness in PEMFC parameter identification compared to its original version. Despite these improvements, the algorithm’s increased complexity leads to higher computational overhead. The Tree Growth Optimizer (TGO) [17] has provided stable convergence and reasonable estimation accuracy for PEMFC models. However, its limited diversification capability may restrict its effectiveness in highly multimodal parameter landscapes. In [18], an improved bald eagle search method is presented for investigating unknown values by reducing differences between measured and estimated data. The Coyote Optimization Algorithm (CO) [19] has leveraged social adaptation mechanisms to improve the robustness and consistency in PEMFC parameter extraction. However, CO often requires larger population sizes to achieve stable results, increasing computational time. The Pathfinder Optimizer (PFO) [20] has demonstrated good tracking capability and dynamic performance in PEMFC modeling. Despite this, it suffers from premature convergence when handling tightly coupled PEMFC parameters. The Black Widow Optimizer (BWO) [21] has shown strong exploitation capability, leading to competitive PEMFC parameter estimation accuracy. Its main drawback is the risk of rapid population reduction, which can lead to decreased diversity and suboptimal solutions. The Neural Network Optimizer (NNO) [22] effectively captured the nonlinear behavior of PEMFC systems and yielded accurate parameter estimation results. However, its training process was computationally intensive and highly dependent on parameter initialization.

Despite the benefits of self-adaptive nature optimizers, they require enhancements in areas such as convergence speed, time load, and statistical analysis. A new optimization technique called Mirage Search Optimization (MSO) is inspired by the physical phenomenon of mirages, in which light bends as a result of temperature-induced atmospheric refractive index gradients [23]. The superior mirage strategy and the inferior mirage strategy are two separate techniques that are derived from this idea. With its distinct inspiration from the physical occurrence of mirages, MSO sets itself apart from previous metaheuristic approaches. It integrates both superior and inferior mirage techniques to establish an evolving equilibrium between exploration and exploitation. In contrast to many algorithms that only use metaphors inspired by biology or society, MSO utilizes optical physics to guide search behavior, enabling agents to explore remote areas of the world and locally refine solutions in an organically adaptable manner. Its fitness-based influence and iteration-dependent agent distribution govern its dual-phase search mechanism, which improves convergence efficiency and prevents premature stagnation. MSO has been effectively used to solve engineering design and path-planning issues, and it is recognized for its ease of execution, speed of convergence, and simplicity. The following are the primary contributions of the paper:

• The use of MSO for defining fuel cell (FC) parameters is illustrated.
• The simulation results of the proposed MSO are compared with the following recent optimizers: the fungal growth optimizer [24], basketball team optimization (BTO) algorithm [25], the Differentiated Creative Search (DCS) [26]; the naked mole rat optimizer (NMRO) [27]; and the Educational Competition Optimizer (ECO) [28].
• The FC modules are tested with varying PH2/PO2 and temperature levels.
• The outcomes and statistical assessments demonstrate the MSO’s superiority compared with the experimental measures.

The remaining sections are arranged as follows: An optimal formulation of the dynamic model of PEMFC is presented in Section 2. Section 3 introduces the MSO for PEMFC, while the simulation results of the MSO when applied to the three PEMFC stacks are presented in Section 4. The key conclusions of this investigation are presented in Section 5.

2. Model of PEMFC

The I-V characteristics (polarization curves) can be mathematically displayed to form the PEMFC model. In this article, the steady-state performance of the PEMFC is described using the simplified electrochemical model proposed by Mann et al. [29]. This paradigm is widely employed in numerous literature analyses. The mathematical model for the output voltage of the PEMFCs stack (V_Stack) is illustrated in Equation (1), which comprises several series-connected cells (N_cells) [30,31,32].

$$V_{stack}=N_{cells}.(E_{Nernst}-v_{act}-v_{\Omega }-v_{conc})$$

(1)

where $v_{act}$ is the cell activation overpotential, $E_{Nernst}$ is the Nernst voltage per cell, $v_{conc}$ is the concentration overpotential, and $v_{\Omega }$ is the cell ohmic voltage drop. The voltage $E_{Nernst}$ can be calculated using (2) under a reference temperature of 25 °C. Thus, these three voltage drop amounts are provided as depicted in Equations (3)–(5) [33].

$$E_{Nernst}=-0.85(T_{fc}-298.15)/1000+4.3085/{10}^5\times T_{fc}ln(P_{H_2}\sqrt{P_{O_2}})+1.229$$

(2)

$$v_{act}=-\left[{\xi }_1+T_{fc}({\xi }_2+{\xi }_{3}ln(C_{O_2})+{\xi }_{4}ln(I_{fc}))\right]$$

(3)

where

$$C_{O_2}={\displaystyle \frac{P_{O_2}}{5.08\times {10}^6}}.exp({\displaystyle \frac{498}{T_{fc}}})$$

(4)

$$v_{\Omega }=I_{fc}(R_m+R_c);R_m={\rho }_{m}l/M_A$$

(5)

where

$${\rho }_m={\displaystyle \frac{181.6\left[1+0.03I_{fc}/M_A+0.062{\left(T_{fc}/303\right)}^2{\left(I_{fc}/M_A\right)}^{2.5}\right]}{\left[\lambda -0.634-3I_{fc}/M_A\right].exp\left[4.18\times \left((T_{fc}-303)/T_{fc}\right)\right]}}$$

(6)

$$v_{conc}=-\beta .ln\left(1-J/J_{max}\right)$$

(7)

where $P_{O2}$ and $P_{H2}$ illustrate the regulating pressures of oxygen (O₂) (atm) and hydrogen (H₂), respectively, while $T_{fc}$ represents the working temperature of the FC (K). Moreover, $C_{O2}$ manifests the concentration of O₂ (mol/cm³), M_A signifies the membrane area (cm), whereas $I_{fc}$ is the operating current (A) and ξ₁ − ξ₄ characterize semi-empirical coefficients [34,35]. In addition, l is the membrane thickness (cm), while R_c and R_m reveal the leads and the membrane ohmic resistances (Ω), respectively. In addition to this, ${\rho }_m$ demonstrates the membrane resistivity (Ω·cm), β is bounded within an empirical range, and λ is treated as a changeable parameter, while J_max and J describe the maximum and actual thermal current densities (A/cm²), respectively [11,34].

$$\beta =\wp .T_{fc}/2\alpha F$$

(8)

where F, $\wp$, and α represent Faraday’s ideal gas constants and the charge transfer coefficient, respectively. A deep look into (6) and (7) reveals that the concentration voltage drop can be replaced with the actual current density and temperature in a linear relationship.

Concentration polarization voltage is predicted to rise with higher current densities and higher cell temperatures [29,31]. To create an appropriate representation of the PEMFC, seven parameters are typically estimated.

The PEMFC’s considerable nonlinear properties and many unknown parameters make precise modeling difficult owing to a lack of manufacturing details. For the model to be accurate, seven crucial parameters must be determined. The summation of the squared error (SSE) that exists between the computed and experimental PEMFC voltages constitutes the model’s figure of significance. This definition frames the parameter estimation as a non-convex optimization problem that depends on SSE minimization as the objective function (FCF), as written in Equation (9) [11,36].

$$FCF=Min(SSE)=Min\left({\displaystyle \sum _{k=1}^{N_{samples}}{\left[V_{FC}^{Exp}(k)-V_{FC}^{Est}(k)\right]}^2}\right)$$

(9)

Therefore, the seven undetermined parameters (λ, ξ₁ − ξ₄, R_c, and β) are optimized using the proposed MSO to achieve the optimal SSE value.

3. MSO for Extraction of PEMFC Parameters

MSO optimizes a target objective function by simulating the trajectory of mirage light rays. The superior mirage strategy and the inferior mirage strategy are two techniques used to update the location of each search agent, which is a possible solution in the search space. These two tactics guide the search process toward the global optimum.

3.1. Step 1: Initialization

Every search agent Zy_i (a potential solution) is started arbitrarily while staying inside the limits of the design parameters:

$$Z{y}_i=\left[Z{y}_{i1},Z{y}_{i2},............,Z{y}_{id}\right]; Z{y}_{id}\in \left[L{L}_d,H{L}_d\right]$$

(10)

where i = 1, 2, …; N_x represents the index of the agent; LL_d and HL_d are the lowest and highest limits of dimension d; and d stands for the number of variables.

$$Z{y}_i=L{L}_i+R_1\times \left(H{L}_i-L{L}_i\right); i=1:N_y$$

(11)

where N_y designates the population size, while R₁ is a random number.

The objective function M_i is assessed for every search agent in the manner described below:

$$M_i=f\left(Z{y}_i\right); i=1:N_y$$

(12)

The solution vector linked to the lowest fitness score is then extracted, and the best solution is saved.

$$Z{y}_{Best}= arg\underset{Z{y}_i}{min} \left(f\left(Z{y}_i\right)\right)$$

(13)

where Zy_Best stands for the best solution discovered.

3.2. Step 2: Superior Mirage Strategy (SMS)

A subgroup of agents employs this stage, which is referred to as global exploration, to investigate distant regions early in the optimization process. First, the following formula is used to determine the number of agents (n_SMS) employing this strategy:

$$n_{SMS}=N_y\times \left(1-{\displaystyle \frac{IT}{I{T}_{mx}}}\right)$$

(14)

where the current and maximum iterations are IT and ITmx. In addition, fewer agents conduct international investigations as IT iterations increase.

Next, the fitness-based influence factor is calculated as follows:

$${\sigma }_i ={ R}_2\times \left({\displaystyle \frac{M_i-M_{Best}}{M_{Best}+\epsilon }}\right)$$

(15)

where ε is a tiny constant designed to prevent division by zero and is set to 10⁻⁸, while R₂ represents an arbitrary number.

Consequently, the following is an update to the agent’s location:

$$Zy\_Ne{w}_i=Z{y}_{Best}+R_3\times {\sigma }_i\times \left(Z{y}_i-Z{y}_{Best}\right)+R_4\times {\sigma }_i\times R_1; i=1:n_{SMS}$$

(16)

where R₁ is a vector of regularly distributed random variables, while R₃ and R₄ represent arbitrary numbers with a uniform distribution. This formula mimics agents recognizing distant optima and leaping in their direction.

3.3. Step 3: Inferior Mirage Strategy

This step is an example of local exploitation, as the surviving agents develop solutions in close proximity to potential locations. The fitness-based influence factor for this goal is calculated using the following method:

$${\theta }_i=R_5\times \left(1-{\displaystyle \frac{M_i}{{\displaystyle \sum _{i=1}^{N_y}{M}_i+\epsilon }}}\right)$$

(17)

where R₅ stands for a random number in this case. Agents who are more fit are encouraged to move more accurately by this aspect. Therefore, the following is an update to the agent’s position:

$$Zy\_Ne{w}_i=Z{y}_i+R_6\times {\theta }_i\times \left(Z{y}_{Best}-Z{y}_i\right)-R_7\times ‖Z{y}_i-Z{y}_{Best}‖\times R_2; i=n_{SMS}+1:N_y$$

(18)

where R₂ represents a vector of regularly distributed random variables, while R₆ and R₇ are random numbers with a uniform distribution.

This update permits some local heterogeneity while guiding individuals in the direction of the optimal solution.

3.4. Step 4: Boundary Control

The variables being controlled are guaranteed to remain within the following boundaries following updates:

$$Zy\_Ne{w}_i=min\left(max\left(Zy\_Ne{w}_i,L{L}_i\right),H{L}_i\right)$$

(19)

This preserves all elements within a legitimate domain.

Each agent (i)’s objective function M_New_i is assessed for the new search agent (Zy_New_i) in the manner described below.

$$M\_Ne{w}_i=f\left(Zy\_Ne{w}_i\right); i=1:N_y$$

(20)

This choice can be modified as follows if the new fitness level surpasses the previous one:

$$Z{y}_i=\left\{\begin{array}{c}Zy\_Ne{w}_i\\ Z{y}_i\end{array}\right. \begin{array}{c}if M\_Ne{w}_i\le M_i\\ Otherwise\end{array}; i=1:N_y$$

(21)

Additionally, if needed, the global best is updated.

$$Z{y}_{Best}=\left\{\begin{array}{c}Zy\_Ne{w}_i\\ Z{y}_{Best}\end{array}\right. \begin{array}{c}if M\_Ne{w}_i\le M_{Best}\\ Otherwise\end{array}; i=1:N_y$$

(22)

Until the maximum number of iterations is reached, steps 2–4 are repeated in the MSO. The best possible solution (Zy_Best) and its matching objective value (M_Best) will be provided at the final stage of the optimization.

Thus, the main steps for identifying the undetermined parameters of the FC in the proposed MSO are shown in Figure 1.

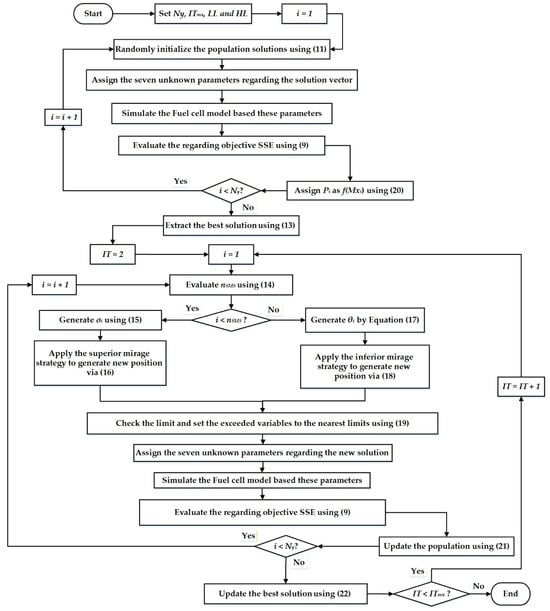
Figure 1. Flowchart of the developed MSO.

The proportion of individuals participating in the superior mirage strategy is gradually reduced as iterations progress, allowing extensive exploration in the early stages and more stable exploitation in later stages. Empirical observations show that higher early participation improves convergence speed by promoting diversity, while reduced participation near convergence limits oscillations and enhances solution stability. The smooth convergence curves and low standard deviation of the final solutions across repeated runs confirm that the adopted proportional variation achieves a robust balance between convergence acceleration and stability.

4. Simulation Results

Three cases of typical commercial PEMFC stacks, namely the Ballard Mark V 5 kW, BCS 500 W, and Modular SR-12 PEM generators, are illustrated in this study to manifest the performance of the proposed MSO to obtain parameter extraction of FCs. Table 1 presents the datasheet of the various FCs. Meanwhile, Table 2 tabulates the upper and lower boundaries of the seven unknown parameters. These bounds are primarily derived from empirical ranges and physical constraints documented in the PEMFC literature, reflecting realistic operating conditions and material properties of the fuel cell stack. In addition, the selected limits also contribute to numerical stability during the optimization process by preventing non-physical or ill-conditioned solutions. This clarification has now been explicitly stated in the text accompanying Table 1 to improve transparency and reproducibility.

Table 1. The datasheet of the various FCs.

Stack Type	Technical Specifications
	Ballard Mark V	Modular SR-12	BCS 500 W
N	35	48	32
L (µm)	178	25	178
Am (cm2)	50.6	62.5	64.0
Jm (A/cm2)	1.500	0.672	0.469
Tc (K)	343	323	333
PH2 (atm)	1.500	1.47628	1
PO2 (atm)	1.000	0.20950	0.2095

Table 2. The upper and lower boundaries of the seven unknown parameters.

Stack Type	Practical Boundaries
	Parameter	Min	Max
N	ξ1 (V)	−1.1997	−0.85320
L (µm)	ξ2 × 10−3 (V/K)	1	5
Am (cm2)	ξ3 × 10−5 (V/K)	3.6	9.8
Jm (A/cm2)	ξ4 × 10−5 (V/K)	−26.00	−9.54
Tc (K)	λ	10	23
PH2 (atm)	Rc (mΩ)	0.1	0.8
PO2 (atm)	β (V)	0.0136	0.5000

The fitness function under a set of realistic constraints is defined as SSE. The population sizes for MSO, ECO, BTO, FGO, and NMRO are each set to 30. The high randomness of the metaheuristics is widely recognized. To verify the accuracy, as determined by the following metrics—mean absolute error (MAE), root mean square error (RMSE), and standard deviation (STD—the minimum SSE results shown are obtained over 55 independent executions.

4.1. BCS 500 W PEMFC Stacks

This stack comprises 32 cells, with a maximum current density of 0.469 A/cm² and a rated power of 500 W [37]. As shown in Table 3, the MSO identifies the stack parameters that yield the optimal performance for this PEMFC model. To illustrate, the MSO achieved a small value of SSE of 1.16978 × 10⁻², which is lower than the ECO, BTO, FGO, and NMRO, with SSE values of 1.170530 × 10⁻², 1.17282 × 10⁻², 1.24770 × 10⁻², and 1.31393 × 10⁻², respectively. Additionally, other newly reported techniques are compared with the MSO to illustrate the robustness of the proposed MSO. The newly reported techniques are the shuffled frog-leaping algorithm (SFLA) [34], the grasshopper optimization algorithm (GOA) [16], an improved algorithm based on the heap-based optimizer IHBO [38], the firefly optimization algorithm (FOA) [34], the imperialist competitive algorithm (ICA) [34], Harris hawks’ optimization (HHO) [39], atom search optimization (ASO) techniques [39], the ant lion optimizer (ALO) [16], the whale optimization algorithm (WOA) [6], the moth-fame optimizer (MFO) [40], the multi-verse optimizer (MVO) [16], the salp swarm optimizer (SSO) [36], the equilibrium optimizer (EO) [38], the sine tree-seed algorithm (STSA) [38], the salp swarm algorithm (SSA) [41], the fractional-order modified Harris hawks optimizer (FMHHO) [42], the modified Harris hawks optimizer (MHHO) [42], the Harris hawks optimizer (HHO) [42], the vortex search algorithm and differential evolution (VSDE) [43], the vortex search algorithm (VSA) [43], and the manta rays foraging optimizer (MRFO) [38]. It can be observed that the MSO outperforms the reported and newly developed techniques in terms of SSE.

Table 3. Parameters extracted using the proposed MSO and compared with those extracted using the reported optimizers for the BCS500W Stack.

Technique	ξ1 (V)	ξ2 × 10−4 (V/K)	ξ3 × 10−5 (V/K)	ξ4 × 10−4 (V/K)	λ	Rc (mΩ)	β (V) × 10−2	SSE × 10−2
MSO	−0.97461791	31.7728	7.68423	−1.93017	20.87724613	0.100000	1.61261	1.16978
ECO	−1.15534264	38.4415	8.48408	−1.92719	23	0.293825	1.62159	1.17053
BTO	−1.08176091	31.1646	5.21882	−1.91813	21.34146173	0.239338	1.55964	1.17282
FGO	−1.0805842	32.6963	6.22000	−1.92747	20.42544107	0.132973	1.56188	1.24770
NMRO	−0.93838167	32.0303	8.53462	−1.76738	15.9389584	0.578885	1.36521	1.31393
IHBO [38]	−1.19970	33.100	4.2000	−1.9300	20.877	0.100	1.613	1.170
HHO [42]	−0.96053	33.505	8.7377	−1.8967	21.821	0.42358	1.5006	1.5753
MFO [40]	−1.0079	33.230	7.9800	−1.9000	20.9189	0.154	1.58	1.190
MRFO [38]	−1.11262	30.600	4.2300	−1.9500	21.705	0.111	1.718	3.683
SFLA [34]	−0.965740	34.760	7.7883354	−0.9540000	15.03229	0.162	1.3600	1.1697
SSO [36]	−0.9719	33.487	7.9111	−0.95435	13.0000	0.10000	5.34	1.219
VSA [43]	−1.0005	3.0053	5.8273	−1.9498	22.322	0.2161	1.58	1.570
STSA [38]	−0.85320	21.800	3.8300	−1.9100	18.062	0.100	1.383	2.135
ASO [39]	−1.0432	36.745	8.8772	1.8775	23.3295	0.581379	1.6495	2.661
EO [38]	−1.09072	33.300	6.4200	−1.9100	22.177	0.267	1.649	1.462
FOA [34]	−1.035664	29.502	3.7669451	−0.9540000	15.029691	0.1622	1.3600	1.1819
ALO [16]	−1.1880	36.840	6.8200	−1.9000	22.5552	0.290	1.60	1.190
GOA [16]	−0.8550	30.320	9.0600	−1.9000	21.0423	0.319	1.46	1.710
ICA [34]	−1.034322	33.202	6.4420795	−0.9540000	15.09701	0.165	1.3600	1.1856
WOA [6]	−1.19693	31.800	3.6000	−1.7700	22.974	0.100	2.216	37.273
MVO [16]	−1.1396	31.910	4.5800	−1.9000	20.5547	0.410	1.41	2.130
SSA [41]	−1.0074	33.470	8.1500	−1.9000	18.9165	0.121	1.50	1.610
FMHHO [42]	−0.87884	30.236	8.2272	−1.1934	22.709	0.40472	1.5289	1.1770
MHHO [42]	−0.91048	30.661	7.9053	−1.9098	19.384	0.10320	1.5212	1.3511
HHO [39]	−1.09311	32.8141	5.67397	−1.89666	20.0436	0.225793	151.48	1.4879
VSDE [43]	−1.1970	42.330	9.7990	−1.9201	20.194	0.1108	1.57	1.214

A statistical comparison of diverse techniques is presented in Table 4 to evaluate the performance of the proposed MSO. Table 4 presents a comparison of the performance of the proposed MSO against a variety of state-of-the-art optimizers for estimating the parameters of the BCS500W fuel cell stack. The techniques are AEO [44], GOA [16], IHBO [38], FOA [34], HHO [39], ASO [39], ALO [16], WOA [6], MFO [40], MVO [16], SSO [36], EO [38], STSA [38], MRFO [38], SSA [41], FMHHO [42], MHHO [42], and HHO [42]. The comparison is based on four key statistical indicators: the best, mean, worst, and standard deviation (STD) values of the objective function over multiple independent runs. The results clearly demonstrate that MSO achieves one of the lowest SSE values (1.16978 × 10⁻²), which is equal to or superior to those of AEO, SCE, ELBA, and SMS. Furthermore, MSO exhibits a very small variation across runs, with a STD of 1.29501 × 10⁻⁵, indicating strong convergence stability and high robustness. In contrast, several well-known methods, such as WOA, MRFO, MHHO, and GOA, show significantly higher worst-case errors and large standard deviations, reflecting performance instability and sensitivity to initial conditions. Additionally, methods such as ECO, FGO, and NMRO exhibit large mean and worst values, suggesting weaker exploitation capability and slower convergence. Overall, the results confirm that MSO provides a well-balanced exploration–exploitation trade-off, achieves high solution precision, and maintains consistent reliability, outperforming most competing techniques in both accuracy and stability for the BCS500W stack modeling problem.

Table 4. Statistical analysis between the proposed MSO and the reported optimizers for the BCS500W Stack.

Technique	Best (× 10−2)	Mean (×10−2)	Worst (×10−2)	STD
MSO	1.16978	1.17008	1.17763	1.29501 × 10−5
DCS	1.16980	1.17030	1.18071	1.55897 × 10−5
ECO	1.17053	1.93494	3.19384	5.86024 × 10−3
FGO	1.24770	1.59397	2.43486	2.36582 × 10−3
NMRO	1.31393	12.9488	62.3830	1.32501 × 10−1
BTO	1.17282	1.19227	1.28847	2.28992 × 10−2
ALO [16]	1.19	20.60	60.52	0.1880
FOA [34]	1.1819	-	-	-
MFO [40]	1.19	4.78	13.51	0.0434
AEO [44]	1.16978	1.170103	1.1791996	1.6902 × 10−5
SSO [36]	1.219	-	2.25060	2.03 × 10−2
WOA [6]	37.273	256.370	851.732	2.55770
ASO [39]	2.661	-	-	-
FMHHO [42]	1.770	37.371	13.498	0.13008
EO [38]	1.462	4.646	13.414	0.03633
MHHO [42]	1.3511	24.067	55.450	0.15958
MRFO [38]	3.683	39.107	113.428	0.25386
HHO [39]	1.4879	-	-	-
GOA [16]	1.71	43.8549	221.0571	67.4693
IHBO [38]	1.170	1.174	1.185	6 × 10−5
MVO [16]	2.13	5.25	13.56	0.1565
SSA [41]	1.61	16.23	47.80	0.1565
STSA [38]	2.135	62.114	340.177	0.70331
HHO [42]	1.5753	28.200	42.233	0.13165

For the BCS-500 W fuel cell case study, non-parametric statistical analysis, including the Wilcoxon rank-sum test, Friedman test, and Cliff’s delta effect size analysis, were applied, as shown in Table 5, Table 6 and Table 7. The Wilcoxon rank-sum test yielded extremely small p-values (p ≪ 0.05) for all pairwise comparisons between MSO and BTO, ECO, NMRO, and FGO, even after Bonferroni adjustment. The Friedman test also revealed a highly significant overall difference among the algorithms (p = 5.264 × 10⁻³⁶), with MSO consistently achieving the lowest average rank. Moreover, Cliff’s delta analysis reported very large effect sizes (|δ| ≥ 0.991), with values approaching −1, indicating near-complete dominance of MSO. These results confirm the robustness, reliability, and decisive performance advantage of MSO for PEMFC parameter estimation.

Table 5. Wilcoxon rank-sum (pairwise) for BCS500 PEMFC.

Comparison	p-Value	Conclusion
MSO vs. BTO	3.323 × 10−21	Significant
MSO vs. ECO	2.325 × 10−21	Significant
MSO vs. NMRO	1.625 × 10−21	Significant
MSO vs. FGO	1.442 × 10−21	Significant

Table 6. Friedman test for BCS-500 W PEMFC.

Algorithm	Average Rank	Final Rank
MSO	1.00	1st
NMRO	2.10	3rd
BTO	3.35	5th
FGO	3.77	2nd
ECO	4.77	4th

Friedman test p-value: p = 5.264 × 10⁻³⁶.

Table 7. Statistical comparison results for BCS-500 W PEMFC.

Comparison	Wilcoxon p-Value	Bonferroni adj. p	Cliff’s δ	Effect
MSO vs. BTO	3.323 × 10−21	3.323 × 10−21	−0.991	Very large
MSO vs. ECO	2.325 × 10−21	2.325 × 10−21	−0.995	Very large
MSO vs. NMRO	1.625 × 10−21	1.625 × 10−21	−0.999	Very large
MSO vs. FGO	1.442 × 10−21	1.442 × 10−21	−1.000	Very large

Fifty-five independent runs were conducted with the relative optimum SSE value for the MSO, as illustrated in Figure 2. MSO outperformed the recently developed techniques ECO, BTO, FGO, and NMRO.

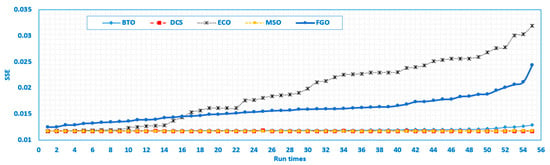
Figure 2. Fifty-five run times for the MSO and the recently developed techniques for the BCS500W Stack.

The convergence characteristics of the MSO are shown in Figure 3. As illustrated, the proposed MSO has the ability to attain the minimum SEE value of 0.011697781 in fewer than 73 iterations, outperforming ECO, BTO, FGO, and NMRO.

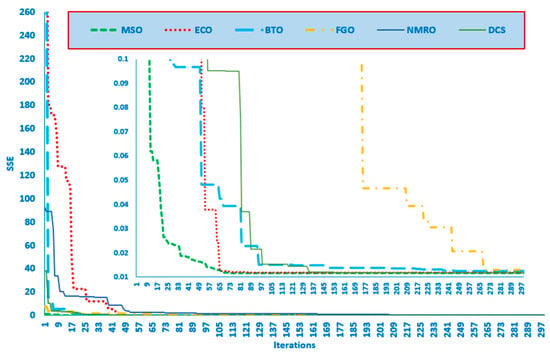
Figure 3. The convergence rate for the MSO and the recently developed techniques for the BCS500W Stack.

The comparison between the simulated and experimental performance presented in Table 8 shows strong agreement across the entire operating range. The absolute error in voltage remained very small (0.0022 to 0.0146 V), corresponding to less than 0.07% VAE, indicating an accurate reproduction of the I–V curve. Similarly, the absolute error in output power was consistently low (0.0017 to 0.2319 W), with PAE values below 0.07%. These results confirm that the proposed model effectively captures the electrical behavior of the PV module, with high precision and stability across different operating points.

Table 8. Simulated and experimental voltage and power, along with the percentage of individual absolute errors, for the BCS500W Stack.

Experimental Order	Experimental Current	Experimental Voltage	Simulated Voltage	Experimental Power	Simulated Power	% of PAE	% of VAE
1	0.6	29	28.99722328	17.4	17.398334	0.009574892	0.00957
2	2.1	26.31	26.30593705	55.251	55.2424678	0.015442595	0.01544
3	3.58	25.09	25.09355523	89.8222	89.8349277	0.014169919	0.01417
4	5.08	24.25	24.25462029	123.19	123.213471	0.019052753	0.01905
5	7.17	23.37	23.37541605	167.5629	167.601733	0.02317524	0.02318
6	9.55	22.57	22.58461499	215.5435	215.683073	0.064754055	0.06475
7	11.35	22.06	22.0713274	250.381	250.509566	0.051348133	0.05135
8	12.54	21.75	21.75846348	272.745	272.851132	0.038912573	0.03891
9	13.73	21.45	21.46126257	294.5085	294.663135	0.052506151	0.05251
10	15.73	21.09	21.08774155	331.7457	331.737175	0.010708622	0.00257
11	17.02	20.68	20.69450943	351.9736	352.22055	0.070161649	0.07016
12	19.11	20.22	20.23098603	386.4042	386.614143	0.05433247	0.05433
13	21.2	19.76	19.77094331	418.912	419.143998	0.055381144	0.05538
14	23	19.36	19.36602477	445.28	445.41857	0.031119667	0.03112
15	25.08	18.86	18.86646633	473.0088	473.170976	0.034285974	0.03429
16	27.17	18.27	18.27472059	496.3959	496.524159	0.025837953	0.02584
17	28.06	17.95	17.95331078	503.677	503.769901	0.018444462	0.01844
18	29.26	17.3	17.29287684	506.198	505.989576	0.041174346	0.04117

Figure 4 and Figure 5 show the simulated and experimental stack power points and voltage points, respectively, versus the stack current of the BCS500W Stack obtained by the MSO. Excellent fitting among the simulated and measured V/I and P/I curves of 18 of the BCS500W Stack is illustrated in Figure 4 and Figure 5, respectively. The outcomes demonstrate that the MSO-based modeling closely matches the experimental data, demonstrating the accuracy with which MSO predicts power and current across a variety of voltage ranges.

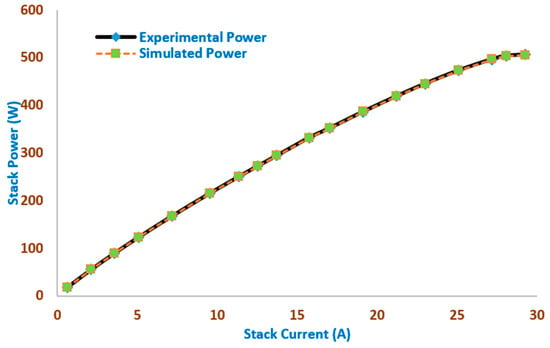
Figure 4. The simulated and experimental stack power points versus stack current of the BCS500W Stack obtained by the MSO.

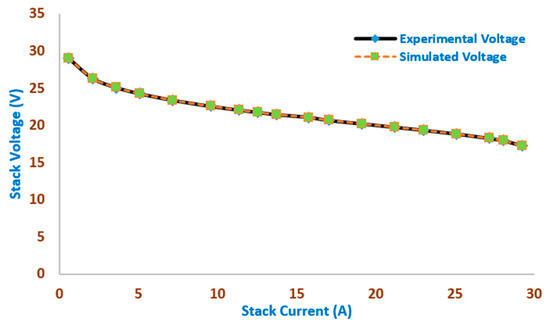
Figure 5. The simulated and experimental stack voltage points versus the stack current of the BCS500W Stack obtained by the MSO.

4.2. Modular SR-12

The parameter extraction approaches are well validated using the Modular SR-12 PEMFC [38]. It was employed to verify the effectiveness of the parameter extraction approach based on the MSO. As described in Table 9, the MSO identified the optimal parameters of the stack that achieved the best values for this PEMFC model. To illustrate, the MSO achieved a small value of SSE of 1.42100 × 10⁻⁴, which is lower than those of ECO, BTO, and FGO, which achieved SSE values of 1.57500 × 10⁻⁴, 1.48159 × 10⁻⁴, and 1.70313 × 10⁻⁴, respectively. Additionally, other newly reported techniques were compared with the MSO to illustrate its robustness. The new reported techniques are AEO [44], SSA [41], SCE [44], MFO [40], STSA [38], EO [38], and FPA [5]. The MSO outperformed the reported technique and the newly developed techniques in this paper in terms of SSE. The findings presented above validate the efficiency of the parameter extraction method of the established MSO-based PEMFC model.

Table 9. Parameters extracted using the proposed MSO and compared with those obtained using the reported optimizers for the Modular SR-12 stack.

Technique	ξ1 (V)	ξ2 × 10−4 (V/K)	ξ3 × 10−5 (V/K)	ξ4 × 10−4 (V/K)	λ	Rc (mΩ)	β (V)	SSE × 10−4
MSO	−0.95606082	27.2023	4.62884	−1.06487	17.7035381	0.205155	0.149778	1.42100
ECO	−0.85358607	22.4937	3.63539	−1.04429	12.92705598	0.317232	0.145352	1.57500
BTO	−1.03815837	33.8185	7.26394	−1.06316	18.1075043	0.227328	0.149645	1.48159
FGO	−1.08747647	34.7412	6.87967	−1.04685	16.88808673	0.278572	0.148655	2.70313
MFO [40]	−1.12876	39.5	9.13	−1.00	20.14571	0.800	0.14274	433.4
EO [38]	−1.08514	31.8	5.03	−1.06	20.39017	0.337	0.14874	12.0
ISA [45]	−1.16993	36.6	6.45	−1.07	13.92287	0.112	0.14915	1.9
WOA [6]	−1.19970	42.7	9.78	−1.08	18.83208	0.119	0.15125	20.2
STSA [38]	−0.85320	22.4	3.60	−1.06	13.0000	0.100	0.14856	8.7
SSA [41]	−1.03331	37.2	9.57	−9.58	14.30103	0.799	0.14212	968.1
MRFO [38]	−1.15570	36.5	6.62	−1.05	20.54620	0.224	0.15288	625.6
FPA [5]	−0.85320	31.0	9.15	−9.54	13.0000	0.571	0.14548	1598.2

A statistical comparison of diverse techniques to evaluate the performance of the proposed MSO is presented in Table 10. Table 10 presents the comparative performance of the proposed MSO against a variety of state-of-the-art optimizers for estimating the parameters of the BCS500W fuel cell stack. The techniques are SSA [41], FPA [5], EO [38], WOA [6], MRFO [38], STSA [38], and MFO [40]. The comparison is based on four key statistical indicators: best, mean, worst, and STD values of the objective function over multiple independent runs. The results clearly demonstrate that MSO achieves one of the lowest SSE values (1.42100 × 10⁻⁴), which is equal to or superior to those shown in Table 10. Furthermore, MSO exhibits very little variation across runs, with a STD of 1.15177 × 10⁻⁵, indicating strong convergence stability and high robustness. In contrast, several well-known methods, such as WOA, MRFO, STSA, SSA, FPA, and EO, show significantly higher worst-case errors and large standard deviations, reflecting performance instability and sensitivity to initial conditions. Additionally, methods such as ECO, FGO, and NMRO exhibit large mean and worst values, suggesting weaker exploitation capability and slower convergence. The results confirm that MSO provides a well-balanced exploration–exploitation trade-off, achieves high solution precision, and maintains consistent reliability, outperforming most competing techniques in both accuracy and stability for the BCS500W stack modeling problem.

Table 10. Statistical analysis between the proposed MSO and the reported optimizers for the Modular SR-12 stack.

Technique	Best (×10−4)	Mean (×10−4)	Worst (×10−4)	STD
MSO	1.42100	1.48367	1.93191	1.15177 × 10−5
BTO	1.48159	6.99296	32.0308	7.29238 × 10−4
ECO	1.57500	141.058	753.539	1.55999 × 10−2
FGO	2.70313	42.9074	119.151	2.89831 × 10−3
SSA [41]	968.1	1802.8	3663.0	0.08660
FPA [5]	1589.2	11575.5	51239.5	1.04838
EO [38]	12.0	195.2	739.6	0.02002
WOA [6]	20.2	33349.5	39.29097	9.85066
MRFO [38]	625.6	7872.7	40135.5	0.89801
STSA [38]	8.7	1000.2	3351.3	0.09099
MFO [40]	433.4	1321.6	3518.4	0.05970

For the SR-12 fuel cell case study, rigorous non-parametric statistical tests were conducted to validate the superiority of the proposed MSO. The Wilcoxon rank-sum test was applied as shown in Table 11, which revealed extremely small p-values (p ≪ 0.05) for all pairwise comparisons between MSO and BTO, ECO, NMRO, and FGO. Furthermore, the Friedman test was applied, as shown in Table 12, which indicates a highly significant overall difference among all algorithms (p = 4.605 × 10⁻³⁸), with MSO consistently achieving the top rank. In addition, Cliff’s delta effect size analysis was applied, as shown in Table 13, which yielded very large effect magnitudes (|δ| ≥ 0.945), with values approaching −1, indicating near-complete dominance of MSO over all competing optimizers. These findings are observed even after Bonferroni adjustment, confirming the statistically significant performance improvements. These results collectively demonstrate the robustness, reliability, and decisive superiority of the proposed MSO for PEM fuel cell parameter estimation.

Table 11. Wilcoxon rank-sum (pairwise) for SR-12 PEMFC.

Comparison	p-Value	Conclusion
MSO vs. BTO	6.55 × 10−18	Significant
MSO vs. ECO	1.36 × 10−19	Significant
MSO vs. NMRO	8.82 × 10−20	Significant
MSO vs. FGO	7.91 × 10−20	Significant

Table 12. Friedman test for SR-12 PEMFC.

Algorithm	Average Rank	Final Rank
MSO	1.00	1st
BTO	3.42	3rd
ECO	4.78	5th
NMRO	2.05	2nd
FGO	3.75	4th

Friedman test p-value: p = 4.605 × 10⁻³⁸.

Table 13. Statistical comparison results for SR-12 PEMFC.

Comparison	Wilcoxon p-Value	Bonferroni adj. p	Cliff’s δ	Effect
MSO vs. BTO	6.55 × 10−18	6.55 × 10−18	−0.945	Very large
MSO vs. ECO	1.36 × 10−19	1.36 × 10−19	−0.993	Very large
MSO vs. NMRO	8.82 × 10−20	8.82 × 10−20	−0.999	Very large
MSO vs. FGO	7.91 × 10−20	7.91 × 10−20	−1.000	Very large

Table 14 presents a detailed comparison between the experimental and simulated electrical characteristics of the SR_12 Module Stack, including voltage, power, and their corresponding percentage absolute errors. Across all 20 operating points, the simulated voltages and powers produced by the proposed model closely follow the experimental data, demonstrating the high accuracy and reliability of the modeling process. The percentage voltage absolute error (%VAE) and the percentage power absolute error (%PAE) remain extremely low—mostly below 0.01%—indicating excellent agreement between the measured and predicted values. This low level of error across the entire current range confirms the robustness of the proposed method in accurately estimating the voltage–current behavior and power output of the SR_12 stack under varying operating conditions. These results further validate the capability of the optimization algorithm to acheive precise parameter identification and high-fidelity simulation performance.

Table 14. Simulated and experimental voltage and power, along with the percentage of individual absolute errors, for the SR_12 Module Stack.

Experimental Order	Experimental Current	Experimental Voltage	Simulated Voltage	Experimental Power	Simulated Power	% of PAE	% of VAE
1	0.42	44.25	44.25037979	18.585	18.5851595	0.000858281	0.000858281
2	1.68	41.71	41.71043753	70.0728	70.073535	0.001048971	0.001048971
3	2.52	40.87	40.86838698	102.9924	102.988335	0.003946721	0.003946721
4	3.36	40.22	40.21720505	135.1392	135.129809	0.00694915	0.00694915
5	6.3	38.53	38.53346836	242.739	242.760851	0.009001715	0.009001715
6	7.14	38.13	38.13339187	272.2482	272.272418	0.008895532	0.008895532
7	10.08	36.85	36.85204741	371.448	371.468638	0.00555607	0.00555607
8	13.02	35.66	35.65522589	464.2932	464.231041	0.013387863	0.013387863
9	14.7	34.98	34.97959043	514.206	514.199979	0.001170863	0.001170863
10	17.64	33.78	33.77821961	595.8792	595.847794	0.005270543	0.005270543
11	19.32	33.07	33.06741837	638.9124	638.862523	0.007806576	0.007806576
12	20.58	32.52	32.5167898	669.2616	669.195534	0.009871455	0.009871455
13	22.68	31.55	31.55507998	715.554	715.669214	0.016101351	0.016101351
14	25.2	30.3	30.30411412	763.56	763.663676	0.013577968	0.013577968
15	27.3	29.15	29.15098678	795.795	795.821939	0.003385166	0.003385166
16	29.4	27.86	27.85860782	819.084	819.04307	0.004997074	0.004997074
17	31.5	26.37	26.37120978	830.655	830.693108	0.004587728	0.004587728
18	33.6	24.6	24.59655773	826.56	826.44434	0.013992963	0.013992963
19	35.28	22.86	22.85964874	806.5008	806.488407	0.001536579	0.001536579
20	36.96	20.66	20.66124792	763.5936	763.639723	0.00604028	0.00604028

The convergence characteristics of the MSO are denoted in Figure 6. It is illustrated that the proposed MSO is capable of attaining the minimum SSE value of 1.42100 × 10⁻⁴ in fewer than 81 iterations, compared with ECO, BTO, FGO, and DCS.

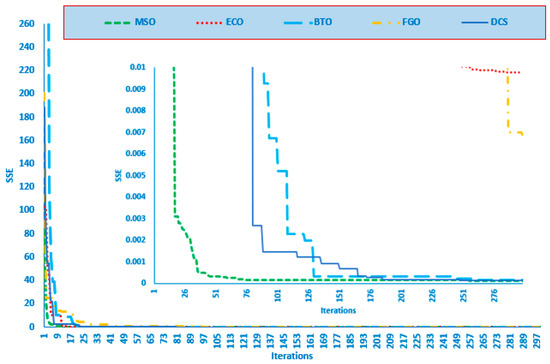
Figure 6. The convergence rate for the MSO and the recently developed techniques for the SR_12 Module Stack.

Fifty-five independent runs were conducted with the relative optimum SSE value for the MSO, as illustrated in Figure 7. As shown, the MSO outperformed the recently developed techniques, namely ECO, BTO, and FGO.

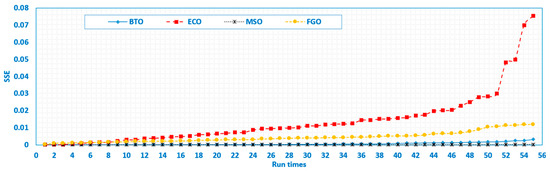
Figure 7. Fifty-five run times for the MSO and the recently developed techniques for the SR_12 Module Stack.

Figure 8 and Figure 9 represent the simulated and experimental stack power points and voltage points, respectively, versus the stack current of the SR_12 Module Stack obtained by the MSO. Excellent fitting among the simulated and measured V/I and P/I curves of 18 of the SR_12 Module Stack is illustrated in Figure 8 and Figure 9, respectively. The outcomes demonstrate that the MSO-based modeling closely matches the experimental data, demonstrating the accuracy with which MSO predicts power and current across a variety of voltage ranges.

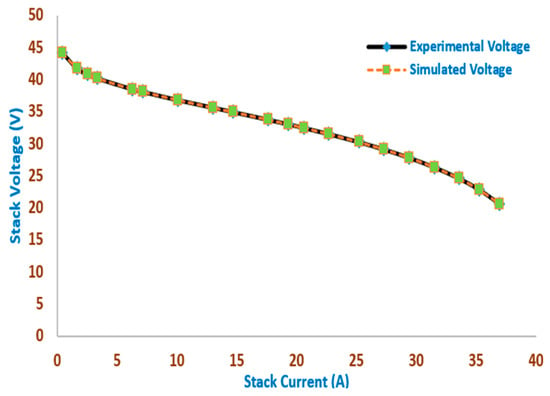
Figure 8. The simulated and experimental stack voltage points versus the stack current of the SR_12 Module Stack obtained by the MSO.

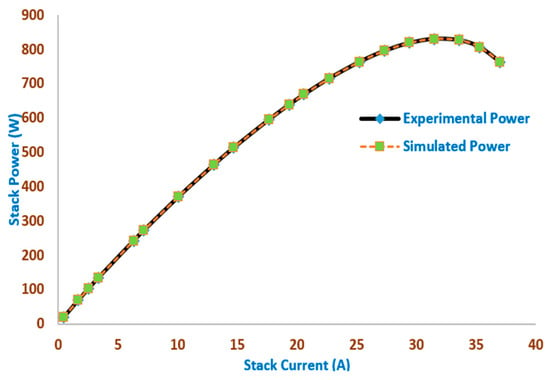
Figure 9. Simulated and experimental stack power points versus stack current for the SR_12 Module Stack obtained by MSO.

4.3. Ballard Mark V

The Ballard Mark V fuel cell system with a 5 kW rated capacity is utilized, and the datasheet for the device is gathered from Reference [14]. Table 15 displays the optimal values of the generated PEMFC model using MSO-based parameter extraction. This is employed to verify the effectiveness of the parameter extraction approach based on MSO. As described in Table 15, the MSO identifies the optimal parameters of the stack that achieve the best values for this PEMFC model. To illustrate, the MSO achieved a small value of SSE of 0.852056, which was lower than those achieved by ECO, BTO, and DCS, which were 0.852058, 0.852475, and 0.852063, respectively. Additionally, other new reported techniques were compared with the MSO to illustrate the robustness of the proposed MSO. The newly reported techniques are the artificial ecosystem-based optimizer (AEO) [44], the neural network algorithm (NNA) [22], the flower pollination algorithm FPA [5], the enhanced Levy flight bat algorithm (ELBA) [44], the whale optimization algorithm (WOA) [6], the chaotic grasshopper optimization algorithm (CGOA) [41], shuffled complex evolution (SCE) [44], GHO [39], the grass fibrous root optimization algorithm (GRA) [41], the improved chimp optimization algorithm (ICHOA1) [46], marine predators and political optimizers (MPA) [47], and the artificial bee colony differential evolution optimizer (ABCDE) [44]. The results indicate that the MSO outperformed the reported techniques and the newly developed techniques in this paper in terms of SSE. The findings presented above validate the efficiency of the parameter extraction method of the established MSO-based PEMFC model.

Table 15. Parameters extracted using the proposed MSO and compared with those obtained using the reported optimizers for the Ballard Mark V.

Technique	ξ1 (V)	ξ2 × 10−4 (V/K)	ξ3 × 10−5 (V/K)	ξ4 × 10−4 (V/K)	λ	Rc (mΩ)	β (V) × 10−2	SSE
MSO	−1.16946819	41.3826	8.31100	−1.63052	23	0.1000	1.36000	0.852056
ECO	−1.1997	35.1110	3.60344	−1.31915	22.99711376	0.5087	1.36000	0.852058
BTO	−1.16960568	39.5056	7.00851	−1.60888	22.98266713	0.10818	1.39243	0.852475
DCS	−0.87763114	33.5219	8.77050	−1.63078	22.99934736	0.100035	1.36041	0.852063
MPA [47]	−1.20000	39.0000	5.3700	−1.4400	21.755	1.0000	1.4000	1.0200
GHO [39]	−0.85320	34.1730	9.8000	−1.59555	22.8458	0.1000	1.3600	0.8710
ABCDE [44]	−1.19561	42.18852	8.34036	−1.62830	23.0000	0.1000	1.3600	0.85360751
AEO [44]	−0.85374	28.29006	5.52997	−1.62830	23.0000	0.1000	1.3600	0.85360751
NNA [22]	−0.97997	36.94600	9.0871	−1.62820	23.0000	0.1000	1.3600	0.8536
GRA [41]	−2.38000	35.80000	8.1700	−1.6620	22.0000	0.1000	1.5000	1.5900
SCE [44]	−1.05568	39.65265	9.44389	−1.62830	23.0000	0.1000	1.3600	0.85360752
WOA [6]	−1.19900	35.70000	4.2200	−1.3000	20.6690	1.1000	1.4000	1.3220
FPA [5]	−1.20000	36.30000	3.6000	−1.5100	22.6260	1.0000	1.4000	1.0690
ELBA [44]	−1.11514	41.88070	9.79741	−1.62830	23.0000	0.1000	1.3600	0.853607527
CGOA [41]	−3.14000	42.80000	6.9600	−1.8830	22.0000	0.1000	5.3000	1.8600
ICHOA1 [46]	−1.20000	40.60000	7.1200	−1.6000	23.0000	1.0000	1.4000	0.8540

A statistical comparison of diverse techniques to evaluate the performance of the proposed MSO is shown in Table 16. Table 16 presents the comparative performance of the proposed MSO against a variety of state-of-the-art optimizers for parameter estimation of the BCS500W fuel cell stack. The techniques are ABCDE [44], ICHOA1 [46], AEO [44], FPA [5], SCE [44], ELBA [44], MPA [47], and WOA [6]. The comparison is based on four key statistical indicators: best, mean, worst, and STD values of the objective function over multiple independent runs. The results clearly demonstrate that MSO achieves one of the lowest SSE values (0.852056), which is equal to or superior to those shown in Table 16. Furthermore, MSO exhibits very little variation across runs, with a STD of 6.77 × 10⁻¹⁴, indicating strong convergence stability and high robustness. In contrast, several well-known methods, such as ABCDE [44], ICHOA1 [46], AEO [44], FPA [5], SCE [44], ELBA [44], MPA [47], and WOA [6], show significantly higher worst-case errors and large standard deviations, reflecting performance instability and sensitivity to initial conditions. Additionally, methods such as ECO, DCS, and BTO exhibit large mean and worst values, suggesting weaker exploitation capability and slower convergence. To illustrate, the results confirm that MSO provides a well-balanced exploration–exploitation trade-off, achieves high solution precision, and maintains consistent reliability, outperforming most competing techniques in both accuracy and stability for the Ballard Mark V stack modeling problem.

Table 16. Statistical analysis comparing the proposed MSO with reported optimizers for the Ballard Mark V.

Technique	Best	Mean	Worst	STD
MSO	0.852056	0.852056	0.852056	6.77 × 10−14
BTO	0.852475	0.854174	0.860694	0.001657
DCS	0.852063	0.852167	0.852634	0.000134
ECO	0.852058	0.949698	1.537371	0.183117
ABCDE [44]	0.853608	0.853608	0.85360751	7.6746 × 10−15
ICHOA1 [46]	0.854	0.854	0.854	3.60 × 10−7
AEO [44]	0.853608	0.853609	0.85366619	1.0533 × 10−5
FPA [5]	1.069	2.237	4.512	0.591
SCE [44]	0.853608	0.853608	0.85360751	4.0235 × 10−15
ELBA [44]	0.853608	0.853607	0.85360754	4.9757 × 10−9
MPA [47]	1.020	2.025	4.304	0.658
WOA [6]	1.322	4.124	46.678	8.157

The convergence characteristics of the MSO are shown in Figure 10. The results illustrate that the proposed MSO achieved the minimum SEE of 0.852056 in fewer than 30 iterations, outperforming ECO, BTO, and DCS.

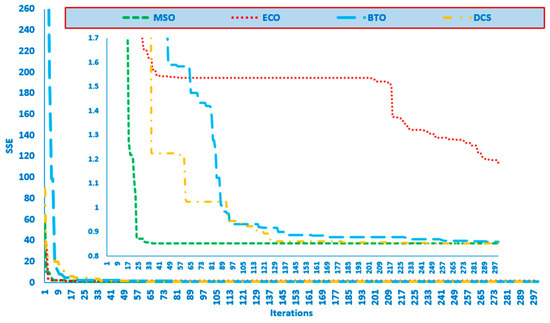
Figure 10. The convergence rate for the MSO and the recently developed techniques for the Ballard Mark V Stack.

Fifty-five independent runs were conducted with the relative optimum SSE value for the MSO, as illustrated in Figure 11. The results show that the MSO outperformed the recently developed techniques, namely ECO, BTO, and FGO.

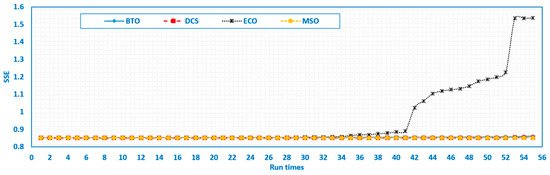
Figure 11. Fifty-five run times for the MSO and the recently developed techniques for the Ballard Mark V Stack.

Table 17 presents a detailed comparison between the experimental and simulated electrical characteristics of the Ballard Mark V Stack, including voltage, power, and their corresponding percentage absolute errors. Across all 13 operating points, the simulated voltages and powers produced by the proposed model closely follow the experimental data, demonstrating the high accuracy and reliability of the modeling process. These results further validate the capability of the optimization algorithm to acheive precise parameter identification and high-fidelity simulation performance.

Table 17. Simulated and experimental voltage and power, along with the percentage of individual absolute errors, for the Ballard Mark V Stack.

Experimental Order	Experimental Current	Experimental Voltage	Simulated Voltage	Experimental Power	Simulated Power	% of PAE	% of VAE
1	5.06	33.25	32.93924409	168.245	166.672575	0.934604251	0.934604251
2	10.626	30.8	31.06977086	327.2808	330.147385	0.875879423	0.875879423
3	16.192	29.75	29.80761669	481.712	482.644929	0.193669548	0.193669548
4	20.24	28.7	29.03785876	580.888	587.726261	1.177208238	1.177208238
5	27.83	28	27.75033506	779.24	772.291825	0.891660486	0.891660486
6	34.408	26.6	26.7081686	915.2528	918.974665	0.406648872	0.406648872
7	37.444	26.25	26.23402266	982.905	982.306744	0.060866067	0.060866067
8	43.01	25.2	25.35942629	1083.852	1090.70892	0.632643989	0.632643989
9	48.07	24.5	24.54386153	1177.715	1179.82342	0.179026645	0.179026645
10	56.166	23.8	23.85827925	1336.7508	1320.70791	0.244870792	1.2001405
11	61.226	22.05	22.21087714	1350.0333	1359.88316	0.729601532	0.729601532
12	67.298	21	20.93019085	1413.258	1408.55998	0.332424543	0.332424543
13	71.852	19.6	19.75034814	1408.2992	1419.10201	0.767082324	0.767082324

Figure 12 and Figure 13 represent the simulated and experimental stack power points and voltage points, respectively, versus the stack current of the Ballard Mark V Stack obtained by the MSO. Excellent fitting among the simulated and measured V/I and P/I curves of 13 of the SR_12 Module Stack is illustrated in Figure 12 and Figure 13, respectively. The outcomes demonstrate that the MSO-based modeling closely matches the experimental data, demonstrating the accuracy with which MSO predicts power and current across a variety of voltage ranges.

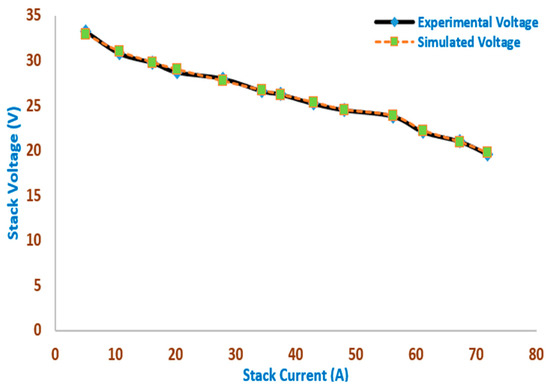
Figure 12. The simulated and experimental stack voltage points versus the stack current of the Ballard Mark V Stack obtained by the MSO.

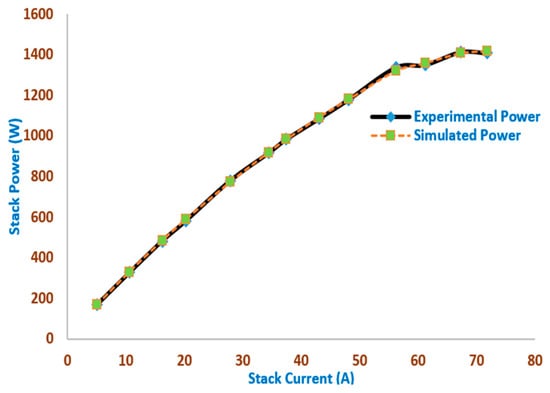
Figure 13. The simulated and experimental stack power points versus the stack current of the Ballard Mark V Stack obtained by the MSO.

5. Conclusions

In this paper, a novel MSO is proposed to effectively extract the PEMFC model’s unidentified parameters. The final objective was to create a precise PEMFC model that delivers accurate FC simulation and modeling results. This is necessary because in the manufacturer’s datasheets, there are a number of unknown parameters. The total squared error between the measured and output voltages model the FC issue that is being optimized. The fitness function is directly minimized using the MSO while adhering to the limits of the issue. By contrasting the numerical model results with the experimental findings of the three commercial PEMFC stacks under study, the suggested MSO’s effectiveness is assessed. For each case study, the simulated results match the experimental findings. Additionally, the MSO results are compared with those from other optimization techniques, demonstrating that the MSO offers a more precise assessment of the PEMFC model. This leads to the MSO-based model having a significant advantage over the other optimization method-based models in the literature.Future work can extend the application of the proposed MSO beyond PEMFC parameter identification to a wider range of power system and energy-related problems [48,49]. In particular, MSO can be employed for parameter estimation and control tuning in renewable energy systems such as photovoltaic arrays [50], wind energy conversion systems [51], batteries [52], electric vehicles [53], and hybrid microgrids, where accurate modeling is essential for reliable operation. Moreover, its strong optimization capability makes it a promising tool for solving optimal power flow [54], economic dispatch [55], unit commitment, and energy management problems [56,57] in modern power systems with high penetration of renewables and energy storage.