Weighted Approximation by Szász–Mirakyan–Durrmeyer Operators Reproducing Exponential Functions

Abstract

We examine a Szász–Mirakyan–Durrmeyer type operator that reproduces the functions 1 and $e^{2ax}$ for a fixed parameter $a>0.$ While its exponential reproduction property has been described in the classical literature, the effect of exponential weights on its approximation behavior has not been studied. In this work, we provide a detailed analysis of the operator in weighted spaces and show that combining exponential reproduction with weighted norms improves the approximation behavior for exponentially growing functions. We also prove that the corresponding sequence of operator norms remains uniformly bounded for a family of exponential weights, ensuring the stability of the operators in the weighted framework. Moreover, we establish new Korovkin-type approximation theorems involving weighted convergence and obtain sharp uniform error estimates in the presence of exponential weights. These results extend the classical theory to weighted exponential settings and highlight several quantitative features that do not arise in the classical case.

1. Introduction

The theory of approximation has long been a fundamental area of research in mathematical analysis and has provided the basis for many developments in numerical analysis and functional analysis. One of the main frameworks in this field is the use of positive linear operators, which play a central role in approximating continuous functions over both bounded and unbounded intervals.

In recent years, there has been growing interest in constructing generalized and modified forms of classical operators that preserve certain test functions or their linear combinations. Such modifications are often intended to improve approximation properties or to adapt the operators to weighted function spaces. In this direction, new types of Szász–Mirakyan operators have been introduced in the literature [1].

A significant milestone in this line of research was the contribution of King [2], who introduced a modification of the Bernstein operators that preserves quadratic test functions and inspired many subsequent studies. Similarly, Duman and Özarslan [3] proposed Szász–Mirakyan-type operators on the interval $[0,\infty )$ with improved approximation properties. Further generalizations and related results concerning Bernstein and King-type constructions were reported in [4,5,6].

Szász–Mirakyan operators and their various modifications have been extensively studied, particularly because of their ability to reproduce exponential functions. Acar et al. [7] introduced a version that preserves both the constant function and the exponential function $e^{2ax}$, obtaining corresponding approximation results. Other exponential-preserving forms were analyzed in [8,9], further extending the scope of these constructions. More recently, ref. [10] studied extended Beta-type Szász–Mirakyan operators under weighted settings, providing new insights into their approximation behavior.

However, the classical Szász–Mirakyan operators are not suitable for approximating integrable functions. To overcome this limitation, Mazhar and Totik [11] proposed an integral modification in the Durrmeyer sense, defined by

$$S_m(f;x)=m\sum _{k=0}^{\infty }{e}^{-mx}{\displaystyle \frac{{\left(mx\right)}^k}{k!}}{\int }_0^{\infty }{e}^{-mt}{\displaystyle \frac{{\left(mt\right)}^k}{k!}}f\left(t\right)dt.$$

(1)

Later studies, such as [12,13], examined related extensions, including the generalized Baskakov–Durrmeyer–Schurer and exponential-type operators on unbounded intervals.

Parallel developments have also emerged for operators based on Appell, Beta, and Gamma structures, offering different perspectives on integral and exponential modifications of Szász–Mirakyan and Durrmeyer operators.

Ayman-Mursaleen et al. [14] proposed integral forms based on Appell polynomials, while Nasiruzzaman et al. [15] introduced generalized $\alpha$–Szász–Gamma operators. These constructions show that polynomial and gamma-type modifications can improve approximation flexibility, especially on unbounded intervals.

In a related direction, ref. [16] presented results on wavelet-type Baskakov operators preserving quadratic functions, showing improved approximation behavior.

These studies show an increasing interest in exponential and integral generalizations and give a broader view of the behavior of these operators.

Following these developments, Deniz, Aral, and Gupta [17] introduced a Szász–Mirakyan–Durrmeyer-type operator that reproduces both the constant function and $e^{2ax}$ for a fixed parameter $a>0$:

$$S_m^{\ast }(f;x)=m\sum _{k=0}^{\infty }{e}^{-m{\alpha }_m\left(x\right)}{\displaystyle \frac{{\left(m{\alpha }_m\left(x\right)\right)}^k}{k!}}{\int }_0^{\infty }{e}^{-mt}{\displaystyle \frac{{\left(mt\right)}^k}{k!}}f\left(t\right)dt,m\in \mathbb{N},x\ge 0,$$

(2)

where

$${\alpha }_m\left(x\right)={\displaystyle \frac{m}{m-2a}}\left[2ax-ln\left({\displaystyle \frac{m}{m-2a}}\right)\right], m>2a.$$

(3)

Direct verification shows that

$$S_m^{\ast }(1;x)=1\mathrm{and}{S}_m^{\ast }(e^{2at};x)=e^{2ax}$$

for all $x\ge 0$ and for all $m\in \mathbb{N}.$ Throughout the paper, the notation has been harmonized to ensure consistency across the weighted and unweighted settings, and the index n used in the classical literature has been replaced by m for uniformity.

The operators $S_m^{\ast }$, designed to reproduce exponential functions, are naturally suited for analysis in exponentially weighted spaces. These operators offer computational advantages, particularly in evaluating exponential moments. Unlike the classical Szász–Mirakyan–Durrmeyer operators, which are defined in the standard unweighted setting, the present work focuses on their behavior in these weighted spaces. Such a setting allows a more realistic treatment of functions with exponential growth, which frequently arise in applications of approximation theory.

The purpose of this paper, inspired by the approach in [17], is to study the weighted approximation properties of these operators and to extend previous results by analyzing their behavior in such weighted settings. By applying a Korovkin-type theorem adapted to exponential weights, several weighted approximation results are established. Furthermore, using suitably defined moduli of continuity, we derive quantitative estimates describing the rate of uniform convergence in exponential norms.

Considering the large number of operator constructions in approximation theory, this study emphasizes the analytical significance of the proposed operator, which bridges classical and weighted frameworks by incorporating exponential reproduction.

Finally, to illustrate the theoretical results, a section is devoted to the numerical examples, where tables and graphs demonstrate the efficiency of the proposed operators in the weighted setting.

2. Auxiliary Results

In what follows, we outline several straightforward properties of the operators introduced in (2).

Lemma 1.

Regarding the operator family ${\left(S_m^{\ast }\right)}_{m\ge 1},$ we obtain the following results

$$S_m^{\ast }(1;x)=1,$$

$$\begin{array}{ccc}\hfill S_m^{\ast }(e^{at};x)& =& e^{{\displaystyle \frac{am{\alpha }_m\left(x\right)}{m-a}}}{\displaystyle \frac{m}{m-a}}\hfill \\ & =& e^{{\displaystyle \frac{m-2a}{m-a}}ax}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}},m>2a,\hfill \end{array}$$

$$S_m^{\ast }(e^{2at};x)=e^{2ax},$$

$$\begin{array}{ccc}\hfill S_m^{\ast }\left({\left(e^{at}-e^{ax}\right)}^2;x\right)& =& 2e^{2ax}-2e^{ax}{e}^{{\displaystyle \frac{m-2a}{m-a}}ax}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}\hfill \\ & =& 2e^{2ax}\left(1-e^{ax\left({\displaystyle \frac{m-2a}{m-a}}-1\right)}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}+e^{ax\left({\displaystyle \frac{m-2a}{m-a}}-1\right)}-e^{ax\left({\displaystyle \frac{m-2a}{m-a}}-1\right)}\right)\hfill \\ & =& 2e^{2ax}\left(\left(1-e^{{\displaystyle \frac{-a^2}{m-a}}x}\right)+e^{{\displaystyle \frac{-a^2}{m-a}}x}\left({\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}-1\right)\right)\hfill \\ & =& 2e^{2ax}\left(\left(1-e^{{\displaystyle \frac{-a^2}{m-a}}x}\right)+e^{{\displaystyle \frac{-a^2}{m-a}}x}\left(\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1\right)\right).\hfill \end{array}$$

(4)

Proof. 

Let $m>2a.$ Then, we have

$$\begin{array}{ccc}\hfill S_m^{\ast }(e^{at};x)& =& m\sum _{k=0}^{\infty }{e}^{-m{\alpha }_m\left(x\right)}{\displaystyle \frac{{\left(m{\alpha }_m\left(x\right)\right)}^k}{k!}}{\int }_0^{\infty }{e}^{-mt}{\displaystyle \frac{{\left(mt\right)}^k}{k!}}{e}^{at}dt\hfill \\ & =& m\sum _{k=0}^{\infty }{e}^{-m{\alpha }_m\left(x\right)}{\displaystyle \frac{{\left(m{\alpha }_m\left(x\right)\right)}^k}{k!}}{\displaystyle \frac{m^k}{k!}}{\int }_0^{\infty }{e}^{-t(m-a)}{t}^{k}dt\hfill \\ & =& {\displaystyle \frac{m}{m-a}}\sum _{k=0}^{\infty }{e}^{-m{\alpha }_m\left(x\right)}{\displaystyle \frac{{\left(m{\alpha }_m\left(x\right)\right)}^k}{k!}}{\left({\displaystyle \frac{m}{m-a}}\right)}^k\hfill \\ & =& {\displaystyle \frac{m}{m-a}}{e}^{m{\alpha }_m\left(x\right){\displaystyle \frac{a}{m-a}}}\hfill \\ & =& e^{{\displaystyle \frac{m-2a}{m-a}}ax}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}.\hfill \end{array}$$

□

Lemma 2.

For the operators ${\left(S_m^{\ast }\right)}_{m\ge 1}$ we have

$S_m^{\ast }(e_0;x)=1,$

$S_m^{\ast }(e_1;x)={\alpha }_m\left(x\right)+{\displaystyle \frac{1}{m}},$

$S_m^{\ast }(e_2;x)={\alpha }_m^2\left(x\right)+{\displaystyle \frac{4{\alpha }_m\left(x\right)}{m}}+{\displaystyle \frac{2}{m^2}}$.

Lemma 3.

By Lemma 1, the central moments ${\mu }_{m,r}^{\alpha }\left(x\right)=S_m^{\ast }({(t-x)}^r,x), r=0,1,2,$ for $m>2a$ are given by:

$$\begin{array}{ccc}\hfill {\mu }_{m,0}^{\alpha }\left(x\right)& =& 1,\hfill \\ \hfill {\mu }_{m,1}^{\alpha }\left(x\right)& =& {\alpha }_m\left(x\right)-x+{\displaystyle \frac{1}{m}},\hfill \\ \hfill {\mu }_{m,2}^{\alpha }\left(x\right)& =& {\left({\alpha }_m\left(x\right)-x\right)}^2+{\displaystyle \frac{2(2{\alpha }_m\left(x\right)-x)}{m}}+{\displaystyle \frac{2}{m^2}},\hfill \\ \hfill {\mu }_{m,4}^{\alpha }\left(x\right)& =& {\left({\alpha }_m\left(x\right)-x\right)}^4+{\displaystyle \frac{4(4{\alpha }_m^3\left(x\right)-9x{\alpha }_m^2\left(x\right)+6x^2{\alpha }_m\left(x\right)-x^3}{m}},\hfill \\ & & +{\displaystyle \frac{12(6{\alpha }_m^2\left(x\right)-6x{\alpha }_m\left(x\right)+x^2}{m^2}}+{\displaystyle \frac{24(4{\alpha }_m\left(x\right)-x)}{m^3}}+{\displaystyle \frac{24}{m^4}}.\hfill \end{array}$$

The following limits hold.

$$\underset{m\to \infty }{lim}m\left({\alpha }_m\left(x\right)-x+{\displaystyle \frac{1}{m}}\right)=-2ax$$

and

$$\underset{m\to \infty }{lim}m\left({\left({\alpha }_m\left(x\right)-x\right)}^2+{\displaystyle \frac{2(2{\alpha }_m\left(x\right)-x)}{m}}+{\displaystyle \frac{2}{m^2}}\right)=2x$$

$$\underset{m\to \infty }{lim}{m}^2{\mu }_{m,4}^{\alpha }\left(x\right)=12x^2.$$

3. Weighted Approximation

To analyze the behavior of the modified Szász–Mirakyan–Durrmeyer operators in exponential weighted spaces, we first recall some basic notions related to weighted approximation and operator norms. These concepts clarify how the operators act on functions with exponential growth and provide the foundation for establishing convergence results in the weighted setting.

In this section, we construct a framework for weighted approximation using exponential weight functions and derive direct approximation theorems of Korovkin type. We focus on the exponential weighted spaces $C_{{\rho }_a}$ and $B_{{\rho }_a}$, examine the boundedness of the associated operators, and prove convergence theorems that describe their asymptotic behavior as $m\to \infty .$

Assume that for $k=1,2$ the functions ${\rho }_k$ are continuous on $\mathbb{R}$ and satisfy ${\rho }_k\ge 1,$ with the additional property that they are unbounded. Define $B_{{\rho }_k}:=\left\{f:\left|f\left(x\right)\right|\le M_f{\rho }_k\left(x\right), x\in I\right\},$ where I is an unbounded interval. Also, let $C_{{\rho }_k}=\left\{f:f\in B_{{\rho }_k}, f\mathrm{continuous}\right\}$ denote the corresponding spaces of continuous functions defined on $I.$ The space $B_{{\rho }_k}$ is referred to as a weighted space, and with the ${\rho }_k$-norm it becomes a Banach space.

$${∥f∥}_{{\rho }_k}=\underset{x\in I}{sup}{\displaystyle \frac{\left|f\left(x\right)\right|}{{\rho }_k\left(x\right)}}.$$

A positive linear operator L acting on the space $C_{{\rho }_1}$ is said to map this space into $B_{{\rho }_2}$ whenever the function $L{\rho }_1$ belongs the $B_{{\rho }_2}.$$L{\rho }_1\in B_{{\rho }_2}.$

1.

Consider a positive linear operator $L:C_{{\rho }_1}\left(\mathbb{R}\right)\to B_{{\rho }_2}\left(\mathbb{R}\right)$. In this situation, its operator norm can be expressed as

$${∥L∥}_{C_{{\rho }_1}\to B_{{\rho }_2}}={∥L{\rho }_1∥}_{{\rho }_2}.$$

2.

Let ${\left\{A_n\right\}}_{n\in \mathbb{N}}$ be a sequence of positive linear operators $A_n:C_{{\rho }_1}\left(\mathbb{R}\right)\to B_{{\rho }_2}\left(\mathbb{R}\right)$. Assume that there exists a constant $M>0$ such that, ${\rho }_1\left(x\right)\le M{\rho }_2\left(x\right)$ for all $x\in \mathbb{R}$. If, in addition, the condition

$$\underset{n\to \infty }{lim}{∥A_n\left({\rho }_1\right)-{\rho }_1∥}_{{\rho }_2}=0$$

is satisfied, then the operator norms ${∥A_n∥}_{C_{{\rho }_1}\to B_{{\rho }_2}}$ form a uniformly bounded sequence.

Theorem 1.

Assume that ${lim}_{x\to \infty }{\displaystyle \frac{{\rho }_1\left(x\right)}{{\rho }_2\left(x\right)}}=0$. Let $\left\{A_n\right\}$ be a family of positive linear operators acting between the spaces

$$A_n:C_{{\rho }_1}\left(\mathbb{R}\right)\to B_{{\rho }_2}\left(\mathbb{R}\right).$$

Moreover, these operators satisfy

$$\underset{n\to \infty }{lim}{∥A_n\left({\rho }_1^{\upsilon }\right)-{\rho }_1^{\upsilon }∥}_{{\rho }_2}=0,$$

for $\upsilon =0,1,2$. Under these assumptions,

$$\underset{n\to \infty }{lim}{∥A_n\left(f\right)-f∥}_{{\rho }_2}=0$$

holds for every $f\in C_{{\rho }_1}$ (see [18]).

It should be noted that the findings presented in Theorem 1 concerning operators that preserve exponential functions were obtained under the framework of a single weight function. In contrast, the goal of this section is to formulate a direct approximation theorem within a weighted setting, complemented by a weighted variant of the Korovkin-type result. The statements established here pertain to exponential weighted function spaces equipped with different types of weight functions. More precisely, we focus on the exponential weighted space $B_{{\rho }_a}$ where $a>0$ is fixed. This space consists of all real-valued functions on ${\mathbb{R}}^{+}$ that satisfy $\left|f\left(x\right)\right|\le M_f{\rho }_a\left(x\right),$ for some positive constant $M_f$, with the weight given by ${\rho }_a\left(x\right)=e^{ax}$. We also denote by $C_{{\rho }_a}$ the collection of continuous functions belonging to $B_{{\rho }_a}.$ When endowed with the norm

$${∥f∥}_{{\rho }_a}=\underset{x\in {\mathbb{R}}^{+}}{sup}{\displaystyle \frac{\left|f\left(x\right)\right|}{{\rho }_a\left(x\right)}},$$

this space becomes a normed linear space.

Let $C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right)$ denote the class of functions $f\in C_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$ for which ${lim}_{x\to \infty }{\displaystyle \frac{f\left(x\right)}{{\rho }_a\left(x\right)}}$ exists as a finite constant.

In what follows, we describe the precise assumptions ensuring that the operator family ${\left(S_m^{\ast }\right)}_{m\ge 1}$ acts from $C_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$ into $B_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$ and, moreover, does so with operator norms that remain uniformly bounded across all $m.$

Lemma 4.

Assume that $0<a<b.$ We work with the sequence of positive linear operators ${\left(S_m^{\ast }\right)}_{m\ge 1}$ which map the weighted space $C_{{\rho }_a}$ into $C_{{\rho }_b}$. Throughout our analysis, we require that their operator norms remain uniformly bounded; that is, ${∥S_m^{\ast }∥}_{C_{{\rho }_a}\to C_{{\rho }_b}}$ is controlled by a constant independent of $m.$

Proof. 

The representation given in (2) confirms that the family $\left(S_m^{\ast }\right)$ consists of positive linear operators. Moreover, we have

$$\begin{array}{ccc}\hfill {∥S_m^{\ast }\left({\rho }_a\right)∥}_{{\rho }_b}& =& \underset{x\in {\mathbb{R}}^{+}}{sup}{\displaystyle \frac{e^{\frac{m-2a}{m-a}ax}}{e^{bx}}}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}\hfill \end{array}$$

(5)

$$\begin{array}{ccc} & \le & 1,\hfill \end{array}$$

(6)

which shows that each operator $S_m^{\ast }$ indeed sends functions from $C_{{\rho }_a}$ into the space $C_{{\rho }_b}.$ In addition, for every $x\in {\mathbb{R}}^{+}$ we obtain

$${∥S_m^{\ast }\left({\rho }_a\right)-{\rho }_a∥}_{{\rho }_b}=sup{\displaystyle \frac{\left|S_m^{\ast }({\rho }_a;x)-{\rho }_a\left(x\right)\right|}{{\rho }_b\left(x\right)}}$$

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\left|S_m^{\ast }({\rho }_a;x)-{\rho }_a\left(x\right)\right|}{{\rho }_b\left(x\right)}}& =& e^{-bx}\left|e^{{\displaystyle \frac{m-2a}{m-a}}ax}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}-e^{ax}\right|\hfill \\ & \le & e^{-bx}\left|e^{ax{\displaystyle \frac{m-2a}{m-a}}}-e^{ax}\right|\hfill \\ & =& e^{(a-b)x}\left(1-e^{\left({\displaystyle \frac{m-2a}{m-a}}-1\right)ax}\right)\hfill \end{array}$$

Using the classical inequality $1-e^{-x}\le x$ for $x\ge 0$, we obtain $1-e^{-x}\le x$ for $x\ge 0,$ we get

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\left|S_m^{\ast }({\rho }_a;x)-{\rho }_a\left(x\right)\right|}{{\rho }_b\left(x\right)}}& \le & e^{(a-b)x}\left(1-{\displaystyle \frac{m-2a}{m-a}}\right)ax\hfill \\ & =& {\displaystyle \frac{ax}{e^{(b-a)x}}}\left(1-{\displaystyle \frac{m-2a}{m-a}}\right).\hfill \end{array}$$

Function $f\left(x\right)$ attains its maximum value at $x={\displaystyle \frac{1}{b-a}}$. Thus,

$$\begin{array}{ccc}\hfill {∥S_m^{\ast }\left({\rho }_a\right)-{\rho }_a∥}_{{\rho }_b}& =& \underset{x\in {\mathbb{R}}^{+}}{sup}{e}^{-bx}\left|e^{ax}{\displaystyle \frac{m-2a}{m-a}}-e^{ax}\right|\hfill \end{array}$$

(7)

$$\begin{array}{ccc} & \le & {\displaystyle \frac{a}{(b-a)e}}\left(1-{\displaystyle \frac{m-2a}{m-a}}\right).\hfill \end{array}$$

(8)

□

Remark 1.

The boundedness of the operator norms holds under the natural parameter restrictions $m>2a>0$ and $0<a<b$. These assumptions, together with sufficiently large values of m guarantee that

$${\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}<1,$$

which ensures that the supremum in the definition of the operator norm remains finite. If these conditions are not satisfied (for instance, when $b\le a$), the exponential term does not decay and the norm may become unbounded. Hence, these restrictions together with taking m sufficiently large are essential for the validity of the uniform boundedness result.

Theorem 2.

Assume that $0<a<b.$ For every function $f\in C_{{\rho }_a}\left({\mathbb{R}}^{+}\right),$ we obtain

$$\underset{m\to \infty }{lim}{∥S_m^{\ast }\left(f\right)-f∥}_{{\rho }_b}=0.$$

Proof. 

We make use of the general result stated in Theorem 1. In line with this theorem, we now verify that the operator meets the necessary requirements. Specifically, we show that

$$\underset{m\to \infty }{lim}{∥S_m^{\ast }\left({\rho }_a^{\lambda }\right)-{\rho }_a^{\lambda }∥}_{{\rho }_b}=0,\lambda =0,1,2.$$

For $\lambda =0$ and $\lambda =2,$ this conclusion follows directly from Lemma 1. When $\lambda =1,$ the desired convergence is guaranteed by the relation established in (8). □

Remark 2.

This theorem demonstrates that the sequence of modified Szász–Mirakyan–Durrmeyer operators $S_m^{\ast }$ provides uniform convergence in exponential weighted spaces. Hence, for every function $f\in C_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$, the operators reproduce the given function in the weighted norm ${\rho }_b$ as $m\to \infty .$ This result confirms the validity of the operators in the exponential framework and forms a basic step for the subsequent quantitative estimates. Moreover, this theorem not only establishes the convergence of the operator defined between two different weighted spaces but also reveals the structural behavior of the test functions within these weighted spaces.

Corollary 1.

Let $f\in C_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$ for some $a>0.$ Under these conditions, the operators $S_m^{\ast }$ satisfy Moreover, this pointwise convergence becomes uniform when restricted to any compact interval $[x_1,x_2]$ with $0\le x_1\le x_2.$

Theorem 3.

Assume that $0<a<b.$ For each $f\in C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right)$ we obtain

$$\underset{m\to \infty }{lim}{∥S_m^{\ast }\left(f\right)-f∥}_{{\rho }_b}=0.$$

Proof. 

For each $x_0>0,$

$$\begin{array}{ccc}\hfill \underset{x\in {\mathbb{R}}^{+}}{sup}{\displaystyle \frac{\left|S_m^{\ast }(f;x)-f\left(x\right)\right|}{e^{bx}}}& \le & \underset{x\le x_0}{sup}{\displaystyle \frac{\left|S_m^{\ast }(f;x)-f\left(x\right)\right|}{e^{bx}}}+\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|S_m^{\ast }(f;x)-f\left(x\right)\right|}{e^{bx}}}\hfill \\ & \le & {∥S_m^{\ast }\left(f\right)-f∥}_{C[0,x_0]}+{∥f∥}_{{\rho }_a}\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|S_m^{\ast }(e^{at},x)\right|}{e^{bx}}}+\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|f\left(x\right)\right|}{e^{bx}}}.\hfill \end{array}$$

First expression in the inequality vanishes as $m\to \infty$, which follows directly from Corollary 1. Applying Lemma 1, we observe that for any fixed $x_0>0,$

$$\underset{x\ge x_0}{sup}{\displaystyle \frac{\left|S_m^{\ast }(e^{at},x)\right|}{e^{bx}}}\le e^{x_0\left(a-b\right)}{\displaystyle \frac{m-2a}{m-a}},$$

and the right-hand side approaches zero when m becomes large. Finally, by selecting $x_0$ sufficiently large, the remaining term in the inequality can be made arbitrarily small. □

4. Order of Convergence

Our aim in this section is to quantify the convergence stated in Theorem 1 by means of an appropriate modulus of continuity. To investigate this behavior, we introduce a weighted modulus of continuity for functions in the space $C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right),$ which plays a role similar to that of the classical modulus on compact intervals. This exponential-type modulus turns out to be an effective tool for estimating the speed of convergence of sequences of positive linear operators acting in exponentially weighted spaces.

With this motivation, we consider the weighted modulus of continuity given by

$$\varpi (f‘;\delta )=\underset{\left|t-x\right|\le \delta ,x\ge 0}{sup}{\displaystyle \frac{\left|f\left(t\right)-f\left(x\right)\right|}{e^{at}+e^{ax}}}, \delta \ge 0$$

(9)

for functions $f\in C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right).$ This construction provides a convenient mechanism for controlling the approximation error in terms of the exponential growth imposed by the weight. (See [8]).

Lemma 5.

Given $f\in C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right),$

$$\underset{\delta \to 0}{lim}\varpi (f‘;\delta )=0.$$

Lemma 6.

For any $\lambda >0$ and $C_a^k\left({\mathbb{R}}^{+}\right)$ we have

$$\varpi (f‘;\lambda \delta )\le 2(1+\lambda )\varpi (f‘;\delta ).$$

(10)

The properties derived above, we can now determine the rate at which these operators converge, as described below:

Theorem 4.

Assume that $0<2a<b.$ For $f\in C_{{\rho }_a}^k\left({\mathbb{R}}^{+}\right)$ one has

$${∥S_m^{\ast }\left(f\right)-f∥}_{{\rho }_b}\le 2\left\{2+{\displaystyle \frac{2}{a}}\right\}\varpi \left(f;{\displaystyle \frac{1}{(m-a)e}}+\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1\right)$$

(11)

Proof. 

Making use of the definition of the modulus of smoothness $\varpi \left(f;·\right)$ together with property (10) and selecting $\lambda ={\displaystyle \frac{\left|t-x\right|}{\delta }}, \delta >0,$ we obtain

$$\begin{array}{ccc}\hfill \left|f\left(t\right)-f\left(x\right)\right|& \le & \left(e^{at}+e^{ax}\right)\varpi (f‘;\left|t-x\right|)\hfill \\ & \le & 2\left(e^{at}+e^{ax}\right)\left(1+{\displaystyle \frac{\left|t-x\right|}{\delta }}\right)\varpi (f‘;\delta ).\hfill \end{array}$$

(12)

By the mean value theorem, we can write

$$\left|f\left(t\right)-f\left(x\right)\right|\le 2\left(e^{at}+e^{ax}\right)\left(1+{\displaystyle \frac{\left|e^{at}-e^{ax}\right|}{a\delta }}\right)\varpi (f‘;\delta ).$$

By the Cauchy Schwarz inequality for each $x\in {\mathbb{R}}^{+},$ one has

$$\begin{array}{ccc}\hfill \left|\left(S_m^{\ast }f\right)\left(x\right)-f\left(x\right)\right|& \le & S_m^{\ast }(\left|\left(f\right(t)-f(x)\right|;x)\hfill \\ & \le & 2\varpi (f‘;\delta )S_m^{\ast }\left(\left(e^{at}+e^{ax}\right)\left(1+{\displaystyle \frac{\left|e^{at}-e^{ax}\right|}{a\delta }}\right)\right)\left(x\right)\hfill \\ & =& 2\varpi (f‘;\delta )\left\{\left(S_m^{\ast }(e^{at};x\right)+{\displaystyle \frac{1}{a\delta }}{\left[S_m^{\ast }\left(e^{2t};x\right)\right]}^{1/2}{\left[S_m^{\ast }\left({\left(e^{at}-e^{ax}\right)}^2;x\right)\right]}^{1/2}\right.\hfill \\ & & \left.+e^{ax}\left[S_m^{\ast }\left(1;x\right)\right]+{\displaystyle \frac{e^{ax}}{a\delta }}{\left[S_m^{\ast }\left(1;x\right)\right]}^{1/2}{\left[S_m^{\ast }\left({\left(e^{at}-e^{ax}\right)}^2;x\right)\right]}^{1/2}\right\}\hfill \\ & \le & 2\varpi (f‘;\delta )\left\{\left(S_m^{\ast }(e^{at};x\right)+e^{ax}+{\displaystyle \frac{2e^{ax}}{a\delta }}{\left[S_m^{\ast }\left({\left(e^{at}-e^{ax}\right)}^2;x\right)\right]}^{1/2}\right\}\hfill \end{array}$$

and we have

$${\displaystyle \frac{\left|\left(S_m^{\ast }f\right)\left(x\right)-f\left(x\right)\right|}{e^{bx}}}\le {\displaystyle \frac{2\varpi (f‘;\delta )}{e^{\left(b-2a\right)x}}}\left\{{\displaystyle \frac{\left(S_m^{\ast }(e^{at};x\right)}{e^{2ax}}}+{\displaystyle \frac{e^{ax}}{e^{2ax}}}+{\displaystyle \frac{2}{a\delta }}{\left[{\displaystyle \frac{S_m^{\ast }\left({\left(e^{at}-e^{ax}\right)}^2;x\right)}{e^{2ax}}}\right]}^{1/2}\right\}.$$

From (4), we have

$$\begin{array}{ccc}\hfill \underset{x\in {\mathbb{R}}^{+}}{sup}{\displaystyle \frac{\left|\left(S_m^{\ast }f\right)\left(x\right)-f\left(x\right)\right|}{e^{bx}}}& \le & {\displaystyle \frac{2\varpi (f‘;\delta )}{e^{\left(b-2a\right)x}}}\left\{e^{\left({\displaystyle \frac{m-2a}{m-a}}-2\right)ax}{\displaystyle \frac{m}{m-a}}\sqrt{{\displaystyle \frac{m-2a}{m}}}+1\right.\hfill \\ & & \left.+{\displaystyle \frac{2}{e^{ax}a\delta }}\left[\left(1-e^{{\displaystyle \frac{-a^2}{m-a}}x}\right)+e^{{\displaystyle \frac{-a^2}{m-a}}x}\left(\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1\right)\right]\right\}\hfill \\ & \le & {\displaystyle \frac{2\varpi (f‘;\delta )}{e^{\left(b-2a\right)x}}}\left\{2+{\displaystyle \frac{2}{\delta }}\left({\displaystyle \frac{1}{\left(m-a\right)e}}+\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1\right)\right\}\hfill \end{array}$$

The best possible bound is obtained by choosing $\delta$ to minimize the right-hand side of the above inequality, balancing the terms involving ${\displaystyle \frac{1}{a\delta }}$ and the square-root expression. If we choose $\delta ={\displaystyle \frac{1}{\left(m-a\right)e}}+\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1$, we have the desired result. □

Remark 3.

This theorem gives a quantitative estimate for the rate of convergence of the modified Szász–Mirakyan–Durrmeyer operators in exponential weighted spaces. By introducing the weighted modulus of continuity, the result expresses how the approximation error depends on both the smoothness of the function and the parameter m. It thus provides a clear measure of the operators’ approximation efficiency in the exponential setting.

Example 1.

Let $f\left(x\right)=e^{-x},$ by Theorem 4, we obtain

$${∥S_m^{\ast }\left(f\right)-f∥}_{{\rho }_b}\le 2\left\{2+{\displaystyle \frac{2}{a}}\right\}\varpi \left(f;{\displaystyle \frac{1}{(m-a)e}}+\sqrt{1-{\displaystyle \frac{a^2}{{\left(m-a\right)}^2}}}-1\right).$$

5. Voronovskaya Type Theorem

Theorem 5.

Assume that $f\in C_{{\rho }_a}\left({\mathbb{R}}^{+}\right)$. If f is twice differentiable on ${\mathbb{R}}^{+}$ and $f^{″}$ is continuous at $x,$ the following limit can be established

$$\underset{m\to \infty }{lim}m\left[S_m^{\ast }(f,x)-f\left(x\right)\right]=-2ax{f}^{\prime }\left(x\right)+x{f}^{″}\left(x\right)$$

Proof. 

According to Taylor’s formula, one can find $\eta$ lying between x and t such that

$$f\left(t\right)=f\left(x\right)+f^{\prime }\left(x\right)(t-x)+{\displaystyle \frac{f^{″}\left(x\right)}{2}}{(t-x)}^2+h(t,x){(t-x)}^2,$$

where

$$h(t,x):={\displaystyle \frac{f^{″}\left(\eta \right)-f^{″}\left(x\right)}{2}}$$

and h denotes a continuous function that vanishes as $t\to x$. By applying the operator ${\left(S_m^{\ast }\right)}_{m\ge 1}$ to the above equality, we obtain

$$S_m^{\ast }(f,x)-f\left(x\right)=f^{\prime }\left(x\right){\mu }_{m,1}^{\alpha }\left(x\right)+{\displaystyle \frac{f^{″}\left(x\right)}{2}}{\mu }_{m,2}^{\alpha }\left(x\right)+S_m^{\ast }(h(t,x){(t-x)}^2,x).$$

$$m\left[S_m^{\ast }(f,x)-f\left(x\right)\right]=f^{\prime }\left(x\right)m{\mu }_{m,1}^{\alpha }\left(x\right)+{\displaystyle \frac{f^{″}\left(x\right)}{2}}m{\mu }_{m,2}^{\alpha }\left(x\right)+m{S}_m^{\ast }(h(t,x){(t-x)}^2,x).$$

(13)

A direct calculation yields

$$\underset{m\to \infty }{lim}m{\mu }_{m,1}^{\alpha }\left(x\right)=\underset{m\to \infty }{lim}m\left({\alpha }_m\left(x\right)-x+{\displaystyle \frac{1}{m}}\right)=-2ax.$$

Moreover

$$\underset{m\to \infty }{lim}m{\mu }_{m,2}^{\alpha }\left(x\right)=\underset{m\to \infty }{lim}m\left({\left({\alpha }_m\left(x\right)-x\right)}^2+{\displaystyle \frac{2(2{\alpha }_m\left(x\right)-x)}{m}}+{\displaystyle \frac{2}{m^2}}\right)=2x.$$

For the estimation of the final term in (13), for every $ϵ>0$ choose $\delta >0$ such that $\left|h(t,x)\right|<ϵ$ for $\left|t-x\right|<\delta .$ Therefore, if $\left|t-x\right|<\delta$ then $\left|h(t,x){(t-x)}^2\right|<ϵ{(t-x)}^2,$ while if $\left|t-x\right|\ge \delta ,$ then since $\left|h(t,x)\right|\le M$ we have $\left|h(t,x){(t-x)}^2\right|\le {\displaystyle \frac{M}{{\delta }^2}}{(t-x)}^4.$ So we can write

$$S_m^{\ast }\left(h(t,x){(t-x)}^2,x\right)<ϵ{\mu }_{m,2}^{\alpha }\left(x\right)+{\displaystyle \frac{M}{{\delta }^2}}{\mu }_{m,4}^{\alpha }\left(x\right),$$

and therefore

$$\underset{m\to \infty }{lim}m{S}_m^{\ast }(h(t,x){(t-x)}^2,x)=0.$$

Direct calculations show that

$${\mu }_{m,4}^{\alpha }\left(x\right)=O\left({\displaystyle \frac{1}{m^2}}\right).$$

Thus, $h(t,x)$ represents the remainder term in the Taylor expansion of f around $x.$ Since $f^{″}$ is continuous, $h(t,x)$ is also continuous and satisfies $h(t,x)\to 0$ as $t\to x.$ This property ensures that the operator $S_m^{\ast }$ applied to $h(t,x){(t-x)}^2$ vanishes in the limit, which justifies the passage to the limit and completes the proof. □

Remark 4.

This theorem presents the asymptotic behavior of the modified Szász–Mirakyan–Durrmeyer operators as $m\to \infty .$ The obtained limit formula provides a second-order approximation that relates the deviation of the operators to the first and second derivatives of the function. Hence, it characterizes how the operators approximate smooth functions in exponentially weighted spaces.

Example 1.

Let $f\left(x\right)=e^x,$ by Theorem 5, we obtain

$$\begin{array}{ccc}\hfill \underset{m\to \infty }{lim}m\left[S_m^{\ast }(f,x)-f\left(x\right)\right]& =& -2ax{f}^{\prime }\left(x\right)+x{f}^{″}\left(x\right)\hfill \\ & =& e^x(x-2ax)\hfill \end{array}$$

6. Numerical Results

This section is devoted to numerical examples which illustrate the theoretical results obtained in the previous sections. For this purpose, we use several graphs generated with the Mathematica software package. In all computations, the parameter $a={\displaystyle \frac{1}{2}}$ is fixed. We consider the test function $f\left(x\right)=x^2-e^{-2x}$, where x belongs to the interval $[0, 10]$, since the operators $S_m^{\ast }$ are defined only for non- negative values of $x.$

Figure 1 shows the graphs of the function $f\left(x\right)$ (blue line) together with its approximations $S_m^{\ast }(f;x)$ for $m=5$ (orange line), $m=10$ (green line), $m=25$ (red line), $m=50$ (purple line) and $m=100$ (brown line).

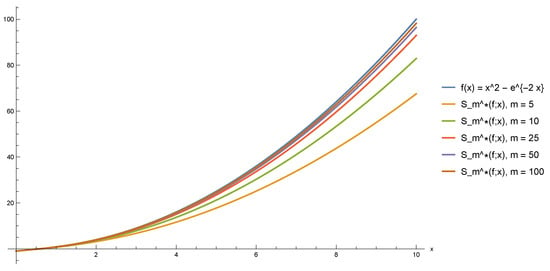
Figure 1. Approximation plot of $S_m^{\ast }(f;x)$ to $f\left(x\right)$. The graphs of $f\left(x\right)=x^2-e^{-2x}$ (blue line) and its approximations $S_m^{\ast }(f,x)$ for $m=5,10,25,50$ and 100 on the interval $[0, 10]$.

It can clearly be seen that, as m increases, the curves of $S_m^{\ast }(f;x)$ become almost indistinguishable from the graph of $f\left(x\right).$ Hence, a larger value of m provides a better approximation, confirming the convergence behavior of the operators.

Figure 2 presents the absolute errors $\left|S_m^{\ast }(f,x)-f\left(x\right)\right|$ for the same values $m=5$, $10, 25, 50$ and 100 on the interval $[0, 10].$

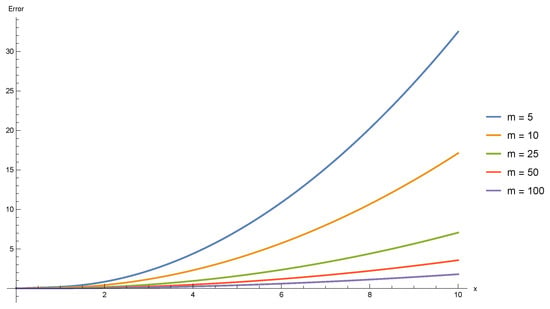
Figure 2. Approximation error plot. The absolute errors $|S_m^{\ast }(f,x)-f\left(x\right)|$ for $m=5,10,25,50$ and 100 over the interval $[0, 10]$.

As expected, the error decreases as m increases, and the operator $S_{100}^{\ast }$ shows the best approximation over the entire interval.

The decrease in error is consistent with the theoretical rate of convergence obtained from the central moments of the operators.

Finally, Table 1 presents the numerical error values $|S_m^{\ast }(f,x)-f\left(x\right)|$ at the discrete points $x=0,1,2,3,$ and 4.

Table 1. Matrix of absolute approximation errors $|S_m^{\ast }(f,x)-f\left(x\right)|$ at the discrete points $x=0,1,2,3,$ and 4 for different m values.

$\mathit{m}$∖$\mathit{x}$	0	1	2	3	4
5	0.04728	0.1952	0.8376	2.235	4.383
10	0.01505	0.09206	0.4206	1.159	2.294
25	0.002845	0.03452	0.1685	0.4744	0.9430
50	0.0007538	0.01678	0.08433	0.2390	0.4758
100	0.0001941	0.008257	0.04218	0.1200	0.2390

For each fixed x, the error decreases monotonically as m increases, once again supporting the theoretical findings on the convergence of $S_m^{\ast }.$

Overall, the numerical and graphical results are in good agreement with the analytical results derived earlier.

7. Conclusions

In this paper, we introduced a modified Szász–Mirakyan operator that reproduces the functions 1 and $e^{2ax},$ providing a more suitable framework for approximating functions with exponential growth. We examined its behavior on exponentially weighted function spaces and proved that the sequence of operator norms remains uniformly bounded, even as the weights vary with the parameter. This stability forms the basis for the operator’s reliable approximation properties. Building on these results, we established Korovkin-type theorems for exponential weighted convergence and derived explicit descriptions of the corresponding uniform approximation errors. Overall, the modified operators offer an effective and stable tool for weighted approximation under exponential growth conditions.