Neural Network-Based Adaptive Finite-Time Control for Pure-Feedback Stochastic Nonlinear Systems with Full State Constraints, Actuator Faults, and Backlash-like Hysteresis

Abstract

This paper addresses the tracking control problem for pure-feedback stochastic nonlinear systems subject to full state constraints, actuator faults, and backlash-like hysteresis. An adaptive finite-time control strategy is proposed, using radial basis function neural networks to approximate unknown system dynamics. By integrating barrier Lyapunov functions with a backstepping design, the method guarantees semi-global practical finite-time stability of all closed-loop signals. The strategy ensures that all states remain within prescribed limits while achieving accurate tracking of the reference signal in finite time. The effectiveness and superiority of the proposed approach are demonstrated through simulations, including a numerical example and a rigid robot manipulator system, with comparisons to existing methods highlighting its advantages.

1. Introduction

In practical engineering applications, stochastic disturbances are a common challenge that can significantly compromise system stability. The presence of higher-order Hessian terms in the stochastic differentiation of Lyapunov functions further increases the complexity of controller design for stochastic nonlinear systems [1,2,3,4]. Compared to deterministic nonlinear systems, this complexity makes the design of effective controllers for stochastic systems more demanding. Recently, the study of stochastic nonlinear systems has attracted considerable attention, and adaptive backstepping methods, initially developed for deterministic systems, have been extended to stochastic scenarios [5,6,7]. For example, a globally adaptive control approach has been proposed for stochastic nonlinear time-delay systems subject to disturbances, ensuring robust performance despite temporal delays and random perturbations [8]. Additionally, an adaptive output-feedback strategy based on dynamic surface control has been developed to handle stochastic nonlinear systems with unmodeled dynamics in both state and input, providing effective control even under unmodeled uncertainties [9]. Moreover, an adaptive control method using output feedback has been presented for stochastic nonlinear systems with dynamic uncertainties, guaranteeing stable and accurate tracking performance despite system uncertainties [10].

However, existing methods are primarily designed for systems in which the nonlinearities are either precisely known or can be linearly parameterized. Such approaches are often inadequate when dealing with stochastic systems that exhibit structured uncertainties. To overcome these limitations, various adaptive fuzzy or neural network-based backstepping control methods have been developed [11]. These methods combine the backstepping design with fuzzy logic systems or neural networks, thereby improving their applicability to stochastic nonlinear systems [12,13]. For example, a recent study proposed an adaptive fuzzy control technique specifically for stochastic nonlinear systems, effectively handling challenges such as dead zones and unmodeled dynamics to ensure robust system performance [14]. Additionally, an event-based dynamic output-feedback adaptive fuzzy control approach has been developed, which utilizes event-triggered mechanisms to improve control efficiency and maintain system stability in the presence of uncertainties [15]. Furthermore, for stochastic nonlinear systems with multiple time-varying delays and input saturation, an adaptive neural control strategy has been introduced, providing effective control by addressing the complications caused by time-varying delays and input saturation [16].

Despite recent advances in control theory, many practical systems, such as rolling mills, biochemical processes, and pendulum dynamics, exhibit nonlinear behaviors that do not conform to standard affine models [17]. In these systems, traditional methods that assume a linear relationship between inputs and state variables are limited, especially in pure-feedback nonlinear systems where the direct use of state variables as control signals is not feasible. This limitation has motivated significant research into methods capable of effectively controlling nonaffine pure-feedback nonlinear systems [18,19]. To address these challenges, several innovative control strategies have been proposed. For instance, event-triggered adaptive fuzzy tracking control has been developed to manage systems with multiple constraints while ensuring accurate tracking performance and system stability [20]. Neural network-based adaptive control methods have also been introduced to handle issues such as time-varying delays and dead-zone inputs in stochastic nonlinear systems, thereby improving robustness and overall performance [21]. Additionally, a fuzzy adaptive tracking control approach has been proposed for constrained nonlinear switched stochastic pure-feedback systems, using fuzzy logic to handle constraints effectively and demonstrating enhanced robustness under varying operating conditions [22]. These developments underscore the ongoing efforts to design specialized control solutions that can manage the complexities present in nonaffine pure-feedback nonlinear systems across a wide range of practical applications.

Adaptive fuzzy and neural network-based backstepping control methods have made significant progress, but they often assume ideal conditions for all system components [23]. In practice, components such as actuators, sensors, and processors may fail unexpectedly during operation [24,25]. Addressing these challenges requires the development of fault-tolerant control strategies to ensure system reliability and safety under adverse conditions. Recent studies have focused on adaptive fuzzy backstepping approaches to handle uncertainties and actuator faults in nonlinear systems [26,27]. For stochastic nonlinear systems with nonstrict-feedback dynamics and actuator faults, adaptive fuzzy tracking control methods have been proposed to maintain accurate tracking performance and ensure system stability [28]. Strategies have also been developed to manage systems with output constraints and actuator faults, aiming to achieve robust control performance despite these limitations [29]. In scenarios involving nonlinear systems affected by Markovian actuator failures and stochastic disturbances, adaptive fault-tolerant stabilization methods have been introduced, providing effective stabilization in the presence of unpredictable actuator failures and noise through adaptive techniques [30]. Furthermore, for large-scale nonlinear systems facing actuator faults and output constraints, adaptive fuzzy fault-tolerant control strategies have been designed, utilizing fuzzy logic to ensure reliable and effective control in complex operational environments [31]. These developments highlight ongoing efforts to design control methodologies capable of mitigating the impact of faults and uncertainties, thereby enhancing the reliability and performance of nonlinear systems in practical applications.

Moreover, in practical engineering applications, control performance can be significantly influenced by hysteresis, a common nonlinearity present in various devices and systems, including electronic relay circuits, military systems, and mechanical actuators [32]. Hysteresis nonlinearities can severely limit system performance, making the development of effective control strategies to address these issues an active area of research. Studying the control of nonlinear systems with hysteresis inputs is crucial for achieving high-performance standards [33,34]. For instance, an adaptive output dynamic feedback control method has been proposed for nonaffine pure-feedback time-delay systems with backlash-like hysteresis [35]. This method effectively manages the challenges posed by nonlinear dynamics and unknown hysteresis effects, ensuring robust control performance. For uncertain nonlinear systems with unknown backlash-like hysteresis, an adaptive prescribed performance tracking control strategy has been developed [36], achieving the desired tracking performance despite uncertainties and hysteresis through adaptive control techniques. Additionally, an event-triggered adaptive fuzzy control approach has been introduced for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis [37]. This method combines fuzzy logic and event-triggered mechanisms to handle uncertainties and unmeasured states effectively, providing robust control performance.

Traditional control strategies typically aim for asymptotic stability, where the closed-loop system response converges over an infinite time horizon. However, in practical applications, finite-time convergence is often a critical performance requirement [38,39,40,41]. Finite-time control offers several advantages, including rapid response, high convergence accuracy, and robust disturbance rejection, making it a highly relevant and promising area of research. Significant progress has been made in this field, demonstrating its importance and potential in practical control applications [42,43,44]. For instance, an observer-based adaptive fuzzy finite-time control design with prescribed performance has been proposed for switched pure-feedback nonlinear systems [45]. This approach integrates fuzzy logic and adaptive techniques within an observer framework to achieve finite-time control objectives with guaranteed performance. In addition, a fuzzy adaptive finite-time output-feedback control strategy has been developed for stochastic nonlinear systems [46], focusing on compensating stochastic disturbances while ensuring finite-time convergence and enhancing robustness in uncertain environments. Observer-based finite-time control methods have also been applied to stochastic nonstrict-feedback nonlinear systems [47], addressing the challenges associated with nonstrict-feedback structures and stochastic disturbances while achieving stable and robust finite-time control performance.

The control approaches discussed above often neglect the consideration of state constraints, which limits their applicability in the tracking control of nonlinear stochastic systems. In industrial control applications, ensuring compliance with safety specifications requires careful management of various state constraints. Violating these constraints can degrade system performance or even cause significant safety hazards, highlighting the critical importance of incorporating state constraints into controller design [48,49,50,51]. To address this challenge, several effective control strategies have been developed, including model predictive control, data-driven control algorithms, and enhanced prescribed performance control methods. Recently, barrier Lyapunov functions (BLFs) have received growing attention for handling state constraints due to their simplicity and effectiveness [52,53,54,55]. For time-varying state-constrained nonlinear stochastic systems, adaptive neural network control strategies have been proposed to manage input saturation while enforcing state constraints [56]. These approaches leverage neural networks to adaptively handle dynamic state constraints in the presence of stochastic uncertainties and input limitations. Additionally, adaptive finite-time control strategies using command filters have been developed for stochastic nonlinear systems with time-varying full-state constraints and input saturation [57]. By integrating command filtering with adaptive neural networks, these methods achieve finite-time control objectives while addressing dynamic constraints and asymmetric saturation effects. In the context of non-triangular high-order nonlinear stochastic systems, adaptive fuzzy control techniques have been employed to handle asymmetric output constraints [58], using fuzzy logic to regulate complex high-order dynamics and ensure effective control performance despite the presence of output constraints.

Based on the discussion above, it is evident that existing finite-time control schemes largely focus on deterministic nonlinear systems and do not adequately address the complexities inherent in stochastic nonlinear systems, particularly those involving actuator faults, full state constraints, and backlash-like hysteresis. This work aims to fill this gap by investigating the use of neural networks in adaptive finite-time control design for pure-feedback stochastic systems. The presence of actuator faults and backlash-like hysteresis poses significant practical challenges that have not been thoroughly explored in previous studies. The motivation for this research stems from the critical need to develop robust control strategies capable of effectively handling these challenges in real-world applications, thereby enhancing system reliability and performance under adverse conditions. To address state constraints, this study incorporates barrier Lyapunov functions (BLFs) to enforce constraints and ensure that all system states remain within predefined safe regions. This approach significantly improves the practical applicability of finite-time control strategies for stochastic nonlinear systems and represents an important contribution to the field. The main contributions of this paper are summarized as follows:

(i)

Compared with the existing studies [29,32], this work develops an adaptive finite-time control framework for stochastic pure-feedback nonlinear systems while simultaneously addressing several practical challenges, including actuator faults, full state constraints, backlash-like hysteresis, and stochastic disturbances. Most existing studies consider only a subset of these issues, whereas the proposed method incorporates all of them within a unified design. This integrated treatment enhances the reliability of the control scheme in realistic environments where multiple uncertainties can occur concurrently.

(ii)

In contrast to earlier works [13,19,29] that primarily concentrate on enforcing output constraints using barrier Lyapunov functions (BLFs), this paper extends the constraint-handling capability to full system states. By embedding BLF techniques into a recursive backstepping structure, the proposed controller guarantees that every system state remains strictly within predefined bounds throughout the entire operation. This development is particularly important for safety-critical applications. Furthermore, the controller ensures finite-time convergence, closed-loop stability, and accurate tracking of the reference signal. Comprehensive simulation results validate the effectiveness of the approach under various fault and disturbance conditions.

(iii)

The proposed method adopts the norm of the neural-network weight vector as the adaptive parameter instead of estimating individual weight components. This strategy significantly reduces the number of adaptive parameters, simplifies the computational burden, and improves robustness against parameter variations. As a result, the control design becomes more compact and better suited for real-time engineering applications.

The remainder of the article is structured as follows: Section 2 introduces the system and provides preliminary information. In Section 3, the stability analysis and details of the adaptive finite-time controller are discussed extensively. Section 4 presents two simulation examples to illustrate the effectiveness of the theoretical results. Finally, Section 5 concludes the article.

Notations. In this study, we consistently use the following notations: $\mathbb{R}$ denotes the set of real numbers; ${\mathbb{R}}^n$ refers to the n-dimensional real space; y indicates the system output; u represents the system input; v is the actual control input; ${\overline{\zeta }}_i={[{\zeta }_1,{\zeta }_2,\dots ,{\zeta }_i]}^T\in {\mathbb{R}}^i$ for $i=1,2,\dots ,n$ denotes the system state vector; and $\parallel X\parallel$ represents the Euclidean norm of the vector X.

2. Problem Formulation and Preliminaries

Consider stochastic pure-feedback nonlinear systems described by [59]

$$\left\{\begin{array}{cc}d{\zeta }_i=f_i({\overline{\zeta }}_i,{\zeta }_{i+1})dt+{\psi }_i\left({\overline{\zeta }}_i\right)dw,\hfill & 1\le i\le n-1,\hfill \\ d{\zeta }_n=f_n({\overline{\zeta }}_n,u)dt+{\psi }_n\left({\overline{\zeta }}_n\right)dw,\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(1)

where the state vector and system output are represented by ${\overline{\zeta }}_n={[{\zeta }_1,{\zeta }_2,\dots ,{\zeta }_n]}^T\in {\mathbb{R}}^n$ and $y\in \mathbb{R}$, respectively. A r-dimensional standard Brownian motion is denoted by w, which is defined on a complete probability space $(\mathrm{\Omega },\mathcal{F},P)$, where the sample space is $\mathrm{\Omega }$, the sigma-field is $\mathcal{F}$, the filtration is ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ and the probability measure is P. Unknown smooth nonlinear functions are $f_i(·):{\mathbb{R}}^{i+1}\to \mathbb{R}$ and ${\psi }_i(·):{\mathbb{R}}^{i+1}\to {\mathbb{R}}^r$. The system input u experiences actuator faults and backlash-like hysteresis.

In this study, each system state is required to remain within the set depicted below

$$\mathrm{\Omega }=\left\{{\zeta }_i\in \mathbb{R}\mid -k_{c_i}<{\zeta }_i<k_{c_i}\right\},\forall t\ge 0,$$

(2)

where $k_{c_i}>0$ represents the constant with $i=1,\dots ,n$.

Define ${\varphi }_i({\overline{\zeta }}_i+1)={\displaystyle \frac{\partial f_i({\overline{\zeta }}_i+1)}{\partial {\zeta }_{i+1}}}$, ${\varphi }_n({\overline{\zeta }}_n,u)={\displaystyle \frac{\partial f_n({\overline{\zeta }}_n,u)}{\partial u}}$.

By applying the mean value theorem [60], there exist ${\zeta }_0^{i+1}$ and $u_0$ such that

$$\left\{\begin{array}{cc}{f}_i\left({\overline{\zeta }}_{i+1}\right)=f_i({\overline{\zeta }}_i,0)+{\varphi }_i({\overline{\zeta }}_i,{\zeta }_0^{i+1}){\zeta }_{i+1}\hfill & \mathrm{for}i=1,\dots ,n-1\hfill \\ f_n({\overline{\zeta }}_n,u)=f_n({\overline{\zeta }}_n,0)+{\varphi }_n({\overline{\zeta }}_n,u_0)u\hfill \end{array}\right.$$

(3)

where ${\zeta }_0^{i+1}$ lies between 0 and ${\zeta }_{i+1}$, and $u_0$ lies between 0 and u.

Then system (1) is equivalent to

$$\left\{\begin{array}{cc}d{\zeta }_i=(f_i({\overline{\zeta }}_i,0)+{\varphi }_i({\overline{\zeta }}_i,{\zeta }_0^{i+1}){\zeta }_{i+1})dt+{\psi }_i\left({\overline{\zeta }}_i\right)dw,\hfill & 1\le i\le n-1,\hfill \\ d{\zeta }_n=(f_n({\overline{\zeta }}_n,0)+{\varphi }_n({\overline{\zeta }}_n,u_0)u)dt+{\psi }_n\left({\overline{\zeta }}_n\right)dw,\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(4)

The system input u is susceptible to actuator faults, where the model for an undetectable fault is described in [39] as

$$u=\varkappa \left(t\right)\rho \left(v\right)+\varpi \left(t\right)$$

(5)

where $\varkappa \left(t\right)\in (0,1]$ denotes the actuation effectiveness, and $\varpi \left(t\right)$ represents an uncontrollable additive actuation fault. The input $\rho \left(v\right)$ is subject to backlash-like hysteresis, which is represented as follows [26]:

$${\displaystyle \frac{d\rho \left(v\right)}{dt}}=\alpha \left({\displaystyle \frac{dv}{dt}}\right)(cv-\rho \left(v\right))+B_1{\displaystyle \frac{dv}{dt}},$$

(6)

where constants $\alpha$, c, and $B_1$ satisfy $c>B_1$. Following an approach [26], one has

$$\rho \left(v\right)=cv\left(t\right)+d\left(v\right),$$

(7)

with

$$d\left(v\right)=({\rho }_0-c{v}_0)e^{-\alpha (v-v_0)\mathrm{sgn}\dot{v}}+e^{-\alpha \mathrm{sgn}\dot{v}}{\int }_{v_0}^v(B_1-c)e^{\alpha \eta \mathrm{sgn}\dot{v}}d\eta ,$$

(8)

where ${\rho }_0$ and $v_0$ represent the initial conditions of u and v. The function $d\left(v\right)$ is bounded such that

$$\left|d\left(v\right)\right|<d^{*}.$$

(9)

• Control Objective.

The aim of this paper is to develop an adaptive finite-time controller for stochastic nonlinear systems (1) in pure-feedback form. The designed controller ensures that within the closed-loop system all signals remain bounded and that the system output y closely follows a specified reference signal $y_d$, while all system states stay within the constraint boundaries.

Assumption 1

([50]). The signs of ${\varphi }_i\left({\overline{\zeta }}_i\right)$ are known, and ∃ constants ${\varphi }_{i0}>0$ and ${\varphi }_{i1}>0$ ensuring $0<{\varphi }_{i0}\le \left|{\varphi }_i\left({\overline{\zeta }}_i\right)\right|\le {\varphi }_{i1}$. Adopting ${\varphi }_{i0}\le {\varphi }_i\left({\overline{\zeta }}_i\right)\le {\varphi }_{i1}$ for simplicity.

Assumption 2

([50]). The reference signal $y_d\left(t\right)$ satisfies $|y_d\left(t\right)|\le A_1<k{c}_1$, and its ith time derivative ${\dot{y}}_d^{\left(i\right)}\left(t\right)$ is bounded by $|{\dot{y}}_d^{\left(i\right)}\left(t\right)|\le C_i$ for $i=1,\dots ,n,$ where $A_1,C_1,\dots ,C_n$ are positive constants.

Assumption 3

([39]). Both $\varpi \left(t\right)$ and $\varkappa \left(t\right)$ are bounded time-varying unknown functions. In particular, ${\varkappa }_{\mathit{min}}>0$ and ${\varpi }_{\mathit{max}}>0$ exist constants such that ${\varkappa }_{\mathit{min}}<\varkappa \left(t\right)\le 1$ and $\left|\varpi \left(t\right)\right|\le {\varpi }_{\mathit{max}}$.

Lemma 1

([50]). For all $|z_i|<k_{b_i}>0$, $i=1,\dots ,n$, one has

$$log{\displaystyle \frac{k_{b_i}^4-z_i^4}{k_{b_i}^4-z_i^4}}\le {\displaystyle \frac{z_i^4}{k_{b_i}^4-z_i^4}}.$$

(10)

Remark 1.

Assumptions 1–3 are necessary to ensure the feasibility, stability, and performance of the proposed control design. Specifically, Assumption 1 represents a controllability condition for the system (4), ensuring that the control gain functions ${\varphi }_i\left({\overline{\zeta }}_i\right)$ have known signs and are bounded away from zero and from above, which guarantees that the control input can effectively influence the system dynamics [50]. Assumption 2 ensures that the reference signal $y_d\left(t\right)$ and its derivatives are bounded, which is required for the recursive backstepping design and barrier Lyapunov function formulation, allowing all system states to remain within prescribed limits while achieving accurate tracking [50]. Assumption 3 characterizes actuator faults and uncertainties, where $\varkappa \left(t\right)\in (0,1]$ denotes the actuation effectiveness and $\varpi \left(t\right)$ represents an uncontrollable additive actuation fault. This assumption allows the controller to compensate for faults and uncertainties, ensuring stable operation and desired performance under partial actuator failures and disturbances [39]. These assumptions are explicitly applied in the controller design and stability analysis throughout the paper.

Remark 2.

Previous research [1] primarily focused on adaptive control techniques tailored for stochastic nonlinear systems structured in strict feedback form rather than pure feedback form. Recent advancements, exemplified by the BLF-based control approach for pure feedback stochastic nonlinear systems [59], have effectively achieved uniformly bounded tracking control. However, these methods have not comprehensively addressed the integration of state constraints into their frameworks. In prior research [46,47], finite-time control schemes for nonlinear stochastic systems have been introduced but faced challenges in fully incorporating comprehensive state constraints into their control strategies. This paper proposes a novel approach using barrier Lyapunov functions (BLFs) and neural networks for finite-time control, specifically to address the complexities of stochastic pure feedback nonlinear systems with state constraints.

2.1. Theory of Neural Network Approximation

As stated in [32], the RBFNNs used in this work will approximate any continuous function $F(·):{\mathbb{R}}^n\to \mathbb{R}$.

$$F_{nn}\left(Z\right)=W^{T}P\left(Z\right)$$

(11)

where the number of nodes in the neural network is indicated by $l>1$, the weight vector is $W={[W_1,\dots ,W_l]}^T\in {\mathbb{R}}^l$ and the basis function vector is $P\left(Z\right)={[P_1\left(Z\right),\dots ,P_l\left(Z\right)]}^T$ with each $P_i\left(Z\right)$ selected as the Gaussian function

$$P_i\left(Z\right)=exp\left(-{\displaystyle \frac{{(Z-{\sigma }_i)}^T(Z-{\sigma }_i)}{{\eta }^2}}\right),$$

(12)

where the length of the Gaussian function is $\eta$ and the center of the receptive field is ${\sigma }_i={[{\sigma }_{i1},\dots ,{\sigma }_{iq}]}^T\in {\mathbb{R}}^n$. With an arbitrary degree of precision, the neural network may estimate any continuous function $F\left(Z\right)$ over a compact set ${\mathrm{\Omega }}_Z\in {\mathbb{R}}^q$ as

$$F\left(Z\right)=W^{*T}P\left(Z\right)+\delta \left(Z\right)$$

(13)

where the approximation error satisfying $\left|\delta \right(Z\left)\right|\le ϵ$ for some small $ϵ>0$ is represented by $\delta \left(Z\right)$ and $W^{*}$ denotes the ideal constant weight vector.

2.2. Stochastic Finite-Time Theory

Consider the following stochastic nonlinear system as [50]

$$d\zeta =f\left(\zeta \right)dt+\psi \left(\zeta \right)d\omega ,$$

(14)

where $\omega$ is a r-dimensional standard Brownian motion, and $\zeta \in {\mathbb{R}}^n$ denotes the state vector of the system, $f(·):{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $\psi (·):{\mathbb{R}}^n\to {\mathbb{R}}^{n\times r}$ represent the local Lipschitz functions.

Definition 1

([47]). Define the differential operator $\mathcal{L}V\left(\zeta \right)$ for a positive function $V\left(\zeta \right)$, which is twice continuously differentiable on ${\mathbb{R}}^n$, with respect to the system (14) as

$$\mathcal{L}V\left(\zeta \right)={\displaystyle \frac{\partial V}{\partial \zeta }}f\left(\zeta \right)+{\displaystyle \frac{1}{2}}Tr\left\{h{\left(\zeta \right)}^T{\displaystyle \frac{{\partial }^{2}V}{\partial {\zeta }^2}}h\left(\zeta \right)\right\},$$

(15)

where $Tr(·)$ denotes the matrix trace.

Definition 2

([50]). For every initial condition $\zeta \left(t_0\right)={\zeta }_0$, the equilibrium point of system (14) achieves semiglobal practical finite-time stability (SGPFS) in probability if there exists a positive ϵ and a finite settling time $T(ϵ,{\zeta }_0)<\infty$ such that

$${\mathbb{E}\left(\right|\zeta \left(t\right)|}^2) <ϵ,\mathit{for}\mathit{all}t\ge t_0+T.$$

(16)

Lemma 2

([47]). For every $z\in \mathbb{R}$, $\vartheta \in \mathbb{R}$, and positive constants $d_1, d_2, d_3$, one has

$${\left|z\right|}^{d_1}{\left|\vartheta \right|}^{d_2}\le {\displaystyle \frac{d_1}{d_2+d_3}}{d}_3{\left|z\right|}^{d_1+d_2}+{\displaystyle \frac{d_2}{d_1+d_2}}{d}_3^{-{\displaystyle \frac{d_1}{d_2}}}{\left|\vartheta \right|}^{d_1+d_2}.$$

(17)

Lemma 3

([27]). For every $(x,y)\in {\mathbb{R}}^2$, one has

$$xy\le {\displaystyle \frac{q^{\kappa }}{\kappa }}{\left|x\right|}^{\kappa }+{\displaystyle \frac{1}{\varsigma q^{\varsigma -1}}}\left|\varsigma \right|y^{\varsigma },$$

(18)

where $q>0$, $\kappa >1$, $\varsigma >1$, and $(\kappa -1)(\varsigma -1)=1$.

Lemma 4

([50]). For system (14), if there exists a twice continuously differentiable function $V:{\mathbb{R}}^n\to {\mathbb{R}}^{+}$, positive constants $a_0>0$, $0<\beta <1$, $b_0>0$, and two functions ${\phi }_1,{\phi }_2\in {\mathcal{K}}_{\infty }$, such that

$$\left\{\begin{array}{c}{\phi }_1\left(\right|\zeta \left|\right)\le V\left(\zeta \right)\le {\phi }_2\left(\right|\zeta \left|\right),\hfill \\ \mathcal{L}V\left(\zeta \right)\le -a_0{V}^{\beta }\left(\zeta \right)+b_0.\hfill \end{array}\right.$$

(19)

Then the stochastic nonlinear system (14) achieves SGPFS. Specifically, for all $0<\eta <1$, define $T_{\mathit{reach}}={\displaystyle \frac{1}{\eta \mu (1-\beta )}}\left[E\left[V^{1-\beta }\left({\zeta }_0\right)\right]-{\displaystyle \frac{\rho }{(1-\eta )\mu }}{\displaystyle \frac{(1-\beta )}{\beta }}\right]$ and let ${\mathrm{\Omega }}_{\zeta }=\{\zeta \mid \mathbb{E}\left[V^{\beta }\left(\zeta \right)\right]\le {\displaystyle \frac{\rho }{(1-\eta )\mu }}\}$. Then, the time required for $\zeta \left(t\right)$ to reach the set ${\mathrm{\Omega }}_{\zeta }$ is bounded by $T_{\mathit{reach}}$; hence, for all $T>T_{\mathit{reach}}$, $\zeta \left(t\right)\in {\mathrm{\Omega }}_{\zeta }$ holds.

3. Controller Design and Stability Analysis

The upcoming sections propose an adaptive tracking control approach for stochastic nonlinear systems (1) using the backstepping technique and barrier Lyapunov function (BLF) in a recursive manner. The design process involves n steps. Steps 1 through $n-1$ focus on designing virtual controllers ${\alpha }_i$ for $i=1,\dots ,n-1$. In Step n, the real controller v is formulated. The backstepping design procedure initiates with the following coordinate transformation:

$$\begin{array}{cc}\hfill z_1& ={\zeta }_1-y_d,\hfill \\ \hfill z_i& ={\zeta }_i-{\alpha }_{i-1},\hfill & \hfill 2\le i\le n,\end{array}$$

(20)

where $y={\zeta }_1$ is the system output, $y_d$ is the desired signal, ${\zeta }_i$ are the state variables of the system, and ${\alpha }_{i-1}$ represents the virtual controller.

Step 1: By using (4) and (20), one has

$$\begin{array}{cc}\hfill d{z}_1& =d{\zeta }_1-d{y}_d\hfill \\ \hfill & =\left[f_1({\zeta }_1,0)+{\varphi }_1({\zeta }_1,{\zeta }_2^0){\zeta }_2-{\dot{y}}_d\right]dt+{\psi }_1\left({\zeta }_1\right)d\omega .\hfill \end{array}$$

(21)

Consider a Lyapunov function candidate as

$$V_1={\displaystyle \frac{1}{4}}log{\displaystyle \frac{k_{b_1}^4}{k_{b_1}^4-z_1^4}}+{\displaystyle \frac{1}{2}}{\varphi }_{10}{\tilde{\theta }}_1^2$$

(22)

where ${\tilde{\theta }}_1={\widehat{\theta }}_1-{\theta }_1$ with ${\widehat{\theta }}_1>0$ is the estimation of ${\theta }_1^{*}={\varphi }_{10}^{-1}{\overline{W}}_1^2$, and $k_{b_1}=k_{c_1}-A_1$,

From (10) and (11), one has

$$\begin{array}{cc}\hfill L{V}_1& ={\displaystyle \frac{z_1^3}{k_{b1}^4-z_1^4}}\left[f_1({\zeta }_1,0)+{\varphi }_1({\zeta }_1,{\zeta }_2^0){\zeta }_2-{\dot{y}}_d\right]\hfill \\ \hfill & +{\displaystyle \frac{z_1^2(3k_{b_1}^4+z_1^4)}{2(k_{b_1}^4-z_1^4)}}{\psi }_1^2\left({\zeta }_1\right)+{\varphi }_{10}\widetilde{{\theta }_1}{\dot{\widehat{\theta }}}_1.\hfill \end{array}$$

(23)

Now formulated the nonlinear unknown function as

$$F_1\left(Z_1\right)=f_1({\zeta }_1,0)-{\dot{y}}_d+{\displaystyle \frac{z_1(3k_{b_1}^4+z_1^4){\psi }_1^4\left({\zeta }_1\right)}{8{(k_{b_1}^4-z_1^4)}^3{l}_1^2}}.$$

(24)

According to the RBFNN approximation in (13), the function $F_1\left(Z_1\right)$ can be approximated as

$$F_1\left(Z_1\right)=W_1^{*}{P}_1\left(Z_1\right)+{\delta }_1\left(Z_1\right),\left|{\delta }_1\left(Z_1\right)\right|\le {ϵ}_1.$$

(25)

where $W_1^{*}$ denotes the ideal weight vector with $\parallel W_1^{*}\parallel \le {\overline{W}}_1,{\overline{W}}_1>0$ and $Z_1={[{\zeta }_1,{\dot{y}}_d,y_d]}^T$ represents the input vector.

From (24) and (25), (23) can be written as

$$\begin{array}{cc}\hfill L{V}_1=& {\displaystyle \frac{z_1^3}{k_{b_1}^4-z_1^4}}{W}_1^{*T}{P}_1\left(Z_1\right)+{\displaystyle \frac{z_1^3}{k_{b_1}^4-z_1^4}}{\delta }_1\left(Z_1\right)\hfill \\ \hfill & +{\displaystyle \frac{z_1^3{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}{\zeta }_2-{\displaystyle \frac{z_1^4{(3k_{b_1}^4+z_1^4)}^2{\psi }_1^4\left({\zeta }_1\right)}{8{(k_{b1}^4-z_1^4)}^4{l}_1^2}}\hfill \\ \hfill & +{\displaystyle \frac{z_1^2(3k_{b_1}^4+z_1^4)}{2{(k_{b_1}^4-z_1^4)}^2}}{\psi }_1^2\left({\zeta }_1\right)+{\varphi }_{10}\widetilde{{\theta }_1}{\dot{\widehat{\theta }}}_1.\hfill \end{array}$$

(26)

By employing Lemma 3, one has

$${\displaystyle \frac{z_1^3}{k_{b_1}^4-z_1^4}}{W}_1^{*T}{P}_1\left(Z_1\right)\le {\displaystyle \frac{{\gamma }_1^2}{2}}+{\displaystyle \frac{1}{2{\gamma }_1^2}}{\displaystyle \frac{z_1^6}{{(k_{b_1}^4-z_1^4)}^2}}{\overline{W}}_1^2{\parallel P_1\left(Z_1\right)\parallel }^2.$$

(27)

$${\displaystyle \frac{z_1^3}{k_{b_1}^4-z_1^4}}{\delta }_1\left(Z_1\right)\le {\displaystyle \frac{{\varphi }_{10}}{2}}{\displaystyle \frac{z_1^6}{{(k_{b_1}^4-z_1^4)}^2}}+{\displaystyle \frac{{ϵ}_1^2}{2{\varphi }_{10}}}.$$

(28)

$$\begin{array}{cc}\hfill {\displaystyle \frac{z_1^2(3k_{b_1}^4+z_1^4)}{2{(k_{b_1}^4-z_1^4)}^2}}{\varphi }_1^2\left({\zeta }_1\right)& \le {\displaystyle \frac{z_1^4{(3k_{b_1}^4+z_1^4)}^2{\psi }_1^4\left({\zeta }_1\right)}{8{(k_{b_1}^4-z_1^4)}^4{l}_1^2}}+{\displaystyle \frac{l_1^2}{2}}.\hfill \end{array}$$

(29)

with ${\gamma }_1>0$, ${\varphi }_{10}>0$, and $l_1>0$ being the design parameters.

The virtual controller ${\alpha }_1$ can be designed as

$$\begin{array}{cc}\hfill {\alpha }_1& =-{\lambda }_1{\displaystyle \frac{z_1^{4\beta -3}}{{(k_{b_1}^4-z_1^4)}^{\beta -1}}}-{\displaystyle \frac{z_1^3}{2(k_{b_1}^4-z_1^4)}}\hfill \\ \hfill & -{\displaystyle \frac{z_1^3{\widehat{\theta }}_1{\parallel P_1\left(Z_1\right)\parallel }^2}{2{\gamma }_1^2(k_{b_1}^4-z_1^4)}}-{\displaystyle \frac{3z_1}{4{(k_{b_1}^4-z_1^4)}^{\frac{1}{3}}}},\hfill \end{array}$$

(30)

with ${\lambda }_1$ being the positive design parameter.

Since $z_2={\zeta }_2-{\alpha }_1$, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{z_1^3{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}{\zeta }_2& ={\displaystyle \frac{z_1^3{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}(z_2+{\alpha }_1)\hfill \\ \hfill & \le {\displaystyle \frac{z_1^3{z}_2{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}-{\lambda }_1{\varphi }_{10}{\displaystyle \frac{z_1^{4\beta }}{{(k_{b_1}^4-z_1^4)}^{\beta }}}\hfill \\ \hfill & -{\displaystyle \frac{{\varphi }_{10}{z}_1^6}{2{(k_{b_1}^4-z_1^4)}^2}}-{\displaystyle \frac{z_1^6{\varphi }_{10}{\widehat{\theta }}_1{\parallel P_1\left(Z_1\right)\parallel }^2}{2{\gamma }_1^2{(k_{b_1}^4-z_1^4)}^2}}\hfill \\ \hfill & -{\displaystyle \frac{3z_1^4{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{4{(k_{b_1}^4-z_1^4)}^{\frac{4}{3}}}}.\hfill \end{array}$$

(31)

By using (27) to (31) into (26) gives

$$\begin{array}{cc}\hfill L{V}_1\le & -{\lambda }_1{\varphi }_{10}{\left({\displaystyle \frac{z_1^4}{k_{b_1}^4-z_1^4}}\right)}^{\beta }+{\displaystyle \frac{z_1^3{z}_2{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}-{\displaystyle \frac{3z_1^4{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{4{(k_{b_1}^4-z_1^4)}^{\frac{4}{3}}}}\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }_1^2}{2}}+{\displaystyle \frac{{ϵ}_1^2}{2{\varphi }_{10}}}+{\displaystyle \frac{l_1^2}{2}}-{\tilde{\theta }}_1{\varphi }_{10}\left[{\displaystyle \frac{z_1^6{\parallel S_1\left(Z_1\right)\parallel }^2}{2{\gamma }_1^2{(2k_{b_1}^4-z_1^4)}^2}}-{\dot{\widehat{\theta }}}_1\right].\hfill \end{array}$$

(32)

From Lemma 3, we have

$$z_1^3{z}_2{\displaystyle \frac{{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{k_{b_1}^4-z_1^4}}\le {\displaystyle \frac{3z_1^4{\varphi }_1({\zeta }_1,{\zeta }_2^0)}{4{(k_{b_1}^4-z_1^4)}^3}}+{\displaystyle \frac{1}{4}}{z}_2^4{\varphi }_1({\zeta }_1,{\zeta }_2^0).$$

(33)

By using (33) into (32), one has

$$\begin{array}{cc}\hfill L{V}_1\le & -{\lambda }_1{\varphi }_{10}{\left[{\displaystyle \frac{z_1^4}{k_{b_1}^4-z_1^4}}\right]}^{\beta }+{\displaystyle \frac{z_2^4}{4}}{\varphi }_1({\zeta }_1,{\zeta }_2^0)+{\displaystyle \frac{{\gamma }_1^2}{2}}+{\displaystyle \frac{{ϵ}_1^2}{2{\varphi }_{10}}}+{\displaystyle \frac{l_1^2}{2}}\hfill \\ \hfill & -{\tilde{\theta }}_1{\varphi }_{10}\left[z_1^6{\parallel P_1\left(Z_1\right)\parallel }^2{\displaystyle \frac{2{\gamma }_1^2}{{(k_{b_1}^4-z_1^4)}^2}}-{\dot{\widehat{\theta }}}_1\right].\hfill \end{array}$$

(34)

Step $\mathit{i}$ ($\mathbf{2}\le \mathit{i}\le \mathit{n}-\mathbf{1}$): From (4) and (20), one has

$$\begin{array}{cc}\hfill d{z}_i& =d{\zeta }_i-d{\alpha }_{i-1}\hfill \\ \hfill & =[f_i({\zeta }_i,0)+{\varphi }_i({\zeta }_i,{\zeta }_{i+1}^0){\zeta }_{i+1}-L{\alpha }_{i-1}]dt+\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)dw\hfill \end{array}$$

(35)

where

$$\begin{array}{cc}\hfill L{\alpha }_{i-1}& =\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{f}_j\left({\overline{\zeta }}_{j+1}\right)+\sum _{j=0}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial y^{\left(j\right)}}}{\dot{y}}^{{(j+1)}_d}+\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\theta }}_j}}{\dot{\widehat{\theta }}}_j\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\sum _{j,k=1}^{i-1}{\displaystyle \frac{{\partial }^2{\alpha }_{i-1}}{\partial {\zeta }_j\partial {\zeta }_k}}{\psi }_j{\psi }_k.\hfill \end{array}$$

(36)

Take the following Lyapunov function candidate as

$$V_i=V_{i-1}+{\displaystyle \frac{1}{4}}log{\displaystyle \frac{k_{b_i}^4}{k_{b_i}^4-z_i^4}}+{\displaystyle \frac{1}{2}}{\varphi }_{i0}{\tilde{\theta }}_i,$$

(37)

where ${\tilde{\theta }}_i={\widehat{\theta }}_i-{\theta }_i^{*}$ and ${\widehat{\theta }}_i>0$ represents the estimation of ${\theta }_i^{*}={\varphi }_{i0}^{-1}{\overline{W}}_i^2$, and $k_{b_i}=k_{c_i}-A_i\left(\right|{\alpha }_{i-1}|<A_i)$.

By employing (35) and (37), becomes

$$\begin{array}{cc}\hfill L{V}_i& =L{V}_{i-1}+{\displaystyle \frac{z_i^3}{k_{b_i}^4-z_i^4}}\left[f_i({\overline{\zeta }}_i,0)+{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0){\zeta }_{i+1}-L{\alpha }_{i-1}\right]\hfill \\ & +{\displaystyle \frac{z_i^2(3k_{b_i}^4+z_i^4)}{{(2k_{b_i}^4-z_i^4)}^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2+{\varphi }_{i0}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i.\hfill \end{array}$$

(38)

Now formulated the nonlinear unknown function as

$$\begin{array}{cc}\hfill F_i\left(Z_i\right)& =f_i({\overline{\zeta }}_i,0)-L{\alpha }_{i-1}+{\displaystyle \frac{(k_{b_i}^4-z_i^4)}{4}}{z}_i{\varphi }_{i-1}({\overline{\zeta }}_{i-1},{\zeta }_i^0)\hfill \\ \hfill & +{\displaystyle \frac{z_i{(3k_{b_i}^4+z_i^4)}^2}{8{(k_{b_i}^4-z_i^4)}^3{l}_i^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4.\hfill \end{array}$$

(39)

According to the RBFNN approximation in (13), the function $F_i\left(Z_i\right)$ can be approximated as

$$F_i\left(Z_i\right)=W^{*T}{P}_i\left(Z_i\right)+{\delta }_i\left(Z_i\right),\left|{\delta }_i\left(Z_i\right)\right|\le {ϵ}_i.$$

(40)

where $W_i^{*}$ signifies the optimal weight vector with $\parallel W_i^{*}\parallel \le {\overline{W}}_i$ and ${\overline{W}}_i>0$$Z_i={[{\overline{\zeta }}_i^T,{\overline{\theta }}_{i-1}^T,{\overline{y}}_{\left(i\right)d}^T]}^T$ represents the input vector with ${\overline{\theta }}_{i-1}^T={[{\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_{n-1}]}^T$.

By employing (39) and (40), (38) becomes

$$\begin{array}{cc}\hfill L{V}_i=& L{V}_{i-1}+{\displaystyle \frac{z_i^3}{k_{b_i}^4-z_i^4}}{W}_i^{*T}{P}_i\left(Z_i\right)+{\displaystyle \frac{z_i^3}{k_{b_i}^4-z_i^4}}{\delta }_i\left(Z_i\right)-{\displaystyle \frac{z_i^4}{4}}{\varphi }_{i-1}({\overline{\zeta }}_{i-1},{\zeta }_i^0)\hfill \\ \hfill & +{\displaystyle \frac{z_i^3{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0){\zeta }_{i+1}}{k_{b_i}^4-z_i^4}}-{\displaystyle \frac{z_i^4{(3k_{b_i}^4+z_i^4)}^2}{8{(k_{b_i}^4-z_i^4)}^4{l}_i^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4\hfill \\ \hfill & +{\displaystyle \frac{z_i^2(3k_{b_i}^4+z_i^4)}{2{(k_{b_i}^4-z_i^4)}^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2+{\varphi }_{i0}{\tilde{\theta }}_i{\dot{\widehat{\theta }}}_i.\hfill \end{array}$$

(41)

By utilizing Lemma 3, one has

$${\displaystyle \frac{z_i^3}{k_{b_i}^4-z_i^4}}{W}_i^{*T}{P}_i\left(Z_i\right)\le {\displaystyle \frac{{\gamma }_i^2}{2}}+{\displaystyle \frac{1}{2{\gamma }_i^2}}{\displaystyle \frac{z_i^6}{{(k_{b_i}^4-z_i^4)}^2}}{\overline{W}}_i^2{\parallel P_i\left(Z_i\right)\parallel }^2$$

(42)

$${\displaystyle \frac{z_i^3}{k_{b_i}^4-z_i^4}}{\delta }_i\left(Z_i\right)\le {\displaystyle \frac{{\varphi }_{i0}}{2}}{\displaystyle \frac{z_i^6}{{(k_{b_i}^4-z_i^4)}^2}}+{\displaystyle \frac{{ϵ}_i^2}{2{\varphi }_{i0}}}$$

(43)

$$\begin{array}{cc}\hfill {\displaystyle \frac{z_i^2(3k_{b_i}^4+z_i^4)}{2{(k_{b_i}^4-z_i^4)}^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2& \le {\displaystyle \frac{z_i^4{(3k_{b_i}^4+z_i^4)}^2{\psi }_i^4\left({\zeta }_i\right)}{8{(k_{b_i}^4-z_i^4)}^4{l}_i^2}}{\left({\psi }_i-\sum _{j=1}^{i-1}{\displaystyle \frac{\partial {\alpha }_{i-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4+{\displaystyle \frac{l_i^2}{2}}\hfill \end{array}$$

(44)

with ${\gamma }_i>0$, ${\varphi }_{i0}>0$, and $l_i>0$ being the constants.

The virtual controller ${\alpha }_i$ can be formulated as

$$\begin{array}{cc}\hfill {\alpha }_i& =-{\lambda }_i{\displaystyle \frac{z_i^{4\beta -3}}{{(k_{b_i}^4-z_i^4)}^{\beta -1}}}-{\displaystyle \frac{z_i^3}{2(k_{b_i}^4-z_i^4)}}\hfill \\ \hfill & -{\displaystyle \frac{z_i^3{\widehat{\theta }}_i{\parallel P_i\left(Z_i\right)\parallel }^2}{2{\gamma }_i^2(k_{b_i}^4-z_i^4)}}-{\displaystyle \frac{3z_i}{4{(k_{b_i}^4-z_i^4)}^{\frac{1}{3}}}},\hfill \end{array}$$

(45)

with ${\lambda }_i$ being the positive design parameter.

As $z_{i+1}={\zeta }_{i+1}-{\alpha }_i$, one has

$$\begin{array}{cc}\hfill {\displaystyle \frac{z_i^3{\varphi }_i({\zeta }_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}{\zeta }_{i+1}& ={\displaystyle \frac{z_i^3{\varphi }_i({\zeta }_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}(z_{i+1}+{\alpha }_i)\hfill \\ \hfill & \le {\displaystyle \frac{z_i^3{z}_{i+1}{\varphi }_i({\zeta }_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}-{\lambda }_i{\varphi }_{i0}{\displaystyle \frac{z_i^{4\beta }}{{(k_{b_i}^4-z_i^4)}^{\beta }}}\hfill \\ \hfill & -{\displaystyle \frac{{\varphi }_{i0}{z}_i^6}{2{(k_{b_i}^4-z_i^4)}^2}}-{\displaystyle \frac{z_i^6{\varphi }_{i0}{\widehat{\theta }}_i{\parallel P_i\left(Z_i\right)\parallel }^2}{2{\gamma }_i^2{(k_{b_i}^4-z_i^4)}^2}}\hfill \\ \hfill & -{\displaystyle \frac{3z_i^4{\varphi }_i({\zeta }_i,{\zeta }_{i+1}^0)}{4{(k_{b_i}^4-z_i^4)}^{\frac{4}{3}}}}.\hfill \end{array}$$

(46)

By using (42)–(46) into (41) gives

$$\begin{array}{cc}\hfill L{V}_i& \le L{V}_{i-1}-{\lambda }_i{\varphi }_{i0}{\left({\displaystyle \frac{z_i^4}{k_{b_i}^4-z_i^4}}\right)}^{\beta }+{\displaystyle \frac{{\gamma }_i^2}{2}}+{\displaystyle \frac{{ϵ}_i^2}{2{\varphi }_{i0}}}+{\displaystyle \frac{l_i^2}{2}}\hfill \\ \hfill & +{\displaystyle \frac{z_i^3{z}_{i+1}{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}-{\displaystyle \frac{z_i^4}{4}}{\varphi }_{i-1}({\overline{\zeta }}_{i-1},{\zeta }_i^0)-{\displaystyle \frac{3z_i^4{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{4{(k_{b_i}^4-z_i^4)}^{4/3}}}\hfill \\ \hfill & -{\tilde{\theta }}_i{\varphi }_{i0}\left({\displaystyle \frac{z_i^6{\parallel P_i\left(Z_i\right)\parallel }^2}{2{\gamma }_i^2{(k_{b_i}^4-z_i^4)}^2}}-{\dot{\widehat{\theta }}}_i\right).\hfill \end{array}$$

(47)

In accordance with the derivation steps mentioned earlier, $L{V}_{i-1}$ is expressed as

$$\begin{array}{cc}\hfill L{V}_{i-1}& \le -\sum _{j=1}^{i-1}{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^{i-1}{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^{i-1}{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}+{\displaystyle \frac{l_j^2}{2}}\hfill \\ \hfill & +{\displaystyle \frac{z_i^4}{4}}{\varphi }_{i-1}({\overline{\zeta }}_{i-1},{\zeta }_i^0)-\sum _{j=1}^{i-1}{\tilde{\theta }}_j{\varphi }_{j0}\left({\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{2{\gamma }_j^2{(k_{b_j}^4-z_j^4)}^2}}-{\dot{\widehat{\theta }}}_j\right).\hfill \end{array}$$

(48)

By using (48) into (47), one has

$$\begin{array}{cc}\hfill L{V}_i& \le -\sum _{j=1}^i{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+{\displaystyle \frac{z_i^3{z}_{i+1}{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}-{\displaystyle \frac{3z_i^4{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{4{(k_{b_i}^4-z_i^4)}^{4/3}}}\hfill \\ \hfill & +\sum _{j=1}^i{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^i{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}+\sum _{j=1}^i{\displaystyle \frac{l_j^2}{2}}-\sum _{j=1}^i{\tilde{\theta }}_j{\varphi }_{j0}\left({\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{2{\gamma }_j^2{(k_{b_j}^4-z_j^4)}^2}}-{\dot{\widehat{\theta }}}_j\right).\hfill \end{array}$$

(49)

By employing Lemma 3, we have

$${\displaystyle \frac{z_i^3{z}_{i+1}{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{k_{b_i}^4-z_i^4}}\le {\displaystyle \frac{3z_i^4{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)}{4{(k_{b_i}^4-z_i^4)}^{4/3}}}+{\displaystyle \frac{1}{4}}{z}_{i+1}^4{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0).$$

(50)

By employing (50) into (49), we have

$$\begin{array}{cc}\hfill L{V}_i\le & -\sum _{j=1}^i{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+{\displaystyle \frac{1}{4}}{z}_{i+1}^4{\varphi }_i({\overline{\zeta }}_i,{\zeta }_{i+1}^0)+\sum _{j=1}^i{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^i{\displaystyle \frac{{\delta }_j^2}{2{\varphi }_{j0}}}+\sum _{j=1}^i{\displaystyle \frac{l_j^2}{2}}\hfill \\ \hfill & -\sum _{j=1}^i{\tilde{\theta }}_j{\varphi }_{j0}\left({\displaystyle \frac{z_j^6{\parallel S_j\left(Z_j\right)\parallel }^2}{2{\gamma }_j^2{(k_{b_j}^4-z_j^4)}^2}}-{\dot{\widehat{\theta }}}_j\right).\hfill \end{array}$$

(51)

Step $\mathit{n}$: Based on the relationships described in (4), (5), (7), and (20), we can deduce the following

$$\begin{array}{cc}\hfill d{z}_n& =d{\zeta }_n-d{\alpha }_{n-1}\hfill \\ \hfill =& [f_n({\overline{\zeta }}_n,0)+{\varphi }_n({\overline{\zeta }}_n,u^0)(\varkappa \left(t\right)cv+\varkappa \left(t\right)d\left(v\right)+\varpi \left(t\right))-L{\alpha }_{n-1}]dt\hfill \\ \hfill & +\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)dw\hfill \end{array}$$

(52)

with

$$\begin{array}{cc}\hfill L{\alpha }_{n-1}& =\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{f}_j\left({\overline{\zeta }}_{j+1}\right)+\sum _{j=0}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial y^{\left(j\right)}}}{\dot{y}}^{{(j+1)}_d}+\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\widehat{\theta }}_j}}{\dot{\widehat{\theta }}}_j\hfill \\ & +{\displaystyle \frac{1}{2}}\sum _{j,k=1}^{n-1}{\displaystyle \frac{{\partial }^2{\alpha }_{n-1}}{\partial {\zeta }_j\partial {\zeta }_k}}{\psi }_j{\psi }_k.\hfill \end{array}$$

(53)

Take the following Lyapunov function candidate as

$$V_n=V_{n-1}+{\displaystyle \frac{1}{4}}log{\displaystyle \frac{k_{b_n}^4}{k_{b_n}^4-z_n^4}}+{\displaystyle \frac{1}{2}}{\varphi }_{n0}{\tilde{\theta }}_n,$$

(54)

with ${\tilde{\theta }}_n={\widehat{\theta }}_n-{\theta }_n^{*}$ and ${\widehat{\theta }}_1>0$ being the estimation of ${\theta }_n^{*}={\varphi }_{n0}^{-1}{\overline{W}}_n^2$, and $k_{b_n}=k_{c_n}-A_n\left(\right|{\alpha }_{n-1}|<A_n)$.

By using (52) into (54), we have

$$\begin{array}{cc}\hfill L{V}_n& =L{V}_{n-1}+{\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}\left[f_n({\overline{\zeta }}_n,0)+{\varphi }_n({\overline{\zeta }}_n,u^0)(\varkappa \left(t\right)cv+\varkappa \left(t\right)d\left(v\right)+\varpi \left(t\right))-L{\alpha }_{n-1}\right]\hfill \\ & +{\displaystyle \frac{z_n^2(3k_{b_n}^4+z_n^4)}{{(2k_{b_n}^4-z_n^4)}^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2+{\varphi }_{n0}{\tilde{\theta }}_n{\dot{\widehat{\theta }}}_n.\hfill \end{array}$$

(55)

By applying (9), Lemma 3, Assumptions 1 and 3, we obtain

$${\displaystyle \frac{{\zeta }_n^3{\varphi }_n({\overline{\zeta }}_n,u^0)\varkappa \left(t\right)d\left(v\right)}{k_{b_n}^4-z_n^4}}\le {\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4+{\displaystyle \frac{1}{4}}{d}^{*2},$$

(56)

$${\displaystyle \frac{{\zeta }_n^3{\varphi }_n({\overline{\zeta }}_n,u^0)\varpi \left(t\right)}{k_{b_n}^4-z_n^4}}\le {\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2,$$

(57)

By using (56) and (57) into (55), we have

$$\begin{array}{cc}\hfill L{V}_n& =L{V}_{n-1}+{\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}\left[f_n({\overline{\zeta }}_n,0)+{\varphi }_n({\overline{\zeta }}_n,u^0)\varkappa \left(t\right)cv-L{\alpha }_{n-1}\right]\hfill \\ & +{\displaystyle \frac{z_n^2(3k_{b_n}^4+z_n^4)}{{(2k_{b_n}^4-z_n^4)}^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2+{\varphi }_{n0}{\tilde{\theta }}_n{\dot{\widehat{\theta }}}_n\hfill \\ \hfill & +{\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2\hfill \end{array}$$

(58)

Now, formulated the nonlinear unknown function as

$$\begin{array}{cc}\hfill F_n\left(Z_n\right)& =f_n({\overline{\zeta }}_n,0)-L{\alpha }_{n-1}+{\displaystyle \frac{(k_{b_n}^4-z_n^4)}{4}}{z}_n{\varphi }_{n-1}({\overline{\zeta }}_{n-1},{\zeta }_n^0)\hfill \\ & +{\displaystyle \frac{z_n{(3k_{b_n}^4+z_n^4)}^2}{8{(k_{b_n}^4-z_n^4)}^3{l}_n^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4\hfill \\ \hfill & +{\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4+{\displaystyle \frac{3\varphi \left(n0\right)}{4{(k_{b_n}^4-z_n^4)}^2}}{\zeta }_n^4.\hfill \end{array}$$

(59)

According to the RBFNN approximation in (13), the function $F_i\left(Z_i\right)$ can be approximated as

$$F_n\left(Z_n\right)=W^{*T}{P}_n\left(Z_n\right)+{\delta }_n\left(Z_n\right),\left|{\delta }_n\left(Z_n\right)\right|\le {ϵ}_n.$$

(60)

where $Z_n={[{\overline{\zeta }}_n^T,{\overline{\theta }}_{n-1}^T,{\overline{y}}_{\left(n\right)d}^T]}^T$ denotes the input vector with ${\overline{\theta }}_{n-1}^T={[{\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_{n-1}]}^T$, and $W_n^{*}$ signifies the optimal weight vector with $\parallel W_n^{*}\parallel \le {\overline{W}}_n$ and ${\overline{W}}_n>0$.

By employing (59) and (60) into (58), we have

$$\begin{array}{cc}\hfill L{V}_n=& L{V}_{n-1}+{\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}{W}_n^{*T}{P}_n\left(Z_n\right)+{\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}{\delta }_n\left(Z_n\right)-{\displaystyle \frac{z_n^4}{4}}{\varphi }_{n-1}({\overline{\zeta }}_{n-1},{\zeta }_n^0)\hfill \\ \hfill & +{\displaystyle \frac{z_n^3{\varphi }_n({\overline{\zeta }}_n,u^0)\varkappa \left(t\right)cv}{k_{b_n}^4-z_n^4}}-{\displaystyle \frac{z_n^4{(3k_{b_n}^4+z_n^4)}^2}{8{(k_{b_n}^4-z_n^4)}^4{l}_n^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4\hfill \\ \hfill & +{\displaystyle \frac{z_n^2(3k_{b_n}^4+z_n^4)}{2{(k_{b_n}^4-z_n^4)}^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2+{\varphi }_{n0}{\tilde{\theta }}_n{\dot{\widehat{\theta }}}_n\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(61)

By using Lemma 3, we have

$${\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}{W}_n^{*T}{P}_n\left(Z_n\right)\le {\displaystyle \frac{{\gamma }_n^2}{2}}+{\displaystyle \frac{1}{2{\gamma }_n^2}}{\displaystyle \frac{z_n^6}{{(k_{b_n}^4-z_n^4)}^2}}{\overline{W}}_n^2{\parallel P_n\left(Z_n\right)\parallel }^2.$$

(62)

$${\displaystyle \frac{z_n^3}{k_{b_n}^4-z_n^4}}{\delta }_n\left(Z_n\right)\le {\displaystyle \frac{{\varphi }_{n0}}{2}}{\displaystyle \frac{z_n^6}{{(k_{b_n}^4-z_n^4)}^2}}+{\displaystyle \frac{{ϵ}_n^2}{2{\varphi }_{n0}}}.$$

(63)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{z_n^2(3k_{b_n}^4+z_n^4)}{2{(k_{b_n}^4-z_n^4)}^2}}& {\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^2\hfill & \hfill \le {\displaystyle \frac{z_n^4{(3k_{b_n}^4+z_n^4)}^2{\psi }_n^4\left({\zeta }_n\right)}{8{(k_{b_n}^4-z_n^4)}^4{l}_n^2}}{\left({\psi }_n-\sum _{j=1}^{n-1}{\displaystyle \frac{\partial {\alpha }_{n-1}}{\partial {\zeta }_j}}{\psi }_j\right)}^4\\ \hfill & +{\displaystyle \frac{l_n^2}{2}}.\hfill \end{array}$$

(64)

with ${\gamma }_n>0$, ${\varphi }_{n0}>0$, and $l_n>0$ being the constants.

Now, formulate the real controller v as

$$\begin{array}{cc}\hfill v& =-{\lambda }_n{\displaystyle \frac{z_n^{4\beta -3}}{{(k_{b_n}^4-z_n^4)}^{\beta -1}}}-{\displaystyle \frac{z_n^3}{2(k_{b_n}^4-z_n^4)}}-{\displaystyle \frac{z_n^3{\widehat{\theta }}_n{\parallel P_n\left(Z_n\right)\parallel }^2}{2{\gamma }_n^2(k_{b_n}^4-z_n^4)}},\hfill \end{array}$$

(65)

with ${\lambda }_n$ being the positive design parameter.

By using (65) and Assumption 3, we can derive

$${\displaystyle \frac{z_n^3{\varphi }_n({\overline{x}}_n,u_0)\varkappa \left(t\right)cv\left(t\right)}{k_{b_n}^4-z_n^4}}\le -{\lambda }_n{\varphi }_{n0}{\left({\displaystyle \frac{z_n^4}{k_{bn}^4-z_n^4}}\right)}^{\beta }-{\displaystyle \frac{{\varphi }_{n0}{z}_n^6}{2{(k_{bn}^4-z_n^4)}^2}}-{\displaystyle \frac{z_n^6{\varphi }_{n0}{\widehat{\theta }}_n{\parallel P_n\left(Z_n\right)\parallel }^2}{2{\gamma }_n^2{(k_{b_n}^4-z_n^4)}^2}}.$$

(66)

By using (62)–(66) into (61), one has

$$\begin{array}{cc}\hfill L{V}_n\le & L{V}_{n-1}-{\lambda }_n{\varphi }_{n0}{\left({\displaystyle \frac{z_n^4}{k_{bn}^4-z_n^4}}\right)}^{\beta }-{\displaystyle \frac{z_n^4}{4}}{\varphi }_{n-1}({\overline{\zeta }}_{n-1},{\zeta }_n^0)\hfill \\ \hfill & +{\displaystyle \frac{{\gamma }_n^2}{2}}+{\displaystyle \frac{{ϵ}_n^2}{2{\varphi }_{n0}}}+{\displaystyle \frac{l_n^2}{2}}+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2-{\tilde{\theta }}_n{\varphi }_{n0}\left({\displaystyle \frac{z_n^6{\parallel P_n\left(Z_n\right)\parallel }^2}{2{\gamma }_n^2{(k_{bn}^4-z_n^4)}^2}}-{\dot{\widehat{\theta }}}_n\right).\hfill \end{array}$$

(67)

In accordance with the derivation steps mentioned earlier, $L{V}_{n-1}$ is expressed as

$$\begin{array}{cc}\hfill L{V}_{n-1}& \le -\sum _{j=1}^{n-1}{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^{n-1}{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^{n-1}{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}+{\displaystyle \frac{l_j^2}{2}}\hfill \\ \hfill & +{\displaystyle \frac{z_n^4}{4}}{\varphi }_{n-1}({\overline{\zeta }}_{n-1},{\zeta }_n^0)-\sum _{j=1}^{n-1}{\tilde{\theta }}_j{\varphi }_{j0}\left({\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{2{\gamma }_j^2{(k_{b_j}^4-z_j^4)}^2}}-{\dot{\widehat{\theta }}}_j\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(68)

By using (68) into (67), we have

$$\begin{array}{cc}\hfill L{V}_n& \le -\sum _{j=1}^n{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{bj}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^n{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^n{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}\hfill \\ \hfill & +\sum _{j=1}^n{\displaystyle \frac{l_j^2}{2}}-\sum _{j=1}^n{\tilde{\theta }}_j{\varphi }_{j0}\left({\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{2{\gamma }_j^2{(k_{bj}^4-z_j^4)}^2}}-{\dot{\widehat{\theta }}}_j\right)+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(69)

The formulation of adaptation laws ${\widehat{\theta }}_j$ is as follows:

$${\dot{\widehat{\theta }}}_j=-{\sigma }_j{\widehat{\theta }}_j+{\displaystyle \frac{1}{2{\gamma }_j^2}}{\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{{(k_{bj}^4-z_j^4)}^2}},j=1,\dots ,n$$

(70)

with ${\sigma }_j$ being the positive design parameters.

By employing (70) into (69), one has

$$\begin{array}{cc}\hfill L{V}_n& \le -\sum _{j=1}^n{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{bj}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^n{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^n{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}+\sum _{j=1}^n{\displaystyle \frac{l_j^2}{2}}\hfill \\ \hfill & -\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j{\widehat{\theta }}_j+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(71)

Theorem 1.

Considering the pure-feedback stochastic nonlinear system (1) with integrated actuator faults and backlash-like hysteresis, and under Assumptions 1–3 along with the inclusion of virtual controllers (30), (45), real controller (65), and adaptive laws (70), we guarantee the boundedness of all system variables. Additionally, the tracking error converges to zero in finite time, ensuring that all state variables remain within their specified boundaries.

Proof. 

Utilizing Lemma 3, one can deduce

$$-{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j{\widehat{\theta }}_j\le -{\displaystyle \frac{1}{2}}{\sigma }_j{\varphi }_{j0}{\left({\tilde{\theta }}_j\right)}^2+{\displaystyle \frac{1}{2}}{\sigma }_j{\varphi }_{j0}{\left({\theta }_j^{*}\right)}^2,j=1,\dots ,n.$$

(72)

By applying (72) to (71), we obtain

$$\begin{array}{cc}\hfill L{V}_n\le & -\sum _{j=1}^n{\lambda }_j{\varphi }_{j0}{\left({\displaystyle \frac{z_j^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^n{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^n{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}+\sum _{j=1}^n{\displaystyle \frac{l_j^2}{2}}-{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\theta }_j^{*2}+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(73)

It can be demonstrated using Lemma 1 that $log{\displaystyle \frac{k_{b_i}^4}{k_{b_i}^4-z_i^4}}\le {\displaystyle \frac{z_i^4}{k_{b_i}^4-z_i^4}}$, which implies $|log{\displaystyle \frac{k_{b_i}^4}{k_{b_i}^4-z_i^4}}{|}^{\beta }\le {\left|{\displaystyle \frac{z_i^4}{k_{b_i}^4-z_i^4}}\right|}^{\beta }$ holds for $0<\beta <1$. Thus, it follows

$$\begin{array}{cc}\hfill L{V}_n& \le -\sum _{j=1}^n{\lambda }_j{\varphi }_{j0}{\left(log{\displaystyle \frac{k_{b_j}^4}{k_{b_j}^4-z_j^4}}\right)}^{\beta }+\sum _{j=1}^n{\displaystyle \frac{{\gamma }_j^2}{2}}+\sum _{j=1}^n{\displaystyle \frac{{ϵ}_j^2}{2{\varphi }_{j0}}}\hfill \\ \hfill & +\sum _{j=1}^n{\displaystyle \frac{l_j^2}{2}}-{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_1+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\theta }_j^{*2}+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(74)

Let $z={\displaystyle \frac{1}{2}}{\sum }_{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2$, $d_1=\beta$, $d_2=1-\beta$, and $d_3=\beta -1$. From Lemma 2, one can derive

$${\left({\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2\right)}^{\beta }\le {\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2+(1-\beta ){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}.$$

(75)

Moreover, we have

$$-{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2\le -{\left({\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2\right)}^{\beta }+(1-\beta ){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}},$$

(76)

By using (76) into (74), we have

$$\begin{array}{cc}\hfill L{V}_n& \le -\sum _{j=1}^n{\lambda }_j{\varphi }_{j0}log{{\displaystyle \frac{k_{bj}^4}{k_{bj}^4-z_j^4}}}^{\beta }-{\left({\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\tilde{\theta }}_j^2\right)}^{\beta }+\sum _{j=1}^n{\displaystyle \frac{{\gamma }_j^2}{2}}\hfill \\ \hfill & +\sum _{j=1}^n{\displaystyle \frac{{ϵ}_j^2{\varphi }_{j0}}{2}}+\sum _{j=1}^n{\displaystyle \frac{l_j^2}{2}}+{\displaystyle \frac{1}{2}}\sum _{j=1}^n{\sigma }_j{\varphi }_{j0}{\theta }_j^{*2}+(1-\beta ){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2.\hfill \end{array}$$

(77)

Let

$$a_0=min\{4\beta {\lambda }_j{\varphi }_{j0},{ϵ}_j^{\beta }\}$$

(78)

$$\begin{array}{cc}\hfill b_0& =\sum _{j=1}^n{\gamma }_j^2+\sum _{j=1}^n{ϵ}_j^2{\varphi }_{j0}+\sum _{j=1}^n{l}_j^2+{\displaystyle \frac{1}{4}}{d}^{*2}+{\displaystyle \frac{1}{4}}{\varpi }_{\max }^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\sum _{j=1}^n{ϵ}_j{\varphi }_{j0}{\theta }_j^{*2}+(1-\beta ){\beta }^{{\displaystyle \frac{\beta }{1-\beta }}}\hfill \end{array}$$

(79)

Then, utilizing Lemma 2, (77) can be expressed as

$$L{V}_n\le -a_0{V}^{\beta }+b_0.$$

(80)

Let $T^{*}={\displaystyle \frac{1}{\eta \mu (1-\beta )}}\left[\mathbb{E}\left[V^{1-\beta }(\zeta \left(0\right),\tilde{\theta }\left(0\right))\right]-{\left({\displaystyle \frac{b_0}{(1-\eta )a_0}}\right)}^{{\displaystyle \frac{(-\beta )}{\beta }}}\right]$, where $\zeta \left(0\right)={[{\zeta }_1\left(0\right),\dots ,{\zeta }_n\left(0\right)]}^T$ and $\tilde{\theta }\left(0\right)={[{\tilde{\theta }}_1\left(0\right),\dots ,{\tilde{\theta }}_n\left(0\right)]}^T$. From Lemma 4, for all $t\ge T^{*}$,

$$\mathbb{E}\left[V^{\beta }(\zeta ,\tilde{\theta })\right]\le {\displaystyle \frac{b_0}{(1-\eta )a_0}},$$

(81)

which implies that the closed-loop systems are SGPFS.

Given that ${\zeta }_1=z_1+y_d\left(t\right)$ and considering $-A_1<y_d\left(t\right)<A_1$, it follows that $-k_{b_1}-A_1<{\zeta }_1<k_{b_1}+A_1$. By defining $k_{b_1}=k_{c_1}-A_1$ and $-k_{b_1}=A_1-k_{c_1}$, we obtain $-k_{c_1}<{\zeta }_1<k_{c_1}$. Since ${\zeta }_1$, $z_1$, $y_d$, and ${\widehat{\theta }}_1$ are all bounded, it follows that ${\alpha }_1$ is also bounded with $-A_2<{\alpha }_1<A_2$. Considering ${\zeta }_2=z_2+{\alpha }_1$, it consequently holds that $-k_{b_2}-A_2<{\zeta }_2<k_{b_2}+A_2$. Defining $k_{b_2}=k_{c_2}-A_2$ and $-k_{b_2}=A_2-k_{c_2}$ results in $-k_{c_2}<{\zeta }_2<k_{c_2}$. Similarly, for $i=3,\dots ,n$, it follows that $-k_{c_i}\le {\zeta }_i\le k_{c_i}$. Therefore, all state constraints are satisfied, completing the proof. □

Figure 1 illustrates the block diagram of the proposed control methodology. This diagram visually represents the structure and interaction of various components within the control scheme.

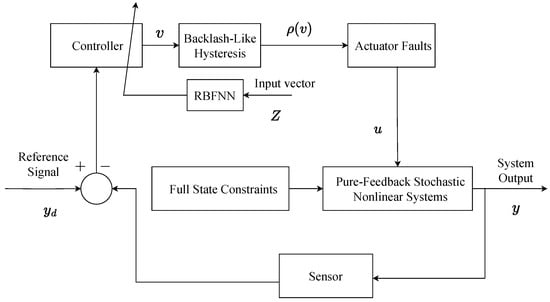
Figure 1. Block diagram of the proposed control method.

Remark 3.

While existing literature extensively covers methods for achieving full state constraints in infinite-time tracking control problems [32,36], practical industrial systems often require achieving control objectives within finite time. This paper addresses this gap by detailing an adaptive finite-time control approach for stochastic nonlinear systems. The method accommodates full state constraints, actuator faults, and backlash-like hysteresis, enhancing its applicability to real-world industrial settings.

Remark 4.

From (30), (45), and (65), it is observed that the estimation of the neural network weight vector’s norm is prioritized over tracking the complete weight vector itself. This strategic use of adaptive law (70) ensures that only n parameters need updating across the entire system. As a result, this approach substantially minimizes the online computational load required by the controller.

Remark 5.

Theorem 1 indicates that the tracking error $z_1$ is influenced by the parameters $a_0$ and $b_0$. Reducing ${\gamma }_i$ while increasing ${\lambda }_i$ and ${\sigma }_i$ can result in smaller tracking errors, improving the system’s tracking performance. However, increasing ${\lambda }_i$ and ${\sigma }_i$ or decreasing ${\gamma }_i$ also leads to higher control energy consumption. Therefore, careful selection of these design parameters is crucial to achieve a proper balance between tracking accuracy and control efficiency. In practical implementation, the parameters are determined through a systematic trial and error procedure. Initially, moderate values of ${\lambda }_i$, ${\sigma }_i$, and ${\gamma }_i$ are chosen and the system is simulated. Based on the observed tracking performance and control energy, the parameters are iteratively adjusted. This process is repeated until satisfactory tracking accuracy is obtained while maintaining reasonable control effort, ensuring the controller performs effectively under the given system constraints and uncertainties.

Remark 6.

The proposed adaptive finite-time control scheme has strong application value in practical engineering systems where reliability and safety are essential. The ability to handle actuator faults, backlash-like hysteresis, stochastic disturbances, and full state constraints simultaneously makes the method suitable for multi-agent coordination, robotic manipulators, autonomous vehicles, and other safety-critical systems. In such applications, ensuring that all system states remain within prescribed bounds while achieving fast and accurate tracking is crucial for maintaining stable and safe operation.

4. Simulation Results

To illustrate the efficacy and reliability of the proposed control strategy, a numerical example and a practical example involving a rigid robot manipulator are presented in this section.

Example 1.

Consider the pure-feedback stochastic nonlinear system as

$$\left\{\begin{array}{c}d{\zeta }_1=({\zeta }_1^2+5{\zeta }_2+0.5sin{\zeta }_1^2)dt+sin{\zeta }_{1}dw,\hfill \\ d{\zeta }_2=({\zeta }_2^{2}sin{\zeta }_2^2+3u+sin{u}^2)dt+cos\left({\zeta }_1{\zeta }_2\right)dw,\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(82)

where ${\zeta }_1$ and ${\zeta }_2$ are the state variables with $\left|\zeta \right|<k_{c_1}=1.5$, $|{\zeta }_2| <k_{c_2}=2$, y is the system output, and u is the system output. The control objective is for the system output y to track the reference signal $y_d=0.6sin\left(0.5t\right)+0.5sin\left(t\right)$.

The model of actuator fault (4) is taken as

$$u\left(v\right)\left\{\begin{array}{cc}v,\hfill & if t<10\hfill \\ (0.2+0.8exp(-0.2t))\rho \left(v\right)+{cos}^2\left({\zeta }_1\right){\zeta }_2,\hfill & otherwise.\hfill \end{array}\right.$$

(83)

where $\varkappa \left(t\right)=0.2+0.8exp(-0.2t))$, and $\varpi \left(t\right)={cos}^2\left({\zeta }_1\right){\zeta }_2$. The parameter of the backlash-like hysteresis (5) are chosen as $B_1=0.345$, $\alpha =1$, and $c=3.1635$.

The virtual controller ${\alpha }_1$, real controller v, and the adaptive law ${\widehat{\theta }}_j$ are chosen as

$$\begin{array}{cc}\hfill {\alpha }_1& =-{\lambda }_1{\displaystyle \frac{z_1^{4\beta -3}}{{(k_{b_1}^4-z_1^4)}^{\beta -1}}}-{\displaystyle \frac{z_1^3}{2(k_{b_1}^4-z_1^4)}}\hfill \\ \hfill & -{\displaystyle \frac{z_1^3{\widehat{\theta }}_1{\parallel P_1\left(Z_1\right)\parallel }^2}{2{\gamma }_1^2(k_{b_1}^4-z_1^4)}}-{\displaystyle \frac{3z_1}{4{(k_{b_1}^4-z_1^4)}^{\frac{1}{3}}}},\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill v& =-{\lambda }_2{\displaystyle \frac{z_2^{4\beta -3}}{{(k_{b_2}^4-z_2^4)}^{\beta -1}}}-{\displaystyle \frac{z_2^3}{2(k_{b_2}^4-z_2^4)}}-{\displaystyle \frac{z_2^3{\widehat{\theta }}_2{\parallel P_2\left(Z_2\right)\parallel }^2}{2{\gamma }_2^2(k_{b_2}^4-z_2^4)}},\hfill \end{array}$$

(85)

$${\dot{\widehat{\theta }}}_j=-{\sigma }_j{\widehat{\theta }}_j+{\displaystyle \frac{1}{2{\gamma }_j^2}}{\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{{(k_{bj}^4-z_j^4)}^2}},j=1,2.$$

(86)

The initial condition are set as ${[{\zeta }_1\left(0\right),{\zeta }_2\left(0\right)]}^T={[0.5,0.5]}^T$, ${[{\widehat{\theta }}_1\left(0\right),{\widehat{\theta }}_2\left(0\right)]}^T={[0,0]}^T$. The design parameters are ${\lambda }_1=6$, ${\lambda }_2=4$, ${\sigma }_1=0.01$, ${\sigma }_2=0.01$, ${\gamma }_1=0.3$, ${\gamma }_2=0.3$, $\beta ={\displaystyle \frac{118}{121}}$, $k_{b_1}=1.1$, $k_{b_2}=1.74$.

The RBF neural networks are set up as follows: $W_1^T{P}_1\left(Z_1\right)$ consists of 49 nodes evenly spread across the interval $[-5,5]\times [-5,5]$ with a width of two, while $W_2^T{P}_2\left(Z_2\right)$ includes 343 nodes uniformly distributed over $[-5,5]\times [-5,5]\times [-5,5]$ with the width 2.

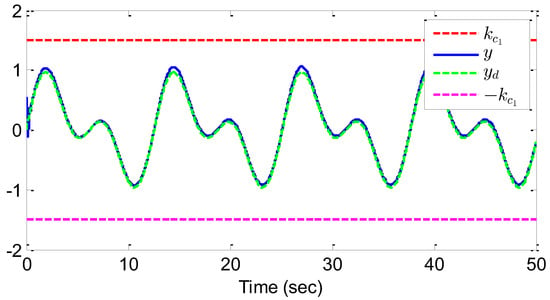
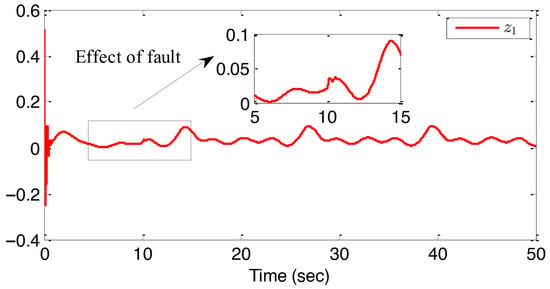
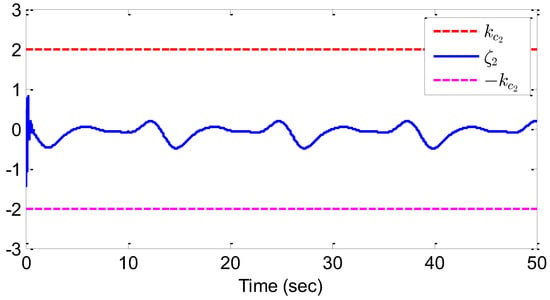
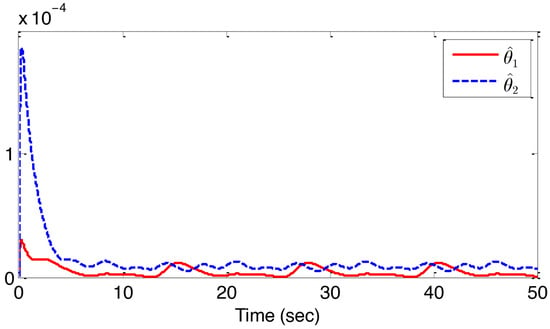
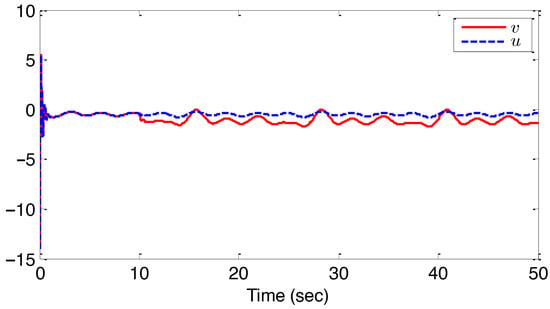
The results from Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 highlight important observations. Figure 2 shows how the output y closely tracks the expected signal $y_d$ within a finite time, while ensuring all states remain within their specified bounds. Figure 3 details the tracking error $z_1$ between the output and the reference signal. In Figure 4, the state ${\zeta }_2$ adheres to its defined constraints. Figure 5 illustrates the stabilization of the adaptive parameters ${\widehat{\theta }}_1$ and ${\widehat{\theta }}_2$. Finally, Figure 6 presents the behavior of both the actual control input v and the system input u. These figures collectively demonstrate the efficacy of the proposed control method in maintaining system variables within bounds and achieving convergence in tracking error.

Figure 2. Trajectories of y and $y_d$ for example 1.

Figure 3. The response of the tracking error $z_1$ for example 1.

Figure 4. The response of the state variable ${\zeta }_2$ for example 1.

Figure 5. Trajectories of the adaptive laws ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$ for example 1.

Figure 6. Control input v and system input u for example 1.

To evaluate the effectiveness of the proposed finite-time adaptive control scheme, a comparison is made with the existing adaptive control method reported in [48]. The performance metrics used for the comparison are defined as follows [60]:

$$\begin{array}{cc}\hfill \mathit{Output}\mathit{Index}& =\sum _{k=1}^M{[y\left(k\right)-y_d\left(k\right)]}^2,\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill \mathit{Control}\mathit{Effort}\mathit{Index}& =\sum _{k=1}^M{\left[u\left(k\right)\right]}^2,\hfill \end{array}$$

(88)

where M represents the total number of sampling points. The indexes are calculated over the simulation period from 0 to 50 s with a sampling interval of 0.01 s. Table 1 presents a detailed comparison of the proposed method with the existing method reported in [48]. It is evident that the proposed finite-time adaptive control scheme achieves smaller output tracking errors and comparable or reduced control effort compared to the existing method. This demonstrates the superior performance of the proposed strategy in ensuring accurate tracking while maintaining efficient control input.

Table 1. Performance comparison between the proposed method and the existing method [48] for example 1.

Indexes	Proposed Method	Existing Method [48]
Output Index	7.7010	8.1984
Control Effort Index	1990.8969	1917.3034

The improved performance of the proposed method can be attributed to the integration of finite-time adaptive control with barrier Lyapunov functions, which enforces state constraints and accelerates convergence of the tracking error. By contrast, the existing method in [48] relies on conventional adaptive control, which does not explicitly guarantee finite-time convergence or effectively handle state constraints. Consequently, the proposed strategy not only achieves faster and more accurate tracking but also maintains all system states within predefined safe bounds, highlighting its practical advantages in stochastic nonlinear systems with actuator faults and hysteresis.

Example 2.

To further substantiate the efficacy of the proposed approach, we examine a practical scenario involving a rigid robot manipulator system affected by stochastic disturbances [18]. The system dynamics are governed by

$$\left\{\begin{array}{c}{\dot{\zeta }}_1={\zeta }_2,\hfill \\ {\dot{\zeta }}_2={\displaystyle \frac{1}{I_c}}(m_l\ddot{q}-m_{g}rcos\left({\zeta }_1\right)+u),\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(89)

where ${\zeta }_1$ and ${\zeta }_2$ denote the state variables, y represents the system output, and u is the actual control input. Specifically, ${\zeta }_1$ and ${\zeta }_2$ correspond to the angular position and relative angular velocity of the manipulator, respectively. Parameters $m_l$, $m_g$, r, and $l_m$ denote the load mass, gravitational constant, length of the manipulator, and $I_c={\displaystyle \frac{4}{3}}{m}_l^2$ represents the inertia coefficient. Given the presence of stochastic disturbances inherent in practical rigid robot manipulator systems, the system (89) is adjusted as follows:

$$\left\{\begin{array}{c}d{\zeta }_1={\zeta }_2+0.1sin\left({\zeta }_1^2\right)d\omega ,\hfill \\ d{\zeta }_2={\displaystyle \frac{1}{I_c}}(m_l{l}_m{g}_{r}cos\left({\zeta }_1\right)+u)+0.1{\zeta }_{2}cos\left({\zeta }_1\right)d\omega ,\hfill \\ y={\zeta }_1,\hfill \end{array}\right.$$

(90)

where ${\zeta }_1$ and ${\zeta }_2$ are the state variables, with $\left|\zeta \right|<k_{c_1}=1.5$, $|{\zeta }_2|< k_{c_2}=1.5$, y is the system output, and u is the system output. The control objective is for the system output y to track the reference signal $y_d=sin\left(t\right)$.

The model of actuator fault (4) is taken as

$$u\left(v\right)\left\{\begin{array}{cc}v,\hfill & if t<10\hfill \\ (0.2+0.8exp(-0.2t))\rho \left(v\right)+{cos}^2\left({\zeta }_1\right){\zeta }_2,\hfill & otherwise.\hfill \end{array}\right.$$

(91)

where $\varkappa \left(t\right)=0.2+0.8exp(-0.2t))$, and $\varpi \left(t\right)={cos}^2\left({\zeta }_1\right){\zeta }_2$. The parameter of the backlash-like hysteresis (5) are chosen as $B_1=0.345$, $\alpha =1$, and $c=3.1635$.

The virtual controller ${\alpha }_1$, real controller v, and the adaptive law ${\widehat{\theta }}_j$ are chosen as

$$\begin{array}{cc}\hfill {\alpha }_1& =-{\lambda }_1{\displaystyle \frac{z_1^{4\beta -3}}{{(k_{b_1}^4-z_1^4)}^{\beta -1}}}-{\displaystyle \frac{z_1^3}{2(k_{b_1}^4-z_1^4)}}\hfill \\ \hfill & -{\displaystyle \frac{z_1^3{\widehat{\theta }}_1{\parallel P_1\left(Z_1\right)\parallel }^2}{2{\gamma }_1^2(k_{b_1}^4-z_1^4)}}-{\displaystyle \frac{3z_1}{4{(k_{b_1}^4-z_1^4)}^{\frac{1}{3}}}},\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill v& =-{\lambda }_2{\displaystyle \frac{z_2^{4\beta -3}}{{(k_{b_2}^4-z_2^4)}^{\beta -1}}}-{\displaystyle \frac{z_2^3}{2(k_{b_2}^4-z_2^4)}}-{\displaystyle \frac{z_2^3{\widehat{\theta }}_2{\parallel P_2\left(Z_2\right)\parallel }^2}{2{\gamma }_2^2(k_{b_2}^4-z_2^4)}},\hfill \end{array}$$

(93)

$${\dot{\widehat{\theta }}}_j=-{\sigma }_j{\widehat{\theta }}_j+{\displaystyle \frac{1}{2{\gamma }_j^2}}{\displaystyle \frac{z_j^6{\parallel P_j\left(Z_j\right)\parallel }^2}{{(k_{bj}^4-z_j^4)}^2}},j=1,2.$$

(94)

The initial conditions are set as ${[{\zeta }_1\left(0\right), {\zeta }_2\left(0\right)]}^T={[0.5, 0.5]}^T$ and ${[{\widehat{\theta }}_1\left(0\right), {\widehat{\theta }}_2\left(0\right)]}^T={[0, 0]}^T$. The design parameters are ${\lambda }_1=6$, ${\lambda }_2=4$, ${\sigma }_1=0.01$, ${\sigma }_2=0.01$, ${\gamma }_1=0.3$, ${\gamma }_2=0.3$, $\beta ={\displaystyle \frac{118}{121}}$, $k_{b_1}=1.1$, and $k_{b_2}=1.74$. The RBF neural networks are configured as follows: $W_1^T{P}_1\left(Z_1\right)$ consists of 49 nodes evenly distributed across the interval $[-5,5]\times [-5,5]$ with a width of 2, while $W_2^T{P}_2\left(Z_2\right)$ includes 343 nodes uniformly spread over $[-5,5]\times [-5,5]\times [-5,5]$ with a width of 2.

The simulation results, depicted in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, highlight several significant findings. Figure 7 illustrates the accurate tracking of the output y with the desired signal $y_d$ within a finite time, ensuring all states remain within their specified limits. Figure 8 presents the tracking error $z_1$ between the output and the reference signal. In Figure 9, the state ${\zeta }_2$ is shown to adhere to its designated constraints. Figure 10 demonstrates the rapid stabilization of the adaptive parameters ${\widehat{\theta }}_1$ and ${\widehat{\theta }}_2$. Finally, Figure 11 provides an overview of the actual control input v alongside the system input u. Together, these figures collectively affirm the effectiveness of the proposed control method in maintaining bounded system variables and achieving convergence in tracking error.

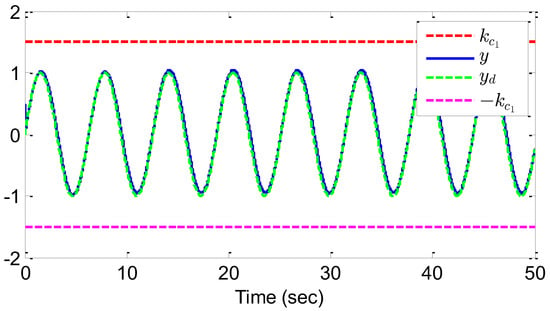
Figure 7. Trajectories of y and $y_d$ for example 2.

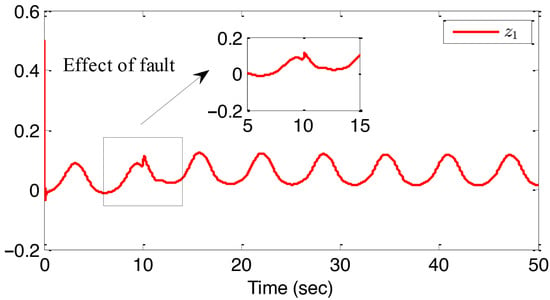
Figure 8. The response of the tracking error $z_1$ for example 2.

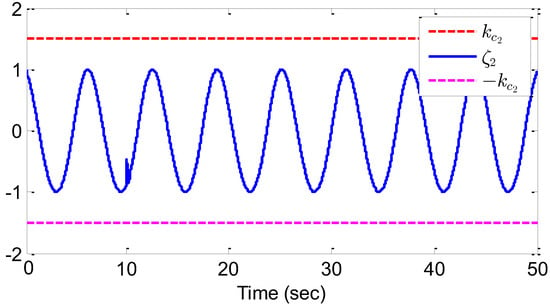
Figure 9. The response of the state variable ${\zeta }_2$ for example 2.

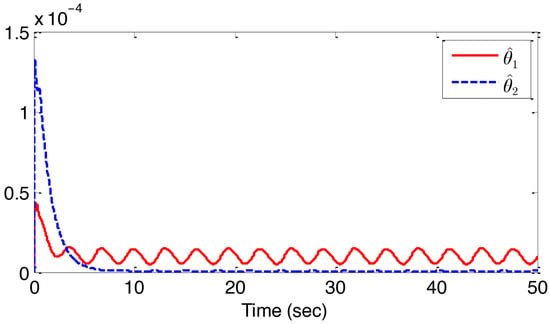
Figure 10. Trajectories of the adaptive laws ${\widehat{\theta }}_1$, ${\widehat{\theta }}_2$ for example 2.

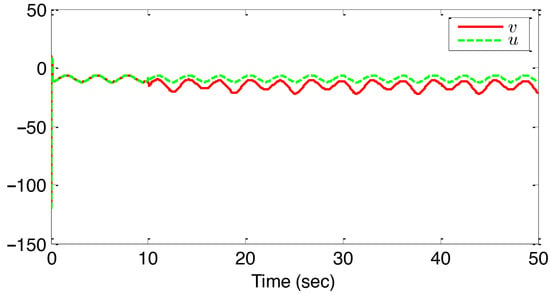
Figure 11. Control input v and system input u for example 2.

Similar to the Example 1, performance indexes are used to compare the effectiveness of the proposed finite-time adaptive control method with the existing traditional adaptive control scheme reported in [48]. Table 2 presents the comparison results. The proposed finite-time adaptive control method achieves smaller tracking errors while maintaining comparable control effort relative to the traditional adaptive control scheme. These results demonstrate that the proposed strategy provides faster convergence and improved accuracy, while effectively handling system uncertainties and constraints.

Table 2. Performance comparison between the proposed method and the existing method [48] for example 2.

Indexes	Proposed Method	Existing Method [48]
Output Index	7.2229	9.1997
Control Effort Index	3045.0747	2630.9075

The superior performance of the proposed method arises from the integration of finite-time adaptive control with barrier Lyapunov functions, which ensures rapid tracking and enforces state constraints. In contrast, the traditional method does not explicitly guarantee finite-time convergence or fully enforce state constraints, which accounts for the observed differences in performance.

Remark 7.

The feasibility of Theorem 1 is guaranteed by the design of the virtual and real controllers along with the adaptive laws, which ensure that all state variables remain within prescribed boundaries and that the tracking error converges in finite time. The controller parameters can be chosen systematically using a trial-and-error procedure or by following the stability analysis guidelines. The practical applicability of Theorem 1 is further illustrated through simulations, including a numerical example and a rigid robot manipulator system. The results demonstrate that the proposed controller can be effectively implemented, confirming the feasibility of Theorem 1 in both theoretical and practical scenarios.

Remark 8.

The proposed adaptive finite-time control methodology can be potentially extended to other classes of nonlinear systems. For instance, it can be applied to networked multi-agent systems using pinning-based neural control with self-regulation intermediate event-triggered mechanisms [61], as well as to multiple networked mechanical systems employing event-based adaptive sliding-mode containment control under parameter uncertainties [62]. The key design principles, including adaptive neural network approximation, barrier Lyapunov functions, and finite-time backstepping, provide a systematic framework to ensure stability, handle state constraints, and achieve accurate tracking in these more complex scenarios. Therefore, the proposed approach demonstrates flexibility and applicability beyond the stochastic pure-feedback nonlinear systems considered in this study.

5. Conclusions

This article presents an adaptive finite-time control method for pure-feedback stochastic nonlinear systems subject to actuator faults, full state constraints, and backlash-like hysteresis. The proposed approach employs RBFNNs to approximate unknown system functions. By integrating the Barrier Lyapunov Function with the backstepping technique, the method ensures semiglobal practical finite-time stability of all signals in the closed-loop system, maintaining system states within predefined boundaries and enabling the output to track the reference signal efficiently within finite time. Simulation results demonstrate the effectiveness of the proposed control scheme. Compared to the existing adaptive control method [48], the proposed strategy achieves lower tracking errors and reduced control effort, as reflected in Table 1 and Table 2. For instance, the output tracking index and control input index indicate a significant improvement, highlighting the capability of the method to handle actuator faults, hysteresis, and state constraints effectively. These quantitative comparisons clearly confirm the superior performance and reliability of the proposed control approach. The insights from this study suggest several directions for further research. Future work can focus on addressing input quantization effects and extending the control methodology to achieve fixed-time stability for stochastic nonlinear systems. Additionally, applying the proposed strategy to more complex practical systems, such as multi-degree-of-freedom robotic manipulators or networked cyber–physical systems, can validate its scalability and robustness. Integration of advanced learning-based estimation and optimization techniques may further improve performance under uncertainties and external disturbances, offering a pathway to develop more practical and resilient control strategies in related research areas.