Proper Strict Efficiency in Set Optimization with Partial Set Order Relation

Abstract

This paper is devoted to the investigation of the proper strict efficient solutions to a set optimization problem with a partial set order relation. Firstly, the notion of proper strict efficient solution defined by the Minkowski difference is introduced, and it is worth mentioning that the introduced strict efficiency is different from those in the existing literature. Secondly, a class of generalized contingent derivatives for set-valued maps is proposed, which are characterized in terms of a set criterion. Finally, the necessary and sufficient optimality conditions and a scalarization theorem for proper strict efficiency are established. Some concrete examples are given to illustrate the obtained results.

1. Introduction

Set optimization is a primary approach to addressing set-valued optimization problems and has been widely studied in uncertain multi-objective programming [1], optimality conditions [2], and higher-order derivatives [3,4]. Kuroiwa [5] pointed out that there is a lack of a total order relationship between sets, so it is necessary to introduce some set order relations to enable the comparison between two sets. Currently, Jahn [6] has already summarized some order relations, including the upper set order relation, lower set order relation, minmax set order relation, and others. However, the order relations presented in [6] are preorder relations. To address this, Karaman et al. [7] defined a kind of partial set order relation using the Minkowski difference.

Strict efficiency is an important concept for optimization problems, and it has been applied in sensitivity analysis [8] and convergence analysis of algorithms [9]. Because of the wide applications of strict efficiency, many authors have been interested in extending it to the set-valued maps. For example, Flores [10] developed a kind of strict local efficient solutions and obtained optimality conditions for a set-valued optimization problem; Mohamed [11] proposed the concept of directional strict efficiency and established its optimality for a set-valued equilibrium problem; Another strict efficiency associated with preference mappings was presented in [12], and its higher-order optimality theorems for a set-valued optimization problem were obtained. For more details on strict efficiency, see [13,14,15,16,17,18]. Recently, Huerga et al. [19] presented the notion of Henig proper strict efficient solution for a set optimization problem with a lower set order relation and investigated some of its properties. Motivated by [19], this paper attempts to introduce a class of proper strict efficient solutions for a set optimization problem related to the partial set order relation and establish its optimality conditions.

The derivative and its generalization are powerful tools to establish optimality conditions for set optimization problems. For instance, Yao [3] introduced the notion of generalized radial derivative and used it to derive second-order optimality conditions for a set optimization problem with a lower set order relation; Yu [4] applied a kind of higher-order radial derivative to establish optimality theorems for a constrained set optimization problem with respect to a weak lower set order relation. Our purpose is to give a class of generalized contingent derivatives of set-valued maps and employ them to construct optimality conditions for a set optimization problem associated with the partial set order relation. Further, Khushboo et al. [20] established a scalarization theorem for the partial set order relation using the oriented distance. This paper aims to obtain the corresponding scalarization results via a different function.

This paper is organized as follows: Section 2 recalls some basic notions, definitions, and lemmas needed in the sequel. Section 3 introduces the concept of a proper strict efficient solution for a set optimization problem and discusses some of its properties. Section 4 gives a kind of generalized contingent derivative defined by a set criterion and utilizes it to establish necessary and sufficient optimality conditions for proper strict efficient solution. Finally, a scalarization theorem is obtained in Section 5.

2. Preliminaries

Let $X,$ Y be two normed spaces, and let $\mathbb{N}$ and ${\mathbb{R}}^n$ be the set of natural numbers and n-dimensional Euclidean space, respectively. $\mathbb{B}(\overline{x},r)$ stands for the open ball with center $\overline{x}\in {\mathbb{R}}^n$ and radius $r>0$, and

$${\mathbb{R}}_{+}^n=\{x\in {\mathbb{R}}^n:x_i\ge 0,i=1,\dots ,n\},{\mathbb{R}}_{++}^n=\{x\in {\mathbb{R}}^n:x_i>0,i=1,\dots ,n\}.$$

Let $E\subset X$ be a nonempty subset; $intE$, $coE$, and $E^c$ denote the interior, the convex hull, and the complement of E, respectively; and let the cone generated by E be $coneE=\{\lambda x:\lambda \ge 0,x\in E\}$. The tangent cone of set E at $\overline{x}\in E$ is given by (see [21])

$$T(E;\overline{x}):=\{d\in X:\exists t_n\to 0^{+},\exists d_n\to d,s.t.\overline{x}+t_n{d}_n\in E,\forall n\in \mathbb{N}\}.$$

(1)

Given a set-valued map $F:X\rightrightarrows Y$, we denote the domain, graph, epigraph, and profile map of F, respectively, by

$$dom\left(F\right):=\{x\in X:F(x)\ne \varnothing \},gr\left(F\right):=\left\{\right(x,y)\in X\times Y:y\in F(x\left)\right\},$$

$$epi\left(F\right):=\{(x,y)\in X\times Y:y\in F\left(x\right)+K\},F_{+}\left(x\right):=F\left(x\right)+K.$$

Throughout the paper, let $K\subset Y$ be a nonempty pointed closed convex cone, and let $P\left(Y\right)$ denote the family of all nonempty bounded subsets in Y. For $A,B\in P\left(Y\right)$, the algebraic sum and Minkowski difference of A and B are defined by [7]

$$A+B:=\{a+b:a\in A,b\in B\},A\dot{-}B:=\{y\in Y:y+B\subset A\}=\bigcap _{b\in B}(A-b).$$

Lemma 1 

([2,7]). Let $A,B\in P\left(Y\right)$ and $y\in Y.$ Then the following assertions hold:

(i) $A\dot{-}A=\left\{0\right\}$;

(ii) $(y+A)\dot{-}B=y+\left(A\dot{-}B\right)$;

(iii) $A\dot{-}(y+B)=-y+\left(A\dot{-}B\right)$;

(iv) $A\dot{-}y=A-y$.

Next, we recall a partial set order relation defined by the Minkowski difference.

Definition 1 

([7]). Let $A,B\in P\left(Y\right)$ be arbitrary chosen sets. The partial set order relation with respect to K, denoted by ${⪯}_K^m$, is defined as

$$A{⪯}_K^{m}B⟺\left(A\dot{-}B\right)\cap (-K)\ne \varnothing .$$

3. Proper Strict Efficiency

Let $F:X\rightrightarrows Y$ be a set-valued map and $\Omega \subset X$ be a nonempty subset. We consider the following Set Optimization Problem

$$\left(\mathrm{SOP}\right)\min F\left(x\right),\mathrm{s}.\mathrm{t}.x\in \Omega .$$

It is always assumed that $F\left(x\right)\dot{-}F\left(y\right)$ is nonempty for all $x,y\in \Omega$ in the paper.

Definition 2 

([20]). In problem (SOP), $\overline{x}\in \Omega$ is called a ${⪯}_K^m$-efficient solution, denoted by $\overline{x}\in E(F,{⪯}_K^m)$, if there is no $x\in \Omega$ such that $F\left(x\right){⪯}_K^{m}F\left(\overline{x}\right)$ and $F\left(x\right)\ne F\left(\overline{x}\right)$, that is,

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing orF\left(\overline{x}\right)=F\left(x\right),\forall x\in \Omega .$$

Next, we introduce two concepts of strict efficient solutions related to ${⪯}_K^m$ for problem (SOP).

Definition 3. 

In problem (SOP),

(i) $\overline{x}\in \Omega$ is called a strict ${⪯}_K^m$-efficient solution, denoted by $\overline{x}\in S(F,{⪯}_K^m)$, if $F\left(x\right){\cancel{⪯}}_K^m F\left(\overline{x}\right)$ for all $x\in \Omega \setminus \left\{\overline{x}\right\}$, i.e.,

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(2)

(ii) $\overline{x}\in \Omega$ is called a proper strict ${⪯}_K^m$-efficient solution, denoted by $\overline{x}\in P(F,{⪯}_K^m)$, if there exists $\alpha >0$ such that

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(3)

Here is an example to illustrate the concepts of Definition 3.

Example 1. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =[1,+\infty )$ and

$$F\left(x\right)=\{(a,b)\in {\mathbb{R}}^2:a=x,b\ge x^2+1\},\forall x\in \Omega .$$

Let $\overline{x}=1$, it yields $F\left(1\right)=\{(a,b)\in {\mathbb{R}}^2:a=1,b\ge 2\}$. Since

$$F\left(x\right)\dot{-}F\left(1\right)=\left\{(x,x^2)\right\}\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{1\right\},$$

we obtain $\overline{x}=1$ is a strict ${⪯}_K^m$-efficient solution. In addition, there exists $\alpha ={\displaystyle \frac{1}{3}}$ such that

$$\left(F\left(x\right)\dot{-}F\left(1\right)\right)\cap \left(\mathbb{B}(0,{\displaystyle \frac{1}{3}}(x-1))-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{1\right\}.$$

Thus, $\overline{x}=1$ is also a proper strict ${⪯}_K^m$-efficient solution.

Remark 1. 

 (i) In terms of form, Definition 3 (ii) of this paper differs from those in [10]. If $F\left(\overline{x}\right)=\left\{\overline{y}\right\}$, it follows from Lemma 1 (iv) that $F\left(x\right)\dot{-}F\left(\overline{x}\right)=F\left(x\right)\dot{-}\left\{\overline{y}\right\}=F\left(x\right)-\overline{y}$. Then, Definition 3 (ii) reduces to the strict efficient solution in [10].

(ii) In terms of applicability, Definition 3 (i) of this paper is distinct from those in [19]. In [19], $\overline{x}\in \Omega$ is called the strict ${⪯}_H^l$-Henig proper solution of problem (SOP) if there is no $x\in \Omega \setminus \left\{\overline{x}\right\}$ such that $F\left(x\right){⪯}_H^{l}F\left(\overline{x}\right)$, that is,

$$F\left(\overline{x}\right)\cancel{\subset }F\left(x\right)+H,\forall x\in \Omega \setminus \left\{\overline{x}\right\},$$

where H is a pointed closed convex cone and $K\setminus \left\{0\right\}\subset intH$. An example is given below to illustrate the validity of Remark 1 (ii).

Example 2. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =\{0,1,2\}$, $H=\{(x,y)\in {\mathbb{R}}^2:y\ge -{\displaystyle \frac{1}{2}}x,y\ge -2x\}$ and

$$\begin{array}{c}\hfill F\left(x\right)=\left\{\begin{array}{c}co\left\{\right(0,0),(3,0\left)\right\},x=0,\hfill \\ co\left\{\right(-3,1),(0,1\left)\right\},x=1,\hfill \\ co\left\{\right(-6,2),(-3,2\left)\right\},x=2.\hfill \end{array}\right.\end{array}$$

Let $\overline{x}=0$, there exists $\alpha ={\displaystyle \frac{1}{4}}$ such that

$$\left(F\left(x\right)\dot{-}F\left(0\right)\right)\cap (\mathbb{B}(0,{\displaystyle \frac{1}{4}}x)-K)=\varnothing ,\forall x\in \Omega \setminus \left\{0\right\}.$$

Hence, $\overline{x}=0$ is a proper strict ${⪯}_K^m$-efficient solution.

However, as seen in Figure 1, there exists $\widehat{x}=1\in \Omega \setminus \left\{0\right\}$ such that

$$F\left(0\right)\subset F\left(1\right)+H.$$

Thus, $\overline{x}=0$ is not a strict ${⪯}_H^l$-Henig proper solution.

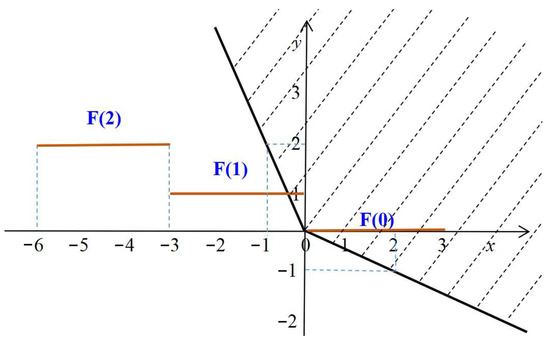
Figure 1. Illustrations of $F\left(x\right)$ and H.

Remark 2. 

In problem (SOP), if $F\left(\overline{x}\right)=\left\{\overline{y}\right\}$ is single-valued, then $F\left(x\right)\dot{-}\left\{\overline{y}\right\}=F\left(x\right)-\overline{y}$. The proper strict ${⪯}_K^m$-efficient solution becomes the following form

$$\left(F\left(x\right)-\overline{y}\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

In this case, it is also different from the Henig proper minimal solution defined in literature [19]. A point $\overline{x}\in \Omega$ is called a Henig proper minimal solution of problem (SOP) if there exists $\overline{y}\in F\left(\overline{x}\right)$ such that

$$\left(F\left(x\right)-\overline{y}\right)\cap (-H\setminus \left\{0\right\})=\varnothing ,\forall x\in \Omega ,$$

where H is a pointed closed convex cone and $K\setminus \left\{0\right\}\subset intH$. This fact can be illustrated by the following two examples.

Example 3. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =[0,2]$, and $H=\{(x,y)\in {\mathbb{R}}^2:y\ge -{\displaystyle \frac{1}{2}}x,y\ge -2x\}$. Define

$$\begin{array}{c}\hfill F\left(x\right)=\left\{\begin{array}{c}\left\{\right(0,1\left)\right\},x=[0,1),\hfill \\ \left\{1\right\}\times [1,3],x=[1,2].\hfill \end{array}\right.\end{array}$$

Take $\overline{x}=0$, we derive $\overline{y}=(0,1)\in F\left(\overline{x}\right)$. Due to

$$\left(F\left(x\right)-\overline{y}\right)\cap (-H\setminus \left\{0\right\})=\varnothing ,\forall x\in \Omega ,$$

we conclude $\overline{x}=0$ is a Henig proper minimal solution.

However, for any $\alpha >0$, there exists $\widehat{x}={\displaystyle \frac{1}{2}}\in \Omega \setminus \left\{0\right\}$ such that

$$F\left({\displaystyle \frac{1}{2}}\right)\dot{-}F\left(\overline{x}\right)=F\left({\displaystyle \frac{1}{2}}\right)-\overline{y}=\left\{(0,0)\right\}\cap (\mathbb{B}(0,{\displaystyle \frac{\alpha }{2}})-K)\ne \varnothing .$$

Consequently, $\overline{x}=0$ is not a proper strict ${⪯}_K^m$-efficient solution.

Example 4. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =[0,1]$, $H=\{(x,y)\in {\mathbb{R}}^2:y\ge -{\displaystyle \frac{1}{2}}x,y\ge -2x\}$ and

$$\begin{array}{c}\hfill F\left(x\right)=\left\{\begin{array}{c}\left\{\right(0,0\left)\right\},x=0,\hfill \\ co\{(-x,x+{\displaystyle \frac{3}{2}}),(-x-1,x+{\displaystyle \frac{3}{2}})\},x\ne 0.\hfill \end{array}\right.\end{array}$$

Let $\overline{x}=0$, then $\overline{y}=(0,0)\in F\left(0\right)$. For all $x\in \Omega \setminus \left\{0\right\}$, there exists $\alpha ={\displaystyle \frac{1}{4}}$ such that

$$\left(F\left(x\right)\dot{-}F\left(0\right)\right)=\left(F\left(x\right)-\overline{y}\right)\cap (\mathbb{B}(0,{\displaystyle \frac{1}{4}}x)-K)=\varnothing .$$

Hence, $\overline{x}=0$ is a proper strict ${⪯}_K^m$-efficient solution.

However, there exists $\widehat{x}=1\in \Omega \setminus \left\{0\right\}$ such that

$$\left(F\left(1\right)-\overline{y}\right)\cap (-H\setminus \left\{0\right\})\ne \varnothing .$$

Thus, $\overline{x}=0$ is not a Henig proper minimal solution.

Some properties of the proper strict ${⪯}_K^m$-efficient solution are listed below.

Lemma 2. 

In problem (SOP), the following statements hold:

(i) $P(F,{⪯}_K^m)\subset S(F,{⪯}_K^m)\subset E(F,{⪯}_K^m)$;

(ii) If $K_1\subset K_2\subset Y$, then $P(F,{⪯}_{K_2}^m)\subset P(F,{⪯}_{K_1}^m)$ and $S(F,{⪯}_{K_2}^m)\subset S(F,{⪯}_{K_1}^m)$;

(iii) $P(F,{⪯}_K^m)=P(F+K,{⪯}_K^m)$;

(iv) $S(F,{⪯}_K^m)=S(F+K,{⪯}_K^m)$.

Proof. 

(i) Firstly, we prove $P(F,{⪯}_K^m)\subset S(F,{⪯}_K^m)$. Let $\overline{x}\in P(F,{⪯}_K^m)$, then there exists $\alpha >0$ such that

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(4)

Suppose that $\overline{x}\notin S(F,{⪯}_K^m)$, there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)\ne \varnothing .$$

This means that there exists $k\in K$ such that

$$-k\in F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right).$$

Since $-k\in -K$ and $-K\subset \mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )-K$, one has

$$-k\in \mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )-K.$$

Consequently, we conclude

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )-K\right)\ne \varnothing ,$$

which contradicts Equation (4). Therefore, $P(F,{⪯}_K^m)\subset S(F,{⪯}_K^m)$ holds.

Now, we verify $S(F,{⪯}_K^m)\subset E(F,{⪯}_K^m)$. Take $\overline{x}\in S(F,{⪯}_K^m)$, it holds

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(5)

Assume that $\overline{x}\notin E(F,{⪯}_K^m)$, then there exists $\widehat{x}\in \Omega$ such that

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)\ne \varnothing andF\left(\widehat{x}\right)\ne F\left(\overline{x}\right).$$

If $\widehat{x}=\overline{x}$, it yields $F\left(\widehat{x}\right)=F\left(\overline{x}\right)$, which contradicts $F\left(\widehat{x}\right)\ne F\left(\overline{x}\right)$. Hence, there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that $\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)\ne \varnothing$. This is a contradiction to Equation (5). Consequently, $S(F,{⪯}_K^m)\subset E(F,{⪯}_K^m)$ holds.

(ii) It follows from Definition 3 that the proof is obvious.

(iii) Assume that $\overline{x}\in P(F+K,{⪯}_K^m)$, there exists $\alpha >0$ such that

$$\left((F\left(x\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(6)

Since K is a pointed closed convex cone, we get $F\left(x\right)\subset F\left(x\right)+K$. Combined with Equation (6), hence,

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

This indicates that $\overline{x}\in P(F,{⪯}_K^m)$.

Next, we testify $P(F,{⪯}_K^m)\subset P(F+K,{⪯}_K^m)$ holds. Let $\overline{x}\in P(F,{⪯}_K^m)$, then there exists $\alpha >0$ such that

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

This indicates that for any $b\in \mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )$ and any $k\in K$

$$b-k\notin F\left(x\right)\dot{-}F\left(\overline{x}\right),\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(7)

Suppose that $\overline{x}\notin P(F+K,{⪯}_K^m)$, then there exists $\widehat{x}\in W\setminus \left\{\overline{x}\right\}$ such that for any $\alpha >0$

$$\left((F\left(\widehat{x}\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )-K\right)\ne \varnothing .$$

This means that there exist $\widehat{b}\in \mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )$ and $\widehat{k}\in K$ such that $\widehat{b}-\widehat{k}\in (F\left(\widehat{x}\right)+K)\dot{-}F\left(\overline{x}\right)$. Since

$$\begin{array}{ccc}\hfill \widehat{b}-\widehat{k}\in (F\left(\widehat{x}\right)+K)\dot{-}F\left(\overline{x}\right)& \iff & \widehat{b}-\widehat{k}+F\left(\overline{x}\right)\subset F\left(\widehat{x}\right)+K\hfill \\ & \iff & \widehat{b}-\widehat{k}+\overline{y}=\widehat{y}+k,\forall \overline{y}\in F\left(\overline{x}\right),\exists \widehat{y}\in F\left(\widehat{x}\right),\exists k\in K\hfill \\ & \iff & \widehat{b}-\widehat{k}-k+\overline{y}=\widehat{y},\forall \overline{y}\in F\left(\overline{x}\right),\exists \widehat{y}\in F\left(\widehat{x}\right),\exists k\in K\hfill \\ & \iff & \widehat{b}-\widehat{k}-k+F\left(\overline{x}\right)\subset F\left(\widehat{x}\right),\exists k\in K\hfill \\ & \iff & \widehat{b}-\widehat{k}-k\in F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right),\exists k\in K,\hfill \end{array}$$

and K is a convex cone, we have $\widehat{k}+k\in K$. Therefore, there exist $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$, $\widehat{b}\in \mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )$ and $(k+\widehat{k})\in K$ such that

$$\widehat{b}-(\widehat{k}+k)\in F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right),$$

which contradicts Equation (7). This implies that $P(F,{⪯}_K^m)\subset P(F+K,{⪯}_K^m)$. Hence, $P(F,{⪯}_K^m)=P(F+K,{⪯}_K^m)$ is true.

(iv) Let $\overline{x}\in S(F+K,{⪯}_K^m)$. By Definition 3, one has

$$\left((F\left(x\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(8)

Since K is a pointed closed convex cone, we have $F\left(x\right)\subset F\left(x\right)+K$. Hence,

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\},$$

which implies that $\overline{x}\in S(F,{⪯}_K^m)$. This shows that $S(F+K,{⪯}_K^m)\subset S(F,{⪯}_K^m)$ holds.

Conversely, if $\overline{x}\in S(F,{⪯}_K^m)$, then

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(9)

Assume that $\overline{x}\notin S(F+K,{⪯}_K^m)$, there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that

$$\left((F\left(\widehat{x}\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap (-K)\ne \varnothing .$$

Hence, there exists $k\in K$ such that $-k+F\left(\overline{x}\right)\subset F\left(\widehat{x}\right)+K$. Since

$$\begin{array}{ccc}\hfill -k+F\left(\overline{x}\right)\subset F\left(\widehat{x}\right)+K& \iff & -k+\overline{y}=\widehat{y}+\widehat{k},\forall \overline{y}\in F\left(\overline{x}\right),\exists \widehat{y}\in F\left(\widehat{x}\right),\exists \widehat{k}\in K\hfill \\ & \iff & -k-\widehat{k}+\overline{y}=\widehat{y},\forall \overline{y}\in F\left(\overline{x}\right),\exists \widehat{y}\in F\left(\widehat{x}\right),\exists \widehat{k}\in K\hfill \\ & \iff & -k-\widehat{k}+F\left(\overline{x}\right)\subset F\left(\widehat{x}\right),\exists \widehat{k}\in K\hfill \\ & \iff & -k-\widehat{k}\in F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right),\exists \widehat{k}\in K,\hfill \end{array}$$

and K is a convex cone, one has $k+\widehat{k}\in K$. Thus, there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that

$$-(k+\widehat{k})\in F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right),$$

which contradicts Equation (9). Hence, we have $\overline{x}\in S(F+K,{⪯}_K^m)$, that is, $S(F,{⪯}_K^m)\subset S(F+K,{⪯}_K^m)$. This shows that $S(F,{⪯}_K^m)=S(F+K,{⪯}_K^m)$ holds. □

In some practical problems, in order to make a rapid and effective decision, people prefer to acquire a smaller decision set. By Lemma 2 (i), it yields $P(F,{⪯}_K^m)\subset S(F,{⪯}_K^m)\subset E(F,{⪯}_K^m)$. This implies that the solution sets $P(F,{⪯}_K^m)$ and $S(F,{⪯}_K^m)$ are two refinements of the solution set $E(F,{⪯}_K^m)$. Therefore, it is of practical significance and value to explore the solution sets $P(F,{⪯}_K^m)$ and $S(F,{⪯}_K^m)$. The following Example 5 is provided to illustrate this fact.

Example 5. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$ and $\Omega =\{1,2,3\}$. Define

$$\begin{array}{c}\hfill F\left(x\right)=\left\{\begin{array}{c}\{(a,b)\in {\mathbb{R}}^2:{(a-1)}^2+{(b-2)}^2=1\},x=1,\hfill \\ \{(a,b)\in {\mathbb{R}}^2:{(a-2)}^2+{(b-1)}^2=1\},x=2,3.\hfill \end{array}\right.\end{array}$$

As seen in Figure 2, since

$$\left(F\left(y\right)\dot{-}F\left(x\right)\right)\cap (-K)=\varnothing orF\left(x\right)=F\left(y\right),\forall x,y\in \Omega ,$$

we get $E(F,{⪯}_K^m)=\{1,2,3\}$. In this case, a decision-maker does not know how to make the choice.

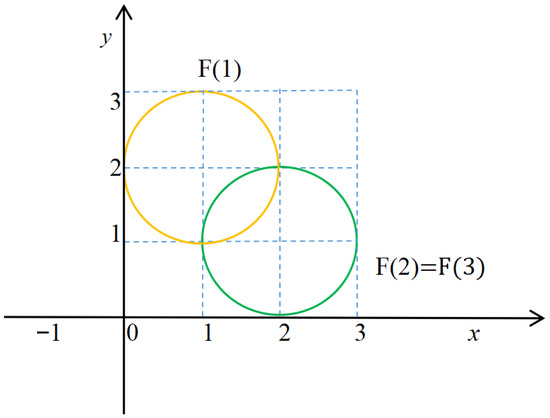
Figure 2. Illustrations of $F\left(x\right)$.

However, we claim $P(F,{⪯}_K^m)=S(F,{⪯}_K^m)=\left\{1\right\}$. Indeed, since

$$F\left(2\right)\dot{-}F\left(1\right)=\left\{(1,-1)\right\},F\left(3\right)\dot{-}F\left(1\right)=\left\{(1,-1)\right\},$$

it leads to

$$\left(F\left(x\right)\dot{-}F\left(1\right)\right)\cap (-K)=\varnothing ,\forall x\in \Omega \setminus \left\{1\right\}.$$

Thus, $\overline{x}=1\in S(F,{⪯}_K^m)$. But, if take $\overline{x}=2$ or $\overline{x}=3$, we have

$$\left(F\left(2\right)\dot{-}F\left(3\right)\right)\cap (-K)\ne \varnothing ,\left(F\left(3\right)\dot{-}F\left(2\right)\right)\cap (-K)\ne \varnothing .$$

Consequently, $\overline{x}=2,3\notin S(F,{⪯}_K^m)$. Furthermore, due to

$$\left(F\left(3\right)\dot{-}F\left(2\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-2\parallel )-K\right)\ne \varnothing ,\forall \alpha >0,$$

$$\left(F\left(2\right)\dot{-}F\left(3\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-3\parallel )-K\right)\ne \varnothing ,\forall \alpha >0,$$

we get $x=2,3\notin P(F,{⪯}_K^m)$. But, when $\overline{x}=1$, for all $x\in \Omega \setminus \left\{1\right\}$, there exists $\alpha ={\displaystyle \frac{1}{3}}$ such that

$$\left(F\left(x\right)\dot{-}F\left(1\right)\right)\cap \left(\mathbb{B}(0,{\displaystyle \frac{1}{3}}\parallel x-1\parallel )-K\right)=\varnothing .$$

Thus, $P(F,{⪯}_K^m)=\left\{1\right\}$.

In literature [10], it has been pointed out that the notation ${lim\; sup}_{x\to \overline{x},x\in \Omega }F\left(x\right)$ denotes the set of all cluster points of sequences $y_n\in F\left(x_n\right)$ with $x_n\to \overline{x}$ and $x_n\in \Omega \setminus \left\{\overline{x}\right\}$. Next, we present an equivalent characterization of proper strict ${⪯}_K^m$-efficient solution, which will play a crucial role in the proof of optimality conditions in Section 4.

Proposition 1. 

In problem (SOP), let $\overline{x}\in \Omega$. $\overline{x}\in P(F,{⪯}_K^m)$ if and only if

$$0\notin \underset{x\to \overline{x},x\in \Omega }{lim\; sup}{\displaystyle \frac{(F\left(x\right)+K)\dot{-}F\left(\overline{x}\right)}{\parallel x-\overline{x}\parallel }}.$$

(10)

Proof. 

Suppose that Equation (10) is not true. Then there exist $x_n\in \Omega \setminus \left\{\overline{x}\right\}$, ${\theta }_n\in (F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right)$ such that $x_n\to \overline{x}$ and

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\theta }_n}{\parallel x_n-\overline{x}\parallel }}=0.$$

This means that for any $\epsilon >0$, there exists $n_{\epsilon }\in \mathbb{N}$, for all $n\ge n_{\epsilon }$, we have $x_n\in \Omega$, $\parallel x_n-\overline{x}\parallel <\epsilon$ and $\parallel {\theta }_n\parallel <\epsilon \parallel x_n-\overline{x}\parallel$. Therefore,

$${\theta }_n\in \mathbb{B}\left(0,\epsilon \parallel x_n-\overline{x}\parallel \right).$$

Since K is a pointed closed convex cone, we get $\mathbb{B}(0,\epsilon \parallel x_n-\overline{x}\parallel )\subset \mathbb{B}(0,\epsilon \parallel x_n-\overline{x}\parallel )-K$. Thus,

$${\theta }_n\in \mathbb{B}(0,\epsilon \parallel x_n-\overline{x}\parallel )-K.$$

Since $\overline{x}\in P(F,{⪯}_K^m)$, according to Lemma 2 (iii), we derive $\overline{x}\in P(F+K,{⪯}_K^m)$. Consequently, there exists $\alpha >0$ such that

$$\left((F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x_n-\overline{x}\parallel )-K\right)=\varnothing .$$

(11)

Let $\epsilon \le \alpha$, then there exists $n_{\epsilon }\in \mathbb{N}$ such that for all $n\ge n_{\epsilon }$ and $x_n\in \Omega$

$${\theta }_n\in \mathbb{B}(0,\epsilon \parallel x_n-\overline{x}\parallel )-K\subset \mathbb{B}(0,\alpha \parallel x_n-\overline{x}\parallel )-K.$$

This contradicts Equation (11).

Conversely. Assume that $\overline{x}\notin P(F,{⪯}_K^m)$. It follows from Lemma 2 (iii) that $\overline{x}\notin P(F+K,{⪯}_K^m)$. Thus, for any $\alpha >0$, there exists $x_n\in \Omega \setminus \left\{\overline{x}\right\}$ such that

$$\left((F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap \mathbb{B}(0,\alpha \parallel x_n-\overline{x}\parallel )\ne \varnothing .$$

This means that there exists $b\in \mathbb{B}(0,\alpha \parallel x_n-\overline{x}\parallel )$ such that

$$b+F\left(\overline{x}\right)\subset F\left(x_n\right)+K.$$

Hence, for any $\overline{y}\in F\left(\overline{x}\right)$, there exist $y_n\in F\left(x_n\right)$, $k_n\in K$ such that

$$y_n+k_n-\overline{y}=b\in \mathbb{B}(0,\alpha \parallel x_n-\overline{x}\parallel ).$$

Particularly, take $\alpha ={\displaystyle \frac{1}{n}}$, then $y_n+k_n-\overline{y}\in \mathbb{B}(0,{\displaystyle \frac{1}{n}}\parallel x_n-\overline{x}\parallel )$, that is,

$$\parallel y_n+k_n-\overline{y}\parallel <{\displaystyle \frac{1}{n}}\parallel x_n-\overline{x}\parallel .$$

Thus, we conclude

$${\displaystyle \frac{y_n+k_n-\overline{y}}{\parallel x_n-\overline{x}\parallel }}\to 0,$$

which contradicts Equation (10). This completes the proof. □

4. Optimality Conditions

This section aims to introduce a class of generalized contingent derivatives and apply them to establish necessary and sufficient optimality conditions for the proper strict ${⪯}_K^m$-efficient solution of problem (SOP). Before that, we give the notion of a generalized contingent cone.

Definition 4. 

Let $S,W\in P\left(Y\right)$. The generalized contingent cone of S on W is defined by

$$T(S;W):=\{d\in X:\exists t_n\to 0^{+},\exists d_n\to d,s.t.t_n{d}_n\in S\dot{-}W,\forall n\in \mathbb{N}\}.$$

(12)

Remark 3. 

(i) It is obvious that if $S\dot{-}W=\varnothing$, then $T(S;W)=\varnothing$.

(ii) Due to $S\dot{-}W=\{y\in Y:y+W\subset S\}={\bigcap }_{\overline{x}\in W}(S-\overline{x})$, then Equation (12) can be equivalently expressed as

$$\begin{array}{ccc}\hfill T(S;W)& =& \{d\in X:\exists t_n\to 0^{+},\exists d_n\to d,s.t.t_n{d}_n+W\subset S,\forall n\in \mathbb{N}\}\hfill \\ & =& \{d\in X:\exists t_n\to 0^{+},\exists d_n\to d,s.t.\forall \overline{x}\in W,\overline{x}+t_n{d}_n\in S,\forall n\in \mathbb{N}\}.\hfill \end{array}$$

(iii) If $W=\left\{\overline{x}\right\}$ is single-valued and $\overline{x}\in S$, then the generalized contingent cone $T(S;W)$ reduces to the contingent cone $T(S;\overline{x})$ in literature [21], that is, Equation (1).

Next, we give an example of a generalized contingent cone.

Example 6. 

Let $S=\{(x,y)\in {\mathbb{R}}^2:{(x-1)}^2+y^2=1\}$ and $W=\{(x,y)\in {\mathbb{R}}^2:{(x-{\displaystyle \frac{1}{2}})}^2+y^2={\displaystyle \frac{1}{4}}\}$. By a simple calculation, we have $S\dot{-}W\ne \varnothing$ and $T(S;W)=\{(d_1,d_2)\in {\mathbb{R}}^2:d_1\ge 0,d_2\in \mathbb{R}\}$.

Lemma 3. 

Let $S_1,S_2,W\in P\left(Y\right)$. The following statements hold:

(i) If $S_1\subset S_2$, then $T(S_1;W)\subset T(S_2;W)$;

(ii) $T(S_1\cap S_2;W)\subset T(S_1;W)\cap T(S_2;W)$.

Proof. 

(i) For any $d\in T(S_1;W)$, by Definition 4, there exist $t_n\to 0^{+}$, $d_n\to d$ such that $t_n{d}_n\in S_1\dot{-}W$, $\forall n\in \mathbb{N}$, that is,

$$t_n{d}_n+W\subset S_1,\forall n\in \mathbb{N}.$$

(13)

Since $S_1\subset S_2$, by means of Equation (13), we have

$$t_n{d}_n+W\subset S_2,\forall n\in \mathbb{N}.$$

According to Remark 3, then $d\in T(S_2;W)$. By the arbitrariness of d, hence, $T(S_1;W)\subset T(S_2;W)$ holds.

(ii) For any $d\in T(S_1\cap S_2;W)$, there exist $t_n\to 0^{+}$, $d_n\to d$ such that $t_n{d}_n\in (S_1\cap S_2)\dot{-}W$, $\forall n\in \mathbb{N}$, that is,

$$t_n{d}_n+W\subset S_1\cap S_2,\forall n\in \mathbb{N}.$$

(14)

Due to $(S_1\cap S_2)\subset S_1$ and $(S_1\cap S_2)\subset S_2$, we derive from Equation (14) that

$$t_n{d}_n+W\subset S_1,t_n{d}_n+W\subset S_2,\forall n\in \mathbb{N},$$

which means that $d\in T(S_1;W)$ and $d\in T(S_2;W)$ by Remark 3. Thus, the conclusion is valid. □

Based on the above generalized contingent cone, we now introduce the concepts of generalized contingent derivative and generalized contingent epiderivative.

Definition 5. 

Let $F:X\rightrightarrows Y$ be a set-valued map, $\overline{x}\in dom\left(F\right)$ and $(v,u)\in X\times Y$.

(i) The generalized contingent derivative of F at $\overline{x}$ is the set-valued map $D_{c}F\left(\overline{x}\right):X\rightrightarrows Y$ defined by

$$\begin{array}{ccc}\hfill D_{c}F\left(\overline{x}\right)\left(v\right)& :=& \left\{u\in Y:(v,u)\in T\left(gr\left(F\right);\left\{\overline{x}\right\}\times F\left(\overline{x}\right)\right)\right\}\hfill \\ & =& \left\{u\in Y:\exists t_n\to 0^{+},\exists v_n\to v,\exists u_n\to u,s.t.t_n{u}_n\in F(\overline{x}+t_n{v}_n)\dot{-}F\left(\overline{x}\right),\forall n\in \mathbb{N}\right\}.\hfill \end{array}$$

(ii) The generalized contingent epiderivative of F at $\overline{x}$ is the set-valued map $D_c{F}_{+}\left(\overline{x}\right):X\rightrightarrows Y$ defined by

$$\begin{array}{ccc}\hfill D_c{F}_{+}\left(\overline{x}\right)\left(v\right)& :=& \left\{u\in Y:(v,u)\in T\left(epi\left(F\right);\left\{\overline{x}\right\}\times F\left(\overline{x}\right)\right)\right\}\hfill \\ & =& \left\{u\in Y:\exists t_n\to 0^{+},\exists v_n\to v,\exists u_n\to u,s.t.t_n{u}_n\in (F(\overline{x}+t_n{v}_n)+K)\dot{-}F\left(\overline{x}\right),\forall n\in \mathbb{N}\right\}.\hfill \end{array}$$

Here is an example of a generalized contingent derivative.

Example 7. 

Let $X=Y=\mathbb{R}$, $F:X\rightrightarrows Y$ be given by

$$F\left(x\right)=[x^2-1,x^2+1].$$

It is clear that $dom\left(F\right)=\mathbb{R}$. For any $x,v\in \mathbb{R}$, we get $D_{c}F\left(x\right)\left(v\right)=\left\{2xv\right\}$. Indeed, assume that $u\in D_{c}F\left(x\right)\left(v\right)$, then there exist $t_n\to 0^{+}$, $v_n\to v$, $u_n\to u$ such that

$$t_n{u}_n\in F(x+t_n{v}_n)\dot{-}F\left(x\right)=\left[{(x+t_n{v}_n)}^2-1,{(x+t_n{v}_n)}^2+1\right]\dot{-}\left[x^2-1,x^2+1\right].$$

Hence, we have $t_n{u}_n=2t_n{v}_{n}x+t_n^2{v}_n^2$, that is,

$$u_n=2x{v}_n+t_n{v}_n^2.$$

This implies that $D_{c}F\left(x\right)\left(v\right)=\left\{2xv\right\}$.

Remark 4. 

(i) By Remark 3 (i), it yields that if $F(\overline{x}+t_n{v}_n)\dot{-}F\left(\overline{x}\right)=\varnothing$, then $D_{c}F\left(\overline{x}\right)\left(v\right)=\varnothing$.

(ii) It is clear that $0\in D_{c}F\left(\overline{x}\right)\left(0\right)$ and $D_{c}F\left(\overline{x}\right)\left(\lambda v\right)=\lambda D_{c}F\left(\overline{x}\right)\left(v\right)$ for all $\lambda >0$.

(iii) If $F\left(\overline{x}\right)=\left\{\overline{y}\right\}$ is single-valued, then the generalized contingent derivative $D_{c}F\left(\overline{x}\right)\left(v\right)$ reduces to the contingent derivative $D_{c}F(\overline{x},\overline{y})\left(v\right)$ in literature [21], i.e.,

$$D_{c}F(\overline{x},\overline{y})\left(v\right)=\left\{u\in Y:\exists t_n\to 0^{+},\exists v_n\to v,\exists u_n\to u,s.t.\overline{y}+t_n{u}_n\in F(\overline{x}+t_n{v}_n),\forall n\in \mathbb{N}\right\}.$$

Further, since $F(\overline{x}+t_n{v}_n)\dot{-}F\left(\overline{x}\right)={\bigcap }_{\overline{y}\in F\left(\overline{x}\right)}(F(\overline{x}+t_n{v}_n)-\overline{y})$, by the above definitions, it is clear that $D_{c}F\left(\overline{x}\right)\left(v\right)\subset {\bigcap }_{\overline{y}\in F\left(\overline{x}\right)}{D}_{c}F(\overline{x},\overline{y})\left(v\right)$. However, ${\bigcap }_{\overline{y}\in F\left(\overline{x}\right)}{D}_{c}F(\overline{x},\overline{y})\left(v\right)\subset D_{c}F\left(\overline{x}\right)\left(v\right)$ is not necessarily true. The following example justifies this fact.

Example 8. 

Let $X=Y=\mathbb{R}$, and

$$\begin{array}{c}\hfill F\left(x\right)=\left\{\begin{array}{c}\{1,2\},x=0,\hfill \\ \left\{0\right\}\cup \left[\right|x|+1,|x|+3],x\ne 0.\hfill \end{array}\right.\end{array}$$

Then $dom\left(F\right)=\mathbb{R}$. Take $\overline{x}=0$, for any $v\in X$, we have

$$D_{c}F\left(0\right)\left(v\right)={\mathbb{R}}_{+},\bigcap _{\overline{y}\in F\left(0\right)}{D}_{c}F(0,\overline{y})\left(v\right)=\mathbb{R}.$$

Thus, ${\bigcap }_{\overline{y}\in F\left(0\right)}{D}_{c}F(0,\overline{y})\left(v\right)\cancel{\subset }{D}_{c}F\left(0\right)\left(v\right)$.

Next, two necessary optimality conditions of proper strict ${⪯}_K^m$-efficient solution are established by using the above generalized derivatives.

Theorem 1. 

In problem (SOP), let $\overline{x}\in \Omega$. If $\overline{x}\in P(F,{⪯}_K^m)$, then

$$D_{c}F\left(\overline{x}\right)\left(v\right)\cap (-K)=\varnothing ,\forall v\in \Omega \setminus \left\{0\right\}.$$

Proof. 

Since $\overline{x}\in P(F,{⪯}_K^m)$, there exists $\alpha >0$ such that

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

This is equivalent to

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\subset {\left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)}^c,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

Suppose that there exists $\widehat{u}\in D_{c}F\left(\overline{x}\right)\left(\widehat{v}\right)\cap (-K)$ for some $\widehat{v}\in \Omega \setminus \left\{0\right\}$. Then there exist $t_n\to 0^{+}$, $u_n\to \widehat{u}$, $v_n\to \widehat{v}$ and ${\theta }_n\in F(\overline{x}+t_n{v}_n)\dot{-}F\left(\overline{x}\right)$ such that ${\displaystyle \frac{{\theta }_n}{t_n}}=u_n\to \widehat{u}$. Let $x_n=\overline{x}+t_n{v}_n$, we have ${\displaystyle \frac{x_n-\overline{x}}{t_n}}=v_n\to \widehat{v}$ and

$${\displaystyle \frac{{\theta }_n}{\parallel x_n-\overline{x}\parallel }}={\displaystyle \frac{t_n}{\parallel x_n-\overline{x}\parallel }}·{\displaystyle \frac{{\theta }_n}{t_n}}={\displaystyle \frac{1}{\parallel v_n\parallel }}{u}_n\to {\displaystyle \frac{1}{\parallel \widehat{v}\parallel }}\widehat{u}\in -K.$$

(15)

Moreover, since

$${\displaystyle \frac{{\theta }_n}{\parallel x_n-\overline{x}\parallel }}\in {\displaystyle \frac{F\left(x_n\right)\dot{-}F\left(\overline{x}\right)}{\parallel x_n-\overline{x}\parallel }}\subset {\left(\mathbb{B}\right(0,\alpha )-K)}^c,$$

and ${\left(\mathbb{B}(0,\alpha )-K\right)}^c$ is closed, it follows from Equation (15) that

$${\displaystyle \frac{1}{\parallel \widehat{v}\parallel }}\widehat{u}\in {\left(\mathbb{B}(0,\alpha )-K\right)}^c.$$

Due to $-K\subset \mathbb{B}(0,\alpha )-K$, together with Equation (15), we get

$${\left(\mathbb{B}(0,\alpha )-K\right)}^c\cap (-K)\ne \varnothing ,$$

which contradicts ${\left(\mathbb{B}(0,\alpha )-K\right)}^c\cap (-K)=\varnothing$. □

Theorem 2. 

In problem (SOP), let $\overline{x}\in \Omega$. If $\overline{x}\in P(F,{⪯}_K^m)$, then

$$D_c{F}_{+}\left(\overline{x}\right)\left(v\right)\cap (-K)=\varnothing ,\forall v\in \Omega \setminus \left\{0\right\}.$$

Proof. 

If $\overline{x}\in P(F,{⪯}_K^m)$, according to Lemma 2 (iii), we derive $\overline{x}\in P(F+K,{⪯}_K^m)$. Thus, there exists $\alpha >0$ such that

$$\left((F\left(x\right)+K)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

That is,

$$\left((F\left(x\right)+K)\dot{-}F\left(\overline{x}\right)\right)\subset {\left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)}^c,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

By a similar method to Theorem 1, we can obtain the corresponding result. □

Next, we give a lemma, which will play an important role in the proof of sufficient condition.

Lemma 4. 

In problem (SOP), let $\overline{x}\in \Omega$ and $v\in X\setminus \left\{0\right\}$. Then

$$0\notin D_c{F}_{+}\left(\overline{x}\right)\left(v\right)⟺D_c{F}_{+}\left(\overline{x}\right)\left(v\right)\cap (-K)=\varnothing .$$

Proof. 

The necessity is obvious since K is a cone.

Next, we prove sufficiency. Suppose that $D_c{F}_{+}\left(\overline{x}\right)\left(v\right)\cap (-K)\ne \varnothing$. Then there exists $k\in K$ such that $-k\in D_c{F}_{+}\left(\overline{x}\right)\left(v\right)$. This implies that there exist $t_n\to 0^{+}$, $v_n\to v$ and ${\theta }_n\in (F(\overline{x}+t_n{v}_n)+K)\dot{-}F\left(\overline{x}\right)$ such that ${\displaystyle \frac{{\theta }_n}{t_n}}\to -k$. This is equivalent to

$${\displaystyle \frac{{\theta }_n+t_{n}k}{t_n}}\to 0.$$

(16)

Since $0\notin D_c{F}_{+}\left(\overline{x}\right)\left(v\right)$, for any $t_n\to 0^{+}$, $v_n\to v$ and ${\theta }_n\in (F(\overline{x}+t_n{v}_n)+K)\dot{-}F\left(\overline{x}\right)$, we have ${\displaystyle \frac{{\theta }_n}{t_n}}\nrightarrow 0$. According to ${\theta }_n\in (F(\overline{x}+t_n{v}_n)+K)\dot{-}F\left(\overline{x}\right)$, we have

$${\theta }_n+F\left(\overline{x}\right)\subset F(\overline{x}+t_n{v}_n)+K.$$

Note that K is a convex cone and $k\in K$, consequently,

$${\theta }_n+t_{n}k+F\left(\overline{x}\right)\subset F(\overline{x}+t_n{v}_n)+K+K\subset F(\overline{x}+t_n{v}_n)+K,$$

that is,

$${\theta }_n+t_{n}k\in (F(\overline{x}+t_n{v}_n)+K)\dot{-}F\left(\overline{x}\right).$$

Hence, we get ${\displaystyle \frac{{\theta }_n+t_{n}k}{t_n}}\nrightarrow 0$, which contradicts Equation (16). The proof is completed. □

Now, we present a sufficient optimality condition for the proper strict ${⪯}_K^m$-efficient solution.

Theorem 3. 

In problem (SOP), let X be finite-dimensional, and $\overline{x}\in \Omega$. If

$$D_c{F}_{+}\left(\overline{x}\right)\left(v\right)\cap (-K)=\varnothing ,\forall v\in T(\Omega ;\overline{x})\setminus \left\{0\right\},$$

then, $\overline{x}\in P(F,{⪯}_K^m)$.

Proof. 

Since $D_c{F}_{+}\left(\overline{x}\right)\left(v\right)\cap (-K)=\varnothing$ for all $v\in T(\Omega ;\overline{x})\setminus \left\{0\right\}$, by Lemma 4, we have

$$0\notin D_c{F}_{+}\left(\overline{x}\right)\left(v\right),\forall v\in T(\Omega ;\overline{x})\setminus \left\{0\right\}.$$

(17)

Suppose that $\overline{x}\notin P(F,{⪯}_K^m)$. In view of Proposition 1, then there exist $x_n\in \Omega \setminus \left\{\overline{x}\right\}$, ${\theta }_n\in (F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right)$ such that $x_n\to \overline{x}$ and

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\theta }_n}{\parallel x_n-\overline{x}\parallel }}=0.$$

(18)

It follows from $x_n\to \overline{x}$ that $\parallel x_n-\overline{x}\parallel \to 0^{+}$. Since X is finite-dimensional, we can suppose

$$v_n={\displaystyle \frac{x_n-\overline{x}}{\parallel x_n-\overline{x}\parallel }}\to v\in T(\Omega ;\overline{x})\setminus \left\{0\right\}.$$

By ${\theta }_n\in (F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right)$ and Equation (18), we derive

$$\parallel x_n-\overline{x}\parallel ·{\displaystyle \frac{{\theta }_n}{\parallel x_n-\overline{x}\parallel }}\in (F\left(x_n\right)+K)\dot{-}F\left(\overline{x}\right),$$

which implies that $0\in D_c{F}_{+}\left(\overline{x}\right)\left(v\right)$. This contradicts Equation (17). □

Remark 5. 

It is worth noting that the proof of the sufficient optimality condition in Theorem 3 does not require any assumptions of convexity and compactness; in this case, it is different from the results of the literatures [19,22].

We give an example to explain that Theorem 3 holds even if the map F is not convex and compact.

Example 9. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =[0,+\infty )$ and

$$F\left(x\right)=\left(co\left\{\right(x-1,x),(x+1,x+1\left)\right\}\bigcup co\left\{\right(x,x-1),(x+1,x+1\left)\right\}\right)\setminus \left\{(x+1,x+1)\right\},\forall x\in \Omega .$$

As seen in Figure 3, it is clear that F is not convex and compact on $\Omega$. Let $\overline{x}=0$, then $F\left(0\right)=\left(co\left\{\right(-1,0),(1,1\left)\right\}\bigcup co\left\{\right(0,-1),(1,1\left)\right\}\right)\setminus \left\{(1,1)\right\}$. By a direct calculation, we have $T(\Omega ;0)=[0,+\infty )$, and $D_c{F}_{+}\left(0\right)\left(v\right)={\mathbb{R}}_{++}^2$ for all $v\in T(\Omega ;0)\setminus \left\{0\right\}$. Thus,

$$D_c{F}_{+}\left(0\right)\left(v\right)\cap (-K)=\varnothing ,\forall v\in T(\Omega ;0)\setminus \left\{0\right\}.$$

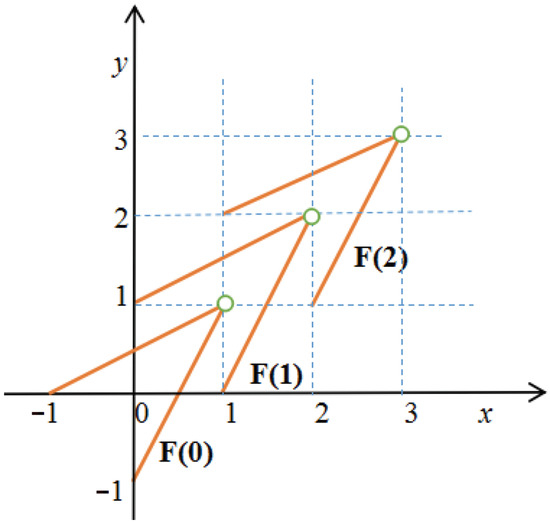
Figure 3. Illustrations of $F\left(x\right)$.

In addition, for all $x\in \Omega \setminus \left\{0\right\}$, there exists $\alpha ={\displaystyle \frac{1}{3}}$ such that

$$\left(F\left(x\right)\dot{-}F\left(0\right)\right)\cap \left(\mathbb{B}(0,{\displaystyle \frac{1}{3}}x)-K\right)=\varnothing .$$

Hence, $\overline{x}=0$ is a proper strict ${⪯}_K^m$-efficient solution of problem (SOP).

5. Scalarization

Throughout this section, let $e\in intK\ne \varnothing$. In literature [7], a scalar function ${\mathcal{I}}_e:P\left(Y\right)\times P\left(Y\right)\to \mathbb{R}\cup \{\pm \infty \}$ is defined as follows:

$${\mathcal{I}}_e(A,B):=inf\{t\in \mathbb{R}:A{⪯}_K^{m}te+B\}.$$

(19)

The following lemmas summarize some properties of the function ${\mathcal{I}}_e$.

Lemma 5 

([7]). Let $A,B\in P\left(Y\right)$. The following assertions hold:

(i) ${\mathcal{I}}_e(A,A)=0$;

(ii) If $A\dot{-}B$ is nonempty, then $-\infty <{\mathcal{I}}_e(A,B)<+\infty$;

(iii) If $A\dot{-}B$ is compact and K is closed, then ${\mathcal{I}}_e(A,B)\le 0⟺A{⪯}_K^{m}B$.

Lemma 6. 

Let $\epsilon \ge 0$, $A,B\in P\left(Y\right)$ and $A\dot{-}B$ be nonempty. Then ${\mathcal{I}}_e(A,B+\epsilon e)={\mathcal{I}}_e(A,B)-\epsilon$.

Proof. 

It follows from Equation (19) and Lemma 1 that

$$\begin{array}{ccc}\hfill {\mathcal{I}}_e(A,B+\epsilon e)& =& inf\{t\in \mathbb{R}:A{⪯}_K^{m}te+(B+\epsilon e)\}\hfill \\ & =& inf\{t\in \mathbb{R}:((-\epsilon -t)e+\left(A\dot{-}B\right))\cap (-K)\ne \varnothing \}\hfill \\ & =& inf\{(r-\epsilon )\in \mathbb{R}:(-re+\left(A\dot{-}B\right))\cap (-K)\ne \varnothing \}\hfill \\ & =& inf\{r\in \mathbb{R}:(-re+\left(A\dot{-}B\right))\cap (-K)\ne \varnothing \}-\epsilon \hfill \\ & =& inf\{r\in \mathbb{R}:A{⪯}_K^{m}re+B\}-\epsilon \hfill \\ & =& {\mathcal{I}}_e(A,B)-\epsilon .\hfill \end{array}$$

□

Let $\overline{x}\in \Omega$. Considering the following scalar problem

$$\left(\mathrm{P}\right)\mathrm{m}\mathrm{i}\mathrm{n}{\mathcal{I}}_e(F\left(x\right),F\left(\overline{x}\right)),\mathrm{s.t.}x\in \Omega .$$

Definition 6. 

A point $\overline{x}\in \Omega$ is called proper strict minimizer solution of problem (P), denoted by $P_{{\mathcal{I}}_e}$, if there exists a $\beta >0$ such that

$${\mathcal{I}}_e(F\left(x\right),F\left(\overline{x}\right))-{\mathcal{I}}_e(F\left(\overline{x}\right),F\left(\overline{x}\right))-\beta \parallel x-\overline{x}\parallel >0,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

Next, we present a relationship between the proper strict ${⪯}_K^m$-efficient solution of problem (SOP) and the proper strict minimizer solution of problem (P).

Theorem 4. 

Let $\overline{x}\in \Omega$ and $F\left(x\right)\dot{-}F\left(y\right)$ be nonempty and compact for all $x,y\in \Omega$. Then $P_{{\mathcal{I}}_e}=P(F,{⪯}_K^m)$.

Proof. 

Firstly, we prove $P_{{\mathcal{I}}_e}\subset P(F,{⪯}_K^m)$ holds. Assume that $\overline{x}\in P_{{\mathcal{I}}_e}$, but $\overline{x}\notin P(F,{⪯}_K^m)$, then there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that for any $\alpha >0$

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )-K\right)\ne \varnothing .$$

(20)

Since $0\in e-intK$, and $e-intK$ is an open set, then 0 is an interior point of $e-intK$. According to the definition of interior points, there exists $\delta >0$ such that the neighborhood $\mathbb{B}(0,\delta )\subset e-intK$. Furthermore, due to $e-intK\subset e-K$, we conclude that $\mathbb{B}(0,\delta )\subset e-K$. For any $\beta >0$, then

$$\mathbb{B}(0,\delta \beta \parallel \widehat{x}-\overline{x}\parallel )\subset \beta \parallel \widehat{x}-\overline{x}\parallel e-K.$$

Since K is a convex cone, we get

$$\mathbb{B}(0,\delta \beta \parallel \widehat{x}-\overline{x}\parallel )-K\subset \beta \parallel \widehat{x}-\overline{x}\parallel e-K-K\subset \beta \parallel \widehat{x}-\overline{x}\parallel e-K.$$

Together with Equation (20), one has

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\beta \parallel \widehat{x}-\overline{x}\parallel e-K\right)\ne \varnothing .$$

This is equivalent to

$$\left(F\left(\widehat{x}\right)\dot{-}\left(\beta \parallel \widehat{x}-\overline{x}\parallel e+F\left(\overline{x}\right)\right)\right)\cap (-K)\ne \varnothing .$$

Hence,

$$F\left(\widehat{x}\right){⪯}_K^m\beta \parallel \widehat{x}-\overline{x}\parallel e+F\left(\overline{x}\right).$$

According to Lemma 5 (iii), we have

$${\mathcal{I}}_e(F\left(\widehat{x}\right),\beta \parallel \widehat{x}-\overline{x}\parallel e+F\left(\overline{x}\right))\le 0.$$

By Lemma 6, it holds

$${\mathcal{I}}_e(F\left(\widehat{x}\right),\beta \parallel \widehat{x}-\overline{x}\parallel e+F\left(\overline{x}\right))={\mathcal{I}}_e(F\left(\widehat{x}\right),F\left(\overline{x}\right))-\beta \parallel \widehat{x}-\overline{x}\parallel .$$

Thus,

$${\mathcal{I}}_e(F\left(\widehat{x}\right),F\left(\overline{x}\right))\le \beta \parallel \widehat{x}-\overline{x}\parallel .$$

Note that ${\mathcal{I}}_e(F\left(\overline{x}\right),F\left(\overline{x}\right))=0$, we obtain

$${\mathcal{I}}_e(F\left(\widehat{x}\right),F\left(\overline{x}\right))-{\mathcal{I}}_e(F\left(\overline{x}\right),F\left(\overline{x}\right))-\beta \parallel \widehat{x}-\overline{x}\parallel \le 0.$$

which contradicts $\overline{x}\in P_{{\mathcal{I}}_e}$.

Next, we prove $P(F,{⪯}_K^m)\subset P_{{\mathcal{I}}_e}$ is true. Let $\overline{x}\in P(F,{⪯}_K^m)$, there exists $\alpha >0$ such that

$$\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

This means that

$$\left(\mathbb{B}(0,\alpha \parallel x-\overline{x}\parallel )-K\right)\subset {\left(F\left(x\right)\dot{-}F\left(\overline{x}\right)\right)}^c,\forall x\in \Omega \setminus \left\{\overline{x}\right\}.$$

(21)

Suppose that $\overline{x}\notin P_{{\mathcal{I}}_e}$, then there exists $\widehat{x}\in \Omega \setminus \left\{\overline{x}\right\}$ such that for any $\beta >0$

$${\mathcal{I}}_e(F\left(\widehat{x}\right),F\left(\overline{x}\right))-{\mathcal{I}}_e(F\left(\overline{x}\right),F\left(\overline{x}\right))-\beta \parallel \widehat{x}-\overline{x}\parallel \le 0.$$

Due to ${\mathcal{I}}_e(F\left(\overline{x}\right),F\left(\overline{x}\right))=0$, we arrive at

$${\mathcal{I}}_e(F\left(\widehat{x}\right),F\left(\overline{x}\right))\le \beta \parallel \widehat{x}-\overline{x}\parallel .$$

It follows from Lemmas 5 and 6 that

$$F\left(\widehat{x}\right){⪯}_K^m\beta \parallel \widehat{x}-\overline{x}\parallel e+F\left(\overline{x}\right).$$

Therefore,

$$\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)\cap \left(\beta \parallel \widehat{x}-\overline{x}\parallel e-K\right)\ne \varnothing .$$

(22)

Due to ${\displaystyle \frac{\alpha }{2\parallel e\parallel }}\parallel \widehat{x}-\overline{x}\parallel e<\alpha \parallel \widehat{x}-\overline{x}\parallel$, we have ${\displaystyle \frac{\alpha }{2\parallel e\parallel }}\parallel \widehat{x}-\overline{x}\parallel e\in \mathbb{B}(0,\alpha \parallel \widehat{x}-\overline{x}\parallel )$. By Equation (21), it leads to

$$\left({\displaystyle \frac{\alpha }{2\parallel e\parallel }}\parallel \widehat{x}-\overline{x}\parallel e-K\right)\subset {\left(F\left(\widehat{x}\right)\dot{-}F\left(\overline{x}\right)\right)}^c.$$

which contradicts Equation (22). This completes the proof. □

We give an example to illustrate Theorem 4.

Example 10. 

In problem (SOP), let $X=\mathbb{R}$, $Y={\mathbb{R}}^2$, $K={\mathbb{R}}_{+}^2$, $\Omega =[-2,+\infty )$ and

$$F\left(x\right)=\{(a,b)\in {\mathbb{R}}^2:{(a-x)}^2+{(b-x)}^2=1\},\forall x\in \Omega .$$

Then $intK={\mathbb{R}}_{++}^2\ne \varnothing$. Let $\overline{x}=-2$, there exists $\alpha ={\displaystyle \frac{1}{2}}$ such that

$$\left(F\left(x\right)\dot{-}F(-2)\right)\cap \left(\mathbb{B}(0,{\displaystyle \frac{1}{2}}\parallel x+2\parallel )-K\right)=\varnothing ,\forall x\in \Omega \setminus \{-2\}.$$

Thus, $\overline{x}=-2\in P(F,{⪯}_K^m)$. Now, we testify $\overline{x}=-2\in P_{{\mathcal{I}}_e}$. Indeed, take $e=(1,1)$, $\beta ={\displaystyle \frac{1}{4}}$, due to ${\mathcal{I}}_e(F\left(x\right),F(-2))=x+2$ and

$${\mathcal{I}}_e(F\left(x\right),F(-2))-\beta \parallel x-(-2)\parallel ={\displaystyle \frac{3}{4}}(x+2)>0,\forall x\in \Omega \setminus \{-2\},$$

we get from Definition 6 that $\overline{x}=-2\in P_{{\mathcal{I}}_e}$.

6. Conclusions

In this paper, we have introduced the notion of proper strict efficient solution for a set optimization problem with a partial set order relation and emphasized that this proper strict efficient solution differs from those defined in the literature [10,19]; the corresponding results have been summarized in Remarks 1 and 2. We have also proposed a class of generalized contingent derivatives, different from the literature [21]; they are given by set criteria, not vector criteria. Finally, two necessary optimality conditions, a sufficient optimality condition, and a scalarization theorem for proper strict efficient solution are established.

It is worth mentioning that the results obtained in the paper do not need any assumptions of convexity and compactness, which are distinct from the conclusions in the literature [19,22]. On the other hand, our sufficient optimality condition holds only in finite-dimensional spaces, and it will be interesting to continue to explore the case in infinite-dimensional spaces.