Numerical Methods for Partial Inverse Spectral Problems with Frozen Arguments on Star-Shaped Graphs

Abstract

In this paper, the authors investigate a partial inverse spectral problem for Sturm–Liouville operators with frozen arguments on star-shaped graphs. The problem is to reconstruct the potential on one edge from the known potentials on the other edges together with two sequences of eigenvalues from a prescribed spectral set. The proposed approach is constructive. First, the characteristic function associated with the given spectral data is constructed, allowing the unknown potential contribution to be isolated. The potential is then recovered by expanding the resulting expressions in an appropriate Riesz basis and solving a corresponding system of linear equations. Based on established uniqueness results, this procedure yields a constructive numerical algorithm. Numerical examples demonstrate reliable reconstruction for both smooth and piecewise continuous potentials, providing a practical scheme for frozen-argument problems on star graphs.

1. Introduction

Inverse spectral problems concern the recovery of differential operators from spectral data such as eigenvalues or eigenfunctions. Since the classical work of Ambarzumyan, Borg, Levinson, Gelfand, and Levitan [1,2,3,4], this area has grown into an important branch of analysis and mathematical physics.

In recent decades, this research field has remained highly active. Numerous researchers, including V.A. Yurko, V. Pivovarchik, S.A. Buterin, N.P. Bondarenko, S. Avdonin, C.F. Yang, and many others, continue to expand its boundaries and contribute to both the classical and generalized Sturm–Liouville problems, particularly with regard to uniqueness theorems, reconstruction algorithms, and stability of solutions. Over the past two decades, the theory has been extended to more general structures known as quantum (metric) graphs. A quantum graph consists of multiple edges, each treated as an interval and connected at vertices, with differential operators such as the Sturm–Liouville operator defined on the edges and appropriate coupling conditions imposed at the vertices. Quantum graphs provide a mathematical model for wave propagation on networks and have found applications in physics, chemistry, engineering, and spectral geometry (see [5] for a survey and [6,7,8,9,10,11] for further references).

Among these developments, inverse spectral problems on star-shaped graphs have received particular attention. Bondarenko [12] obtained uniqueness theorems for partial inverse problems of Sturm–Liouville operators on star-shaped graphs, where one seeks to reconstruct unknown data on a selected edge from spectral information and known data on the remaining edges; Avdonin and Kravchenko [13] proposed numerical algorithms for the self-adjoint case on a star-shaped graph; more recently, Shieh, Tsai, and Wu [14] studied nonlocal Sturm–Liouville operators with frozen arguments on star-shaped graphs and proved uniqueness theorems for the corresponding partial inverse problems. However, despite these advances, a constructive numerical reconstruction algorithm for the frozen-argument case has not been available.

The aim of this paper is to fill this gap. We develop and implement a numerical algorithm for reconstructing an unknown potential on one edge of a star-shaped graph with frozen arguments, using known potentials on the other edges together with the partial spectral data. Several numerical experiments are provided, covering both smooth and piecewise continuous potentials.

To precisely formulate the problem under consideration, let $G_n$ (see Figure 1) be a star-shaped graph with equal edges of length $\pi$; $G_n$ consists of edges $\{E_1,E_2,\dots ,E_n\}$ and vertices $\{V_0,V_1,\dots ,V_n\},$ where $V_0$ is the inner vertex and $V_i$ is an outer vertex which is connected to $V_0$ by $E_i.$ Each edge $E_i$ is parameterized by the variable $x\in [0,\pi ],$ the vertex $V_0$ corresponds to the point $x=\pi$, and the vertex $V_i$ corresponds to $x=0$.

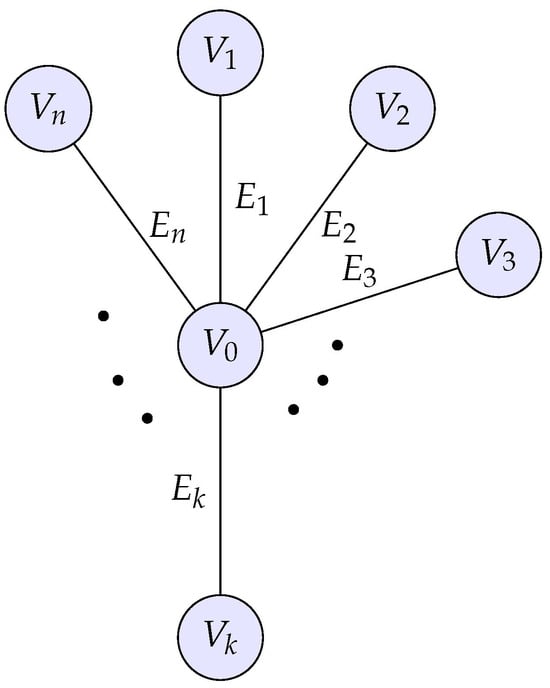
Figure 1. A star-shaped graph $G_n$.

In the graph, each edge $E_i$ is equipped with an ordinary Sturm–Liouville equation

$$l_i\left(y_i\right):=-y_i^{\prime \prime }\left(x\right)+p_i\left(x\right)y_i\left(x\right)=\lambda y_i\left(x\right),0<x<\pi ,$$

(1)

or a nonlocal Sturm–Liouville equation

$$l_i\left(y_i\right):=-y_i^{\prime \prime }\left(x\right)+p_i\left(x\right)\sum _{k=1}^{m_i}{y}_i\left(a_{i,k}\right)=\lambda y_i\left(x\right),a_{i,k}\in (0,\pi ),0<x<\pi ,$$

(2)

where $p_i\left(x\right)$ is a real-valued $L^2$-function on $(0,\pi )$. Let $F_i:={\left\{a_{i,k}\right\}}_{k=1}^{m_i}$ denote the set of frozen arguments on edge $E_i.$ Briefly, we denote $Q_i:=(p_i,F_i).$ We agree that if $F_i=⌀,$ then the differential equation on $E_i$ is an ordinary Sturm–Liouville equation. Denote $L(Q_1,Q_2,\dots ,Q_n)$ the boundary problem on $G_n$ which consists of the differential system

$$l_i\left(y_i\right)=\lambda y_i\left(x\right),0<x<\pi$$

(3)

associated with boundary conditions

$$y_i\left(0\right)=0,1\le i\le n$$

(4)

and Kirchhoff conditions

$$y_1\left(\pi \right)=y_2\left(\pi \right)=\dots =y_n\left(\pi \right);\sum _{i=1}^n{y}_i^{\prime }\left(\pi \right)=0.$$

(5)

A number $\lambda \in \mathbb{C}$ is an eigenvalue of (3)–(5) if there exist non-trivial functions $\{y_1\left(x\right),y_2\left(x\right),\dots ,y_n\left(x\right)\}$ which satisfy (3)–(5). The purpose is to retrieve the potentials $\{p_1\left(x\right),p_2\left(x\right),\dots ,p_n\left(x\right)\}$ from the information of the eigenvalues of (3)–(5).

The remainder of this paper is organized as follows: Section 2 presents the necessary preliminaries and Section 3 introduces the numerical algorithm and provide simulation results, followed by a concluding discussion.

2. Preliminaries

In this section, we introduce the basic notation used throughout the paper along with preliminary results. We also briefly discuss a characteristic feature of nonlocal Sturm–Liouville problems, namely, the possible lack of uniqueness of solutions. As an illustration, consider the boundary value problem

$$-y^{″}\left(x\right)+\{y(\pi /4)+y(\pi /2)+y(3\pi /4)\}=\lambda y\left(x\right),y\left(0\right)=y\left(\pi \right)=0.$$

For $\lambda =4,$ this problem admits more than one linearly independent solution, which highlights the non-uniqueness phenomenon in nonlocal settings.

As such, the analysis of inverse spectral problems relies heavily upon the construction of the characteristic function associated with the operator. In the case of star-shaped graphs, the characteristic function can be constructed from the differential operators defined on individual edges. For this purpose, we recall the following lemma.

Lemma 1 

([14]). Denote $S_i(x,\lambda )$ as the solution of

$$l_i\left(y_i\right)=\lambda y_i\left(x\right),0<x<\pi ,$$

associated with the initial condition $S_i(0,\lambda )=0.$ Denote $\rho :=\sqrt{\lambda }$; then, $S_i(x,\lambda )$ satisfies the integral equation

$$\begin{array}{c}\hfill S_i(x,\lambda )={\displaystyle \frac{sin\rho x}{\rho }}+{\int }_0^x{p}_i\left(t\right){\displaystyle \frac{sin\rho (x-t)}{\rho }}{S}_i(t,\lambda )dt\end{array}$$

(6)

for $F_i=⌀$. Otherwise,

$$\begin{array}{c}\hfill S_i(x,\lambda )=A_i\left(\lambda \right){\displaystyle \frac{sin\rho x}{\rho }}+\sum _{k=1}^{m_i}{S}_i\left(a_{i,k}\right){\int }_0^x{p}_i\left(x\right){\displaystyle \frac{sin\rho (x-t)}{\rho }}dt,\end{array}$$

(7)

where $A_i\left(\lambda \right)$ is an undetermined constant which can be chosen as either 0 or 1 depending on the specific form of $p_i\left(x\right)$ and the value λ.

For consistency, we denote ${▵}_i^{(0,0)}\left(\lambda \right)$ the characteristic function of

$$l_i\left(y_i\right)=\lambda y_i\left(x\right),0<x<\pi ,$$

associated with Dirichlet boundary conditions $y_i\left(0\right)=y_i\left(\pi \right)=0,$ and denote ${▵}_i^{(0,1)}\left(\lambda \right)$ the characteristic function of

$$l_i\left(y_i\right)=\lambda y_i\left(x\right),0<x<\pi ,$$

associated with Dirichlet–Neumann boundary conditions $y_i\left(0\right)=y_i^{\prime }\left(\pi \right)=0.$ According to [15],

$$\begin{array}{c}\hfill {▵}_i^{(0,0)}\left(\lambda \right)=\left\{\begin{array}{cc}{S}_i(\pi ,\lambda ),\hfill & if{F}_i=⌀,\hfill \\ {\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{sin\rho \pi }{{\rho }^2}}\left(\sum _{k=1}^{m_i}{\int }_0^{a_{i,k}}{p}_i\left(t\right)sin\rho (a_{i,k}-t)dt\right)+\sum _{k=1}^{m_i}{\displaystyle \frac{sin\rho a_{i,k}}{{\rho }^2}}{\int }_0^{\pi }{p}_i\left(t\right)sin\rho (\pi -t)dt,\hfill & if{F}_i\ne ⌀,\hfill \end{array}\right.\end{array}$$

(8)

and

$$\begin{array}{c}\hfill {▵}_i^{(0,1)}\left(\lambda \right)=\left\{\begin{array}{cc}{S}_i^{\prime }(\pi ,\lambda ),\hfill & if{F}_i=⌀,\hfill \\ cos\rho \pi -cos\rho \pi \left(\sum _{k=1}^{m_i}{\int }_0^{a_{i,k}}{p}_i\left(t\right){\displaystyle \frac{sin\rho (a_{i,k}-t)}{\rho }}dt\right)+\sum _{k=1}^{m_i}{\displaystyle \frac{sin\rho a_{i,k}}{\rho }}{\int }_0^{\pi }{p}_i\left(t\right)cos\rho (\pi -t)dt,\hfill & if{F}_i\ne ⌀.\hfill \end{array}\right.\end{array}$$

(9)

Then, the characteristic function of (3)–(5) is stated in the following theorem.

Theorem 1 

(Theorem 2.4, [14]). The characteristic function ${\chi }_n\left(\lambda \right)$ of $L(Q_1,Q_2,\dots ,Q_n)$ is

$${\chi }_n\left(\lambda \right)=\sum _{k=1}^n{▵}_k^{(0,1)}\left(\lambda \right)\prod _{j=1,j\ne k}^n{▵}_j^{(0,0)}\left(\lambda \right).$$

(10)

At the end of this section, several preliminary results that will be used in the subsequent analysis are presented. In fact, the characteristic functions allow the following integral forms (refer to [12,14]):

$$\left\{\begin{array}{cc}{▵}_i^{(0,0)}\left(\lambda \right)\hfill & ={\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{{\omega }_{i}cos\rho \pi }{{\rho }^2}}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{K}_i\left(t\right)cos\rho tdt,\hfill \\ {▵}_i^{(0,1)}\left(\lambda \right)\hfill & =cos\rho \pi +{\displaystyle \frac{{\omega }_{i}sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{\rho }}{\int }_0^{\pi }{H}_i\left(t\right)sin\rho tdt\hfill \end{array}\right.$$

(11)

for $F_i=⌀,$$w_i={\displaystyle \frac{1}{2}}{\int }_0^{\pi }{p}_i\left(t\right)dt$ and

$$\left\{\begin{array}{cc}{▵}_i^{(0,0)}\left(\lambda \right)\hfill & ={\displaystyle \frac{sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{N}_i\left(t\right)cos\rho tdt,\hfill \\ {▵}_i^{(0,1)}\left(\lambda \right)\hfill & =cos\rho \pi +{\displaystyle \frac{1}{\rho }}{\int }_0^{\pi }{W}_i\left(t\right)sin\rho tdt\hfill \end{array}\right.$$

(12)

for $F_i\ne ⌀.$ The functions $K_i\left(t\right),H_i\left(t\right),N_i\left(t\right),$ and $W_i\left(t\right)$ are derived from suitable substitutions into Equations (8) and (9), and play essential roles in reconstructing the characteristic function. Readers can refer to [12,14,16] for details.

3. Reconstruction Algorithm and Numerical Experiments

The uniqueness theorems for both ordinary and nonlocal Sturm–Liouville problems on star-shaped graphs have been established in [12,14]. Moreover, a numerical method for the ordinary Sturm–Liouville problem on star-shaped graphs was implemented in [13]. In this work, we focus on the nonlocal problem on star-shaped graphs. The characteristic function and behavior of eigenvalues shall be used to solve our inverse problem.

Theorem 2 

([14]). Suppose that the problem $L(Q_1,Q_2,\dots ,Q_n)$ consists of l ordinary Sturm–Liouville equations at edges $E_{i_1},E_{i_2},\dots ,E_{i_l}$ and $n-l$ nonlocal Sturm–Liouville equations, where $0\le l<n.$ Then, the characteristic function ${\chi }_n\left(\lambda \right)$ of $L(Q_1,Q_2,\dots Q_n)$ is

$$\begin{array}{cc}\hfill {\chi }_n\left(\lambda \right)=& \sum _{k=1}^n{▵}_k^{(0,1)}\left(\lambda \right)\prod _{j=1,j\ne k}^n{▵}_j^{(0,0)}\left(\lambda \right)\hfill \\ \hfill =& \sum _{k=1}^l\left[(cos\rho \pi +{\displaystyle \frac{w_{i_k}sin\rho \pi }{\rho }}+o\left({\displaystyle \frac{1}{\rho }}\right))\prod _{j=1,j\ne k}^l({\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{w_{i_j}cos\rho \pi }{{\rho }^2}}+o\left({\displaystyle \frac{1}{{\rho }^2}}\right))\right]{({\displaystyle \frac{sin\rho \pi }{\rho }}+o\left({\displaystyle \frac{1}{{\rho }^2}}\right))}^{n-l}\hfill \\ \hfill & +(n-l)\left[\prod _{j=1}^l({\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{w_{i_j}cos\rho \pi }{{\rho }^2}}+o\left({\displaystyle \frac{1}{{\rho }^2}}\right))\right](cos\rho \pi +o\left({\displaystyle \frac{1}{\rho }}\right)){({\displaystyle \frac{sin\rho \pi }{\rho }}+o\left({\displaystyle \frac{1}{{\rho }^2}}\right))}^{n-l-1},\hfill \end{array}$$

(13)

where $w_{i_j}={\displaystyle \frac{1}{2}}{\int }_0^{\pi }{p}_{i_j}\left(x\right)dx,1\le j\le l.$ Moreover, the spectral set consists of sequences ${\left\{{\lambda }_{k,j}\right\}}_{k=1}^{\infty },j=0,1,\dots ,n-1,$ where

$$\begin{array}{cc}\hfill {\rho }_{k,0}& =\sqrt{{\lambda }_{k,0}}=k-(1/2)+{\displaystyle \frac{A_l}{\pi k}}+o\left({\displaystyle \frac{1}{k}}\right),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\rho }_{k,j}& =\sqrt{{\lambda }_{k,j}}=k+O\left({\displaystyle \frac{1}{k}}\right),j=1,2,\dots ,n-1,\hfill \end{array}$$

(15)

and $A_l={\displaystyle \frac{1}{n}}{\sum }_{1\le k\le l}{w}_{i_k}.$

Proof. 

Set $\rho =\sqrt{\lambda }$. Using standard asymptotic analysis (as $\left|\rho \right|\to \infty$) on (13), we have

$$\begin{array}{c}\hfill {\chi }_n\left(\lambda \right)={\displaystyle \frac{ncos\rho \pi {sin}^{n-1}\rho \pi }{{\rho }^{n-1}}}+{\displaystyle \frac{{sin}^{n-2}\rho \pi }{{\rho }^n}}\left[(1-n{cos}^2\rho \pi )\sum _{k=1}^l{\omega }_{i_k}\right]+o\left({\displaystyle \frac{1}{{\rho }^n}}\right).\end{array}$$

(16)

Applying Rouché’s theorem near integers and half-integers together with the local Taylor expansions of $sin\left(\rho \pi \right)$ and $cos\left(\rho \pi \right)$ yields

$${\rho }_{k,j}=k+O\left(\frac{1}{k}\right)(j=1,\dots ,n-1),{\rho }_{k,0}=k-\frac{1}{2}+{\displaystyle \frac{A_l}{\pi k}}+o\left(\frac{1}{k}\right),$$

which are (15) and (14), respectively.    □

The asymptotic forms (14) and (15) ensure that ${\{sin\left({\rho }_{k,0}x\right)\}}_{k\in N}$ and $\left\{1\right\}\cup {\{cos\left({\rho }_{k,1}x\right)\}}_{k\in N}$ form Riesz bases in $L^2(0,\pi )$, since they are quadratically closed to ${\{sin(k-1/2)x\}}_{k\in N}$ and ${\{coskx\}}_{k\in N\cup \left\{0\right\}}$ separately.

In this section, we shall solve the following inverse problem.

(IP 1). Given $Q_1,Q_2,\dots ,Q_{n-1},$$F_n$, ${\left\{{\lambda }_{k,j}\right\}}_{k=1}^{\infty }$, $j=0,1,$ reconstruct an approximated potential $p_n\left(x\right)$ on the edge $E_n.$

Next, we briefly describe how one can determine the potential for the setting of the problem. Given two sequences of eigenvalues ${\left\{{\lambda }_{k,j}\right\}}_{k=1}^{\infty },j=0,1$ which satisfy (14) and (15), ${\chi }_n\left({\lambda }_{k,j}\right)=0,$ and (10) then leads to

$${\displaystyle \frac{{▵}_n^{(0,1)}\left({\lambda }_{k,j}\right)}{{▵}_n^{(0,0)}\left({\lambda }_{k,j}\right)}}=-\sum _{i=1}^{n-1}{\displaystyle \frac{{▵}_i^{(0,1)}\left({\lambda }_{k,j}\right)}{{▵}_i^{(0,0)}\left({\lambda }_{k,j}\right)}}:=g_{k,j}.$$

(17)

To solve the inverse problem (IP 1), we assume the following conditions:

(i) 

${▵}_i^{(0,0)}\left({\lambda }_{k,j}\right)\ne 0,$ for all $i,k,j$.

(ii) 

${\sum }_{k=1}^{m_n}sin\rho a_{n,k}=0$ has no solution in $\mathbb{N}.$

There are two cases we want to deal with.

Case (1): $F_n\ne ⌀.$ Under condition (ii), ${▵}_n^{(0,0)}\left(\lambda \right)$ determines $p_n\left(x\right)$ uniquely (refer [15] for details). Equations (12) and (17) yield

$${\displaystyle \frac{g_{k,j}}{{\rho }_{k,j}^2}}{\int }_0^{\pi }{N}_n\left(t\right)cos\left({\rho }_{k,j}t\right)dt-{\displaystyle \frac{1}{{\rho }_{k,j}}}{\int }_0^{\pi }{W}_n\left(t\right)sin\left({\rho }_{k,j}t\right)dt=-g_{k,j}{\displaystyle \frac{sin\left({\rho }_{k,j}\pi \right)}{{\rho }_{k,j}}}+cos\left({\rho }_{k,j}\pi \right).$$

(18)

Let

$${\kappa }_{k,j}={\int }_0^{\pi }{N}_n\left(t\right)cos\left({\rho }_{k,j}t\right)dt\mathrm{and}{\gamma }_{k,j}={\int }_0^{\pi }{W}_n\left(t\right)sin\left({\rho }_{k,j}t\right)dt.$$

Then, by (14) and (15), $g_{k,j}$ in (17) has the following estimates:

$$g_{k,j}={\displaystyle \frac{cos{\rho }_{k,j}\pi +({\gamma }_{k,j}/{\rho }_{k.j})}{sin{\rho }_{k,j}\pi /{\rho }_{k,j}+({\kappa }_{k,j}/{\rho }_{k.j}^2)}}=\left\{\begin{array}{cc}O\left(1\right)\hfill & \mathrm{for}j=0,\hfill \\ O\left(k^2\right)\hfill & \mathrm{for}j=1.\hfill \end{array}\right.$$

For the two cases of Equation (18), $j=0$ and $j=1$, multiplying them by $-{\rho }_{k,0}$ and ${\rho }_{k,1}^2/g_{k,1}$, respectively, we can obtain the following two estimates:

$${\displaystyle \frac{-g_{k,0}}{{\rho }_{k,0}}}{\int }_0^{\pi }{N}_n\left(t\right)cos\left({\rho }_{k,0}t\right)dt+{\int }_0^{\pi }{W}_n\left(t\right)sin\left({\rho }_{k,0}t\right)dt\in l^2$$

and

$${\int }_0^{\pi }{N}_n\left(t\right)cos\left({\rho }_{k,1}t\right)dt-{\displaystyle \frac{{\rho }_{k,1}}{g_{k,1}}}{\int }_0^{\pi }{W}_n\left(t\right)sin\left({\rho }_{k,1}t\right)dt\in l^2.$$

The last two estimates allow for subsequent approximation procedures.

We define the inner product

$$⟨\left(\begin{array}{c}{f}_1\left(t\right)\\ f_2\left(t\right)\end{array}\right),\left(\begin{array}{c}{g}_1\left(t\right)\\ g_2\left(t\right)\end{array}\right)⟩={\int }_0^{\pi }(f_1\left(t\right)\overline{g_1}\left(t\right)+f_2\left(t\right)\overline{g_2}\left(t\right))dt$$

(19)

on $L^2(0,\pi )\oplus L^2(0,\pi ).$ Because $N_n\left(t\right)$ and $W_n\left(t\right)$ are real-valued functions and

$$\left\{\left[\begin{array}{c}1\\ 0\end{array}\right],{\left[\begin{array}{c}cos{\rho }_{k,1}t\\ -{\displaystyle \frac{{\rho }_{k,1}}{g_{k,1}}}sin{\rho }_{k,1}t\end{array}\right]}_{k\ge 1},{\left[\begin{array}{c}-{\displaystyle \frac{g_{k,0}}{{\rho }_{k,0}}}cos{\rho }_{k,0}t\\ sin{\rho }_{k,0}t\end{array}\right]}_{k\ge 1}\right\}$$

is a Riesz base for $L^2(0,\pi )\oplus L^2(0,\pi )$ (refer to [14,17]), $N_n\left(x\right)$ and $W_n\left(x\right)$ can be uniquely determined by Equation (18). In particular, if $F_n$ consists of one single point, then the potential can be reconstructed analytically according the following theorem.

Theorem 3. 

$F_n=\left\{a\right\}$; then, $p_n\left(x\right)$ can be uniquely determined by $Q_1,Q_2,\dots ,Q_{n-1}$ and two sequences ${\left\{{\lambda }_{k,j}\right\}}_{k=1}^{\infty },$$j=0,1$ which satisfy the asymptotic behavior in (14) and (15).

Proof. 

We shall write

$$\begin{array}{c}\hfill {▵}_n^{(0,0)}\left(\lambda \right)={\displaystyle \frac{sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{N}_n\left(t\right)cos\rho tdt\end{array}$$

(20)

and

$$\begin{array}{c}\hfill {▵}_n^{(0,1)}\left(\lambda \right)=cos\rho \pi +{\displaystyle \frac{1}{\rho }}{\int }_0^{\pi }{W}_n\left(t\right)sin\rho tdt.\end{array}$$

(21)

According to [14] and Equation (18), $N_n\left(x\right)$ and $W_n\left(x\right)$ can be determined uniquely. As indicated in [14,16,18],

$$N_n\left(x\right)={\displaystyle \frac{1}{2}}\left\{\begin{array}{cc}{p}_n(\pi -a+x)+p_n(\pi -a-x),\hfill & x\in (0,a),\hfill \\ -p_n(\pi +a-x)+p_n(\pi -a-x),\hfill & x\in (a,\pi -a),\hfill \\ -p_n(\pi +a-x)-p_n(x-\pi +a),\hfill & x\in (\pi -a,\pi )\hfill \end{array}\right.$$

(22)

and

$$W_n\left(x\right)={\displaystyle \frac{1}{2}}\left\{\begin{array}{cc}{p}_n(\pi -a+x)-p_n(\pi -a-x),\hfill & x\in (0,a),\hfill \\ p_n(\pi +a-x)-p_n(\pi -a-x),\hfill & x\in (a,\pi -a),\hfill \\ p_n(\pi +a-x)+p_n(x-\pi +a),\hfill & x\in (\pi -a,\pi ),\hfill \end{array}\right.$$

(23)

where we assume $0<a<\pi /2$; otherwise, the forms of $N_n\left(x\right)$ and $W_n\left(x\right)$ will be a little different, though the arguments following are the same. Equations (22) and (23) yield

$$p_n(\pi -a+x)=N_n\left(x\right)+W_n\left(x\right);p_n(\pi -a-x)=N_n\left(x\right)-W_n\left(x\right),x\in (0,a)$$

(24)

and

$$p_n(\pi +a-x)-p_n(\pi -a-x)=W_n\left(x\right)-N_n\left(x\right),x\in (a,\pi -a).$$

(25)

Hence,

$$p_n\left(t\right)=\left\{\begin{array}{cc}{N}_n(t-\pi +a)+W_n(t-\pi +a),\hfill & t\in (\pi -a,\pi ),\hfill \\ N_n(\pi -a-t)-W_n(\pi -a-t),\hfill & t\in (\pi -2a,\pi -a),\hfill \\ p_n(t+2a)+N_n(\pi -a-t)-W_n(\pi -a-t),\hfill & t\in (0,\pi -2a).\hfill \end{array}\right.$$

(26)

Because the functions $N_n\left(x\right)$ and $W_n\left(x\right)$ are fully known, we can directly determine $p_n\left(x\right)$ on the intervals $(\pi -a,\pi )$ and $(\pi -2a,\pi -a)$. By iteratively applying the third case in (26), we can subsequently recover $p_n\left(x\right)$ on $(\pi -4a,\pi -2a)$, then on $(\pi -6a,\pi -4a)$ and so on, moving backwards. This iterative procedure ultimately reconstructs $p_n\left(x\right)$ on the entire interval $(0,\pi -2a)$. This completes the proof.    □

On the other hand, if $F_n$ contains more than one argument point, then (22) and (23) fail to hold; hence, the potential $p_n\left(x\right)$ has no the simple representation. However, $p_n\left(x\right)$ can be reconstructed theoretically by using (18) and the Riesz basis property of a system of vector functions (refer to [14] for details).

For approximation, we write

$$\left(\begin{array}{c}{N}_n\left(x\right)\\ W_n\left(x\right)\end{array}\right)\cong \sum _{k=0}^m{\alpha }_{k,1}\left(\begin{array}{c}coskx\\ 0\end{array}\right)+\sum _{k=1}^m{\alpha }_{k,0}\left(\begin{array}{c}0\\ sin(k-1/2)x\end{array}\right),$$

(27)

where

$${\alpha }_{k,1}={\displaystyle \frac{2}{\pi }}{\int }_0^{\pi }{N}_n\left(t\right)cosktdt\mathrm{and}{\alpha }_{k,0}={\displaystyle \frac{2}{\pi }}{\int }_0^{\pi }{W}_n\left(t\right)sin(k-(1/2))tdt.$$

Plugging (27) into (18),

$$\begin{array}{cc}\hfill & ⟨\left(\begin{array}{c}{\displaystyle \frac{g_{l,j}}{{\rho }_{l,j}^2}}cos{\rho }_{l,j}t\\ {\displaystyle \frac{-1}{{\rho }_{l,j}}}sin{\rho }_{l,j}t\end{array}\right),\left(\begin{array}{c}{N}_n\left(t\right)\\ W_n\left(t\right)\end{array}\right)⟩\hfill \\ \hfill & =\sum _{k=0}^m{\alpha }_{k,1}⟨\left(\begin{array}{c}{\displaystyle \frac{g_{l,j}}{{\rho }_{l,j}^2}}cos{\rho }_{l,j}t\\ {\displaystyle \frac{-1}{{\rho }_{l,j}}}sin{\rho }_{l,j}t\end{array}\right),\left(\begin{array}{c}coskt\\ 0\end{array}\right)⟩+\sum _{k=1}^m{\alpha }_{k,0}⟨\left(\begin{array}{c}{\displaystyle \frac{g_{l,j}}{{\rho }_{l,j}^2}}cos{\rho }_{l,j}t\\ {\displaystyle \frac{-1}{{\rho }_{l,j}}}sin{\rho }_{l,j}t\end{array}\right),\left(\begin{array}{c}0\\ sin(k-(1/2\left)\right)t\end{array}\right)⟩\hfill \\ \hfill & =-g_{l,j}{\displaystyle \frac{sin{\rho }_{l,j}\pi }{{\rho }_{l,j}}}+cos{\rho }_{l,j}\pi ,\hfill \end{array}$$

(28)

that is,

$$\begin{array}{cc}\hfill & \sum _{k=0}^m{\alpha }_{k,1}{\displaystyle \frac{g_{l,j}}{{\rho }_{l,j}^2}}{\int }_0^{\pi }cos{\rho }_{l,j}tcosktdt+\sum _{k=1}^m{\alpha }_{k,0}\left({\displaystyle \frac{-1}{{\rho }_{l,j}}}\right){\int }_0^{\pi }sin{\rho }_{l,j}tsin(k-1/2)tdt\hfill \\ \hfill =& -g_{l,j}{\displaystyle \frac{sin{\rho }_{l,j}\pi }{{\rho }_{l,j}}}+cos{\rho }_{l,j}\pi ,\hfill \end{array}$$

(29)

where $l=1-j,2-j,\dots ,m$ and $j=0,1.$ Then, ${(N_n\left(x\right),W_n\left(x\right))}^t$ can be solved from (29). Comparing (8) and (12), we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{sin\rho \pi }{{\rho }^2}}\left(\sum _{k=1}^{m_n}{\int }_0^{a_{n,k}}{p}_n\left(t\right)sin\rho (a_{n,k}-t)dt\right)+\sum _{k=1}^{m_n}{\displaystyle \frac{sin\rho a_{n,k}}{{\rho }^2}}{\int }_0^{\pi }{p}_n\left(t\right)sin\rho (\pi -t)dt\hfill \\ \hfill & ={\displaystyle \frac{sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{N}_n\left(t\right)cos\rho tdt.\hfill \end{array}$$

(30)

Substituting $\rho =k$ in (30) with $k\le m$, we have

$${\int }_0^{\pi }{p}_n\left(t\right)sink(\pi -t)dt={\displaystyle \frac{{\int }_0^{\pi }{N}_n\left(t\right)cosktdt}{{\sum }_{j=1}^{m_n}sink{a}_{n,j}}}={\displaystyle \frac{(\pi /2){\alpha }_{k,1}}{{\sum }_{j=1}^{m_n}sink{a}_{n,j}}}.$$

(31)

Equation (31) facilitates the derivation of an approximation of the sine series of $p_n\left(x\right),$ i.e.,

$$p_n\left(t\right)=\sum _{k=1}^m{\displaystyle \frac{{\alpha }_{k,1}}{{\sum }_{j=1}^{m_n}sink{a}_{n,j}}}sink(\pi -t).$$

(32)

Alternatively, an approximation of $p_n\left(x\right)$ can be obtained through the following:

$${\int }_0^{\pi }{p}_n\left(t\right)cos(k-1/2)(\pi -t)dt={\displaystyle \frac{{\int }_0^{\pi }{W}_n\left(t\right)sin(k-1/2)tdt}{{\sum }_{j=1}^{m_n}sin(k-1/2)a_{n,j}}}={\displaystyle \frac{(\pi /2){\alpha }_{k,0}}{{\sum }_{j=1}^{m_n}sin(k-1/2)a_{n,j}}}.$$

(33)

Hence,

$$p_n\left(t\right)=\sum _{k=1}^m{\displaystyle \frac{{\alpha }_{k,0}}{{\sum }_{j=1}^{m_n}sin(k-1/2)a_{n,j}}}cos\left[(k-1/2)(\pi -t)\right].$$

(34)

For convenience, we call (34) the C-Series.

Case (2): $F_n=⌀.$ For this case, (11) and (17) yield

$$\begin{array}{cc}\hfill & {\displaystyle \frac{g_{k,j}}{{\rho }_{k,j}^2}}{\int }_0^{\pi }{K}_n\left(t\right)cos{\rho }_{k,j}\left(t\right)dt-{\displaystyle \frac{1}{{\rho }_{k,j}}}{\int }_0^{\pi }{H}_n\left(t\right)sin{\rho }_{k,j}\left(t\right)dt\hfill \\ \hfill =& -g_{k,j}({\displaystyle \frac{sin{\rho }_{k,j}\pi }{{\rho }_{k,j}}}-{\displaystyle \frac{{\omega }_{n}cos{\rho }_{k,j}\pi }{{\rho }_{k,j}^2}})+cos{\rho }_{k,j}\pi +{\displaystyle \frac{{\omega }_{n}sin{\rho }_{k,j}\pi }{{\rho }_{k,j}}}.\hfill \end{array}$$

(35)

According to (14),

$${\omega }_n=\underset{k\to \infty }{lim}n\pi k({\rho }_{k,0}-k+{\displaystyle \frac{1}{2}})-\sum _{j=1}^{l-1}{\omega }_{i_j}\cong n\pi m({\rho }_{m,0}-m+{\displaystyle \frac{1}{2}})-\sum _{j=1}^{l-1}{\omega }_{i_j}.$$

(36)

Similar to Case (1), we can obtain ${(K_n\left(x\right),H_n\left(x\right))}^t$. Then, we can solve

$${▵}_n^{(0,1)}\left(\lambda \right)=cos\rho \pi +{\displaystyle \frac{{\omega }_{n}sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{\rho }}{\int }_0^{\pi }{H}_n\left(t\right)sin\rho tdt=0$$

(37)

to obtain the Dirichlet–Neumann spectrum ${\sigma }_{DN}\left(p_n\right)$ corresponding to potential $p_n\left(x\right).$ On the other hand, we also solve

$${▵}_n^{(0,0)}\left(\lambda \right)={\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{{\omega }_{n}cos\rho \pi }{{\rho }^2}}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{K}_n\left(t\right)cos\rho tdt=0$$

(38)

to obtain the Dirichlet spectrum ${\sigma }_{DD}\left(p_n\right)$ corresponding to $p_n\left(x\right).$ Then, ${\sigma }_{DN}\left(p_n\right)$ and ${\sigma }_{DD}\left(p_n\right)$ can uniquely determine $p_n\left(x\right).$ Alternatively, the Weyl function for $p_n\left(x\right)$ is

$$M_n\left(\lambda \right)={\displaystyle \frac{cos\rho \pi +{\displaystyle \frac{{\omega }_{n}sin\rho \pi }{\rho }}+{\displaystyle \frac{1}{\rho }}{\int }_0^{\pi }{H}_n\left(t\right)sin\rho tdt}{{\displaystyle \frac{sin\rho \pi }{\rho }}-{\displaystyle \frac{{\omega }_{n}cos\rho \pi }{{\rho }^2}}+{\displaystyle \frac{1}{{\rho }^2}}{\int }_0^{\pi }{K}_n\left(t\right)cos\rho tdt}},$$

(39)

which can also help to reconstruct $p_n\left(x\right).$

Before presenting the numerical experiments, we briefly outline the algorithm for approximating $N_n\left(x\right)$ and $W_n\left(x\right)$. The procedures for $K_n\left(t\right)$ and $H_n\left(t\right)$ are analogous, and are consequently omitted (see Algorithm 1).

Algorithm 1 Algorithm for obtaining approximation of ${\mathit{N}}_{\mathit{n}}\left(\mathit{x}\right)$ and ${\mathit{W}}_{\mathit{n}}\left(\mathit{x}\right)$

Step 1: Using (29), construct a coefficient matrix $A={\left(A_{i,j}\right)}_{0\le i,j\le 2m},$ where $$\left\{\begin{array}{cc}{A}_{2l-1+j,k}={\displaystyle \frac{g_{l,j}}{{\rho }_{l,j}^2}}{\int }_0^{\pi }cos{\rho }_{l,j}tcosktdt,\hfill & \mathrm{for}l=1-j,2-j,\dots ,m;j=0,1\mathrm{and}0\le k\le m,\hfill \\ A_{2l-1+j,k+m}=\left({\displaystyle \frac{-1}{{\rho }_{l,j}}}\right){\int }_0^{\pi }sin{\rho }_{l,j}tsin(k-1/2)tdt,\hfill & \mathrm{for}l=1-j,2-j,\dots ,m;j=0,1\mathrm{and}1\le k\le m.\hfill \end{array}\right.$$ Step 2: Using (29), construct a vector $b={\left(b_k\right)}_{k=0}^{2m},$ where $$b_{2l-1+j}=-g_{l,j}{\displaystyle \frac{sin{\rho }_{l,j}\pi }{{\rho }_{l,j}}}+cos{\rho }_{l,j}\pi \mathrm{for}l=1-j,2-j,\dots ,m\mathrm{and}j=0,1.$$ Step 3: Solve the linear system $Ax=b.$ Then, $${\alpha }_{k,1}=x_{k}0\le k\le m;{\alpha }_{k,0}=x_{m+k}1\le k\le m.$$ Step 4: Using Equation (32) or (34), reconstruct an approximation of potential function $p_n\left(x\right)$.

In the following, we provide several numerical examples computed using Mathematica 14.1 with WorkingPrecision = 30. Next, we shall present some numerical experiments.

Example 1. 

Let $p_1\left(x\right)=0,$$F_1=⌀,$$p_2\left(x\right)=x/2,$$F_2=\{1/2\},$$P_3\left(x\right)=x^2(1-x/\pi ),$ and $F_3=\left\{\sqrt{3}\right\}.$ We pick the following two sequences of approximated (computed) square root of eigenvalues from the spectral set of the nonlocal problem on a three-edged graph. Note that the computed eigenvalues are inexact due to the use of numerical solvers; therefore, we treat them as noisy measurements.

Case 1: Assuming $Q_1\left(x\right)$, $Q_2\left(x\right)$ and $F_3$ are known a priori, for this case, we obtain the recovered potentials

$$p_{3,s}\left(x\right)=\sum _{k=1}^{20}{b}_{k,3}sink(\pi -x)$$

or

$$p_{3,c}\left(x\right)=\sum _{k=1}^{20}{c}_{k,3}cos(k-1/2)(\pi -x).$$

The list of coefficients $\{b_{k,3},c_{k,3}\}$ is presented below (Table 1 and Table 2).

Table 1. Approximated square roots of eigenvalues.

k	${\mathit{\rho }}_{\mathit{k},0}$	${\mathit{\rho }}_{\mathit{k},1}$
1	0.701670979849780482802884683945	1.14419713214781285821337805721
2	1.53253047542152205042869966746	1.92606881071834693862126739038
3	2.53611149714040329694142277640	2.99530323823089127956398317338
4	3.49716816406192161502486908049	3.97968558095450765939906602447
5	4.49601464239664136172762681980	5.00036300941891543708369963789
6	5.49969429743679017457895059081	5.99881342368587646071097182829
⋮	⋮	⋮
18	17.4999401763010990138773834483	17.9995761788640423800696265217
19	18.4999694278934314570173748406	18.9999313730510288442448032663
20	19.5000330173038898996481752409	20.0000004992489194016841930157

Table 2. Coefficients $\{b_{k,3},c_{k,3}\}$ of the approximated potential.

k	${\mathit{b}}_{\mathit{k},3}$	${\mathit{c}}_{\mathit{k},3}$
1	1.2732376158578581123836	1.2677493131113754386767
2	0.4774612728400880111861	−0.2714647240108379473994
3	0.04715698204247169024987	0.3703614031143858306897
4	0.05968371021266308305825	−0.12546627491921589416838
5	0.010185906619608655653099	0.10977280291750229098440
6	0.017683791469507794191816	−0.05713409595112502632124
⋮	⋮	⋮
18	0.0006537749468139297943053	−0.006280049788959601006533
19	0.00018552948565125628916774	0.006034355880384813018389
20	0.0004774309458339084200947	−0.005079474283679086772172

The comparison between the exact potential $p_3\left(x\right)$ and the recovered potential is illustrated in Figure 2. It is evident that $p_3\left(x\right)$ is smooth and vanishes at both endpoints. The approximation closely matches the exact potential, which can be attributed to the appropriateness of the chosen bases in (32) and (34).

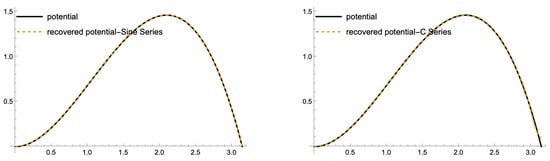
Figure 2. Approximated potential for $p_3\left(x\right)$.

Case 2: Assuming $Q_1\left(x\right)$, $Q_3\left(x\right)$, and $F_2$ are known a priori, for this case we obtain the recovered potentials

$$p_{2,s}\left(x\right)=\sum _{k=1}^{20}{b}_{k,2}sink(\pi -x)$$

or

$$p_{2,c}\left(x\right)=\sum _{k=1}^{20}{c}_{k,2}cos(k-1/2)(\pi -x).$$

The list of coefficients $\{b_{k,2},c_{k,2}\}$ is presented below (Table 3).

Table 3. Coefficients $\{b_{k,2},c_{k,2}\}$ of the approximated potential.

k	${\mathit{b}}_{\mathit{k},2}$	${\mathit{c}}_{\mathit{k},2}$
1	1.000014583263539309	1.273241987070193787
2	0.500015920073165111	0.1414903788305458901
3	0.3333336215285048484	0.0509248152647319274
4	0.2500085390717648115	0.02598486848036296669
5	0.2000004760838436230	0.01572179271809543313
6	0.1666716766940862663	0.01052273889360826647
⋮	⋮	⋮
18	0.0555627415323602532	0.001039008537001434613
19	0.0526421358095932992	0.000931770630550529962
20	0.0500010530135964570	0.000835804356132458430

The comparison between the exact potential $p_2\left(x\right)$ and the recovered potential is illustrated in Figure 3.

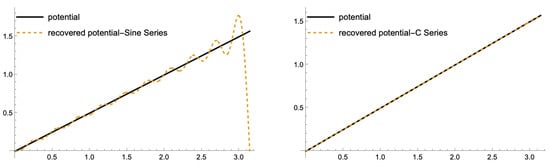
Figure 3. Approximated potential for $p_2\left(x\right)$.

Notice that the sine series approximation is not as good as that of the C-Series for this case. The sine series approximation tends to be inaccurate near the endpoints, a phenomenon often attributed to the Gibbs effect.

Case 3: Assume that $Q_2$ and $Q_3$ are known a priori and that $F_1=⌀.$ In this case, the Sturm–Liouville operator on edge $e_1$ reduces to an ordinary form. To recover $p_1\left(x\right),$ both the Dirichlet eigenvalues and Dirichlet–Neumann eigenvalues are required. To this end, we must first compute the functions $K_n\left(t\right)$ and $H_n\left(t\right),$ which are then used to determine the Dirichlet and Dirichlet–Neumann spectral data. For this case, we take

$$\omega ={\displaystyle \frac{1}{2}}{\int }_0^{\pi }{p}_1\left(t\right)dt\cong 50\ast (49.4999980-49.5)\cong 0.$$

We immediately obtain the coefficients ${\alpha }_{k,1}={\alpha }_{k,0}=0$ by applying the linear system in (35) for $1\le k\le m.$ Hence,

$${▵}_1^{(0,0)}\left(\lambda \right)={\displaystyle \frac{sin\rho \pi }{\rho }},{▵}_1^{(0,1)}\left(\lambda \right)=cos\rho \pi ,$$

which leads to the conclusion that $p_1\left(x\right)\cong 0.$

Finally, we shall present a case in which the potential is not continuous at some point inside $(0,\pi ).$

Example 2. 

In this example, we take $p_1\left(x\right)=0,$$F_1=⌀,$$p_2\left(x\right)=x/2,$$F_2=\{1/2\},$$F_2=\left\{\sqrt{3}\right\}$, and

$$p_3\left(x\right)=\left\{\begin{array}{cc}1+x,\hfill & 0\le x\le 1,\hfill \\ 6-x,\hfill & 1<x\le \pi ,\hfill \end{array}\right.$$

is a piecewise continuous function. Again, the picked computed eigenvalues are as below (Table 4).

Table 4. Approximated square roots of eigenvalues for piecewise function $p_3\left(x\right)$.

k	${\mathit{\rho }}_{\mathit{k},0}$	${\mathit{\rho }}_{\mathit{k},1}$
1	0.737803560298703641388370068300	1.15588799519209921118721826664
2	1.90606729751227334913492299737	1.95813054797355361249891022202
3	2.64224878175953888791029268734	2.94555842678532895160130874327
4	3.50431127427502397388784261329	3.94549412972677073692409506690
5	4.49869305437664852427777028651	5.00558963396096082945795930486
6	5.49851355852333249633577285758	5.99417977918890294709122884411
⋮	⋮	⋮
18	17.4994949655067843825938901652	17.9995739601314368987132337680
19	18.5006810143870193327397320706	18.9999477171102423759503830322
20	19.5007050905545662052763763262	20.0000180704282308865331522241
⋮	⋮	⋮
49	48.5000114638397143292852383530	48.9999119356279372873826055065
50	49.4998918021879152025642752803	49.9999184829462541785280225335

Using forty computed eigenvalues to recover the potential yields the approximation shown in Figure 4, which is clearly unsatisfactory. To enhance the reconstruction accuracy, we can increase the number of eigenvalues to $100.$ The resulting approximation displayed in Figure 5 shows an improvement.

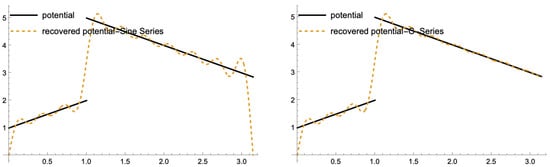
Figure 4. Approximated potential for $p_3\left(x\right)$ with 40 eigenvalues.

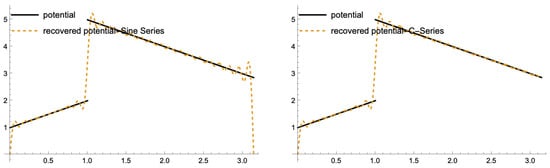
Figure 5. Approximated potential for $p_3\left(x\right)$ with 100 eigenvalues.

The reader might wonder whether our theory and algorithm can be extended to the case of star graphs with unequal edge lengths. The answer is affirmative. Although we omit the technical details here, interested readers are encouraged to explore this extension independently.

4. Conclusions

In this paper, we have studied the partial inverse spectral problem for nonlocal Sturm–Liouville operators with frozen arguments on a star-shaped graph. We have presented a constructive solution by recovering one unknown coefficient on a selected edge using a partial set of spectral data. We have formulated an algorithm for numerical reconstruction and validated its effectiveness through various examples, including both smooth and piecewise continuous potentials. Our experiments demonstrate that the proposed method provides accurate reconstructions with sufficiently many eigenvalues. The performance of sine-type and cosine-type series reconstructions has also been compared. Although the present study is primarily theoretical, the proposed method provides qualitative insight into the influence of graph and frozen arguments on system behavior.