Generalized Synchronization of a Novel Hyperchaotic System and Application in Secure Communication

Abstract

In this paper, a generalized synchronization (GS) framework for identical hyperchaotic systems is presented. The main objective is to achieve generalized synchronization with guaranteed global stability and effective convergence, which remains a key challenge in synchronization-based secure communication systems. The proposed controller is systematically derived to ensure global asymptotic convergence of the synchronization errors for arbitrary initial conditions and distinct scaling factors. This formulation unifies complete, anti-, and generalized synchronization within a single control structure. To demonstrate the applicability of the proposed method, it is integrated into an image encryption algorithm, where the hyperchaotic trajectories of the drive system generate highly random permutation and diffusion sequences. Simulation results verify that the designed controller achieves effective generalized synchronization and that the encrypted images exhibit uniform histograms and low pixel correlation, indicating strong security and resistance to statistical attacks.

1. Introduction

The study of hyperchaotic systems has attracted significant attention over the past few decades due to their complex nonlinear dynamics and wide-ranging applications in science and engineering. Since the pioneering work of Pecora and Carroll [1], who first introduced the concept of chaos synchronization, researchers have extensively explored synchronization phenomena in nonlinear dynamical systems. These efforts have led to the development of several synchronization types, including complete synchronization, anti-synchronization, projective synchronization, and generalized synchronization [2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Among them, generalized synchronization (GS) is regarded as the most comprehensive form, as it allows for a relationship between the drive and response systems. Hyperchaotic systems, which possess more than one positive Lyapunov exponent, provide even richer dynamic behavior and higher sensitivity to initial conditions compared to simple chaotic systems. Such properties make them especially attractive for secure communication and cryptographic applications, where unpredictability and sensitivity are key requirements [16,17,18,19,20,21,22,23]. Several recent studies have investigated advanced synchronization strategies and their applications in secure communication and encryption. Generalized modified projective synchronization has been employed in secure communication schemes based on newly proposed four-dimensional fractional-order hyperchaotic systems, highlighting the effectiveness of scaling-based synchronization in fractional-order settings [24]. Some studies have addressed synchronization and the FPGA implementation of multiscroll Hopfield neural networks using non-polynomial memristors [25]. Recent work has addressed fixed-time interlayer synchronization in voltage-flux time-delayed memristive neural networks using Lyapunov-based control and demonstrated its effectiveness in secure communication applications [26]. In addition, Mittag–Leffler synchronization of fractional-order chaotic neural networks with time-varying delays has been studied using hybrid control techniques and applied to biometric image encryption. These works highlight the role of advanced control designs in enhancing synchronization robustness and encryption performance [27].

Although these studies provide valuable contributions by addressing specific synchronization types, control strategies, or implementation platforms, they are typically restricted to fractional-order models, neural network-based systems, hardware-oriented realizations, or particular synchronization objectives. In contrast, the present work considers a continuous-time hyperchaotic system and develops a generalized synchronization framework within a unified analytical setting, which is subsequently applied to secure communication.

The main contributions of this paper are summarized as follows:

• A generalized synchronization framework is rigorously formulated for identical hyperchaotic systems by defining appropriate error dynamics with diagonal scaling matrices. This formulation provides a unified mathematical setting that encompasses complete and anti-synchronization as special cases.
• A control law is analytically derived to stabilize the resulting error system. By constructing a quadratic Lyapunov function, sufficient conditions are established to ensure that the synchronization error dynamics are globally asymptotically stable for arbitrary initial conditions and nonzero scaling factors.
• The proposed synchronization framework is further exploited to generate high-quality chaotic sequences from the drive-system trajectories. These sequences are systematically incorporated into a permutation diffusion image encryption algorithm, thereby demonstrating the practical applicability of the theoretical results.

The contents of this paper are organized as follows: Section 2 defines the novel hyperchaotic system. Section 3 proposes the methodology of generalized synchronization. The chaos-generalized synchronization of the introduced chaotic system with itself as a drive response system is investigated in Section 4. A numerical example is provided to show the effectiveness of the method in Section 5. The implementation of the proposed method is presented in Section 6, where secure image encryption is achieved using the drive system’s trajectories to generate permutation and diffusion keys. Moreover, statistical evaluations, including histogram and pixel correlation analysis, confirm that the proposed scheme ensures strong security and robustness against cryptanalytic attacks. Finally, the paper is concluded in Section 7.

2. The Novel Hyperchaotic System

The considered novel hyperchaotic system defined in [28] is expressed as follows:

$$\begin{array}{cc}\hfill \dot{x}& =a(y-x)+u,\hfill \\ \hfill \dot{y}& =bx+kxz,\hfill \\ \hfill \dot{z}& =-cz-hxy,\hfill \\ \hfill \dot{u}& =xz-dy,\hfill \end{array}$$

where the system parameters are given by $a=10, b=40, c=2.5, h=1, k=16, d=2.$ The corresponding phase portraits and projections of the system variables are illustrated in Figure 1, where subfigures (a)–(h) represent different two dimensional projections and three-dimensional attractors of the novel hyperchaotic system.

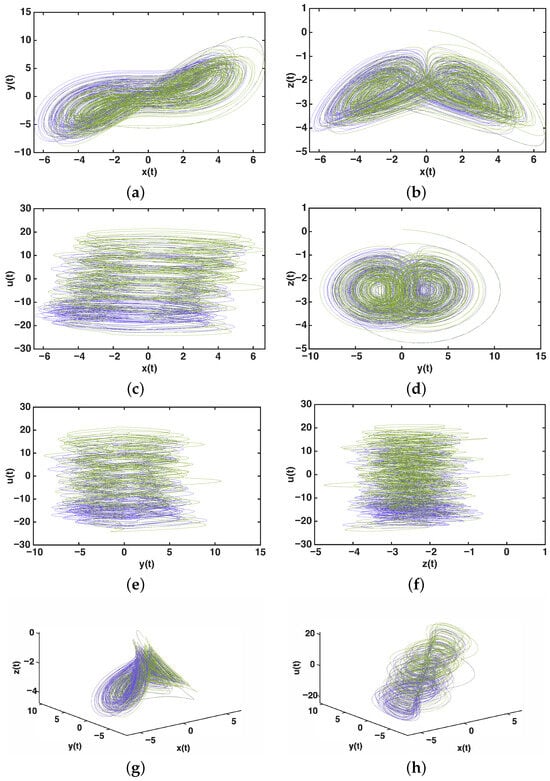
Figure 1. Phase portraits of the novel hyperchaotic system: (a) trajectory in the $(x, y)$ plane; (b) trajectory in the $(x, z)$ plane; (c) trajectory in the $(x, u)$ plane; (d) trajectory in the $(y, z)$ plane; (e) trajectory in the $(y, u)$ plane; (f) trajectory in the $(z, u)$ plane; (g) 3D attractor $(x, y, z)$; (h) 3D attractor $(x, y, u)$. The green trajectory represents the numerical solution obtained using the default settings of the ODE45 solver, while the purple trajectory corresponds to the solution computed with a higher relative tolerance (RelTol = 10⁻⁶).

3. The Scheme of General Synchronization

We consider the drive and response systems shown in the following form:

$$\begin{array}{cc}\hfill \dot{x}& =\Phi \left(x\right)\hfill \\ \hfill \dot{y}& =\Omega \left(y\right)+v(x, y, t),\hfill \end{array}$$

where $x={(x_1, x_2,\dots ,x_n)}^T$ and $y={(y_1, y_2,\dots ,y_n)}^T$$\in R^n$ are state vectors, $\Phi , \Omega :R^n\to R^n$ are continuous nonlinear functions, and $v(x, y, t)$ is the controller vector to be designed [29].

Definition 1.

It is said that the drive and response systems achieve generalized synchronization if the following equation holds:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\left|\right|e\left(t\right)\left|\right|=\underset{t\to \infty }{lim}\left|\right|y\left(t\right)-\Lambda x\left(t\right)\left|\right|=0\end{array}$$

where the diagonal matrix ($\Lambda =diag\{{\alpha }_1, {\alpha }_2,\dots ,{\alpha }_n\}, {\alpha }_i\in \mathbb{R}\setminus \left\{0\right\},i=\{1,\dots ,n\}$) is a scaling factor that can be chosen to realize different types of synchronization.

Remark 1.

The generalized synchronization framework includes several classical synchronization schemes as special cases, depending on the choice of the scaling matrix (Λ).

• If $\Lambda =I_n$, where $I_n$ denotes the $n\times n$ identity matrix, the generalized synchronization reduces to complete synchronization, that is,

  $$\underset{t\to \infty }{lim}\parallel y\left(t\right)-x\left(t\right)\parallel =0.$$
• If $\Lambda =-I_n$, the generalized synchronization becomes anti-synchronization, where the state variables of the drive and response systems evolve in opposite directions, i.e.,

  $$\underset{t\to \infty }{lim}\parallel y\left(t\right)+x\left(t\right)\parallel =0.$$

4. Generalized Synchronization Between Two Identical Systems

Here, we present the novel hyperchaotic dynamical system with generalized synchronization. The novel hyperchaotic drive system is described as follows:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =a(y_1-x_1)+u_1,\hfill \\ \hfill {\dot{y}}_1& =b{x}_1+k{x}_1{z}_1,\hfill \\ \hfill {\dot{z}}_1& =-c{z}_1-h{x}_1{y}_1,\hfill \\ \hfill {\dot{u}}_1& =x_1{z}_1-d{y}_1,\hfill \end{array}$$

(1)

where $x_1, y_1, z_1$, and $u_1$ denote the drive states. The corresponding response system, including the control input ($v_i$), is given by

$$\begin{array}{cc}\hfill {\dot{x}}_2& =a(y_2-x_2)+u_2+v_1,\hfill \\ \hfill {\dot{y}}_2& =b{x}_2+k{x}_2{z}_2+v_2,\hfill \\ \hfill {\dot{z}}_2& =-c{z}_2-h{x}_2{y}_2+v_3,\hfill \\ \hfill {\dot{u}}_2& =x_2{z}_2-d{y}_2+v_4,\hfill \end{array}$$

(2)

where $x_2, y_2, z_2$, and $u_2$ denote the response states and $v_i,i=1, 2, 3, 4$ is the control signal to be designed.

To establish generalized synchronization between the drive (1) and response (2) systems, we define the error vectors as follows:

$$\begin{array}{cc}\hfill e_x& =x_2-{\alpha }_1{x}_1,\hfill \\ \hfill e_y& =y_2-{\alpha }_2{y}_1,\hfill \\ \hfill e_z& =z_2-{\alpha }_3{z}_1,\hfill \\ \hfill e_u& =u_2-{\alpha }_4{u}_1.\hfill \end{array}$$

(3)

Then, by differentiating the error variables (3), we obtain

$$\begin{array}{cc}\hfill {\dot{e}}_x& =e_u+a{e}_y-a{e}_x+a({\alpha }_2-{\alpha }_1)y_1+({\alpha }_4-{\alpha }_1)u_1+v_1,\hfill \\ \hfill {\dot{e}}_y& =b\left(e_x+({\alpha }_1-{\alpha }_2)x_1\right)+k\left(e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_2)\right)+v_2,\hfill \\ \hfill {\dot{e}}_z& =-c{e}_z-h\left(e_x{e}_y+{\alpha }_2{y}_1{e}_x+{\alpha }_1{x}_1{e}_y+x_1{y}_1({\alpha }_1{\alpha }_2-{\alpha }_3)\right)+v_3,\hfill \\ \hfill {\dot{e}}_u& =e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z-d\left(e_y+({\alpha }_2-{\alpha }_4)y_1\right)+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_4)+v_4.\hfill \end{array}$$

The main purpose is to determine controllers ($v_i,i=1,2,3,4$) that could stabilize the error variables of the system. For this, the following theorem is presented:

Theorem 1.

For a given nonzero scaling factor (${\alpha }_i$, where $i=1, 2, 3, 4$), the generalized synchronization among the drive and response systems will occur with the following control inputs chosen.

$$\begin{array}{cc}\hfill v_1& =-e_u-a{e}_y+a({\alpha }_1-{\alpha }_2)y_1+({\alpha }_1-{\alpha }_4)u_1\hfill \\ \hfill v_2& =b\left(({\alpha }_2-{\alpha }_1)x_1-e_x\right)+k\left(x_1{z}_1({\alpha }_2-{\alpha }_1{\alpha }_3)-e_x{e}_z-{\alpha }_3{z}_1{e}_x-{\alpha }_1{x}_1{e}_z\right)-f{e}_y\hfill \\ \hfill v_3& =-h\left(x_1{y}_1({\alpha }_3-{\alpha }_1{\alpha }_2)-e_x{e}_y-{\alpha }_2{y}_1{e}_x-{\alpha }_1{x}_1{e}_y\right)\hfill \\ \hfill v_4& =-e_x{e}_z-{\alpha }_3{z}_1{e}_x-{\alpha }_1{x}_1{e}_z-d\left(({\alpha }_4-{\alpha }_2)y_1-e_y\right)+x_1{z}_1({\alpha }_4-{\alpha }_1{\alpha }_3)-g{e}_u.\hfill \end{array}$$

(4)

where $f,g>0$ are design parameters.

Proof. 

Consider the following Lyapunov function:

$$V=\frac{1}{2}\left(e_x^2+e_y^2+e_z^2+e_u^2\right).$$

(5)

The time derivative of the Lyapunov function (5) is

$$\begin{array}{cc}\hfill \dot{V}& =e_x{\dot{e}}_x+e_y{\dot{e}}_y+e_z{\dot{e}}_z+e_u{\dot{e}}_u.\hfill \\ \hfill & =e_x\left(e_u+a{e}_y-a{e}_x+a({\alpha }_2-{\alpha }_1)y_1+({\alpha }_4-{\alpha }_1)u_1+v_1\right)\hfill \\ \hfill & +e_y\left(b\left(e_x+({\alpha }_1-{\alpha }_2)x_1\right)+k\left(e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_2)\right)+v_2\right)\hfill \\ \hfill & +e_z\left(-c{e}_z-h\left(e_x{e}_y+{\alpha }_2{y}_1{e}_x+{\alpha }_1{x}_1{e}_y+x_1{y}_1({\alpha }_1{\alpha }_2-{\alpha }_3)\right)+v_3\right)\hfill \\ \hfill & +e_u\left(e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z-d\left(e_y+({\alpha }_2-{\alpha }_4)y_1\right)+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_4)+v_4\right),\hfill \end{array}$$

substituting the above control input (4) to cancel cross terms and ensure negative definiteness:

$$\begin{array}{cc}\hfill \dot{V}& =e_x\left(e_u+a{e}_y-a{e}_x+a({\alpha }_2-{\alpha }_1)y_1+({\alpha }_4-{\alpha }_1)u_1-e_u-a{e}_y+a({\alpha }_1-{\alpha }_2)y_1+({\alpha }_1-{\alpha }_4)u_1\right),\hfill \\ \hfill & +e_y(b\left(e_x+({\alpha }_1-{\alpha }_2)x_1\right)+k\left(e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_2)\right)\hfill \\ \hfill & +b\left(({\alpha }_2-{\alpha }_1)x_1-e_x\right)+k\left(x_1{z}_1({\alpha }_2-{\alpha }_1{\alpha }_3)-e_x{e}_z-{\alpha }_3{z}_1{e}_x-{\alpha }_1{x}_1{e}_z\right)-f{e}_y),\hfill \\ \hfill & +e_z(-c{e}_z-h\left(e_x{e}_y+{\alpha }_2{y}_1{e}_x+{\alpha }_1{x}_1{e}_y+x_1{y}_1({\alpha }_1{\alpha }_2-{\alpha }_3)\right)\hfill \\ \hfill & -h\left(x_1{y}_1({\alpha }_3-{\alpha }_1{\alpha }_2)-e_x{e}_y-{\alpha }_2{y}_1{e}_x-{\alpha }_1{x}_1{e}_y\right)),\hfill \\ \hfill & +e_u(e_x{e}_z+{\alpha }_3{z}_1{e}_x+{\alpha }_1{x}_1{e}_z-d\left(e_y+({\alpha }_2-{\alpha }_4)y_1\right)+x_1{z}_1({\alpha }_1{\alpha }_3-{\alpha }_4)\hfill \\ \hfill & -e_x{e}_z-{\alpha }_3{z}_1{e}_x-{\alpha }_1{x}_1{e}_z-d\left(({\alpha }_4-{\alpha }_2)y_1-e_y\right)+x_1{z}_1({\alpha }_4-{\alpha }_1{\alpha }_3)-g{e}_u),\hfill \\ \hfill \Rightarrow \dot{V}=& -a{e}_x^2-f{e}_y^2-c{e}_z^2-g{e}_u^2.\hfill \end{array}$$

Then, we obtain

$$\begin{array}{c}\hfill \dot{V}=-e^{T}Pe,\mathrm{where}e=\left[\begin{array}{c}{e}_x\\ e_y\\ e_z\\ e_u\end{array}\right],P=\left[\begin{array}{cccc}a& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& c& 0\\ 0& 0& 0& g\end{array}\right],\end{array}$$

since $a, f, c$, and $g>0$ and the matrix (P) is positive definite, which implies that $\dot{V}$ is negative definite. Consequently, the error system is globally asymptotically stable, and generalized synchronization between the identical hyperchaotic systems is achieved. □

5. Numerical Simulations

To substantiate the analytical results and assess the effectiveness of the proposed synchronization schemes, a series of numerical simulations was carried out using the designed novel hyperchaotic drive response systems. The synchronization performance is evaluated through the temporal evolution of the error variables ($e_x\left(t\right), e_y\left(t\right), e_z\left(t\right), e_u\left(t\right)$), which are defined as follows:

$$e_x=x_2-{\alpha }_1{x}_1,e_y=y_2-{\alpha }_2{y}_1,e_z=z_2-{\alpha }_3{z}_1,e_u=u_2-{\alpha }_4{u}_1.$$

We assume that the initial conditions are given by

$$\begin{array}{c}\hfill {[x_1\left(0\right), y_1\left(0\right), z_1\left(0\right), u_1\left(0\right)]}^T={[1,-0.3, 0.7, -0.5]}^T{[x_2\left(0\right), y_2\left(0\right), z_2\left(0\right), u_2\left(0\right)]}^T={[5, -4, -6, 9]}^T.\end{array}$$

In the first case, the complete synchronization behavior was achieved by setting all scaling factors to ${\alpha }_i=1$, as presented in Figure 2. In the second case, the anti-synchronization phenomenon appears in Figure 3 when ${\alpha }_i=-1$, as the state variables of the response system evolved in an opposite phase to those of the drive system. Finally, for the generalized synchronization, different scaling factors of ${\alpha }_i={[2, 6, 4, 5]}^T$ were considered to demonstrate the system’s ability to achieve stable convergence, even under non-identical mappings, as illustrated in Figure 4. These results demonstrate that the proposed controller provides a unified and effective synchronization mechanism for multiple synchronization modes.

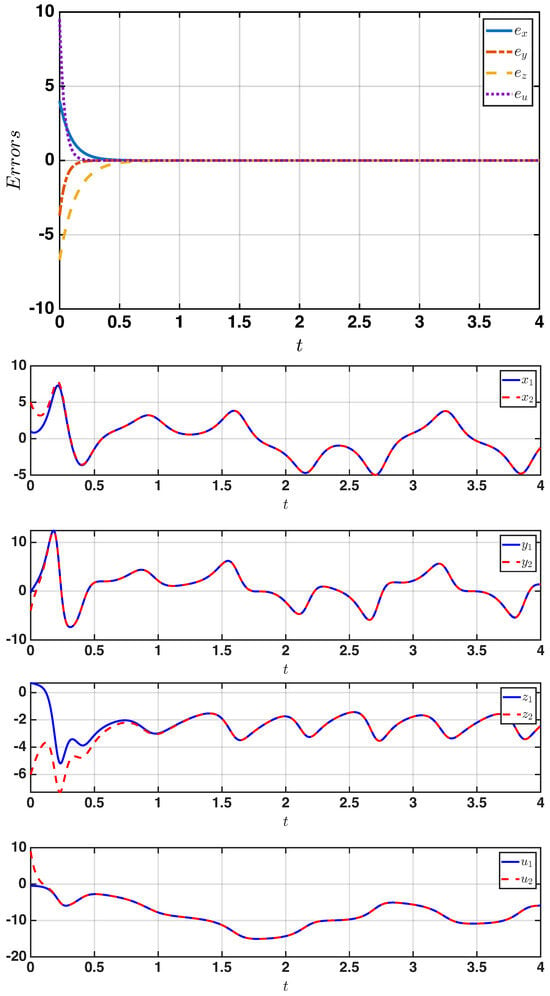
Figure 2. Complete synchronization results showing (top) drive response trajectories, and (bottom) phase portraits $(x, y, z, u)$ under ${\alpha }_i=1$.

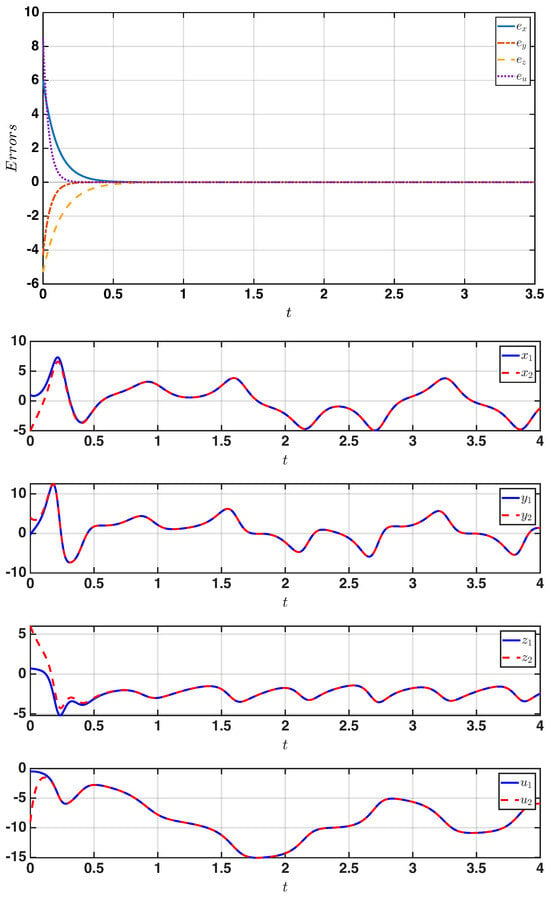
Figure 3. Anti-synchronization results showing (top) drive response trajectories and (bottom) phase portraits $(x, y, z, u)$ under ${\alpha }_i=-1$.

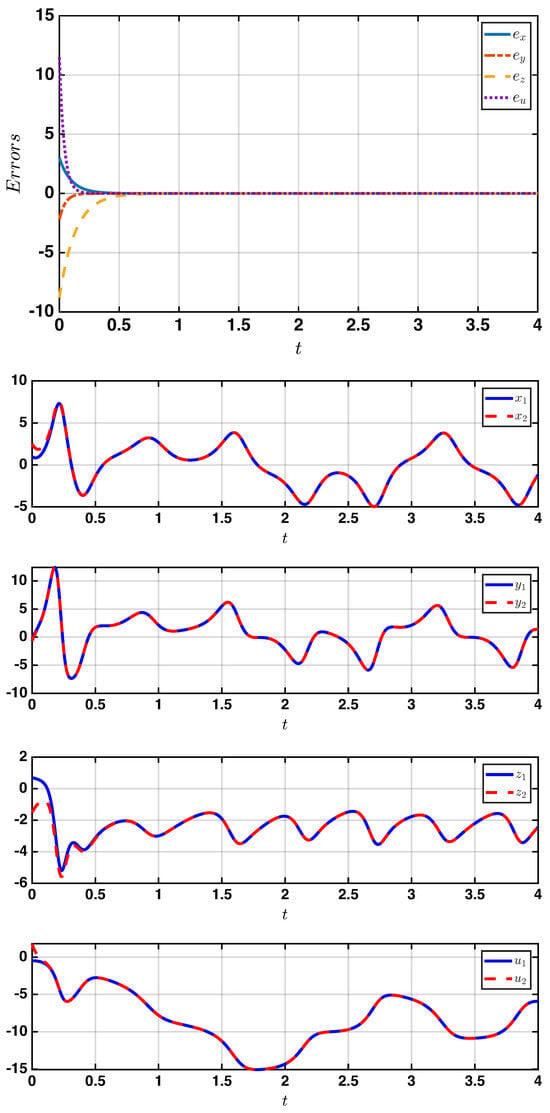
Figure 4. Generalized synchronization results showing the drive response trajectories (top) and phase portraits (bottom).

6. Chaotic Image Encryption and Decryption Process

This section describes the proposed chaotic image encryption scheme, which combines permutation and diffusion mechanisms driven by a hyperchaotic synchronization system. Figure 5 illustrates a schematic depiction of the proposed encoding technique. Below are the procedures followed during encryption.

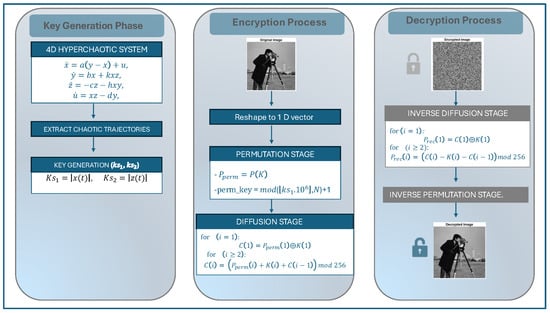
Figure 5. Proposed permutation diffusion-based image encryption and decryption scheme.

6.1. Novel Hyperchaotic System Modeling

We consider a four-dimensional novel hyperchaotic system defined as follows:

$$\begin{array}{cc}\hfill \dot{x}& =a(y-x)+u,\hfill \\ \hfill \dot{y}& =bx+kxz,\hfill \\ \hfill \dot{z}& =-cz-hxy,\hfill \\ \hfill \dot{u}& =xz-dy,\hfill \end{array}$$

The system generates chaotic trajectories $\left(x\right(t), y(t), z(t), u(t\left)\right)$, which are obtained using numerical integration with the fourth-order Runge–Kutta solver (ode45)and a sufficiently small step size of $t\in [0, 65],\Delta t={10}^{-4}$. From the obtained chaotic trajectories, two state variables of the drive system are extracted, namely

$$x_1\left(t\right)\mathrm{and}{z}_1\left(t\right),$$

which serve as the sources of chaotic key streams. To guarantee sufficient length for image encryption, the generated sequences are extended when necessary.

6.2. Key Generation

The absolute-valued chaotic sequences are defined as

$$k{s}_1\left(i\right)=|x_1\left(i\right)|,k{s}_2\left(i\right)=\left|z_1\left(i\right)\right|,i=1, 2,\dots ,N,$$

where N denotes the total number of pixels in each image channel. These sequences are normalized and mapped as follows:

Image Preprocessing

The plaintext image is resized to $256\times 256$ pixels. For grayscale images, the image is directly reshaped into a one-dimensional pixel vector. For color images, the encryption process is applied independently to each RGB channel. Each channel is reshaped into a one-dimensional vector:

$$P={[p_1, p_2,\dots ,p_N]}^T.$$

where $p_i\in \{0, 1,\dots ,255\}$ denotes the intensity value of the i-th pixel in the plaintext image and N is the total number of pixels in each channel.

• Permutation Key Generation
  A permutation key is generated from the chaotic sequence ($k{s}_1$) as follows:

  $$\mathrm{perm}\_\mathrm{key}\left(i\right)=\left(⌊k{s}_1\left(i\right)\times {10}^6⌋modN\right)+1.$$
  By sorting the permutation key in ascending order, a permutation index vector ($\pi$) is obtained, which determines the scrambling order of pixel positions. The permuted pixel sequence is given by

  $$P_{\mathrm{perm}}\left(i\right)=P\left(\pi \left(i\right)\right).$$
  This permutation stage effectively disrupts the strong spatial correlation among adjacent pixels in the original image.
• Diffusion Key Generation
  A diffusion key stream is derived from the second chaotic sequence as

  $$K\left(i\right)=⌊k{s}_2\left(i\right)\times {10}^6⌋\mathrm{mod}256,$$

  where $K\left(i\right)$ is an 8-bit integer sequence used to modify pixel intensities during the diffusion process.

6.3. Diffusion Stage

The diffusion process is performed sequentially to enhance sensitivity to plaintext changes. The first encrypted pixel is computed using the bitwise XOR operation:

$$C\left(1\right)=P_{\mathrm{perm}}\left(1\right)\oplus K\left(1\right).$$

For the remaining pixels, a feedback-based diffusion rule is applied:

$$C\left(i\right)=\left(P_{\mathrm{perm}}\left(i\right)+K\left(i\right)+C(i-1)\right)\mathrm{mod}256,i=2, 3,\dots ,N.$$

This chained diffusion mechanism ensures that a slight change in any pixel propagates throughout the entire ciphertext image.

6.4. Decryption Process

Decryption applies the inverse operations:

• Inverse Diffusion:

  $$P_{\mathrm{rec}}\left(1\right)=C\left(1\right)\oplus K\left(1\right),$$

  $$P_{\mathrm{rec}}\left(i\right)=\left(C\left(i\right)-K\left(i\right)-C(i-1)\right)\mathrm{mod}256,i\ge 2.$$
• Inverse Permutation: Construct the inverse index $\text{inv\_perm}$ such that

  $$P=P_{\mathrm{rec}}\left(\text{inv\_perm}\right).$$

The reconstructed image matches the original, with no information loss.

6.5. Validation

The encryption scheme is validated using the following metrics:

• Histogram Analysis: Encrypted images exhibit uniform distributions.
• Correlation Coefficient: Near-zero correlation for adjacent pixels in encrypted images.

The successful reconstruction of the original images, along with uniform histograms and low pixel correlation, confirms that the proposed framework provides a reliable and secure foundation for the encryption process.

Figure 6 presents visual and statistical analyses of the image encryption process using the proposed chaotic system. The top section illustrates the grayscale image encryption results, including the original, encrypted, and decrypted images, along with their corresponding histograms and pixel correlation plots. The bottom section presents the same evaluation for a colored (RGB) image, demonstrating consistent encryption performance across different image types.

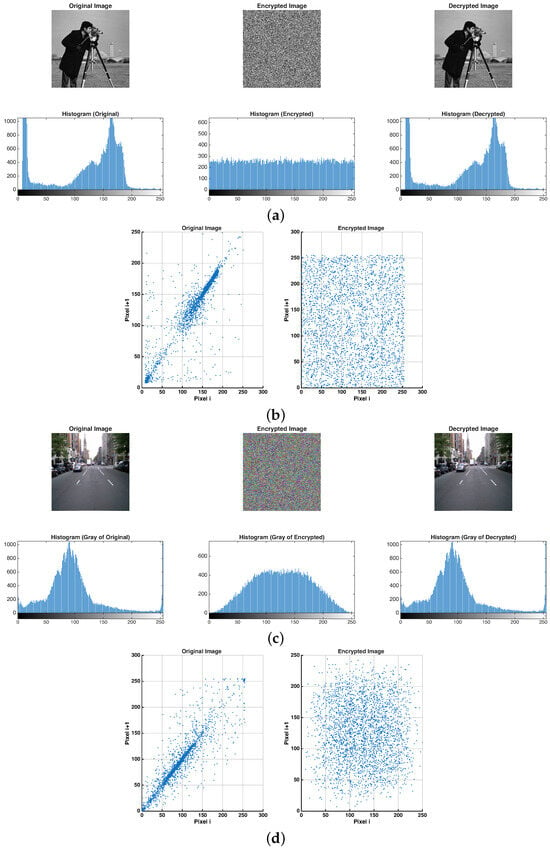
Figure 6. Subfigures (a,b) show the grayscale case, including the original, encrypted, and decrypted images with their corresponding histograms and pixel correlation plots, while (c,d) represent the corresponding results for the colored case.

7. Conclusions

In this study, a generalized synchronization scheme for identical hyperchaotic systems was successfully presented and systematically analyzed. The proposed method guarantees global asymptotic convergence of synchronization errors based on Lyapunov stability analysis and extends the synchronization capability to cases with distinct scaling factors (${\alpha }_i$). Numerical simulations confirm the effectiveness of the designed controllers, showing that the synchronization errors rapidly approach zero for complete, anti-, and generalized synchronization cases. Furthermore, the developed synchronization framework was applied to image encryption, where the hyperchaotic trajectories of the drive system provide secure and highly sensitive keys. The encrypted images exhibit uniform histograms, low pixel correlations, and perfect reconstruction upon decryption, confirming the robustness and efficiency of the proposed scheme. This approach demonstrates that generalized synchronization not only stabilizes complex hyperchaotic systems but also provides a powerful and reliable foundation for secure communication and information protection applications.