Identical Neighbor Structure: Effects on Spectrum and Independence in CN_s Cartesian Product of Graphs

Abstract

In this study, we introduced a novel graph product derived from the standard Cartesian product and investigated its structural properties, with a particular emphasis on its independence number and spectral characteristics in relation to identical neighbor structures. A key finding is that the spectrum of this newly defined product graph consists entirely of integral eigenvalues, a significant property with applications in chemistry, network theory, and combinatorial optimization. We defined $C{N}_s$ vertices as the vertices having an identical set of neighbors and classified graphs containing such vertices as $C{N}_s$ graphs. Furthermore, we introduced the $C{N}_s$ Cartesian product for these graphs. To formally characterize the relationships between $C{N}_s$ vertices, we constructed an $n\times n$ $C{N}_s$ matrix, where an entry is 1 if the corresponding pair of vertices are $C{N}_s$ vertices and 0 otherwise. Utilizing this matrix, we established that the spectrum of the $C{N}_s$ Cartesian product consists exclusively of integral eigenvalues. This finding enhances our understanding of graph spectra and their relation to structural properties.

1. Introduction

In graph theory, two fundamental concepts that provide valuable insights into a graph’s structure are its spectrum and independence number. The spectrum of a graph, derived from the eigenvalues of its adjacency matrix, serves as a powerful tool for analyzing key properties such as connectivity, robustness, and structural patterns [1]. By capturing how vertices and edges interact through these eigenvalues, the spectrum offers a comprehensive framework for understanding the behavior of complex networks.

Another essential concept in graph theory is the independent set and the independence number, both of which have numerous applications [2]. A subset S of the vertex set of a graph G is called an independent (or stable) set if no two vertices $u,v\in S$ are adjacent in G. The largest independent sets in G are referred to as $\alpha$-sets. The independence number, denoted as $\alpha \left(G\right)$, represents the size of the largest independent set in the graph. The study of independent sets and the independence number is crucial for understanding graph properties such as sparsity, connectivity, and optimization potential in various practical applications [3]. Moreover, ref. [4] provides a relatively straightforward method to estimate upper and lower bounds for the independence number in terms of the graph spectrum.

Spectral graph theory [5] explores the relationship between graph properties and the spectrum of various graph matrices. By examining the eigenvalues of the adjacency matrix [6,7], it is possible to derive significant structural properties of the graph. For instance, the second-largest eigenvalue provides insights into the graph’s expansion and randomness properties, while the smallest eigenvalue is closely related to the independence number and chromatic number. The Cauchy eigenvalue interlacing theorem further reveals information about graph substructures, making the spectrum a useful invariant in graph analysis.

Graph theory provides a foundational framework for analyzing and understanding complex systems characterized by interconnected elements. A central concept in this framework is that of common neighbors [8], which encapsulates the immediate connections between vertices and plays a crucial role in studying structural relationships within a graph.

To lay the groundwork for our study, we build upon the concept of twin vertices [9] in a graph G. Twin vertices are pairs of vertices a and b that have exactly the same neighbors, meaning both are connected to the same set of other vertices without any differences in their connections. This concept plays a crucial role in identifying structural similarities within a graph.

In this paper, we introduce the concept of $C{N}_s$ vertices, which generalizes twin vertices, and apply the equivalence relation they establish to define $C{N}_s$ sets within a graph. These sets provide a deeper understanding of the graph’s structure by grouping together vertices that share similar connection patterns. This generalization enables a more comprehensive characterization of the newly defined $C{N}_s$ Cartesian product.

A key approach to quantifying the relationship between neighboring vertices in a graph is through the $C{N}_s$ matrix. This matrix systematically represents the identical neighbors shared among pairs of vertices, offering valuable insights into the structural patterns and connectivity dynamics within the graph.

In this study, we explored the $C{N}_s$ Cartesian product, a method of combining two graphs to analyze how their neighborhood relationships interact. Our primary focus is on examining the adjacency spectrum of the resulting product graph using the $C{N}_s$ matrix. Additionally, we investigate how the vertices with identical neighbors in the factor graphs influence the independence number of the product graph.

The study of the $C{N}_s$ vertices in a graph and its spectral properties has significant implications across multiple domains, including structural engineering [10], deep learning [11], and optimization [12]. The cable dome structure is an advanced prestressed space system that utilizes a network of cables and compression elements to achieve high structural efficiency, expansive spans, and an aesthetically appealing design. Its importance [10] in modern architecture and engineering makes it a preferred solution for large-scale public buildings, including stadiums, exhibition halls, terminals, and transportation hubs. A key spectral property of such graphs is that the largest eigenvalue of the adjacency matrix of this graph is directly associated with maximum force transmission within the structure and determines its load-bearing efficiency and structural stability.

Deep learning models such as Transformers [11] process long-range dependencies in student performance data. Similarly, graph neural networks (GNNs) leverage spectral properties to model complex dependencies in educational and networked systems. The phenomenon of emergent abilities in GNNs, where performance dramatically improves beyond a certain scale [13], is closely tied to spectral properties. In particular, the largest eigenvalue of the adjacency matrix influences long-range learning dependencies in GNNs.

A physics-informed neural network (PINN)-based resilience framework for multi-state systems (MSS) [14] and the concept of a service function chain (SFC) [15] share graph-based modeling, stability analysis, and adaptive optimization, making them relevant across engineering, network resilience, and AI-driven forecasting. The discounted infinite horizon optimal control problem for stochastic learning networks (SLN) [12] is also deeply connected to spectral graph theory, particularly through Markov decision processes (MDPs) and value iteration.

Our objective is to understand how identical neighborhoods impact the spectrum and independence number of the $C{N}_s$ Cartesian product. Understanding these properties is crucial for applications in structural engineering, deep learning, network resilience, and optimization. Through this study, we bridge graph theoretical concepts with real-world applications, enhancing our ability to design more efficient, stable, and scalable systems across multiple domains. To achieve this, we analyze undirected graphs represented by $G=(V,E)$, where V is the set of vertices and E is the set of edges. A crucial metric in this investigation is the concept of graph energy, as defined in the literature [16]. This metric, denoted by $\mathcal{E}$, is calculated as the sum of the absolute eigenvalues of the adjacency matrix of G, providing a quantitative measure of the graph’s structural properties.

By incorporating the energy metric into our analysis, we aim to gain deeper insights into how common neighborhoods influence the organization of complex systems represented by the $C{N}_s$ Cartesian product of graphs. Through the examination of the adjacency spectrum, we seek to identify significant patterns that reveal the underlying structural properties and interconnectedness within these intricate networks. Ultimately, this investigation aims to bridge theoretical concepts with practical applications, enhancing our understanding of graph dynamics and their real-world implications.

2. Preliminaries

In graph theory, the study of product graphs offers valuable insights into the structural properties and interactions of complex systems. A product graph is formed by combining two or more graphs, leading to new structures with unique characteristics. One such product is the Cartesian product, which has been extensively studied [17] for its role in various applications, including network design, computer science, and chemistry.

In this work, we introduce a new type of product graph inspired by the Cartesian product, that focuses on the concept of identical neighbors. We refer to this new construction as the $C{N}_s$ Cartesian product. The idea of vertices with identical neighbors, referred to as $C{N}_s$ vertices, plays a critical role in understanding relationships between vertices, as vertices with identical neighbors exhibit a high level of structural similarity within a graph. These vertices form the foundation of the newly defined product graph.

This research bridges theoretical graph concepts with practical applications, providing a framework for understanding how identical neighborhoods and the resulting spectrum can impact various fields, such as network design, protein folding, and stability analysis in complex systems. Through the concept of the $C{N}_s$ Cartesian product, we aim to offer a novel perspective on graph dynamics and their underlying mathematical structures. Before proceeding further, let us discuss some fundamental terminologies:

Definition 1

([18]). Let G be a graph with vertex set V and edge set E. The neighborhood $N\left(v\right)$ of a vertex $v\in V$ is the set of all neighbors of v. i.e., $N\left(v\right)=\{u:\{u,v\}\in E\}$.

Definition 2

([19,20]). The spectrum S(G) of an undirected graph G of order n is defined as the non-increasing sequence of the n real eigenvalues of the adjacency matrix of G. It has been found that certain graphs have an integral spectrum, i.e., each eigenvalue is an integer. Such graphs are called integral graphs. If ${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_k$ are distinct eigenvalues of a graph G with corresponding multiplicities $p_1,p_2,\dots ,p_k$, then the spectrum of G denoted as $S\left(G\right)$ is represented as ${\lambda }_1^{p_1},{\lambda }_2^{p_2},\dots ,{\lambda }_k^{p_k}$.

Definition 3

([21]). The nullity $\eta \left(G\right)$ of a graph G is the multiplicity of the eigenvalue zero in the spectrum of G.

Definition 4

([22]). If a graph has eigenvalue 0, then it is called a singular graph; otherwise, it is called a nonsingular graph.

Definition 5.

Let G be a graph with $V=\{v_1,v_2,\dots ,v_n\}$ vertices. Then two vertices $v_i,v_j$: $1\le i,j\le n$ are $C{N}_s$ vertices if $N\left(v_i\right)=N\left(v_j\right)$.

Definition 6

([9]). Let $G=(V,E)$ be a graph. Two vertices (a and b) are twin vertices in G if and only if they have the same neighborhood. In addition, if the edge $(a,b)$ belongs to E, a and b are called true twins; otherwise, they are called false twins.

Definition 7.

Let G be a graph with vertex set $V=\{v_1,v_2,\dots ,v_n\}$. The vertices with the same neighborhood are called $C{N}_s$ vertices. The pair of $C{N}_s$ vertices are false twins [9], and the presence of such vertices makes a graph $C{N}_s$. A graph G is said to be a $C{N}_s$ graph if it contains at least one pair of $C{N}_s$ vertices. A graph that is not a $C{N}_s$ graph is called a $D{N}_s$ graph.

Definition 8.

$C{N}_s$ matrix of a finite graph G with vertex set $V=\{v_1,v_2,\dots ,v_n\}$ is an $n\times n$ matrix denoted as $C{N}_s\left(G\right)$, defined by $C{N}_s\left(G\right)=\left[c_{ij}\right]$, where

$$c_{ij}=\left\{\begin{array}{cc}1\hfill & if{v}_{i}and{v}_{j}areC{N}_{s}vertices,\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

Definition 9.

The set of all eigenvalues of the $C{N}_s$ matrix of a graph G is called the $C{N}_s$ spectrum of G. The sum of absolute values of these eigenvalues is called $C{N}_s$ energy of the graph and is denoted as ${\mathcal{E}}_{CN}$.

Also, the $C{N}_s$ spectral radius is defined as the largest absolute value of the eigenvalues in the $C{N}_s$ spectrum.

Definition 10.

The multiplicity of the eigenvalue 0 in the $C{N}_s$ spectrum of a graph is called $C{N}_s$ nullity and is denoted as ${\eta }_{CN}$.

Example 1.

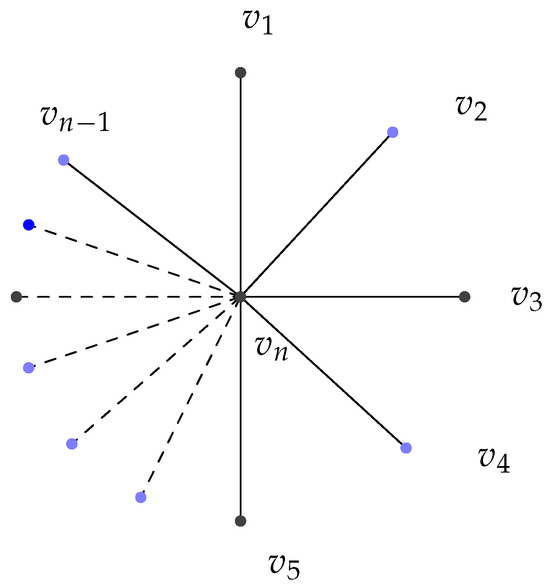
Consider the graph in Figure 1.

Figure 1. $S_n$.

Here, $\{v_1,v_2,\dots ,v_{n-1}\}$ are $C{N}_s$ vertices. Hence, the Star graph $S_n:n\ge 3$ is a $C{N}_s$ graph.

Now, $C{N}_s$ matrix is $\left[\begin{array}{cc}{J}_{n-1}-I_{n-1}& 0\\ 0& 0\end{array}\right]$, where $J_{n-1}$ is the matrix of order $n-1\times n-1$ with all entries being 1.

The eigenvalues of $J_n-I_n$ [6] are $-1$ with multiplicity $n-1$ and $n-1$ with multiplicity 1.

Hence, the $C{N}_s$ spectrum of $S_n$ is $0^1,{(-1)}^{n-2},{(n-2)}^1$.

So the $C{N}_s$ energy, ${\mathcal{E}}_{CN}\left(S_n\right)=2n-4$, and $C{N}_s$ nullity, ${\eta }_{CN}\left(S_n\right)=1$.

Remark 1.

The concept “Common Neighborhood” partitions the vertex set of a graph G into disjoint sets so that we can introduce the following definition.

Definition 11.

Let $G=(V,E)$ be a graph and $v\in V$ be a vertex of G. Then CN set corresponding to v is denoted by $C{N}_G\left(v\right)$ or simply $CN\left(v\right)$ and is defined as $C{N}_G\left(v\right)=\{u\in V:N\left(v\right)=N\left(u\right)\}$.

Example 2.

Consider the cycle graph $C_4$ shown in Figure 2, then $C{N}_G\left(v_1\right)=\{v_1,v_2\}$, which is also the CN set for $v_2$. Similarly, the CN set for $v_3$ and $v_4$ is $\{v_3,v_4\}$. Hence, $C_4$ has two CN sets-$\{v_1,v_2\},\{v_3,v_4\}$

Figure 2. $C_4$.

Also, in Example 1, the CN sets are $\{v_1,v_2,\dots ,v_{n-1}\},\left\{v_n\right\}$.

Definition 12.

A vertex whose CN set is a singleton is called a DN vertex. A CN set containing two elements is referred to as a Binary CN set.

In the Example 1, $v_n$ is a DN vertex, whereas in Example 2, the graph contains no DN vertices.

In Example 2, the sets $\{v_1,v_2\}$ (both have $v_3,v_4$ as neighbors) and $\{v_3,v_4\}$ (both have $v_1,v_2$ as neighbors) are binary CN sets.

Definition 13

([23]). Let A be an $m\times n$ matrix and B be a $p\times q$ matrix. The Kronecker product, denoted by $A\otimes B$, is an $\left(mp\right)\times \left(nq\right)$ matrix, defined as $A\otimes B=\left[\begin{array}{cccc}{a}_{11}B& a_{12}B& \dots & a_{1n}B\\ a_{21}B& a_{22}B& \dots & a_{2n}B\\ \dots & \dots & \dots & \dots \\ a_{m1}B& a_{m2}B& \dots & a_{mn}B\end{array}\right]$ where each entry $a_{ij}$ of A is multiplied by the entire matrix B.

Theorem 1

([23]). The spectrum of the Kronecker product of two matrices A and B consists of the pairwise product of the eigenvalues of A and B.

Definition 14

([24]). If A is an $m\times m$ matrix and B is an $n\times n$ matrix, then the Kronecker sum $A\oplus B$ of A and B is defined as: $A\oplus B=I_m\otimes B+A\otimes I_n$, where $I_m$ and $I_n$ are the identity matrices of order m and n, respectively, and ⊗ denotes the Kronecker product.

Theorem 2

([24]). The spectrum of the Kronecker sum of two matrices A and B consists of the pairwise sum of the eigenvalues of A and B. This means that if ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{k_1}$ are the eigenvalues of A and ${\mu }_1,{\mu }_2,\dots ,{\mu }_{k_2}$ are the eigenvalues of B, then the eigenvalues of the Kronecker sum $A\oplus B=I_m\otimes B+A\otimes I_n$ are given by:

$${\lambda }_i+{\mu }_j\mathit{for}\mathit{each}i=1,2,\dots ,k_1\mathit{and}j=1,2,\dots ,k_2.$$

3. ${\mathit{CN}}_{\mathit{s}}$ Spectrum of ${\mathit{CN}}_{\mathit{s}}$ Graphs

In this section, we evaluated the $C{N}_s$ spectrum of $C{N}_s$ graphs and used this analysis to achieve our ultimate goal: determining the adjacency spectrum of the $C{N}_s$ Cartesian product of two $C{N}_s$ graphs.

Theorem 3.

Let G be a $C{N}_s$ graph. Then $C{N}_s$ spectrum of G contains only integral values.

Proof. 

Consider a graph G with $CN$ sets of sizes $r_1,r_2,\dots ,r_k$, where each $r_i\ne 1:1\le i\le k$. Then we can label the vertices of G in such a way that the $C{N}_s$ matrix of G has a structure of block matrices with non-zero entries occurring only in k diagonal blocks and is given by $B_{ii}=J_{r_i}-I_{r_i}:i=1,2,\dots ,k$. Here, $J_{r_i}$ denotes an all-one’s square matrix of size $r_i$, while $I_{r_i}$ signifies the identity matrix of size $r_i$.

The eigenvalues of the matrix $J_n-I_n$, ref. [19] are characterized by two distinct values: $-1$ with multiplicity $n-1$, and $n-1$ with multiplicity 1. Hence, the non-zero elements in the $C{N}_s$ spectrum of G are tabulated as

Eigenvalue	−1	−1	……	−1	$r_1-1$	$r_2-1$	……	$r_k-1$
Multiplicity	$r_1-1$	$r_2-1$	……	$r_k-1$	1	1	……	1

Now, if the graph G has some DN vertices, then the CN set corresponding to these vertices will be singleton, and the diagonal block corresponding to the CN set will be a zero matrix of order 1; therefore, the eigenvalues corresponding to these DN vertices are 0. If G has r number of DN vertices and k number of CN sets with $r_1,r_2,\dots ,r_k$ (where each $r_i\ne 1,$ $i=1,2,\dots ,k$) elements, then the $C{N}_s$ spectrum of G consists of the following eigenvalues:

•

0 with multiplicity r (equal to the number of DN vertices).

•

−1 with multiplicity $r_1+r_2+\cdots +r_k-k$.

•

$r_1-1,r_2-1,\dots ,r_k-1$, each with multiplicity 1.

Also, if G has n number of vertices, then $n=r_1+r_2+\cdots +r_k+r$.

Hence, the $C{N}_s$ spectrum of G is $0^r,{(-1)}^{n-r-k},{(r_1-1)}^1,{(r_2-1)}^1,\dots ,{(r_k-1)}^1$.

Clearly, all these values are integers. Hence, the proof is complete. □

Remark 2.

The complement of a $C{N}_s$ graph is not necessarily $C{N}_s$, and the complement of a $D{N}_s$ graph may indeed be $C{N}_s$. An example is given below.

Example 3.

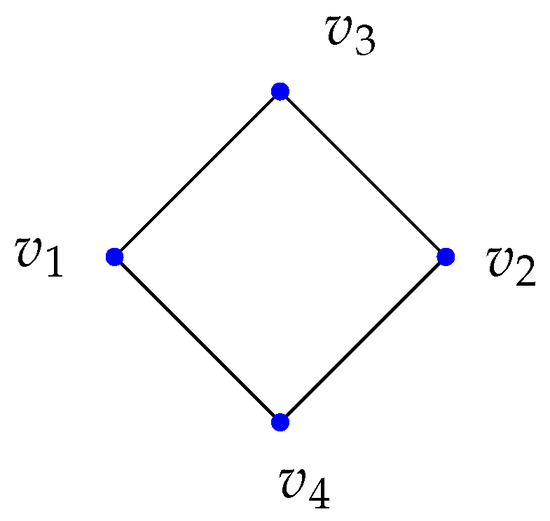
For instance, consider Figure 3, where $G=C_4$ is a $C{N}_s$ graph, but its complement shown is not.

Figure 3. $C_4$ is $C{N}_s$ but $C_4^c$ is not.

Theorem 4.

If a $C{N}_s$ graph with n vertices has k number of CN sets with cardinality $r_1,r_2,\dots ,r_k$ where each $r_i>1:i=1,2,\dots ,k$ and r number of DN vertices, then $C{N}_s$ energy of G is $2(n-r-k)$.

Proof. 

Clearly, $n=r_1+r_2+\cdots +r_k+r$. Theorem 3 gives the $C{N}_s$ eigenvalues and hence the $C{N}_s$ energy of G

$$\begin{array}{cc}\hfill {\mathcal{E}}_{CN}& =r_1+r_2+\cdots +r_k-k+r_1-1+r_2-1+\cdots +r_k-1\hfill \\ \hfill & =2(r_1+r_2+\cdots +r_k-k)=2(n-r-k).\hfill \end{array}$$

□

Theorem 5.

The $C{N}_s$ nullity of a $C{N}_s$ graph G is exactly the number of $DN$ vertices in G.

Proof. 

By Theorem 3, the multiplicity of the eigenvalue 0 is exactly the number of DN vertices for a $C{N}_s$ graph. Hence the $C{N}_s$ nullity is the number of DN vertices in G. □

4. ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product

The $C{N}_s$ Cartesian product is a novel graph product operation that extends the traditional Cartesian product of graphs by incorporating the concept of common neighbors. The $C{N}_s$ Cartesian product focuses on the common neighbors of vertices to provide a new perspective on how vertices in different graphs can be connected. In the traditional Cartesian product of two graphs, the vertices of the resulting graph are formed by combining the vertices of the original graphs, and edges are established based on the adjacency relations in the original graphs. However, the $C{N}_s$ Cartesian product introduces a twist: the adjacency of vertices in the product graph is determined not only by the original graph’s adjacency relations but also by the common neighborhood structure within each graph.

Definition 15.

Let $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ be two graphs. Then the $C{N}_s$ Cartesian product of $G_1$ and $G_2$ is denoted by $G_1⊚G_2$ and has $V_1\times V_2$ as its vertex set. Two vertices $(u_1,v_1)$ and $(u_2,v_2)$ are adjacent if and only if

• $u_1=u_2$ and $v_1,v_2$ are $C{N}_s$ vertices in $G_2$.

or

• $u_1,u_2$ are $C{N}_s$ vertices in $G_1$ and $v_1=v_2$.

The $C{N}_s$ Cartesian product of $S_4$ and $P_3$ is depicted in Figure 4.

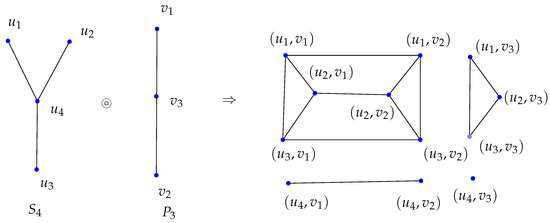
Figure 4. $S_4⊚P_3$.

The standard Cartesian product of $S_4$ and $P_3$ is depicted in Figure 5.

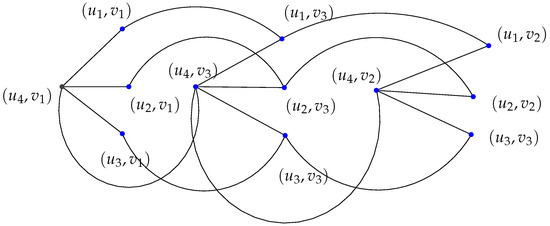
Figure 5. $S_4\square P_3$.

The $C{N}_s$ Cartesian product focuses on pairs of $C{N}_s$ veritices (false twins), making it a subset of the complement of the standard Cartesian product of the same graphs.

5. Properties of ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product

In this section, we explore and identify some fundamental properties of the $C{N}_s$ Cartesian product graph that are shared with standard graph products [18]. These properties provide insights into the behavior and characteristics of the graph, contributing to a deeper understanding of its structure and potential applications.

• If $G_1=(V_1,E_1),G_2=(V_2,E_2)$ are two graphs of order $n_1$ and $n_2$ respectively, then the order of $G_1⊚G_2$ is $n_1{n}_2$.
  This result follows from the fact that the vertex set of $G_1⊚G_2$ is the cross product of $V_1\times V_2.$ Here, $G_1$ and $G_2$ are of order $n_1,n_2$, respectively, and hence the order of $G_1⊚G_2$ is $n_1{n}_2$.
• If $G_1,G_2$ are any two graphs, then $G_1⊚G_2\cong G_2⊚G_1$.
  To explain this symmetry, let $V_1$ and $V_2$ be the vertex sets of $G_1$ and $G_2$, respectively. Then the vertex set of $G_1⊚G_2$ is the Cartesian product, $V_1\times V_2$ and that of $G_2⊚G_1$ is $V_2\times V_1$. According to the definition of $C{N}_s$ Cartesian product, the connectivity between the vertices is preserved in the same manner for both $G_1⊚G_2$ and $G_2⊚G_1$. Hence, $G_1⊚G_2\cong G_2⊚G_1$.
• If $G_1,G_2,$ and $G_3$ are any three graphs, then $(G_1⊚G_2)⊚G_3=G_1⊚(G_2⊚G_3)$.
  To demonstrate this property, consider the vertex set $V_1,V_2,V_3$ of $G_1,G_2,G_3$, then the vertex set for $(G_1⊚G_2)⊚G_3$ and $G_1⊚(G_2⊚G_3)$ is $V_1\times V_2\times V_3$. According to the definition of $C{N}_s$ Cartesian product, the connectivity between the vertices will be preserved in same manner for both $(G_1⊚G_2)⊚G_3$ and $G_1⊚(G_2⊚G_3)$. Hence, $(G_1⊚G_2)⊚G_3=G_1⊚(G_2⊚G_3)$.
• If $G_1,G_2$ are any two $D{N}_s$ graphs with $n_1$ and $n_2$ vertices, respectively, then $G_1⊚G_2$ is a null graph with $n_1{n}_2$ vertices.
  Given $G_1$ and $G_2$ are two $D{N}_s$ graphs. Hence, it has no $C{N}_s$ vertices. But two vertices $(u_1,v_1)$ and $(u_2,v_2)$ are adjacent in $G_1⊚G_2$ if and only if either $u_1,u_2$ or $v_1,v_2$ (not both) are $C{N}_s$ vertices in $G_1$ or $G_2$, respectively. Being that $G_1$ and $G_2$ are $D{N}_s$ graphs, there are no such cases. Hence, $G_1⊚G_2$ has no edges and becomes a null graph.

6. More About the ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product

In this section, we examine the critical role of binary CN sets in identifying the $C{N}_s$ Cartesian product as a $C{N}_s$ graph. These binary CN sets are crucial for preserving the defining traits of a $C{N}_s$ graph within the product structure. Furthermore, we note that the newly formed product graph also inherits binary CN sets, which significantly impact both its structure and spectral characteristics. This analysis offers valuable insights into how binary CN sets shape the overall behavior of the $C{N}_s$ Cartesian product.

Theorem 6.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs, each having at least one binary CN set, then $G_1⊚G_2$ is also a $C{N}_s$ graph.

Proof. 

Let $\{u_i,u_k\}$ be a binary CN set of $G_1$ and $\{v_j,v_m\}$ be a binary CN set of $G_2$. Then, the vertices $(u_i,v_j),(u_k,v_m)$ in $G_1⊚G_2$ form a CN set because they share common neighbors, namely $\{(u_i,v_m),(u_k,v_j)\}$. Hence, $G_1⊚G_2$ is a $C{N}_s$ graph. □

Theorem 7.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs, each having at least one binary CN set, then the $C{N}_s$ Cartesian product $G_1⊚G_2$ will contain at least two binary CN sets.

Proof. 

Let $\{u_i,u_k\}$ be a binary CN set of $G_1$ and $\{v_j,v_m\}$ be a binary CN set of $G_2$. Then, the vertices $(u_i,v_j)$ and $(u_k,v_m)$ in $G_1⊚G_2$ have identical neighbors as $\{(u_i,v_m),(u_k,v_j)\}$, and the vertices $(u_i,v_m)$ and $(u_k,v_j)$ also have identical neighbors $(u_i,v_j),(u_k,v_m)$. Thus, the two binary CN sets of $G_1⊚G_2$ are $\{(u_i,v_j),(u_k,v_m)\}$ and $\{(u_i,v_m),(u_k,v_j)\}$. □

Theorem 8.

Let $G_1$ and $G_2$ be two $C{N}_s$ graphs with $n_1$ and $n_2$ vertices, respectively. Also, assume that the number of CN sets of $G_1$ and $G_2$ are $k_1$ and $k_2$, respectively, with all the CN sets of $G_1$ and $G_2$ having more than one element being binary. Then $C{N}_s$ energy of $G_1⊚G_2$ is $4k_1{k}_2$. Moreover, the $C{N}_s$ nullity of $G_1⊚G_2$ is $n_1{n}_2-4k_1{k}_2$.

Proof. 

The $C{N}_s$ matrix of $G_1⊚G_2$ is a block matrix where the $2k_1{k}_2$ diagonal blocks are given by $J_2-I_2$, where $J_2$ is a $2\times 2$ matrix with all elements equal to 1 and $I_2$ is the identity matrix of order 2. The characteristic polynomial of $J_2-I_2$ is ${\lambda }^2-1$, and all other blocks in the matrix are zero matrices. Therefore, the $C{N}_s$ spectrum of $G_1⊚G_2$ is $\{1^{2k_1{k}_2},-1^{2k_1{k}_2},0^{n_1{n}_2-4k_1{k}_2}\}$ so that the $C{N}_s$ nullity of $G_1⊚G_2$ is $n_1{n}_2-4k_1{k}_2$. And $C{N}_s$ energy is $2k_1{k}_2+2k_1{k}_2=4k_1{k}_2$. □

Theorem 9.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs with no binary CN sets, then $G_1⊚G_2$ is a $D{N}_s$ graph.

Proof. 

Let $\{u_1,u_2,u_3,\dots ,u_n\}:n>2$ be an arbitrary CN set of $G_1$ and let $\{v_1,v_2,\dots ,v_m\}:m>2$ be an arbitrary CN set of $G_2$. Now, consider the vertices $(u_i,v_j),(u_k,v_j):1\le i,k\le n,1\le j\le m$ of $G_1⊚G_2$. Since $u_i,u_k:1\le i,k\le n$ are $C{N}_s$ vertices in $G_1$, the neighborhood of $(u_i,v_j)$ contains $(u_k,v_j)$; the neighborhood of $(u_k,v_j)$ contains $(u_i,v_j)$ for $j=1,2,\dots ,m$ and has no self loops. Hence, no vertices in $G_1⊚G_2$ have identical neighbors. Therefore, $G_1⊚G_2$ is a $D{N}_s$ graph. □

Theorem 10.

If $G_1$ and $G_2$ are two $D{N}_s$ graphs, then $G_1⊚G_2$ is also a $D{N}_s$ graph.

Proof. 

Given that $G_1$ and $G_2$ are $D{N}_s$ graphs. Therefore, $G_1$ and $G_2$ have no $C{N}_s$ vertices. By definition, $G_1⊚G_2$ has no edges. Therefore, $G_1⊚G_2$ is a null graph and is a $D{N}_s$ graph. □

Theorem 11.

If $G_1$ is a $C{N}_s$ graph and $G_2$ is a $D{N}_s$ graph, then $G_1⊚G_2$ is also a $D{N}_s$ graph.

Proof. 

Let $u_i,u_j$ be $C{N}_s$ vertices of $G_1$ and $v_k$ be an arbitrary vertex of $G_2.$ Then $(u_i,v_k),(u_j,v_k)$ are adjacent in $G_1⊚G_2.$ Since $G_2$ is a $D{N}_s$ graph, there does not exists a vertex $v_l$ in $G_2$ such that $v_k$ and $v_l$ have common neighbors. Thus, we cannot make the vertices $(u_j,v_l)$ and $(u_j,v_k)$ adjacent in $G_1⊚G_2$. Hence, the vertices $(u_i,v_k)$ and $(u_j,v_l)$ have no common neighbors. Therefore, there do not exist any $C{N}_s$ vertices in $G_1⊚G_2$. □

Theorem 12.

If $(u,v)$ is a vertex of $G_1⊚G_2$, then neighbors of $(u,v)$ in $G_1⊚G_2$ is $N_{G_1⊚G_2}\left((u,v)\right)$ $= \{(C{N}_{G_1}\left(u\right)-u)\times \left\{v\right\}\}\cup \{\left\{u\right\}\times (C{N}_{G_2}\left(v\right)-v)\}$.

Proof. 

By the definition of $G_1⊚G_2$, two vertices $(u_1,v_1)$ and $(u_2,v_2)$ are adjacent if:

• $u_1=u_2$ and $v_1,v_2$ are $C{N}_s$ vertices in $G_2$, or
• $u_1,u_2$ are $C{N}_s$ vertices in $G_1$ and $v_1=v_2$.

Therefore, to determine the neighbors of a vertex $(u,v)$, we need to consider:

• all vertices in the $CN$ set of u in $G_1$, excluding u itself, and
• all vertices in the $CN$ set of v in $G_2$, excluding v itself.

Thus, the neighborhood of $(u,v)$ in $G_1⊚G_2$ is given by:

$N_{G_1⊚G_2}\left((u,v)\right)=\{(C{N}_{G_1}\left(u\right)-u)\times \left\{v\right\}\}\cup \{\left\{u\right\}\times (C{N}_{G_2}\left(v\right)-v)\}$.

Hence the proof is complete. □

Corollary 1.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs with $n_1$ and $n_2$ vertices, respectively, the number of edges in the product graph $G_1⊚G_2$ is given by

$${\displaystyle n_1\sum _{c_i\in \mathcal{C}\left(G_2\right)}\left(\genfrac{}{}{0pt}{}{n\left(c_i\right)}{2}\right)+n_2\sum _{c_i\in \mathcal{C}\left(G_1\right)}\left(\genfrac{}{}{0pt}{}{n\left(c_i\right)}{2}\right),}$$

where $\mathcal{C}\left(G_1\right),\mathcal{C}\left(G_2\right)$ are the collections of all CN sets of $G_1,G_2$, respectively, which are not singletons, and $n\left(c_i\right)$ denotes the number of vertices in each CN set $c_i$.

Proof. 

By the Theorem 12, the number of edges drawn from the vertex $(u,v)$ in $G_1⊚G_2$ is the total of $n_1$ times number of ways of selecting two elements from the CN set of v in $G_2$ and $n_2$ times the number of ways of selecting two elements from the CN set of u in $G_1.$

Number of edges in ${\displaystyle G_1⊚G_2=n_1\sum _{c_i\in \mathcal{C}\left(G_2\right)}\left(\genfrac{}{}{0pt}{}{n\left(c_i\right)}{2}\right)+n_2\sum _{c_i\in \mathcal{C}\left(G_1\right)}\left(\genfrac{}{}{0pt}{}{n\left(c_i\right)}{2}\right).}$ □

Corollary 2.

If u and v are two DN vertices of $G_1$ and $G_2$, respectively, then $(u,v)$ is an isolated vertex in $G_1⊚G_2$.

Proof. 

Since u and v are DN vertices of $G_1$ and $G_2$, respectively, $C{N}_{G_1}\left(u\right)=\left\{u\right\}$ and $C{N}_{G_2}\left(v\right)=\left\{v\right\}$. By the Theorem 11, the neighborhood of $(u,v)$ in $G_1⊚G_2$, $N_{G_1⊚G_2}\left((u,v)\right)=\varphi$.

Hence, $(u,v)$ is an isolated vertex in $G_1⊚G_2$. □

Corollary 3.

The number of isolated vertices in $G_1⊚G_2$ is given by the product of number of DN vertices in $G_1$ and the number of DN vertices in $G_2$.

Proof. 

If u and v are DN vertices of $G_1$ and $G_2$, respectively, then by the above corollary, $(u,v)$, is an isolated vertex in $G_1⊚G_2$. Hence, the number of isolated vertices in $G_1⊚G_2$ is the product of the number of DN vertices in $G_1$ and the number of DN vertices in $G_2$. □

Corollary 4.

If the graphs $G_1$ and $G_2$ have $d_1$ and $d_2$ DN vertices, respectively, and contain $r_1$ and $r_2$ binary CN sets, then the components of $G_1⊚G_2$ contain $r_1{d}_1+r_2{d}_2$ path of length 2.

Proof. 

Let $u,v$ be arbitrary DN vertices of $G_1$ and $G_2$, respectively. Also, let $\{u_1,u_2\},\{v_1,v_2\}$ be a binary CN set of $G_1$ and $G_2,$ respectively. Then, in the graph $G_1⊚G_2$, the pairs $(u,v_1)$ and $(u,v_2)$ are adjacent. Since $\{v_1,v_2\}$ is a binary CN set, no other edges exist between $(u,v_1)$ and $(u,v_2)$, forming a path of length 2. Similarly, the pairs $(v,u_1),(v,u_2)$ form a path of length 2. Since the graphs have $d_1,d_2$ DN vertices and $r_1,r_2$ binary CN sets, the components of $G_1⊚G_2$ consist of $r_1{d}_1+r_2{d}_2$ path of length 2. □

Theorem 13.

The $C{N}_s$ Cartesian product of two arbitrary graphs will always result in a disconnected graph.

Proof. 

We know that the $C{N}_s$ Cartesian product of two $D{N}_s$ graphs always results in a null graph and is therefore disconnected.

Next, consider the $C{N}_s$ Cartesian product of a $C{N}_s$ graph and a trivial graph. In this case also, the distinct CN sets of the $C{N}_s$ graph corresponds to distinct components, and hence, the $C{N}_s$ Cartesian product graph is disconnected. Now, consider a graph $G_1$, which is a $C{N}_s$ graph with CN sets $c_1,c_2,\dots ,c_n$, and a $D{N}_s$ graph $G_2$ with vertex set $V\left(G_2\right)=\{u_1,u_2,\dots ,u_m\}$. In the $C{N}_s$ Cartesian product $G_1⊚G_2$, vertices of the form $(v_i,u)$ and $(v_j,u)$, where $i,j=1,2,\dots ,n$ and $u\in V\left(G_2\right)$, are adjacent if and only if $v_i$ and $v_j$ belong to the same CN set of $G_1$. However, if $v_i$ and $v_j$ belong to different CN sets, the vertices $(v_i,u)$ and $(v_j,u)$ are not adjacent. As a result, there are $n\times m$ components in $G_1⊚G_2$, confirming that the product graph is disconnected.

Next, consider two $C{N}_s$ graphs, $G_1$ and $G_2$, with CN sets $c_1,c_2,\dots ,c_n$ and $s_1,s_2,\dots ,s_q$, respectively, where at least one of the sets contains more than one element. Vertices of the form $(v_i,u)$ and $(v_j,u)$, where $i,j=1,2,\dots ,n$ and $u\in V\left(G_2\right)$, are adjacent if and only if $v_i$ and $v_j$ belong to the same CN set of $G_1$. Similarly, vertices like $(v,u_i)$ and $(v,u_j)$ are adjacent if and only if $u_i$ and $u_j$ belong to the same CN set of $G_2$. Hence there are $n\times q$ components in $G_1⊚G_2$. Therefore, the product graph $G_1⊚G_2$ is also disconnected. □

Corollary 5.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs with $r_1$ and $r_2$ CN sets, respectively, then $G_1⊚G_2$ has $r_1{r}_2$ components.

Corollary 6.

If graph $G_1$ has $p_1$ CN sets with $k_1$ elements, and graph $G_2$ has $p_2$ CN sets with $k_2$ elements, then the number of isomorphic components with $k_1{k}_2$ elements is $p_1{p}_2$.

7. Independence Number of the ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product Graph

In graph theory, the independence number of a graph is a fundamental measure that captures the largest set of mutually nonadjacent vertices, known as an independent set. This number plays a critical role in understanding the structure and behavior of graphs, particularly in terms of their sparsity, connectivity, and combinatorial properties.

For the $C{N}_s$ Cartesian product, understanding the independence number becomes especially important. The independent set in this graph consists of vertex pairs that are mutually nonadjacent, determined by their shared neighbor relationships within the individual graphs. Investigating the independence number of these product graphs provides important structural insights, such as the nature of disjoint components and how they interconnect.

Here, we investigate how the independence number is affected by the interplay between the CN sets of the input graphs $G_1$ and $G_2$ and how this number reflects the overall organization of the product graph. By studying the independence number in the context of the $C{N}_s$ Cartesian product, we aim to deepen our understanding of the graph’s structural properties and their potential applications in various fields such as network theory, optimization, and computational biology.

Theorem 14.

Let $G_1$ and $G_2$ be two $C{N}_s$ graphs with CN sets $c_1,c_2,\dots ,c_{r_1}$ in $G_1$ and $s_1,s_2,\dots ,s_{r_2}$ in $G_2$. The independence number of the $C{N}_s$ Cartesian product of these two graphs is given by ${\displaystyle \sum _{i=1}^{r_1}}{\displaystyle \sum _{j=1}^{r_2}}min(n\left(c_i\right),n\left(s_j\right))$, where $n\left(c_i\right)$ denote the number of vertices in each CN set $c_i$.

Proof. 

Given that $G_1$ and $G_2$ are two $C{N}_s$ graphs with $r_1$ and $r_2$ CN sets, respectively. We will prove that the independent set constructed in the following way for the $C{N}_s$ Cartesian product $G_1⊚G_2$ is a maximum independent set. The independent set is constructed by considering the CN sets of $G_1$ and $G_2$. If two distinct vertices $u_i,u_k$ in $G_1$ and $v_j,v_l$ in $G_2$ belong to the same CN set of $G_1$ and $G_2$, respectively, then by the definition of the $C{N}_s$ Cartesian product, the vertices $(u_i,v_j)$ and $(u_k,v_l$) are nonadjacent in a component of $G_1⊚G_2$. Since $G_1$ and $G_2$ have $r_1$ and $r_2$ CN sets, respectively, by Corollary 6, the graph $G_1⊚G_2$ has $r_1{r}_2$ components. To construct an independent set, we take the union of nonadjacent vertices from each component.

Now, consider an arbitrary component of $G_1⊚G_2$, formed by the CN sets $c_i=\{u_1,u_2,\dots ,u_{k_i}\}$ from $G_1$ and $s_j=\{v_1,v_2,\dots ,v_{k_j}\}$ from $G_2$.

• If $n\left(c_i\right)=n\left(s_j\right)=k$(say), then $\{(u_1,v_1),(u_2,v_2),\dots ,(u_k,v_k)\}$ is the independent set for $G_1⊚G_2$.
• If $n\left(c_i\right)>n\left(s_j\right)$ i.e., $k_i>k_j$, then $\{(u_1,v_1),(u_2,v_2),\dots ,(u_{k_j},v_{k_j})\}$ is the independent set for $G_1⊚G_2$.
• If $n\left(c_i\right)<n\left(s_j\right)$ i.e., $k_i<k_j$, then $\{(u_1,v_1),(u_2,v_2),\dots ,(u_{k_i},v_{k_i})\}$ is the independent set for $G_1⊚G_2$.

Since we have selected mutually nonadjacent vertices, the set formed is indeed an independent set. Furthermore, it is an independent set that contains the largest possible number of vertices. In other words, no independent set in the graph has more vertices than this one. Therefore, the maximum independent set for the component formed by $c_i\times s_j$ contains $min(k_i,k_j)$ elements.

Thus, the maximum independent set of $G_1⊚G_2$ is the disjoint union of the largest independent sets from each component of $G_1⊚G_2$. The size of the independent set we have constructed is the largest possible, as it fully utilizes the capacity of mutually nonadjacent vertices from each component. Additionally, if we attempt to add any further vertex pairs to this set, at least one of them would be adjacent to a vertex in the constructed independent set, violating its independence. Hence, the independence number of $G_1⊚G_2$ is ${\displaystyle \sum _{i=1}^{r_1}}{\displaystyle \sum _{j=1}^{r_2}}min(c_i,s_j)$. □

8. Main Results on ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product

This section focuses on the primary goal of our work. We conducted a detailed analysis to identify the adjacency spectrum of the $C{N}_s$ Cartesian product, which is a crucial aspect of understanding the graph’s structural properties. By examining the eigenvalues of the adjacency matrix, we were able to determine the spectrum, which reveals how the vertices of the graph are connected and how these connections influence the overall behavior of the graph.

Theorem 15.

If $G_1$ is a $C{N}_s$ graph with $p_1$ vertices and $G_2$ is a $C{N}_s$ graph with $p_2$ vertices, then the adjacency matrix of $G_1⊚G_2$ is given by

$$I_{p_1}\otimes C{N}_s\left(G_2\right)+C{N}_s\left(G_1\right)\otimes I_{p_2}$$

i.e., the Kronecker sum of $C{N}_s\left(G_1\right)$ and $C{N}_s\left(G_2\right)$.

Proof. 

Let $\{u_1,u_2,\dots ,u_{p_1}\}$ be the vertices of $G_1$ and $\{v_1,v_2,\dots ,v_{p_2}\}$ be the vertices of $G_2$. The adjacency matrix of $G_1⊚G_2$ can be constructed using block matrices as given in Table 1:

Table 1. The adjacency matrix of $G_1⊚G_2$ as block matrices.

	$(u_1,v_1),\dots \dots ,(u_1,v_{p_2})$	$(u_2,v_1),\dots \dots ,(u_2,v_{p_2})$	$\dots \dots$	$(u_{p_1},v_1),\dots ,(u_{p_1},v_{p_2})$
$(u_1,v_1)$
⋮	$B_{11}$	$B_{12}$	$\dots \dots$	$B_{1p_2}$
$(u_1,v_{p_2})$
$(u_2,v_1)$
⋮	$B_{21}$	$B_{22}$	$\dots \dots$	$B_{2p_2}$
$(u_2,v_{p_2})$
⋮	⋮	⋮	⋮	⋮
⋮	⋮	⋮	⋮	⋮
$(u_{p_1},v_1)$
⋮	$B_{p_{2}1}$	$B_{p_{1}2}$	$\dots \dots$	$B_{p_1{p}_2}$
$(u_{p_1},v_{p_2})$

Each block in the diagonal are determined by the CN sets of $G_2$. The diagonal blocks are exactly the matrix $C{N}_s\left(G_2\right)$ and the non-diagonal blocks are nonzero in the place where 1 occurs in the matrix $C{N}_s\left(G_1\right)$ and in such blocks the diagonal elements have only entry as 1 and is determined by $C{N}_s$ vertices of $G_1$.

Hence, the adjacency matrix of $G_1⊚G_2$ is given by

$$I_{p_1}\otimes C{N}_s\left(G_2\right)+C{N}_s\left(G_1\right)\otimes I_{p_2}.$$

□

Corollary 7.

The eigenvalues of $G_1⊚G_2$ is the pairwise sum of spectrum of $C{N}_s\left(G_1\right)$ and $C{N}_s\left(G_2\right)$.

Corollary 8.

Let $G_1$ and $G_2$ be two $C{N}_s$ graphs with $k_1$ and $k_2$ number of DN vertices. Also, if $G_1$ has CN sets of order $r_1,r_2,\dots ,r_{p_1}$ and $G_2$ has CN sets of order $t_1,t_2,\dots ,t_{p_2}$, then

(i)

the nullity of $G_1⊚G_2$ is $k_1\times k_2$.

(ii)

the distinct eigenvalues of $G_1⊚G_2$ are

$0,-1,-2,r_1-1,r_2-1,\dots ,r_{n_1}-1,t_1-1,t_2-1,\dots ,t_{p_2}-1,$

$r_1-2,r_2-2,\dots ,r_{n_1}-2,t_1-2,t_2-2,\dots ,t_{p_2}-2,$

$r_1+t_1-2,r_1+t_2-2,\dots ,r_1+t_{p_2}-2,$

$r_2+t_1-2,r_2+t_2-2,\dots ,r_2+t_{p_2}-2,$

$\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots$

$r_{p_1}+t_1-2,r_{p_1}+t_2-2,\dots ,r_{p_1}+t_{p_2}-2.$

(iii)

If $G_1$ or $G_2$ or both have no DN vertices, then $G_1⊚G_2$ is non-singular.

Proof. 

The eigenvalues of $C{N}_s\left(G_1\right)$ are given as follows:

Eigenvalue	0	$-1$	$-1$	……	$-1$	$r_1-1$	$r_2-1$	……	$r_{p_1}-1$
Multiplicity	$k_1$	$r_1-1$	$r_2-1$	……	$r_{p_1}-1$	1	1	……	1

The eigenvalues of $C{N}_s\left(G_2\right)$ are as follows:

Eigenvalue	0	$-1$	$-1$	……	$-1$	$t_1-1$	$t_2-1$	……	$t_{p_2}-1$
Multiplicity	$k_2$	$t_1-1$	$t_2-1$	……	$t_{p_2}-1$	1	1	……	1

If $G_1$ and $G_2$ have $n_1$ and $n_2$ vertices, respectively, then $n_1=k_1+r_1+r_2+\cdots +r_{p_1}$ and $n_2=k_2+t_1+t_2+\cdots +t_{p_2}$. Also, the eigenvalues of $G_1⊚G_2$ are the pairwise sums of the spectra of $C{N}_s\left(G_1\right)$ and $C{N}_s\left(G_2\right)$, resulting in the eigenvalues of $G_1⊚G_2$, as shown in the following Table 2:

Table 2. The eigenvalues of $G_1⊚G_2$.

Eigenvalues	Multiplicity
0	$k_1\times k_2$
−1	$k_2(r_1+r_2+\cdots +r_{p_1}-p_1)+k_1(t_1+t_2+\cdots +t_{p_2}-p_2)$ $=k_2(n_1-k_1-p_1)+k_1(n_2-k_2-p_2)$
−2	$(r_1+r_2+\cdots +r_{p_1}-p_1)(t_1+t_2+\cdots +t_{p_2}-p_2)$ $=(n_1-k_1-p_1)(n_2-k_2-p_2)$
$r_1-1,r_2-1,\dots ,r_{p_1}-1$	$k_2$
$t_1-1,t_2-1,\dots ,t_{p_2}-1$	$k_1$
$r_1-2,r_2-2,\dots ,r_{p_1}-2$	$t_1+t_2+\cdots +t_{p_2}-p_2=n_2-k_2-p_2$
$t_1-2,t_2-2,\dots ,t_{p_2}-2$	$r_1+r_2+\cdots +r_{p_1}-p_1=n_1-k_1-p_1$
$r_1+t_1-2,r_1+t_2-2,\dots ,r_1+t_{p_2}-2$	1
$r_2+t_1-2,r_2+t_2-2,\dots ,r_2+t_{p_2}-2$	1
⋮	⋮
$r_{p_1}+t_1-2,r_{p_1}+t_2-2,\dots ,r_{p_1}+t_{p_2}-2$	1

□

Theorem 16.

Let $G_1$ and $G_2$ be two $C{N}_s$ graphs with $n_1$ and $n_2$ vertices, respectively, with $k_1$ and $k_2$ number of DN vertices. Also, $G_1$ has CN sets of order $r_1,r_2,\dots ,r_{p_1}$ and $G_2$ has CN sets of order $t_1,t_2,\dots ,t_{p_2}$. Then, the energy of $G_1⊚G_2$ is

$2\left[(n_2-k_2-p_2)(n_1-p_1)+(n_1-k_1-p_1)(n_2-p_2)\right]$.

Proof. 

By the above corollary, we get energy of $G_1⊚G_2$ by adding all the eigenvalues.

$$\begin{array}{cc}\hfill \mathcal{E}(G_1⊚G_2)& =k_1(N_2-k_2-n_2)+k_2(N_1-k_1-n_1)+2(N_1-k_1-n_1)(N_2-k_2-n_2)\hfill \\ \hfill & +k_2(N_1-k_1-n_1)+k_1(N_2-k_2-n_1)+(N_2-k_2-n_2)(N_1-k_1-2n_1)\hfill \\ \hfill & +(N_1-k_1-n_1)(N_2-k_2-2n_2)\hfill \\ \hfill & +n_2{r}_1+N_2-k_2-2n_2+n_2{r}_2+N_2-k_2-2n_2+\cdots +n_2{r}_{n_1}+N_2-k_2-2n_2\hfill \\ \hfill & =2k_1(N_2-k_2-n_2)+2k_2(N_1-k_1-n_1)+2(N_1-k_1-n_1)(N_2-k_2-n_2)\hfill \\ \hfill & +(N_2-k_2-n_2)(N_1-k_1-2n_1)+(N_1-k_1-n_1)(N_2-k_2-2n_2)\hfill \\ \hfill & +n_2(N_1-k_1)+n_1(N_2-k_2-2n_2)\hfill \\ \hfill & =2\left[(N_2-k_2-n_2)(N_1-n_1)+(N_1-k_1-n_1)(N_2-n_2)\right].\hfill \end{array}$$

□

If $G_1$ and $G_2$ are two $C{N}_s$ graphs, then energy of $G_1⊚G_2$ is always even.

Corollary 9.

If $G_1$ and $G_2$ are two $C{N}_s$ graphs with no DN vertices, then the energy of $G_1⊚G_2$ is a multiple of 4.

9. Open Problems on the Symmetry of ${\mathit{CN}}_{\mathit{s}}$ Cartesian Product Graphs

9.1. Open Problem 1: Characterization of Automorphism Groups of the $C{N}_s$ Cartesian Product

Given the automorphism groups $\mathrm{Aut}\left(G_1\right)$ and $\mathrm{Aut}\left(G_2\right)$, determine the structure of $\mathrm{Aut}(G_1⊚G_2)$ in the context of the $C{N}_s$ Cartesian product.

• Under what conditions does $\mathrm{Aut}(G_1⊚G_2)$ decompose as a direct or semi-direct product of $\mathrm{Aut}\left(G_1\right)$ and $\mathrm{Aut}\left(G_2\right)$?
• What are necessary and sufficient conditions for $\mathrm{Aut}(G_1⊚G_2)$ to be isomorphic to $\mathrm{Aut}\left(G_1\right)\times \mathrm{Aut}\left(G_2\right)$ in the $C{N}_s$ Cartesian product setting?

9.2. Open Problem 2: Vertex-Transitivity of the $C{N}_s$ Cartesian Product Graph

If $G_1$ and $G_2$ are vertex-transitive, does it follow that $G_1⊚G_2$ is vertex-transitive under the $C{N}_s$ Cartesian product?

• Identify graph-theoretic properties of $G_1$ and $G_2$ that guarantee vertex-transitivity of $G_1⊚G_2$.
• Are there counterexamples where both $G_1$ and $G_2$ are vertex-transitive, but $G_1⊚G_2$ is not in the $C{N}_s$ Cartesian product framework?

9.3. Open Problem 3: Edge-Transitivity and Arc-Transitivity in the $C{N}_s$ Cartesian Product

Under what conditions is $G_1⊚G_2$ edge-transitive or arc-transitive in the $C{N}_s$ Cartesian product, given that $G_1$ and $G_2$ possess these properties?

• Develop criteria for when edge-transitivity or arc-transitivity is preserved under the $C{N}_s$ Cartesian product operation.
• Investigate whether symmetry-breaking phenomena can occur, leading to cases where $G_1⊚G_2$ has fewer symmetry properties than $G_1$ and $G_2$.

9.4. Open Problem 4: Relationship Between Symmetric Graphs and Their $C{N}_s$ Cartesian Product

If $G_1$ and $G_2$ are symmetric graphs (i.e., arc-transitive and vertex-transitive), is $G_1⊚G_2$ necessarily symmetric in the $C{N}_s$ Cartesian product?

• Are there additional symmetry conditions required for the $C{N}_s$ Cartesian product graph to be arc-transitive?
• Can the classification of known symmetric graphs be extended to include their $C{N}_s$ Cartesian product graphs?

10. Conclusions and Future Scope

In this paper, we introduced and examined the concept of the $C{N}_s$ Cartesian product of graphs, with a focus on how identical neighbor structures impact both the spectrum and independence number of the graph. By analyzing the adjacency spectrum using the $C{N}_s$ matrix and considering the influence of vertices with identical neighbors, we gained deeper insights into the interplay between graph structure and its spectral properties. The study further highlighted the effects of these identical neighbors on the independence number, illustrating the strong connection between spectral characteristics and the structural components of complex networks. To advance this exploration, we defined a $C{N}_s$ matrix based on the neighborhood relationships of vertices within a graph. By applying the $C{N}_s$ matrices of two graphs, we determined the adjacency matrix for their $C{N}_s$ Cartesian product. Our analysis revealed that the $C{N}_s$ Cartesian product of graphs, where vertices have identical neighborhoods comprising two elements, consistently results in integral graphs. Additionally, we observed that the energy of these graphs is always an even number. These findings contribute to a deeper understanding of the spectral properties of graphs generated by the $C{N}_s$ Cartesian product, with potential implications for the analysis and behavior of complex networks across various domains. Study of $C{N}_s$ vertices opens multiple avenues for future research. It can provide new insights into graph classification and optimization. Additionally, extending these concepts to weighted graphs and directed networks may enhance their applicability in areas like network resilience, social network analysis, and bioinformatics. The spectral characteristics of $C{N}_s$ graphs can contribute to machine learning frameworks and AI-driven learning systems.