Classifications of Several Classes of Armendariz-like Rings Relative to an Abelian Monoid and Its Applications

Abstract

Let M be an Abelian monoid. A necessary and sufficient condition for the class $\mathcal{A}r{m}_M$ of all Armendariz rings relative to M to coincide with the class $\mathcal{A}rm$ of all Armendariz rings is given. As a consequence, we prove that $\mathcal{A}r{m}_M$ has exactly three cases: the empty set, $\mathcal{A}rm$, and the class of all rings. If N is an Abelian monoid, then we prove that $\mathcal{A}r{m}_{M\times N}=\mathcal{A}r{m}_M\bigcap \mathcal{A}r{m}_N$, which gives a partial affirmative answer to the open question of Liu in 2005 (whether R is $M\times N$-Armendariz if R is M-Armendariz and N-Armendariz). We also show that the other Armendariz-like rings relative to an Abelian monoid, such as M-quasi-Armendariz rings, skew M-Armendariz rings, weak M-Armendariz rings, M-$\pi$-Armendariz rings, nil M-Armendariz rings, upper nil M-Armendariz rings and lower nil M-Armendariz rings can be handled similarly. Some conclusions on these classes have, therefore, been generalized using these classifications.

1. Introduction

All rings in this paper are associative with identity element $1\ne 0$. A semigroup is a nonempty set closed under an associative binary operation. A semigroup with unity is called a monoid. A monoid with a commutative binary operation is called an Abelian monoid. Unless otherwise specified, $ϵ$ will always stand for the unity element of a monoid, and the monoid operation is written multiplicatively. We denote the multiplicative monoid of positive integers by $({\mathbb{Z}}^{+},·)$. The additive monoid of nonnegative integers is denoted by $(\mathbb{N},+)$, and the operation is written additively. The field of rational numbers is denoted by $\mathbb{Q}$. A relation on an arbitrary set is called a partial order if it is reflexive, transitive, and antisymmetric. A partial order is denoted by ≤ and the notation $\xi >\eta$ or $\eta <\xi$ is used to mean $\eta \le \xi$ and $\eta \ne \xi$. A partial order ≤ on a monoid M is said to be compatible with the monoid operation if $\xi \le \eta$ implies $\zeta \xi \le \zeta \eta$ and $\xi \zeta \le \eta \zeta$ for $\xi ,\eta ,\zeta \in M$. A monoid M with a compatible partial order ≤ is denoted by $(M,\le )$. We may use the notation ${\le }_M$ to denote the compatible total order on a monoid M. ${\le }_M$ is said to be strict if $\xi <\eta$ implies $\zeta \xi <\zeta \eta$ and $\xi \zeta <\eta \zeta$ for $\xi ,\eta ,\zeta \in M$. $M^n$ designates the Cartesian product of n copies of M. For a ring R, we denote by $N_{\ast }(R)$, $N^{\ast }(R)$ and $N(R)$ the prime radical, the upper nilradical (i.e., the sum of nil ideals), and the set of all nilpotent elements of R, respectively. It is well known that $N_{\ast }(R)\subseteq N^{\ast }(R)\subseteq N(R)$.

Many authors have studied various generalizations and properties of Armendariz rings. We will list the concepts involved in this paper as follows.

$(a)$ In ref. [1], a ring R is said to have the Armendariz property (or is an Armendariz ring) if whenever polynomials $f(x)=a_0+a_{1}x+\cdots +a_m{x}^m$ and $g(x)=b_0+b_{1}x+\cdots +b_n{x}^n\in R\left[x\right]$ satisfy $f(x)g(x)=0$, we have $a_i{b}_j=0$ for every i and j. The term Armendariz ring was chosen because Armendariz noted in ([2], Lemma 1) that reduced rings (i.e., rings without non-zero nilpotent elements) satisfy this condition. We use $\mathcal{A}rm$ to denote the class of all Armendariz rings. It is well known that $\mathcal{A}rm$ is a nonempty proper subclass of the class of all rings.

$(b)$ In [3], a ring R is quasi-Armendariz if whenever $f(x)={\sum }_{i=0}^m{a}_i{x}^i$, $g(x)={\sum }_{j=0}^n{b}_j{x}^j\in R\left[x\right]$ satisfy $f(x)R\left[x\right]g(x)=0$, we have $a_{i}R{b}_j=0$ for every i and j. We use $\mathcal{Q}Arm$ to denote the class of all quasi-Armendariz rings. It is well known that $\mathcal{Q}Arm$ is a nonempty proper subclass of the class of all rings.

$(c)$ Let $\alpha$ be an endomorphism of a ring R and $I_R$ the identity endomorphism of R. In [4], R is called a skew Armendariz ring with the endomorphism $\alpha$ (simply, an $\alpha$-skew Armendariz ring) if for $f(x)={\sum }_{i=0}^m{a}_i{x}^i$, $g(x)={\sum }_{j=0}^n{b}_j{x}^j$ in $R[x;\alpha ]$, $f(x)g(x)=0$ implies $a_i{\alpha }^i(b_j)=0$ for all $0\le i\le m$, and $0\le j\le n.$ We define the class

$$\mathcal{S}Arm:=\{R:R\mathrm{is}\alpha -\mathrm{skew}\mathrm{Armendariz}\mathrm{for}\mathrm{some}\alpha \mathrm{such}\mathrm{that}{\alpha }^t=I_R\mathrm{for}\mathrm{some}\mathrm{positive}\mathrm{integer}t\}.$$

It is immediate from the definition that $\mathcal{A}rm\subseteq \mathcal{S}Arm$, and so $\mathcal{S}Arm$ is nonempty. The following example shows that there exists a ring R such that R is not $\alpha$-skew Armendariz for any endomorphism $\alpha$ of R. Therefore, $\mathcal{S}Arm$ is a proper subclass of the class of all rings.

Example 1. 

We consider the matrix ring $R=M_2({\mathbb{Z}}_2)$ over the ring of integers modulo 2. If R is α-skew Armendariz for an endomorphism α of R, then $\alpha (e)=e$ for each idempotent element $e\in R$ by [5] and so $\alpha =I_R$. Thus, R is Armendariz, which is a contradiction. Therefore R is not in $\mathcal{S}Arm$.

$(d)$ In [6], a ring R is called weak Armendariz if whenever polynomials $f(x)=a_0+a_{1}x+\cdots +a_m{x}^m$, $g(x)=b_0+b_{1}x+\cdots +b_n{x}^n\in R\left[x\right]$ satisfy $f(x)g(x)=0$, then $a_i{b}_j\in N(R)$ for each $i,j$. We use $\mathcal{W}Arm$ to denote the class of all weak Armendariz rings. It is well known that $\mathcal{W}Arm$ is a nonempty proper subclass of the class of all rings.

$(e)$ In [7], a ring R is called π-Armendariz if whenever $f(x)g(x)\in N(R[x])$ for $f(x)={\sum }_{i=0}^m{a}_i{x}^i$, $g(x)={\sum }_{j=0}^n{b}_j{x}^j$ in $R\left[x\right]$ we obtain $a_i{b}_j\in N(R)$ for all $i,j$. We use $\pi Arm$ to denote the class of all $\pi$-Armendariz rings. It is known that $\pi Arm$ is a nonempty proper subclass of the class of all rings by ([7], Example 2.3).

$(f)$ In [8], a ring R is said to be nil-Armendariz if whenever $f(x),g(x)\in R\left[x\right]$ satisfy $f(x)g(x)\in N(R)\left[x\right]$ then we have $ab\in N(R)$ for all $a\in coef(f(x))$ and $b\in coef(g(x))$. We use $\mathcal{N}Arm$ to denote the class of all nil-Armendariz rings. It is known that $\mathcal{N}Arm$ is a nonempty proper subclass of the class of all rings by ([8], Example 5.5) or ([9], Example 2.34). It is immediate from the definition that $\mathcal{N}Arm\subseteq \mathcal{W}Arm$.

$(g)$ In [10], for a ring R and polynomials $f(x)$, $g(x)$ over R, the following condition

$$f(x)g(x)\in N^{\ast }(R)\left[x\right]\Rightarrow ab\in N^{\ast }(R),\forall a\in coef(f(x)),b\in coef(g(x))$$

(†)

is studied. It is well known that a ring R satisfies the condition $(†)$ if and only if R is nil-Armendariz by ([10], Theorem 11). For the convenience of writing below, we also use ${\mathcal{N}}^{\ast }Arm$ to denote the class of all nil-Armendariz rings.

$(h)$ In [11], a ring R is said to be Armendariz-over-prime-radical (APR) if whenever two polynomials $f(x),g(x)\in R\left[x\right]$ satisfy $f(x)g(x)\in N_{\ast }(R)\left[x\right]$ then $ab\in N_{\ast }(R)$ for all $a\in coef(f(x))$ and $b\in coef(g(x))$. We use ${\mathcal{N}}_{\ast }Arm$ to denote the class of all APR rings. It is known that ${\mathcal{N}}_{\ast }Arm$ is a nonempty proper subclass of the class of all rings by ([11], Example 1.8).

These previous concepts have their analogs in semigroup rings. We conclude this section with some definitions to keep in mind in the sequel.

$(a^{\prime })$ Let M be a monoid and $R\left[M\right]$ the monoid ring of M over a coefficient ring R. In [12], R is called an M-Armendariz ring (an Armendariz ring relative to M), if whenever elements $\Phi =a_1{\xi }_1+\cdots +a_n{\xi }_n$, $\Psi =b_1{\eta }_1+\cdots +b_m{\eta }_m\in R\left[M\right]$ satisfy $\Phi \Psi =0$, then $a_i{b}_j=0$ for each $i,j$. We use $\mathcal{A}r{m}_M$ to denote the class of all Armendariz rings relative to M. It is clear that $\mathcal{A}r{m}_{(\mathbb{N},+)}=\mathcal{A}rm$ and $\mathcal{A}r{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings. It is immediate from the definition that $\mathcal{A}r{m}_M\subseteq \mathcal{A}r{m}_N$ when N is a submonoid of M.

$(b^{\prime })$ Let M be a monoid. In [13,14] and independently in [15], a ring R is called an M-quasi-Armendariz ring (a quasi-Armendariz ring relative to the monoid M) if whenever $\Phi =a_1{\xi }_1+a_2{\xi }_2+\cdots +a_n{\xi }_n,\Psi =b_1{\eta }_1+b_2{\eta }_2+\cdots +b_m{\eta }_m\in R\left[M\right]$ satisfy $\Phi R\left[M\right]\Psi =0$, then $a_{i}R{b}_j=0$ for each $i,j$. We use $\mathcal{Q}Ar{m}_M$ to denote the class of all quasi-Armendariz rings relative to the monoid M. It is clear that $\mathcal{Q}Ar{m}_{(\mathbb{N},+)}=\mathcal{Q}Arm$ and $\mathcal{Q}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings. If M is an Abelian monoid and N is a submonoid of M, then $\mathcal{Q}Ar{m}_M\subseteq \mathcal{Q}Ar{m}_N$ by ([14], Lemma 1.14) and ([15], Proposition 3.2).

$(c^{\prime })$ Let R be a ring, M a monoid, $\omega :M\to End(R)$ a monoid homomorphism and $I_R$ the identity endomorphism of R. In [16], R is called a skew Armendariz ring relative to M (or simply skew M-Armendariz) if whenever two elements $\Phi ={\sum }_{i=1}^m{a}_i{\xi }_i$ and $\Psi ={\sum }_{j=1}^n{b}_j{\eta }_j$ of $R\ast M$ satisfy $\Phi \Psi =0$, then $a_i{\omega }_{{\xi }_i}(b_j)=0$ for each $1\le i\le m$ and $1\le j\le n$, where $R\ast M$ is the skew monoid ring (induced by the monoid homomorphism $\omega$). We define the class

$$\begin{array}{cc}\hfill \mathcal{S}Ar{m}_M:=& \{R:R\mathrm{is}\mathrm{skew}M-\mathrm{Armendariz}\mathrm{for}\mathrm{some}\omega \mathrm{such}\mathrm{that}\mathrm{for}\mathrm{each}\\ & \xi \in M,\mathrm{there}\mathrm{exists}\mathrm{a}\mathrm{positive}\mathrm{integer}t\mathrm{with}{({\omega }_{\xi })}^t=I_R\}.\end{array}$$

It is clear that $\mathcal{S}Ar{m}_{(\mathbb{N},+)}=\mathcal{S}Arm$, $\mathcal{A}r{m}_M\subseteq \mathcal{S}Ar{m}_M$, $\mathcal{S}Ar{m}_M\subseteq \mathcal{S}Ar{m}_N$ when N is a submonoid of M. We know that $\mathcal{S}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

$(d^{\prime })$ Let R be a ring and M a monoid. In [17], R is called a weak M-Armendariz ring if whenever $\Phi =a_1{\xi }_1+\cdots +a_m{\xi }_m,\Psi =b_1{\eta }_1+\cdots +b_n{\eta }_n$ in $R\left[M\right]$ satisfy $\Phi \Psi =0$, then $a_i{b}_j\in N(R)$ for each i and j. We use $\mathcal{W}Ar{m}_M$ to denote the class of all weak M-Armendariz rings. It is immediate from the definition that $\mathcal{W}Ar{m}_{(\mathbb{N},+)}=\mathcal{W}Arm$, $\mathcal{W}Ar{m}_M\subseteq \mathcal{W}Ar{m}_N$ when N is a submonoid of M. We know that $\mathcal{W}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

$(e^{\prime })$ Let R be a ring and M a monoid. In [18], R is called an M-π-Armendariz ring (a $\pi$-Armendariz ring relative to M), if whenever $\Phi =a_1{\xi }_1+\cdots +a_n{\xi }_n$, $\Psi =b_1{\eta }_1+\cdots +b_m{\eta }_m\in R\left[M\right]$ satisfy $\Phi \Psi \in N(R[M])$, then $a_i{b}_j\in N(R)$ for each $i,j$. We use $\pi {Arm}_M$ to denote the class of all M-$\pi$-Armendariz rings. It is immediate from the definition that $\pi Ar{m}_{(\mathbb{N},+)}=\pi Arm$, $\pi Ar{m}_M\subseteq \pi Ar{m}_N$ when N is a submonoid of M. We know that $\pi Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

$(f^{\prime })$ Let R be a ring and M a monoid. In [19] and independently in [20,21], R is said to be nil-Armendariz relative to M (nil M-Armendariz or M-nil-Armendariz) if whenever element $\Phi ={\sum }_{i=1}^m{a}_i{\xi }_i$ and $\Psi ={\sum }_{j=1}^n{b}_j{\eta }_j$ in $R\left[M\right]$ satisfy $\Phi \Psi \in N(R)\left[M\right]$, then $a_i{b}_j\in N(R)$ for each i and j. We use $\mathcal{N}Ar{m}_M$ to denote the class of all nil M-Armendariz rings. It is immediate from the definition that $\mathcal{N}Ar{m}_{(\mathbb{N},+)}=\mathcal{N}Arm$, $\mathcal{N}Ar{m}_M\subseteq \mathcal{N}Ar{m}_N$ when N is a submonoid of M. We know that $\mathcal{N}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

$(g^{\prime })$ Let R be a ring and M a monoid. In [22], R is said to be upper nil M-Armendariz if whenever elements $\Phi ={\sum }_{i=1}^m{a}_i{\xi }_i$ and $\Psi ={\sum }_{j=1}^n{b}_j{\eta }_j$ in $R\left[M\right]$ satisfy $\Phi \Psi \in N^{\ast }(R)\left[M\right]$, then $a_i{b}_j\in N^{\ast }(R)$ for each i and j. We use ${\mathcal{N}}^{\ast }Ar{m}_M$ to denote the class of all upper nil M-Armendariz rings. It is clear that ${\mathcal{N}}^{\ast }Ar{m}_{(\mathbb{N},+)}={\mathcal{N}}^{\ast }Arm$ and ${\mathcal{N}}^{\ast }Ar{m}_M\subseteq {\mathcal{N}}^{\ast }Ar{m}_N$ when N is a submonoid of M. It is immediate from the definition that ${\mathcal{N}}^{\ast }Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

$(h^{\prime })$ Let R be a ring and M a monoid. In [22], a ring R is said to be lower nil M-Armendariz, if whenever element $\Phi ={\sum }_{i=1}^m{a}_i{\xi }_i$, $\Psi ={\sum }_{j=1}^n{b}_j{\eta }_j\in R\left[M\right]$ satisfy $\Phi \Psi \in N_{\ast }(R)\left[M\right]$, then $a_i{b}_j\in N_{\ast }(R)$ for all i, j. We use ${\mathcal{N}}_{\ast }Ar{m}_M$ to denote the class of all nil M-Armendariz rings. It is immediate from the definition that ${\mathcal{N}}_{\ast }Ar{m}_{(\mathbb{N},+)}={\mathcal{N}}_{\ast }Arm$, ${\mathcal{N}}_{\ast }Ar{m}_M\subseteq {\mathcal{N}}_{\ast }Ar{m}_N$ when N is a submonoid of M. We know that ${\mathcal{N}}_{\ast }Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings.

The following statement may bring convenience. When “Armendariz rings” appear, we consider them to be the rings in $(a)$. When “Armendariz-like rings” appear, we consider them to be the rings in $(a)$, $(b)$, $(c)$, $(d)$, $(e)$, $(f)$, $(g)$, and $(h)$. When “Armendariz rings relative to an Abelian monoid” appear, we consider them to be the rings in $(a^{\prime })$. When “Armendariz-like rings relative to an Abelian monoid” appear, we consider them to be the rings in $(a^{\prime })$, $(b^{\prime })$, $(c^{\prime })$, $(d^{\prime })$, $(e^{\prime })$, $(f^{\prime })$, $(g^{\prime })$, and $(h^{\prime })$.

In this article, we focus on the influence of monoid M on these classes mentioned in $(a^{\prime })$ to $(h^{\prime })$, especially when M is commutative. In Section 2, classifications of these classes are given. As a consequence (see Theorem 2), we understand that ${♯}_M$ has exactly three cases: the empty set, ♯, and the class of all rings, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

Section 3 is devoted to several applications of these classifications. We determine the class of Abelian monoids that admits a compatible strict total order in a new way (see Proposition 5). That is, M is cancellative and torsion-free if and only if ${♯}_M$ is nonempty. The open question of [12] asked whether R is $M\times N$-Armendariz if R is M-Armendariz and N-Armendariz. This question and the corresponding questions in other classes of Armendariz-like rings are answered in the affirmative for Abelian monoids (see Proposition 6) because we understand that $\mathcal{A}r{m}_{M\times N}=\mathcal{A}r{m}_M\bigcap \mathcal{A}r{m}_N$. We also obtained the same results (see Propositions 7–9) without assuming $G(M)=\left\{ϵ\right\}$ which cannot be removed in much original literature. Finally, a generalization of the Lemma 3 is given (see Theorem 3), which says that multiplication behaves of a finite set of elements of M can be the same as addition does for a finite set of nonnegative integers.

2. Classifications of These Classes

Recall that an element $\xi$ of a monoid M is left cancellative if $\xi {\eta }_1=\xi {\eta }_2$ implies ${\eta }_1={\eta }_2$ for ${\eta }_1,{\eta }_2\in M$. The right cancellativity is defined similarly. If every element is left and right cancellative, M is said to be cancellative. The results similar to the following two propositions can be found in the literature (see ([22], Lemma 2.2), ([15], Proposition 2.13), ([23], Lemma 4.2), ([24], Proposition 2.27), ([17], Lemma 2) and ([20], Lemma 2.4)). We give proofs for completeness.

Proposition 1. 

If an Abelian monoid M is not cancellative, then the class ${♯}_M$ is empty, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

Proof. 

Suppose $\xi \in M$ is not left cancellative. Then there are ${\eta }_1,{\eta }_2\in M$ such that $\xi {\eta }_1=\xi {\eta }_2$ and ${\eta }_1\ne {\eta }_2$.

In the special case $♯=\mathcal{Q}Arm$, if $\mathcal{Q}Ar{m}_M$ is not empty, then there is a ring $R\in \mathcal{Q}Ar{m}_M$. Thus, $(1\xi )R\left[M\right](1{\eta }_1+(-1){\eta }_2)=0$, giving a contradiction.

If $♯\ne \mathcal{Q}Arm$ and $R\in {♯}_M$, then $(1\xi )(1{\eta }_1+(-1){\eta }_2)=0$, which is also a contradiction. □

The converse of Proposition 1 need not hold by ([12], Lemma 1.11).

Proposition 2. 

If an Abelian monoid M contains a non-unity element of finite order, then the class ${♯}_M$ is empty, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

Proof. 

Suppose there is $ϵ\ne \xi \in M$ with ${\xi }^m={\xi }^n$ for some positive integers $m<n$. Let

$$k=\min \{l\in {\mathbb{Z}}^{+}:{\xi }^r={\xi }^l\mathrm{for}\mathrm{some}\mathrm{positive}\mathrm{integer}r<l\}.$$

Then the choice of k implies that the set $\{{\xi }^r,\cdots ,{\xi }^{k-1}\}$ has cardinality $k-r$ for a positive integer $r<k$ such that ${\xi }^r={\xi }^k$.

In the special case $♯=\mathcal{Q}Arm$, if $\mathcal{Q}Ar{m}_M$ is not empty, then there is a ring $R\in \mathcal{Q}Ar{m}_M$. Thus, for any $a_1{\zeta }_1+\cdots +a_n{\zeta }_n\in R\left[M\right]$,

$$(1{\xi }^r+\cdots +1{\xi }^{k-1})(a_1{\zeta }_1+\cdots +a_n{\zeta }_n)(1ϵ+(-1)\xi )=0,$$

giving a contradiction.

If $♯\ne \mathcal{Q}Arm$ and $R\in {♯}_M$, then $(1{\xi }^r+\cdots +1{\xi }^{k-1})(1ϵ+(-1)\xi )=0$, giving a contradiction. □

Lemma 1. 

Let M be a monoid whose all non-unity elements have infinite order, and let $\xi ,\eta \in M$ be such that $⟨\xi ⟩\bigcap ⟨\eta ⟩\ne Ø$. If

$$p^{\prime }=\min \{p\in {\mathbb{Z}}^{+}:{\xi }^p={\eta }^q\mathit{for}\mathit{some}\mathit{positive}\mathit{integer}q\}$$

and

$$q^{\prime }=\min \{q\in {\mathbb{Z}}^{+}:{\xi }^p={\eta }^q\mathit{for}\mathit{some}\mathit{positive}\mathit{integer}p\},$$

then ${\xi }^{p^{\prime }}={\eta }^{q^{\prime }}$.

Proof. 

If $\xi =ϵ$, then $\eta =ϵ$. So $p^{\prime }=q^{\prime }=1$ and ${\xi }^{p^{\prime }}={\eta }^{q^{\prime }}$.

If $\xi \ne ϵ$, then $\eta \ne ϵ$. So ${\xi }^{p^{\prime }}={\eta }^{q^{″}}$ and ${\xi }^{p^{″}}={\eta }^{q^{\prime }}$ for some positive integers $p^{″}$ and $q^{″}$. We claim that $p^{\prime }=p^{″}$. Otherwise, if $p^{\prime }<p^{″}$, then $p^{\prime }{q}^{\prime }<p^{″}{q}^{″}$. Since ${\eta }^{q^{\prime }{p}^{\prime }}={\xi }^{p^{\prime }{p}^{″}}={\eta }^{q^{″}{p}^{″}}$, we have $q^{\prime }{p}^{\prime }=q^{″}{p}^{″}$, giving a contradiction. It follows that ${\xi }^{p^{\prime }}={\xi }^{p^{″}}={\eta }^{q^{\prime }}$. □

Recall that a monoid M is torsion-free if ${\xi }^n={\eta }^n$ implies $\xi =\eta$ for any $\xi ,\eta \in M$ and any positive integer n.

Proposition 3. 

Let M be an Abelian monoid. If M is not torsion-free, then the class ${♯}_M$ is empty, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

Proof. 

Suppose M is not torsion-free. Then there are distinct elements $\xi ,\eta \in M$ such that ${\xi }^n={\eta }^n$ for a positive integer n. If ${♯}_M$ is not empty, then all non-unity elements of M have infinite order by Proposition 2. Hence $\xi \ne ϵ$ and $\eta \ne ϵ$. Let

$$p^{\prime }=\min \{p\in {\mathbb{Z}}^{+}|\exists q\in {\mathbb{Z}}^{+},{\xi }^p={\eta }^q\},q^{\prime }=\min \{q\in {\mathbb{Z}}^{+}|\exists p\in {\mathbb{Z}}^{+},{\xi }^p={\eta }^q\}.$$

By Lemma 1, ${\xi }^{p^{\prime }}={\eta }^{q^{\prime }}$. Then ${\eta }^{n{p}^{\prime }}={\xi }^{p^{\prime }n}={\eta }^{q^{\prime }n}$. Thus, $n{p}^{\prime }=n{q}^{\prime }$ and so $p^{\prime }=q^{\prime }$. For convenience, let $r=p^{\prime }=q^{\prime }$. Since ${♯}_M$ is not empty, there is a ring $R\in {♯}_M$.

In the special case $♯=\mathcal{Q}Ar{m}_M$, for any $a_1{\zeta }_1+\cdots +a_n{\zeta }_n\in R\left[M\right]$,

$$(1{\xi }^{r-1}+1{\xi }^{r-2}\eta +\cdots +1\xi {\eta }^{r-2}+1{\eta }^{r-1})(a_1{\zeta }_1+\cdots +a_n{\zeta }_n)(1\xi +(-1)\eta )=0,$$

giving a contradiction.

If $♯\ne \mathcal{Q}Ar{m}_M$, then

$$(1{\xi }^{r-1}+1{\xi }^{r-2}\eta +\cdots +1\xi {\eta }^{r-2}+1{\eta }^{r-1})(1\xi +(-1)\eta )=0,$$

which is also a contradiction. □

Example 2. 

The multiplicative Abelian monoid $(\mathbb{Z},\times )$ of integers is not torsion-free. Then the class ${♯}_{(\mathbb{Z},\times )}$ is empty for each $♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}$ by Proposition 3.

Remark 1. 

Notice that the converse of Proposition 3 is not true in general. For instance, the multiplicative Abelian monoid $(\mathbb{N},\times )$ of nonnegative integers is torsion-free but not cancellative. So, these classes in Proposition 3 are empty by Proposition 1.

Recall that a monoid M is called a u.p.-monoid (unique product monoid) if for any two nonempty finite subsets $A,B\subseteq M$ there exists an element $\xi \in M$ uniquely presented in the form $\eta \zeta$ where $\eta \in A$ and $\zeta \in B$. In ([25], Proposition 5.1), it is shown that for any nontrivial u.p.-monoid M (i.e., $M\ne \left\{ϵ\right\}$ and M is a u.p.-monoid), the class $\mathcal{A}r{m}_M$ is contained in $\mathcal{A}rm$. Now we have the following.

Proposition 4. 

If M is an Abelian monoid, then

$${♯}_M\subseteq ♯\mathit{if}\mathit{and}\mathit{only}\mathit{if}M\ne \left\{ϵ\right\},$$

where $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$.

Proof. 

If ${♯}_M\subseteq ♯$, then $M\ne \left\{ϵ\right\}$ follows from the fact that ${♯}_{\left\{ϵ\right\}}$ coincides with the class of all rings and ♯ is a proper subclass of the class of all rings.

If $M\ne \left\{ϵ\right\}$, we claim that ${♯}_M\subseteq ♯$. First, we may assume that ${♯}_M$ is not empty, for the result is trivially true otherwise. Then M contains a non-unity element of infinite order by Proposition 2. Thus, $(\mathbb{N},+)$ is isomorphic to a submonoid of M. Therefore, ${♯}_M\subseteq {♯}_{(\mathbb{N},+)}=♯$. □

By Proposition 4, we know that when M is an Abelian monoid, the only class ${♯}_M$ which contains ♯ as a proper subclass is ${♯}_{\left\{ϵ\right\}}$, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

Corollary 1. 

If M is an Abelian monoid, then

$$M=\left\{ϵ\right\}\mathit{if}\mathit{and}\mathit{only}\mathit{if}{♯}_M\mathit{is}\mathit{the}\mathit{class}\mathit{of}\mathit{all}\mathit{rings},$$

where $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$.

Proof. 

If $M=\left\{ϵ\right\}$, then it is easy to see that ${♯}_M$ is the class of all rings.

On the other hand, assume that ${♯}_M$ is the class of all rings. If $M\ne \left\{ϵ\right\}$, then ${♯}_M\subseteq ♯$ by Proposition 4, giving a contradiction. □

The following lemma is an easy observation that will simplify our work of checking whether a ring has Armendariz-like properties relative to an Abelian monoid. The proof of it is elementary and will be omitted.

Lemma 2. 

Let $\Phi =a_1{\xi }_1+a_2{\xi }_2+\cdots +a_n{\xi }_n$ and $\Psi =b_1{\xi }_1+b_2{\xi }_2+\cdots +b_n{\xi }_n$. The following statements hold for any monoid M:

1. 

A ring R is an M-Armendariz ring if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi =0$, then $a_i{b}_j=0$ for each $i,j$;

2. 

A ring R is M-quasi-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi R\left[M\right]\Psi =0$, then $a_{i}R{b}_j=0$ for each $i,j$;

3. 

Let $\omega :M\to End(R)$ be a monoid homomorphism. A ring R is skew M-Armendariz if and only if whenever Φ, Ψ of $R\ast M$ satisfy $\Phi \Psi =0$, then $a_i{\omega }_{{\xi }_i}(b_j)=0$ for each $i,j$;

4. 

A ring R is weak M-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi =0$, then $a_i{b}_j\in N(R)$ for each i and j;

5. 

A ring R is M-π-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi \in N(R[M])$, then $a_i{b}_j\in N(R)$ for each i and j;

6. 

A ring R is nil M-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi \in N(R)\left[M\right]$, then $a_i{b}_j\in N(R)$ for each i and j;

7. 

A ring R is upper nil M-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi \in N^{\ast }(R)\left[M\right]$, then $a_i{b}_j\in N^{\ast }(R)$ for each i and j;

8. 

A ring R is lower nil M-Armendariz if and only if whenever Φ, $\Psi \in R\left[M\right]$ satisfy $\Phi \Psi \in N_{\ast }(R)\left[M\right]$, then $a_i{b}_j\in N_{\ast }(R)$ for each i and j.

To characterize the connection between $(\mathbb{N},+)$ and a cancellative, torsion-free Abelian monoid M, we present the following lemma, which is crucial in this paper.

Lemma 3. 

Let M be any Abelian monoid that is both torsion-free and cancellative. Assume that ${\xi }_1,\cdots ,{\xi }_n\in M$. For each positive integer m, there are n elements $r_1,\cdots ,r_n$ in $(\mathbb{N},+)$ such that

$${\xi }_{i_1}\cdots {\xi }_{i_m}={\xi }_{j_1}\cdots {\xi }_{j_m}ifandonlyif{r}_{i_1}+\cdots +r_{i_m}=r_{j_1}+\cdots +r_{j_m},$$

for each $i_k,j_k\in \{1,\cdots ,n\},k=1,\cdots ,m$.

Proof. 

Since M is a torsion-free and cancellative Abelian monoid, we can embed M in its quotient group G. Let $\sigma :M\to G$ be the embedding. As it is torsion-free and Abelian, G then embeds into $V=\mathbb{Q}{\otimes }_{\mathbb{Z}}G$, which is a $\mathbb{Q}$-vector space (A similar argument can be found in the proof of ([26], Theorem 6.31)). Let $\delta :G\to V$ be the embedding. As we are only concerned with a subsemigroup of M generated by $\{{\xi }_1,\cdots ,{\xi }_n\}$, we can reduce to the case that the $\mathbb{Q}$-vector space V is finite-dimensional. After clearing denominators, we can think of the coordinates of $\delta \sigma ({\xi }_i)$ with respect to a basis as finite tuples of integers. Moreover, by adding the same sufficiently large positive integer to each entry of these tuples, we can think of them as finite tuples of nonnegative integers. Without loss of generality, we may assume that

$$\begin{array}{cc}\hfill \delta \sigma ({\xi }_1)& =(r_{10},\cdots ,r_{1s}),\hfill \\ \hfill \delta \sigma ({\xi }_2)& =(r_{20},\cdots ,r_{2s}),\hfill \\ \hfill & ⋮\hfill \\ \hfill \delta \sigma ({\xi }_n)& =(r_{n0},\cdots ,r_{ns}),\hfill \end{array}$$

where each $r_{ij}$ is a nonnegative integer, $1\le i\le n,0\le j\le s$. Choose a positive integer

$$k>\max \{m{r}_{ij}:1\le i\le n,0\le j\le s\}.$$

Let $r_i=r_{i0}{p}^s+\cdots +r_{is}{p}^0,i=1,\cdots ,n$. By the uniqueness of p-ary representation and the injectivity of $\sigma$ and $\delta$, we have

$${\xi }_{i_1}\cdots {\xi }_{i_m}={\xi }_{j_1}\cdots {\xi }_{j_m}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{r}_{i_1}+\cdots +r_{i_m}=r_{j_1}+\cdots +r_{j_m},$$

for each $i_k,j_k\in \{1,\cdots ,n\},k=1,\cdots ,m$. □

Example 3. 

Let M be the submonoid of $({\mathbb{Z}}^{+},·)$ generated by $\{1,2,3,4\}$. The quotient group G of M is the subgroup of the multiplicative group of positive rational numbers $({\mathbb{Q}}^{+},·)$ generated by $\{1,2,3,4\}$. Let $\sigma :M\to G$ be the embedding. As it is torsion-free and Abelian, G then embeds into the $\mathbb{Q}$-vector space $V=\mathbb{Q}{\otimes }_{\mathbb{Z}}G$. Let $\delta :G\to V$ be the embedding. The set $\{1\otimes 2,1\otimes 3\}$ is a basis of V. The coordinates of $\delta \sigma (1),\delta \sigma (2),\delta \sigma (3)$ and $\delta \sigma (4)$ with respect to the basis are $(0,0),(1,0),(0,1)$ and $(2,0)$, respectively. We think of them as quinary representations, then $r_1=0,r_2=5,r_3=1$, and $r_4=10$. Therefore $i_1{i}_2=j_1{j}_2\mathit{if}\mathit{and}\mathit{only}\mathit{if}{r}_{i_1}+r_{i_2}=r_{j_1}+r_{j_2}$ for each $i_1,i_2,j_1,j_2\in \{1,2,3,4\}$.

It is obvious that ${♯}_M=♯$ if $M=(\mathbb{N},+)$, where

$$♯\in \{\mathcal{A}rm,\mathcal{Q}Arm,\mathcal{S}Arm,\mathcal{W}Arm,\pi Arm,\mathcal{N}Arm,{\mathcal{N}}^{\ast }Arm,{\mathcal{N}}_{\ast }Arm\}.$$

The following theorem shows that the equality ${♯}_M=♯$ holds for any cancellative, infinite, and torsion-free Abelian monoid M.

Theorem 1. 

If M is an Abelian monoid, then

$${♯}_M=♯\mathit{if}\mathit{and}\mathit{only}\mathit{if}M\mathit{is}\mathit{cancellative},\mathit{infinite}\mathit{and}\mathit{torsion}-\mathit{free},$$

where $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$.

Proof. 

If ${♯}_M=♯$, then M is cancellative and torsion-free by Propositions 1 and 3. Since ${♯}_{\left\{ϵ\right\}}$ coincides with the class of all rings, M is not a singleton. By Proposition 2, M is infinite.

On the other hand, if M is cancellative, infinite, and torsion-free, then ${♯}_M\subseteq ♯$ by Proposition 4. For the reverse inclusion, we divide the proof into the following three cases.

Case 1: $♯=\pi Arm$. Take any $R\in \pi Arm$. Let

$$\Phi =a_1{\xi }_1+\cdots +a_n{\xi }_n,\Psi =b_1{\xi }_1+\cdots +b_n{\xi }_n\in R\left[M\right]$$

with $\Phi \Psi \in N(R[M])$. If the index of nilpotency of $\Phi \Psi$ in $R\left[M\right]$ is m, then there are n elements $r_1,\cdots ,r_n$ in $(\mathbb{N},+)$ such that

$${\xi }_{i_1}\cdots {\xi }_{i_{2m}}={\xi }_{j_1}\cdots {\xi }_{j_{2m}}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{r}_{i_1}+\cdots +r_{i_{2m}}=r_{j_1}+\cdots +r_{j_{2m}}$$

for each $i_k,j_k\in \{1,\cdots ,n\}$, $k=1,\cdots ,2m$, by Lemma 3. Let

$$f(x)=a_1{x}^{r_1}+\cdots +a_n{x}^{r_n},g(x)=b_1{x}^{r_1}+\cdots +b_n{x}^{r_n}\in R\left[x\right].$$

Then ${(f(x)g(x))}^m=0$. Thus, $a_i{b}_j\in N(R)$ for all i and j. So $R\in \pi Ar{m}_M$ by Lemma 2.

Case 2: $♯\ne \mathcal{S}Arm$ and $♯\ne \pi Arm$. Take any $R\in ♯$. Let

$$\Phi =a_1{\xi }_1+\cdots +a_n{\xi }_n,\Psi =b_1{\xi }_1+\cdots +b_n{\xi }_n\in R\left[M\right].$$

There are n elements $r_1,\cdots ,r_n$ in $(\mathbb{N},+)$ such that

$${\xi }_{i_1}{\xi }_{i_2}={\xi }_{j_1}{\xi }_{j_2}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{r}_{i_1}+r_{i_2}=r_{j_1}+r_{j_2},$$

for each $i_1,i_2,j_1,j_2\in \{1,\cdots ,n\}$ by Lemma 3. Let

$$f(x)=a_1{x}^{r_1}+\cdots +a_n{x}^{r_n},g(x)=b_1{x}^{r_1}+\cdots +b_n{x}^{r_n}\in R\left[x\right].$$

The following statements are obvious.

• If $\Phi \Psi =0$, then $f(x)g(x)=0$;
• If $\Phi R\left[M\right]\Psi =0$, then $f(x)R\left[x\right]g(x)=0$;
• If $\Phi \Psi \in N(R)\left[M\right]$, then $f(x)g(x)\in N(R)\left[x\right]$;
• If $\Phi \Psi \in N^{\ast }(R)\left[M\right]$, then $f(x)g(x)\in N^{\ast }(R)\left[x\right]$;
• If $\Phi \Psi \in N_{\ast }(R)\left[M\right]$, then $f(x)g(x)\in N_{\ast }(R)\left[x\right]$.

Given these facts, it is not hard to show that $R\in {♯}_M$.

Case 3: $♯=\mathcal{S}Arm$. Take any $R\in \mathcal{S}Arm$ with the endomorphism $\alpha$ such that ${\alpha }^t=I_R$ for some positive integer t. It follows from ([27], Corollary 2) that $R\in \mathcal{A}rm$. Since $\mathcal{A}rm\subseteq \mathcal{A}r{m}_M$ by Case 2, it follows that $R\in \mathcal{A}r{m}_M$. Please note that $\mathcal{A}r{m}_M\subseteq \mathcal{S}Ar{m}_M$. Therefore $R\in \mathcal{S}Ar{m}_M$. □

Now, we have a complete classification of these classes of Armendariz-like rings relative to an Abelian monoid.

Theorem 2. 

Let M be an Abelian monoid. Then, the following assertions hold for $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}:$

1. 

If $M=\left\{ϵ\right\}$, then ${♯}_M$ coincides with the class of all rings;

2. 

If M is cancellative, infinite and torsion-free, then ${♯}_M=♯$;

3. 

If M is not cancellative or it is not torsion-free, then ${♯}_M$ is empty.

Proof. 

Assume that M is cancellative and torsion-free. If $M=\left\{ϵ\right\}$, then (1) holds. If $M\ne \left\{ϵ\right\}$, then M is infinite. Hence (2) holds by Theorem 1. Assume that M is not cancellative, or it is not torsion-free, then ${♯}_M$ is empty by Propositions 1 and 3. □

In [20], a ring R is called nil-Armendariz relative to monoid $\mathbb{Z}$, if whenever $f(x)=a_{-m}{x}^{-m}+\cdots +a_p{x}^p$, $g(x)=b_{-n}^{-n}+\cdots +b_q{x}^q\in R[x,x^{-1}]$ satisfy $f(x)g(x)\in N(R)[x,x^{-1}]$, then $a_i{b}_j\in N(R)$ for each $i,j$. We denote the additive group of integers by $(\mathbb{Z},+)$. By Theorem 2, we know that ${♯}_{(\mathbb{Z},+)}=♯$ for $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$. So, the class of all nil-Armendariz rings relative to monoid $\mathbb{Z}$ coincides with the class $\mathcal{N}Arm$ of all nil-Armendariz rings. One may suspect that the only nonempty class ${♯}_M$ contained in ♯ is ♯ itself. This, however, may not always be the case. Notice that when a monoid M is not commutative, $\mathcal{A}r{m}_M$ may be nonempty and strictly contained in $\mathcal{A}rm$ by ([25], Example 5.2).

3. Applications

The following proposition determines the class of Abelian monoids that admits a compatible strict total order in a new way.

Proposition 5. 

Let M be an Abelian monoid. The following are equivalent for each $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}:$

1. 

M is cancellative and torsion-free;

2. 

M admits a compatible strict total order;

3. 

${♯}_M$ is nonempty.

Proof. 

Statements $(1)$ and $(2)$ are equivalent by ([28], Corollary 3.4).

$(1)\Rightarrow (3).$ If $M=\left\{ϵ\right\}$, then ${♯}_M$ coincides with the class of all rings. If $M\ne \left\{ϵ\right\}$, then M is infinite because M is cancellative and torsion-free. Thus, ${♯}_M=♯$ by Theorem 1.

$(3)\Rightarrow (1).$ This follows immediately from Propositions 1 and 3. □

As a consequence of Proposition 5, we obtain the following corollary, which is known for finitely generated Abelian groups (see ([12], Theorem 1.14), ([14], Theorem 1.16), ([24], Proposition 2.26), ([17], Theorem 2), ([29], Theorem 2.8), ([19], Theorem 2.10), ([20] Theorem 2.24) and ([9], Theorem 2.40)).

Corollary 2. 

If M is a cancellative Abelian monoid, then

$$M\mathit{is}\mathit{torsion}-\mathit{free}\mathit{if}\mathit{and}\mathit{only}\mathit{if}{♯}_M\mathit{is}\mathit{nonempty},$$

where $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$.

The author of [12] asked whether R is $M\times N$-Armendariz if R is M-Armendariz and N-Armendariz. In ([12], Propositions 2.6 and 2.7), affirmative results exist in the particular case. In ([22], Theorems 2.7 and 2.8), affirmative results exist in the much more general cases. In ([15], Theorem 3.3), ([17], Theorem 3), ([18], Theorem 2.17) and ([20], Theorem 2.29), there are partial answers for $\mathcal{Q}Ar{m}_M$, $\mathcal{W}Ar{m}_M$, $\pi Ar{m}_M$ and $\mathcal{N}Ar{m}_M$, respectively. The following proposition gives a positive answer to the open question mentioned above for Abelian monoids.

Proposition 6. 

If M and N are Abelian monoids, then

$${♯}_{M\times N}={♯}_M\bigcap {♯}_N,$$

for all $♯\in \{\mathcal{A}rm$, $\mathcal{Q}Arm$, $\mathcal{S}Arm$, $\mathcal{W}Arm$, $\pi Arm$, $\mathcal{N}Arm$, ${\mathcal{N}}^{\ast }Arm$, ${\mathcal{N}}_{\ast }Arm\}$.

Proof. 

We may assume that $M\ne \left\{ϵ\right\}$ and $N\ne \left\{ϵ\right\}$ for the result is trivially true otherwise. We know that ${♯}_{M\times N}\subseteq {♯}_M\bigcap {♯}_N$ is true because both M and N can be considered to be submonoids of $M\times N$. Let us prove the reverse inclusion. If ${♯}_M$ or ${♯}_N$ is empty, the reverse inclusion is trivially true. If ${♯}_M$ and ${♯}_N$ are both nonempty, then M and N are both cancellative, infinite and torsion-free by Theorem 2. So $M\times N$ is cancellative, infinite and torsion-free. Then ${♯}_{M\times N}=♯={♯}_M={♯}_N$ by Theorem 1. Therefore ${♯}_{M\times N}={♯}_M\bigcap {♯}_N$. □

We denote by $G(M)$ the largest subgroup of M. $G(M)=\left\{ϵ\right\}$ is an important condition in much literature. We will show how to obtain the same conclusion without using this condition in the following three propositions. We know that a ring R is Armendariz if and only if $R\left[x\right]$ is Armendariz by ([30], Theorem 2). From ([12], Proposition 2.6), if R is Armendariz and M-Armendariz, where M is a commutative and cancellative monoid with $G(M)=\left\{ϵ\right\}$, then $R\left[M\right]$ is Armendariz. Now, we have the following conclusion.

Proposition 7. 

Let R be a ring and M an Abelian monoid. The following are equivalent:

1. 

R is M-Armendariz;

2. 

$R\left[x\right]$ is M-Armendariz;

3. 

$R[x,x^{-1}]$ is M-Armendariz;

4. 

$R\left[M\right]$ is M-Armendariz.

Proof. 

We may assume that $M\ne \left\{ϵ\right\}$ and that $\mathcal{A}r{m}_M$ is not empty, for the result is trivially true otherwise. By Theorem 2, we have $\mathcal{A}r{m}_M=\mathcal{A}rm=\mathcal{A}r{m}_{(\mathbb{Z},+)}$ and M is a cancellative, infinite and torsion-free Abelian monoid. Statements $(1)$ and $(2)$ are equivalent by ([30], Theorem 2). If $(3)$ or $(4)$ holds, then $(1)$ holds true because a subring of an M-Armendariz ring is M-Armendariz.

$(1)\Rightarrow (3)$. If $R\in \mathcal{A}r{m}_M$, then $R\left[x\right]\in \mathcal{A}r{m}_M$ by ([30], Theorem 2). So $R\left[(\mathbb{N},+)\right]\in \mathcal{A}r{m}_{(\mathbb{Z},+)}$ because $R\left[x\right]\cong R[(\mathbb{N},+)]$. It is well known that if R is M-Armendariz and N-Armendariz, then R is $M\times N$-Armendariz if and only if $R\left[N\right]$ is M-Armendariz, if and only if $R\left[M\right]$ is N-Armendariz (see [12]). So $R\left[(\mathbb{Z},+)\right]\in \mathcal{A}r{m}_M$. Then $R[x,x^{-1}]\in \mathcal{A}r{m}_M$ because $R[x,x^{-1}]\cong R[(\mathbb{Z},+)]$.

$(1)\Rightarrow (4)$. Let $R\in \mathcal{A}r{m}_M$. Since $M\times M$ is also a cancellative, infinite, and torsion-free Abelian monoid, we have $\mathcal{A}r{m}_M=\mathcal{A}rm=\mathcal{A}r{m}_{M\times M}$ by Theorem 1. Then $R\left[M\right]\in \mathcal{A}r{m}_M$ because $R\in \mathcal{A}r{m}_{M\times M}$. □

Proposition 7 gives the following:

Corollary 3. 

Let R be a ring and M an Abelian monoid. If R is Armendariz and M-Armendariz, then $R\left[M\right]$ is Armendariz.

Proof. 

If $M=\left\{ϵ\right\}$, then $R\left[M\right]\cong R$ is Armendariz.

If $M\ne \left\{ϵ\right\}$, then $\mathcal{A}r{m}_M=\mathcal{A}rm$ by Theorem 2. As an immediate consequence of Proposition 7, we have $R\left[M\right]\in \mathcal{A}rm$. □

Remark 2. 

Notice that the converse of Corollary 3 is not always true. On the one hand, it is true when $M=(\mathbb{N},+)$ is the additive Abelian monoid of nonnegative integers. On the other hand, it is not true when $M=(\{1,-1\},\times )$ is the multiplicative Abelian group of $\pm 1$ and $R={\mathbb{Z}}_2$ is the ring of integers modulo 2.

It was shown in ([15], Propositions 3.5 and 3.6) that if R is M-quasi-Armendariz and quasi-Armendariz where M is an Abelian monoid with $G(M)=\left\{ϵ\right\}$, then $R\left[M\right]$ is quasi-Armendariz and $R\left[x\right]$ is M-quasi-Armendariz. Now, we have the following conclusion.

Proposition 8. 

Let R be a ring and M an Abelian monoid. If R is M-quasi-Armendariz, then $R\left[x\right]$ and $R\left[M\right]$ are M-quasi-Armendariz.

Proof. 

If $M=\left\{ϵ\right\}$, then $\mathcal{Q}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings, and the result is trivially true.

If $M\ne \left\{ϵ\right\}$, then M is cancellative and torsion-free by Propositions 1 and 3. Thus, M is infinite and so $\mathcal{Q}Ar{m}_M=\mathcal{Q}Arm$ by Theorem 2. Hence $R\in \mathcal{Q}Arm$ and so $R\left[x\right]\in \mathcal{Q}Arm$ by ([3], Theorem 3.16). Therefore, we have $R\left[x\right]\in \mathcal{Q}Ar{m}_M$. Next, we show that $R\left[M\right]\in \mathcal{Q}Ar{m}_M$. Suppose that

$$(\sum _i{\Phi }_i{x}^i)(R\left[M\right])\left[x\right](\sum _j{\Psi }_j{x}^j)=0,$$

where ${\Phi }_i={\sum }_p{a}_{ip}{\xi }_p$, ${\Psi }_j={\sum }_q{b}_{jq}{\eta }_q\in R\left[M\right]$ and ${\xi }_p$, ${\eta }_q\in M$. We will show that ${\Phi }_{i}R\left[M\right]{\Psi }_j=0$ for all i and j. It is easy to see that there exists an isomorphism of rings

$$(R[M])\left[x\right]\to (R[x])\left[M\right]$$

via

$$\sum _i(\sum _p{a}_{ip}{\xi }_p)x^i\mapsto \sum _p(\sum _i{a}_{ip}{x}^i){\xi }_p.$$

Thus, we have $({\sum }_p({\sum }_i{a}_{ip}{x}^i){\xi }_p)(R\left[x\right])\left[M\right]({\sum }_q({\sum }_j{b}_{jq}{x}^j){\eta }_q)=0$. Since $R\left[x\right]$ is M-quasi-Armendariz, it follows that $({\sum }_i{a}_{ip}{x}^i)R\left[x\right]({\sum }_j{b}_{jq}{x}^j)=0$. Thus, $a_{ip}R{b}_{jq}=0$ for all i, j, p and q since $R\in \mathcal{Q}Ar{m}_M\subseteq \mathcal{Q}Arm$. Now it easy to see that ${\Phi }_{i}R\left[M\right]{\Psi }_j=0$ for all i and j. □

Proposition 8 gives the following:

Corollary 4. 

Let R be a ring and M an Abelian monoid. If R is M-quasi-Armendariz and quasi-Armendariz, then $R\left[M\right]$ is quasi-Armendariz and $R\left[x\right]$ is M-quasi-Armendariz.

Proof. 

If $M=\left\{ϵ\right\}$, then $R\left[M\right]\cong R$ is quasi-Armendariz and $\mathcal{Q}Ar{m}_M$ coincides with the class of all rings. If $M\ne \left\{ϵ\right\}$, then $\mathcal{Q}Ar{m}_M=\mathcal{Q}Arm$ by Theorem 2. As an immediate consequence of Proposition 8 we have $R\left[M\right]\in \mathcal{Q}Arm$ and $R\left[x\right]\in \mathcal{Q}Ar{m}_M$. □

It was shown in ([17], Propositions 7) that if R is a semicommutative and weak M-Armendariz where M is an Abelian and cancellative monoid such that $G(M)=\left\{ϵ\right\}$, then $R\left[M\right]$ is weak Armendariz. Now, we have the following conclusion.

Proposition 9. 

Let M be an Abelian monoid. If R is semicommutative and weak M-Armendariz, then $R\left[M\right]$ is weak M-Armendariz.

Proof. 

If $M=\left\{ϵ\right\}$, then $\mathcal{W}Ar{m}_{\left\{ϵ\right\}}$ coincides with the class of all rings, and the result is trivially true.

If $M\ne \left\{ϵ\right\}$, then M is cancellative and torsion-free by Propositions 1 and 3. Thus, M is infinite and $\mathcal{W}Ar{m}_M=\mathcal{W}Arm$ by Theorem 2. Next, we show that $R\left[M\right]\in \mathcal{W}Arm$. Suppose that

$$(\sum _i{\Phi }_i{x}^i)(\sum _j{\Psi }_j{x}^j)=0,$$

where ${\Phi }_i={\sum }_{p=1}^n{a}_{ip}{\xi }_p$, ${\Psi }_j={\sum }_{p=1}^n{b}_{jp}{\xi }_p\in R\left[M\right]$ and ${\xi }_p\in M$. By the isomorphism of rings in the proof of Proposition 8, we have

$$(\sum _{p=1}^n(\sum _i{a}_{ip}{x}^i){\xi }_p)(\sum _{p=1}^n(\sum _j{b}_{jp}{x}^j){\xi }_p)=0.$$

There are n elements $r_1,\cdots ,r_n$ in $(\mathbb{N},+)$ such that

$${\xi }_{i_1}{\xi }_{i_2}={\xi }_{j_1}{\xi }_{j_2}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{r}_{i_1}+r_{i_2}=r_{j_1}+r_{j_2},$$

for each $i_1,i_2,j_1,j_2\in \{1,\cdots ,n\}$ by Lemma 3. Let

$$\lambda =\sum _{p=1}^n(deg(\sum _i{a}_{ip}{x}^i)+deg(\sum _j{b}_{jp}{x}^j)),$$

where the degree is as polynomials in x and the degree of the zero polynomial is taken to be 0. Then

$$\sum _{p=1}^n(\sum _i{a}_{ip}{x}^i)x^{\lambda r_p},\sum _{p=1}^n(\sum _j{b}_{jp}{x}^j)x^{\lambda r_p}\in R\left[x\right],$$

and the set of coefficients of the ${{\sum }_i{a}_{ip}{x}^i}^{,}$s (resp., ${{\sum }_j{b}_{jp}{x}^j}^{,}$s) equals the set of coefficients of ${\sum }_{p=1}^n({\sum }_i{a}_{ip}{x}^i)x^{\lambda r_p}$ (resp., ${\sum }_{p=1}^n({\sum }_j{b}_{jp}{x}^j)x^{\lambda r_p})$. Since

$$(\sum _{p=1}^n(\sum _i{a}_{ip}{x}^i)x^{\lambda r_p})(\sum _{p=1}^n(\sum _j{b}_{jp}{x}^j)x^{\lambda r_p})=0$$

and $R\in \mathcal{W}Arm$, we have each $a_{ip}{b}_{jq}\in N(R)$. From ([6], Lemma 3.1), ${\Phi }_i{\Psi }_j\in N(R)\left[M\right]$. Thus, we have ${\Phi }_i{\Psi }_j\in N(R\left[M\right])$ by ([17], Lemma 3). □

Example 4. 

Let us consider the additive Abelian group $(\mathbb{Z},+)$ of integers. Obvious $G((\mathbb{Z},+))=(\mathbb{Z},+)\ne \left\{ϵ\right\}$. If R is semicommutative and weak $(\mathbb{Z},+)$-Armendariz, then $R[(\mathbb{Z},+)]$ is weak $(\mathbb{Z},+)$-Armendariz by Proposition 9.

Proposition 9 gives the following:

Corollary 5. 

Let M be an Abelian monoid. If R is semicommutative and weak M-Armendariz, then $R\left[M\right]$ is weak Armendariz.

Proof. 

If $M=\left\{ϵ\right\}$, then $R\left[M\right]\cong R$ is weak Armendariz by ([6], Corollary 3.4).

If $M\ne \left\{ϵ\right\}$, then $\mathcal{W}Ar{m}_M\subseteq \mathcal{W}Arm$ by Proposition 4. As an immediate consequence of Proposition 9 we have $R\left[M\right]\in \mathcal{W}Arm$. □

Let M be any Abelian monoid that is both torsion-free and cancellative. By Lemma 3, given a finite set of elements of M, their multiplication behaves in the same way as addition does for a finite set of nonnegative integers. However, as in Example 3, we have $2<3$ while $r_3<r_2$. This further motivates our discussion of another choice for $r_i$ in Theorem 3. In the proof of Theorem 3, it will be convenient to use the following definition.

Definition 1. 

Let m be a positive integer. Assume that two Abelian monoids $(M,{\le }_M)$ and $(N,{\le }_N)$ admit a compatible strict total order, respectively. Two n-tuples $({\xi }_1,\cdots ,{\xi }_n)\in M^n$ and $({\eta }_1,\cdots ,{\eta }_n)\in N^n$ are in the same order of degree m if for each $(i_1,\cdots ,i_n)$, $(j_1,\cdots ,j_n)\in {\mathbb{N}}^n$ with $i_1+\cdots +i_n=j_1+\cdots +j_n\le m$, all the following three conditions hold:

1. 

${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}{<}_M{\xi }_1^{j_1}\cdots {\xi }_n^{j_n}$ if and only if ${\eta }_1^{i_1}\cdots {\eta }_n^{i_n}{<}_N{\eta }_1^{j_1}\cdots {\eta }_n^{j_n}$;

2. 

${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}={\xi }_1^{j_1}\cdots {\xi }_n^{j_n}$ if and only if ${\eta }_1^{i_1}\cdots {\eta }_n^{i_n}={\eta }_1^{j_1}\cdots {\eta }_n^{j_n}$;

3. 

${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}{>}_M{\xi }_1^{j_1}\cdots {\xi }_n^{j_n}$ if and only if ${\eta }_1^{i_1}\cdots {\eta }_n^{i_n}{>}_N{\eta }_1^{j_1}\cdots {\eta }_n^{j_n}$.

Example 5. 

Let $({\mathbb{Z}}^{+},·)$ and $(\mathbb{N},+)$ be Abelian monoids with the usual ordering.

Two 3-tuples $(1,2,3)\in {({\mathbb{Z}}^{+})}^3$ and $(0,7,11)\in {\mathbb{N}}^3$ are in the same order of degree 10. However, they are not in the same order of degree 11, as

$$2^{11}<1^4·3^{7}while11\times 7=4\times 0+7\times 11.$$

Two 4-tuples $(1,2,3,4)\in {({\mathbb{Z}}^{+})}^4$ and $(0,7,11,14)\in {\mathbb{N}}^4$ are in the same order of degree 6. However, they are not in the same order of degree 7, as

$$2^1·4^5<3^{7}while1\times 7+5\times 14=7\times 11.$$

Two 5-tuples $(1,2,3,4,5)\in {({\mathbb{Z}}^{+})}^5$ and $(0,7,11,14,16)\in {\mathbb{N}}^5$ are in the same order of degree 2. However, they are not in the same order of degree 3, as

$$2·3·4<1·5·5while7+11+14=0+16+16.$$

Theorem 3. 

Assume that the Abelian monoid $(M,\le )$ admits a compatible strict total order. Let $({\xi }_1,\cdots ,{\xi }_n)\in M^n$. For each positive integer m, there are n elements $r_1,\cdots ,r_n$ in $(\mathbb{N},+)$ such that $({\xi }_1,\cdots ,{\xi }_n)\in M^n$ and $(r_1,\cdots ,r_n)\in {\mathbb{N}}^n$ are in the same order of degree m.

Proof. 

Let $n\ge 2$. It suffices to assume that ${\xi }_1<\cdots <{\xi }_n$. Choose a positive integer m. By induction hypothesis, there exists $(r_1,\cdots ,r_{n-1})\in {\mathbb{N}}^{n-1}$ such that $({\xi }_1,\cdots ,{\xi }_{n-1})$ and $(r_1,\cdots ,r_{n-1})$ are in the same order of degree $m^{\prime }$ (in Case 1 it suffices to take $m^{\prime }=2m^2$).

Case 1. There exists an equality

$${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}={\xi }_1^{j_1}\cdots {\xi }_n^{j_n}with{i}_1+\cdots +i_n=j_1+\cdots +j_n\le m$$

(1)

such that $i_n\ne j_n$.

Without loss of generality, we may assume that $i_n>j_n$. By replacing each $r_i$ with $m!·r_i$, we can assume that all the integers $r_1,\cdots ,r_{n-1}$ are divisible by $m!$. We define

$$r_n={\displaystyle \frac{1}{i_n-j_n}}·\left(j_1{r}_1+\cdots +j_{n-1}{r}_{n-1}-(i_1{r}_1+\cdots +i_{n-1}{r}_{n-1})\right).$$

(2)

Since $i_n-j_n\le m$ and each $r_i$ is divisible by $m!$, it follows that $r_n$ is an integer. Furthermore, since ${\xi }_1^{i_n-j_n}<{\xi }_n^{i_n-j_n}$, it follows from (1) that

$${\xi }_1^{i_1}\cdots {\xi }_{n-1}^{i_{n-1}}{\xi }_1^{i_n}<{\xi }_1^{j_1}\cdots {\xi }_{n-1}^{j_{n-1}}{\xi }_1^{j_n},$$

and since $(r_1,\cdots ,r_{n-1})$ and $({\xi }_1,\cdots ,{\xi }_{n-1})$ are in the same order of degree $m^{\prime }$, we obtain

$$i_1{r}_1+\cdots +i_{n-1}{r}_{n-1}+i_n{r}_1<j_1{r}_1+\cdots +j_{n-1}{r}_{n-1}+j_n{r}_1.$$

It follows from (2) that $(i_n-j_n)r_1<(i_n-j_n)r_n$ and thus $r_1<r_n$, which shows that $r_n$ is a positive integer.

Now, let us consider any expression

$${\xi }_1^{s_1}\cdots {\xi }_n^{s_n}★{\xi }_1^{t_1}\cdots {\xi }_n^{t_n}with{s}_1+\cdots +s_n=t_1+\cdots +t_n\le m$$

(3)

such that $s_n>t_n$, where $★\in \{<,=,>\}$. We show that

$$s_1{r}_1+\cdots +s_n{r}_n★t_1{r}_1+\cdots +t_n{r}_n.$$

(4)

It follows from (1) and (3) that

$${({\xi }_1^{j_1}\cdots {\xi }_{n-1}^{j_{n-1}})}^{s_n-t_n}{({\xi }_1^{s_1}\cdots {\xi }_{n-1}^{s_{n-1}})}^{i_n-j_n}★{({\xi }_1^{i_1}\cdots {\xi }_{n-1}^{i_{n-1}})}^{s_n-t_n}{({\xi }_1^{t_1}\cdots {\xi }_{n-1}^{t_{n-1}})}^{i_n-j_n}$$

and since $(r_1,\cdots ,r_{n-1})$ and $({\xi }_1,\cdots ,{\xi }_{n-1})$ are in the same order of degree $m^{\prime }$, we obtain

$$\begin{array}{cc}& (s_n-t_n)(j_1{r}_1+\cdots +j_{n-1}{r}_{n-1})+(i_n-j_n)(s_1{r}_1+\cdots +s_{n-1}{r}_{n-1})\hfill \\ \hfill ★& (s_n-t_n)(i_1{r}_1+\cdots +i_{n-1}{r}_{n-1})+(i_n-j_n)(t_1{r}_1+\cdots +t_{n-1}{r}_{n-1}).\hfill \end{array}$$

Hence

$$\begin{array}{cc}& \left((s_n-t_n)(i_1{r}_1+\cdots +i_{n-1}{r}_{n-1}+i_n{r}_n)\right.\left.+(i_n-j_n)(s_1{r}_1+\cdots +s_{n-1}{r}_{n-1})\right)\hfill \\ \hfill ★& ((s_n-t_n)(i_1{r}_1+\cdots +i_{n-1}{r}_{n-1})+(s_n-t_n)j_n{r}_n+(i_n-j_n)(t_1{r}_1+\cdots +t_{n-1}{r}_{n-1}))\hfill \end{array}$$

by (2). Then (4) holds.

Case 2: The following three conditions are established simultaneously.

• Each equation ${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}={\xi }_1^{j_1}\cdots {\xi }_n^{j_n}$ with $i_1+\cdots +i_n=j_1+\cdots +j_n\le m$ has $i_n=j_n$;
• Each inequality ${\xi }_1^{i_1^{\prime }}\cdots {\xi }_n^{i_n^{\prime }}<{\xi }_1^{j_1^{\prime }}\cdots {\xi }_n^{j_n^{\prime }}$ with $i_1^{\prime }+\cdots +i_n^{\prime }=j_1^{\prime }+\cdots +j_n^{\prime }\le m$ has $i_n^{\prime }\le j_n^{\prime }$;
• Each inequality ${\xi }_1^{i_1^{\prime \prime }}\cdots {\xi }_n^{i_n^{″}}>{\xi }_1^{j_1^{″}}\cdots {\xi }_n^{j_n^{″}}$ with $i_1^{″}+\cdots +i_n^{″}=j_1^{″}+\cdots +j_n^{″}\le m$ has $i_n^{″}\ge j_n^{″}$.

Without loss of generality, we may assume these inequalities can be reduced to

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\xi }_1^{i_{11}}\cdots {\xi }_{n-1}^{i_{1,n-1}}& <{\xi }_1^{j_{11}}\cdots {\xi }_{n-1}^{j_{1,n-1}}{\xi }_n^{p_1},\hfill \\ \hfill {\xi }_1^{i_{21}}\cdots {\xi }_{n-1}^{i_{2,n-1}}& <{\xi }_1^{j_{21}}\cdots {\xi }_{n-1}^{j_{2,n-1}}{\xi }_n^{p_2},\hfill \\ \hfill & ⋮\hfill \\ \hfill {\xi }_1^{i_{l1}}\cdots {\xi }_{n-1}^{i_{l,n-1}}& <{\xi }_1^{j_{l1}}\cdots {\xi }_{n-1}^{j_{l,n-1}}{\xi }_n^{p_l},\hfill \end{array}\right.\end{array}$$

(5)

where $0<p_1,p_2,\cdots ,p_l\le m$. Multiplying the appropriate power of the inequalities in (5) by some of ${\xi }_1,\cdots ,{\xi }_{n-1}$, we have

$${\xi }_1^{i_{l+1,1}}\cdots {\xi }_{n-1}^{i_{l+1,n-1}}<{\xi }_1^{j_{l+1,1}}\cdots {\xi }_{n-1}^{j_{l+1,n-1}}{\xi }_n^{p_{l+1}}$$

with the unified right side, where $p_{l+1}$ is the lowest common multiple of $p_1$, $\cdots ,p_l$. Let

$$\xi ={\xi }_1^{i_{l+2,1}}\cdots {\xi }_{n-1}^{i_{l+2,n-1}}$$

be the maximum amount of these ${\xi }_1^{i_{l+1,1}}\cdots {\xi }_{n-1}^{i_{l+1,n-1}}$. There is $r_n\in {\mathbb{Z}}^{+}$ sufficiently large to make the inequality

$$i_{l+2,1}{r}_1+\cdots +i_{l+2,n-1}{r}_{n-1}<j_{l+1,1}{r}_1+\cdots +j_{l+1,n-1}{r}_{n-1}+p_{l+1}{r}_n$$

true. Since $(r_1,\cdots ,r_{n-1})$ and $({\xi }_1,\cdots ,{\xi }_{n-1})$ are in the same order of degree $m^{\prime }$, we have

$$i_{l+1,1}{r}_1+\cdots +i_{l+1,n-1}{r}_{n-1}<j_{l+1,1}{r}_1+\cdots +j_{l+1,n-1}{r}_{n-1}+p_{l+1}{r}_n$$

by the maximality of $\xi$. Then, we have the following inequalities

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill i_{11}{r}_1+\cdots +i_{1,n-1}{r}_{n-1}& <j_{11}{r}_1+\cdots +j_{1,n-1}{r}_{n-1}+p_1{r}_n,\hfill \\ \hfill i_{21}{r}_1+\cdots +i_{2,n-1}{r}_{n-1}& <j_{21}{r}_1+\cdots +j_{2,n-1}{r}_{n-1}+p_2{r}_n,\hfill \\ \hfill & ⋮\hfill \\ \hfill i_{l1}{r}_1+\cdots +i_{l,n-1}{r}_{n-1}& <j_{l1}{r}_1+\cdots +j_{l,n-1}{r}_{n-1}+p_l{r}_n.\hfill \end{array}\right.\end{array}$$

(6)

Case 3: The following three conditions are established simultaneously.

• Each equation ${\xi }_1^{i_1}\cdots {\xi }_n^{i_n}={\xi }_1^{j_1}\cdots {\xi }_n^{j_n}$ with $i_1+\cdots +i_n=j_1+\cdots +j_n\le m$ has $i_n=j_n$;
• There exist inequalities

  $${\xi }_1^{i_{11}}\cdots {\xi }_n^{i_{1n}}<{\xi }_1^{j_{11}}\cdots {\xi }_n^{j_{1n}}$$

  such that $i_{11}+\cdots +i_{1n}=j_{11}+\cdots +j_{1n}\le m$ and $i_{1n}<j_{1n};$
• There exist inequalities

  $${\xi }_1^{j_{21}}\cdots {\xi }_n^{j_{2n}}<{\xi }_1^{k_{21}}\cdots {\xi }_n^{k_{2n}}$$

  such that $j_{21}+\cdots +j_{2n}=k_{21}+\cdots +k_{2n}\le m$ and $j_{2n}>k_{2n}$.

As in Case 2, we may assume that those inequalities can be rewritten as

$${\xi }_1^{i_{31}}\cdots {\xi }_{n-1}^{i_{3,n-1}}<{\xi }_1^{j_{31}}\cdots {\xi }_{n-1}^{j_{3,n-1}}{\xi }_n^p$$

(7)

and

$${\xi }_1^{j_{31}}\cdots {\xi }_{n-1}^{j_{3,n-1}}{\xi }_n^p<{\xi }_1^{k_{31}}\cdots {\xi }_{n-1}^{k_{3,n-1}}$$

(8)

with the unified item ${\xi }_1^{j_{31}}\cdots {\xi }_{n-1}^{j_{3,n-1}}{\xi }_n^p$, where $0<p\le m$. Let $\eta ={\xi }_1^{i_{41}}\cdots {\xi }_{n-1}^{i_{4,n-1}}$ be the maximum value of the left side of (7) and $\zeta ={\xi }_1^{k_{41}}\cdots {\xi }_{n-1}^{k_{4,n-1}}$ the minimum value of the right side of (8). By the density of rational numbers, there is a rational number $r_n$ satisfying the following inequality

$$i_{41}{r}_1+\cdots +i_{4,n-1}{r}_{n-1}<j_{31}{r}_1+\cdots +j_{3,n-1}{r}_{n-1}+p{r}_n<k_{41}{r}_1+\cdots +k_{4,n-1}{r}_{n-1}.$$

Since $({\xi }_1,\cdots ,{\xi }_{n-1})$ and $(r_1,\cdots ,r_{n-1})$ are in the same order of degree $m^{\prime }$, we have

$$i_{31}{r}_1+\cdots +i_{3,n-1}{r}_{n-1}<j_{31}{r}_1+\cdots +j_{3,n-1}{r}_{n-1}+p{r}_n$$

(9)

and

$$j_{31}{r}_1+\cdots +j_{3,n-1}{r}_{n-1}+p{r}_n<k_{31}{r}_1+\cdots +k_{3,n-1}{r}_{n-1},$$

(10)

by the maximality of $\eta$ and the minimality of $\zeta$, respectively. Choose a positive integer $\lambda$ such that $\lambda r_n$ is an integer. By replacing each $r_i$ with $\lambda r_i$ for all $i\in \{1,\cdots ,n\}$, we still have (9) and (10). □

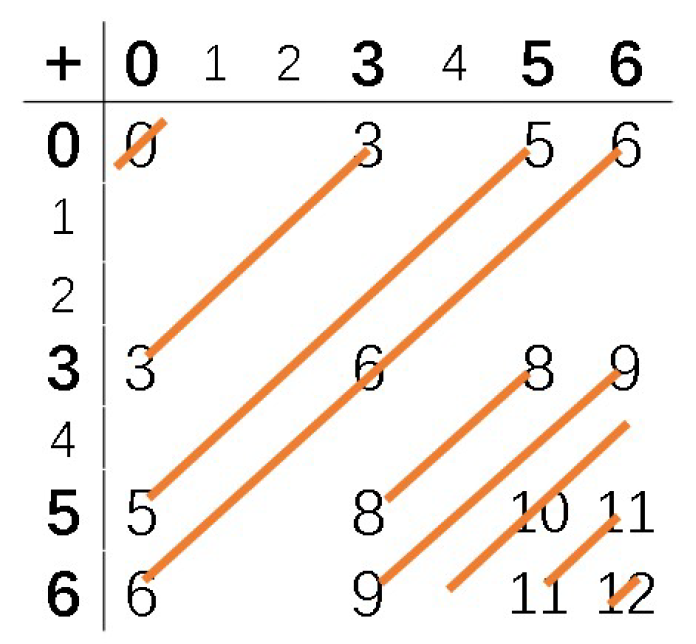
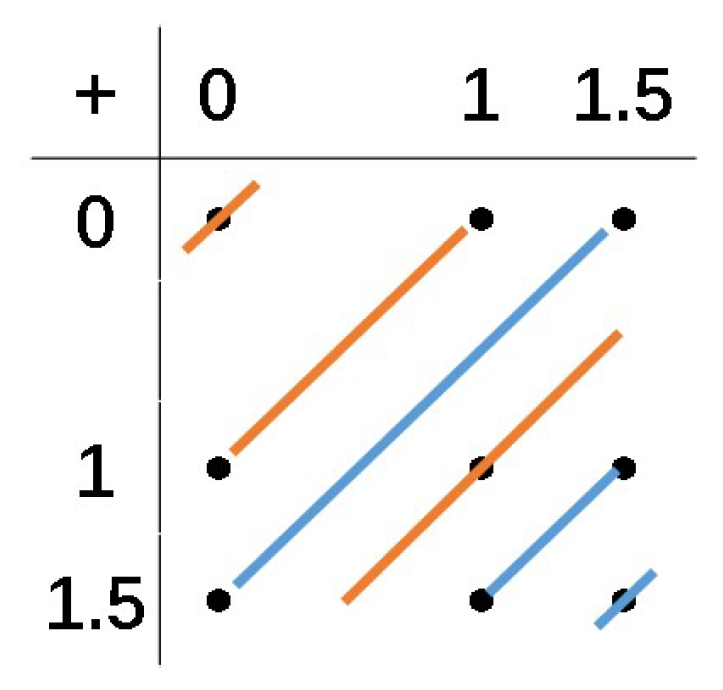
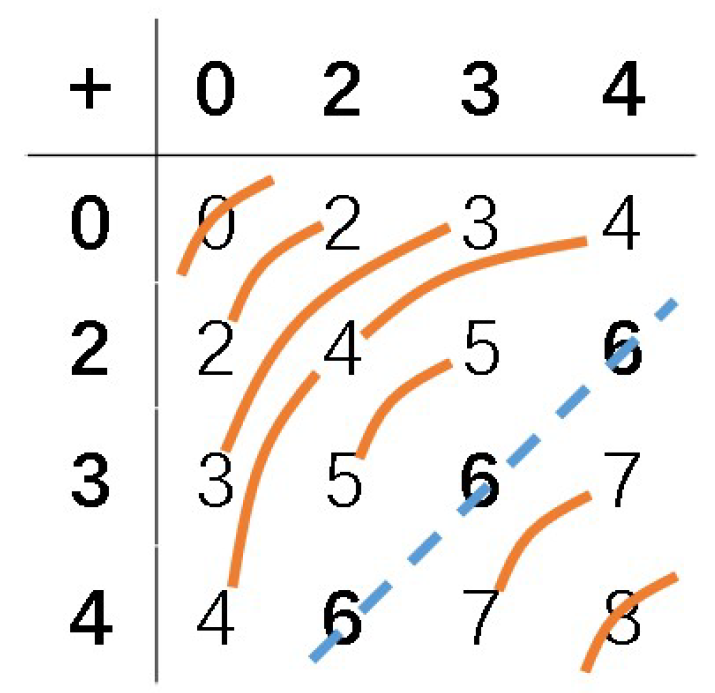
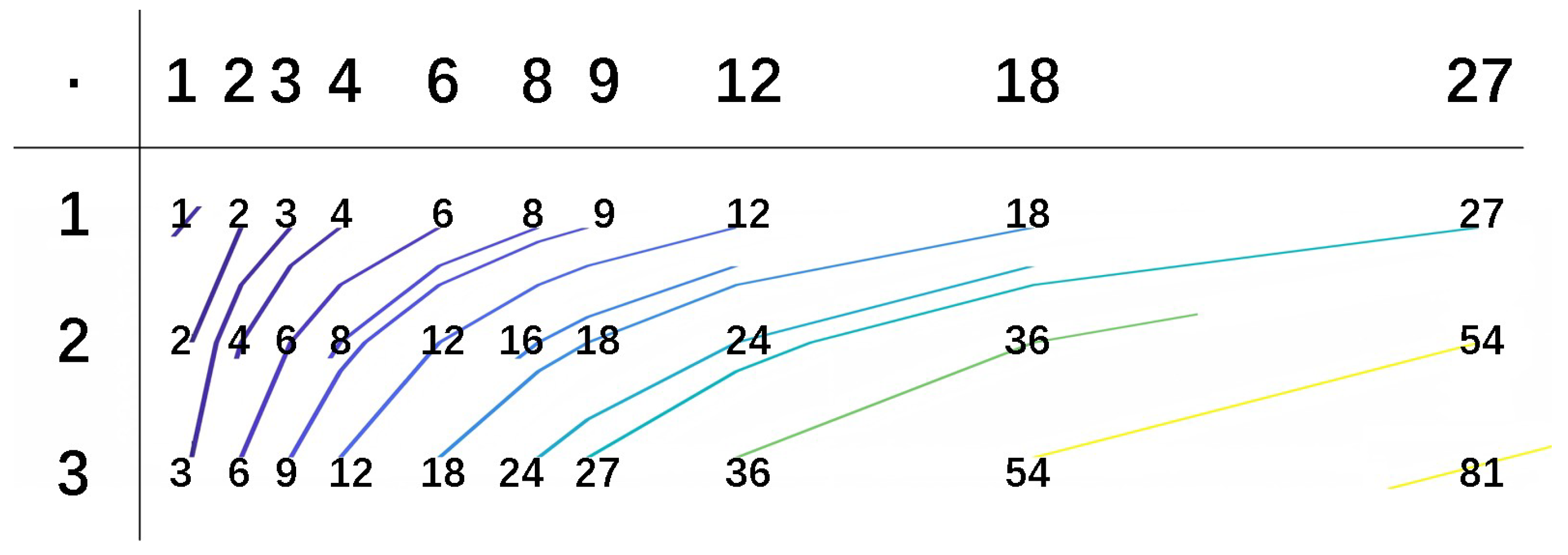
The value of $r_i$ can be calculated using various methods (detailed discussion can be found in Appendix A).

4. Conclusions

In this paper, we explore the necessary and sufficient conditions under which the class of all Armendariz-like rings, relative to an Abelian monoid M, coincides with the class of all Armendariz-like rings. We have shown that M-Armendariz-like rings are, indeed, Armendariz-like rings for any nontrivial Abelian monoid M. We have established a connection between a cancellative, torsion-free Abelian monoid M and the monoid of nonnegative integers under addition. We provide a partial affirmative resolution to an open question posed by Liu in 2005. All monoids considered in this paper have been assumed to be commutative but some of the results in this paper are meaningful for noncommutative monoids. For instance, we have that Propositions 1 and 2 hold for noncommutative monoid when $♯\ne \mathcal{Q}Arm$. In addition to these classes of Armendariz-like rings relative to a monoid mentioned above, many papers further propose the study of rings with an analog of the Armendariz condition defined concerning power series rings where the Lemma 3 seems to not be generalizable to infinitely many elements.