Robust Estimation of L₁-Modal Regression Under Functional Single-Index Models for Practical Applications

Abstract

We propose a robust procedure to estimate the conditional mode of a univariate outcome O given a Hilbertian explanatory variable I, under the assumption that $(O,I)$ follow a single-index structure. The estimator is constructed using the M-estimator for the conditional density, and we establish its complete convergence. We discuss the estimator’s advantages in addressing challenges within functional data analysis, particularly robustness and reliability. We then evaluate both the performance and practical implementation of our method via Monte Carlo simulations. Furthermore, we carry out an empirical study to showcase the improved reliability and robustness of this estimator compared to conventional approaches. In particular, our methodology is applied to predict fuel quality based on spectrometry data, illustrating its strong potential in real-world scenarios.

1. Introduction

In typical regression analyses, one aims to identify a possible relationship between the variables $\left\{(X_i,Y_i)\right\}$ by finding a function that minimizes the mean squared error criterion. It is well established that this minimizer corresponds to the regression function

$$r(x,\psi )=\mathbb{E}\left(\Psi \left(O\right)\mid I=x\right),$$

where $\Psi :\mathbb{R}\to \mathbb{R}$ is a bounded measurable function. A substantial body of work has been devoted to the nonparametric estimation of this function, utilizing an array of smoothing techniques, such as kernel methods, spline smoothing, local polynomials, and orthogonal expansions, to capture the potentially complex structure of the relationship between O and I. For comprehensive discussions on theoretical developments and practical applications in both independent and dependent settings, readers are referred to [1,2,3,4,5,6,7,8].

Under the classic setting where $\Psi \left(O\right)=O$, the conditional expectation $\mathbb{E}(O\mid I=x)$ is commonly estimated via least-squares regression (or robust/weighted variants) to summarize how the response O depends on the covariate I. However, such a mean-based framework can be unsuitable for data characterized by strong skewness, multiple modes, or the presence of outliers. For instance, in domains such as economics (e.g., wages, prices, and expenditures) or nutrition (e.g., energy intake), the arithmetic mean may be a poor representation of the central tendency. As a concrete illustration, consider the following conditional density function:

$$\psi (y\mid x)={\displaystyle \frac{1}{2\sqrt{2\pi }}}\left\{exp\left(-\frac{1}{2}{(y-x)}^2\right)+exp\left(-\frac{1}{2}{(y+x)}^2\right)\right\}.$$

Here, the conditional mean is

$$m\left(x\right)=\mathbb{E}(O\mid I=x)=\frac{1}{2}(x-x)=0,$$

implying that the usual regression function is constant and thus unhelpful for prediction purposes in this scenario.

Mode regression (MR) emerges as a compelling alternative when the conditional density exhibits heavy tails, significant skewness, or multiple local modes. Unlike mean regression, which can be heavily influenced by outliers or fail to capture multimodal structures, MR focuses on estimating the most frequent (modal) values of Y given X. The advantages of MR over classical mean-based approaches in such circumstances were first observed by [9] and further emphasized by [10]. For detailed reviews and methodological extensions, see [11,12,13].

Building on these ideas, the present work focuses on mode estimation within a functional single index (FSI) framework, offering new insights and methodologies for robustly capturing the salient features of complex data distributions.

The FSI framework is widely adopted because it enhances nonparametric estimation through the projection of the functional input onto a principal direction. This approach combines the interpretability of a linear model with the flexibility of a nonparametric procedure, achieved by applying a suitable link function. Although there is a substantial body of research on single-index models in finite-dimensional settings (see [14,15] for early investigations and [16,17,18] for more recent advances), the extension to functional data was first introduced by [19,20], who proposed a kernel-based estimator for conditional expectation under an FSI assumption. Quantile regression under an FSI model was discussed in [21], where both the unknown link function and the slope were estimated using a B-spline method. A compact single functional index model with a specific coefficient function was examined in [22], whereas [18] addressed nonparametric models tied to the conditional distribution in the FSI setting. Multi-index scenarios under functional inputs are considered in [23], with established asymptotic properties for kernel-smoothing methods when estimating unknown parameters. Additional works relevant to nonparametric conditional density estimation with Hilbertian regressors in an FSI framework can be found in [24,25]. In [26], the estimation of a functional single-index regression model is addressed under the setting where responses may be randomly missing, and the data follow a strongly mixing time series structure. Under general conditions, the proposed estimator is shown to achieve a uniform, almost complete convergence rate, and its asymptotic normality is also established. In [27], a robust nonparametric estimation procedure is introduced for regression functions using a kernel-based approach. The covariates are i.i.d. functional data linked to a single-index model, and the methodology accommodates censored observations. In [28], a robust estimator grounded in Huber’s loss function is proposed for a functional single-index model with a parameter of fixed dimension. This work further extends to high-dimensional settings by developing a robust $L_1$ estimator of the unknown parameter, achieved through an adaptive lasso penalty. An extensive overview of functional semiparametric modeling is provided in [29,30,31,32].

A second focus of this contribution concerns conditional mode functions, which were introduced in functional statistics by [33]. Since that foundational work, a considerable number of studies have analyzed the interplay between functional predictors and a scalar response. For instance, ref. [34] explored functional M-regression, ref. [35] investigated functional linear local regression, and [36] dealt with relative error functional regression. Within this general framework, the nonparametric conditional mode has attracted growing attention. Seminal work by [37] established the asymptotic distribution of a kernel-based modal regression estimator under independent and identically distributed observations, later generalized to dependent samples in [38]. The complete consistency of the kernel-based modal regression estimator for spatio-functional data was studied by [39], who also demonstrated $L_p$ consistency in [40]. A distribution-free version of the modal regression estimator for ergodic functional time series, accommodating missing-at-random (MAR) data in the response, was introduced by [41], who proved its almost sure consistency. Additionally, ref. [42] analyzed a local linear estimator for modal regression and derived its asymptotic distribution. For recent advances in FSI modeling, see [43,44,45,46], among others.

1.1. Contribution

In contrast to previous research, this study offers a novel strategy that merges modal and quantile regression. Instead of relying on the usual definition of the conditional mode as the point that maximizes the conditional density, we redefine the conditional mode by minimizing the derivative of the conditional quantile. This perspective establishes a direct link between modal regression and quantile regression, providing a robust alternative for estimating the mode function. Our estimator is developed under the functional single-index (FSI) framework, which integrates robust estimation with single-index modeling to improve both robustness and efficiency. It is well recognized that using the FSI approach enhances convergence by projecting the functional predictor onto its principal direction. A major theoretical contribution of this work is the derivation of complete consistency for the proposed estimator, with explicit convergence rates provided. In addition, we examine how selecting the functional index influences efficiency. Finally, an empirical analysis illustrates the method’s straightforward implementation and compares its performance against standard estimators from earlier research.

1.2. Organization of the Paper

The paper is structured as follows. In the next section, we present the underlying model together with the robust modal regression estimator. In Section 3, we demonstrate that this estimator achieves complete consistency, subject to certain mild conditions that relate to the functional space of the model and the nature of the data. Section 4 explores the performance of the estimator on both synthetic and real datasets. In particular, for the real-data application, we illustrate how to determine the chemical composition of fuel by examining the spectrometry curves of the processed energy product. Some concluding observations are provided in Section 5. Finally, in order to maintain a clear narrative and foster a deeper comprehension of our proofs, all the detailed mathematical developments are postponed to Section 6.

2. Robust Estimator of Modal Regression in the FSI Structure

In this section, we introduce the FSI-mode estimator and provide a detailed examination of its conceptual alignment with the conditional quantile. Consider a pair of input–output random variables $(I,O)$ taking values in $\mathcal{F}\times \mathrm{I}\mathrm{R}$, where $\mathcal{F}$ is an inner product space equipped with the inner product $⟨·,·⟩$. Let ${(I_i,O_i)}_{1\le i\le n}$ be n independent and identically distributed samples from the same distribution as $(I,O)$. In the framework of an FSI model, the dependence of O on I is described via a functional index $\nu \in \mathcal{F}$, satisfying the following

$$\mathrm{I}\mathrm{E}[O\mid I]=\mathrm{I}\mathrm{E}[O\mid ⟨\nu ,I⟩].$$

(1)

Typically, to guarantee the identifiability of this FSI model, one assumes that the regression operator $r\left(u\right)=\mathrm{I}\mathrm{E}[O\mid I=u]$ is differentiable and that $\nu$ is chosen so that $⟨\nu ,v_1⟩=1$, where $v_1$ is the first vector of an orthonormal basis of $\mathcal{F}$; for instance, see [19]. As in the finite-dimensional case, the FSI approach is highly effective in mitigating the impact of the infinite-dimensional setting when constructing estimators.

Throughout what follows, we fix a point $u\in \mathcal{F}$ and consider a neighborhood $N_u$ of u. We assume that the conditional distribution function of O given $⟨\nu ,I⟩=⟨\nu ,u⟩$, denoted by $C{D}_{\nu }(·\mid u)$, is strictly increasing and that it has a continuous density $PD{F}_{\nu }(t\mid u)$ with respect to the Lebesgue measure on $\mathrm{I}\mathrm{R}$. We define the SFI mode as the maximizer of this conditional density over a given compact set S:

$$Mo{d}_{\nu }\left(u\right)=arg\underset{t\in S}{max}PD{F}_{\nu }\left(t\mid ⟨\nu ,u⟩\right).$$

In order to connect the mode function $Mod$ to the conditional quantile $CQ$, which is known to be more robust, we use the relationship that, for any $q\in C{D}_{\nu }^{-1}(S\mid u)=[a_u,b_u]\subset (0,1)$,

$$C{Q}^{\prime }(q\mid u)={\displaystyle \frac{\partial CQ(q\mid u)}{\partial q}}={\displaystyle \frac{1}{PD{F}_{\nu }\left(CQ(q\mid u)\mid u\right)}},$$

where $CQ(q\mid u)$ is the conditional quantile of order q given $⟨\nu ,I⟩=⟨\nu ,u⟩$. It follows that the function $Mo{d}_{\nu }\left(u\right)$ satisfies the following:

$$Mo{d}_{\nu }\left(u\right)=CQ\left(q_{\nu }\mid u\right),$$

(2)

with

$$q_{\nu }=arg\underset{q\in [a_u,b_u]}{min}C{Q}^{\prime }(q\mid u).$$

Hence, a robust estimator of the FSI mode is given by

$$\widehat{{Mod}_{\nu }}\left(u\right)=\widehat{CQ}\left(\widehat{q_{\nu }}\mid u\right),$$

(3)

where

$$\widehat{q_{\nu }}=arg\underset{q\in [a_u,b_u]}{min}\widehat{C{Q}^{\prime }}(q\mid u).$$

Here, $\widehat{CQ}$ and $\widehat{C{Q}^{\prime }}$, respectively, denote estimators for the conditional quantile and its derivative. First, for $q\in (0,1)$, the derivative $C{Q}^{\prime }(q\mid u)$ is estimated by

$$\widehat{C{Q}^{\prime }}(q\mid u)={\displaystyle \frac{\widehat{CQ}(q+b_n\mid u)-\widehat{CQ}(q-b_n\mid u)}{2b_n}},$$

where $b_n$ is a sequence of positive real numbers. Second, the qth conditional quantile $CQ(q\mid u)$ is defined as the solution in t of the following optimization problem:

$$\underset{t\in \mathrm{I}\mathrm{R}}{min}\mathrm{I}\mathrm{E}\left[L_q(O-t)\mid ⟨\nu ,I⟩=⟨\nu ,u⟩\right],$$

(4)

with the loss function $L_q\left(s\right)=(2q-1)s+\left|s\right|$. Consequently, its robust estimator is obtained by solving

$$\widehat{CQ}(q\mid u)=arg\underset{t\in \mathrm{I}\mathrm{R}}{min}\widehat{\Phi }\left(t,q\mid u\right),$$

(5)

where

$$\widehat{\Phi }\left(t,q\mid u\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\mathbf{H}\left(c_n^{-1}{d}_{\nu }(u,I_i)\right)L_q\left(O_i-t\right)}}{{\displaystyle \sum _{i=1}^n\mathbf{H}\left(c_n^{-1}{d}_{\nu }(u,I_i)\right)}}},d_{\nu }(x,y)=\left|⟨\nu ,x-y⟩\right|,$$

$\mathbf{H}$ denotes a kernel function, and $c_n$ is a sequence of positive real numbers tending to zero as $n\to \infty$.

Our main objective is to derive the asymptotic properties of the estimator $\widehat{Mo{d}_{\nu }}\left(u\right)$ relative to the true mode $Mo{d}_{\nu }\left(u\right)$. Under standard assumptions, which will be detailed in the next section, we establish convergence properties and asymptotic distributions for $\widehat{Mo{d}_{\nu }}\left(u\right)$.

3. Main Results

We begin by introducing C and $C^{\prime }$ as generic positive constants. Additionally, we define $B(u,r)=\{u^{\prime }\in \mathcal{F}:d_{\nu }(u^{\prime },u)<r\}$. The following are essential conditions necessary for establishing the almost complete convergence (a.co.). Consider a sequence of real-valued random variables $\left(z_n\right)$ for $n\in \mathbb{N}$. The sequence $\left(z_n\right)$ is said to converge almost completely (a.co.) to zero if, for any $ϵ>0$, the series

$$\sum _{n=1}^{\infty }\mathbb{P}\left(\right|z_n|>ϵ)$$

is finite. Moreover, the rate of this convergence is said to be of order $u_n$ (with $u_n\to 0$), denoted by $z_n=O_{a.co.}\left(u_n\right)$, if there exists $ϵ>0$ such that

$$\sum _{n=1}^{\infty }\mathbb{P}\left(\right|z_n|>ϵu_n)<\infty .$$

By the Borel–Cantelli lemma, this implies ${\displaystyle \frac{|z_n|}{u_n}}\to 0$ almost surely, thus indicating that almost complete convergence entails both almost sure convergence and convergence in probability of the estimator $\widehat{{\mathrm{Mod}}_{\nu }}\left(u\right)$ for ${\mathrm{Mod}}_{\nu }\left(u\right)$.

(CO1)

$\mathbb{P}(u\in B(u,r))={\zeta }_u\left(r\right)>0$, where ${\zeta }_u\left(r\right)\to 0$ as $r\to 0$.

(CO2)

The function $CQ(·\mid u)$ belongs to the class $C^3\left([a_u,b_u]\right)$, and $C{D}_{\nu }(·\mid u)$ satisfies the following Lipschitz condition:

$$\mathrm{For}\mathrm{all}(u_1,u_2)\in N_u,|C{D}_{\nu }(t\mid u_1)-C{D}_{\nu }(t\mid u_2)|\le C{d}_{\nu }^b(u_1,u_2)\mathrm{for}\mathrm{some}b>0,$$

where $N_u$ represents a neighborhood of u.

(CO3)

$\mathbf{H}$ is a function supported on $(0,1)$, and there exist constants $C^{\prime }$ and C such that $0<C^{\prime }<\mathbf{H}\left(t\right)<C<\infty$.

(CO4)

The smoothing parameters $c_n$ and $b_n$ satisfy ${lim}_{n\to \infty }{\displaystyle \frac{logn}{n{b}_n{\zeta }_u\left(c_n\right)}}=0$.

These conditions, (CO1) through (CO4), are standard in the context of functional statistics under a distribution-free framework. Specifically, condition (CO1) plays a critical role in such data analyses, as the function ${\zeta }_u(·)$ can often be explicitly determined for various continuous processes [33].

Condition (CO2) is a regularity assumption designed to facilitate the exploration of the functional space associated with the model. This assumption significantly affects the bias term in the convergence rate of $\widehat{{\mathrm{Mod}}_{\nu }}\left(u\right)$. Furthermore, conditions (CO3) and (CO4) pertain to the kernel function $\mathbf{H}$ and the bandwidth parameters $c_n$ and $b_n$. These technical requirements simplify the proof of the estimator $\widehat{{\mathrm{Mod}}_{\nu }}\left(u\right)$’s consistency.

It should be noted that these conditions are less restrictive than those used in earlier studies, such as those mentioned in [33]. Unlike traditional approaches that rely on two-kernel functions, our methodology estimates only a single kernel, which introduces significant simplifications.

The main asymptotic results derived from this study are summarized in the theorem below.

Theorem 1. 

Under assumptions (CO1)–(CO4) and if ${\displaystyle \underset{q\in (0,1)}{inf}\frac{{\partial }^{3}CQ(q\mid u)}{\partial q}>0}$ we have the following:

$$\widehat{Mo{d}_{\nu }}\left(u\right)-Mo{d}_{\nu }\left(u\right)=O\left(c_n^{b/2}\right)+O\left(b_n^{1/2}\right)+O\left({\left({\displaystyle \frac{logn}{n{b}_n{\zeta }_u\left(c_n\right)}}\right)}^{{\displaystyle \frac{1}{4}}}\right)a.co.$$

4. Computational Study

4.1. Simulation Results

In this section, we present an empirical investigation to evaluate the practical usability of the constructed estimators. Specifically, our objective is to demonstrate the feasibility of employing various data-driven selection strategies to determine the functional index and smoothing parameters $c_n$ and $b_n$. A key challenge in this analysis lies in constructing functional regressors in practice. To address this, we simulate data using two distinct types of curves: (i) smooth curves and (ii) rough curves. The generation of these curves is defined as follows:

$$\left\{\begin{array}{cc}{I}_i\left(t\right)=B_i{cos}^2(a_i+\pi t)+(1-B_i)cos(a_i+\pi t)+a_{i}t,\hfill & \mathrm{Smooth}\mathrm{curves},\\ I_i\left(t\right)=c_{i}t+{\eta }_t^i,\hfill & \mathrm{Rough}\mathrm{curves},\end{array}\right.$$

where $a_i\sim N(0,0.8)$, $B_i\sim \mathrm{Bernoulli}\left(0.8\right)$, $c_i\sim \mathrm{Uniform}(0,1)$, and ${\eta }_t^i\sim N(t,0.7)$. The curves $I_i\left(t\right)$ are discretized over a grid of 110 equidistant points in the interval $[-2,2]$. Examples of the resulting curves are visualized in Figure 1.

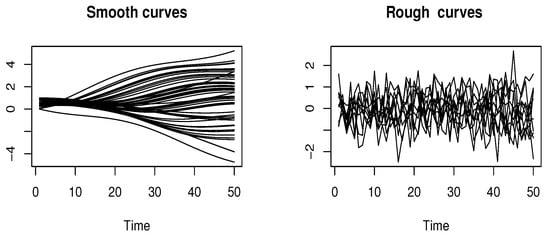
Figure 1. Functional input variables: smooth curves (left) and rough curves (right).

To simulate the output variables O, we employ two semiparametric models:

$$O_i=r\left(⟨\nu ,I_i⟩\right)+{ϵ}_i,i=1,\dots ,n=120,$$

(6)

where ${ϵ}_i$ are independent realizations from a normal distribution $\mathcal{N}(0,1)$. Here, the conditional mode $Mod\left(\right)$ of the model is linked to the distribution of the noise ${ϵ}_i$. For the purposes of this study, we generate O using the link function $r\left(x\right)=3log(1+x^2)$, and $\nu$ represents the first eigenfunction corresponding to the largest eigenvalue of the covariance operator associated with the process ${\left(I_i\right)}_i$. In practical scenarios, the functional index $\nu$ is typically unknown, making its accurate estimation crucial for FSI structures. We explore two well-known approaches for estimating $\nu$, both based on cross-validation principles: The functional index is selected by minimizing the cross-validation error:

$$CV\left(\nu \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(O_i-\widehat{Mo{d}_{\nu }}\left(I_i\right))}^2.$$

The optimal index ${\nu }_{opt}$ is chosen as follows:

$${\nu }_{opt}=arg\underset{\nu \in {\mathcal{C}}_n}{min}CV\left(\nu \right),$$

(7)

where ${\mathcal{C}}_n$ denotes the subset of candidate indices defined by the following:

$${\mathcal{C}}_n=\left\{\nu \in H:\nu =\sum _{j=1}^k{l}_j{e}_j,\parallel \nu \parallel =1,\exists j\mathrm{such}\mathrm{that}⟨\nu ,e_j⟩>0\right\}.$$

Here, ${\left(e_j\right)}_{j=1,\dots ,k}$ are basis functions obtained via Karhunen–Loève decomposition, and ${\left(l_j\right)}_j$ are calibration constants, typically chosen from $\{-1,0,1\}$. The second approach maximizes the pseudo-log-likelihood of the conditional density:

$${\nu }_{opt}^{\prime }=arg\underset{\nu \in {\mathcal{C}}_n}{max}\widehat{L}\left(\nu \right),$$

(8)

where

$$\widehat{L}\left(\nu \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}log{\widetilde{PDF}}_{\nu }(O_i\mid ⟨\nu ,I_i⟩),$$

and ${\widetilde{PDF}}_{\nu }$ represents the double-kernel estimator of the conditional density:

$${\widetilde{PDF}}_{\nu }(t\mid ⟨\nu ,u⟩)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\mathbf{H}\left(c_n^{-1}{d}_{\nu }(u,I_i)\right)\mathbf{H}\left(c_n^{-1}(t-O_i)\right)}}{{\displaystyle c_n\sum _{i=1}^n\mathbf{H}\left(c_n^{-1}{d}_{\nu }(u,I_i)\right)}}}.$$

The smoothing parameter $c_n$ is also selected using the same optimization rules over the subsets $({\mathcal{C}}_n,{\mathcal{H}}_n)$, where ${\mathcal{H}}_n$ represents a sequence of bandwidths indexed by k (e.g., $k\in \{5,10,15,\dots ,50\}$). The kernel $\mathbf{H}$ used in this study is the quadratic kernel defined on $(0,1)$, which aligns with the assumptions of the FSI model. To assess the performance, we compare the estimated mode ${\left(\widehat{Mo{d}_{\nu }}\left(I_i\right)\right)}_i$ with the true mode ${\left(Mod\left(I_i\right)\right)}_i$ by computing the mean squared error (MSE):

$$MSE={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(Mo{d}_{\nu }\left(I_i\right)-\widehat{Mo{d}_{{\nu }_{opt}}}\left(I_i\right))}^2.$$

Additionally, we present plots comparing the estimated and true modes for both smooth and rough cases.

In addition, we report the $MSE$ of different situations in the following table.

The results presented in Figure 2 and Figure 3 and Table 1 illustrate that the selection of both the functional index and the smoothing parameter plays a crucial role in determining the accuracy of the estimation. It is evident that the criterion defined in (7) performs exceptionally well in both the rough and smooth cases. Conversely, the rule described in (8) appears to be particularly well-suited for scenarios involving smoother data. Overall, the FSI-estimator proves to be computationally efficient, with multiple strategies available for parameter selection in its construction. Each of these selection methods delivers reliable and computationally efficient outcomes.

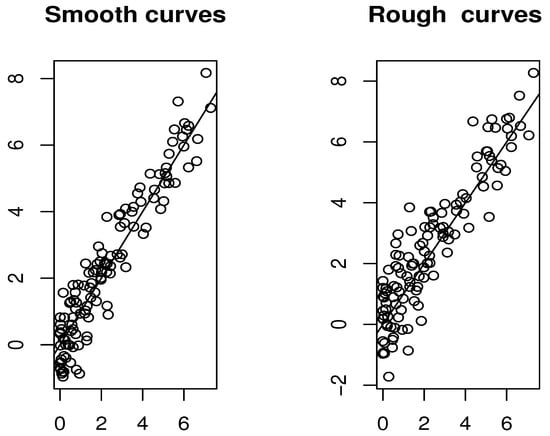
Figure 2. Comparison of the prediction results using the cross-validation (7) rule.

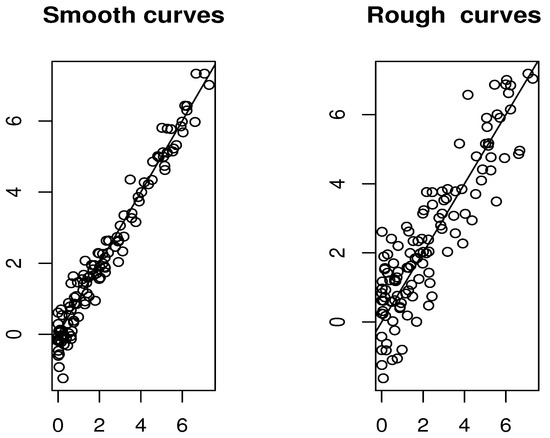
Figure 3. Comparison of the prediction results using the cross-validation (8) rule.

Table 1. MSE of the estimators.

Selector	Curves	MSE
Rule (7)	Smooth curves	0.42
	Rough curves	0.56
Rule (8)	Smooth curves	0.29
	Rough curves	0.87

4.2. Real Data Application

In this section, we demonstrate how our proposed model can be utilized for prediction tasks. As an illustrative example, we investigate the chemical composition of yogurt, with particular emphasis on forecasting its riboflavin content. Riboflavin plays a pivotal role in various metabolic processes, including the breakdown of fatty acids and amino acids, and is crucial for maintaining the integrity of skin, eyesight, and mucous membranes. Consequently, riboflavin levels are often used as an indicator of yogurt quality.

Although a similar type of analysis has been conducted previously (see [47]), our contribution introduces a functional single-index (FSI) approach that combines the near-infrared (NIR) spectral curves with a robust estimation procedure. The aim is to enhance predictive performance compared to traditional methods. The NIR data used in this study can be found at http://www.models.life.ku.dk/Yogurt (accessed on 20 September 2024). These spectral measurements were obtained using a BioView spectro-fluorometer, yielding absorbance profiles at 120 wave points between 270–550 nm and at wavelengths ranging from 310–590 nm. The dataset contains 115 spectral curves $I_i\left(t\right)$, as illustrated in Figure 4. Additional details regarding this dataset can be found in [48].

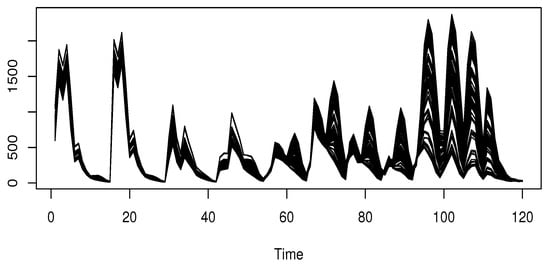
Figure 4. Spectral curves of the yogurt dataset.

For the predictive comparison, we focus on three modal regression estimators: $\widehat{Mo{d}_{{\nu }_{opt}}}$ (FSI-robust), $\widetilde{Mo{d}_{{\nu }_{opt}}}$ (FSI-standard), and $\overline{Mod}$ (nonparametric-standard). They are defined by

$$\widetilde{Mo{d}_{{\nu }_{opt}}}\left(u\right)=arg\underset{t}{max}{\widetilde{PDF}}_{{\nu }_{opt}}(t\mid ⟨\nu ,u⟩),\overline{Mod}\left(u\right)=arg\underset{t}{max}\overline{PDF}(t\mid ⟨\nu ,u⟩),$$

where

$$\overline{PDF}(t\mid u)={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\mathbf{H}\left(c_n^{-1}(u-I_i)\right)\mathbf{H}\left(c_n^{-1}(t-O_i)\right)}}{{\displaystyle c_n\sum _{i=1}^n\mathbf{H}\left(c_n^{-1}(u-I_i)\right)}}}.$$

All three estimators employ consistent parameter selection criteria, including the same kernel function and cross-validation strategy for choosing smoothing parameters. To evaluate predictive performance, the 115 available observations were randomly split into training (80 observations) and testing (35 observations) sets. The quality of each estimator was measured using the mean squared error (MSE):

$$\begin{array}{c}\hfill MSE\left(\nu \right)={\displaystyle \frac{1}{35}}\sum _{k=1}^{35}{(O_k-\dot{Mod}\left(I_k\right))}^2,\end{array}$$

(9)

where $(I_k,O_k)$ denotes the test set, and $\dot{Mod}$ stands for one of the three estimators.

This splitting procedure was repeated 70 times to assess the stability and robustness of the predictions. Figure 5 provides a box plot of the MSE values, according to (9), for the three estimators across all runs.

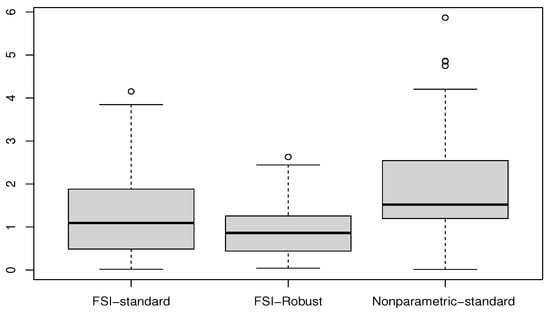
Figure 5. Box plots of MSE values for the three predictors.

Overall, all estimators demonstrate strong performance; however, FSI-based methods exhibit a distinct advantage. This superiority is particularly evident in the interquartile range (IQR) presented in Figure 5, which highlights the greater consistency of $\widehat{Mo{d}_{{\nu }_{opt}}}$. Specifically, the IQR for $\widehat{Mo{d}_{{\nu }_{opt}}}$ is approximately $0.5$, which is notably smaller than those of $\widetilde{Mo{d}_{{\nu }_{opt}}}$ and $\overline{Mod}$, respectively. These findings align with theoretical expectations, as the FSI framework, when integrated with a robust quantile-based approach, effectively mitigates the challenges posed by the high-dimensional nature of the functional regressor.

5. Conclusions and Prospects

In this work, we propose a robust methodology for estimating modal regression by exploiting the quantile function. We construct the estimator and establish its asymptotic properties through complete consistency. The functional structure is captured via a single-index smoothing algorithm, which is particularly effective for enhancing the precision of the estimator. Meanwhile, incorporating the quantile function bolsters the model’s robustness. Our asymptotic findings hold under general assumptions, thereby accommodating a broad class of functional data and/or continuous-time processes. Empirical evidence underscores both the simplicity of implementing the proposed estimator and its advantageous properties in terms of robustness and accuracy, especially when juxtaposed with alternative methods. Furthermore, the work presented here paves the way for various future research directions. As an illustration, exploring a local linear estimator for modal regression could prove promising, given that local linear approaches are well known for mitigating bias and thus advancing asymptotic performance. Another important yet unresolved question concerns the asymptotic normality of the robust estimator since its resolution would be pivotal for constructing confidence intervals and performing hypothesis testing.

One area not addressed in this paper concerns the optimal selection of smoothing parameters with the specific goal of minimizing the mean square error (MSE) of the proposed kernel estimators. This issue is highly pertinent within the broader domain of kernel-based nonparametric estimation and clearly merits a dedicated investigation. Although it is an integral component in refining our approach, we have opted to postpone a detailed analysis of smoothing parameter selection, potentially using cross-validation or other optimization strategies, to forthcoming work.

Moreover, there are numerous other directions for future research. For instance, one might consider linear or partially linear extensions of robust modal regression. Another more intricate avenue would involve accommodating censored data or functional time series, requiring a level of mathematical rigor that exceeds the scope of the present contribution.

A further question that naturally arises is how to extend our findings to other widely used nonparametric estimation techniques, such as wavelet-based estimators [49], delta sequence estimators [50], k-nearest neighbor (kNN) estimators, and various local linear estimators [51]. Given the versatility of these methods within functional data analysis, integrating the bias correction techniques introduced here could potentially enhance their performance in a variety of contexts.

6. The Mathematical Developments

In this section, we establish the main theoretical results of the paper. The proof of Theorem 1 relies on standard analytical arguments. In particular, we begin by writing the following:

$$\begin{array}{ccc}\hfill \widehat{Mo{d}_{\nu }}\left(u\right)-Mo{d}_{\nu }\left(u\right)& =& \widehat{CQ}(\widehat{q_{\nu }}\mid u)-CQ(q_{\nu }\mid u)\hfill \\ \hfill & =& \widehat{CQ}(\widehat{q_{\nu }}\mid u)-CQ(\widehat{q_{\nu }}\mid u)+CQ(\widehat{q_{\nu }}\mid u)-CQ(q_{\nu }\mid u)\hfill \\ \hfill & \le & \underset{q\in [a_u,b_u]}{max}\left|\widehat{CQ}(q\mid u)-CQ(q\mid u)\right|+CQ(\widehat{q_{\nu }}\mid u)-CQ(q_{\nu }\mid u).\hfill \end{array}$$

Next, by applying a Taylor expansion, we obtain

$$CQ(\widehat{q_{\nu }}\mid u)-CQ(q_{\nu }\mid u)=(\widehat{q_{\nu }}-q_{\nu })C{Q}^{\prime }(q_{\nu }^{*}\mid u),\mathrm{where}{q}_{\nu }^{*}\in (\widehat{q_{\nu }},q_{\nu }).$$

(10)

Since $q_{\nu }$ is the minimizer of $C{Q}^{\prime }(·\mid u)$, it follows that

$$C{Q}^{\prime }(\widehat{q_{\nu }}\mid u)-C{Q}^{\prime }(q_{\nu }\mid u)={(\widehat{q_{\nu }}-q_{\nu })}^2{t}^{‴}(q_{\nu }^{**}\mid u),\mathrm{with}{q}_{\nu }^{**}\in (\widehat{q_{\nu }},q_{\nu }).$$

(11)

Moreover,

$$\begin{array}{c}C{Q}^{\prime }(\widehat{q_{\nu }}\mid u)-C{Q}^{\prime }(q_{\nu }\mid u)\hfill \\ =\left(C{Q}^{\prime }(\widehat{q_{\nu }}\mid u)-\widehat{C{Q}^{\prime }}(\widehat{q_{\nu }}\mid u)\right)+\left(\widehat{C{Q}^{\prime }}(\widehat{q_{\nu }}\mid u)-C{Q}^{\prime }(q_{\nu }\mid u)\right)\hfill \\ \le \left|C{Q}^{\prime }(\widehat{q_{\nu }}\mid u)-\widehat{C{Q}^{\prime }}(\widehat{q_{\nu }}\mid u)\right|+\left|\underset{q}{min}\widehat{C{Q}^{\prime }}(q\mid u)-\underset{q}{min}C{Q}^{\prime }(q\mid u)\right|\hfill \\ \le 2\underset{q\in [a_u,b_u]}{max}\left|\widehat{C{Q}^{\prime }}(q\mid u)-C{Q}^{\prime }(q\mid u)\right|.\hfill \end{array}$$

(12)

Combining (10)–(12) leads to

$$\begin{array}{c}{\displaystyle \left|\widehat{Mo{d}_{\nu }}\left(u\right)-Mo{d}_{\nu }\left(u\right)\right|}\hfill \\ \le C\left(\underset{q\in [a_u,b_u]}{max}\left|\widehat{CQ}(q\mid u)-CQ(q\mid u)\right|+\sqrt{\underset{q\in [a_u,b_u]}{max}\left|\widehat{C{Q}^{\prime }}(q\mid u)-C{Q}^{\prime }(q\mid u)\right|}\right).\hfill \end{array}$$

From the definition of $\widehat{C{Q}^{\prime }}(q\mid u)$ and for sufficiently large n, we have

$$\begin{array}{l}\widehat{C{Q}^{\prime }}(q\mid u)-C{Q}^{\prime }(q\mid u)\\ {\displaystyle =\frac{\left[\widehat{CQ}(q+b_n\mid u)-CQ(q+b_n\mid u)\right]+\left[CQ(q-b_n\mid u)-\widehat{CQ}(q-b_n\mid u)\right]}{2b_n}}\hfill \\ {\displaystyle +\frac{CQ(q+b_n\mid u)-CQ(q\mid u)+CQ(q\mid u)-CQ(q-b_n\mid u)-2b_{n}C{Q}^{\prime }(q\mid u)}{2b_n}}\hfill \\ {\displaystyle \le C{b}_n^{-1}\underset{q\in (a_u-b_n,b_u+b_n)}{max}\left|\widehat{CQ}(q\mid u)-CQ(q\mid u)\right|+O\left(b_n\right).}\hfill \end{array}$$

It follows that

$$\underset{q\in [0,1]}{max}\left|\widehat{CQ}(q\mid u)-CQ(q\mid u)\right|.$$

Hence, Theorem 1 is implied by the following proposition.

Proposition 1. 

Under the assumptions of Theorem 1, we have

$$\underset{q\in (0,1)}{sup}|\widehat{CQ}(q\mid u)-CQ(q\mid u)|=O\left(c_n^b\right)+O_{a.co.}\left({\left({\displaystyle \frac{logn}{n{\zeta }_u\left(c_n\right)}}\right)}^{{\displaystyle \frac{1}{2}}}\right).$$

In order to establish this proposition, we draw upon the lemmas presented below.

Lemma 1. 

Suppose that $\left\{{\mathbf{F}}_n\right\}$ is a sequence of real-valued random functions, each of which is monotonically decreasing in n, and let $\left\{C_n\right\}$ be a sequence of real-valued random variables satisfying

$$C_n=o_{a.co.}\left(1\right)\mathrm{and}\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)+\chi \xi -C_n\right|=o_{a.co.}\left(1\right),$$

for some positive constants χ and M. Then, for any real sequence $\left\{{\varsigma }_n\right\}$ such that ${\mathbf{F}}_n\left({\varsigma }_n\right)=o_{a.co.}\left(1\right)$, it follows that

$$\sum _{n=1}^{\infty }\mathrm{I}\mathrm{P}\left\{|{\varsigma }_n|\ge M\right\}<\infty .$$

Proof of Lemma 1. 

Let $\eta >0$. We begin by noting that

$$\mathrm{I}\mathrm{P}\left(|{\varsigma }_n|\ge M\right)=\mathrm{I}\mathrm{P}\left(|{\varsigma }_n|\ge M,\left|{\mathbf{F}}_n\left({\varsigma }_n\right)\right|<\eta \right)+\mathrm{I}\mathrm{P}\left(\left|{\mathbf{F}}_n\left({\varsigma }_n\right)\right|\ge \eta \right).$$

Hence,

$$\mathrm{I}\mathrm{P}\left(|{\varsigma }_n|\ge M\right)\le \mathrm{I}\mathrm{P}\left(\underset{\left|\xi \right|\ge M}{inf}\left|{\mathbf{F}}_n\left(\xi \right)\right|<\eta \right)+\mathrm{I}\mathrm{P}\left(\left|{\mathbf{F}}_n\left({\varsigma }_n\right)\right|\ge \eta \right).$$

Since we have ${\mathbf{F}}_n\left({\varsigma }_n\right)=o_{\mathrm{a}.\mathrm{co}.}\left(1\right)$, the remaining task is to show that

$$\sum _n\mathrm{I}\mathrm{P}\left(\underset{\left|\xi \right|\ge M}{inf}\left|{\mathbf{F}}_n\left(\xi \right)\right|<\eta \right)<\infty .$$

To proceed, we use the fact that ${\mathbf{F}}_n$ is a decreasing function, which allows us to write

$$\underset{\left|\xi \right|\ge M}{inf}\left|{\mathbf{F}}_n\left(\xi \right)\right|=\in PD{F}_{\nu }\left(-{\mathbf{F}}_n\left(M\right),{\mathbf{F}}_n(-M)\right).$$

Consequently, it will suffice to prove

$$\sum _n\mathrm{I}\mathrm{P}\left(\left[-{\mathbf{F}}_n\left(M\right)\right]\le \eta \right)<\infty \mathrm{and}\sum _n\mathrm{I}\mathrm{P}\left(\left[{\mathbf{F}}_n(-M)\right]\le \eta \right)<\infty .$$

For the first claimed result, we write

$$\begin{array}{ccc}{\displaystyle \sum _n\mathrm{I}\mathrm{P}\left(-{\mathbf{F}}_n\left(M\right)\le \eta \right)}\hfill & \le & \sum _n\mathrm{I}\mathrm{P}\left(-{\mathbf{F}}_n\left(M\right)\le \eta ,M\chi -2\eta \ge max\right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(M\chi -2\eta \le max\right)}\hfill \\ & \le & {\displaystyle \sum _n\mathrm{I}\mathrm{P}\left({\mathbf{F}}_n\left(M\right)\ge -\eta ,M\chi -C_n\ge 2\eta \right)}\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(M\chi -2\eta \le C_n\right)}\hfill \\ & {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left(\left|{\mathbf{F}}_n\left(M\right)+\chi M-C_n\right|\ge \eta \right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(|C_n|\ge \chi M-2\eta \right)}\hfill \\ & \le & {\displaystyle \sum _n\mathrm{I}\mathrm{P}\left(\underset{|{\xi }_1|\le M}{max}\left|{\mathbf{F}}_n\left({\xi }_1\right)+\chi {\xi }_1-C_n\right|\ge \eta \right)}\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(|C_n|\ge \chi M-2\eta \right).}\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}\hfill {\displaystyle \sum _n\mathrm{I}\mathrm{P}\left({\mathbf{F}}_n(-M)\le \eta \right)}& {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left({\mathbf{F}}_n(-M)\le \eta ,2\eta -M\chi \le C_n\right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(2\eta -M\chi \ge C_n\right)}\hfill \\ & {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left(-{\mathbf{F}}_n(-M)\ge -\eta ,C_n+M\chi \ge 2\eta \right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(M\chi -2\eta \le -C_n\right)}\hfill \\ & {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left(-\left({\mathbf{F}}_n(-M)-\chi M-C_n\right)\ge \eta \right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(|C_n|\ge \chi M-2\eta \right)}\hfill \\ & {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left(\left|{\mathbf{F}}_n(-M)+\chi (-M)-C_n\right|\ge \eta \right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(|C_n|\ge \chi M-2\eta \right)}\hfill \\ & {\displaystyle \le }& \sum _n\mathrm{I}\mathrm{P}\left(\underset{|{\xi }_1|\le M}{max}\left|{\mathbf{F}}_n\left({\xi }_1\right)+\chi {\xi }_1-C_n\right|\ge \eta \right)\hfill \\ & & {\displaystyle +\sum _n\mathrm{I}\mathrm{P}\left(|C_n|\ge \chi M-2\eta \right).}\hfill \end{array}$$

Finally, let us select $\eta$ such that

$$\eta >{\displaystyle \frac{\chi M}{2}}.$$

Building on this choice and invoking conditions of the lemma, we thereby conclude that

$$\sum _n\mathrm{I}\mathrm{P}\left(|{\varsigma }_n|\ge M\right)<\infty .$$

Hence, the proof is complete. □

Proof of Proposition 1. 

We begin by invoking Lemma 1 for the function

$${\mathbf{F}}_n\left(\xi \right)={\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _{i=1}^n\left(q-1{\mathrm{I}}_{\{O_i\le \xi +CQ(q\mid u)\}}\right){\mathbf{H}}_i,$$

where

$${\varsigma }_n=\widehat{CQ}(q\mid u)-CQ(q\mid u)\mathrm{and}{C}_n={\mathbf{F}}_n\left(0\right).$$

Under this framework, we derive the Bahadur representation of the quantile. Since ${\mathbf{F}}_n\left({\varsigma }_n\right)=0$, it remains to check that the conditions required by Lemma 1 are satisfied. In particular, we must show

$$C_n=o_{a.co.}\left(1\right),$$

(13)

and that there exist constants $M>0$ and $\chi >0$ such that

$$\underset{\left|\xi \right|\le M}{max}\left|{\mathbf{F}}_n\left(\xi \right)+\chi \xi -C_n\right|=o_{a.co.}\left(1\right).$$

(14)

For (13), we derive

$${\xi }_i=\left(q-1{\mathrm{I}}_{{\displaystyle [O_i\le CQ(q\mid u)]}}\right){\mathbf{H}}_i-\mathrm{I}\mathrm{E}\left[\left(q-1{\mathrm{I}}_{{\displaystyle [O_i\le CQ(q\mid u)]}}\right){\mathbf{H}}_i\right].$$

We also consider the expression

$$C_n-\mathbb{E}\left[C_n\right]={\displaystyle \frac{1}{n\mathbb{E}\left[{\mathbf{H}}_1\right]}}\sum _{i=1}^n{\xi }_i.$$

To analyze this, we apply Bernstein’s inequality to the random variables ${\xi }_i$. By assumption, we have the following bounds:

$$|{\xi }_i|\le C\mathrm{and}\mathbb{E}\left[{\xi }_i^2\right]\le C{\zeta }_u\left(c_n\right).$$

These conditions allow us to establish the rate of convergence:

$$C_n-\mathbb{E}\left[C_n\right]=O_{\mathrm{a}.\mathrm{co}.}\left(\sqrt{{\displaystyle \frac{logn}{n{\zeta }_u\left(c_n\right)}}}\right).$$

Next, we examine the expectation $\mathbb{E}\left[C_n\right]$:

$$\begin{array}{cc}\hfill \mathbb{E}\left[C_n\right]& ={\displaystyle \frac{1}{\mathbb{E}\left[{\mathbf{H}}_1\right]}}\mathbb{E}\left[\left(q-{\mathbf{1}}_{[O_1\le CQ(q\mid u)]}\right){\mathbf{H}}_1\right]\hfill \\ \hfill & \le {\displaystyle \frac{1}{\mathbb{E}\left[{\mathbf{H}}_1\right]}}\mathbb{E}\left|PD{F}_{\nu }(CQ(q\mid u)\mid u)-PD{F}_{\nu }(CQ(q\mid u)\mid u){\mathbf{H}}_1\right|\hfill \\ \hfill & =O\left(c_n^b\right).\hfill \end{array}$$

Combining these results, we deduce that

$$|C_n|=O\left(c_n^b\right)+O_{\mathrm{a}.\mathrm{co}.}\left(\sqrt{{\displaystyle \frac{logn}{n{\zeta }_u\left(c_n\right)}}}\right).$$

For (14), we have

$$\underset{\left|\xi \right|\le M}{sup}|{\mathbf{F}}_n\left(\xi \right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]|=O_{a.co.}\left(\sqrt{{\displaystyle \frac{logn}{n{\zeta }_u\left(h\right)}}}\right)$$

(15)

and the bias term

$$\underset{\left|\xi \right|\le M}{sup}|\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]+PD{F}_{\nu }(t_q\left(u\right)\mid u)\xi |=O\left(c_n^b\right).$$

(16)

In order to investigate (15), we begin by noting that

$$[-M,M]\subset \bigcup _{j=1}^{d_n}[{\xi }_j-l_n,{\xi }_j+l_n],\mathrm{for}{\xi }_j\in [-M,M]\mathrm{and}{l}_n=d_n^{-1}=1/\sqrt{n}.$$

Hence, for every $\xi \in [-M,M]$, let

$$j\left(\xi \right)=arg\underset{j}{min}\left|\xi -{\xi }_j\right|.$$

We then decompose the following:

$$\begin{array}{c}{\displaystyle \underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]\right|}\hfill \\ \le \underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)\right|+\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)-C_n\right]\right|\hfill \\ +\underset{\left|\xi \right|\le M}{max}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)\right]\right|.\hfill \end{array}$$

Because

$$\left|{\mathbf{1}}_{\{Y<a\}}-{\mathbf{1}}_{\{Y<b\}}\right|\le {\mathbf{1}}_{\left\{|Y-b|\le |a-b|\right\}},$$

we find

$$\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_j\right)\right|\le {\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _i{\mathcal{X}}_i,$$

where

$${\mathcal{X}}_i=\underset{\left|\xi \right|\le M}{sup}{\mathbf{1}}_{\left\{|O_i-{\xi }_{j\left(\xi \right)}-CQ(q\mid u)|\le C{l}_n\right\}}{\mathbf{H}}_i.$$

Clearly, $\left|{\mathcal{X}}_i\right|\le C$, and

$$\mathrm{I}\mathrm{E}\left[{\mathcal{X}}_i\right]=O\left(l_n{\zeta }_u\left(h\right)\right),\mathrm{I}\mathrm{E}\left[{\mathcal{X}}_i^2\right]=O\left(l_n{\zeta }_u\left(h\right)\right).$$

By using

$$l_n=o\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right),$$

(17)

we deduce

$$\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_j\right)\right|=O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right).$$

Next, we observe that

$$\underset{\left|\xi \right|\le M}{max}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_j\right)\right]\right|\le {\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\mathrm{I}\mathrm{E}\left[{\mathcal{X}}_1\right]\le C{l}_n,$$

and consequently,

$$\underset{\left|\xi \right|\le M}{sup}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-{\mathbf{F}}_n\left({\xi }_j\right)\right]\right|=o\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right).$$

We now turn to

$$\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left({\xi }_j\right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left({\xi }_j\right)-C_n\right]\right|.$$

Notice that

$${\mathbf{F}}_n\left({\xi }_j\right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left({\xi }_j\right)-C_n\right]={\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _{i=1}^n{\mathcal{Y}}_i,$$

with

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_i& =& \left({\mathbf{1}}_{\{O_i\le CQ(q\mid u)\}}-{\mathbf{1}}_{\{O_i\le {\xi }_j+CQ(q\mid u)\}}\right){\mathbf{H}}_i\hfill \\ & -& \mathrm{I}\mathrm{E}\left[\left({\mathbf{1}}_{\{O_i\le CQ(q\mid u)\}}-{\mathbf{1}}_{\{O_i\le {\xi }_j+CQ(q\mid u)\}}\right){\mathbf{H}}_i\right].\hfill \end{array}$$

Clearly, $\left|{\mathcal{Y}}_i\right|\le C$ and

$$\mathrm{I}\mathrm{E}{\left[{\mathcal{Y}}_i\right]}^2\le C{\zeta }_u\left(h\right).$$

Hence, there exists $\eta >0$ such that

$$\begin{array}{cc}\hfill & \sum _n\mathrm{I}\mathrm{P}\left(\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left({\xi }_{j\left(\xi \right)}\right)-C_n\right]\right|\ge \eta \sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right)\hfill \\ \hfill & \le \sum _n{d}_n\underset{j}{max}\mathrm{I}\mathrm{P}\left(\left|{\mathbf{F}}_n\left({\xi }_j\right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left({\xi }_j\right)-C_n\right]\right|\ge \eta \sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right)<\infty ,\hfill \end{array}$$

which completes the proof of (15). Concerning (16), we write

$$\begin{array}{c}{\displaystyle \mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]}\hfill \\ =-{\displaystyle \frac{1}{\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\mathrm{I}\mathrm{E}\left[\left(1{\mathrm{I}}_{\left[O_1\le \xi +CQ(q\mid u)\right]}-1{\mathrm{I}}_{\left[O_1\le CQ(q\mid u)\right]}\right){\mathbf{H}}_i\right]\hfill \\ =-{\displaystyle \frac{1}{\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\mathrm{I}\mathrm{E}\left[\left(PD{F}_{\nu }(\xi +CQ(q\mid u)\mid u)-PD{F}_{\nu }(CQ(q\mid u)\mid u)\right){\mathbf{H}}_1\right]\hfill \\ =-{\displaystyle \frac{1}{\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\mathrm{I}\mathrm{E}\left[\left(PD{F}_{\nu }(\xi +CQ(q\mid u)\mid u)-PD{F}_{\nu }(CQ(q\mid u)\mid u)\right){\mathbf{H}}_1\right]+O\left(c_n^b\right)\hfill \\ =-{\displaystyle \frac{\xi PD{F}_{\nu }(CQ(q\mid u)\mid u)}{\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]+O\left(c_n^b\right)+o\left(\xi \right).\hfill \end{array}$$

implying

$$\begin{array}{ccc}\hfill \mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]& =& -PD{F}_{\nu }(t_q\left(u\right)\mid u)\xi +O\left(c_n^b\right)+o\left(\xi \right).\hfill \end{array}$$

Therefore,

$$\widehat{CQ}(q\mid u)-CQ(q\mid u)={\varsigma }_n={\displaystyle \frac{1}{PD{F}_{\nu }(t_q\left(u\right)\mid u)}}{c}_n+O\left({\displaystyle \underset{\left|\xi \right|\le M}{max}|{\mathbf{F}}_n\left(\xi \right)+\chi \xi -C_n|}\right).$$

(18)

Now, we use the Bahadur representation to state the uniform consistency of

$$\widehat{CQ}(q\mid u)-CQ(q\mid u).$$

So, all that remains is

$$\underset{q\in [0,1]}{sup}|C_n-\mathrm{I}\mathrm{E}\left[C_n\right]|\mathrm{and}\underset{q\in [0,1]}{sup}\underset{\left|\xi \right|\le M}{sup}|{\mathbf{F}}_n\left(\xi \right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]|.$$

For the sake of shortness, we only prove the second one. Indeed, we keep the notation of the first part and we use the compactness $[0,1]$ once again. Therefore,

$$[0,1]\subset \bigcup _{k=1}^{d_n}[q_k-l_n,q_k+l_n],for{q}_k\in [0,1].$$

Next, for each $q\in [0,1]$, define $\mathbf{H}\left(q\right)=arg{min}_k\left|q-q_k\right|$ and consider the corresponding term as a function of $\xi$ and q. To simplify notation, set

$${\mathbf{U}}_n(\xi ,q)={\mathbf{F}}_n\left(\xi \right)-C_n.$$

Hence,

$$\begin{array}{c}{\displaystyle \underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n(\xi ,q)-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q)\right]\right|}\hfill \\ \le \underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right|\hfill \\ +\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})\right|\hfill \\ +\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})\right]\right|\hfill \\ +\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})\right]-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q_{\mathbf{H}\left(q\right)})\right]\right|\hfill \\ +\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q_{\mathbf{H}\left(q\right)})\right]-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q)\right]\right|.\hfill \end{array}$$

Therefore, it follows that

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right|\le {\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _i{\mathcal{X}}_i^0,$$

where

$${\mathcal{X}}_i^0=\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}{\mathbf{1}}_{\left\{\left|O_i-{\xi }_{j\left(\xi \right)}-CQ\left(q\mid u\right)\right|\le C{l}_n\right\}}{\mathbf{H}}_i.$$

Since

$$\left|{\mathcal{X}}_i^0\right|\le C,\mathrm{I}\mathrm{E}\left[{\mathcal{X}}_i^0\right]=O\left(l_n{\zeta }_u\left(h\right)\right),\mathrm{and}\mathrm{I}\mathrm{E}\left[{\left({\mathcal{X}}_i^0\right)}^2\right]=O\left(l_n{\zeta }_u\left(h\right)\right),$$

we deduce

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right|=O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right),$$

and

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right]\right|=o\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right).$$

Similarly, we obtain

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})\right|\le {\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _i{\mathcal{X}}_i^1,$$

where

$${\mathcal{X}}_i^1=\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left({\mathbf{1}}_{\{\mid O_i-{\xi }_{j\left(\xi \right)}-CQ(q\mid u)\mid \le C{l}_n\}}+{\mathbf{1}}_{\{\mid O_i-CQ(q_{\mathbf{H}\left(q\right)}\mid u)\mid \le C{l}_n\}}\right){\mathbf{H}}_i.$$

Because

$$\left|{\mathcal{X}}_i^1\right|\le C,\mathrm{I}\mathrm{E}\left[{\mathcal{X}}_i^1\right]=O\left(l_n{\zeta }_u\left(h\right)\right),\mathrm{I}\mathrm{E}\left[{\left({\mathcal{X}}_i^1\right)}^2\right]=O\left(l_n{\zeta }_u\left(h\right)\right),$$

we again conclude

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right|=O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right),$$

and

$$\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n(\xi ,q)-{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q)\right]\right|=o\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right).$$

To handle the final term, similarly define

$${\mathbf{U}}_n({\xi }_j,q_k)-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n({\xi }_j,q_k)\right]={\displaystyle \frac{1}{n\mathrm{I}\mathrm{E}\left[{\mathbf{H}}_1\right]}}\sum _{i=1}^n{\mathcal{Y}}_i^{\prime },$$

where

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_i^{\prime }& =& \left({\mathbf{1}}_{\{O_i\le CQ(q_k\mid u)\}}-{\mathbf{1}}_{\{O_i\le {\xi }_j+CQ(q_k\mid u)\}}\right){\mathbf{H}}_i\hfill \\ & & -\mathrm{I}\mathrm{E}\left[\left({\mathbf{1}}_{\{O_i\le CQ(q_k\mid u)\}}-{\mathbf{1}}_{\{O_i\le {\xi }_j+CQ(q_k\mid u)\}}\right){\mathbf{H}}_i\right].\hfill \end{array}$$

Using Bernstein’s inequality, we note that

$$\left|{\mathcal{Y}}_i^{\prime }\right|\le C\mathrm{and}\mathrm{I}\mathrm{E}\left[{\left({\mathcal{Y}}_i^{\prime }\right)}^2\right]\le C{\zeta }_u\left(h\right).$$

Hence, there exists $\eta >0$ such that

$$\begin{array}{c}{\displaystyle \sum _n\mathrm{I}\mathrm{P}\left(\underset{\left|\xi \right|\le M}{sup}\underset{q\in [0,1]}{sup}\left|{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n({\xi }_{j\left(\xi \right)},q_{\mathbf{H}\left(q\right)})\right]\right|\ge \eta \sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right)}\hfill \\ \le \sum _n{d}_n^2\underset{j}{max}\underset{k}{max}\mathrm{I}\mathrm{P}\left(\left|{\mathbf{U}}_n({\xi }_j,q_k)-\mathrm{I}\mathrm{E}\left[{\mathbf{U}}_n({\xi }_j,q_k)\right]\right|\ge \eta \sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right)<\infty .\hfill \end{array}$$

It follows that

$$\underset{q\in [0,1]}{sup}\underset{\left|\xi \right|\le M}{sup}\left|{\mathbf{F}}_n\left(\xi \right)-C_n-\mathrm{I}\mathrm{E}\left[{\mathbf{F}}_n\left(\xi \right)-C_n\right]\right|=O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(c_n\right)}}\right).$$

Moreover, one can show

$$\underset{q\in [0,1]}{sup}\left|C_n-\mathrm{I}\mathrm{E}\left[C_n\right]\right|=O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right).$$

Thus, combining these bounds yields

$$\underset{q\in [0,1]}{sup}\left|\widehat{CQ}(q\mid u)-CQ(q\mid u)\right|=O\left(c_n^b\right)+O_{a.co.}\left(\sqrt{\frac{logn}{n{\zeta }_u\left(h\right)}}\right),$$

which completes the proof of the proposition. □