Homothetic Covering of Crosspolytopes

Abstract

The exact value of ${\Gamma }_m\left(K\right)$, which is the least positive number $\gamma$ such that a convex body K can be covered by m translates of $\gamma K$, is usually difficult to obtain. We present exact values of ${\Gamma }_{14}\left(B_1^3\right)$, ${\Gamma }_{11}\left(B_1^4\right)$, ${\Gamma }_{2n}\left(B_1^n\right)$, ${\Gamma }_{2n+1}\left(B_1^n\right)$, and ${\Gamma }_{2n+2}\left(B_1^n\right)$, where $B_1^n$ is the unit ball of ${\mathbb{R}}^n$ endowed with the taxicab norm.

1. Introduction

A compact convex set K whose interior $\mathrm{int}K$ is not empty is called a convex body. Denote by $\mathrm{ext}K$ the set of extreme points of K, $\mathrm{cl}K$ the closure of K, and $\mathrm{bd}K$ the boundary of K. Let ${\mathcal{K}}^n$ be the set of all convex bodies in ${\mathbb{R}}^n$. We denote by $c\left(K\right)$ the smallest number of translates of $\mathrm{int}K$ needed to cover K. Concerning the least upper bound of $c\left(K\right)$ for each $K\in {\mathcal{K}}^n$, there is a long-standing conjecture:

Conjecture 1 (Hadwiger’s covering conjecture).

For each $K\in {\mathcal{K}}^n$, we have

$$c\left(K\right)\le 2^n;$$

the equality holds if and only if K is a parallelotope.

This conjecture has been studied by many authors, and it is completely solved only in the two-dimensional case (cf. [1]). M. Lassak [2] proved that $c\left(K\right)\le 8$ holds for each centrally symmetric convex body in ${\mathcal{K}}^3$. A. Prymak [3] showed that $c\left(K\right)\le 14$ holds for each $K\in {\mathcal{K}}^3$. More details and references about this conjecture can be found in [4,5,6]. For each $K\in {\mathcal{K}}^n$ and each $m\in {\mathbb{Z}}^{+}$, set

$${\Gamma }_m\left(K\right):=\inf \left\{\gamma \ge 0|\exists \left\{c_i|i\in \left[m\right]\right\}\subseteq {\mathbb{R}}^n\mathrm{s}.\mathrm{t}.K\subseteq \bigcup _{i\in \left[m\right]}(c_i+\gamma K)\right\},$$

where $\left[m\right]=\left\{i\in \mathbb{Z}|1\le i\le m\right\}$. By standard compactness arguments, one can show that “inf” in the definition of ${\Gamma }_m\left(K\right)$ can be replaced with “min”. The map ${\Gamma }_m(·):{\mathcal{K}}^n\to [0,1]$ is called the m-covering functional. A set C of m points satisfying $K\subseteq {\Gamma }_m\left(K\right)K+C$ is called an m-optimal configuration of K.

Estimating ${\Gamma }_p\left(K\right)$ for special convex bodies $K\in {\mathcal{K}}^n$ plays an important role in Chuanming Zong’s quantitative program to attack Conjecture 1; see [7]. However, it is not easy to obtain m-optimal configurations even for convex bodies like the Euclidean unit disk and simplices (cf. Figure 6 in [8,9]). Several algorithms have been introduced to find near-optimal configurations for convex bodies; see [10,11,12]. In most cases, it is more difficult to show the optimality of a nice configuration. We will find several optimal configurations for crosspolytopes and prove the optimality theoretically. Since SageMath provides facilities to handle convex polytopes, many details in our proofs can be checked by computer programs.

A convex body $K\in {\mathcal{K}}^n$ is said to be an n-dimensional crosspolytope if there exist n linearly independent vectors $v_1,\cdots ,v_n$ such that $K=\mathrm{conv}\left\{\pm v_1,\cdots ,\pm v_n\right\}$. Each n-dimensional crosspolytope is affinely equivalent to

$$B_1^n=\left\{x=(x_1,x_2\cdots ,x_n)|{\Vert x\Vert }_1=\sum _{i\in \left[n\right]}\left|x_i\right|\le 1\right\},$$

which is the closed unit ball of ${\ell }_1^n$. In [13], Y. Lian showed that

$${\Gamma }_{10}\left(B_1^3\right)={\Gamma }_{11}\left(B_1^3\right)={\Gamma }_{12}\left(B_1^3\right)={\Gamma }_{13}\left(B_1^3\right)={\displaystyle \frac{3}{5}},$$

and claimed that

$${\Gamma }_{14}\left(B_1^3\right)={\Gamma }_{15}\left(B_1^3\right)={\Gamma }_{16}\left(B_1^3\right)={\Gamma }_{17}\left(B_1^3\right)={\displaystyle \frac{4}{7}}.$$

We shall show that the correct value of ${\Gamma }_{14}\left(B_1^3\right)$ is $7/13$. For each $m\in [2n,2n+2]$, an m-optimal configuration for $B_1^n$ is presented. The exact value of ${\Gamma }_{11}\left(B_1^4\right)$ is also determined. Our methods are different from the ones used in [14].

For each $x\in {\mathbb{R}}^n$, denote by $p_i\left(x\right)$ the i-th coordinate of x. Denote by $\#A$ the cardinality of a finite set A. Let $\left\{e_i|i\in \left[n\right]\right\}$ be the canonical basis of ${\mathbb{R}}^n$. A nonempty subset A of ${\ell }_1^n$ is said to be ε-separated for some positive $\epsilon$ if the distance (with respect to the taxicab norm) between each pair of points in A is at least $\epsilon$.

Our main results are the following:

Theorem 1.

${\Gamma }_{14}\left(B_1^3\right)=7/13$.

Theorem 2.

${\Gamma }_{2n}\left(B_1^n\right)={\Gamma }_{2n+1}\left(B_1^n\right)={\Gamma }_{2n+2}\left(B_1^n\right)=(n-1)/n$.

It follows that ${\Gamma }_{11}\left(B_1^4\right)\le {\Gamma }_{10}\left(B_1^4\right)=3/4$. In fact, the corresponding equality holds.

Theorem 3.

${\Gamma }_{11}\left(B_1^4\right)=3/4$.

2. Homothetic Covering of ${\mathit{B}}_{\mathbf{1}}^{\mathbf{3}}$

2.1. Notations

We collect in this subsection several notations and basic results that will be used. Set

$$\begin{array}{c}{O}_1=\left\{x|p_i\left(x\right)\ge 0,\forall i\in \left[3\right]\right\},O_2=\left\{x|p_1\left(x\right)\ge 0,p_2\left(x\right)\ge 0,p_3\left(x\right)\le 0\right\},\\ O_3=\left\{x|p_1\left(x\right)\ge 0,p_2\left(x\right)\le 0,p_3\left(x\right)\ge 0\right\},O_4=\left\{x|p_1\left(x\right)\le 0,p_2\left(x\right)\ge 0,p_3\left(x\right)\ge 0\right\},\end{array}$$

$O_5=-O_4$, $O_6=-O_3$, $O_7=-O_2$, and $O_8=-O_1$. Two orthants O and $O^{\prime }$ of ${\mathbb{R}}^3$ are said to be adjacent (denoted by $O\sim O^{\prime }$) if the intersection of them is two-dimensional. The adjacency between orthants is collected in Table 1.

Table 1. Adjacency of orthants.

Orthant	Signs	Adjacent Orthants	Orthant	Signs	Adjacent Orthants
$O_1$	(+, +, +)	2, 3, 4	$O_5$	(+, −, −)	2, 3, 8
$O_2$	(+, +, −)	1, 5, 6	$O_6$	(−, +, −)	2, 4, 8
$O_3$	(+, −, +)	1, 5, 7	$O_7$	(−, −, +)	3, 4, 8
$O_4$	(−, +, +)	1, 6, 7	$O_8$	(−, −, −)	5, 6, 7

For each $j\in \left[8\right]$, set $f_j=(\mathrm{sgn}{p}_1\left(x\right),\mathrm{sgn}{p}_2\left(x\right),\mathrm{sgn}{p}_3\left(x\right))$, where $x\in \mathrm{int}{O}_j$. For example, we have $f_1=(1,1,1)$, $f_2=(1,1,-1)$, $f_3=(1,-1,1)$, and $f_4=(-1,1,1)$. Let

$$F=\left\{\pm f_i|i\in \left[4\right]\right\} \mathrm{and} F_i=\left\{f\in F|⟨e_i|f⟩=1\right\},\forall i\in \left[3\right].$$

Clearly,

$$B_1^3=\left\{x\in {\mathbb{R}}^3|⟨x|f⟩\le 1,\forall f\in F\right\}$$

(1)

and

$$F=-F_j\bigsqcup F_j,\forall j\in \left[3\right].$$

(2)

For each $\alpha \in \mathbb{R}$ and each $g\in {\mathbb{R}}^3\setminus \left\{o\right\}$, set

$$H_{g,\alpha }=\left\{x|⟨x|g⟩=\alpha \right\},H_{g,\alpha }^{+}=\left\{x|⟨x|g⟩\ge \alpha \right\},\mathrm{and}{H}_{g,\alpha }^{-}=\left\{x|⟨x|g⟩\le \alpha \right\}.$$

Let $\mathcal{G}$ be the group generated by permutations of the standard basis vectors and reflections with respect to coordinate hyperplanes, and $Q_1$, $Q_2$, $Q_3$, and $Q_4$ be the linear transforms in $\mathcal{G}$ with matrices

$$\left(\begin{array}{ccc}0& 0& -1\\ 0& 1& 0\\ -1& 0& 0\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& -1\\ 0& -1& 0\end{array}\right),\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right),\mathrm{and}\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right),$$

(3)

respectively. It can be verified that, for each $\gamma >0$ and each $m\in {\mathbb{R}}^3$, we have

$$\gamma B_1^3+m=\left\{x+m|⟨x+m|f⟩\le ⟨m|f⟩+\gamma ,\forall f\in F\right\}.$$

(4)

Thus, for each $y\in \gamma B_1^3+m$ and each $f\in F$, we have

$$⟨m|-f⟩+\gamma \le 2\gamma +⟨y|-f⟩.$$

(5)

Let $P_0=\left\{\pm 6e_1,\pm 6e_2,\pm 6e_3\right\}$, $P_1=\left\{(2,2,-2),(5,5,4),(-4,5,-5),(5,-4,-5)\right\}$, and $P=P_0\cup P_1\cup (-P_1)$. We will show that P is a 14-optimal configuration of $13B_1^3$. Set

$$K_i=6e_i+7B_1^3,\forall i\in \left[3\right].$$

By (1), we have

$$\begin{array}{cc}\hfill K_i& =6e_i+\left\{x\in {\mathbb{R}}^3|⟨x|f⟩\le 7,\forall f\in F\right\}\hfill \\ \hfill & =\left\{x+6e_i|x\in {\mathbb{R}}^3\mathrm{and}⟨x|f⟩\le 7,\forall f\in F\right\}\hfill \\ \hfill & =\left\{x\in {\mathbb{R}}^3|⟨x|f⟩\le 13\mathrm{and}⟨x|-f⟩\le 1,\forall f\in F_i\right\}.\hfill \end{array}$$

(6)

Similarly,

$$-K_i=\left\{x|⟨x|f⟩\le 1\mathrm{and}⟨x|-f⟩\le 13,\forall f\in F_i\right\}.$$

(7)

Let $k\in \left[8\right]$ and $k_1,k_2,k_3\in \left[8\right]$ be integers such that, for each $i\in \left[3\right]$, $O_k\sim O_{k_i}$ and $f_{k_i}$ differs from $f_k$ only in its i-th coordinate. Put

$$G_k=\left\{f_{k_1},f_{k_2},f_{k_3}\right\}.$$

The following lemma can also be verified by a computer program based on SageMath; see [15].

Lemma 1.

For each $k\in \left[8\right]$, the closure of

$$U_k:=(13B_1^3\setminus (7B_1^3+P_0))\cap O_k=(13B_1^3\setminus (\left(\bigcup _{i\in \left[3\right]}{K}_i\right)\cup \left(\bigcup _{i\in \left[3\right]}(-K_i)\right)))\cap O_k$$

is the simplex $S_k:=\left\{x|⟨x|f⟩\ge 1,\forall f\in G_k;⟨x|f_k⟩\le 13\right\}$ contained in $\mathrm{int}{O}_k$.

Proof. 

It suffices to show that $U_k=\Delta :=\left\{x|⟨x|f⟩>1,\forall f\in G_k;⟨x|f_k⟩\le 13\right\}$.

Let $x\in U_k$. We have $⟨x|f⟩\le 13,\forall f\in F$. For each $i\in \left[3\right]$, there exist $g_{k,i},h_{k,i}\in F_i$ such that $⟨x|-g_{k,i}⟩>1$ and $⟨x|h_{k,i}⟩>1$. Clearly,

$$⟨x|f_{k_i}⟩\ge ⟨x|-g_{k,i}⟩>1,\forall i\in \left[3\right].$$

Thus, $x\in \Delta$. Therefore, $U_k\subseteq \Delta$.

Clearly, $\Delta \subseteq 13B_1^3\cap \mathrm{int}{O}_k$. Note that, for each $i\in \left[3\right]$, we have $G_k\cap F_i\ne \varnothing$ and $-G_k\cap F_i\ne \varnothing$. By (6) and (7), we have

$$\Delta \cap (\left(\bigcup _{i\in \left[3\right]}{K}_i\right)\cup \left(\bigcup _{i\in \left[3\right]}(-K_i)\right))=\varnothing .$$

Thus, $\Delta \subseteq U_k$. This completes the proof. □

For each $k\in \left[8\right]$, set

$$T_k=S_k\cap \mathrm{bd}\left(13B_1^3\right) \mathrm{and} \mathcal{T}:=\left\{T_k|k\in \left[8\right]\right\}.$$

There exists $Q\in \mathcal{G}$ such that $S_k=Q\left(S_1\right)$ and $T_k=Q\left(T_1\right)$.

It can be verified that (see also [15])

$$E:=\bigcup _{k\in \left[8\right]}\mathrm{ext}{T}_k=\{(\pm 1,\pm 6,\pm 6),(\pm 6,\pm 1,\pm 6),(\pm 6,\pm 6,\pm 1)\}.$$

(8)

Set $V:=\left\{v_k|k\in \left[8\right]\right\}$ and $C:=\left\{c_k|k\in \left[8\right]\right\}$, where, for each $k\in \left[8\right]$, $v_k$ is the point in

$$\mathrm{ext}{S}_k\setminus \mathrm{ext}{T}_k=\{(\pm 1,\pm 1,\pm 1)\}\cap O_k,$$

and $c_k$ is the point in $\{(\pm 4,\pm 4,\pm 5)\}\cap T_k$. See Table 2 for more details.

Table 2. The set $\mathrm{ext}{T}_k$, $v_k$, and $c_k$, for each $k\in \left[8\right]$.

k	$\mathrm{ext}{\mathit{T}}_{\mathit{k}}$	${\mathit{v}}_{\mathit{k}}$	${\mathit{c}}_{\mathit{k}}$
1	$\left\{(6,1,6),(1,6,6),(6,6,1)\right\}$	$(1,1,1)$	$(4,4,5)$
2	$\left\{(6,1,-6),(1,6,-6),(6,6,-1)\right\}$	$(1,1,-1)$	$(4,4,-5)$
3	$\left\{(6,-1,6),(1,-6,6),(6,-6,1)\right\}$	$(1,-1,1)$	$(4,-4,5)$
4	$\left\{(-6,1,6),(-1,6,6),(-6,6,1)\right\}$	$(-1,1,1)$	$(-4,4,5)$
5	$\left\{(6,-1,-6),(1,-6,-6),(6,-6,-1)\right\}$	$(1,-1,-1)$	$(4,-4,-5)$
6	$\left\{(-6,1,-6),(-1,6,-6),(-6,6,-1)\right\}$	$(-1,1,-1)$	$(-4,4,-5)$
7	$\left\{(-6,-1,6),(-1,-6,6),(-6,-6,1)\right\}$	$(-1,-1,1)$	$(-4,-4,5)$
8	$\left\{(-6,-1,-6),(-1,-6,-6),(-6,-6,-1)\right\}$	$(-1,-1,-1)$	$(-4,-4,-5)$

Lemma 2.

Suppose that $k\in \left[8\right]$, $m\in {\mathbb{R}}^3$, and $x\in \mathrm{ext}{T}_k\cap (m+\gamma B_1^3)$. If $f_x\in F$ is given by

$$p_i\left(f_x\right)=\left\{\begin{array}{cc}\mathrm{sgn}{p}_i\left(x\right),\hfill & |p_i\left(x\right)| =6,\hfill \\ -\mathrm{sgn}{p}_i\left(x\right),\hfill & |p_i\left(x\right)| =1,\hfill \end{array}\right.$$

(9)

then

$$⟨m|-f_x⟩\le \gamma -11.$$

(10)

If $\gamma B_1^3+m$ contains another point $y\in \mathrm{ext}{T}_k$, then

$$-1-\gamma \le ⟨m|-f_x⟩\le \gamma -11.$$

(11)

Proof. 

By (4), we have $⟨x|f_x⟩=11\le ⟨m|f_x⟩+\gamma$, which implies (10).

Assume that $|p_{i_0}\left(x\right)| =1$. For each $y\in \mathrm{ext}{T}_k\setminus \left\{x\right\}$, we have $|p_{i_0}\left(y\right)| =6$ and

$$⟨y|-f_x⟩=\mathrm{sgn}{p}_{i_0}\left(x\right)p_{i_0}\left(y\right)+\sum _{i\in \left[3\right]\setminus \left\{i_0\right\}}(-\mathrm{sgn}{p}_i\left(x\right))p_i\left(y\right)=-1.$$

By (4), we have $⟨y|-f_x⟩=-1\le ⟨m|-f_x⟩+\gamma$, from which (11) follows. □

Take $y=(6,1,-6)\in \mathrm{ext}{T}_2\cap (\gamma B_1^3+m)$ for example. We have $f_y=(1,-1,-1)=-f_4$. From (10), it follows that $⟨m|f_4⟩\le \gamma -11$. By (4), we have

$$⟨x|f_4⟩\le ⟨m|f_4⟩+\gamma \le 2\gamma -11,\forall x\in \gamma B_1^3+m.$$

(12)

If $y=(6,1,6)\in \mathrm{ext}{T}_1\cap (\gamma B_1^3+m)$, then $f_y=(1,-1,1)=f_3$. By (10), we have

$$⟨x|-f_3⟩\le ⟨m|-f_3⟩+\gamma \le 2\gamma -11,\forall x\in \gamma B_1^3+m.$$

(13)

We end this subsection with the following result.

Lemma 3.

${\Gamma }_{14}\left(B_1^3\right)\le 7/13$.

Proof. 

We only need to prove that $13B_1^3\subseteq 7B_1^3+P$. By Lemma 1 and

$$-\bigcup _{k\in \{1,2,5,6\}}{S}_k=\bigcup _{k\in \{3,4,7,8\}}{S}_k,$$

it suffices to show that

$$\bigcup _{k\in \{1,2,5,6\}}{S}_k\subseteq 7B_1^3+P_1.$$

(14)

Clearly,

$$S_1=(H_{f_1,7}^{+}\cap S_1)\cup (H_{f_1,7}^{-}\cap S_1).$$

It can be verified that

$$\mathrm{ext}(S_1\cap H_{f_1,7}^{+})\subseteq 7B_1^3+(5,5,4) \mathrm{and} \mathrm{ext}(S_1\cap H_{f_1,7}^{-})\subseteq 7B_1^3+(2,2,-2).$$

Hence,

$$S_1\subseteq (7B_1^3+(2,2,-2))\cup (7B_1^3+(5,5,4)).$$

(15)

Note that

$$\begin{array}{c}{Q}_1\left(S_1\right)=S_6,Q_2\left(S_1\right)=S_5,\\ Q_1(2,2,-2)=Q_2(2,2,-2)=(2,2,-2),\\ Q_1(5,5,4)=(-4,5,-5),Q_2(5,5,4)=(5,-4,-5).\end{array}$$

These equalities and (15) show that

$$S_5\cup S_6\subseteq 7B_1^3+\left\{(-4,5,-5),(5,-4,-5),(2,2,-2)\right\}.$$

Clearly, $Q_3\left(S_1\right)=S_2$. By Lemma 1,

$$S_2=H_{f_2,13}^{-}\cap H_{f_1,1}^{+}\cap H_{-f_3,1}^{+}\cap H_{-f_4,1}^{+}.$$

Straightforward calculations show that (see Table 3 and [15])

$$\begin{array}{c}\mathrm{ext}(S_2\cap H_{f_1,9}^{+})\subseteq 7B_1^3+(5,5,4),\\ \mathrm{ext}(S_2\cap H_{-f_3,9}^{+})\subseteq 7B_1^3+(-4,5,-5),\\ \mathrm{ext}(S_2\cap H_{-f_4,9}^{+})\subseteq 7B_1^3+(5,-4,-5),\\ \mathrm{ext}(S_2\cap H_{f_1,9}^{-}\cap H_{-f_3,9}^{-}\cap H_{-f_4,9}^{-})\subseteq 7B_1^3+(2,2,-2).\end{array}$$

Table 3. The proof of (14).

Polytope	Vertices	Center
$S_1\cap H_{f_1,7}^{+}$	$\left\{(6,6,1),(6,1,6),(1,6,6),(1,3,3),(3,3,1),(3,1,3)\right\}$	$(5,5,4)$
$S_1\cap H_{f_1,7}^{-}$	$\left\{(3,3,1),(3,1,3),(1,1,1),(1,3,3)\right\}$	$(2,2,-2)$
$S_5\cap H_{f_5,7}^{+}$	$\left\{(6,-6,-1),(6,-1,-6),(1,-6,-6),(1,-3,-3),(3,-3,-1),(3,-1,-3)\right\}$	$(5,-4,-5)$
$S_5\cap H_{f_5,7}^{-}$	$\left\{(3,-3,-1),(3,-1,-3),(1,-1,-1),(1,-3,-3)\right\}$	$(2,2,-2)$
$S_6\cap H_{f_6,7}^{+}$	$\left\{(-6,6,-1),(-6,1,-6),(-1,6,-6),(-1,3,-3),(-3,3,-1),(-3,1,-3)\right\}$	$(-5,5,-5)$
$S_6\cap H_{f_6,7}^{-}$	$\left\{(-3,3,-1),(-3,1,-3),(-1,1,-1),(-1,3,-3)\right\}$	$(2,2,-2)$
$S_2\cap H_{f_1,9}^{-}\cap H_{-f_3,9}^{-}\cap H_{-f_4,9}^{-}$	$\left\{\right(2,6,-5),(5,6,-2),(6,5,-2),(6,2,-5),(5,5,-1),$ $(1,1,-1),(5,1,-5),(2,5,-6),(1,5,-5),(5,2,-6)\}$	$(2,2,-2)$
$S_2\cap H_{f_1,9}^{+}$	$\left\{(6,6,-1),(6,5,-2),(5,5,-1),(5,6,-2)\right\}$	$(5,5,4)$
$S_2\cap H_{-f_3,9}^{+}$	$\left\{(2,6,-5),(2,5,-6),(1,6,-6),(1,5,-5)\right\}$	$(-4,5,-5)$
$S_2\cap H_{-f_4,9}^{+}$	$\left\{(6,2,-5),(5,2,-6),(5,1,-5),(6,1,-6)\right\}$	$(5,-4,-5)$

Hence,

$$\begin{array}{c}{S}_2\subseteq 7B_1^3+\left\{(2,2,-2),(5,5,4),(-4,5,-5),(5,-4,-5)\right\}.\hspace{1em}\square \end{array}$$

2.2. Auxiliary Lemmas

In the rest of Section 2, $\gamma$ will always be a number in $(0,7)$. Let $k,j\in \left[8\right]$. $S_k$ ($T_k$, resp.) and $S_j$ ( $T_j$, resp.) are said to be adjacent (denoted by $S_k\sim S_j$ or $T_k\sim T_j$) if they are contained in adjacent orthants. The following lemma is of fundamental importance for this section.

Lemma 4.

Suppose that $k,j\in \left[8\right]$ are distinct, $m\in {\mathbb{R}}^3$, and $S_j\nsim S_k$. If $T_k\cap (\gamma B_1^3+m)\ne \varnothing$; then, $S_j\cap (\gamma B_1^3+m)=\varnothing$. In particular, a translate of $\gamma B_1^3$ intersects at most two members of $\mathcal{T}$, which are adjacent.

Proof. 

Fix $x\in T_k\cap (\gamma B_1^3+m)$. Clearly, $⟨x|f_k⟩=13$.

Let $y\in 13B_1^3\cap O_j\cap (\gamma B_1^3+m)$. By (4) and (5), we have

$$⟨y|-f_k⟩\le ⟨m|-f_k⟩+\gamma \le 2\gamma +⟨x|-f_k⟩=2\gamma -13<1.$$

Since $S_j\nsim S_k$, there are two possible cases.

Case 1. $\mathrm{sgn}{p}_i\left(y\right)=-\mathrm{sgn}{p}_i\left(x\right),\forall i\in \left[3\right]$. Then, for each $g\in F$, we have

$$⟨y|g⟩\le \sum _{i\in \left[3\right]}\left|p_i\left(y\right)\right|=⟨y|-f_k⟩<1.$$

Case 2. There exists a unique $i_0\in \left[3\right]$ such that $\mathrm{sgn}{p}_{i_0}\left(x\right)=\mathrm{sgn}{p}_{i_0}\left(y\right)$. Then, for each $g\in \mathrm{sgn}{p}_{i_0}\left(x\right)F_{i_0}$, we have

$$⟨y|-g⟩\le \sum _{i\in \left[3\right]\setminus \left\{i_0\right\}}|p_i\left(y\right)|-\mathrm{sgn}{p}_{i_0}\left(x\right)p_{i_0}\left(y\right)=⟨y|-f_k⟩<1.$$

In both cases, by Lemma 1, we have $y\notin S_j$.

To complete the proof, it is sufficient to note that among any three distinct orthants, there is a pair that are not adjacent. □

Lemma 5.

Let $m\in {\mathbb{R}}^3$.

(a) 

If there exists a $k\in \left[8\right]$ such that $T_k\subseteq \gamma B_1^3+m$, then $⟨m|-f_k⟩+\gamma <-5$.

(b) 

If $(\gamma B_1^3+m)\cap V\ne \varnothing$, then, for each $k\in \left[8\right]$, $\gamma B_1^3+m$ contains at most two points in $\mathrm{ext}{T}_k$.

(c) 

For each $k\in \left[8\right]$, $S_k$ cannot be covered by a single translate of $\gamma B_1^3$.

Proof. 

We only need to show (a) and (b).

(a). Take $x\in \mathrm{ext}{T}_k$. By Lemma 2, we have

$$-8<-1-\gamma \le ⟨m|-f_x⟩<-4.$$

Since a point is in $\mathrm{ext}{T}_k$ if and only if its coordinates is a permutation of the coordinates of x, we have

$$\begin{array}{c}\mathrm{sgn}{p}_1\left(x\right)p_1\left(m\right)-\mathrm{sgn}{p}_2\left(x\right)p_2\left(m\right)-\mathrm{sgn}{p}_3\left(x\right)p_3\left(m\right)\in (-8,-4),\\ -\mathrm{sgn}{p}_1\left(x\right)p_1\left(m\right)-\mathrm{sgn}{p}_2\left(x\right)p_2\left(m\right)+\mathrm{sgn}{p}_3\left(x\right)p_3\left(m\right)\in (-8,-4),\\ -\mathrm{sgn}{p}_1\left(x\right)p_1\left(m\right)+\mathrm{sgn}{p}_2\left(x\right)p_2\left(m\right)-\mathrm{sgn}{p}_3\left(x\right)p_3\left(m\right)\in (-8,-4).\end{array}$$

It follows that

$$⟨m|-f_k⟩=-\sum _{i\in \left[3\right]}\mathrm{sgn}{p}_i\left(x\right)p_i\left(m\right)<-12.$$

Thus,

$$⟨m|-f_k⟩+\gamma <\gamma -12<-5.$$

(16)

(b). Assume the contrary that there exists $k\in \left[8\right]$ such that $\mathrm{ext}{T}_k\subseteq \gamma B_1^3+m$. Let $v\in V\cap (\gamma B_1^3+m)$. By (4), we have $-3\le ⟨v|-f_k⟩\le ⟨m|-f_k⟩+\gamma$. By (16), $⟨m|-f_k⟩+\gamma <-5$, which is a contradiction. □

Let $T_k$ and $T_j$ be adjacent, with the signs of their $i_0$-th coordinates being opposite. Set

$$D_{kj}=\left\{x\in \mathrm{ext}{T}_k\left|\right|p_{i_0}\left(x\right)|=6\right\}\mathrm{and}{N}_{kj}=\left\{x\in \mathrm{ext}{T}_k\left|\right|p_{i_0}\left(x\right)|=1\right\}.$$

Clearly, $\#D_{kj}=\#D_{jk}=2$ and $\#N_{kj}=\#N_{jk}=1$. Let $x\in D_{kj}$ and $y\in D_{jk}$. We write $x\equiv y$ if $|p_i\left(x\right)|=|p_i\left(y\right)|,\forall i\in \left[3\right]$. Otherwise, we write $x\not\equiv y$ and we have ${\Vert x-y\Vert }_1={\Vert (1,6,6)-(6,1,-6)\Vert }_1=22$. Thus, if $x\not\equiv y$, then they cannot be covered by a single translate of $\gamma B_1^3$.

Clearly, we have

Lemma 6.

Suppose that $T_k\sim T_j$ and B is a translate of $\gamma B_1^3$.

(a) 

$\#(B\cap (D_{kj}\bigsqcup D_{jk}))\le 2$ and $\#(B\cap (\mathrm{ext}{T}_k\cup \mathrm{ext}{T}_j))\le 4$.

(b) 

If $\#(B\cap \mathrm{ext}{T}_k)=\#(B\cap \mathrm{ext}{T}_j)=2$, then there exist $x\in D_{kj}\cap B$ and $y\in D_{jk}\cap B$ such that $x\equiv y$, and $x^{\prime }\in N_{kj}\cap B$ and $y^{\prime }\in N_{jk}\cap B$.

Lemma 7.

Let $m\in {\mathbb{R}}^3$. Suppose that $T_k\sim T_j$. If $c_j\in \gamma B_1^3+m$, then

(a) 

$(\gamma B_1^3+m)\cap D_{kj}=\varnothing$,

(b) 

$\#((\gamma B_1^3+m)\cap {\bigcup }_{k\in \left[8\right]\setminus \left\{j\right\}}\mathrm{ext}{T}_k)\le 1=\#N_{kj}$.

Proof. 

(a). By applying a transformation in $\mathcal{G}$ if necessary, we may assume that $k\in \{2,3,4\}$ and $j=1$. Suppose that the $i_0$-th coordinates of $T_k$ and $T_1$ are with the opposite sign. Let $x\in D_{k1}\cap (\gamma B_1^3+m)$. Then, one of the coordinates of x is 1 and $p_{i_0}\left(x\right)=-6$. By Lemma 2, one coordinate of $-f_x$ (see (9) for the definition) is $-1$ and the other two are 1. It follows that $⟨c_1|-f_x⟩\ge 3>2\gamma -11$. If $c_1\in \gamma B_1^3+m$, then, by (4), we have $2\gamma -11<⟨c_1|-f_x⟩\le ⟨m|-f_x⟩+\gamma$, which contradicts (10). Hence, $(\gamma B_1^3+m)\cap D_{k1}=\varnothing$.

(b). It follows from Lemma 4 and Lemma 7a. □

Suppose that $T_k\sim T_j$. Lemma 7 shows that a translate of $\gamma B_1^3$ containing $c_j$ cannot contain any point in $D_{kj}$. Conversely, a translate of $\gamma B_1^3$ containing a point in $D_{kj}$ cannot contain $c_j$. Particularly, in the case of Lemma 6b, $(\gamma B_1^3+m)\cap C=\varnothing$.

Lemma 8.

Let B be a translate of $\gamma B_1^3$.

(a) 

If $\{c_1,(1,6,6),(5,6,2)\}\subseteq B$, then $B\cap C=\left\{c_1\right\}$.

(b) 

If $\{c_2,(1,6,-6),(5,6,-2)\}\subseteq B$, then $B\cap C=\left\{c_2\right\}$.

Proof. 

By symmetry, we only need to prove (a). By Lemma 4, $B\cap C\subseteq \left\{c_1,c_2,c_3,c_4\right\}$. Lemma 7 and the fact $(1,6,6)\in D_{12}\cap D_{13}$ show that $c_2,c_3\notin B$. The distance from $c_4=(-4,4,5)$ to $(5,6,2)$ is 14. Thus, $c_4\notin B$. □

Lemma 9.

Let $m\in {\mathbb{R}}^3$.

(a) 

If $\{(1,6,-6),(6,1,-6),(6,6,1)\}\subseteq \gamma B_1^3+m$, then $v_1\notin \gamma B_1^3+m$.

(b) 

If $\left\{(1,6,6),(6,1,6),v_1\right\}\subseteq \gamma B_1^3+m$, then $\{(5,6,2),(6,5,2)\}\notin \gamma B_1^3+m$.

(c) 

If $\left\{(6,1,-6),(6,6,1),v_1\right\}\subseteq \gamma B_1^3+m$, then $c_2\notin \gamma B_1^3+m$.

Proof. 

(a). By the hypothesis and (4), we have

$$\begin{array}{c}1·(6-p_1\left(m\right))+(-1)·(1-p_2\left(m\right))+(-1)·(-6-p_3\left(m\right))\le \gamma ,\\ (-1)·(1-p_1\left(m\right))+1·(6-p_2\left(m\right))+(-1)·(-6-p_3\left(m\right))\le \gamma ,\\ 1·(6-p_1\left(m\right)+1·(6-p_2\left(m\right))+1·(1-p_3\left(m\right))\le \gamma .\end{array}$$

Adding these inequalities, we have

$$-p_1\left(m\right)-p_2\left(m\right)+p_3\left(m\right)+35\le 3\gamma \mathrm{and} ⟨m|-f_2⟩+\gamma \le 4\gamma -35<-7.$$

By $⟨v_1|-f_2⟩=-1>⟨m|-f_2⟩+\gamma$ and (4), $v_1\notin \gamma B_1^3+m$.

(b). By the hypothesis and (4), we have

$$\begin{array}{c}1·\left(6-p_1\left(m\right)\right)+(-1)·\left(1-p_2\left(m\right)\right)+1·\left(6-p_3\left(m\right)\right)\le \gamma ,\\ (-1)·\left(1-p_1\left(m\right)\right)+1·\left(6-p_2\left(m\right)\right)+1·\left(6-p_3\left(m\right)\right)\le \gamma ,\\ (-1)·\left(1-p_1\left(m\right)\right)+(-1)·\left(1-p_2\left(m\right)\right)+(-1)·\left(1-p_3\left(m\right)\right)\le \gamma .\end{array}$$

It follows that

$$p_1\left(m\right)+p_2\left(m\right)-p_3\left(m\right)+19\le 3\gamma \mathrm{and} ⟨m|f_2⟩+\gamma \le 4\gamma -19<7.$$

By $⟨(5,6,2)|f_2⟩=⟨(6,5,2)|f_2⟩=9>⟨m|f_2⟩+\gamma$ and (4), we have $(5,6,2),(6,5,2)\notin \gamma B_1^3+m$.

(c). By the hypothesis and (4), we have

$$\begin{array}{c}1·\left(6-p_1\left(m\right)\right)+(-1)·\left(1-p_2\left(m\right)\right)+(-1)·(-6-p_3\left(m\right))\le \gamma ,\\ 1·\left(6-p_1\left(m\right)\right)+1·\left(6-p_2\left(m\right)\right)+1·(1-p_3\left(m\right))\le \gamma ,\\ (-1)·\left(1-p_1\left(m\right)\right)+(-1)·\left(1-p_2\left(m\right)\right)+1·\left(1-p_3\left(m\right)\right)\le \gamma .\end{array}$$

Therefore,

$$-p_1\left(m\right)+p_2\left(m\right)-p_3\left(m\right)+23\le 3\gamma \mathrm{and} ⟨m|-f_3⟩+\gamma \le 4\gamma -23<5.$$

By $⟨c_2|-f_3⟩=5>⟨m|-f_3⟩+\gamma$ and (4), we have $c_2\notin \gamma B_1^3+m$. □

Lemma 10.

Let $m\in {\mathbb{R}}^3$. If $(\gamma B_1^3+m)\cap \mathrm{ext}\left(13B_1^3\right)\ne \varnothing$, then

$$(\gamma B_1^3+m)\cap \left(\bigcup _{k\in \left[8\right]}{S}_k\right)=\varnothing .$$

Proof. 

By symmetry, we only need to consider the case when $13e_1\in \gamma B_1^3+m$. By (5), we have

$$⟨m|-f⟩+\gamma \le 2\gamma +⟨13e_1|-f⟩=2\gamma -13<1,\forall f\in F_1.$$

Let $x\in \gamma B_1^3+m$. By (4), we have

$$⟨x|-f⟩\le ⟨m|-f⟩+\gamma <1,\forall f\in F_1.$$

By (6), (7), and Lemma 1, we have $x\notin {\displaystyle \bigcup _{k\in \left[8\right]}}{S}_k$. □

In the rest of this section, $M\subseteq {\mathbb{R}}^3$ is a set satisfying $13B_1^3\subseteq \gamma B_1^3+M$,

$$M_0=\left\{m\in M|(\gamma B_1^3+m)\cap \mathrm{ext}\left(13B_1^3\right)\ne \varnothing \right\}.$$

Let $x,y\in \mathrm{ext}\left(13B_1^3\right)$ be distinct. Then, ${\Vert x-y\Vert }_1=26$, which implies that $\#M_0\ge 6$. Set $M_1=M\setminus M_0$. By Lemma 10,

$$\bigcup _{k=1}^8{S}_k\subseteq \gamma B_1^3+M_1.$$

(17)

Set ${\mathcal{M}}_1=\left\{\gamma B_1^3+m|m\in M_1\right\}$.

Recall that A 2-regular graph is a graph where each vertex is connected to exactly two other vertices.

Lemma 11.

Let ${\mathcal{T}}^{\prime }\subseteq \mathcal{T}$ and ${\mathcal{M}}_1^{\prime }\subseteq {\mathcal{M}}_1$ be two sets satisfying $\#{\mathcal{T}}^{\prime }=\#{\mathcal{M}}_1^{\prime }=k\in \left[8\right]$, $G^{\prime }$ be the bipartite graph with bipartitions ${\mathcal{T}}^{\prime }$ and ${\mathcal{M}}_1^{\prime }$, where $T\in {\mathcal{T}}^{\prime }$ and $B\in {\mathcal{M}}_1^{\prime }$ are connected by an edge if and only if $T\cap B\ne \varnothing$. If

(a) 

$\bigcup {\mathcal{T}}^{\prime }\subseteq \bigcup {\mathcal{M}}_1^{\prime }$,

(b) 

no member of ${\mathcal{T}}^{\prime }$ can be covered by a single translate of ${\mathcal{M}}_1$,

(c) 

and $G^{\prime }$ is 2-regular,

then, for each pair of distinct members $T_i$ and $T_j$ of ${\mathcal{T}}^{\prime }$, no member of ${\mathcal{M}}_1^{\prime }$ can contain two points in $\mathrm{ext}{T}_i$ and two points in $\mathrm{ext}{T}_j$ simultaneously.

Proof. 

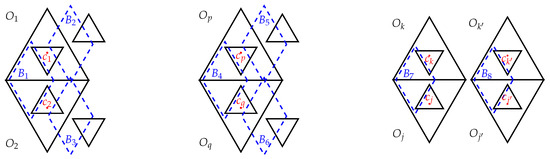
By the hypothesis, each member of ${\mathcal{T}}^{\prime }$ is covered by exactly two members of ${\mathcal{M}}_1^{\prime }$, and each member of ${\mathcal{M}}_1^{\prime }$ intersects exactly two members of ${\mathcal{T}}^{\prime }$.

Assume the contrary that there exist $B_1\in {\mathcal{M}}_1^{\prime }$ and distinct $T_i$,$T_j\in {\mathcal{T}}^{\prime }$ such that $B_1$ contains two points in $\mathrm{ext}{T}_i$ and two points in $\mathrm{ext}{T}_j$. By Lemma 4, $T_i\sim T_j$. Without loss of generality, we may assume that $i=1,j=2$. By Lemma 6, we may also assume (exchange the first two coordinates if necessary) that

$$\{(6,6,1),(6,1,6),(6,1,-6),(6,6,-1)\}\subseteq B_1.$$

Let $B_2$ and $B_3$ be members of ${\mathcal{M}}_1^{\prime }$ such that $T_1\subseteq B_1\cup B_2$ and $T_2\subseteq B_1\cup B_3$. See Figure 1. By Lemma 7,

$$C\cap B_1=\varnothing \mathrm{and} B_2\ne B_3.$$

Figure 1. The covering configuration described in Lemma 11.

Note that $\{(6,1,6),(6,1,-6)\}\subseteq B_1$. By (10), we have $B_1\subseteq H_{f_4,3}^{-}\cap H_{-f_3,3}^{-}$.

Then, $T_1\cap H_{f_4,3}^{+}\subseteq B_2$ and $T_2\cap H_{-f_3,3}^{+}\subseteq B_3$. It can be verified that (see also [15])

$$\begin{array}{c}\mathrm{ext}(T_1\cap H_{f_4,3}^{+})=\left\{(5,6,2),(5,2,6),(1,6,6)\right\}\subseteq B_2,\\ \mathrm{ext}(T_2\cap H_{-f_3,3}^{+})=\left\{(5,6,-2),(5,2,-6),(1,6,-6)\right\}\subseteq B_3.\end{array}$$

From Lemma 8, it follows that

$$C\cap B_2=\left\{c_1\right\} \mathrm{and} C\cap B_3=\left\{c_2\right\}.$$

(18)

By Lemma 7, $B_1\cup B_2\cup B_3$ contains at most eight points of ${\bigcup }_{T\in {\mathcal{T}}^{\prime }}\mathrm{ext}T$. Clearly, $k>3$. Since $(3k-8)/(k-3)>3$, there exists $B_4\in {\mathcal{M}}_1^{\prime }$ that contains two points in $\mathrm{ext}{T}_p$ and two points in $\mathrm{ext}{T}_q$, where $p,q\notin \{1,2\}$. Let $B_5$ and $B_6$ be two members of ${\mathcal{M}}_1^{\prime }$ such that $T_p\subseteq B_4\cup B_5$ and $T_q\subseteq B_4\cup B_6$. As above, we have $B_5\ne B_6$. By (18), we have

$$B_5,B_6\notin \left\{B_1,B_2,B_3,B_4\right\} \mathrm{and} k\ge 6.$$

By Lemma 7 again, $B_5\cup B_6$ can cover at most two points in

$$\left(\bigcup _{T\in {\mathcal{T}}^{\prime }}\mathrm{ext}T\right)\setminus (B_1\cup B_2\cup B_3\cup B_4).$$

Therefore, at least $3k-(8+6+2)=3k-16$ points in ${\bigcup }_{T\in {\mathcal{T}}^{\prime }}\mathrm{ext}T$ remain uncovered, while the number of the remaining translates of $\gamma B_1^3$ is $k-6$. Thus, $k>6$.

If $k=7$, then there exists a member of ${\mathcal{M}}_1^{\prime }$ containing five points in E, which contradicts Lemma 6. If $k=8$, then the remaining two members $B_7$ and $B_8$ of ${\mathcal{M}}_1^{\prime }$ contain eight points of ${\bigcup }_{\{T\in {\mathcal{T}}^{\prime }\}}\mathrm{ext}T$. By Lemma 7, $B_7\cup B_8$ contains no point in C, which is a contradiction. □

Lemma 12.

If $\#M_1=8$, then there exist $m_0\in M_1$ and $k_0\in \left[8\right]$ such that $T_{k_0}\subseteq \gamma B_1^3+m_0$.

Proof. 

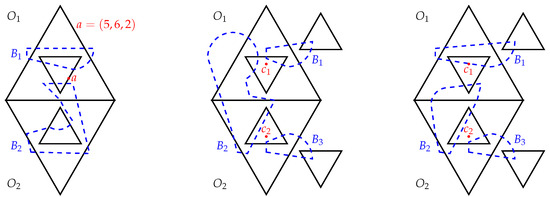
Let $G^{\prime }$ be the bipartite graph defined as in Lemma 11 with bipartitions $\mathcal{T}$ and ${\mathcal{M}}_1$. By Lemma 4, the total number of edges is at most 16.

Assume the contrary that, for each $m\in M_1$ and $k\in \left[8\right]$, $T_k\setminus (\gamma B_1^3+m)\ne \varnothing$. Then, for each $k\in \left[8\right]$, the degree of $T_k$ in $G^{\prime }$ is at least two. Thus, $G^{\prime }$ is 2-regular.

Let

$$\begin{array}{c}N=\max \left\{\#((\gamma B_1^3+m)\cap \left(\bigcup _{i\in \left[8\right]}\mathrm{ext}{T}_k\right))|m\in M_1\right\}.\end{array}$$

Clearly, $N\ge 24/8=3$. By Lemmas 4 and 6, $N\le 4$. By Lemmas 6 and 11, we only need to consider the case when $N=3$. For each $m\in M_1$, we have

$$(E\cap (\gamma B_1^3+m))\cap (\gamma B_1^3+M_1\setminus \left\{m\right\})=\varnothing .$$

(19)

Then, for each $m\in M_1$, there exists a unique $\{k,j\}\subseteq \left[8\right]$ such that $\gamma B_1^3+m$ contains one point in $\mathrm{ext}{T}_k$ and two points in $\mathrm{ext}{T}_j$, where $T_j\sim T_k$.

Let $B_1$ and $B_2$ be two members of ${\mathcal{M}}_1$ such that $T_1\subseteq B_1\cup B_2$. Without loss of generality, we may assume that

$$\#(B_2\cap \mathrm{ext}{T}_1)=1 \mathrm{and} \#(B_2\cap \mathrm{ext}{T}_2)=2.$$

See Figure 2.

Figure 2. The cases in Lemma 12, when $N=3$.

We claim that $v_1\in B_1\cup B_2$. Otherwise, there exists $B^{\prime }$ in ${\mathcal{M}}_1$ such that $v_1\in S_1\cap B^{\prime }$. By Lemma 4, $B^{\prime }\cap \left({\cup }_{k\in \{5,6,7,8\}}{T}_k\right)=\varnothing$. From (19), it follows that $\#(B^{\prime }\cap {\bigcup }_{k\in \{2,3,4\}}\mathrm{ext}{T}_k)=3$, which contradicts Lemma 4 since $T_2,T_3$, and $T_4$ are pairwise nonadjacent.

There are two cases.

Case a. $(6,6,-1)\notin B_2$. Then, $D_{21}\subseteq B_2$. It follows that $B_2\cap T_1=N_{12}=\left\{(6,6,1)\right\}$. By Lemma 9a, $v_1\notin B_2$. Thus,

$$\left\{(1,6,6),(6,1,6),v_1\right\}\subseteq B_1.$$

(20)

By Lemma 9b, $(5,6,2)\notin B_1$. Since ${\left|\right|(5,6,2)-(6,1,-6)\left|\right|}_1=14$, $(5,6,2)\notin B_2$. Clearly, $(5,6,2)=(1/5)(1,6,6)+(4/5)(6,6,1)\in T_1$, which is a contradiction.

Case b. $(6,6,-1)\in B_2$. Without loss of generality, we may assume (exchange the first two coordinates if necessary) that $(6,1,-6)\in B_2$. By Lemma 6, $(1,6,6)\notin B_2$. Then, either $(6,1,6)$ or $(6,6,1)$ is contained in $B_2$.

If $\left\{(6,1,-6),(6,6,-1),(6,1,6)\right\}\subseteq B_2$, then, by $(6,1,6)\in B_2$ and Lemma 7, $c_2\notin B_2$. By Lemma 7b and (19), there exists a member of ${\mathcal{M}}_1$ containing $c_2$ that contains at most two points in E, which is a contradiction.

Now, assume that $\left\{(6,1,-6),(6,6,-1),(6,6,1)\right\}\subseteq B_2$. We claim that $v_1\in B_2$. Otherwise, (20) holds, which yields a contradiction as in Case a. From Lemma 9c, it follows that $c_2\notin B_2$, which contradicts Lemma 7b and (19). □

Corollary 1.

If $\#M_1=8$, then there exist $m\in M_1$ and distinct $k_0,j_0\in \left[8\right]$ such that

$$T_{k_0}\subseteq \gamma B_1^3+m \mathit{and} T_{j_0}\cap (\gamma B_1^3+m)\ne \varnothing .$$

Proof. 

Set

$$\begin{array}{c}I=\left\{k\in \left[8\right]|\exists m\in M_1\mathrm{s}.\mathrm{t}.T_k\subseteq \gamma B_1^3+m\right\},\\ J=\left\{m\in M_1|\exists k\in \left[8\right]\mathrm{s}.\mathrm{t}.T_k\subseteq \gamma B_1^3+m\right\}.\end{array}$$

Let

$$\begin{array}{c}{\mathcal{T}}_1=\left\{T_k|k\in I\right\},{\mathcal{T}}_2=\left\{T_{k^{\prime }}|k^{\prime }\in \left[8\right]\setminus I\right\},\\ {\mathcal{M}}_1^1=\left\{\gamma B_1^3+m|m\in J\right\}, \mathrm{and} {\mathcal{M}}_1^2=\left\{\gamma B_1^3+m^{\prime }|m^{\prime }\in M_1\setminus J\right\}.\end{array}$$

Assume the contrary that, for each $m\in M_1$ and each $k\in \left[8\right]$ satisfying $T_k\subseteq \gamma B_1^3+m$, we have

$$\left(\bigcup _{i\in \left[8\right]\setminus \left\{k\right\}}{T}_i\right)\cap (\gamma B_1^3+m)=\varnothing .$$

(21)

Thus, $\#I\le \#J$.

Considering the bipartite graph G defined as in Lemma 11 with bipartitions $\mathcal{T}$ and ${\mathcal{M}}_1$. Each member of ${\mathcal{M}}_1^1$ has degree 1 in G and, by Lemma 4, each member of ${\mathcal{M}}_1^2$ has degree at most 2. Thus, the total number L of edges of G satisfies

$$L\le 2(8-\#J)+\#J=16-\#J.$$

Each member of ${\mathcal{T}}_1$ has degree at least 1 and each member of ${\mathcal{T}}_2$ has degree at least 2. Therefore, we have $L\ge 16-\#I$. It follows that $L=16-\#I=16-\#J$, and the subgraph $G^{\prime }$ of G with bipartitions ${\mathcal{T}}_2$ and ${\mathcal{M}}_1^2$ is 2-regular.

By Lemma 5, we have $\left[8\right]\setminus I\ne \varnothing$. By Lemma 12, there exist $k\in I$ and $m\in J$ such that $T_k\subseteq \gamma B_1^3+m$. From Lemma 5b, it follows that $v_k\notin \gamma B_1^3+m$. Then, there exists an $m^{\prime }\in M_1$ such that $v_k\in \gamma B_1^3+m^{\prime }$. By Lemma 4, $\gamma B_1^3+m^{\prime }$ can only intersect with the three members of $\mathcal{T}$ that are adjacent to $T_k$. Note that these three members of $\mathcal{T}$ are pairwise nonadjacent. From Lemma 5b and Lemma 4, it follows that $\gamma B_1^3+m^{\prime }$ contains at most two points in $E\setminus \mathrm{ext}{T}_k$ and $m^{\prime }\in M_1\setminus J$.

Clearly, $(\#E-3\#I-2)/(8-\#I-1)>3$. By the pigeon hole principle and Lemma 6, there exist $m_1\in M_1\setminus J$ and $k_1,k_2\in \left[8\right]\setminus I$ such that $\gamma B_1^3+m_1$ contains two points in $\mathrm{ext}{T}_{k_1}$ and two points in $\mathrm{ext}{T}_{k_2}$, which contradicts Lemma 11. □

2.3. The Proof of Theorem 1

Suppose the contrary that there exists a set $M\subseteq {\mathbb{R}}^3$ with $\#M=14$ such that $13B_1^3\subseteq \gamma B_1^3+M$. By (17), we have ${\bigcup }_{k=1}^8{S}_k\subseteq \gamma B_1^3+M_1$, where $\#M_1\le 8$.

By Corollary 1, without loss of generality, we may assume that there exists $m_1\in M_1$ such that

$$T_1\subseteq \gamma B_1^3+m_1 \mathrm{and} T_2\cap (\gamma B_1^3+m_1)\ne \varnothing .$$

(22)

Lemma 13.

$\mathrm{conv}\left\{(3,1,3),(1,3,3),(3,3,1),v_1\right\}\subseteq S_1\setminus (\gamma B_1^3+m_1)$.

Proof. 

Take $x\in T_2\cap (\gamma B_1^3+m_1)$, then $⟨m_1|f_2⟩+\gamma \ge 13=⟨x|f_2⟩$, which is equivalent to

$$-p_1\left(m_1\right)-p_2\left(m_1\right)+p_3\left(m_1\right)\le \gamma -13.$$

By $T_1\subseteq \gamma B_1^3+m_1$, we have

$$\begin{array}{c}(6-p_1\left(m_1\right))-(1-p_2\left(m_1\right))+(6-p_3\left(m_1\right))\le \gamma ,\\ -(1-p_1\left(m_1\right))+(6-p_2\left(m_1\right))+(6-p_3\left(m_1\right))\le \gamma .\end{array}$$

It follows that $⟨m_1|-f_1⟩+22\le 3\gamma -13$. Hence, $⟨m_1|-f_1⟩+\gamma <-7$.

By (4), we have

$$S_1\cap (\gamma B_1^3+m_1)\subseteq S_1\cap \left\{x|⟨x|-f_1⟩<-7\right\}.$$

It can be verified that (see also [15])

$$\mathrm{conv}\left\{(3,1,3),(1,3,3),(3,3,1),v_1\right\}\subseteq S_1\cap H_{f_1,7}^{-}\subseteq S_1\setminus (\gamma B_1^3+m_1).\hspace{1em}\square$$

Set

$$\begin{array}{c}{a}_2=(6,5,-2),a_3=(6,-1,6),a_4=(-1,6,6),a_5=(4,-3,-6),\\ a_6=(-3,4,-6),a_7=(-2,-6,5),a_8=(-6,-4,-3),\end{array}$$

and $A=\left\{a_k|k\in \left[8\right]\setminus \left\{1\right\}\right\}$. It can be verified that $a_k\in T_k,\forall k\in \left[8\right]\setminus \left\{1\right\}$, and A is 14-separated. For each $k\in \left[8\right]\setminus \left\{1\right\}$, there exists $m_k\in M_1$ such that $a_k\in \gamma B_1^3+m_k$. Clearly, if $k,j\in \left[8\right]\setminus \left\{1\right\}$ are distinct, then $m_k$ and $m_j$ are distinct. By ${\left|\right|a_2-(1,6,6)\left|\right|}_1=14$, we have $a_2\notin \gamma B_1^3+m_1$. By Lemma 4, $m_1\ne m_k,\forall k\in \left[8\right]\setminus \left\{1\right\}$. Hence, $\#M_1=8$ and $M_1=\left\{m_k|k\in \left[8\right]\right\}$. Set

$$B_k=\gamma B_1^3+m_k,\forall k\in \left[8\right].$$

Put

$$A^{\prime }=Q_4\left(A\right)=\left\{a_3,a_4,a_5,a_6\right\}\cup \left\{a_7^{\prime },a_8^{\prime },a_2^{\prime }\right\},$$

where $a_7^{\prime }=Q_4\left(a_7\right)=(-6,-2,5)\in T_7$, $a_8^{\prime }=Q_4\left(a_8\right)=(-4,-6,-3)\in T_8$, and $a_2^{\prime }=Q_4\left(a_2\right)=(5,6,-2)\in T_2$. Since $Q_4$ is a linear isometry on ${\ell }_1^3$, $A^{\prime }$ is also 14-separated.

Clearly, if $i,k\in \left[8\right]$ are distinct and $T_k\cap B_i\ne \varnothing$, then by Lemma 4, $T_i\sim T_k$.

Since $A^{\prime }$ is 14-separated, $a_2^{\prime }\notin B_k,\forall k\in \left[8\right]\setminus \left\{1,2\right\}$. From ${\left|\right|a_2^{\prime }-(6,1,6)\left|\right|}_1=14$, it follows that $a_2^{\prime }\notin B_1$. Thus,

$$a_2^{\prime }\in B_2\setminus \left(\bigcup _{k\in \left[8\right]\setminus \left\{2\right\}}{B}_k\right).$$

On the one hand, neither $T_1$ nor $T_2$ is adjacent to any of $T_7$ and $T_8$ (see Table 1); thus, $a_7^{\prime },a_8^{\prime }\notin B_1\cup B_2$. On the other hand, since $A^{\prime }$ is 14-separated, $a_7^{\prime },a_8^{\prime }\notin B_k,\forall k\in \left\{3,4,5,6\right\}$. Thus, $a_7^{\prime },a_8^{\prime }\in B_7\cup B_8$. Hence, either

$$\{a_7^{\prime },a_7\}\subseteq B_7 \mathrm{and} \{a_8,a_8^{\prime }\}\subseteq B_8,$$

(23)

or

$$\{a_8^{\prime },a_7\}\subseteq B_7 \mathrm{and} \{a_8,a_7^{\prime }\}\subseteq B_8.$$

(24)

By Lemma 4 and Table 1, $T_2\subseteq B_1\cup B_2\cup B_5\cup B_6$. Since $(1,6,6),(6,1,6)\in B_1$ and

$$\begin{array}{c}\hfill \left|\right|(5,2,-6)-(1,6,6)\left|\right|=\left|\right|(6,2,-5)-(1,6,6)\left|\right|=20,\\ \hfill \left|\right|(2,5,-6)-(6,1,6)\left|\right|=\left|\right|(2,6,-5)-(6,1,6)\left|\right|=20,\end{array}$$

we have

$$\{(5,2,-6),(6,2,-5),(2,5,-6),(2,6,-5)\}\subseteq (B_2\cup B_5\cup B_6)\cap T_2.$$

(25)

Lemma 14.

$(5,2,-6),(6,2,-5)\notin B_6$.

Proof. 

By Lemma 4 and Table 1, we obtain all possible locations of points listed in Table 4.

Table 4. Possible k such that $p\in B_k$.

p	Coordinates	k	p	Coordinates	k
$p_1\in T_6$	$(-6,4,-3)$	$2,4,6,8$	$p_4\in T_6$	$(-5,6,-2)$	$2,4,6,8$
$p_2\in T_8$	$(-3,-4,-6)$	$5,6,7,8$	$p_5\in S_1$	$(1,3,3)$	$1,2,3,4$
$p_3\in T_5$	$(5,-6,-2)$	$2,3,5,8$	$p_6\in T_3$	$(6,-5,2)$	$1,3,5,7$

Suppose the contrary that one of the two points $(5,2,-6)$ and $(6,2,-5)$ is in $B_6$. By

$${\left|\right|(5,2,-6)-p_1\left|\right|}_1={\left|\right|(6,2,-5)-p_1\left|\right|}_1=16,$$

$p_1\notin B_6$. By ${\left|\right|a_4-p_1\left|\right|}_1=16$ and ${\left|\right|a_2-p_1\left|\right|}_1=14$, $p_1\notin B_2\cup B_4$. Thus, $p_1\in B_8\cap T_6$. Since $B_8$ intersects both $T_8$ and $T_6$, $a_7^{\prime }\in B_7$ and $a_8^{\prime }\in B_8$.

Note that $p_2\in T_8$. By ${\left|\right|p_1-p_2\left|\right|}_1={\left|\right|a_7-p_2\left|\right|}_1=14$, $p_2\notin B_7\cup B_8$. Since $B_6$ intersects both $T_2$ and $T_6$, $p_2\notin B_6$. Thus, $p_2\in B_5\cap T_8$.

By Table 4 and ${\left|\right|p_2-p_3\left|\right|}_1={\left|\right|a_8-p_3\left|\right|}_1={\left|\right|a_3-p_3\left|\right|}_1=14$, we have $p_3\in B_2$.

By ${\left|\right|(5,2,-6)-p_4\left|\right|}_1={\left|\right|(6,2,-5)-p_4\left|\right|}_1=18$, $p_3\in B_2$, ${\left|\right|p_3-p_4\left|\right|}_1=22$, and ${\left|\right|a_8^{\prime }-p_4\left|\right|}_1=14$, we have $p_4\in B_4$.

Clearly, $p_5\in O_1$. By Lemma 13, $p_5\notin B_1$. Moreover, $p_4\in B_4\cap T_6$, $p_3\in B_2\cap T_5$, and neither $O_6$ nor $O_5$ is adjacent to $O_1$. By Lemma 4, $p_5\notin B_2\cup B_4$. Thus, $p_5\in B_3$.

Since $p_6\in T_3$, $B_1\cap T_1\ne \varnothing$, and $B_1\cap T_2\ne \varnothing$, we have $p_6\notin B_1$. By ${\left|\right|p_5-p_6\left|\right|}_1=14$ and ${\left|\right|a_7^{\prime }-p_6\left|\right|}_1=18$, $p_6\notin B_3\cup B_7$. By $p_2\in B_5\cap T_8$, $B_5$ intersects both $T_5$ and $T_8$, we have $p_6\notin B_5$, a contradiction. □

Corollary 2.

$(2,5,-6),(2,6,-5)\notin B_5$.

Proof. 

Since $13B_1^3\subseteq \gamma B_1^3+M$, we have $13B_1^3\subseteq \gamma B_1^3+Q_4\left(M\right)$. From $T_2=Q_4\left(T_2\right)$ and $T_1=Q_4\left(T_1\right)$, it follows that

$$T_1\subseteq \gamma B_1^3+Q_4\left(m_1\right)\mathrm{and}(\gamma B_1^3+Q_4\left(m_1\right))\cap T_2\ne \varnothing .$$

Thus, $Q_4\left(M\right)$ is a configuration satisfying (22), where $m_1$ is replaced with $Q_4\left(m_1\right)$. Let $m_k^{\prime }$ be the point in $Q_4\left(M\right)$ satisfying $a_k\in \gamma B_1^3+m_k^{\prime }$. Then, since

$$a_6=Q_4\left(a_5\right)\in \gamma B_1^3+Q_4\left(m_5\right),$$

we have $m_6^{\prime }=Q_4\left(m_5\right)$. Applying Lemma 14 on $Q_4\left(M\right)$, we have $(5,2,-6),(6,2,-5)\notin \gamma B_1^3+Q_4\left(m_5\right)$. It follows that $(2,5,-6),(2,6,-5)\notin B_5$. □

By ${\left|\right|a_8-p_3\left|\right|}_1={\left|\right|a_3-p_3\left|\right|}_1=14$ and Table 4, we have $p_3\notin B_3\cup B_8$.

Lemma 15.

$(4,3,-6)\in B_2$.

Proof. 

By Table 1, we only need to show that $(4,3,-6)\notin B_1\cup B_5\cup B_6$.

By $(6,1,6)\in T_1$ and ${\left|\right|(4,3,-6)-(6,1,6)\left|\right|}_1=16$, we have $(4,3,-6)\notin B_1$.

Next, we claim that $(4,3,-6)\notin B_5$. Otherwise, since ${\left|\right|(4,3,-6)-p_3\left|\right|}_1=14$, we would have $p_3\in B_2$. By ${\left|\right|(2,5,-6)-p_3\left|\right|}_1={\left|\right|(2,6,-5)-p_3\left|\right|}_1=18$, (25), and Corollary 2, we have $(2,5,-6),(2,6,-5)\in B_6$.

By Table 1, $(-6,1,-6)$ is contained in $B_2\cup B_4\cup B_6\cup B_8$. By

$${\left|\right|(-6,1,-6)-a_4\left|\right|}_1=22,{\left|\right|(-6,1,-6)-a_2\left|\right|}_1=20,\mathrm{and}{\left|\right|(-6,1,-6)-(2,6,-5)\left|\right|}_1=14,$$

we have $(-6,1,-6)\in B_8$. Hence, $B_8$ intersects both $T_6$ and $T_8$. By Lemma 4, $B_8\cap T_7=\varnothing$, and therefore $a_7^{\prime }\in B_7$. Since ${\left|\right|a_7^{\prime }-(-1,-6,-6)\left|\right|}_1=20$, we have $(-1,-6,-6)\notin B_7$. In the current situation, $B_5$ intersects both $T_5$ and $T_2$, and $B_6$ intersects both $T_6$ and $T_2$. By Lemma 4 and Table 1, $(-1,-6,-6)\in B_8\cap T_8$.

By Table 1, ${\left|\right|(-6,6,-1)-(-1,-6,-6)\left|\right|}_1=22$, and

$${\left|\right|(-6,6,-1)-a_2\left|\right|}_1={\left|\right|(-6,6,-1)-(2,5,-6)\left|\right|}_1=14,$$

we have $(-6,6,-1)\in B_4\cap T_6$.

By Table 1 and Lemma 13, $p_5\in B_k\cap S_1$ for some $k\in \left\{2,3,4\right\}$. Since $B_4$ intersects $T_6$, $B_2$ intersects $T_5$, $O_5\nsim O_1$, and $O_6\nsim O_1$, we have, by Lemma 4, $p_5\in B_3\cap (S_1\setminus T_1)$.

Clearly, $p_6\in T_3$. Since $B_1$ intersects both $T_1$ and $T_2$, $p_6\notin B_1$. By

$${\left|\right|p_5-p_6\left|\right|}_1=14 \mathrm{and} {\left|\right|a_7^{\prime }-p_6\left|\right|}_1=18,$$

$p_6\in B_5\cap T_3$. Hence, $B_5$ intersects $T_2$, $T_3$, and $T_5$, which contradicts Lemma 4.

In the rest of this section, we show that $(4,3,-6)\notin B_6$. Otherwise, by

$${\left|\right|p_1-(4,3,-6)\left|\right|}_1={\left|\right|a_2-p_1\left|\right|}_1=14,$$

and ${\left|\right|a_4-p_1\left|\right|}_1=16$, we have $p_1\in B_8$. Since $B_8$ intersects both $T_6$ and $T_8$, we have $a_7^{\prime }\in B_7$. By

$${\left|\right|p_2-p_1\left|\right|}_1=14 \mathrm{and} {\left|\right|a_7-p_2\left|\right|}_1=14,$$

we have $p_2\notin B_7\cup B_8$. By $(4,3,-6)\in B_6\cap T_2$ and Lemma 4, $p_2\notin B_6$. Thus, $p_2\in B_5\cap T_8$. By Table 4 and

$${\left|\right|p_2-p_3\left|\right|}_1={\left|\right|a_3-p_3\left|\right|}_1={\left|\right|a_8-p_3\left|\right|}_1=14,$$

we have $p_3\in B_2\cap T_5$. Since $B_2$ intersects both $T_2$ and $T_5$, $(-5,6,-2)\notin B_2$. By Table 4,

$${\left|\right|(4,3,-6)-p_4\left|\right|}_1=16, \mathrm{and} {\left|\right|a_8^{\prime }-p_4\left|\right|}_1=14,$$

we have $p_4\in B_4\cap T_6$. Since $B_4$ intersects $T_6$ and $O_6\nsim O_1$, and $B_2$ intersects $T_5$ and $O_5\nsim O_1$, $p_5\notin B_2\cup B_4$. By Lemma 13, $p_5\notin B_1$. Thus, $p_5\in B_3\cap (S_1\setminus T_1)$.

Clearly, $p_6\in T_3$. Since $B_1$ intersects both $T_1$ and $T_2$, $(6,-5,2)\notin B_1$. By

$${\left|\right|p_5-p_6\left|\right|}_1=14,{\left|\right|a_7^{\prime }-p_6\left|\right|}_1=18,$$

and Lemma 4, we have $p_6\in B_5\cap T_3$, contradicting the fact that $B_5$ intersects both $T_5$ and $T_8$. □

Lemma 16.

If $\left\{(5,2,-6),(6,2,-5)\right\}⊈B_5$, then $\left\{(5,2,-6),(6,2,-5)\right\}\subseteq B_2$.

If $\left\{(2,5,-6),(2,6,-5)\right\}⊈B_6$, then $\left\{(2,5,-6),(2,6,-5)\right\}\subseteq B_2$.

Proof. 

We prove the first statement and the other one can be obtained by arguments as in the proof of Corollary 2.

By Lemma 14, either $(5,2,-6)\in B_2$ or $(6,2,-5)\in B_2$.

Case a $(5,2,-6)\in B_2$. By (4), for each $f\in -F_3$, we have

$$\begin{array}{c}⟨m_2|f⟩+\gamma -⟨(6,2,-5)|f⟩\ge ⟨(5,2,-6)|f⟩-⟨(6,2,-5)|f⟩=⟨-1,0,-1|f⟩\ge 0.\end{array}$$

By (4) and $a_2=(6,5,-2)\in B_2$, for each $f\in F_3$, we have

$$\begin{array}{c}⟨m_2|f⟩+\gamma -⟨(6,2,-5)|f⟩\ge ⟨(6,5,-2)|f⟩-⟨(6,2,-5)|f⟩=⟨(0,3,3)|f⟩\ge 0.\end{array}$$

By (4) again, we have $\left\{(5,2,-6),(6,2,-5)\right\}\subseteq B_2$.

Case b $(6,2,-5)\in B_2$. By (4), we have

$$\begin{array}{c}⟨m_2|f⟩+\gamma -⟨(5,2,-6)|f⟩\ge ⟨(6,2,-5)|f⟩-⟨(5,2,-6)|f⟩=⟨(1,0,1)|f⟩\ge 0,\forall f\in F_1.\end{array}$$

From $(4,3,-6)\in B_2$ and (4), it follows that

$$\begin{array}{c}⟨m_2|f⟩+\gamma -⟨(5,2,-6)|f⟩\ge ⟨(4,3,-6)|f⟩-⟨(5,2,-6)|f⟩=⟨-1,1,0|f⟩\ge 0,\forall f\in -F_1.\end{array}$$

By (4), we have $\left\{(5,2,-6),(6,2,-5)\right\}\subseteq B_2$. □

If $\left\{(5,2,-6),(6,2,-5)\right\}\subseteq B_5\cap T_2$, then by

$$\left|\right|(5,2,-6)-(6,-6,-1)\left|\right|=14 \mathrm{and} \left|\right|(6,2,-5)-(1,-6,-6)\left|\right|=14,$$

we have $(6,-6,-1),(1,-6,-6)\notin B_5$. Thus,

$$\left\{(6,-6,-1),(1,-6,-6)\right\}\subseteq (B_2\cup B_3\cup B_8)\cap T_5.$$

(26)

If $\left\{(2,5,-6),(2,6,-5)\right\}\subseteq B_6\cap T_2$, then one can verify that

$$\left\{(-6,6,-1),(-6,1,-6)\right\}\subseteq (B_2\cup B_4\cup B_8)\cap T_6.$$

(27)

Lemma 17.

We have

$$\{(2,5,-6),(2,6,-5),(5,2,-6),(6,2,-5)\}\subseteq B_2.$$

(28)

Proof. 

We show that $\left\{(5,2,-6),(6,2,-5)\right\}\subseteq B_2$. The inclusion $\{(2,5,-6),(2,6,-5)\}\subseteq B_2$ can be proved by similar arguments as in the proof of Corollary 2.

By Lemma 16, we only need to show that $\left\{(5,2,-6),(6,2,-5)\right\}⊈B_5$. By Lemmas 4 and 13, $(3,1,3)\in B_2\cup B_3\cup B_4$. Thus, it suffices to show that, if $\left\{(5,2,-6),(6,2,-5)\right\}$ is a subset of $B_5$, then $(3,1,3)\notin B_2\cup B_3\cup B_4$.

First, we show that $(3,1,3)\notin B_2$. Otherwise, by

$${\left|\right|(2,5,-6)-(3,1,3)\left|\right|}_1={\left|\right|(2,6,-5)-(3,1,3)\left|\right|}_1=14,$$

we have $(2,5,-6),(2,6,-5)\notin B_2\cap T_2$. By Corollary 2, we have $\left\{(2,5,-6),(2,6,-5)\right\}\subseteq B_6$. By Lemma 4 and the facts $(3,1,3)\in B_2\cap S_1$, $O_5\nsim O_1$, and $O_6\nsim O_1$, we have

$$B_2\cap T_5=B_2\cap T_6=\varnothing ,$$

which, together with ${\left|\right|a_4-(-6,1,-6)\left|\right|}_1=22$ and (27), shows that $(-6,1,-6)\in B_8\cap T_6$.

Similarly, by ${\left|\right|(6,2,-5)-(1,-6,-6)\left|\right|}_1=14$, ${\left|\right|a_3-(1,-6,-6)\left|\right|}_1=22$, and (26), we have $(1,-6,-6)\in B_8\cap T_5$. It follows that $B_8$ intersects both $T_5$ and $T_6$, which are not adjacent, which is a contradiction.

Next, we show that $(3,1,3)\notin B_3$. Suppose that this is not true. From $O_5\nsim O_1$ and Lemma 4, it follows that $T_5\cap B_3=\varnothing$. Thus, $(6,-6,-1)\notin B_3$. By

$${\left|\right|(6,-6,-1)-a_2^{\prime }\left|\right|}_1=14,$$

we have $(6,-6,-1)\notin B_2$. By (26), we have $(6,-6,-1)\in B_8$, which is impossible since ${\left|\right|(6,-6,-1)-a_8\left|\right|}_1=16$.

In the rest of this section, we show that $(3,1,3)\notin B_4$. Otherwise, by

$${\left|\right|(3,1,3)-(-6,5,2)\left|\right|}_1={\left|\right|(3,1,3)-(-5,6,2)\left|\right|}_1=14,$$

we have $(-6,5,2),(-5,6,2)\notin B_4$. By Table 1, $(-5,6,2)\in B_1\cup B_6\cup B_7$. Since $B_1$ intersects both $T_1$ and $T_2$ and ${\left|\right|a_7-(-5,6,2)\left|\right|}_1=18$, we have $(-5,6,2)\in B_6\cap T_4$. By

$${\left|\right|a_4-(-6,1,-6)\left|\right|}_1=22,{\left|\right|a_2-(-6,1,-6)\left|\right|}_1=20,\mathrm{and}{\left|\right|(-5,6,2)-(-6,1,-6)\left|\right|}_1=14,$$

we have $(-6,1,-6)\in B_8\cap T_6$. By (26),

$${\left|\right|a_2-(1,-6,-6)\left|\right|}_1=20,\mathrm{and}{\left|\right|a_3-(1,-6,-6)\left|\right|}_1=22,$$

we have $(1,-6,-6)\in B_8\cap T_5$. Then, $B_8$ intersects both $T_5$ and $T_6$, which are not adjacent, which is a contradiction. □

Corollary 3.

We have

$$\left\{(3,1,3),p_5\right\}\subseteq B_3\cup B_4.$$

(29)

Proof. 

By Table 1 and Lemma 13, these two points are in $B_2\cup B_3\cup B_4$. By Lemma 17 and ${\left|\right|(5,2,-6)-p_5\left|\right|}_1={\left|\right|(2,5,-6)-(3,1,3)\left|\right|}_1=14$, we have $p_5,(3,1,3)\notin B_2$. □

Lemma 18.

We have $(3,3,1)\in B_2$.

Proof. 

By Table 1 and Lemma 13, $(3,3,1)\in B_2\cup B_3\cup B_4$. We show that $(3,3,1)\notin B_3$, and $(3,3,1)\notin B_4$ can be proved by similar arguments as in the proof of Corollary 2.

Otherwise, $(3,3,1)\in B_3\cap S_1$. By Lemma 4, $B_3$ may only intersect $T_1$ and $T_3$. Since

$$\begin{array}{c}{\left|\right|(2,-6,5)-(3,3,1)\left|\right|}_1={\left|\right|(2,-5,6)-(3,3,1)\left|\right|}_1=14,\end{array}$$

we have $(2,-6,5),(2,-5,6)\notin B_3$. Since $B_1$ intersects both $T_1$ and $T_2$, and

$${\left|\right|(2,-6,5)-a_5\left|\right|}_1={\left|\right|(2,-5,6)-a_5\left|\right|}_1=16,$$

we have $(2,-5,6),(2,-6,5)\subseteq B_7\cap T_3$. Thus, $B_7$ intersects both $T_3$ and $T_7$. By Lemma 4, $\left\{a_8^{\prime },a_8\right\}\subseteq B_8$.

Since $B_3$ intersects $S_1$ and $T_3$, $(-6,-6,1),(-6,-1,6)\notin B_3$. By

$$\begin{array}{c}{\left|\right|a_4-(-6,-6,1)\left|\right|}_1=22,{\left|\right|(2,-5,6)-(-6,-6,1)\left|\right|}_1=14,\\ {\left|\right|a_8^{\prime }-(-6,-1,6)\left|\right|}_1=16, \mathrm{and} {\left|\right|(2,-6,5)-(-6,-1,6)\left|\right|}_1=14,\end{array}$$

we have $(-6,-6,1)\in B_8\cap T_7$ and $(-6,-1,6)\in B_4\cap T_7$.

Since $O_7\nsim O_1$, we have $B_4\cap S_1=\varnothing$. Thus, $p_5\notin B_4$. By Lemma 13, $p_5\notin B_1$. By (28) and ${\left|\right|p_5-(5,2,-6)\left|\right|}_1=14$, we have $p_5\in B_3\cap S_1$. By

$${\left|\right|p_5-p_6\left|\right|}_1=14,{\left|\right|(1,6,6)-p_6\left|\right|}_1=20,\mathrm{and}{\left|\right|p_6-a_7^{\prime }\left|\right|}_1=18,$$

we have $p_6\in B_5\cap T_3$.

Since $B_8$ intersects both $T_8$ and $T_7$, $(1,-6,-6)\notin B_8$. By ${\left|\right|(3,3,1)-(1,-6,-6)\left|\right|}_1=18$ and ${\left|\right|p_6-(1,-6,-6)\left|\right|}_1=14$, we have $(1,-6,-6)\in B_2\cap T_5$. By (28) and

$${\left|\right|(1,-6,-6)-(6,2,-5)\left|\right|}_1=14,$$

this is impossible. □

Lemma 19.

If $(6,1,-6),(1,6,-6)\in B_2$, then $v_2\notin B_2$.

Proof. 

From (4) and $a_2$, $a_2^{\prime }\in B_2$, it follows that

$$\begin{array}{c}|6-p_1\left(m_2\right)| + |1-p_2\left(m_2\right)| + |-6-p_3\left(m_2\right)| \le \gamma ,\end{array}$$

(30)

$$\begin{array}{c}|1-p_1\left(m_2\right)| + |6-p_2\left(m_2\right)| + |-6-p_3\left(m_2\right)| \le \gamma ,\end{array}$$

(31)

$$\begin{array}{c}|6-p_1\left(m_2\right)| + |5-p_2\left(m_2\right)| + |-2-p_3\left(m_2\right)| \le \gamma ,\end{array}$$

(32)

$$\begin{array}{c}|5-p_1\left(m_2\right)| + |6-p_2\left(m_2\right)| + |-2-p_3\left(m_2\right)| \le \gamma .\end{array}$$

(33)

Taking the sum of (30) and (32), the sum of (31) and (33), and the sum of (30) and (31), and applying the triangle inequality, we obtain

$$|6-p_1\left(m_2\right)| \le \gamma -4,|6-p_2\left(m_2\right)| \le \gamma -4,\mathrm{and}|-6-p_3\left(m_2\right)| \le \gamma -5.$$

Hence,

$$⟨m_2|-f_2⟩+\gamma \le \gamma -10+\gamma -10+\gamma -11+\gamma <-3=⟨(1,1,-1)|-f_2⟩.$$

By (4), we have $v_2\notin B_2$. □

Lemma 20.

Either $(3,1,3)\notin B_3$ or $p_5\notin B_4$.

Proof. 

Assume the contrary that $(3,1,3)\in B_3\cap S_1$ and $p_5\in B_4\cap S_1$. By (4), we have

$$-5=⟨(3,1,3)|-f_3⟩\le ⟨m_3|-f_3⟩+\gamma .$$

By (16), $T_3⊈B_3$. Clearly, $B_1\cap T_3=\varnothing$. Thus, by Table 1, we have

$$\varnothing \ne T_3\setminus B_3\subseteq B_5\cup B_7.$$

(34)

Similarly, we have

$$\varnothing \ne T_4\setminus B_4\subseteq B_6\cup B_7.$$

(35)

By Lemma 18, $B_2$ can only intersect $T_1$ and $T_2$. Moreover, $B_3$ can only intersect $T_1$ and $T_3$, and $B_4$ can only intersect $T_1$ and $T_4$. It follows that

$$T_5\subseteq B_5\cup B_8,T_6\subseteq B_6\cup B_8,\mathrm{and}{T}_7\subseteq B_7\cup B_8.$$

(36)

By

$${\left|\right|a_4-(-2,-2,1)\left|\right|}_1={\left|\right|a_3-(-2,-2,1)\left|\right|}_1=14,$$

the midpoint $(-2,-2,1)$ of $(-3,-3,1)$ and $(-1,-1,1)$ is in $B_7\cup B_8$. If $(-2,-2,1)\in B_7$, then, by (4), we have

$$-5=⟨(-2,-2,1)|-f_7⟩\le ⟨m_7|-f_7⟩+\gamma .$$

By (16), we have $T_7\setminus B_7\ne \varnothing$. By (36), $T_7\setminus B_7\subseteq B_8$. In this situation, by Lemma 4, $B_8$ cannot intersect $T_5$ and $T_6$. Thus, by (36),

$$T_5\subseteq B_5 \mathrm{and} T_6\subseteq B_6.$$

(37)

If $(-2,-2,1)\in B_8$ then, by Lemma 4, $B_8$ cannot intersect $T_5$ and $T_6$. By (36) again, we have (37). It follows that $(-6,6,-1)\in B_6\cap T_6$.

By ${\left|\right|(6,1,-6)-(1,6,6)\left|\right|}_1=22$ and ${\left|\right|(6,1,-6)-(-6,6,-1)\left|\right|}_1=22$, $(6,1,-6)\notin B_1\cup B_6$. If $(6,1,-6)\in B_5\cap T_2$, then, since $O_2\nsim O_3$, $B_5$ does not intersect $T_3$. By (34), $B_7\cap T_3\ne \varnothing$. Since $O_3\nsim O_4$, by (35), $B_6\cap T_4\ne \varnothing$. Since $O_2$, $O_3$, and $O_4$ are not adjacent to $O_8$, by Lemma 4, $S_8\subseteq B_8$, which contradicts Lemma 5b. Thus, $(6,1,-6)\in B_2\cap T_2$. Similarly, we have $(1,6,-6)\in B_2\cap T_2$.

By Lemma 19, $v_2\in B_1\cup B_5\cup B_6$. By $T_1\subseteq B_1$, (37), and Lemma 5b, this is impossible. □

Clearly, by (29) and Lemma 20, $(3,1,3)\in B_4\mathrm{or}{p}_5\in B_3$.

Lemma 21.

If $(3,1,3)\in B_4$, then $(-1,6,-6)\in B_8$. If $p_5\in B_3$, then $(6,-1,-6)\in B_8$.

Proof. 

Suppose that $(3,1,3)\in B_4$. By $B_1\cap T_2\ne \varnothing$,

$${\left|\right|(3,1,3)-(-6,5,2)\left|\right|}_1=14,{\left|\right|a_7-(-6,5,2)\left|\right|}_1=18,$$

and Lemma 4, $(-6,5,2)\in B_6\cap T_4$.

By ${\left|\right|(-6,5,2)-(-1,6,-6)\left|\right|}_1=14$, $(3,1,3)\in B_4\cap S_1$, and $(3,3,1)\in B_2\cap S_1$, we have $(-1,6,-6)\in B_8\cap T_6$.

Now, suppose that $p_5\in B_3$. As in the proof of Corollary 2, we have $(3,1,3)\in Q_4\left(B_3\right)$. By the first case, we have $(-1,6,-6)\in (\gamma B_1^3+Q_4\left(m_8^{\prime }\right))\cap T_6$, where $m_8^{\prime }$ is defined as in Corollary 2. Then, either $(-1,6,-6)\in Q_4\left(B_7\right)\cap T_6$ or $(-1,6,-6)\in Q_4\left(B_8\right)\cap T_6$. If $(-1,6,-6)\in Q_4\left(B_7\right)\cap T_6$, then $B_7\cap T_5\ne \varnothing$ and $m_8^{\prime }\in B_7$, which contradicts Lemma 4. Hence, $(6,-1,-6)\in B_8\cap T_5$. □

If $(3,1,3)\in B_4$, then $(-1,6,-6)\in B_8\cap T_6$. Hence, by Lemma 4, (23) holds. However, this is in contradiction to ${\left|\right|(-1,6,-6)-a_8^{\prime }\left|\right|}_1=18$. If $p_5\in B_3$, then $(6,-1,-6)\in B_8\cap T_5$, which is in contradiction to ${\left|\right|(6,-1,-6)-a_8\left|\right|}_1=18$. This completes the proof of Theorem 1.

3. A $\mathbf{(}\mathbf{2}\mathit{n}\mathbf{+}\mathbf{2}\mathbf{)}$-Optimal Configuration of ${\mathit{B}}_{\mathbf{1}}^{\mathit{n}}$

In this section, we always assume $n\ge 3$. Let

$$A_n=\left\{(\pm {\displaystyle \frac{1}{n}},\pm {\displaystyle \frac{1}{n}},\cdots ,\pm {\displaystyle \frac{1}{n}})\right\}\subseteq B_1^n.$$

For each $x,y\in A_n$ and $k\in \left[n\right]\cup \left\{0\right\}$, set

$$I(x,y)=\#\left\{i\in \left[n\right]|p_i\left(x\right)=p_i\left(y\right)\right\} \mathrm{and} D_x^k=\left\{z\in A_n|I(x,z)=k\right\}.$$

If $\gamma <(n-1)/n$ and $c\in {\mathbb{R}}^n$, then, for each pair $x,y$ of points in $(\gamma B_1^n+c)\cap A_n$, we have

$${\left|\right|x-y\left|\right|}_1\le 2\gamma <{\displaystyle \frac{2(n-1)}{n}},$$

which implies that $I(x,y)\ge 2$.

Let S be a maximal subset of $A_n$ such that $I(p,q)\ge 2$, $\forall p,q\in S$. Then, for each $p\in S$, we have $D_p^0=\left\{-p\right\}$, $S\subseteq A_n\setminus (D_p^1\cup D_p^0)$ and

$$S\subseteq \bigcap _{p\in S}(A_n\setminus (D_p^1\cup D_p^0))=A_n\setminus \bigcup _{p\in S}(D_p^1\cup D_p^0)\subseteq A_n\setminus (-S).$$

(38)

Therefore, we obtain that $\#S\le 2^{n-1}$.

Lemma 22.

If $\gamma <(n-1)/n$ and $c\in {\mathbb{R}}^n$, then $\#((\gamma B_1^n+c)\cap A_n)<2^{n-1}$.

Proof. 

Set $S=(\gamma B_1^n+c)\cap A_n$. Then, $\#S\le 2^{n-1}$. Assume the contrary that $\#S=\#(-S)=2^{n-1}$. Then, by (38), ${\bigcup }_{p\in S}{D}_p^1\subseteq -S$. Clearly,

$$D_p^k=\left\{x\in A_n|I(p,x)=k\right\}=-D_p^{n-k}=\left\{x\in A_n|I(p,-x)=n-k\right\}.$$

It follows that

$$D_p^{n-1}\subseteq S,\forall p\in S.$$

(39)

Let $k\in [n-1]$ and $p\in S$. Take $x\in D_p^{n-k-1}$. Without loss of generality, we may assume that

$$p_i\left(x\right)=p_i\left(p\right)⟺i\in [n-k-1].$$

Let $u\in A_n$ be the point satisfying

$$p_n\left(u\right)=-p_n\left(x\right)=p_n\left(p\right) \mathrm{and} p_i\left(x\right)=p_i\left(u\right),\forall i\in [n-1].$$

Then, $u\in D_p^{n-k}$ and $x\in D_u^{n-1}$. Hence,

$$D_p^{n-k-1}\subseteq \bigcup _{u\in D_p^{n-k}}{D}_u^{n-1},\forall p\in S,\forall k\in [n-1].$$

(40)

For each $k\in \left[n\right]$, we show by induction that

$$D_p^{n-k}\subseteq S,\forall p\in S.$$

(41)

The case when $k=1$ follows from (39). Suppose that (41) holds for all $k\in \left[m\right]$, where $m\in [n-1]$. For each $p\in S$, by (39) and (40), we have

$$D_p^{n-(m+1)}\subseteq \bigcup _{u\in D_p^{n-m}}{D}_u^{n-1}\subseteq S.$$

Hence, (41) holds for each $k\in \left[n\right]$. It follows that $D_p^0\subseteq S$, $\forall p\in S$, which is impossible. □

Lemma 23.

For $p,q\in A_n$, $D_p^1=D_q^1$ if and only if $p=q$.

Proof. 

We only need to show that $D_p^1\ne D_q^1$, when $p\ne q$. If $p=-q$, then, since $n\ge 3$, $D_p^1\ne D_q^1$. Otherwise, there exists $k\in [n-1]$ such that $p\in D_q^k$. Without loss of generality, we may assume that $p_i\left(p\right)=p_i\left(q\right)⟺i\in \left[k\right]$. Suppose that $u\in A_n$ is given by

$$\begin{array}{c}\hfill p_i\left(u\right)=\left\{\begin{array}{cc}{p}_i\left(p\right),\hfill & i=1,\hfill \\ -p_i\left(p\right),\hfill & i\ne 1.\hfill \end{array}\right.\end{array}$$

Then, $u\in D_p^1$ and, since $p_1\left(u\right)=p_1\left(q\right)$ and $p_n\left(u\right)=p_n\left(q\right)$, $u\notin D_q^1$. □

Lemma 24.

If $c\in {\mathbb{R}}^4$ and $\gamma <3/4$, then $\#((\gamma B_1^4+c)\cap A_4)\le 5$.

Proof. 

Let $S=(\gamma B_1^4+c)\cap A_4$. Then, $I(p,q)\ge 2,\forall p,q\in S$. Assume the contrary that $\#S\ge 6$. By (38), we have

$$\#S\le \#A_4-\#(\left(\bigcup _{p\in S}{D}_p^1\right)\setminus (-S))-\#S.$$

Then, $\#(\left({\bigcup }_{p\in S}{D}_p^1\right)\setminus (-S))\le 4$. Clearly, $\#D_x^1=4$, $\forall x\in A_4$. By Lemma 23, we have $\#\left({\bigcup }_{p\in S}{D}_p^1\right)\ge 5$. Hence, ${\bigcup }_{p\in S}{D}_p^1\cap (-S)\ne \varnothing$. Thus, there exist $p_0,u_0\in S$ such that $-u_0\in D_{p_0}^1=-D_{p_0}^3$. Moreover, since $S\subseteq D_{p_0}^2\bigsqcup D_{p_0}^3\bigsqcup \left\{p_0\right\}$, $\#S\ge 6$, and $\#D_{p_0}^3\le 4$, there exists a point $v_0\in D_{p_0}^2\cap S$.

Let $u\in D_{p_0}^3\cap S$ and $v\in D_{p_0}^2\cap S$. There exists a unique integer $i\left(u\right)\in \left[4\right]$ such that $p_{i\left(u\right)}\left(u\right)=-p_{i\left(u\right)}\left(p_0\right)$. If $p_{i\left(u\right)}\left(u\right)=-p_{i\left(u\right)}\left(v\right)$, then $p_{i\left(u\right)}\left(v\right)=p_{i\left(u\right)}\left(p_0\right)$. Thus, there is exactly one integer $j\in \left[4\right]\setminus \left\{i\left(u\right)\right\}$ such that $p_j\left(v\right)=p_j\left(p_0\right)=p_j\left(u\right)$. Then, for each $i\in \left[4\right]\setminus \left\{i\left(u\right),j\right\}$, we have $p_i\left(v\right)=-p_i\left(p_0\right)=-p_i\left(u\right)$. Thus, $v\in D_u^1$, which is impossible. Therefore, $p_{i\left(u\right)}\left(u\right)=p_{i\left(u\right)}\left(v\right)$. In particular, we have

$$\begin{array}{c}{p}_{i\left(u\right)}\left(v_0\right)=p_{i\left(u\right)}\left(u\right)=-p_{i\left(u\right)}\left(p_0\right),\forall u\in D_{p_0}^3\cap S,\\ p_{i\left(u_0\right)}\left(v\right)=p_{i\left(u_0\right)}\left(u_0\right)=-p_{i\left(u_0\right)}\left(p_0\right),\forall v\in D_{p_0}^2\cap S.\end{array}$$

Since $v_0\in D_{p_0}^2\cap S$, $\#(D_{p_0}^3\cap S)\le 2$. By $u_0\in D_{p_0}^3\cap S$, we have $\#(D_{p_0}^2\cap S)\le 3$.

From $\#S\ge 6$, it follows that $\#(D_{p_0}^3\cap S)=2$ and $\#(D_{p_0}^2\cap S)=3$. Suppose that $D_{p_0}^3\cap S=\left\{u_0,u_1\right\}$. For each $v\in D_{p_0}^2\cap S$, we have

$$p_{i\left(u_0\right)}\left(v\right)=p_{i\left(u_0\right)}\left(u_0\right)=-p_{i\left(u_0\right)}\left(p_0\right) \mathrm{and} p_{i\left(u_1\right)}\left(v\right)=p_{i\left(u_1\right)}\left(u_1\right)=-p_{i\left(u_1\right)}\left(p_0\right).$$

Thus, $\#(D_{p_0}^2\cap S)=1$, which is a contradiction. □

Proof of Theorem 2. 

Let

$$C=\{\pm ({\displaystyle \frac{1}{n}},0,\cdots ,0),\pm (0,{\displaystyle \frac{1}{n}},\cdots ,0),\pm (0,0,\cdots ,{\displaystyle \frac{1}{n}})\}.$$

First, we show that $B_1^n\subseteq ((n-1)/n)B_1^n+C$. It is clear that $o\in ((n-1)/n)B_1^n+c$, $\forall c\in C$. Thus, it is suffices to show that $\mathrm{bd}{B}_1^n\subseteq ((n-1)/n)B_1^n+C$. For each $x\in \mathrm{bd}{B}_1^n$, let j be an integer in $\left[n\right]$ such that $\left|p_j\left(x\right)\right|={\max }_{i\in \left[n\right]}\left|p_i\left(x\right)\right|$. Take $c^{\prime }\in C$ such that $p_j\left(c^{\prime }\right)=1/n\mathrm{sgn}\left(p_j\left(x\right)\right)$. Since $x\in \mathrm{bd}{B}_1^n$, we have $\left|p_j\left(x\right)\right|\ge 1/n$. Then,

$${\left|\right|x-c^{\prime }\left|\right|}_1=\sum _{i\in \left[n\right]\setminus \left\{j\right\}}|p_i\left(x\right)-p_i\left(c^{\prime }\right)| + |p_j\left(x\right)-p_j\left(c^{\prime }\right)|=\sum _{i\in \left[n\right]}\left|p_i\left(x\right)\right|-{\displaystyle \frac{1}{n}}={\displaystyle \frac{n-1}{n}}.$$

Hence,

$${\Gamma }_{2n+2}\left(B_1^n\right)\le {\Gamma }_{2n+1}\left(B_1^n\right)\le {\Gamma }_{2n}\left(B_1^n\right)\le {\displaystyle \frac{n-1}{n}}.$$

Next, we show that ${\Gamma }_{2n+2}\left(B_1^n\right)\ge (n-1)/n$. Otherwise, there exists $\gamma \in (0,(n-1)/n)$ and $M\subseteq {\mathbb{R}}^n$ with $\#M=2n+2$ such that $B_1^n\subseteq \gamma B_1^n+M$. For each $x\in A_n$ and each point $y\in \mathrm{ext}{B}_1^n$, we have ${\Vert x-y\Vert }_1\ge 2(n-1)/n$. Since $\mathrm{ext}{B}_1^n$ is 2-separated and $\#\left(\mathrm{ext}{B}_1^n\right)=2n$, $A_n$ is contained in at most two translates of $\gamma B_1^n$. Hence, there exists a $c^{\prime }\in M$ such that $\#((\gamma B_1^n+c^{\prime })\cap A_n)\ge 2^{n-1}$. By Lemma 22, this is a contradiction. □

Proof of Theorem 3. 

Since ${\Gamma }_{11}\left(B_1^4\right)\le {\Gamma }_8\left(B_1^4\right)=3/4$, we only need to show that ${\Gamma }_{11}\left(B_1^4\right)\ge 3/4$. Otherwise, there exists $\gamma \in (0,3/4)$ and $\left\{c_k|k\in \left[11\right]\right\}\subseteq {\mathbb{R}}^4$ such that $B_1^4\subseteq \gamma B_1^4+C$. For each vertex v of $B_1^4$ and each point $a\in A_4$, we have ${\Vert v-a\Vert }_1\ge 3/2>2\gamma$. Then, we may assume, with loss of generality, that $A_4\subseteq \gamma B_1^4+\left\{c_k|k\in \left[3\right]\right\}$. By Lemma 24, $\#((\gamma B_1^4+\left\{c_k\right\})\cap A_4)\le 5$, $\forall k\in \left[3\right]$. Since $\#A_4=16$, this is impossible. □