Centralized and Decentralized Event-Triggered Nash Equilibrium-Seeking Strategies for Heterogeneous Multi-Agent Systems

Abstract

This paper addresses the event-triggered Nash equilibrium-seeking problem for non-cooperative games played by heterogeneous multi-agent systems. Unlike homogeneous multi-agent systems, heterogeneous multi-agent systems consist of agents with different dynamic structures, making it difficult to design control schemes and construct event-triggering conditions for such systems. In this paper, a novel centralized event-triggered Nash equilibrium-seeking strategy and a novel decentralized event-triggered Nash equilibrium-seeking strategy are proposed. The corresponding centralized and decentralized event-triggering conditions are derived. The convergence properties of the proposed centralized and decentralized strategies are proved. Further theoretical analyses illustrate that Zeno behavior does not exist under the proposed strategies. Finally, the effectiveness and efficiency of both centralized and decentralized strategies are presented through numerical experiments. The experimental results illustrate that under both strategies, heterogeneous multi-agent systems achieve the Nash equilibrium successfully, and the communication consumption among agents is significantly reduced.

1. Introduction

In recent years, game theory has been adopted in various application fields, such as control of unmanned systems [1], multi-agent exploration policies [2], collective decision making [3], communication networks [4], and cooperative advertising strategy [5]. As an important part of game theory, the Nash equilibrium (NE)-seeking problem within multi-agent systems (MASs) has attracted increasing interest among scholars in multi-agent communities [6,7,8,9,10,11,12]. For example, in [6], Ye et al. tackled the distributed NE-seeking problem with constraints on control inputs by introducing a series of consensus-based strategies. In [10], Hua et al. focused on the generalized NE-seeking problem, which concerns the action constraints of the agents. An NE-seeking problem within MASs with strongly connected switching networks was considered by He et al. in [11]. Additionally, Tan et al. addressed an NE-seeking problem with the payoff functions and actions of agents unknown to each other in [12].

In the studies mentioned above, the NE is achieved through continuous-time communication. However, in practice, due to physical limitations, it is often necessary for mobile robots and other autonomous agents to implement controllers that do not depend on continuous-time communications [13,14,15]. It is a widely accepted fact that by introducing an event-triggered mechanism or a periodic sampling scheme, the communication consumption is effectively reduced. Thus, event-triggered mechanisms have attracted tremendous attention [16,17,18]. Many scholars have made efforts to replace continuous communication by introducing event-triggered mechanisms into NE-seeking strategies in recent years [19,20,21,22]. For example, Shi et al. developed an event-triggered strategy to compute the NE in aggregative games in [20]. Another event-triggered strategy was proposed by Shi et al. to solve the generalized NE-seeking problem of networked non-cooperative games in [21]. Those strategies are semi-decentralized. They require agents to have access to certain global information, such as the aggregate value of aggregative games or complete decision information. In [22], for non-cooperative games, Wang et al. proposed a decentralized event-triggered NE-seeking strategy that relies on partial decision information of each agent, such as local action and the estimation of neighbors of an agent.

In most of the above-mentioned studies, the authors studied homogeneous MASs, in which the dynamics of the agents are the same. Specifically, those strategies are designed exclusively for homogeneous MASs that contain only single-integrator or only double-integrator agents. However, this situation is a special case. Heterogeneous MASs, with different dynamic structures or identical dynamic structures but different parameters, are encountered in various applications [23,24,25,26,27,28]. According to [26], there are typically two types of heterogeneous MASs. The first type consists of agents with identical system structures but different parameters. For example, in [27], Li et al. developed an adaptive fuzzy containment control method for nonlinear MASs with time-delayed input. The followers in the MASs have identical system structures but different parameters. The second type of heterogeneous MASs consists of agents with non-identical system structures. For example, in [28], He and Huang considered the NE-seeking problem for high-order-integrator agents. If a multi-agent system consists of single- and double-integrator agents simultaneously, then the multi-agent system is deemed as a second-type heterogeneous multi-agent system. Unlike in the field of game theory, the implementation of an event-triggered mechanism for heterogeneous MASs has long been explored in other scientific fields, such as group consensus [29,30,31,32,33]. For example, in [32], combinational measurements were introduced to handle the pinning exponential synchronization of complex networks. In [33], Li et al. designed a fully distributed event-triggered pinning control scheme to address the group consensus problem for heterogeneous MASs with cooperative–competitive interaction.

Driven by the above discussion, this paper aims to design event-triggered NE-seeking strategies for non-cooperative games played by heterogeneous MASs with both single- and double-integrator agents. In comparison to existing works, the main contributions of this paper are presented as follows.

• Event-triggered NE seeking for non-cooperative games played by heterogeneous MASs comprising both single- and double-integrator agents is studied in this paper. Compared with conventional NE seeking for homogeneous MASs, the NE-seeking problem addressed in this paper is conducted by heterogeneous MASs, which consist of agents with varying dynamic structures, and it introduces an event-triggered mechanism to reduce communication consumption.
• A novel centralized event-triggered NE-seeking (CETNES) strategy and a novel decentralized event-triggered NE-seeking (DETNES) strategy are proposed to address the event-triggered NE-seeking problem for heterogeneous MASs. The corresponding centralized and decentralized event-triggering conditions are derived. The proposed CETNES and DETNES strategies successfully solve the NE-seeking problem for heterogeneous MASs and significantly reduce communication consumption.
• The convergence properties of both the CETNES and DETNES strategies are proved through Lyapunov stability theory. The nonexistence of Zeno behavior for both the CETNES and DETNES strategies is also proved.

The remaining part of this paper is organized as follows. In Section 2, some preliminaries concerning graph theory and mathematical notations are provided. Additionally, the formulation for the NE-seeking problem for non-cooperative games played by heterogeneous MASs is also presented in Section 2. In Section 3, the CETNES and DETNES strategies are proposed. Specifically speaking, in Section 3.1, a novel CETNES strategy is proposed, and detailed theoretical analyses of the CETNES strategy are presented. In Section 3.2, a novel DETNES strategy is designed to address the NE-seeking problem in a fully distributed manner, and detailed theoretical analyses of the DETNES strategy are presented. Moreover, in Section 4, the efficiency and efficacy of the proposed strategies are illustrated through numerical experiments. Finally, the conclusion is provided in Section 5.

2. Preliminaries and Problem Formulation

In this section, to lay the foundation for further investigation, some preliminaries concerning mathematical notation and graph theory are provided. Additionally, the formulation of the NE-seeking problem in non-cooperative games played by heterogeneous MASs is presented.

2.1. Mathematical Notation

In this paper, the notation $M=\mathrm{diag}\left\{l_{ij}\right\}\in {\mathbb{R}}^{n^2\times n^2}$ for $i,j\in \{1,2,\dots ,n\}$ denotes a diagonal matrix with diagonal elements $l_{11},l_{12},\dots ,l_{1n},l_{21},l_{22},\dots ,l_{2n},\dots ,l_{n1},l_{n2},\dots ,l_{nn}$, respectively. Furthermore, ${\lambda }_{\min }\left(O\right)$ denotes the minimum eigenvalue of a symmetric and real matrix $O\in {\mathbb{R}}^{n\times n}$, and ${\left[h_i\right]}_{\mathrm{vec}}=[h_1,h_2,$$\dots ,h_n{]}^{\mathrm{T}}$. Moreover, $\parallel \dots \parallel$ denotes the 2-norm of a matrix or vector and the Kronecker product is denoted by ⊗ [34].

2.2. Graph Theory

Consider $\mathbb{G}=(\mathcal{V},ϵ,\mathcal{A})$ as the communication topology in non-cooperative games that contain n agents. The set of nodes is denoted by $\mathcal{V}=\{{\mathcal{V}}_1,{\mathcal{V}}_2,\dots ,{\mathcal{V}}_n\}$, the set of unordered pairs is defined as $ϵ=\{{ϵ}_{ij}=(i,j)\subseteq \mathcal{V}\times \mathcal{V}\}$, the adjacency matrix is $\mathcal{A}={\left(a_{ij}\right)}_{n\times n}$, where $a_{ij}\ge 0$, the in-degree of the ith node is denoted by $d_i$, and the in-degree matrix is denoted as $\mathcal{D}=\mathrm{diag}\{d_1,\dots ,d_n\}\in {\mathbb{R}}^{n\times n}$, where $d_i={\sum }_{j=1}^n{a}_{ij}$. Moreover, the Laplacian matrix is $\mathcal{L}=\mathcal{D}-\mathcal{A}\in {\mathbb{R}}^{n\times n}$ [35].

2.3. Problem Formulation

Consider non-cooperative games played by heterogeneous MASs with m single-integrator agents and $n-m$ double-integrator agents. The dynamics of the heterogeneous agents are denoted as

$$\left\{\begin{array}{cc}{\dot{x}}_i\left(t\right)=u_i\left(t\right),\hfill & \hspace{1em}i\in S_m,\hfill \\ \left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=v_i\left(t\right),\hfill \\ {\dot{v}}_i\left(t\right)=u_i\left(t\right),\hfill \end{array}\right.\hfill & \hspace{1em}i\in S_{n-m},\hfill \end{array}\right.$$

(1)

where $S_m=\{1,2,\dots ,m\}$; $S_{n-m}=\{m+1,m+2,\dots ,n\}$; $S_n=S_m\cup S_{n-m}$; and $S_n\cap S_{n-m}=\varnothing$. In addition, $x_i\left(t\right)\in \mathbb{R}$, $v_i\left(t\right)\in \mathbb{R}$, and $u_i\left(t\right)\in \mathbb{R}$ denote the position, velocity, and control input for agent i, respectively.

Remark 1. 

Before proceeding, in order to simplify complicated computations, it is necessary to point out that the position, velocity, and control input considered in this paper are scalars. In other words, $x_i\left(t\right)\in \mathbb{R}$, $v_i\left(t\right)\in \mathbb{R}$, and $u_i\left(t\right)\in \mathbb{R}$ belong to 1-dimensional space. Nevertheless, it is easy to extend the main results in this paper to n-dimensional space by adopting the Kronecker product.

The cost function of agent i is $f_i\left(\mathbf{x}\left(t\right)\right)$ for both single-integrator and double-integrator agents, where $\mathbf{x}\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^n$ denotes the position set of all the n agents. The NE ${\mathbf{x}}^{*}=(x_i^{*},{\mathbf{x}}_{-i}^{*})$ is given by

$$f_i(x_i^{*},{\mathbf{x}}_{-i}^{*})\le f_i(x_i\left(t\right),{\mathbf{x}}_{-i}^{*})$$

(2)

for $x_i\left(t\right)\in \mathbb{R},i\in \{1,2,\dots ,n\}$, and ${\mathbf{x}}_{-i}\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_{i-1}\left(t\right),x_{i+1}\left(t\right),\dots ,x_n\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n-1}$.

In order to investigate the convergence properties, the following assumptions are introduced [6].

Assumption 1. 

There exists a graph $\mathbb{G}$ that denotes the communication topology of the n agents, and $\mathbb{G}$ is undirected and connected.

Assumption 2. 

For all $\mathbf{x}\left(t\right),\mathbf{z}\left(t\right)\in {\mathbb{R}}^n$, there is a positive constant m such that

$${\left(\mathbf{x}\left(t\right)-\mathbf{z}\left(t\right)\right)}^{\mathrm{T}}\left(\mathbf{\phi }\left(\mathbf{x}\right(t\left)\right)-\mathbf{\phi }\left(\mathbf{z}\right(t)\right))\ge m{∥\mathbf{x}\left(t\right)-\mathbf{z}\left(t\right)∥}^2,$$

(3)

where vector $\mathbf{\phi }\left(\mathbf{x}\right)={\left[{\phi }_i\left(\mathbf{x}\left(t\right)\right)\right]}_{\mathrm{vec}}\in {\mathbb{R}}^n$, with ${\phi }_i\left(\mathbf{x}\left(t\right)\right)=\partial f_i\left(\mathbf{x}\left(t\right)\right)/\partial x_i\left(t\right)$.

Assumption 3. 

The partial derivative of cost function $f_i\left(\mathbf{x}\left(t\right)\right)$ for each agent is globally Lipschitz, which means that there exists a positive constant $\overline{l}$ such that

$$\left|{\phi }_i\left(\mathbf{x}\left(t\right)\right)-{\phi }_i\left(\mathbf{z}\left(t\right)\right)\right|\le \overline{l}\parallel \mathbf{x}\left(t\right)-\mathbf{z}\left(t\right)\parallel .$$

Remark 2. 

It is obtained from Assumption 2 that for each fixed ${\mathbf{x}}_{-i}$, $f_i(x_i\left(t\right),{\mathbf{x}}_{-i})$ is strongly convex [6]. In addition, it is derived from Assumptions 2 and 3 that the NE ${\mathbf{x}}^{*}$ of the non-cooperative game is unique and the positions of agents are at the NE if and only if $\mathbf{\phi }\left({\mathbf{x}}^{*}\right)={\mathbf{0}}_n$ [36].

3. Main Results

In this section, the CETNES and DETNES strategies for non-cooperative games played by heterogeneous MASs are proposed for the first time. The convergence properties of the proposed strategies are obtained by utilizing Lyapunov stability theory. Furthermore, for both the CETNES and DETNES strategies, the nonexistence of Zeno behavior is proved.

3.1. CETNES Strategy

Suppose that, when adopting the CETNES strategy, all the agents update control input $u_i\left(t\right)$ and exchange information with their neighbors at the same centralized event-triggering time instant. Consider $t_k$ as the kth centralized event-triggering time instant for all agents. For heterogeneous MASs, when $t\in [t_k,t_{k+1})$, the CETNES strategy is proposed as

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}\begin{array}{cccc}\hfill u_i\left(t\right)& =-{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right),\hfill & \hfill & i\in S_m,\hfill \\ \hfill u_i\left(t\right)& =-r\left(v_i\left(t\right)+{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right)\right),\hfill & \hfill & i\in S_{n-m},\hfill \end{array}\hfill \end{array}\right.\hfill \\ \hfill & \begin{array}{c}\hfill {\dot{y}}_{ij}\left(t\right)=-\theta \left(\sum _{q=1}^n{a}_{ik}\left(y_{ij}\left(t_k\right)-y_{qj}\left(t_k\right)\right)+a_{ij}\left(y_{ij}\left(t_k\right)-x_j\left(t_k\right)\right)\right),i\in S_n,\end{array}\hfill \end{array}$$

(4)

where ${\mathbf{y}}_i\left(t\right)={[y_{i1}\left(t\right),y_{i2}\left(t\right),\dots ,y_{in}\left(t\right)]}^{\mathrm{T}}$ denotes the local estimation of $\mathbf{x}\left(t\right)$ of agent i. Moreover, for the double-integrator agents, r is a positive parameter to be determined. For all agents, $\theta$ is a positive parameter to be determined. In addition, $a_{ij}$ is the element of the adjacency matrix $\mathcal{A}$ on the ith row and the jth column.

In this subsection, for agent i, to measure the difference between its own estimation and the actual value of agents position state vector $\mathbf{x}\left(t\right)$ at time t, a vector-valued function ${\mathbf{q}}_i\left(t\right)\in {\mathbb{R}}^n$ is introduced as

$${\mathbf{q}}_i\left(t\right)={\mathbf{y}}_i\left(t\right)-\mathbf{x}\left(t\right).$$

The event-triggered mechanism for the CETNES strategy is determined by a vector-valued function $\mathbf{g}\left(t\right)\in {\mathbb{R}}^{n^2}$, and $\mathbf{g}\left(t\right)$ is defined as

$$\mathbf{g}\left(t\right)=\mathbf{q}\left(t_k\right)-\mathbf{q}\left(t\right),\forall t\in [t_k,t_{k+1}),$$

where $\mathbf{q}\left(t\right)=\mathbf{y}\left(t\right)-{\mathbf{1}}_n\otimes \mathbf{x}\left(t\right)\in {\mathbb{R}}^{n^2}$, with ${\mathbf{1}}_n$ denoting an n-dimensional column vector whose elements are 1, and $\mathbf{y}\left(t\right)={[{\mathbf{y}}_1^{\mathrm{T}}\left(t\right),{\mathbf{y}}_2^{\mathrm{T}}\left(t\right),\dots ,{\mathbf{y}}_n^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2}$. In addition, $\mathbf{g}\left(t\right)={[{\mathbf{g}}_1^{\mathrm{T}}\left(t_k\right),{\mathbf{g}}_2^{\mathrm{T}}\left(t_k\right),\dots ,{\mathbf{g}}_n^{\mathrm{T}}\left(t_k\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2}$, and ${\mathbf{g}}_i\left(t\right)={\mathbf{q}}_i\left(t_k\right)-{\mathbf{q}}_i\left(t\right)\in {\mathbb{R}}^n$.

The event-triggering condition is based on the value relation between $\parallel \mathbf{q}\left(t\right)\parallel$ and $\parallel \mathbf{g}\left(t\right)\parallel$. When the event-triggering condition is satisfied, the event is triggered. Then, the next event-triggering time instant $t_{k+1}$ is reached. The centralized event-triggering condition is given as

$$t_{k+1}=\inf \{t:t>t_k,\parallel \mathbf{g}\left(t\right)\parallel >\rho \parallel \mathbf{q}\left(t\right)\parallel \},$$

(5)

where $\rho$ is a positive parameter to be determined.

Remark 3. 

Compared with the NE-seeking strategy in [6], the proposed CETNES strategy does not require continuous-time information exchange among neighboring players. Therefore, the proposed CETNES strategy reduces the communication consumption.

The convergence properties of the proposed CETNES strategy are given by the following theorem.

Theorem 1. 

Consider non-cooperative games played by heterogeneous MASs following the CETNES strategy (4) and centralized event-triggering condition (5). Suppose that Assumptions 1–3 are satisfied. Then, there exists a positive constant ${\rho }^{*}$. For each $\rho \in (0,{\rho }^{*})$, the NE is asymptotically achieved.

Proof of Theorem 1. 

Firstly, based on the CETNES strategy (4), when $t\in [t_k,t_{k+1})$, the dynamics of the heterogeneous MASs are formulated as

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}{\dot{x}}_i\left(t\right)=-{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right),\hfill & \hspace{1em}i\in S_m,\hfill \\ \left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=v_i\left(t\right),\hfill \\ {\dot{v}}_i\left(t\right)=-r\left(v_i\left(t\right)+{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right)\right),\hfill \end{array}\right.\hfill & \hspace{1em}i\in S_{n-m},\hfill \end{array}\right.\hfill \\ \hfill & \begin{array}{cc}\hfill {\dot{y}}_{ij}\left(t\right)=-\theta \left(\sum _{q=1}^N{a}_{iq}\left(y_{ij}\left(t_k\right)-y_{qj}\left(t_k\right)\right)+a_{ij}\left(y_{ij}\left(t_k\right)-x_j\left(t_k\right)\right)\right),& i\in S_n.\hfill \end{array}\hfill \end{array}$$

(6)

Before proceeding, some notation is introduced for convenience. Let ${\mathbf{y}}_{\mathrm{s}}\left(t\right)={[{\mathbf{y}}_1^{\mathrm{T}}\left(t\right),{\mathbf{y}}_2^{\mathrm{T}}\left(t\right),\dots ,{\mathbf{y}}_m^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{nm}$ and ${\mathbf{y}}_{\mathrm{d}}\left(t\right)={[{\mathbf{y}}_{m+1}^{\mathrm{T}}\left(t\right),{\mathbf{y}}_{m+2}^{\mathrm{T}}\left(t\right),\dots ,{\mathbf{y}}_n^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2-nm}$ denote the estimations of single-integrator and double-integrator agents, respectively. Let ${\mathbf{x}}_{\mathrm{s}}\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_m\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^m$ and ${\mathbf{x}}_{\mathrm{d}}\left(t\right)={[x_{m+1}\left(t\right),x_{m+2}\left(t\right),\dots ,x_n\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n-m}$ denote the position vectors of single-integrator and double-integrator agents, respectively. Moreover, let $\mathbf{y}\left(t\right)={[{\mathbf{y}}_{\mathrm{s}}^{\mathrm{T}}\left(t\right),{\mathbf{y}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2}$ and $\mathbf{x}\left(t\right)={[{\mathbf{x}}_{\mathrm{s}}^{\mathrm{T}}\left(t\right),{\mathbf{x}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right)]}^{\mathrm{T}}\in {\mathbb{R}}^n$. Therefore, the corresponding vector form of (6) is given as

$$\begin{array}{cc}\hfill & \dot{\mathbf{x}}\left(t\right)=\left[\begin{array}{c}-{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right],\hfill \\ \hfill & {\dot{\mathbf{v}}}_{\mathrm{d}}\left(t\right)=-\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right),\hfill \\ \hfill & \dot{\mathbf{y}}\left(t\right)=-\theta \left(\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A\right)\left(\mathbf{g}\left(t\right)+\mathbf{q}\left(t\right)\right),\hfill \end{array}$$

(7)

where ${\dot{\mathbf{v}}}_{\mathrm{d}}\left(t\right)={[v_{m+1}\left(t\right),v_{m+2}\left(t\right),\dots ,v_n\left(t\right)]}^{\mathrm{T}}$, and matrix A is defined as $A=\mathrm{diag}\left\{a_{ij}\right\}\in {\mathbb{R}}^{n^2\times n^2}$ for $i,j\in S_n$. In addition, ${\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)$ and ${\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)$ are defined as

$$\begin{array}{cc}\hfill {\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)& ={\left[{\phi }_1\left({\mathbf{y}}_1\left(t\right)\right),{\phi }_2\left({\mathbf{y}}_2\left(t\right)\right),\dots ,{\phi }_m\left({\mathbf{y}}_m\left(t\right)\right)\right]}^{\mathrm{T}}\in {\mathbb{R}}^{nm}\mapsto {\mathbb{R}}^m,\hfill \\ \hfill {\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)& ={\left[{\phi }_{m+1}\left({\mathbf{y}}_{m+1}\left(t\right)\right),{\phi }_{m+2}\left({\mathbf{y}}_{m+2}\left(t\right)\right),\dots ,{\phi }_n\left({\mathbf{y}}_n\left(t\right)\right)\right]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2-nm}\mapsto {\mathbb{R}}^{n-m}.\hfill \end{array}$$

To prove Theorem 1, the Lyapunov candidate function is given as

$$\begin{array}{c}\hfill V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill V_1\left(t\right)=& {\displaystyle \frac{1}{2}}{\left({\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}\right)}^{\mathrm{T}}\left({\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}\right)+{\displaystyle \frac{1}{2}}{\left({\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}+{\displaystyle \frac{1}{r}}{\mathbf{v}}_{\mathrm{d}}\left(t\right)\right)}^{\mathrm{T}}\left({\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}+{\displaystyle \frac{1}{r}}{\mathbf{v}}_{\mathrm{d}}\left(t\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2r^2}}{\mathbf{v}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right){\mathbf{v}}_{\mathrm{d}}\left(t\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill V_2\left(t\right)=& {\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\mathbf{q}\left(t\right).\hfill \end{array}$$

(10)

with matrix $\mathcal{P}\in {\mathbb{R}}^{n^2\times n^2}$ defined as $\mathcal{P}=(1/2)(\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A)$. From Assumption 1, one knows that $\mathbb{G}$ is connected and undirected. Hence, $\mathcal{L}$ is symmetric and semi-positive definite. In addition, A is a semi-positive definite diagonal matrix. Hence, $\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A$ is symmetric and semi-positive definite. Additionally, in [37], it is proved that $\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A$ is a non-singular matrix for a connected and undirected graph. Therefore, matrix $\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A$ is symmetric and positive definite. Define matrix $\mathcal{Q}$ as $\mathcal{Q}=\mathcal{P}(\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A)+(\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A)\mathcal{P}$. By Assumption 1, $\mathcal{Q}$ is also a symmetric positive definite matrix [6]. It is evident that $V_1\left(t\right)\ge 0$ and $V_2\left(t\right)\ge 0$. Hence, $V\left(t\right)=V_1\left(t\right)+V_2\left(t\right)\ge 0$. Therefore, if ${\dot{V}}_1\left(t\right)+\dot{V_2}\left(t\right)\le 0$, then Theorem 1 is proved.

The time derivative of $V_1\left(t\right)$ is given as

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& ={\left({\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}\right)}^{\mathrm{T}}{\dot{\mathbf{x}}}_{\mathrm{s}}\left(t\right)+{\left({\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}+{\displaystyle \frac{1}{r}}{\mathbf{v}}_{\mathrm{d}}\left(t\right)\right)}^{\mathrm{T}}\left({\dot{\mathbf{x}}}_{\mathrm{d}}\left(t\right)+{\displaystyle \frac{1}{r}}{\dot{\mathbf{v}}}_{\mathrm{d}}\left(t\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{r^2}}{\mathbf{v}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right){\dot{\mathbf{v}}}_{\mathrm{d}}\left(t\right)\hfill \\ \hfill & =-{\left({\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}\right)}^{\mathrm{T}}{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)-{\left({\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}\right)}^{\mathrm{T}}{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)-{\displaystyle \frac{1}{r}}{\mathbf{v}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right){\mathbf{v}}_{\mathrm{d}}\left(t\right)\hfill \\ & -{\displaystyle \frac{2}{r}}{\mathbf{v}}_{\mathrm{d}}^{\mathrm{T}}\left(t\right){\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\hfill \\ \hfill & =-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}{\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-{\displaystyle \frac{1}{r}}{\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)}^{\mathrm{T}}\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{r}}{\mathbf{\phi }}_{\mathrm{d}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right),\hfill \end{array}$$

where ${\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)={[{\mathbf{\phi }}_{\mathrm{s}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right),{\mathbf{\phi }}_{\mathrm{d}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)]}^{\mathrm{T}}\in {\mathbb{R}}^{n^2}\mapsto {\mathbb{R}}^n$. Since $\mathbf{\phi }\left({\mathbf{x}}^{*}\right)={\mathbf{0}}_n$, one further has

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& =-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left({\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)+\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)-\mathbf{\phi }\left({\mathbf{x}}^{*}\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{r}}{\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)}^{\mathrm{T}}\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)+{\displaystyle \frac{1}{r}}{\mathbf{\phi }}_{\mathrm{d}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\hfill \\ \hfill & =-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left({\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\right)-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left(\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)-\mathbf{\phi }\left({\mathbf{x}}^{*}\right)\right)\hfill \\ & -{\displaystyle \frac{1}{r}}{\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)}^{\mathrm{T}}\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)+{\displaystyle \frac{1}{r}}{\mathbf{\phi }}_{\mathrm{d}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right).\hfill \end{array}$$

Under Assumption 2, one has $-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left(\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)-\mathbf{\phi }\left({\mathbf{x}}^{*}\right)\right)\le -m{\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel }^2$. Moreover, under Assumption 3, one obtains $|{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right)-{\phi }_i\left(\mathbf{x}\left(t\right)\right)|\le \overline{l_i}\parallel {\mathbf{y}}_i\left(t\right)-\mathbf{x}\left(t\right)\parallel$, where ${\overline{l}}_i$ is the Lipschitz constant of ${\phi }_i\left(\mathbf{x}\left(t\right)\right)$. Therefore, $∥{\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)∥\le l\parallel \mathbf{y}\left(t\right)-{\mathbf{1}}_n\otimes \mathbf{x}\left(t\right)\parallel =l\parallel \mathbf{q}\left(t\right)\parallel$, where $l=\max \left\{{\overline{l}}_i\right\}$ for $i\in S_n$. Hence,

$$\begin{array}{cc}\hfill {\dot{V}}_1\left(t\right)& =-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left({\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\right)-{\left(\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\right)}^{\mathrm{T}}\left(\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)-\mathbf{\phi }\left({\mathbf{x}}^{*}\right)\right)\hfill \\ & -{\displaystyle \frac{1}{r}}{\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)}^{\mathrm{T}}\left({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\right)+{\displaystyle \frac{1}{r}}{\mathbf{\phi }}_{\mathrm{d}}^{\mathrm{T}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\hfill \\ \hfill & \le l\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel -m\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2-{\displaystyle \frac{1}{r}}{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2+{\displaystyle \frac{1}{r}}{∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2.\hfill \end{array}$$

(11)

As for $V_2\left(t\right)$, the time derivative ${\dot{V}}_2\left(t\right)$ is given as

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& ={\left(\dot{\mathbf{y}}\left(t\right)-{\mathbf{1}}_n\otimes \dot{\mathbf{x}}\left(t\right)\right)}^{\mathrm{T}}\mathcal{P}\mathbf{q}\left(t\right)+{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left(\dot{\mathbf{y}}\left(t\right)-{\mathbf{1}}_n\otimes \dot{\mathbf{x}}\left(t\right)\right)\hfill \\ \hfill & =2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\dot{\mathbf{y}}\left(t\right)-2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}({\mathbf{1}}_n\otimes \dot{\mathbf{x}}\left(t\right)).\hfill \end{array}$$

From Equation (7), one obtains

$$\begin{array}{c}\hfill \dot{\mathbf{x}}\left(t\right)=\left[\begin{array}{c}-{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right]=-{\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)+\left[\begin{array}{c}{\mathbf{0}}_m\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\end{array}\right],\end{array}$$

where ${\mathbf{0}}_m={[0,0,\dots ,0]}_{m\times 1}$. Therefore,

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& =2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes \left({\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\left[\begin{array}{c}{\mathbf{0}}_m\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\end{array}\right]\right)\right)+2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\dot{\mathbf{y}}\left(t\right)\hfill \\ \hfill & =2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes {\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)\right)-2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes \left[\begin{array}{c}{\mathbf{0}}_m\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\end{array}\right]\right)\hfill \\ \hfill & -\theta {\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{Q}\left(\mathbf{q}\left(t\right)+\mathbf{g}\left(t\right)\right)\hfill \\ \hfill & =2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes {\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-{\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\right)+2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\right)\hfill \\ \hfill & -2{\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{P}\left({\mathbf{1}}_n\otimes \left[\begin{array}{c}{\mathbf{0}}_m\\ {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\end{array}\right]\right)-\theta {\mathbf{q}}^{\mathrm{T}}\left(t\right)\mathcal{Q}\left(\mathbf{q}\left(t\right)+\mathbf{g}\left(t\right)\right)\hfill \\ \hfill & \le 2\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathcal{P}\parallel ∥{\mathbf{1}}_n\otimes {\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-{\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)∥+2\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathcal{P}\parallel \parallel {\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\parallel \hfill \\ \hfill & +2\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathcal{P}\parallel \parallel {\mathbf{1}}_n\otimes ({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right))\parallel -\theta {\lambda }_{\min }{\left(\mathcal{Q}\right)\parallel \mathbf{q}\left(t\right)\parallel }^2+\theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{g}\left(t\right)\parallel .\hfill \end{array}$$

(12)

By Assumption 3, one has $∥{\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)∥\le l\parallel \mathbf{y}\left(t\right)-{\mathbf{1}}_n\otimes \mathbf{x}\left(t\right)\parallel =l\parallel \mathbf{q}\left(t\right)\parallel$. Therefore, $\parallel {\mathbf{1}}_n\otimes {\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-{\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\parallel \le \sqrt{n}\parallel {\mathbf{\phi }}_y\left(\mathbf{y}\left(t\right)\right)-\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\parallel \le l\sqrt{n}\parallel \mathbf{y}\left(t\right)-{\mathbf{1}}_n\otimes \mathbf{x}\left(t\right)\parallel =l\sqrt{n}\parallel \mathbf{q}\left(t\right)\parallel$. Moreover, since $\mathbf{\phi }\left({\mathbf{x}}^{*}\right)={\mathbf{0}}_n$, one has $\parallel {\mathbf{1}}_n\otimes \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)\parallel \le \sqrt{n}\parallel \mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)-\mathbf{\phi }\left({\mathbf{x}}^{*}\right)\parallel \le l\sqrt{n}\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel$. In addition, $\parallel {\mathbf{1}}_n\otimes ({\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right))\parallel \le \sqrt{n}\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)\parallel$. Hence, one obtains

$$\begin{array}{cc}\hfill {\dot{V}}_2\left(t\right)& \le 2l\sqrt{n}{\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel }^2+2l\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel -\theta {\lambda }_{\min }\left(\mathcal{Q}\right){\parallel \mathbf{q}\left(t\right)\parallel }^2\hfill \\ \hfill & +2\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel ∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥+\theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{g}\left(t\right)\parallel .\hfill \end{array}$$

(13)

Adding inequalities (11) and (13), one has

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& ={\dot{V}}_1\left(t\right)+{\dot{V}}_2\left(t\right)\hfill \\ \hfill & \le -m\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2-{\displaystyle \frac{1}{r}}{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2-\theta {\lambda }_{\min }\left(\mathcal{Q}\right){\parallel \mathbf{q}\left(t\right)\parallel }^2\hfill \\ \hfill & +l\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel +2l\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel +2l\sqrt{n}{\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel }^2\hfill \\ \hfill & +2\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel ∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥+\theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{g}\left(t\right)\parallel +{\displaystyle \frac{1}{r}}{∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2.\hfill \end{array}$$

(14)

Based on Lyapunov stability theory, one knows that if inequality $\dot{V}\left(t\right)\le 0$ is proved, then Theorem 1 is proved. By observing inequality (14), one sees that there are negative terms and positive terms in inequality (14). In addition, inequality (14) is too complicated to analyze $\dot{V}\left(t\right)$. Therefore, it needs to be simplified. For further investigation, the Young’s inequality [38] is introduced as

$$\left|xy\right|\le {\displaystyle \frac{\gamma }{2}}{x}^2+{\displaystyle \frac{1}{2\gamma }}{y}^2,x,y\in \mathbb{R},\gamma \in {\mathbb{R}}^{+}.$$

By reformulating the positive terms $l\parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel$, $2l\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel$, and $2\sqrt{n}\parallel \mathcal{P}\parallel \parallel \mathbf{q}\left(t\right)\parallel ∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥$, inequality (14) is reformulated as

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& \le -\left(m-{\displaystyle \frac{l}{2{\gamma }_1}}-{\displaystyle \frac{lh}{2{\gamma }_2}}\right){\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel }^2-(\theta {\lambda }_{\min }\left(\mathcal{Q}\right)-lh-{\displaystyle \frac{l{\gamma }_1}{2}}-{\displaystyle \frac{lh{\gamma }_2}{2}}\hfill \\ \hfill & -{\displaystyle \frac{h{\gamma }_3}{2}}{)\parallel \mathbf{q}\left(t\right)\parallel }^2-\left({\displaystyle \frac{1}{r}}-{\displaystyle \frac{h}{{\gamma }_3}}\right)\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\parallel }^2+\theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{g}\left(t\right)\parallel \hfill \\ \hfill & +{\displaystyle \frac{1}{r}}{∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2,\hfill \end{array}$$

(15)

where ${\gamma }_1,{\gamma }_2$, and ${\gamma }_3$ are positive constants to be determined, and constant h is defined as $h=2\sqrt{n}\parallel \mathcal{P}\parallel$ for convenience in algebraic computation. In addition,

$$\begin{array}{cc}\hfill {∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2& ={∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)-{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes \mathbf{x}\left(t\right))+{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes \mathbf{x}\left(t\right))-{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes {\mathbf{x}}^{*})∥}^2\hfill \\ \hfill & \le 2{∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)-{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes \mathbf{x}\left(t\right))∥}^2\hfill \\ \hfill & +2{∥{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes \mathbf{x}\left(t\right))-{\mathbf{\phi }}_{\mathrm{d}}({\mathbf{1}}_{n-m}\otimes {\mathbf{x}}^{*})∥}^2.\hfill \end{array}$$

By Assumption 3, it is derived that

$$\begin{array}{cc}\hfill {∥{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2& \le 2l_{\mathrm{d}}{∥{\mathbf{y}}_{\mathrm{d}}\left(t\right)-{\mathbf{1}}_{n-m}\otimes \mathbf{x}\left(t\right)∥}^2+2l_{\mathrm{d}}\sqrt{n-m}{\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel }^2\hfill \\ \hfill & \le 2l_{\mathrm{d}}{\parallel \mathbf{q}\left(t\right)\parallel }^2+2l_{\mathrm{d}}\sqrt{n-m}{\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel }^2,\hfill \end{array}$$

where $l_{\mathrm{d}}=\max \left\{\overline{l_i}\right\}$ for $i\in S_{n-m}$. Moreover, under the event-triggering condition (5), one has $\parallel \mathbf{g}\left(t\right)\parallel \le \rho \parallel \mathbf{q}\left(t\right)\parallel$. Therefore, inequality (15) is reformulated as

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& \le -\left(m-{\displaystyle \frac{l}{2{\gamma }_1}}-{\displaystyle \frac{lh}{2{\gamma }_2}}-{\displaystyle \frac{2l_{\mathrm{d}}}{r}}\sqrt{n-m}\right){\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel }^2-(\theta {\lambda }_{\min }\left(\mathcal{Q}\right)-lh-{\displaystyle \frac{l{\gamma }_1}{2}}-{\displaystyle \frac{lh{\gamma }_2}{2}}\hfill \\ \hfill & -{\displaystyle \frac{h{\gamma }_3}{2}}-{\displaystyle \frac{2l_{\mathrm{d}}}{r}}{)\parallel \mathbf{q}\left(t\right)\parallel }^2-\left({\displaystyle \frac{1}{r}}-{\displaystyle \frac{h}{{\gamma }_3}}\right)\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right){\parallel }^2+\theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel \parallel \mathbf{g}\left(t\right)\parallel ,\hfill \end{array}$$

For convenience in algebraic computation, define parameters ${\alpha }_1,{\alpha }_2$, and ${\alpha }_3$ as

$$\begin{array}{cc}\hfill {\alpha }_1& =m-{\displaystyle \frac{l}{2{\gamma }_1}}-{\displaystyle \frac{lh}{2{\gamma }_2}}-{\displaystyle \frac{2l_{\mathrm{d}}}{r}}\sqrt{n-m},\hfill \\ \hfill {\alpha }_2& =\theta {\lambda }_{\min }\left(\mathcal{Q}\right)-{\displaystyle \frac{2l_{\mathrm{d}}}{r}}-lh-{\displaystyle \frac{l{\gamma }_1}{2}}-{\displaystyle \frac{lh{\gamma }_2}{2}}-{\displaystyle \frac{h{\gamma }_3}{2}},\hfill \\ \hfill {\alpha }_3& ={\displaystyle \frac{1}{r}}-{\displaystyle \frac{h}{{\gamma }_3}}.\hfill \end{array}$$

Then, one obtains

$$\begin{array}{c}\hfill \dot{V}\left(t\right)\le -{\alpha }_1\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2-{\alpha }_2{\parallel \mathbf{q}\left(t\right)\parallel }^2-{\alpha }_3{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)+{\mathbf{\phi }}_{\mathrm{d}}\left({\mathbf{y}}_{\mathrm{d}}\left(t\right)\right)∥}^2+{\rho \theta \parallel \mathcal{Q}\parallel \parallel \mathbf{q}\left(t\right)\parallel }^2.\end{array}$$

(16)

From inequality (16), one sees that if one can prove that there exists control parameters $\theta$, r, and $\rho$ that guarantee ${\alpha }_1,{\alpha }_2,{\alpha }_3>0$ and ${\alpha }_2-\rho \theta \parallel \mathcal{Q}\parallel >0$, then one obtains $\dot{V}\left(t\right)<0$ and Theorem 1 is proved.

First, we prove that there exists a positive control parameter r that guarantees ${\alpha }_1>0$. Since m, l, and h are positive constant, one obtains that there exist positive ${\gamma }_1$ and ${\gamma }_2$ that guarantee $m-l/2{\gamma }_1-lh/2{\gamma }_2>0$. For fixed ${\gamma }_1$ and ${\gamma }_2$, define a positive constant $r^{*}$ that makes ${\alpha }_1=0$. It is derived that

$$r^{*}={\displaystyle \frac{4l_{\mathrm{d}}{\gamma }_1{\gamma }_2\sqrt{n-m}}{2m{\gamma }_1{\gamma }_2-l{\gamma }_2-lh{\gamma }_1}}.$$

Hence, for any $r>r^{*}$, inequality ${\alpha }_1>0$ holds.

Then, for a fixed r, since h is a positive constant and ${\alpha }_3=1/r-h/{\gamma }_3$, one obtains that there exists a positive ${\gamma }_3$ that guarantees ${\alpha }_3>0$. It is derived that ${\gamma }_3>rh$.

Moreover, we prove that for fixed ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, and r, there exists a positive control parameter r that guarantees ${\alpha }_2>0$. For fixed ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, and r, define a positive constant ${\theta }^{*}$ that makes ${\alpha }_2=0$. It is derived that

$${\theta }^{*}={\displaystyle \frac{2rlh+4l_{\mathrm{d}}+rl{\gamma }_1+rlh{\gamma }_2+rh{\gamma }_3}{2r{\lambda }_{\min }\left(\mathcal{Q}\right)}}.$$

Hence, for any $\theta >{\theta }^{*}$, inequality ${\alpha }_2>0$ holds.

Finally, we prove that for fixed ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, r, and $\theta$, there exists a positive control parameter r that guarantees ${\alpha }_2-\rho \theta \parallel \mathcal{Q}\parallel >0$. For fixed ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, r, and $\theta$, define a positive constant ${\rho }^{*}$ that makes ${\alpha }_2-\rho \theta \parallel \mathcal{Q}\parallel =0$. It is derived that

$${\rho }^{*}={\displaystyle \frac{{\alpha }_2}{\theta \parallel \mathcal{Q}\parallel }}={\displaystyle \frac{2r\theta {\lambda }_{\min }\left(\mathcal{Q}\right)-2rlh-4l_{\mathrm{d}}-rl{\gamma }_1-rlh{\gamma }_2-rh{\gamma }_3}{2r\theta \parallel \mathcal{Q}\parallel }}>0.$$

Hence, for any $\rho >{\rho }^{*}$, inequality ${\alpha }_2>0$ holds. Thus, for $\rho \in (0,{\rho }^{*})$, ${\alpha }_2-\rho \theta \parallel \mathcal{Q}\parallel >0$. Hence, with ${\alpha }_1,{\alpha }_2,{\alpha }_3>0$, it is derived that $\dot{V}\left(t\right)<0$.

Therefore, for properly chosen ${\gamma }_1,{\gamma }_2$, ${\gamma }_3,r,$ and $\theta$, under the event-triggering condition (5), if $\rho \in (0,{\rho }^{*})$, then $\dot{V}\left(t\right)<0$. In addition, following the Proof of Theorem 1, it is evident that $V\left(t\right)$ is positive definite. Through Lyapunov stability theory [39], one obtains that the NE is achieved asymptotically, and $\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}\parallel \to 0$, $\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel \to 0$, and $\parallel \mathbf{q}\left(t\right)\parallel \to 0$ as $t\to \infty$. Thus, the proof is complete. □

Theorem 2. 

Consider non-cooperative games played by heterogeneous MASs following the CETNES strategy (4) and the centralized event-triggering condition (5). Suppose that Assumptions 1–3 are satisfied. Then, there exists no Zeno behavior.

Proof of Theorem 2. 

If the lower bound of the inter-event time interval $t_{k+1}-t_k$ can be determined and inequality $t_{k+1}-t_k>0$ is always satisfied, then Theorem 2 is proved. Since the centralized event-triggering condition is based on the value relation between $\parallel \mathbf{g}\left(t\right)\parallel$ and $\parallel \mathbf{q}\left(t\right)\parallel$, we investigate the time derivative of $\parallel \mathbf{g}\left(t\right)\parallel$. For $t\in [t_k,t_{k+1})$, one has $\dot{\mathbf{g}}\left(t\right)=-\dot{\mathbf{q}}\left(t\right)$. Hence,

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}∥\mathbf{g}\left(t\right)∥}{\mathrm{d}t}}& \le ∥\dot{\mathbf{g}}\left(t\right)∥\hfill \\ \hfill & \le ∥\dot{\mathbf{y}}\left(t\right)-{\mathbf{1}}_n\otimes \dot{\mathbf{x}}\left(t\right)∥\hfill \\ \hfill & \le \parallel \dot{\mathbf{y}}\left(t\right)\parallel +\sqrt{n}\parallel \dot{\mathbf{x}}\left(t\right)\parallel \hfill \\ \hfill & \le c∥\mathbf{q}\left(t_k\right)∥+\sqrt{n}∥\left[\begin{array}{c}{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ -{\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right]∥,\hfill \end{array}$$

where c is a positive constant defined as $c=\theta \parallel \mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A\parallel$. Moreover, by Assumptions 2 and 3, it is derived that

$$\begin{array}{cc}\hfill {∥\left[\begin{array}{c}{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ -{\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right]∥}^2& ={∥{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)∥}^2+{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2\hfill \\ \hfill & \le 2l_{\mathrm{s}}\parallel {\mathbf{y}}_{\mathrm{s}}\left(t\right)-{\mathbf{1}}_m{\otimes \mathbf{x}\left(t\right)\parallel }^2+2l_{\mathrm{s}}\sqrt{m}\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2+{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2\hfill \\ \hfill & \le 2l_{\mathrm{s}}{\parallel \mathbf{q}\left(t\right)\parallel }^2+2l_{\mathrm{s}}\sqrt{m}\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2+{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2,\hfill \end{array}$$

(17)

where $l_{\mathrm{s}}=\max \left\{{\overline{l}}_i\right\}$ for $i\in S_m$. From Equation (9), it is derived that

$$\begin{array}{cc}\hfill V_1\left(t\right)& ={\displaystyle \frac{1}{2}}\parallel {\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}{\parallel }^2+{\displaystyle \frac{1}{2}}{∥{\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}+{\displaystyle \frac{1}{r}}{\mathbf{v}}_{\mathrm{d}}\left(t\right)∥}^2+{\displaystyle \frac{1}{2r^2}}{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2.\hfill \end{array}$$

Since $\parallel {\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}+{\mathbf{v}}_{\mathrm{d}}{\left(t\right)/r\parallel }^2\ge 1/2(\parallel {\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}{\parallel }^2+\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)/r{\parallel }^2)$, one further has

$$\begin{array}{cc}\hfill V_1\left(t\right)& \ge {\displaystyle \frac{1}{2}}\parallel {\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}{\parallel }^2+{\displaystyle \frac{1}{4}}{∥{\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}∥}^2+{\displaystyle \frac{1}{4r^2}}{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)∥}^2+{\displaystyle \frac{1}{2r^2}}{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2\hfill \\ \hfill & \ge {\displaystyle \frac{1}{4}}{\parallel {\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}\parallel }^2+{\displaystyle \frac{1}{4}}{∥\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}∥}^2+{\displaystyle \frac{3}{4r^2}}{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)∥}^2.\hfill \end{array}$$

From Equation (10), it is derived that $V_2\left(t\right)\ge {\lambda }_{\min }\left(\mathcal{P}\right){\parallel \mathbf{q}\left(t\right)\parallel }^2$. Hence, one obtains

$$\begin{array}{cc}\hfill V\left(t\right)& =V_1\left(t\right)+V_2\left(t\right)\hfill \\ \hfill & \ge {\displaystyle \frac{1}{4}}\parallel {\mathbf{x}}_{\mathrm{s}}\left(t\right)-{\mathbf{x}}_{\mathrm{s}}^{*}{\parallel }^2+{\displaystyle \frac{1}{4}}{∥\mathbf{x}\left(t\right)-{\mathbf{x}}^{*}∥}^2+{\displaystyle \frac{3}{4r^2}}{∥{\mathbf{v}}_{\mathrm{d}}\left(t\right)∥}^2+{\lambda }_{\min }\left(\mathcal{P}\right){\parallel \mathbf{q}\left(t\right)\parallel }^2.\hfill \end{array}$$

(18)

By observing inequalities (17) and (18), one sees that inequalities (17) and (18) consist of similar terms ${\parallel \mathbf{q}\left(t\right)\parallel }^2$, $\parallel \mathbf{x}\left(t\right)-{\mathbf{x}}^{*}{\parallel }^2$, and $\parallel {\mathbf{v}}_{\mathrm{d}}{\left(t\right)\parallel }^2$ with different coefficients. Therefore, a value relation between $V\left(t\right)$ and ${∥{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)∥}^2+{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2$ is established. Define ${\eta }_1$ as ${\eta }_1=\max \{2l_{\mathrm{s}},2l_{\mathrm{s}}\sqrt{m},1\}$ and ${\eta }_2$ as ${\eta }_2=\min \{{\lambda }_{\min }\left(\mathcal{P}\right),3/4r^2,1/4\}$. Thus, one obtains

$$\begin{array}{cc}\hfill {\displaystyle \frac{{∥\left[\begin{array}{c}{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ -{\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right]∥}^2}{{\eta }_1}}& \le {\parallel \mathbf{q}\left(t\right)\parallel }^2+\parallel {\mathbf{x}}_{\mathrm{d}}\left(t\right)-{\mathbf{x}}_{\mathrm{d}}^{*}{\parallel }^2+{\parallel {\mathbf{v}}_{\mathrm{d}}\left(t\right)\parallel }^2\le {\displaystyle \frac{V\left(t\right)}{{\eta }_2}}.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill ∥\left[\begin{array}{c}{\mathbf{\phi }}_{\mathrm{s}}\left({\mathbf{y}}_{\mathrm{s}}\left(t\right)\right)\\ -{\mathbf{v}}_{\mathrm{d}}\left(t\right)\end{array}\right]∥& \le \sqrt{{\displaystyle \frac{{\eta }_{1}V\left(t\right)}{{\eta }_2}}}=\sqrt{\eta V\left(t\right)},\hfill \end{array}$$

where $\eta ={\eta }_1/{\eta }_2$. Moreover, as proved in Theorem 1, $\dot{V}\left(t\right)<0$. Hence, for $t\in [t_k,t_{k+1})$, $V\left(t\right)\le V\left(t_k\right)$. Thus, one obtains

$$\begin{array}{cc}\hfill \parallel \dot{\mathbf{g}}\left(t\right)\parallel & \le \sqrt{\eta nV\left(t\right)}+c\parallel \mathbf{q}\left(t_k\right)\parallel \hfill \\ \hfill & \le \sqrt{\eta nV\left(t_k\right)}+c\parallel \mathbf{q}\left(t_k\right)\parallel ,\hfill \end{array}$$

where $V\left(t_k\right)$ is a positive constant for $t\in [t_k,t_{k+1})$. Hence,

$$\begin{array}{cc}\hfill \parallel \mathbf{g}\left(t_{k+1}\right)\parallel & \le {\int }_{t_k}^{t_{k+1}}\parallel \dot{\mathbf{g}}\left(s\right)\parallel \mathrm{d}s\hfill \\ \hfill & \le \left(\sqrt{\eta nV\left(t_k\right)}+c\parallel \mathbf{q}\left(t_k\right)\parallel \right)\left(t_{k+1}-t_k\right).\hfill \end{array}$$

Furthermore, under the event-triggering condition (5), for $t\in [t_k,t_{k+1})$, $\parallel \mathbf{q}\left(t_k\right)\parallel -\parallel \mathbf{q}\left(t\right)\parallel \le \parallel \mathbf{g}\left(t\right)\parallel \le \rho \parallel \mathbf{q}\left(t\right)\parallel$. Therefore, $\parallel \mathbf{q}\left(t\right)\parallel \ge \parallel \mathbf{q}\left(t_k\right)\parallel /(1+\rho )$. Consider the next event-triggering time instant $t_{k+1}$, one has $\parallel \mathbf{g}\left(t_{k+1}\right)\parallel >\rho \parallel \mathbf{q}\left(t\right)\parallel \ge \rho \parallel \mathbf{q}\left(t_k\right)\parallel /(1+\rho )$. Then, it is derived that

$$\left(\sqrt{\eta nV\left(t_k\right)}+c\parallel \mathbf{q}\left(t_k\right)\parallel \right)\left(t_{k+1}-t_k\right)>{\displaystyle \frac{\rho \parallel \mathbf{q}\left(t_k\right)\parallel }{1+\rho }}.$$

Thus, the lower bound of the inter-event time interval is summarized as

$$t_{k+1}-t_k>{\displaystyle \frac{\rho \parallel \mathbf{q}\left(t_k\right)\parallel }{(1+\rho )\left(\sqrt{\eta nV\left(t_k\right)}+c\parallel \mathbf{q}\left(t_k\right)\parallel \right)}}>0,$$

which proves the nonexistence of Zeno behavior. □

3.2. DETNES Strategy

As presented above, the CETNES strategy (4) demands global information to determine whether the condition (5) is satisfied. However, in physical implementations, agents in MASs may not have access to global information. In this subsection, a DETNES strategy is proposed to solve the NE-seeking problem in a fully distributed manner. By adopting the DETNES strategy, each agent determines its own event-triggering time instants only based on local information and information from its neighbors. Let $t_k^i$ denote the kth event-triggering time instant of agent i. For agent i, when $t\in [t_k^i,t_{k+1}^i)$, the DETNES strategy is proposed as

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}\begin{array}{cccc}\hfill u_i\left(t\right)& =-{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right),\hfill & \hfill & i\in S_m,\hfill \\ \hfill u_i\left(t\right)& =-r\left(v_i\left(t\right)+{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right)\right),\hfill & \hfill & i\in S_{n-m},\hfill \end{array}\hfill \end{array}\right.\hfill \\ \hfill & \begin{array}{c}\hfill {\dot{y}}_{ij}\left(t\right)=-\theta \left(\sum _{q=1}^n{a}_{iq}\left(y_{ij}\left(t_k^i\right)-y_{qj}\left(t_{k^{\prime }}^q\right)\right)+a_{ij}\left(y_{ij}\left(t_k^i\right)-x_j\left(t_{k^{\prime }}^j\right)\right)\right),i\in S_n,\end{array}\hfill \end{array}$$

(19)

where $t_{k^{\prime }}^j\in [t_k^i,t_{k+1}^i)$ denotes the latest event-triggering time instant of agent j when $t\in [t_k^i,t_{k+1}^i)$.

Before proceeding, some distributed measurements are introduced to construct the event-triggering condition for the DETNES strategy (19). The definitions of several decentralized measurements are given as

$$\begin{array}{cccccc}\hfill e_{ij}^y\left(t\right)& =y_{ij}\left(t_k^i\right)-y_{ij}\left(t\right),\hfill & \hfill & i,j\in S_n,\hfill & \hfill & t\in [t_k^i,t_{k+1}^i),\hfill \\ \hfill e_i^x\left(t\right)& =x_i\left(t_k^i\right)-x_i\left(t\right),\hfill & \hfill & i\in S_n,\hfill & \hfill & t\in [t_k^i,t_{k+1}^i),\hfill \\ \hfill e_{ij}^x\left(t\right)& =x_j\left(t_{k^{\prime }}^i\right)-x_j\left(t\right),\hfill & \hfill & i,j\in S_n,\hfill & \hfill & t\in [t_k^i,t_{k+1}^i),\hfill \end{array}$$

and

$$e_{ij}^{xy}\left(t\right)=y_{ij}\left(t_k^i\right)-y_{ij}\left(t\right)-x_j\left(t_{k^{\prime }}^i\right)+x_j\left(t\right)=e_{ij}^y\left(t\right)-e_{ij}^x\left(t\right),i\in S_n,j\in {\mathcal{N}}_i,t\in [t_k^i,t_{k+1}^i),$$

where ${\mathcal{N}}_i$ denotes the set of neighbors for agent i.

Define $\mathbf{z}\left(t\right)=(\mathcal{L}\otimes {\mathcal{I}}_{n\times n}+A)\mathbf{q}\left(t\right)\in {\mathbb{R}}^{n^2}$ and ${\mathbf{z}}_i\left(t_k^i\right)=[z_{i1}\left(t_k^i\right),z_{i2}\left(t_k^i\right),\dots ,$$z_{in}\left(t_k^i\right){]}^{\mathrm{T}}\in {\mathbb{R}}^n$. For agent i, the elements of measurement ${\mathbf{z}}_i\left(t\right)$ and ${\mathbf{z}}_i\left(t_k^i\right)$ are given as

$$z_{ij}\left(t\right)=\sum _{q=1}^n{a}_{iq}\left(y_{ij}\left(t\right)-y_{qj}\left(t\right)\right)+a_{ij}\left(y_{ij}\left(t\right)-x_j\left(t\right)\right),$$

and

$$z_{ij}\left(t_k^i\right)=\sum _{q=1}^n{a}_{iq}\left(y_{ij}\left(t_k^i\right)-y_{qj}\left(t_{k^{\prime }}^q\right)\right)+a_{ij}\left(y_{ij}\left(t_k^i\right)-x_j\left(t_{k^{\prime }}^j\right)\right).$$

For agent i, define a decentralized measurement ${\mathbf{\epsilon }}_i\left(t\right)\in {\mathbb{R}}^n$ as

$${\mathbf{\epsilon }}_i\left(t\right)={\mathbf{z}}_i\left(t_k^i\right)-{\mathbf{z}}_i\left(t\right),$$

with the corresponding elements being

$${\epsilon }_{ij}\left(t\right)=\sum _{q=1}^n{a}_{iq}\left(e_{ij}^y\left(t\right)-e_{qj}^y\left(t\right)\right)+a_{ij}\left(e_{ij}^y\left(t\right)-e_{ij}^x\left(t\right)\right).$$

Thus, the decentralized event-triggering condition for agent i is given as

$$\begin{array}{cc}\hfill t_{k+1}^i=\inf \{& t:t>t_k^i,\parallel {\mathbf{\epsilon }}_i\left(t\right)\parallel >\rho \parallel {\mathbf{z}}_i\left(t\right)\parallel \}.\hfill \end{array}$$

(20)

The transmission of information and the updating of the controller for agent i, along with the decentralized measurements ${\mathbf{z}}_i\left(t\right)$ and ${\mathbf{\epsilon }}_i\left(t\right)$ under the event-triggered mechanism, are presented in Figure 1.

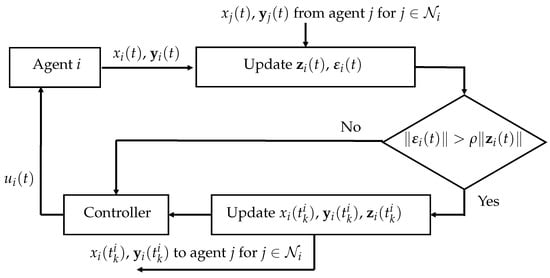
Figure 1. Event-triggered mechanism for agent i under DETNES strategy.

Remark 4. 

Unlike measurements such as $\mathbf{g}\left(t\right)$ and $\mathbf{q}\left(t\right)$, ${\mathbf{\epsilon }}_i\left(t\right)$ and ${\mathbf{z}}_i\left(t\right)$ are computable for agent i without utilizing global information. Therefore, the DETNES strategy (19) solves the NE-seeking problem for non-cooperative games played by heterogeneous MASs in a fully distributed manner.

The convergence property of the DETNES strategy (19) is given by the following theorem.

Theorem 3. 

Consider non-cooperative games played by heterogeneous MASs following the DETNES strategy (19) and the decentralized event-triggering condition (20). Suppose that Assumptions 1–3 are satisfied. Then, there exists a positive constant ${\rho }^{*}$. For each $\rho \in (0,{\rho }^{*})$, the NE is asymptotically achieved.

Proof. 

The detailed proof is presented in Appendix A. □

Theorem 4. 

Consider non-cooperative games played by heterogeneous MASs following the DETNES strategy (19) and the decentralized event-triggering condition (20). Suppose that Assumptions 1–3 are satisfied. Then, there exists no Zeno behavior.

Proof. 

The detailed proof is presented in Appendix B. □

4. Numerical Experiments and Results

In this section, some numerical experiments are conducted to illustrate the efficiency and efficacy of the proposed CETNES strategy (4) and DETNES strategy (19).

Consider a heterogeneous multi-agent system consisting of six agents, in which agents $1,3$, and 5 are single-integrator agents and agents $2,4$, and 6 are double-integrator agents. As shown in Figure 2, the corresponding Laplacian matrix $\mathcal{L}$ of $\mathbb{G}$ is given as

$$\mathcal{L}=\left[\begin{array}{cccccc}1& -1& 0& 0& 0& 0\\ -1& 4& -1& 0& -1& -1\\ 0& -1& 3& -1& -1& 0\\ 0& 0& -1& 2& -1& 0\\ 0& -1& -1& -1& 4& -1\\ 0& -1& 0& 0& -1& 2\end{array}\right]\in {\mathbb{R}}^{6\times 6}.$$

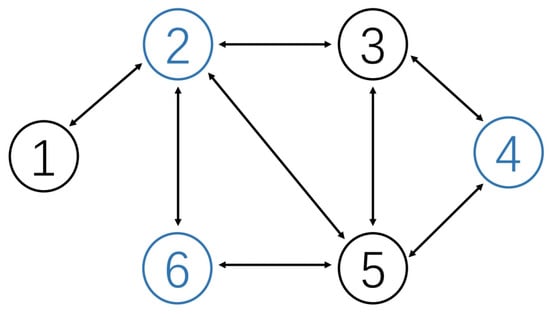
Figure 2. Communication topology $\mathbb{G}$ of heterogeneous multi-agent system consisting of 6 agents, in which agents $1,3$, and 5 are single-integrator agents and agents $2,4$, and 6 are double-integrator agents.

The cost functions of the agents are defined as

$$f_i\left(\mathbf{x}\left(t\right)\right)={\left(x_i\left(t\right)-b_i\right)}^2-p_0{x}_i\left(t\right)\sum _{j\in {\mathcal{N}}_i}{x}_j\left(t\right)+c_0,i\in S_n,$$

(21)

where $b_i,p_0$, and $c_0$ are constants. Set the corresponding constants as $p_0=0.2$, $c_0=3$, and $[b_1,b_2,\dots ,b_6]=[-5,5,-7,7,-9,9]$. Let $\mathbf{\phi }\left({\mathbf{x}}^{*}\right)={\mathbf{0}}_n$; the NE ${\mathbf{x}}^{*}$ is obtained as ${\mathbf{x}}^{*}=[-4.6072,3.9280,-6.8422,$${5.5279,-7.8781,8.6043]}^{\mathrm{T}}$. Moreover, for both CETNES and DETNES strategies, the initial states of the agents are set as $\mathbf{x}\left(0\right)={[10,8,6,4,2,0]}^{\mathrm{T}}$ and ${\mathbf{y}}_i\left(0\right)={[0,0,0,0,0,0]}^{\mathrm{T}}$. In addition, control parameters $\theta$ and r are set as $\theta =25$ and $r=2$, respectively. One can verify that the cost functions (21) satisfy Assumptions 2 and 3, and that the parameters $\theta$ and r satisfy $\theta >{\theta }^{*}$ and $r>r^{*}$.

4.1. Experiment Results of CETNES Strategy

In this subsection, numerical experiments on the NE-seeking problem of non-cooperative games (21) with the CETNES strategy (4) are conducted. The corresponding experiment results are presented in Figure 3 and Figure 4, and Table 1.

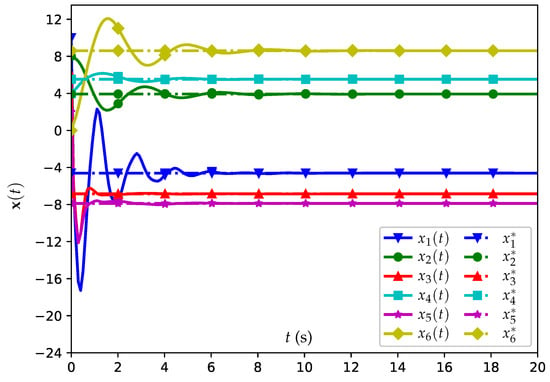
Figure 3. Position trajectories of all agents when using the CETNES strategy (4) with $\rho =0.6$, where $x_i^{*}$ denotes the NE for agent i.

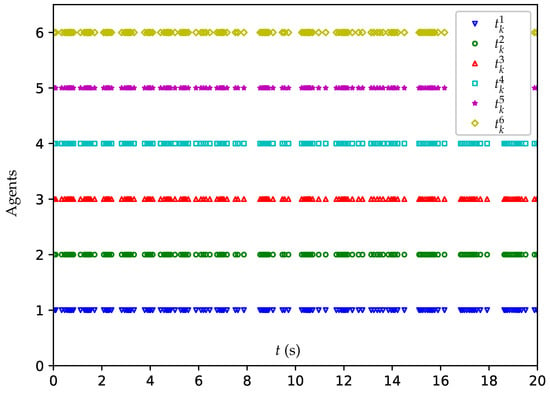
Figure 4. Triggering time sequences of all agents when using the CETNES strategy (4) with $\rho =0.6$.

Table 1. Comparison of CETNES strategy (4) with different values of $\rho$.

$\mathit{\rho }$	Number of Trigger Events	Minimum Inter-Event Time Interval	Maximum Inter-Event Time Interval
0.1	621	0.02 s	0.11 s
0.2	257	0.05 s	0.24 s
0.6	144	0.07 s	0.41 s

The position trajectories of all agents when using the CETNES strategy (4) with $\rho =0.6$ are illustrated in Figure 3. The corresponding centralized triggering time sequences of all agents are illustrated in Figure 4.

From Figure 3, one sees that, driven by the CETNES strategy (4), the heterogeneous multi-agent system successfully converges to the theoretical NE ${\mathbf{x}}^{*}$, as denoted by the dashed lines. Moreover, as illustrated in Figure 4, Zeno behavior does not occur when using the CETNES strategy (4).

Additionally, several numerical experiments of the CETNES strategy (4) with different values of $\rho$ are also conducted, and the corresponding results are presented in Table 1. From Table 1, one sees that, with a larger value of $\rho$, there are more trigger events. In addition, it is evident that, as $\rho$ increases, the minimum and maximum inter-event time intervals also increase.

4.2. Experiment Results of DETNES Strategy

In this subsection, numerical experiments on a non-cooperative game (21) with the DETNES strategy (19) are conducted. The corresponding experiment results are presented in Figure 5 and Figure 6. The initial states and corresponding parameters are set to be the same as those in Section 4.1.

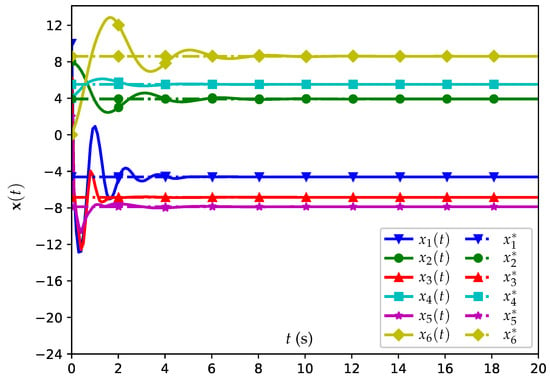
Figure 5. Position trajectories of all agents when using the DETNES strategy (19) with $\rho =0.6$, where $x_i^{*}$ denote the NE for agent i.

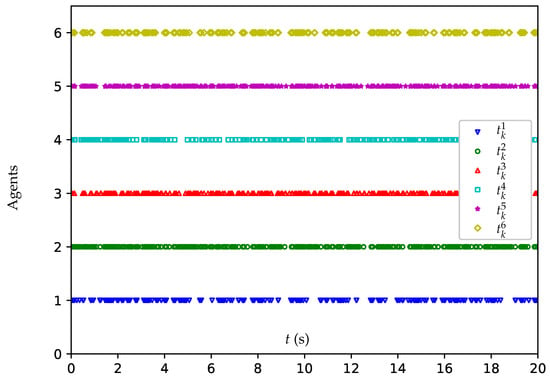
Figure 6. Triggering time sequences of all agents when using the DETNES strategy (19) with $\rho =0.6$.

The position trajectories of all agents when using the DETNES strategy (19) with $\rho =0.6$ are illustrated in Figure 5. The corresponding decentralized triggering time sequences of all agents are illustrated in Figure 6.

4.3. Comparative Experiments

In this subsection, comparative experiments are conducted between the CETNES strategy (4), the DETNES strategy (19), and the periodic sampling control (PSC) strategy. The PSC strategy is based on the method presented in [28]. In [28], He and Huang introduced an NE-seeking strategy for homogeneous MASs consisting of agents with high-order integrator dynamics. Suppose that, under the PSC strategy, all agents periodically transmit their information to their neighbors at $t_p^i=p\tau$, where $\tau >0$ is a constant. Then, for agent i, when $t\in [t_p^i,t_{p+1}^i)$, a PSC strategy is formulated as follows:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}\begin{array}{cccc}\hfill u_i\left(t\right)& =-{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right),\hfill & \hfill & i\in S_m,\hfill \\ \hfill u_i\left(t\right)& =-r\left(v_i\left(t\right)+{\phi }_i\left({\mathbf{y}}_i\left(t\right)\right)\right),\hfill & \hfill & i\in S_{n-m},\hfill \end{array}\hfill \end{array}\right.\hfill \\ \hfill & \begin{array}{c}\hfill {\dot{y}}_{ij}\left(t\right)=-\theta \left(\sum _{q=1}^n{a}_{ik}\left(y_{ij}\left(t_p^i\right)-y_{qj}\left(t_p^i\right)\right)+a_{ij}\left(y_{ij}\left(t_p^i\right)-{\eta }_j\left(t_p^i\right)\right)\right),i\in S_n,\end{array}\hfill \end{array}$$

(22)

where ${\eta }_i\left(t\right)$ is a fictitious output, which is defined as

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}\begin{array}{cccc}\hfill {\eta }_i\left(t\right)& =x_i\left(t\right),\hfill & \hfill & i\in S_m,\hfill \\ \hfill {\eta }_i\left(t\right)& =x_i\left(t\right)+v_i\left(t\right),\hfill & \hfill & i\in S_{n-m}.\hfill \end{array}\hfill \end{array}\right.\hfill \end{array}$$

By introducing the fictitious output ${\eta }_i\left(t\right)$, the PSG strategy (22) ensures that double-integrator agents achieve consensus not only at the position level but also at the velocity level.

In the comparative experiment, the CETNES, DETNES, and PSG strategies are applied to solve the same NE-seeking problem in Section 4.1 and Section 4.2. For the three strategies, the parameters r and $\theta$, as well as the initial states, are set identical to those in Section 4.1 and Section 4.2. Moreover, NE is achieved when $\mathbf{\phi }\left(\mathbf{x}\left(t\right)\right)={\mathbf{0}}_n$. Hence, $\parallel \mathbf{\phi }\left(\mathbf{x}\right(t\left)\right)\parallel$ is chosen as the error that measures the convergence performance of the NE-seeking strategies.

Firstly, several experiments using the PSC strategy (22) with different values of $\tau$ are conducted to find the feasible sampling gap. The corresponding results are presented in Figure 7 and Table 2.

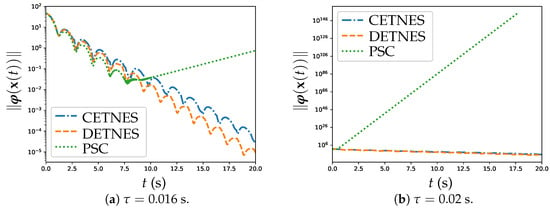
Figure 7. Trajectories of $\parallel \mathbf{\phi }\left(\mathbf{x}\right(t\left)\right)\parallel$ of PSC, CETNES, and DETNES strategies with $\rho =0.1$ and different $\tau$.

Table 2. Convergence performance of PSG with different $\tau$.

$\mathit{\tau }$	Periodic Sampling Times	Whether Convergence
0.01 s	2000	Converge
0.016 s	1250	Do not converge
0.02 s	1000	Do not converge

From Figure 7a,b, it is evident that when the CETNES and DETNES strategies achieve NE successfully, the PSC strategy (22) does not converge and fails to achieve the NE when $\tau =0.016$ s and $\tau =0.02$ s. Moreover, from Table 2, it can be seen that for the PSC strategy (22) to work, the sampling gap $\tau$ needs to be small enough. Therefore, the sampling gap $\tau$ is set to 0.01 s.

Additionally, comparative experiments between the CETNES, DETNES, and PSC strategies are conducted with $\rho =0.1$ and $\tau =0.01$ s. The corresponding results are presented in Figure 8 and Table 3.

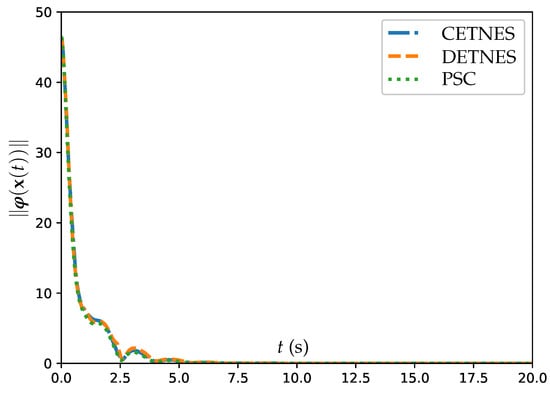
Figure 8. Trajectories of $\parallel \mathbf{\phi }\left(\mathbf{x}\right(t\left)\right)\parallel$ synthesized by the PSC, CETNES, and DETNES strategies with $\rho =0.1$ and $\tau =0.01$ s.

Table 3. Comparison between PSG, CETNES, and DETNES strategies with $\rho =0.1$ and $\tau =0.01$ s.

Agent	Number of Trigger Events for CETNES	Number of Trigger Events for DETNES	Periodic Sampling Times
Agent 1	621	1167	2000
Agent 2	621	1483	2000
Agent 3	621	752	2000
Agent 4	621	917	2000
Agent 5	621	1300	2000
Agent 6	621	706	2000

In addition, to investigate the influence of parameter $\rho$, another comparative experiment is conducted with $\rho =0.6$ and the corresponding results are presented in Table 4. From Table 4, the differences in communication costs for the three strategies are apparent. For the CETNES strategy, the number of trigger events amounts to 144. In contrast, for the DETNES strategy, the number of trigger events for agents varies from 178 to 550 due to the distributed nature. As for the PSG strategy, the periodic sampling time remains 2000. Compared with the experiment results when $\rho =0.1$, it is evident that the number of trigger events increases as $\rho$ decreases. Moreover, due to the centralized event-triggered mechanism, for the same $\rho$, the communication consumption of the CETNES strategy is lower than the DETNES strategy. However, the DETNES strategy has a broader application scenario, as it does not rely on centralized communication or control.

Table 4. Comparison between PSG, CETNES, and DETNES strategies with $\rho =0.6$ and $\tau =0.01$ s.

Agent	Number of Trigger Events for CETNES	Number of Trigger Events for DETNES	Periodic Sampling Times
Agent 1	144	220	2000
Agent 2	144	550	2000
Agent 3	144	323	2000
Agent 4	144	204	2000
Agent 5	144	464	2000
Agent 6	144	178	2000

5. Conclusions

In this paper, the event-triggered NE-seeking problem for non-cooperative games in heterogeneous MASs has been tackled. To solve the NE-seeking problem, novel CETNES and DETNES strategies have been proposed. Theoretical analyses have illustrated the convergence properties of both the CETNES and DETNES strategies, ensuring that both strategies lead to the desired NE without exhibiting Zeno behavior. Through numerical experiments, the effectiveness and efficiency of the proposed strategies have been validated. The experimental results illustrate that both the CETNES and DETNES strategies not only successfully achieve the Nash equilibrium but also significantly reduce the communication consumption among agents. In this paper, the constraints on the agents’ actions are not considered. In practical engineering, heterogeneous MASs may encounter a variety of limitations, and due to their heterogeneous nature, these constraints are more difficult to handle. Generalized (i.e., constrained) Nash equilibrium seeking for heterogeneous MASs may be investigated in our future work.