TFGCRN: Temporal–Frequency Graph Convolutional Recurrent Network for Incomplete Traffic Forecasting

Abstract

Traffic forecasting is a crucial component that underpins an intelligent transportation system. Among the current mainstream forecasting algorithms, spatial–temporal graph neural networks (STGNNs), as the mainstream solution, have been used in traffic forecasting due to their ability to model spatial–temporal dependencies effectively. However, sensor failures caused by factors such as bad weather often lead to incomplete traffic data, which severely prevents STGNNs from modeling spatial–temporal dependencies and consequently degrades forecasting performance. To achieve accurate forecasting under incomplete traffic conditions, this paper proposes a Temporal–Frequency Graph Convolutional Recurrent Network (TFGCRN) model that embeds a Temporal–Frequency Graph Convolutional Network into gated recurrent units. During the recursive modeling process, TFGCRN fully leverages both global and local information to resist the adverse effects of missing values while generating more accurate spatial relationships, thereby achieving precise incomplete traffic forecasting. The experiments on four real-world datasets show that TFGCRN can achieve satisfactory results superior to multiple baselines and effectively adapt to different missing rates. Compared with the state-of-the-art baseline, TFGCRN can reduce forecasting error by 2–6%.

1. Introduction

With the acceleration of urbanization and the rapid increase in the number of motor vehicles, problems such as traffic congestion, frequent accidents, and resource waste have become core bottlenecks that hinder the efficient operation of cities [1,2]. Intelligent transportation systems (ITSs) are the key technological framework to solve these issues [3,4]. As an important part of the ITS, traffic time series forecasting is gradually becoming a crucial technology for addressing traffic congestion and improving travel efficiency [5]. Simply put, traffic time series forecasting involves analyzing traffic data ordered by time to uncover patterns in traffic flow, speed, and other metrics as they change over time, thereby making precise forecasts about future traffic conditions [6]. Using traffic flow and speed data as examples, traffic time series forecasting can accurately capture and predict road congestion states and future changes [7]. By analyzing these patterns, traffic management departments can proactively prepare, such as by deploying additional traffic officers on key routes during peak hours or optimizing signal light timing, thus effectively alleviating traffic pressure [8]. In conclusion, traffic forecasting plays an irreplaceable core role in the construction of ITS [9]. It provides scientific and accurate decision-making support for traffic planners, enabling more rational allocation of traffic resources, injecting strong momentum into the efficient operation of urban traffic, and becoming an indispensable smart solution for modern urban traffic management [10].

To achieve accurate traffic forecasting, various mathematical algorithms have been proposed [11]. The mainstream approaches can be broadly categorized into statistical models and artificial intelligence (AI) models [12,13,14]. The former primarily constructs predictive models based on vehicle dynamics and mathematical formulas [15,16]. Although it has strong interpretability, it is unable to model non-linearity and ignores the spatial dependencies between different traffic time series, limiting its practical value [17]. The latter introduces the concept of non-linear modeling based on mathematical theory, which ensures that the model can capture traffic time series from both temporal and spatial dimensions, thereby achieving better performance than statistical models [18]. Currently, the spatial–temporal graph neural network (STGNN) [19,20,21], as a mainstream AI model, effectively combines the Graph Convolutional Network (GCN) and sequence models to exploit the spatial–temporal dependencies in traffic time series fully, and has thus found widespread application.

However, the effectiveness of STGNNs usually relies on the assumption of data completeness [22]. Specifically, graph convolution requires prior knowledge or node features to model spatial relationships, while sequence models rely on temporal context information to analyze periodicity and local temporal details in the data [23]. In reality, the sensors used for data collection are often affected by factors such as bad weather or component failures, leading to a large number of missing values in the collected data (typically represented as zeros), which leads to existing models often needing to mine incomplete traffic time series and predict future values [24]. In this case, along the temporal dimension, missing values disrupt periodicity and trends while introducing erroneous local details (e.g., abrupt changes or flat segments). In the spatial dimension, missing values alter the patterns among different data streams, causing incorrect spatial relationships during similarity analysis. These phenomena make it difficult for STGNNs to accurately capture spatial–temporal dependencies, resulting in suboptimal forecasting results in incomplete traffic forecasting.

To address the adverse effects caused by missing values and to accurately capture spatiotemporal dependencies, we propose a novel Temporal–Frequency Graph Convolutional Recurrent Network (TFGCRN). The core components of TFGCRN include spatial–temporal embedding, the Temporal–Frequency Graph Convolutional Network (TFGCN), and gated recurrent unit (GRU). Specifically, the spatial–temporal embedding introduces additional global information to mitigate the disruption of both global and local information caused by missing values, which can map missing values to available high-dimensional representations, preventing the model from uncovering incorrect patterns. Then, the TFGCN constructs graph structures from both the frequency and temporal domains to reconstruct spatial relationships from global and local perspectives, aiming to mitigate the impact of missing values on local information and thereby improving the accuracy of modeling spatial relationships. Finally, the TFGCN is embedded into the GRU and replaces all fully connected layers, enabling dynamic extraction of spatial–temporal dependencies and achieving satisfactory results in incomplete traffic forecasting. The main contributions of this paper are as follows:

• To alleviate the adverse effects caused by missing values, this paper proposes the Temporal–Frequency Graph Convolutional Recurrent Network (TFGCRN), which aims to dynamically reconstruct spatial–temporal dependencies from both global and local perspectives, thereby achieving improved performance in incomplete traffic forecasting.
• This paper proposes the Temporal–Frequency Graph Convolutional Network (TFGCN) by leveraging the advantages of frequency and temporal information in capturing global and local spatial relationships. The TFGCN is used to replace all fully connected layers within the GRU, thereby recursively modeling spatial–temporal dependencies.
• Experiments on four real-world datasets demonstrate that TFGCRN outperforms ten mainstream baselines and adapts well to different missing rates, verifying its superiority and robustness.

2. Related Works

2.1. Classic Traffic Forecasting Model

Classical traffic forecasting models mainly establish the mapping between historical observations and future values by combining time series and feature engineering. In this context, long short-term memory (LSTM) networks, convolutional neural networks (CNNs), and ensemble learning have gained widespread attention [25]. Alkarim et al. [26] employ ensemble learning to integrate multiple deep learning models and machine learning models, aiming to achieve stable and accurate forecasting of traffic data changes. Wang et al. [27] combine visual features with traffic flow and introduce deep learning to achieve excellent performance in statistical methods. Chen et al. [28] performed feature fusion based on road mixing rate and anomaly features, and used deep learning models to predict traffic flow changes.

In summary, these works have achieved better results than traditional statistical models and machine learning models. However, due to the lack of sufficient modeling of spatial relationships, they still fail to achieve satisfactory results in spatial–temporal traffic prediction.

2.2. Two-Stage Incomplete Traffic Forecasting Model

Mainstream two-stage models typically follow an imputation + forecasting approach: they first use an imputation model to recover missing values, and then apply a forecasting model on the recovered data to capture spatial–temporal dependencies and generate predictions. Next, we will introduce several mainstream imputation models and forecasting models, respectively.

Imputation models mainly fall into two categories: temporal-based imputation and spatial-based imputation [29]. The former primarily relies on attention mechanisms or transformer models to leverage contextual information for recovering missing values. For example, TA-SAITS [30] employs a bidirectional attention mechanism to effectively ensure high-quality data reconstruction. GPT4TS [31] introduces GPT-2 and patch-based modeling to fully exploit contextual information for imputation. Yang et al. [32] combine frequency-domain information with generative models to enhance the effectiveness of time series imputation. The latter mainly relies on spatial attention mechanisms or graph neural networks to effectively utilize the spatial relationships among different sequences for missing value recovery. For instance, GRIN [33] employs a combination of graph convolution and recurrent neural networks to efficiently reconstruct missing values. SPIN [34] integrates both spatial attention and temporal attention to ensure the reliability of data imputation. Islam et al. [35] combine attention mechanisms with diffusion models to enhance the performance of imputation.

Forecasting models. Currently, the mainstream forecasting models include multi-layer perceptron (MLP), transformer, and spatial–temporal graph neural networks [36,37,38]. The main idea behind MLP and transformer models is to model the temporal dependencies of traffic time series to predict their future values [39,40]. STID [41] uses spatial–temporal encoding with the MLP model to obtain accurate traffic forecasting results. STAEformer [42] combines spatial–temporal encoding with the transformer model to obtain accurate traffic forecasting results. MGSFformer [43] combines the concepts of spatiotemporal attention and multi-scale modeling to achieve accurate time series forecasting. LGSTformer [44] integrates multi-scale temporal convolutions, dynamic–static graph convolutions, and spatiotemporal self-attention to capture spatial–temporal dependencies. Chen et al. [45] introduce the idea of dynamic trend modeling to improve the transformer, achieving excellent forecasting results. Compared to the above two methods, STGNNs [46,47] use graph convolution to extract spatial relationships and sequence models to capture temporal information, thereby better modeling the spatiotemporal dependencies in traffic time series. Zhang [48] proposes dynamic Graph Convolutional Networks with temporal representation learning for traffic flow forecasting. Wang et al. [49] combine a hybrid Graph Convolutional Network with a frequency-domain-based decoupling layer to fully exploit spatial–temporal dependencies, thereby achieving accurate spatial–temporal prediction results. Jiang et al. [50] proposed a dynamic adaptive Graph Convolutional Network to accurately model the spatial relationships among different traffic sequences, thereby improving the accuracy of traffic forecasting.

In summary, the two-stage model can alleviate the impact of missing values to a certain extent, and spatial–temporal graph neural networks, as an effective traffic forecasting model, have been widely applied. However, the two-stage model suffers from an inherent error accumulation problem, which limits its practical value to some extent.

2.3. End-to-End Incomplete Traffic Forecasting Model

To address the issues of two-stage models, recent studies have gradually focused on end-to-end models, which enhance the model’s ability to handle missing values by introducing additional components [51,52]. Yang et al. [53] combine large language models with vision models to improve the accuracy of incomplete traffic forecasting. Zuo et al. [54] combine dynamic graph convolution, temporal convolutional networks, and attention to ensure the model’s ability to handle missing values and achieve incomplete traffic forecasting. Bikram et al. [55] combine graph learning, multi-head attention, and GRU to mitigate the impact of missing values, thereby achieving results superior to those of traditional neural networks. Merlin [56] uses knowledge distillation and contrastive learning to enhance the robustness of deep learning models in handling missing values, thereby achieving satisfactory experimental results in incomplete traffic forecasting. Ivan et al. [57] fully leverage the advantages of down sampling and graph learning to design an STGNN that is effectively suited for incomplete traffic prediction, which significantly enhances the model’s robustness in handling missing values.

In summary, existing end-to-end models improve their ability to handle missing values through additional components (such as graph learning) while avoiding the error accumulation problem inherent in two-stage models. In addition, it can be seen that effectively enhancing the utilization of both global and local spatial relationships in existing models is key to achieving accurate traffic prediction in mainstream end-to-end models. Therefore, one of the core techniques of this paper is the introduction of different graph structures to further construct spatial relationships from both global and local perspectives.

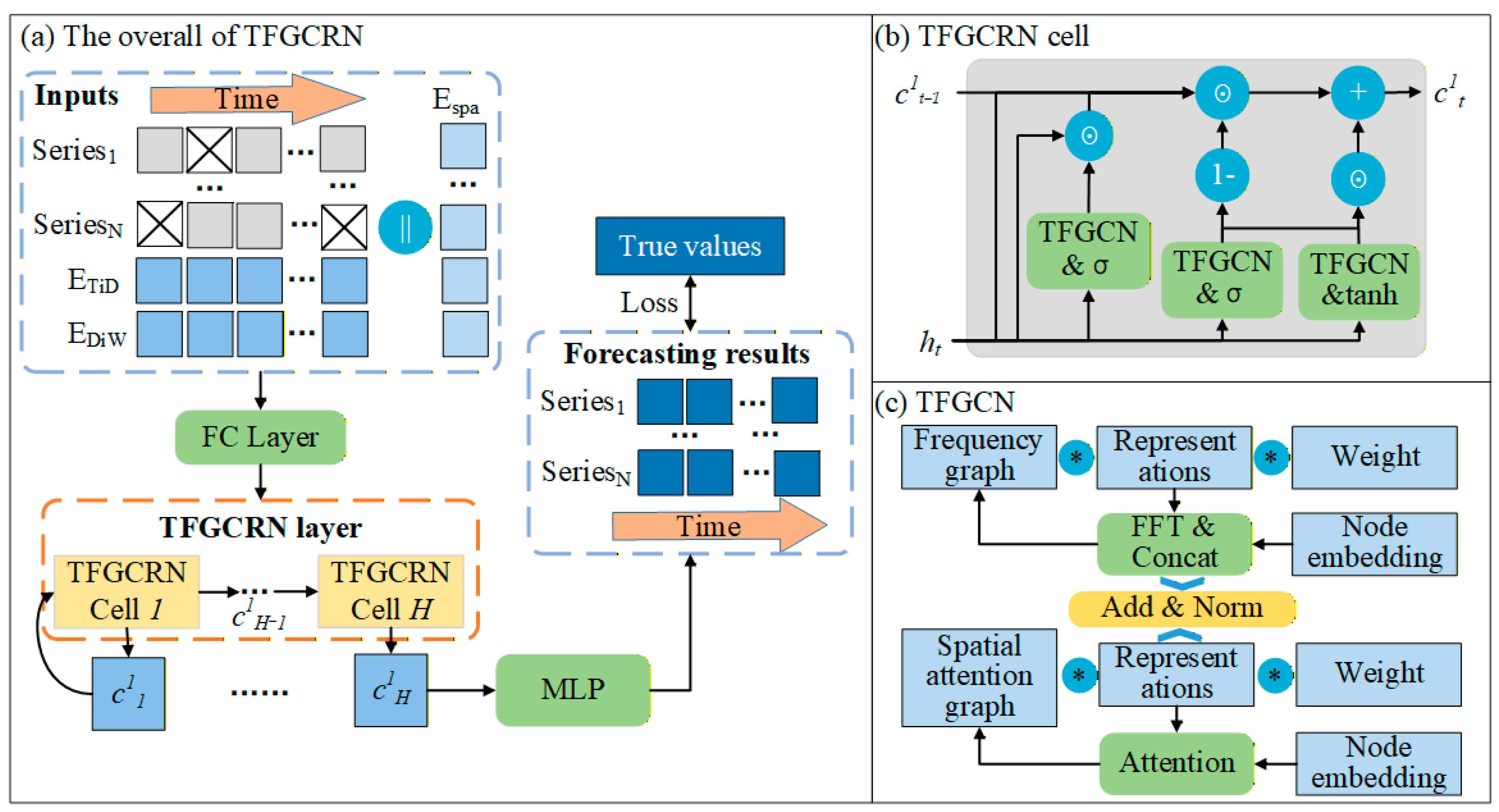
3. Methods

3.1. Preliminaries

Traffic Time Series [58,59]: Traffic time series representation consists of multiple time-varying sequences (typically speed and flow) collected by sensors at different locations, which can be represented by a tensor $X\in {ℝ}^{N_V\times N_H}$. Here, N_V is the number of traffic time series. N_H is the number of time steps.

Incomplete Traffic Forecasting [60,61]: A classic traffic forecasting task involves a given historical observation tensor $X\in {ℝ}^{N_V\times N_H}$, which represents the observations from N_H historical time intervals; the goal of the forecasting model is to predict the values for the next N_F time steps, denoted as $Y\in {ℝ}^{N_V\times N_F}$. The objective of traffic forecasting is to build a mapping function from $X\in {ℝ}^{N_V\times N_H}$ to $Y\in {ℝ}^{N_V\times N_F}$. The main difference in incomplete traffic forecasting lies in the presence of missing values in the historical observation data. Therefore, a random percentage M% of data points are masked from the historical observation tensor $X\in {ℝ}^{N_V\times N_H}$. After this process, a new input feature tensor $X_M\in {ℝ}^{N_V\times N_H}$ is obtained. The core objective is to build a mapping function from $X_M\in {ℝ}^{N_V\times N_H}$ to $Y\in {ℝ}^{N_V\times N_F}$.

3.2. Overall Framework

The overall TFGCRN is shown in Figure 1. The core idea is to integrate TFGCN into the GRU to model spatial relationships from both global and local perspectives recursively. In addition, this paper introduces spatial–temporal embeddings, which aim to provide global information for the input features and alleviate the adverse effects of missing values to some extent. The overall framework and modeling steps are as follows:

Step I: The historical input X_M is mapped to a high-dimensional representation based on spatial–temporal embeddings and fully connected layers.

Step II: The above representation is input into the TFGCRN encoder, where the spatial–temporal dependencies are dynamically mined through recursive modeling.

Step III: The representation of the final time step modeled by the TFGCRN encoder, along with the spatial embedding, is used as the input to the decoder. The final prediction result is obtained through the generative decoder based on the MLP.

3.3. Spatial–Temporal Embedding

The spatial–temporal embeddings can provide effective global information TFGCRN, helping to mitigate the negative impact caused by missing values. It consists of two temporal embeddings ($E_{TiD}$ and $E_{DiW}$) and one spatial embedding ($E_{spa}$). These spatial–temporal embeddings are integrated with the input features X_M through concatenation and fully connected layers [62].

$$H_{in}=\mathrm{FC}(\mathrm{Concat}(X_M\left|\right|E_{TiD}\left|\right|E_{DiW}\left|\right|E_{spa}))$$

(1)

where FC(·) is the fully connected layer. Concat(·) represents concatenating all the tensors. $E_{TiD}$ represents the time point of each value in a day. $E_{DiW}$ represents the specific day of a week. $E_{TiD}$ and $E_{DiW}$ are fixed data obtained by constructing timestamp information from existing time series models [59]. Their dimension is $1\times N_H$. They need to be copied and their dimensions have to be changed to $N_V\times N_H$ before concatenating with X_M. $E_{spa}$ represents the learnable parametric matrix generated for each time series. Its dimension is $N_V\times N_H$. The dimension of H_in will ultimately become $N_V\times N_H\times d$. At this point, the missing values in X_M are mapped to high-dimensional representations.

3.4. Temporal–Frequency Graph Convolution Network

The main function of TFGCN is to effectively combine the advantages of frequency and temporal information to reconstruct spatial relationships from both global and local perspectives. Therefore, we construct two types of graph structures that combine the high-dimensional representations processed by spatial–temporal encoding and learnable node embeddings from different perspectives to establish different spatial relationships.

Spatial attention graph: It first initializes a diagonal matrix $I_N\in {ℝ}^{N_V\times N_V}$ with a value of one, and randomly initializes a learnable parametric node embedding matrix $E_N\in {ℝ}^{N_V\times d}$. The purpose of the diagonal matrix is to ensure that each node preserves its own information while interacting spatially with other nodes, which is a common practice in mainstream-related work [63]. Then, based on the high-dimensional representation $h_{in}\in {ℝ}^{N_V\times d}$ processed by spatial–temporal embedding and the graph embedding matrix $E_N\in {ℝ}^{N_V\times d}$, the signal graph embedding matrix $E_{SAG}\in {ℝ}^{N_V\times d}$ for the spatial attention graph is obtained. $h_{in}\in {ℝ}^{N_V\times d}$ is the high-dimensional representation at a specific time step within the $N_H$ time steps of H_in.

$$E_{SAG}=\mathrm{softmax}({\displaystyle \frac{(W_q{E}_N)\ast {(W_k{h}_{in})}^T}{\sqrt{d_k}}})W_v{h}_{in}$$

(2)

where ∗ is the matrix multiplication. W is the weight coefficient, which is implemented based on a fully connected layer. The dimension of $(W_q{E}_N)$ is $N_V\times d$. ${(W_k{h}_{in})}^T$ is the transpose of $W_k{h}_{in}$. Its dimension is $d\times N_V$. $\mathrm{softmax}(\cdot )$ is the activation function. Its setting is mainly used to handle the last dimension of the matrix. $d_k$ is used to optimize the data distribution. The spatial attention graph $A_{SAG}\in {ℝ}^{N_V\times N_V}$ can be computed as follows:

$$A_{SAG}=(I_N+\mathrm{softmax}(\mathrm{TopK}(\mathrm{ReLU}(E_{SAG}{E}_{SAG}^T)))$$

(3)

where $E_{SAG}^T$ is the transpose of $E_{SAG}$. $\mathrm{TopK}\left(\cdot \right)$ represents the selection of the top K most important nodes.

Frequency graph: It also needs to initialize a diagonal matrix $I_N\in {ℝ}^{N_V\times N_V}$ with a value of one, and randomly initializes a learnable parametric node embedding matrix $E_N\in {ℝ}^{N_V\times d}$. Then, the high-dimensional representation $h_{in}\in {ℝ}^{N_V\times d}$ is processed through Fourier transformation. Based on concatenation and a fully connected layer, it is combined with graph embeddings $E_N\in {ℝ}^{N_V\times d}$ to obtain the signal graph embedding matrix $E_{FG}\in {ℝ}^{N_V\times d}$, which is used for the frequency graph.

$$E_{FG}=\mathrm{FC}(\mathrm{FFT}(h_{in})||E_N)$$

(4)

where $\mathrm{FFT}\left(\cdot \right)$ is the fast Fourier transform function. Since the spatial attention graph already preserves the information related to data amplitude, the frequency graph primarily retains phase information to reflect global patterns. The frequency graph $A_{FG}\in {ℝ}^{N_V\times N_V}$ can be computed as follows:

$$A_{FG}=(I_N+\mathrm{softmax}(\mathrm{TopK}(\mathrm{ReLU}(E_{FG}{E}_{FG}^T)))$$

(5)

TFGCN: Next, this paper implements the effective integration of the above two graph structures using layer normalization and the basic principles of graph convolution and proposes TFGCN. The specific formula is as follows:

$$H_{TFG}=F_{LN}(A_{TG}{H}_{in}{W}_1+b_1+A_{FG}{H}_{in}{W}_2+b_2)$$

(6)

where $F_{LN}\left(\cdot \right)$ is the layer normalization. Through the methods above, the TFGCN effectively integrates frequency graph and spatial attention graph, ensuring a more comprehensive exploration of spatial relationships.

3.5. TFGCRN Cell

The TFGCRN cell is the most crucial structural component of the proposed model. Its core idea is to replace all fully connected layers in the GRU cell with TFGCN, enabling recursive extraction of spatial–temporal dependencies. Specifically, each hidden state $h_t\in {ℝ}^{N_V\times d}$ in the input sequence $H_{in}=\{h_1,h_2,\dots ,h_T\}$ is modeled by a TFGCRN cell, which captures temporal and frequency-domain dependencies through its gated recurrent structure. Based on the basic principles of GRU [64], the formulas for each TFGCRN cell are given as follows:

$$z_t=\sigma (\mathrm{TFGCN}(h_t)+\mathrm{TFGCN}(c_{t-1})+b_z)$$

(7)

$$r_t=\sigma (\mathrm{TFGCN}(h_t)+\mathrm{TFGCN}(c_{t-1})+b_r)$$

(8)

$${\tilde{c}}_t=\tanh (\mathrm{TFGCN}(h_t)+\mathrm{TFGCN}(r_t\odot c_{t-1})+b_c)$$

(9)

$$c_t=(1-z_t)\odot c_{t-1}+z_t\odot {\tilde{c}}_t$$

(10)

where z_t is the update gate. r_t is the reset gate. ${\tilde{c}}_t$ is the candidate hidden state. $\sigma (·)$ is the sigmoid activation function. b is the bias. $\tanh (·)$ is the hyperbolic tangent activation function. $\odot$ is the Hadamard product (element-wise multiplication). b is the bias term with dimension $1\times d$. All other tensors also have dimension $N_V\times d$. Since the spatiotemporal embeddings effectively map missing values into high-dimensional representations and TFGCN models spatial relationships on top of this, the gating mechanism can effectively mitigate the adverse effects caused by zero values.

4. Experiments

4.1. Datasets

To verify the performance of TFGCRN in incomplete traffic forecasting, this section conducts experimental studies on four public datasets, including METR-LA, PEMS-BAY, PEMS04, and PEMS08. METR-LA and PEMS-BAY are traffic speed datasets, while PEMS04 and PEMS08 are traffic flow datasets. The real-world distribution of the data, along with more comprehensive details, can be found in the descriptions provided in the related work [34,65]. The basic statistical information of these datasets is shown in

Table 1. The basic statistical information of these four datasets.

Datasets	METR-LA	PEMS-BAY	PEMS04	PEMS08
Variates	207	325	307	170
Timesteps	34,272	52,116	16,992	17,833
Granularity	5 min	5 min	5 min	5 min

, and their brief descriptions are shown as follows:

• METR-LA: The dataset records traffic speeds measured by loop detectors installed throughout the Los Angeles County road network. It includes observations from 207 sensors collected between 1 March and 30 June 2012. Each sensor provides readings every five minutes, resulting in a total of 34,272 time points.
• PEMS-BAY: The dataset consists of traffic speed records obtained from the California Transportation Agencies (CalTrans) Performance Measurement System (PeMS). It includes measurements from 325 sensors collected between 1 January and 31 May 2017. Each time series was sampled every five minutes, resulting in a total of 52,116 time points.
• PEMS04: The dataset includes traffic flow information sourced from the CalTrans Performance Measurement System (PeMS). It comprises data from 307 sensors collected between 1 January and 28 February 2018. Each series is recorded at five-minute intervals, yielding a total of 16,992 time points.
• PEMS08: The dataset contains traffic flow data obtained from the CalTrans Performance Measurement System (PeMS). It includes observations from 170 sensors recorded between 1 July and 31 August 2018. Each time series was sampled every five minutes, producing a total of 17,833 time points.

4.2. Experimental Setup

Baselines. The baselines adopted in this paper mainly consist of two types: the two-stage model (PatchTST [66] + SAITS [67], DCRNN [68] + GPT4TS [31], FourierGNN [69] + GATGPT [70], and MTGNN [71] + GRIN [33]) and the end-to-end forecasting model (LGnet [72], GC-VRNN [73], RIHGCN [22], GSTAE [74], BiTGraph [75], and GinAR+ [76]). The basic introduction of the adopted baselines is as follows:

• PatchTST + SAITS: The former employs patch encoding and a transformer to perform traffic time series forecasting, while the latter uses an attention mechanism to restore missing values in the data.
• DCRNN + GPT4TS: The former combines GCN and GRU to achieve traffic forecasting, while the latter uses Patch and GPT-2 to restore missing values.
• FourierGNN + GATGPT: The former replaces graph convolution with Fourier computation to perform traffic forecasting, while the latter combines GAT and GPT-2 to restore missing values.
• MTGNN + GRIN: The former combines graph learning and temporal convolutional networks to achieve traffic forecasting, while the latter Employs Graph Convolutional Networks for data recovery.
• LGnet: It combines memory unit components to enhance the performance of recurrent neural networks in incomplete traffic forecasting.
• GC-VRNN: It integrates multi-space GCN with conditional variational RNN to achieve incomplete traffic forecasting.
• RIHGCN: It combines graph convolutions constructed from geographic distances and historical similarity with a bidirectional recurrent imputation mechanism and LSTM to enable incomplete traffic forecasting.
• GSTAE: It proposes a graph-based spatial–temporal autoencoder that follows an encoder–decoder structure for incomplete traffic forecasting.
• BiTGraph: It employs the biased temporal convolution graph neural network to effectively achieve incomplete traffic forecasting.
• GinAR+: It integrates interpolation attention, adaptive graph convolution, and simple recurrent units to achieve incomplete traffic forecasting.

Setting. This paper constructs the comparative experiment from the following perspectives to ensure fairness and robustness:

• In this paper, following mainstream benchmarks [77], all datasets are divided proportionally into training sets, validation sets, and test sets.
• Following mainstream-related works [78], both the historical observation length and the future forecasting length of the model are set to 12, and the evaluation metric is the average performance over the 12-step forecasting.
• This paper is primarily conducted under the classic random-missing setting [79]. Since the distribution of missing values is not fixed, the experimental results can better demonstrate the robustness of the model. The missing rates are set to 25%, 50%, and 75%. All missing values are uniformly set to zero using a random masking approach.
• Currently, most mainstream baselines conduct experiments directly on the datasets used in this paper without additional data cleaning. To ensure a fair comparison, and considering that real-world data naturally contain missing values, we did not perform extra data cleaning so as to better evaluate the model’s performance in realistic settings.
• To ensure stability and robustness, five different random seeds are used for each missing rate, and the final results are reported as the average of the repeated experiments. All models were tested in five repeated trials to ensure their stability and the reproducibility of the experimental results.

Metrics. This paper mainly uses mean absolute error (MAE) [80] and mean absolute percentage error (MAPE) [81] as the main evaluation metrics.

4.3. Main Results

Table 2. The main results of TFGCRN and all baselines on traffic speed datasets.

Datasets	Models	Missing Rate 25%		Missing Rate 50%		Missing Rate 75%
		MAE	MAPE	MAE	MAPE	MAE	MAPE
METR-LA	PatchTST + SAITS	3.83	10.95	3.94	11.23	4.08	11.94
	DCRNN + GPT4TS	3.68	10.24	3.81	10.84	3.96	11.25
	FourierGNN + GATGPT	3.70	10.31	3.84	10.91	3.97	11.44
	MTGNN + GRIN	3.63	10.15	3.75	10.79	3.91	11.24
	LGnet	3.76	10.78	3.88	11.15	4.01	11.71
	GC-VRNN	3.62	9.97	3.71	10.48	3.85	11.14
	RIHGCN	3.57	9.94	3.66	10.41	3.77	10.87
	GSTAE	3.55	9.92	3.67	10.39	3.79	10.92
	BiTGraph	3.54	9.88	3.62	10.36	3.71	10.73
	GinAR+	3.51	9.83	3.59	10.23	3.67	10.58
	TFGCRN	3.44	9.73	3.56	9.92	3.65	10.51
PEMS-BAY	PatchTST + SAITS	2.34	5.45	2.49	5.81	2.81	7.06
	DCRNN + GPT4TS	2.23	5.24	2.37	5.61	2.59	6.28
	FourierGNN + GATGPT	2.27	5.28	2.40	5.68	2.64	6.35
	MTGNN + GRIN	2.21	5.23	2.35	5.63	2.58	6.25
	LGnet	2.31	5.39	2.45	5.71	2.71	6.44
	GC-VRNN	2.17	5.17	2.31	5.52	2.55	6.11
	RIHGCN	2.07	4.92	2.35	5.67	2.62	6.32
	GSTAE	2.12	5.08	2.34	5.61	2.59	6.27
	BiTGraph	2.08	4.96	2.30	5.43	2.51	6.07
	GinAR+	2.05	4.85	2.25	5.37	2.49	5.94
	TFGCRN	2.01	4.82	2.19	5.28	2.36	5.88

and

Table 3. The main results of TFGCRN and all baselines on traffic flow datasets.

Datasets	Models	Missing Rate 25%		Missing Rate 50%		Missing Rate 75%
		MAE	MAPE	MAE	MAPE	MAE	MAPE
PEMS04	PatchTST + SAITS	24.37	17.45	26.04	18.17	27.23	18.67
	DCRNN + GPT4TS	23.17	17.04	25.38	17.41	26.84	18.45
	FourierGNN + GATGPT	22.98	16.61	25.31	17.55	26.67	18.30
	MTGNN + GRIN	23.06	16.64	25.32	17.38	26.73	18.22
	LGnet	23.73	17.22	25.59	17.64	27.04	18.53
	GC-VRNN	22.81	16.52	24.33	17.13	26.43	17.59
	RIHGCN	23.45	17.06	25.17	17.38	26.75	18.02
	GSTAE	22.67	16.48	24.27	17.04	26.07	17.51
	BiTGraph	22.49	16.31	23.73	16.92	25.98	17.45
	GinAR+	22.32	16.05	23.41	16.86	25.72	17.26
	TFGCRN	21.58	15.47	22.76	16.54	24.38	17.15
PEMS08	PatchTST + SAITS	21.43	13.79	22.18	14.25	25.06	16.42
	DCRNN + GPT4TS	20.64	13.56	21.96	14.03	24.58	15.79
	FourierGNN + GATGPT	20.77	13.45	21.91	14.08	24.89	15.85
	MTGNN + GRIN	20.59	13.34	21.78	13.98	24.51	15.68
	LGnet	21.51	13.85	22.14	14.31	24.95	16.26
	GC-VRNN	20.42	13.21	21.67	13.91	23.45	15.06
	RIHGCN	20.53	13.31	21.71	14.08	23.51	15.34
	GSTAE	20.62	13.39	21.83	14.12	23.79	15.63
	BiTGraph	20.21	13.04	21.59	13.82	23.06	14.79
	GinAR+	20.03	12.97	21.55	13.75	22.93	14.52
	TFGCRN	19.79	12.75	21.04	13.52	22.33	14.38

present the main results of TFGCRN and all baselines. It can be observed that TFGCRN achieves satisfactory results across all datasets, demonstrating the superiority and practicality of TFGCRN. The following conclusions can be drawn:

• The forecasting performance of two-stage models is significantly lower than that of end-to-end models, which verifies the value of the end-to-end forecasting framework in the field of incomplete traffic forecasting. The main reason is that two-stage models inevitably suffer from error accumulation, which in turn limits the full exploitation of spatial–temporal dependencies in forecasting models.
• Graph-based end-to-end models achieve better experimental results mainly because graph convolution can effectively model the spatial relationships among different time series, thereby enhancing the modeling of spatiotemporal dependencies and ensuring accurate incomplete traffic forecasting.
• The proposed TFGCRN achieves the best experimental results across all datasets. First, the spatial–temporal embedding mitigates the adverse effects of missing values by introducing additional information. Second, TFGCN leverages both the frequency graph and spatial attention graph to ensure accurate modeling of spatial relationships from global and local perspectives. Finally, by integrating TFGCN into the GRU, the model realizes recursive modeling of spatial–temporal dependencies. Therefore, TFGCRN demonstrates excellent performance in incomplete traffic forecasting tasks.

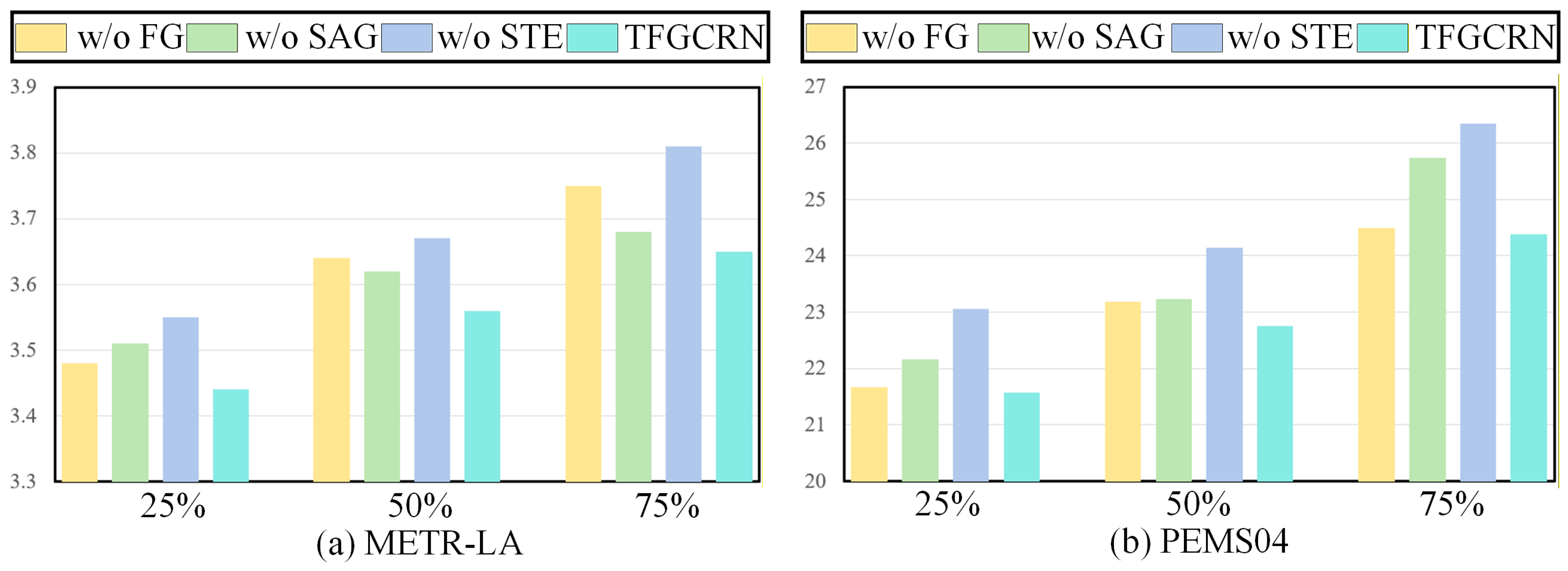
4.4. Ablation Experiment

Ablation experiments can fully evaluate the impact of different components on the results and further validate the motivation of this paper. Therefore, this paper conducts ablation experiments from three perspectives: (1) w/o FG: It represents the removal of the frequency graph, in which case the model mainly relies on the spatial attention graph and local information to construct spatial relationships. (2) w/o SAG: It represents the removal of the spatial attention graph, in which case the model mainly relies on the frequency graph and global information to construct spatial relationships. (3) w/o STE: It represents the removal of spatial–temporal embedding, in which case the model does not use additional spatial–temporal information to alleviate the adverse effects caused by missing values. Figure 2 shows the results of the ablation experiments on METR-LA and PEMS04 datasets. The following conclusions can be drawn:

• The frequency graph has a significant impact when the missing rate is high. This is mainly because, when the missing rate is large, global information helps the model better analyze spatial–temporal dependencies.
• The spatial attention graph has a significant impact when the missing rate is low. This is mainly because, when the missing rate is small, the model can better model spatial dependencies by leveraging local information.
• The spatial–temporal embedding is beneficial to the experimental results under different missing rates. This indirectly confirms that additional spatiotemporal knowledge helps prevent the model from forcing the use of zero values to mine spatial–temporal information, thereby ensuring forecasting accuracy.

The above experimental results demonstrate that spatial–temporal embeddings can significantly improve the model’s forecasting accuracy. Building on this, we further conduct ablation studies in this section. Specifically, we remove the temporal embeddings and the spatial embedding separately, and perform experiments on PEMS-BAY and PEMS08. In addition, the two proposed graph structures, both introduce extra graph embeddings designed to provide additional node identity information, and we also performed further ablation experiments on these components.

Table 4. The ablation experiment of spatial–temporal embedding and node embedding.

Datasets	Models	Missing Rate 25%	Missing Rate 50%	Missing Rate 75%
PEMS-BAY	w/o STE	2.23	2.46	2.62
	w/o EN	2.07	2.24	2.43
	w/o temporal embedding	2.09	2.31	2.54
	w/o spatial embedding	2.12	2.28	2.47
	TFGCRN	2.01	2.19	2.36
PEMS08	w/o STE	22.17	23.42	25.08
	w/o EN	20.16	21.77	23.35
	w/o temporal embedding	21.36	22.65	24.02
	w/o spatial embedding	21.54	22.52	23.47
	TFGCRN	19.79	21.04	22.33

presents the ablation results. It can be observed that removing temporal embeddings leads to a larger performance drop under higher missing rates, mainly because they provide additional timestamp information for each time step, which becomes more beneficial when substantial information is missing. In addition, removing the graph embeddings also degrades the model’s performance, mainly because the node identity information they provide helps the model resist the impact of missing values on graph construction, thereby leading to better results.

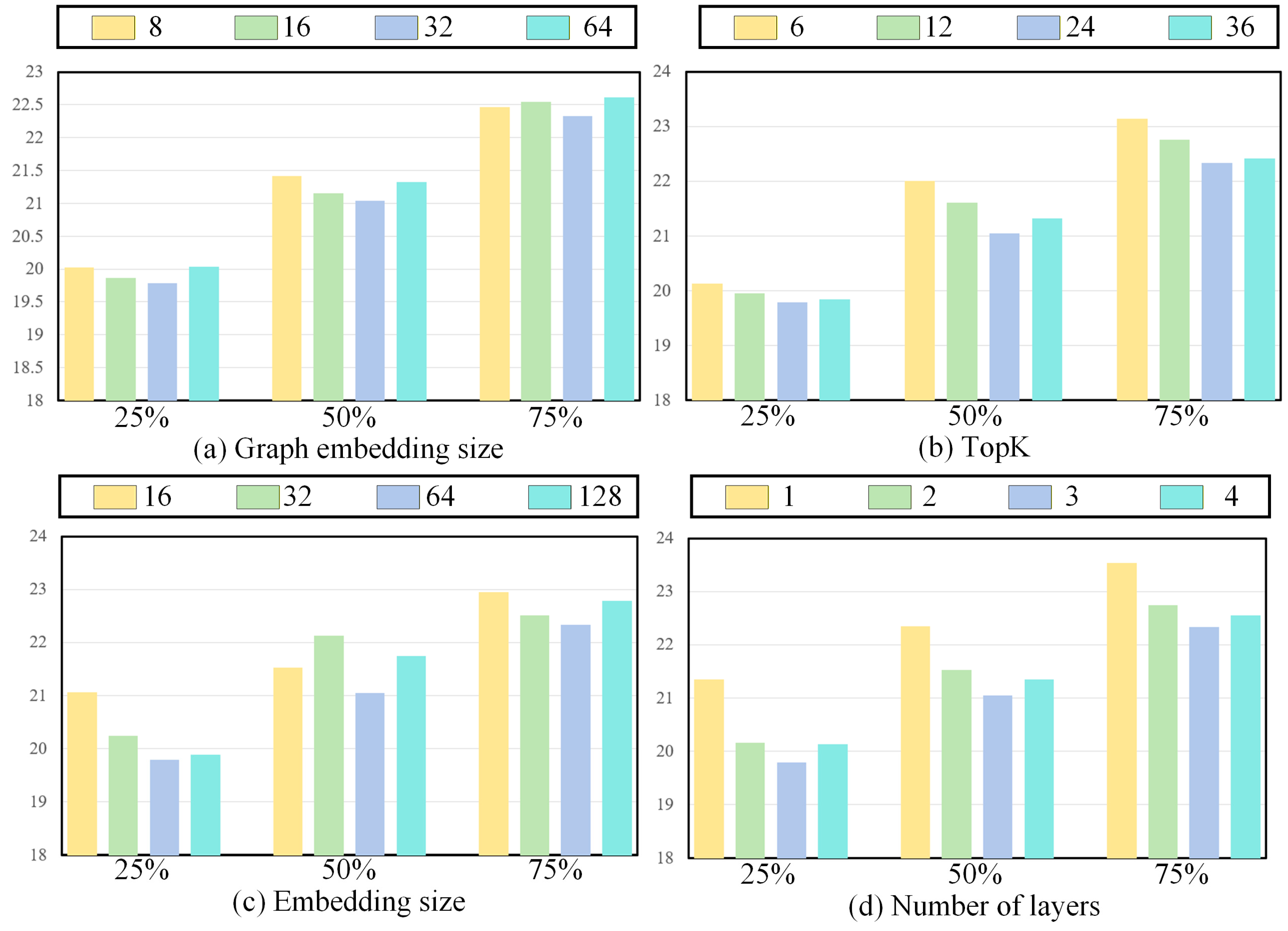
4.5. Hyperparameter Analysis

The model’s hyperparameters can significantly affect its forecasting performance, and a detailed analysis of these hyperparameters helps us to understand the most important aspects and core functions of the model. This paper evaluates the influence of six hyperparameters on the results, including graph embedding size, number of TopK, embedding size, and number of layers.

Table 5. The values of the main hyperparameters of TGCRN.

Config	Values
optimizer	Adam [82]
learning rate	0.002
weight decay	0.0001
embedding size	64
graph embedding size	64
number of layers	3
TopK	24
dropout	0.15
learning rate schedule	MultiStepLR
clip gradient normalization	5
milestone	[1, 5, 25, 50, 75, 100]
discount coefficient	0.5
batch size	32
epoch	101

presents the core hyperparameters of the TFGCRN model, while Figure 3 illustrates the experimental results under different hyperparameter settings (PEMS04 dataset). The following conclusions can be drawn:

• The impact of the graph embedding size on the experimental results is minimal, primarily because TGCRN can generate relatively accurate graph structures with a small number of parameters, ensuring the accuracy of spatial relationships.
• The number of TopK can be increased appropriately, as it allows for a more comprehensive reflection of spatial relationships.
• The embedding size is an important hyperparameter and should not be too large. A larger embedding size may lead to overfitting, which in turn affects forecasting accuracy.
• The number of layers plays a crucial role in forecasting performance. Too few layers may fail to adequately capture and analyze data characteristics, while too many layers can lead to overfitting and other issues.

4.6. Component Replacement Experiment

To further verify the importance of each component in TFGCRN, this section conducts component replacement experiments. Specifically, we replace certain components with other classic network structures to further evaluate the model’s performance. The experiments cover the following aspects: (1) Multi-head attention: It is used to replace the spatial attention graph structure. (2) Graph attention: It is used to replace the spatial attention graph structure. (3) DTW: It is used to replace the FFT in the frequency graph. (4) Single TFGCN: It uses a single TFGCN to model $h_t$ and $c_{t-1}$. (5) LSTM: It used to replace the GRU. (6) Two F_LN: It fuses the information from the two graph structures by first applying normalization and then performing element-wise addition. (7) Mask attention: It replaces the spatiotemporal embeddings with a mask matrix and replaces the spatial attention graph with masked self-attention. In other words, the model directly maps missing values into high-dimensional representations and masks out the positions of missing values when computing spatial relationships.

Table 6. The results of component replacement experiment.

Datasets	Models	Missing Rate 25%	Missing Rate 50%	Missing Rate 75%
PEMS-BAY	Multi-head attention	2.15	2.34	2.54
	Mask attention	2.19	2.41	2.63
	Graph attention	2.13	2.33	2.52
	DTW	2.04	2.22	2.41
	Two FLN	2.07	2.25	2.45
	Single TFGCN	2.08	2.27	2.46
	LSTM	2.05	2.24	2.42
	TFGCRN	2.01	2.19	2.36
PEMS08	Multi-head attention	21.21	22.65	23.92
	Mask attention	21.57	23.06	24.31
	Graph attention	21.03	22.34	23.66
	DTW	20.17	21.56	22.85
	Two FLN	20.11	21.62	22.90
	Single TFGCN	20.58	22.01	23.37
	LSTM	20.04	21.43	22.79
	TFGCRN	19.79	21.04	22.33

presents the results of the component replacement experiments on PEMS-BAY and PEMS08. It can be observed that replacing the proposed components with other general modules leads to a clear performance drop for TFGCRN. Based on the experimental results, we can draw the following conclusions:

• Replacing the spatial attention graph with multi-head attention or graph attention both leads to a clear decline in prediction performance, which demonstrates the stability and effectiveness of incorporating node embeddings, node identity information, and attention-based graph structures.
• Replacing the FFN with DTW does not significantly improve prediction performance, mainly because DTW focuses on local pattern alignment, whereas FFT emphasizes global analysis. In the context of incomplete traffic time series, modeling spatial relationships from a global perspective is more crucial.
• LSTM performs worse than GRU, mainly because a lighter GRU structure can better avoid the noise introduced by missing values along the temporal dimension, thereby improving prediction performance.
• The strategy of fusing graph structures by stacking them before layer normalization yields better prediction results, mainly because this approach preserves the differences between the graph structures and thus provides more comprehensive spatial information.
• Using two separate TFGCNs to model $h_t$ and $c_{t-1}$ leads to better experimental results, mainly because applying graph convolutions with different parameters to these two distinct representations helps capture more complete spatial relationships.
• The performance of masked attention is not satisfactory. On the one hand, removing spatiotemporal embeddings leads to a significant drop in prediction accuracy; on the other hand, masking spatial relationships may cause the model to overlook important information propagation pathways, thereby limiting its predictive performance.

5. Discussion

This paper proposes the Temporal–Frequency Graph Convolutional Recurrent Network for incomplete traffic forecasting. On one hand, the model introduces spatial–temporal embeddings to mitigate the impact of missing values. On the other hand, by incorporating the proposed TFGCN into the GRU, it recursively models spatial–temporal dependencies from both global and local perspectives, thereby achieving accurate incomplete traffic forecasting. This paper will conduct discussions and analyses from the following aspects.

Performance. Compared with mainstream end-to-end forecasting models and two-stage forecasting models, TFGCRN achieves the most satisfactory experimental results across all datasets and missing rates. In addition, ablation studies demonstrate the effectiveness of our proposed TFGCN module. These experimental results collectively verify the superiority of TFGCRN in the field of incomplete traffic forecasting.

Application. From a practical standpoint, missing values are widespread in real-world traffic data. Existing models are often affected by these missing values, leading to inaccurate modeling of spatial–temporal dependencies, which in turn limits their forecasting performance. The proposed TFGCRN leverages the advantages of both the spatial attention graph and the frequency graph to reconstruct spatial relationships from both global and local perspectives. This design ensures the model’s robustness against missing values, thereby demonstrating excellent practicality and application value.

Limitations and Future Work. Although the experimental results collectively demonstrate the performance of TFGCRN, several limitations remain. This work primarily uses spatial–temporal encoding to assist in filling missing values, without considering other important factors such as weather conditions and traffic situations. In the future, we plan to use these additional factors to further enhance the modeling process. In addition, spatial–temporal graph neural networks typically have high computational complexity and therefore require appropriate optimization. The experiments in this paper are mainly conducted on existing datasets. In future studies, we intend to integrate the model into real-world big data platforms to further improve its efficiency and explore its performance and robustness in practical scenarios [83].

6. Conclusions

In this study, we propose a model called the Temporal–Frequency Graph Convolutional Recurrent Network (TFGCRN) to address the negative impact of incomplete traffic data caused by sensor failures on spatial–temporal dependency modeling. By embedding the Temporal–Frequency Graph Convolutional Network into gated recurrent units, TF-GCRN fully leverages both global and local information during the recursive modeling process, mitigating the adverse effects of missing values and generating more accurate spatial relationships, thereby improving the accuracy of incomplete traffic forecasting. Experimental results show that TF-GCRN outperforms several baseline models on four real-world datasets and effectively adapts to different missing rates, demonstrating its superior performance in traffic forecasting tasks. In addition, the ablation study demonstrates that the proposed spatiotemporal embeddings effectively help the model mitigate the interference caused by missing values. Building on this, TFGCN can capture more effective spatial correlations, thereby ensuring strong predictive performance. The component replacement experiment further demonstrates that the designed components can adapt to modeling incomplete traffic time series better than classical networks such as multi-head attention, thereby ensuring the model’s forecasting accuracy.

In the future, we will consider incorporating additional features, such as weather and holiday information, to further enhance forecasting performance. Furthermore, we plan to integrate the model into other big data analytics platforms to enable the practical application of our work.